高二数学抛物线的简单几何性质3
- 格式:pdf
- 大小:1000.32 KB
- 文档页数:8



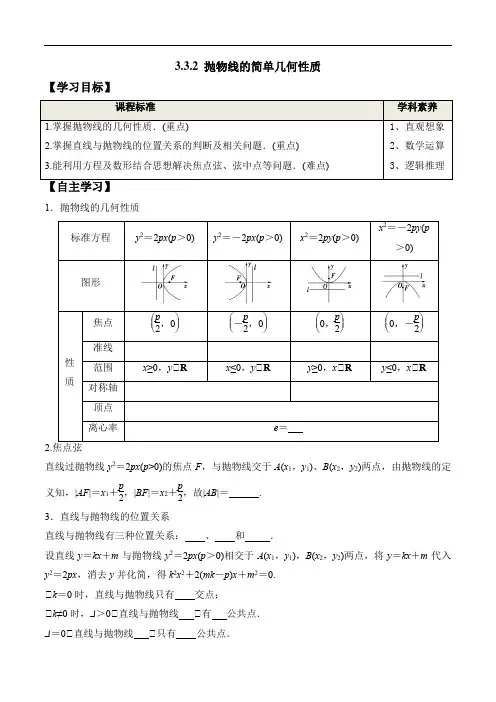
3.3.2 抛物线的简单几何性质【学习目标】1.抛物线的几何性质⎛⎫p ⎛⎫p ⎛⎫p ⎛⎫p 2.直线过抛物线y 2=2px (p >0)的焦点F ,与抛物线交于A (x 1,y 1)、B (x 2,y 2)两点,由抛物线的定义知,|AF |=x 1+p 2,|BF |=x 2+p2,故|AB |= . 3.直线与抛物线的位置关系直线与抛物线有三种位置关系: 、 和 .设直线y =kx +m 与抛物线y 2=2px (p >0)相交于A (x 1,y 1),B (x 2,y 2)两点,将y =kx +m 代入y 2=2px ,消去y 并化简,得k 2x 2+2(mk -p )x +m 2=0. ∈k =0时,直线与抛物线只有 交点;∈k ≠0时,Δ>0∈直线与抛物线 ∈有 公共点. Δ=0∈直线与抛物线 ∈只有 公共点.Δ<0∈直线与抛物线∈ 公共点.【小试牛刀】1.抛物线关于顶点对称.()2.抛物线只有一个焦点,一条对称轴,无对称中心.() 3.抛物线的标准方程虽然各不相同,但是其离心率都相同.() 4.抛物线y2=2px过焦点且垂直于对称轴的弦长是2p.()5.抛物线y=-18x2的准线方程为x=132.()【经典例题】题型一抛物线性质的应用把握三个要点确定抛物线的简单几何性质(1)开口:由抛物线标准方程看图象开口,关键是看准二次项是x还是y,一次项的系数是正还是负.(2)关系:顶点位于焦点与准线中间,准线垂直于对称轴.(3)定值:焦点到准线的距离为p;过焦点垂直于对称轴的弦(又称为通径)长为2p;离心率恒等于1.例1 (1)已知抛物线的顶点在坐标原点,对称轴为x轴且与圆x2+y2=4相交的公共弦长等于23,则抛物线的方程为________.(2)如图,过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=4,求抛物线的方程.[跟踪训练]1 已知抛物线y2=8x.(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是∈OAB 的重心,求∈OAB的周长.题型二直线与抛物线的位置关系直线与抛物线交点问题的解题思路(1)判断直线与抛物线的交点个数时,一般是将直线与抛物线的方程联立消元,转化为形如一元二次方程的形式,注意讨论二次项系数是否为0.若该方程为一元二次方程,则利用判别式判断方程解的个数.(2)直线与抛物线有一个公共点时有两种情形:(1)直线与抛物线的对称轴重合或平行;(2)直线与抛物线相切.例2已知直线l:y=kx+1,抛物线C:y2=4x,当k为何值时,l与C:只有一个公共点;有两个公共点;没有公共点.[跟踪训练]2若抛物线y2=4x与直线y=x-4相交于不同的两点A,B,求证OA∈OB.题型三中点弦及弦长公式“中点弦”问题解题方法例3已知抛物线方程为y2=2px(p>0),过此抛物线的焦点的直线与抛物线交于A,B两点,[跟踪训练]3 过点Q(4,1)作抛物线y2=8x的弦AB,恰被点Q所平分,求AB所在直线的方程.题型四 抛物线的综合应用例4 求抛物线y =-x 2上的点到直线4x +3y -8=0的最小距离.[跟踪训练]4 如图所示,抛物线关于x 轴对称,它的顶点为坐标原点,点P (1,2),A (x 1,y 1),B (x 2,y 2)均在抛物线上. (1)求抛物线的方程及其准线方程;(2)当P A 与PB 的斜率存在且倾斜角互补时,证明:直线AB 的斜率为定值.【当堂达标】1.在抛物线y 2=16x 上到顶点与到焦点距离相等的点的坐标为( ) A .(42,±2) B .(±42,2) C .(±2,42)D .(2,±42)2.以x 轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点,则其方程为( ) A .y 2=8xB .y 2=-8xC .y 2=8x 或y 2=-8xD .x 2=8y 或x 2=-8y3.若抛物线y 2=2x 上有两点A 、B 且AB 垂直于x 轴,若|AB |=22,则抛物线的焦点到直线AB 的距离为( )A .12B .14C .16D .184.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 是抛物线上一点,若OA →·AF →=-4,则点A的坐标是()A.(2,±22)B.(1,±2)C.(1,2)D.(2,22)5.过点P(0,1)与抛物线y2=x有且只有一个交点的直线有()A.4条B.3条C.2条D.1条6.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,则|AB|=________.7.已知AB是过抛物线2x2=y的焦点的弦,若|AB|=4,则AB的中点的纵坐标是________.8.已知抛物线x=-y2与过点(-1,0)且斜率为k的直线相交于A,B两点,O为坐标原点,当∈AOB的面积等于10时,求k的值.9.已知y=x+m与抛物线y2=8x交于A,B两点.(1)若|AB|=10,求实数m的值;(2)若OA∈OB,求实数m的值.10.已知抛物线的顶点在原点,x轴为对称轴,经过焦点且倾斜角为π4的直线l被抛物线所截得的弦长为6,求抛物线的标准方程.【参考答案】【自主学习】x =-p 2 x =p 2 y =-p 2 y =p2 x 轴 y 轴 (0,0) 1 x 1+x 2+p 相离 相切 相交 一个 相交 两个 相切 一个 相离 没有 【小试牛刀】 × √ √ √ × 【经典例题】例1 (1)y 2=3x 或y 2=-3x [根据抛物线和圆的对称性知,其交点纵坐标为±3,交点横坐标为±1,则抛物线过点(1,3)或(-1,3),设抛物线方程为y 2=2px 或y 2=-2px (p >0),则2p =3,从而抛物线方程为y 2=3x 或y 2=-3x .](2)[解] 如图,分别过点A ,B 作准线的垂线,分别交准线于点E ,D , 设|BF |=a ,则由已知得:|BC |=2a ,由定义得:|BD |=a ,故∈BCD =30°,在Rt∈ACE 中,∈|AF |=4,|AC |=4+3a ,∈2|AE |=|AC |,∈4+3a =8,从而得a =43,∈BD ∈FG ,∈43p =23,p =2.因此抛物线的方程是y 2=4x .[跟踪训练]1 解 (1)抛物线y 2=8x 的顶点、焦点、准线方程、对称轴、变量x 的范围分别为(0,0),(2,0),x =-2,x 轴,x ≥0.(2)如图所示,由|OA |=|OB |可知AB ∈x 轴,垂足为点M , 又焦点F 是∈OAB 的重心,则|OF |=23|OM |. 因为F (2,0),所以|OM |=32|OF |=3,所以M (3,0).故设A (3,m ),代入y 2=8x 得m 2=24;所以m =26或m =-26,所以A (3,26),B (3,-26),所以|OA |=|OB |=33,所以∈OAB 的周长为233+4 6. 例2 解 联立⎩⎨⎧y =kx +1,y 2=4x ,消去y ,得k 2x 2+(2k -4)x +1=0.(*)当k =0时,(*)式只有一个解x=14,∈y =1,∈直线l 与C 只有一个公共点⎝ ⎛⎭⎪⎫14,1,此时直线l 平行于x 轴.当k ≠0时,(*)式是一个一元二次方程,Δ=(2k -4)2-4k 2=16(1-k ).∈当Δ>0,即k <1,且k ≠0时,l 与C 有两个公共点,此时直线l 与C 相交;∈当Δ=0,即k =1时,l 与C 有一个公共点,此时直线l 与C 相切; ∈当Δ<0,即k >1时,l 与C 没有公共点,此时直线l 与C 相离. 综上所述,当k =1或0时,l 与C 有一个公共点; 当k <1,且k ≠0时,l 与C 有两个公共点; 当k >1时,l 与C 没有公共点.[跟踪训练]2 [证明] 由⎩⎨⎧y 2=4x ,y =x -4,消去y ,得x 2-12x +16=0.∈直线y =x -4与抛物线相交于不同两点A ,B , ∈可设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=12,x 1x 2=16.∈OA →·OB →=x 1x 2+y 1y 2=x 1x 2+(x 1-4)(x 2-4)=x 1x 2+x 1x 2-4(x 1+x 2)+16=16+16-4×12+16=0,∈OA →∈OB →,即OA ∈OB .例3 解 由题意知焦点F ⎝ ⎛⎭⎪⎫p 2,0,设A (x 1,y 1),B (x 2,y 2),若AB ∈x 轴,则|AB |=2p ≠52p ,不满足题意.所以直线AB 的斜率存在,设为k ,则直线AB 的方程为y =k ⎝ ⎛⎭⎪⎫x -p 2,k ≠0.由⎩⎪⎨⎪⎧y =k ⎝ ⎛⎭⎪⎫x -p 2,y 2=2px ,消去x ,整理得ky 2-2py -kp 2=0.由根与系数的关系得y 1+y 2=2pk ,y 1y 2=-p 2.所以|AB |=⎝ ⎛⎭⎪⎫1+1k 2·y 1-y 22=1+1k 2·y 1+y 22-4y 1y 2=2p ⎝ ⎛⎭⎪⎫1+1k 2=52p ,解得k =±2.所以AB 所在的直线方程为2x -y -p =0或2x +y -p =0.[跟踪训练]3 [解] 法一:(点差法)设以Q 为中点的弦AB 的端点坐标为A (x 1,y 1),B (x 2,y 2),则有y 21=8x 1,y 22=8x 2,∈(y 1+y 2)(y 1-y 2)=8(x 1-x 2).又y 1+y 2=2,∈y 1-y 2=4(x 1-x 2),即y 1-y 2x 1-x 2=4,∈k AB =4. ∈AB 所在直线的方程为y -1=4(x -4),即4x -y -15=0.法二:由题意知AB 所在直线斜率存在,设A (x 1,y 1),B (x 2,y 2),弦AB 所在直线的方程为y=k (x -4)+1.联立⎩⎨⎧y 2=8x ,y =k x -4+1,消去x ,得ky 2-8y -32k +8=0,此方程的两根就是线段端点A ,B 两点的纵坐标.由根与系数的关系得y 1+y 2=8k .又y 1+y 2=2,∈k =4.∈AB 所在直线的方程为4x -y -15=0. 例4 解 方法一 设A (t ,-t 2)为抛物线上的点,则点A 到直线4x +3y -8=0的距离d =|4t -3t 2-8|5=|3t 2-4t +8|5=15⎪⎪⎪⎪⎪⎪3⎝⎛⎭⎪⎫t -232-43+8 =15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫t -232+203=35⎝ ⎛⎭⎪⎫t -232+43. 所以当t =23时,d 有最小值43.方法二 如图,设与直线4x +3y -8=0平行的抛物线的切线方程为4x +3y +m =0,由⎩⎨⎧y =-x 2,4x +3y +m =0,消去y 得3x 2-4x -m =0,∈Δ=16+12m =0,∈m =-43. 故最小距离为⎪⎪⎪⎪⎪⎪-8+435=2035=43.[跟踪训练]4 [解] (1)由题意可设抛物线的方程为y 2=2px (p >0),则由点P (1,2)在抛物线上,得22=2p ×1,解得p =2,故所求抛物线的方程是y 2=4x ,准线方程是x =-1.(2)证明:因为P A 与PB 的斜率存在且倾斜角互补,所以k P A =-k PB ,即y 1-2x 1-1=-y 2-2x 2-1. 又A (x 1,y 1),B (x 2,y 2)均在抛物线上,所以x 1=y 214,x 2=y 224,从而有y 1-2y 214-1=-y 2-2y 224-1,即4y 1+2=-4y 2+2,得y 1+y 2=-4,故直线AB 的斜率k AB =y 1-y 2x 1-x 2=4y 1+y 2=-1. 【当堂达标】1.D [抛物线y 2=16x 的顶点O (0,0),焦点F (4,0),设P (x ,y )符合题意,则有⎩⎨⎧y 2=16x ,x 2+y 2=x -42+y 2∈⎩⎨⎧ y 2=16x ,x =2∈⎩⎨⎧x =2,y =±4 2.所以符合题意的点为(2,±42).] 2. C 解析 设抛物线方程为y 2=2px 或y 2=-2px (p >0),依题意得x =p2,代入y 2=2px 或y 2=-2px 得|y |=p ,∈2|y |=2p =8,p =4. ∈抛物线方程为y 2=8x 或y 2=-8x .3.A [线段AB 所在的直线方程为x =1,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫12,0,则焦点到直线AB 的距离为1-12=12.]4.B [由题意知F (1,0),设A ⎝ ⎛⎭⎪⎫y 204,y 0,则OA →=⎝ ⎛⎭⎪⎫y 204,y 0,AF →=⎝ ⎛⎭⎪⎫1-y 204,-y 0,由OA →·AF →=-4得y 0=±2,∈点A 的坐标为(1,±2),故选B.]5. B 解析 当直线垂直于x 轴时,满足条件的直线有1条; 当直线不垂直于x 轴时,满足条件的直线有2条,故选B.6. 8解析 因为直线AB 过焦点F (1,0),所以|AB |=x 1+x 2+p =6+2=8.7.158 [设A (x 1,y 1),B (x 2,y 2),由抛物线2x 2=y ,可得p =14.∈|AB |=y 1+y 2+p =4,∈y 1+y 2=4-14=154,故AB 的中点的纵坐标是y 1+y 22=158.] 8.解 过点(-1,0)且斜率为k 的直线方程为y =k (x +1)(k ≠0), 由方程组⎩⎨⎧x =-y 2,y =k x +1,消去x 整理得ky 2+y -k =0,Δ=1+4k 2>0,设A (x 1,y 1),B (x 2,y 2),由根与系数之间的关系得y 1+y 2=-1k ,y 1·y 2=-1. 设直线与x 轴交于点N ,显然N 点的坐标为(-1,0). ∈S ∈OAB =S ∈OAN +S ∈OBN =12|ON ||y 1|+12|ON ||y 2|=12|ON ||y 1-y 2|, ∈S ∈AOB =12×1×y 1+y 22-4y 1y 2=12×1k 2+4=10,解得k =±16.9.解 由⎩⎨⎧y =x +m ,y 2=8x ,得x 2+(2m -8)x +m 2=0.由Δ=(2m -8)2-4m 2=64-32m >0,得m <2.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=8-2m ,x 1x 2=m 2,y 1y 2=m (x 1+x 2)+x 1x 2+m 2=8m . (1)因为|AB |=1+k 2x 1+x 22-4x 1x 2=2·64-32m =10,所以m =716,经检验符合题意.(2)因为OA ∈OB ,所以x 1x 2+y 1y 2=m 2+8m =0,解得m =-8或m =0(舍去). 所以m =-8,经检验符合题意.10.[解] 当抛物线焦点在x 轴正半轴上时,可设抛物线标准方程为y 2=2px (p >0),则焦点F ⎝ ⎛⎭⎪⎫p 2,0,直线l 的方程为y =x -p 2.设直线l 与抛物线的交点为A (x 1,y 1),B (x 2,y 2),过点A ,B 向抛物线的准线作垂线,垂足分别为点A 1,点B 1,则|AB |=|AF |+|BF |=|AA 1|+|BB 1|=⎝ ⎛⎭⎪⎫x 1+p 2+⎝ ⎛⎭⎪⎫x 2+p 2=x 1+x 2+p =6, ∈x 1+x 2=6-p .∈ 由⎩⎪⎨⎪⎧y =x -p 2,y 2=2px 消去y ,得⎝ ⎛⎭⎪⎫x -p 22=2px ,即x 2-3px +p 24=0.∈x 1+x 2=3p ,代入∈式得3p =6-p ,∈p =32.∈所求抛物线的标准方程是y 2=3x .当抛物线焦点在x 轴负半轴上时,用同样的方法可求出抛物线的标准方程是y 2=-3x .高考数学:试卷答题攻略一、“六先六后”,因人因卷制宜。







3.3.2 抛物线的简单几何性质教学设计本小节内容选自《普通高中数学选择性必修第一册》人教A版(2019)第三章《圆锥曲线的方程》的第三节《抛物线》。
以下是本节的课时安排:学生已经学习了直线与圆的方程,已经具备了坐标法研究解析几何问题的能力。
本章学习圆锥曲线方程及几何性质,进一步提升用代数方法研究解析几何问题的方法。
1.了解抛物线的简单几何性质,培养数学抽象的核心素养.2.能利用性质解决与抛物线有关的问题.3.能利用方程与数形结合思想解决焦点弦问题,培养数学运算的核心素养.重点:抛物线的标准方程及其推导过程难点:求抛物线标准方程(一)新知导入已知抛物线y2=8x,其轨迹如图所示.(1)观察抛物线y2=8x轨迹可知其上的点的坐标的范围是怎样的?(2)观察抛物线y2=8x的轨迹有什么对称性?【提示】(1)抛物线上的点的横坐标x≥0,纵坐标y∈R.(2)关于x轴对称.(二)抛物线的几何性质知识点一抛物线的几何性质◆抛物线的几何性质向右向左向上向下【点睛】1.对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,其共同点:(1)顶点都为原点;(2)对称轴为坐标轴;(3)准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一;次项系数的绝对值的14(4)焦点到准线的距离均为p.其不同点:(1)对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;2.只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程.【思考】怎样根据抛物线的标准方程判断抛物线的对称轴和开口方向?【提示】开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.【做一做1】(教材P134例3改编)已知抛物线关于y轴对称,顶点在原点,且经过点P(23,-2 ),则抛物线的标准方程是()A.y2=-6x B.x2=-4yC.x2=-6y D.x2=6y解析:由题意,设抛物线方程为x2=-2py(p>0).23,-2在抛物线上,所以12=4p,解得p=3.因为点P()∴抛物线的标准方程为x2=-6y.答案:C知识点二 抛物线的焦点弦长【探究2】斜率为k 的直线l 经过抛物线y 2=2px (p >0)的焦点F ,与抛物线相交于A (x 1,y 1),B (x 2,y 2)两点,你能想到哪些求弦长|AB |的方法?【提示】法一:利用两点间的距离公式; 法二:利用弦长公式|AB |=1+k 2|x 1-x 2|; 法三:|AB |=|AF |+|BF |=x 1+p 2+x 2+p2=x 1+x 2+p . ◆焦点弦直线过抛物线y 2=2px (p >0)的焦点F ,与抛物线交于A (x 1,y 1)、B (x 2,y 2)两点,由抛物线的定义知,|AF |=x 1+p 2,|BF |=x 2+p2,故|AB |=x 1+x 2+p .【做一做2】过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,若x 1+x 2=6,则|AB |=( )A .10B .8C .6D .4解析:|AB |=x 1+x 2+p =6+2=8. 答案:B(三)典型例题1.利用抛物线的几何性质求标准方程例1.已知抛物线的顶点在坐标原点,对称轴为x 轴,且与圆x 2+y 2=4相交的公共弦长等于23,求这条抛物线的方程.[分析] 因为圆和抛物线都关于x 轴对称,所以它们的交点也关于x 轴对称,即公共弦被x 轴垂直平分,于是由弦长等于23,可知交点纵坐标为± 3.[解析] 如图,设所求抛物线的方程为y 2=2px (p >0)或y 2=-2px (p >0),设交点A (x 1,y 1),B (x 2,y 2)(y 1>0,y 2<0), 则|y 1|+|y 2|=23,即y 1-y 2=2 3. 由对称性知y 2=-y 1,∴y 1= 3. 将y 1=3代入x 2+y 2=4得x =±1,∴点(1,3),(-1,3)分别在抛物线y 2=2px ,y 2=-2px 上.∴3=2p 或3=(-2p )×(-1),p =32.故所求抛物线的方程为y 2=3x 或y 2=-3x .【类题通法】根据抛物线的几何性质求抛物线的方程,一般利用待定系数法,先“定形”,再“定量”.但要注意充分运用抛物线定义,并结合图形,必要时还要进行分类讨论.【巩固练习1】1.抛物线的顶点在原点,对称轴重合于椭圆9x 2+4y 2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.[解析] 椭圆的方程可化为x 24+y 29=1,其短轴在x 轴上, ∴抛物线的对称轴为x 轴,∴设抛物线的方程为y 2=2px 或y 2=-2px (p >0). ∵抛物线的焦点到顶点的距离为3,即p2=3, ∴p =6.∴抛物线的标准方程为y 2=12x 或y 2=-12x , 其准线方程分别为x =-3或x =3.2.已知A 、B 是抛物线y 2=2px (p >0)上两点,O 为坐标原点,若|OA |=|OB |,且△ABO 的垂心恰是此抛物线的焦点F ,求直线AB 的方程.[解析] 抛物线的焦点F ⎝ ⎛⎭⎪⎫p 2,0 ∵抛物线关于x 轴对称,|OA |=|OB |,∴△ABO 为等腰三角形. ∴A 、B 两点关于x 轴对称. 设A (x 0,y 0),则B (x 0,-y 0),∵△ABO 的垂心恰为抛物线的焦点,∴BF ⊥OA . 则k BF ·k OA =-1,即-y 0-0x 0-p 2·y 0x 0=-1.又∵y 20=2px 0,∴x 0=52p .∴直线AB 的方程为x =5p2. 2.直线与抛物线的位置关系例2.已知抛物线C 的顶点在原点,焦点在x 轴上,且抛物线上有一点P (4,m )到焦点F 的距离为5.(1)求抛物线C 的方程;(2)若抛物线C 与直线y =x -4相交于不同的两点A 、B , 求证:OA ⊥OB .[分析] (1)可转化为点P 到准线的距离. (2)OA ⊥OB ⇔OA →·OB →=0,即x 1x 2+y 1y 2=0. [解析] (1)解:由题意设抛物线方程为y 2=2px (p >0),其准线方程为x =-p2,∵P (4,m )到焦点的距离等于P 到其准线的距离, ∴4+p2=5,∴p =2,∴抛物线C 的方程为y 2=4x .(2)证明:由⎩⎪⎨⎪⎧y 2=4x ,y =x -4,消去y ,得x 2-12x +16=0,Δ>0,∵直线y =x -4与抛物线相交于不同两点A 、B , ∴可设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=12,x 1x 2=16, ∵OA →·OB →=x 1x 2+y 1y 2=x 1x 2+(x 1-4)(x 2-4)=x 1x 2+x 1x 2-4(x 1+x 2)+16 =16+16-4×12+16=0, ∴OA→⊥OB →,即OA ⊥OB . 轨迹是以C (0,-3)为焦点,以y =3为准线的一条抛物线,其方程为x 2=-12y .【类题通法】将直线方程与抛物线方程联立,转化为一元二次方程,可通过直线与抛物线的位置关系转化为对判别式Δ或者对向量数量积的限制条件,利用限制条件建立不等式或等式,利用根与系数的关系运算求解.【巩固练习2】1.(多选题)过点(-2,1)作直线l ,与抛物线y 2=4x 只有一个公共点,则下列直线l 的方程满足条件的是( )A .y =1B .x +2y =0C .x +y +1=0D .x -2y +4=0解析:由题意知直线l 的斜率存在,设其方程为y -1=k (x +2),由方程组⎩⎪⎨⎪⎧y -1=k (x +2),y 2=4x ,(*)可得ky 2-4y +4(2k +1)=0.①当k =0时,由方程①得y =1,把y =1代入y 2=4x ,得x =14,这时,直线l 与抛物线只有一个公共点⎝ ⎛⎭⎪⎫14,1,此时直线l 的方程为y =1.当k ≠0时,方程①的判别式为Δ=-16(2k 2+k -1).当Δ=0时,即2k 2+k -1=0,解得k =-1或k =12,方程①只有一个解,从而方程组(*)只有一个解,这时直线l 与抛物线只有一个公共点. 此时直线l 的方程为y -1=-1(x +2)或y -1=12(x +2) 即x +y +1=0或x -2y +4=0. 答案:ACD2.已知A ,B 为抛物线E 上不同的两点,若抛物线E 的焦点为(1,0),线段AB 恰被M (2,1)所平分.(1)求抛物线E 的方程; (2)求直线AB 的方程.[解析] (1)由于抛物线的焦点为(1,0),∴p2=1,p =2,所求抛物线方程为y 2=4x .(2)法一:设A (x 1,y 1),B (x 2,y 2),则y 21=4x 1,① y 22=4x 2,②且x 1+x 2=4,y 1+y 2=2,由②-①得(y 1+y 2)(y 2-y 1)=4(x 2-x 1), ∴y 2-y 1x 2-x 1=2, 所以所求直线AB 的方程为y -1=2(x -2), 即2x -y -3=0.法二:显然AB 不垂直于x 轴,故可设弦AB 所在的直线方程为y -1=k (x -2),k ≠0,设A (x 1,y 1),B (x 2,y 2),联立方程⎩⎪⎨⎪⎧y -1=k (x -2),y 2=4x , 消去x 整理得ky 2-4y -8k +4=0,∴y 1+y 2=4k ,又M 点是AB 的中点,∴y 1+y 2=2,∴k =2,故直线AB 的方程为y -1=2(x -2),即2x -y -3=0.3. 抛物线的焦点弦例3.抛物线的顶点在原点,以x 轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线的方程.[解析] 如图,依题意可设抛物线方程为y 2=2px (p >0),则直线方程为y =-x +12p .设直线交抛物线于A (x 1,y 1)、B (x 2,y 2),则由抛物线定义得|AB |=|AF |+|FB |=|AC |+|BD |=x 1+p 2+x 2+p 2,即x 1+x 2+p =8.①又A (x 1,y 1)、B (x 2,y 2)是抛物线和直线的交点,由⎩⎨⎧ y =-x +12p y 2=2px ,消去y 得x 2-3px +p 24=0,∴x 1+x 2=3p ,将其代入①得p =2,∴所求抛物线方程为y 2=4x .当抛物线方程设为y 2=-2px (p >0)时,同理可求得抛物线方程为y 2=-4x .∴抛物线方程为y 2=4x 或y 2=-4x .【类题通法】1.过抛物线焦点的直线与抛物线相交所截得的弦叫作抛物线的焦点弦.2.对于抛物线的焦点弦,利用抛物线的定义,结合平面几何知识可以得出抛物线焦点弦的许多性质,应用起来非常方便.如图,已知线段AB 是抛物线y 2=2px (p >0)的焦点弦,且A (x 1,y 1),B (x 2,y 2),点F 是抛物线的焦点,过A ,B 两点分别作准线l 的垂线AC ,BD ,垂足分别为点C ,D ,点M 为线段AB 的中点,点M ′为线段CD 的中点.(1)几何性质①以过焦点F 的弦AB 为直径的圆与抛物线的准线相切于点M ′,∠AM ′B=90°;②以线段CD 为直径的圆与弦AB 相切于点F ,∠CFD =90°;③通径(过抛物线的焦点且与轴垂直的弦)是所有焦点弦(过焦点的弦)中最短的弦.(2)代数性质①y 1y 2=-p 2,x 1x 2=p 24;②|AB |=x 1+x 2+p =2p sin 2θ(θ为AB 的倾斜角);③1|FA |+1|FB |=2p (定值).【巩固练习3】如图,斜率为43的直线l 经过抛物线y 2=2px 的焦点F (1,0),且与抛物线相交于A 、B 两点.(1)求该抛物线的标准方程和准线方程;(2)求线段AB 的长.[解析] (1)由焦点F (1,0),得p 2=1,解得p =2.所以抛物线的方程为y 2=4x ,其准线方程为x =-1;(2)设A (x 1,y 1),B (x 2,y 2).直线l 的方程为y =43(x -1).与抛物线方程联立,得⎩⎨⎧ y =43(x -1)y 2=4x ,消去y ,整理得4x 2-17x +4=0,由抛物线的定义可知,|AB |=x 1+x 2+p =174+2=254.所以,线段AB 的长为254.(四)操作演练 素养提升1.顶点在原点,焦点为F ⎝ ⎛⎭⎪⎫32,0的抛物线的标准方程是( )A .y 2=32xB .y 2=3xC .y 2=6xD .y 2=-6x2.边长为1的等边三角形AOB ,O 为坐标原点,AB ⊥x 轴,以O 为顶点且过A ,B 的抛物线方程是( )A .y 2=36x B .y 2=-33xC.y2=±36x D.y2=±33x3.过点(1,0)作斜率为-2的直线,与抛物线y2=8x交于A,B两点,则弦AB的长为()A.213 B.215C.217 D.2194.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A 为垂足,如果直线AF的斜率为-3,那么|PF|=________.答案:1.C 2.C 3.B 4. 8【设计意图】通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。