当前位置：文档之家 › 苏汝铿量子力学讲义 第二章 波函数和Schroinger方程

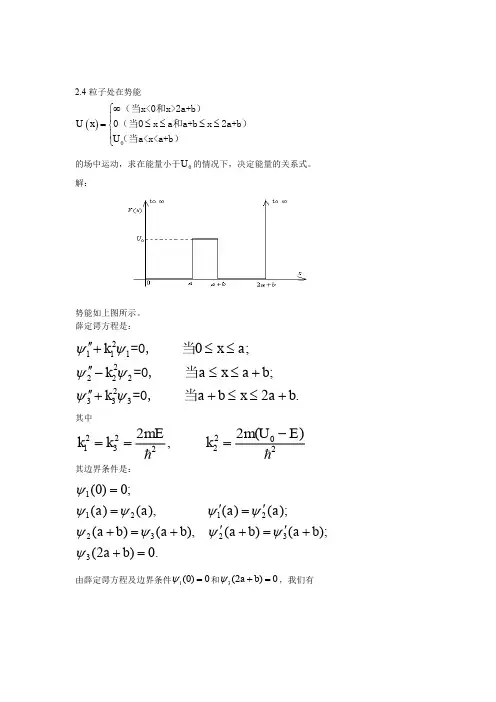
苏汝铿量子力学讲义 第二章 波函数和Schroinger方程

  • 格式：ppt
  • 大小：3.25 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

量子力学答案 苏汝铿 第二章课后答案2#16

量子力学答案 苏汝铿 第二章课后答案2#16

e2 1 8a n2
a
2
me2
e2
e2 4
E
1 me4 1 2 2 ( px py ) 2m 32 2 n2
基态能量为： E
me4 32 2
对应波函数为： 100 ( x, y, z )
2z a

3 2
e

z a
0 z 0 dx3 100 100 z
2m(U 0 E ) 2
可解得径向部分的波函数是
R(r ) Akl jl (kr) (r a) (1) R(r ) Bk l hl (ik r ) (r a)
(1) 式中 jl (r ) 为球贝塞尔函数, hl (ik r ) 为球汉克尔函数
利用在 r a 处波函数 (r ) 及波函数的一阶微商 (r ) 都连续
x2 y 2 2 xy 2 (1 ) 2 (1 )
进行变量代换后的薛定谔方程为：

2 2 2 2 2 2 A 2 2 2 (1 ) (1 ) B( z 2 z ) E 2m z
2.24
2z 4 3 6 2 3 a z e dz a a3 2 me2 0
一 个 质 量 为 m 的 非 相 对 论 粒 子 在 一 势 场 中 运 动 ， 势 场 是
U ( x, y, z ) A( x 2 y 2 2 xy) B( z 2 2 z ) ，其中 A 0 ， B 0 ， 1 ， 是任意
1 x x x 2 ( ) 则 1 ( ) 2 y y y

量子力学(第二版)答案 苏汝铿 第二章课后答案2.16-2#14

量子力学(第二版)答案 苏汝铿 第二章课后答案2.16-2#14

2r 1 a 2 e x dxdydz 3 a 2r 1 3 e a r 2 dxdydz 3a 2r 4 4 而 3 e a r dr 3a 4 a 3 g( )5 4! 3a 2 a2
x
h2 2 h2 h 2 2 x p a 所以 3a 2 3 2
这为适合流超比方程，要使Ｒ（p）在 趋于０则有解
( ) F (S 1
s 1
本征值为
a ), 2s 2, ) 2 Eh
a n 2 Eh
n＝０、１、２…..
且 所以
Enl
2
a2
2h 2 (n s 1)2
2
而 s ( (2l 1) 8 A / h 1) / 2 第 14 组 彭毅 姜麟舜 200431020117 200431020119

2h 2 2ah a3 ( p 2 h / a 2 )2
于是
px | ( p) | px dpx d p y dpz


0
由于被积函数对 px 是奇函数
2 2 px | ( p ) |2 p x dpx d p y dpz

1 | ( p) |2 p 2 dpx d p y dpz 3 8h 5 2 p4 2 5 dp sin d d 3 a 0 0 0 ( p h ) 4 a2 h2 2 3a
a A (a, A 0) ，求粒子的能量本征值。 r r2
14QM-2.1８
设势场为 U (r )
解：由于 E>0 是连续谱，所以仅讨论 E<0 在极坐标中，薛定谔方程的径向方程为
2 2 E l (l 1) R '' (r ) R ' (r ) [ 2 r h r2 2 a 2 A ] R(r ) 0 h 2 r h 2 r2

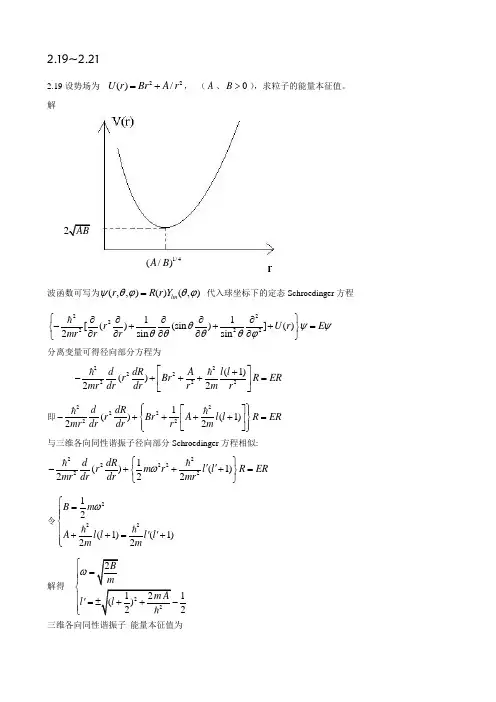
苏汝铿量子力学(第二版)课后习题(含答案)---第二章2.19-2.21#15(延边大学)三年级

苏汝铿量子力学(第二版)课后习题(含答案)---第二章2.19-2.21#15(延边大学)三年级

2.19~2.212.19设势场为22()/U r Br A r =+， （A 、0B >），求粒子的能量本征值。

解波函数可写为(,,)()(,)lm r R r Y ψθϕθϕ= 代入球坐标下的定态Schroedinger 方程22222211[()(sin )]()2sin sin r U r E mr r r θψψθθθθϕ⎧⎫∂∂∂∂∂-+++=⎨⎬∂∂∂∂∂⎩⎭分离变量可得径向部分方程为2222222(1)()22d dR A l l r Br R ER mr dr dr r m r ⎡⎤+-+++=⎢⎥⎣⎦ 即2222221()(1)22d dR r Br A l l R ER mr dr dr r m ⎧⎫⎡⎤⎪⎪-++++=⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭与三维各向同性谐振子径向部分Schroedinger 方程相似:22222221()(1)222d dR r m r l l R ER mr dr dr mr ω⎧⎫''-+++=⎨⎬⎩⎭ 令22212(1)(1)22B m A l l l l m m ω⎧=⎪⎪⎨⎪''++=+⎪⎩解得 222121()22B m m A l l ω⎧=⎪⎪⎨⎪'=±++-⎪⎩三维各向同性谐振子 能量本征值为2AB 1/4(/)A B3()2E N ω=+ 其中2r N n l '=+,,0,1,2,r n l '=（……） 故本题所求能量本征值为223(2)221322228422r n r r r r E n l m A B n m B m A n m ω'=++⎡⎤=-+⎢⎥⎣⎦⎡⎤=++⎢⎥⎣⎦,0,1,2,r n l =（……）2.20 一个质量为m 的粒子被限制在半径为r a =和r b =的两个不可穿透的同心球面之间运动，不存在其他势场。

求粒子的基态能量和基态波函数。

量子力学(第二版)答案 苏汝铿 第二章课后答案2.13-2#13

量子力学(第二版)答案 苏汝铿 第二章课后答案2.13-2#13
2.13 求势场 U ( x)
U 0 e 1
x a
，入射粒子能量 E 0 时的反射系数。
解：该势场的薛定谔方程为：
U d 2 2m 2 ( E x 0 ) 0 2 dx ea 1
令 y (1 e a ) 1 ，则有 y ( y 1)
x
d 2 d 2 2 (1 2 y) ( ) 0 2 dx dy y (1 y ) y
1
1 2m 2 2m( E V0 ) 2 其中 K 2 E ， k 2 a
1 r / a0
1
2.14 设氢原子处在 （i） r 的平均值；
a
3
e
， a0 为第一波尔半径，求：
（ii）势能 e / r 的平均值；
2
（iii）能量概率的分布函数。 解： （1）首先判断题中所给波函数的归一化情况：
十三组成员 ：李俊华 200431020040
扈俊 200431020122
余功硕 200431020039
4
1
令 i ，当 x ，我们有
(1 y)
e
i x / a
eikx ，这时 1 式中 的第一项代表
代表延 x 轴正向传播的平面波，第二代表反射的平面波 因此
AI eikx AReikx , x ，因此
2
A R R AI
(v 1)(v )(2 ) ，当 E 0 时， 和 v 均为纯虚数，即 (v ) 2 (v 1)

（2）
e 2 4 e2 4e2 1 e2 2 r / a0 2 re dr r a3 a 211 a0 0

苏汝铿量子力学讲义第二章波函数和Schroinger方程

苏汝铿量子力学讲义第二章波函数和Schroinger方程
➢ 一维束缚态本征函数的图象
§2.6 一维薛定谔方程的普遍性质
➢ 能量本征函数性质,以x趋近正无穷大为例
§2.6 一维薛定谔方程的普遍性质
➢ 能量本征谱性质
•
振荡解,连续谱,二度简并,散射态
•
指数衰减解
振荡解
本征谱连续,无简并,非束缚态解
§2.6 一维薛定谔方程的普遍性质
• 简并
两端均指数衰减,束缚态解,分立谱,无
➢ 多粒子体系的推广
§2.1 波函数的统计解释
▪ 动量几率分布函数 =>Fourier变换频谱 展开
§2.1 波函数的统计解释
➢
可描写体系状态,
也可描写体系状态
是同一个态,不同自变量
§2.1 波函数的统计解释
➢
代表在
出现单色平面波
态中,
的几率
§2.1 波函数的统计解释
➢ 处在
的粒子,动量无确定值
2 2
2n 1
n 0,1,2,
H
n
2
n
nn
12
n2
nn
1n
2!
2n
3
2
n4
n
1 2
n!
2 n2
n 2
n 2
!
{ n
2
n/2
n 1/ 2
(n为偶数)
n为奇数
En
n
1 2
n 0,1,2,
En1 En
E0
1 2
1 2x2
n x Nne 2 Hn x
§2.3 薛定谔方程
➢ 力学量用算符表示 ➢ 两个惯例
1)只在直角坐标中适用,因为微商不协变 例:二维极坐标下的薛定谔方程

量子力学第二章

量子力学第二章
第二章 波函数和薛定谔方程(波函数的理解) 波函数和薛定谔方程(波函数的理解) 粒子波性 如何描述 波函数 薛定谔方程
光子 E = hv = hω 粒子
E v= h
u hr r r p = n = hk
λ
h h λ= = p 2 E
第二章 波函数和薛定谔方程(波函数的理解) 波函数和薛定谔方程(波函数的理解)
第二章 波函数和薛定谔方程(波函数的理解) 波函数和薛定谔方程(波函数的理解)
怎么理解 ？
分析
经典物理中粒子 有确定的质量 坐标 轨道 仔细分析粒子有确切的轨道是牛顿力学的概念， 仔细分析粒子有确切的轨道是牛顿力学的概念，从来 没有无限精确地为实验证实过 所以很可能坐标和轨道地概念是宏观情况下的近视 同时电荷、质量、 同时电荷、质量、体现出的粒子性与确切坐标和轨道 无必然联系
第二章 波函数和薛定谔方程(波函数的理解) 波函数和薛定谔方程(波函数的理解)
到底电子是什么？波函数是什么？ 到底电子是什么？波函数是什么？ 人们所普通接受的观点为 即不是粒子也不是波电子 即不是粒子也不是波->确切地说不是经典粒 子，也不是经典的波 但人我们说，即是粒子，又是波， 但人我们说，即是粒子，又是波，它是粒子和波动 两重性的矛盾统一， 两重性的矛盾统一，这个波不是经典概念下的波
dτ
r r r 2 dw(r , t ) 空间，几率密度正比与 ω (r , t ) = dτ = c φ (r , t ) 空间，
几率正比与
直接系坐标中 空间区域
r r 2 dw(r , t ) = c φ (r , t ) dτ
2
dw( x, y, z, t ) = c φ ( x, y, z , t ) dxdydz

量子力学第2章 波函数与Schrodinger方程-1

量子力学第2章 波函数与Schrodinger方程-1
两种模糊认识：
1. 波由粒子组成
如水波，声波等 矛盾：不能解释长时间单个电子衍射实验 反例：氢原子
2. 粒子由波组成
粒子的运动速度即波包的群速度
d k k 矛盾： v g dk m
反例：自由粒子
3
波包发散
3
2.1.2．几率波，多粒子系的波函数
电子究竟是什么东西呢？ 是粒子？还是波？
经典概念 1.有一定质量、电荷等“颗粒性”的属性;
1. 扫描电子显微镜
17
SEM
17
电子显微镜下的 流行感冒病毒
18
电子显微镜下 的乙肝病毒
18
电子显微镜下的花粉
19
19
电子显微镜下的灯泡钨丝
20
20
电子显微镜下的光盘表面
21
21
电子显微镜下放大50k倍才观察到碳纳米管的真面目 22
22
2. 扫描隧道显微镜
STM
23
23
0 10
30
50
70
90
(nm)
24
硅晶体表面的STM扫描图象
24
神经细胞的STM扫描图象
25
25
操纵单个原子写出的“100”、“中国”
26
26
镶嵌了48个 Fe 原子的 Cu 表面的扫 描隧道显微镜照片。48 个 Fe 原子形 成“电子围栏”，围栏中的电子形成驻波。
27
27
1959年费曼的演讲《在底部还有很大的空间》
15 15
波函数的意义
2 r , t r , t r , t :几率密度
z
Ψ dV
t 时刻，在 r 端点处单位体
积中发现一个粒子的几率。

量子力学讲义I.波函数与Schrodinger方程（新）

量子力学讲义I.波函数与Schrodinger方程（新）

量子力学讲义I.波函数与Schrodinger方程（新）I.波函数与Schrodinger方程1. 经典波有波函数吗？量子波函数与经典波函数有什么异同？答：波函数就其本义而言不是量子力学特有的概念．任何波都有相应的波图执只是习惯上这一术语通常专用于描述量子态而不常用于经典波．经典波例如沿轴方向传播的平面单色波，波动动量对和的函数——波函数可写为，其复指数形式为，波函数给出了传播方向上时刻在点处的振动状态。

经典波的波函数通常称之为：波的表达式或波运动方程．量子力学中，把德布罗意关系 p ＝k 及 E ＝ω 代入上式就得到自由粒子的波函数 ( 自由粒子的波的表达式 ).经典波与概率狡的唯一共性是叠加相干性。

但概率波函数是态函数，而态的叠加与经典波的叠加有着本质的差别．经典波函数描述的是经典波动量对时空变量的函数关系．量子力学中的概率波函数其意义不同于经典物理中的任何物理量．概率波函数虽是态函执但本身不是力学量．态函数给出的也不是物理量间的关系．概率波函数的意义是：由波函效描述微观体系各种力学量的概率分朽．作为一种约定的处理方法，经典波可表为复指数函数形式但只有它的实部才有物理意义．而概率波函数一般应为复函数．非相对论量子力学中，粒子不产生出不泯灭．粒子一定在全空间中出现，导致了概率被函数归一化问题，而经典波则不存征这个问题．概率波函数乘上一常数后，粒子在空间各点出现的相对概率不变．因而，仍描述原来的状态．而经典波中不同的波幅的波表不同的波动状态，振幅为零的态表示静止态．而量子力学中，振幅处处为零的态表示不存在粒子．另外经典波函数与量子被函数满足各自的、特征不同的波方程．2 ．波函数的物理意义——微观粒子的状态完全由其被函数描述，这里“完全'的含义是什么？波函数归一化的含义又是什么 ?答：按照波函数的统计解释波函数统计地描述了体系的量子态．如已知单粒子 ( 不考虑自旋 ) 波函数为，则不仅可确定粒子的位置概率分布，而且如动员等粒子其他力学且的概率分布也均可通过而完全确定．出于量子理论与经典理论不同，它一般只能预言测量的统计结果．而只要已知体系波函数，便可由它获得该体系的一切可能物理信息．从这个意义上着，有关体系的全部信息显然都已包含在波函数中，所以我们此微现粒子的状态完全由其波函数描述，并把波函数称为态函数．非相对论量子力学中粒子不产生、不泯灭．根据波函数的统计解释，在任何时刻，粒子一定在空间出现，所以，在整个空间中发现粒子是必然事件．概率论中认为必然事件的概率等于1 ．因而，粒子在整个空间中出现的概率即概率密度对整个空间积分应等于1 ．式中积分号下的无限大符号表示对整个空间积分．这个条件称为归一化条件．满足归一化条件的波函数称为归一化波函数．显然，平方可积波函数才可以归一化．3 .证明从单粒子薛定谔方程得出的粒子速度场是非旋的，即求证，其中，为几率密度，为几率流密度。

量子力学答案 苏汝铿 第二章课后答案2.4-2#05

量子力学答案 苏汝铿 第二章课后答案2.4-2#05

由其它边界条件，又有
A1 sin k1a A2e k2 a B2e k2 a , A1k1 cos k1a A2 k2e k2 a B2 k2e k2 a ; A3 sin k1a A2e k2 ( a b ) B2e k2 ( a b ) , A3k1 cos k1a A2 k2e k2 ( a b ) B2 k2e k2 ( a b ) .
改写上式可得关于不全为 0 系数 ( A1 , A2 , B2 , A3 ) 的线性方程组：
A1 sin k1a
A2e k2a
B2e k2a B2 k2 e k2 a
0, 0, A3 sin k1a 0,
A1k1 cos k1a A2 k2e k2 a
A2 ek2 ( a b ) B2e k2 ( a b )
U0 ) U0 )
2.4 粒子处在势能
பைடு நூலகம்
（当x<0和x>2a+b） U x 0（当0 x a和a+b x 2a+b） U（当a<x<a+b） 0
的场中运动，求在能量小于 U 0 的情况下，决定能量的关系式。 解：
势能如上图所示。 薛定谔方程是：
1 k12 1 =0,
由薛定谔方程及边界条件 1 (0) 0 和 3 (2a b) 0 ，我们有
1 ( x) A1 sin k1 x, 2 ( x) A2ek x B2e k x , 3 ( x) A3 sin[k1 ( x 2a b)],
2 2
当0 x a; 当a x a b; 当a b x 2a b.
即

量子力学电子教案(第二章 波函数和 薛定谔方程)

量子力学电子教案(第二章 波函数和 薛定谔方程)

�
i ( E t px x) i + px x i Et i Et
Ψ ( x, t ) = Ψ0 e
与驻波类比
= Ψ0 e
i px x
e
= Ψ ( x) e
式中: 式中: Ψ ( x ) = Ψ e 0
振幅函数
∵ Ψ ( x, t ) = Ψ ( x ) e
i Et
| Ψ ( x, t ) |2 = Ψ Ψ * = Ψ ( x )e
代入 得 即
d Ψ ( x) p x = 2 Ψ ( x) 2 dx
2 2
2 x
*
d 2 Ψ ( x ) 2m + 2 ( E U )Ψ ( x) = 0 2 dx
一维定态薛定谔方程
三维定态薛定谔方程 振幅函数 Ψ = Ψ ( x, y , z )
Ψ Ψ Ψ 2m + 2 + 2 + (E U)Ψ = 0 2 x y z
Ψ(r , t ) = Ψ0e
i ( Et pr )
2. 波函数的强度 波函数的强度——模的平方 模的平方 | Ψ |2 = Ψ Ψ * 波函数与其共轭复数的积 例:一维自由粒子: 一维自由粒子:
| Ψ ( x, t ) | = Ψ Ψ* = Ψ0 e
2
i ( E t px x )
Ψ0 e
x x Ψ = Ψ0 cos ω (t ) = Ψ0 cos 2π (ν t ) λ u 1 E x = Ψ0 cos 2π ( t ) = Ψ0 cos ( Et x p x ) h h p
Ψ(x, t) = Ψ e 0
i ( Et px x)
(取实部) 取实部)
推广 :三维自由粒子波函数

量子力学(第二版)答案 苏汝铿 第二章课后答案2.10-2#07

量子力学(第二版)答案 苏汝铿 第二章课后答案2.10-2#07

x Nne
1 2 x2 2
H n x
Ek
势能平均值
2 p2 2 , 2m 2m x 2
Ep
1 m 2 x 2 2
1 E p n* x m 2 x 2 n x dx 2 m 2 2 2 y2 2 3 N n y e H n y dy 2
a
1 n* x n x
0
An 2 sin 2
0
a
n xdx a

a 2 An 2
a 0 a
1 * x x A2 x 2 a x dx
2 0

a5 2 A 30
得：
A
30 , a5

An
2 a
由态叠加定理有：

2
2m
2
Nn2 e


1 2 x2 2
H n x
2 x2 2 1 2 e H n x dx 2 x
2m
2
N n 2 e

1 y2 2
H n y y 2 1 H n 4nyH n 1 4n n 1 H n 2 e
可想而知，对两个方势垒，则需解八元一次代数方程组，这是不好做的。
我们认为近似处理可以得到： D D1D2 e
2 [ 2 m (U1 E )a 2 m (U 2 E ) c b ]
12.证明对于一维谐振子，无论处在哪个本征态，它的动能平均值恒等于势能平均值。 证明： 一维谐振子的波函数是
6

其中，查表可得：
480 2 ma 2 4 5 2 ma 2

量子力学答案 苏汝铿 第二章课后答案2#02

量子力学答案 苏汝铿 第二章课后答案2#02

d 2W dV ( ) 0 ， 相 应 的 必 有 )， 则 若 满 足 W ( 0) 0， 且 dx 2 dx
d ( ) 0. dx
(1) 证 决定 2 P 和 3D 态能级的 Schondinger 方程是 (2m
1)
批注 [JL1]:
u "
g2 2 u 2 u V u r r g2 6 v 2 v V v r r



u 2 v2 dr r r
(5)
d r
0

r
u r v 2 r dr r r
2
u 2 v 2 dr 0
0
而在 r 很大时 , 由 I r 的特性知 I r 0 , 所以 J r I r dr 0 , 综合上述可知在
U ( x) ( x d ) U ( x) 0 ( x d )
中运动，求：
（i）当势壁离粒子很远时，对束缚态能量的修正值。并据此说明“远离”的意义； （ii）至少存在一个束缚态时， U 0 和 d 应满足的条件。 解： （1） x d 时，势为无穷大，波函数 0
则 U ( x) 的束缚态不超过 V2 ( x) 的束缚态个数，而后者的束缚态个数为 [
2m a 2

] 1，
则所给的势 U ( x) 对应的束缚态个数在 [
2m a 2 m a 2 ] 和[ ] 1 之间 2
v 无节点，且满足
u(0) v(0) 0 ？
uv ' vu ' (
0
r
4 E2 P E3 D )uvdr ' F (r ) ， r '2

量子力学(第二版)答案 苏汝铿 第二章课后答案2.10-2#12

量子力学(第二版)答案 苏汝铿 第二章课后答案2.10-2#12

1 4 2 x 2 2 2 2 m 2 x 2 , 2 2m 2m
2 2 2

m
, x
Vn n x Vdx
2



N n H n e
2 2 2
2m
d
又由厄秘多项式 H n 的递推式 2 H n H 2 n1 2nH n1
2
a 0
2
于是 A 30a
5
下面考虑粒子能量的概率分布和能量的平均值：
2 n sin x 对一个无限深的势阱，其能级为 En 的波函数为： n x a a

0
a
x 是各个能级的波函数的叠加，故设
x cn n x cn
n n
2 n sin x a a
2 D exp 2m U 0 E b a
U1
又
a
U2
b
D R 1 ，D 是贯穿系数，R 是反射系数，
所以 D 是粒子透过势垒的概率，而由概率论知识， 粒子连续贯穿两个方势垒的概率等于 分别单独贯穿这两个势垒的概率之积。 于是
E
图 2
a b

a
0
5 2 E x dx 2 ma
2
2.10
设两个方势垒的形状分别是：
0 U x U1
x 0 , 0 x a
0 U x U 2
a x b, x c b x c
U
E
图1
求粒子连续贯穿两个方势垒的贯穿系数。 解：如图（1） ，对低能入射，贯穿一个方势垒的贯穿系数为

量子力学(第二版)【苏汝铿】课后习题解答

量子力学(第二版)【苏汝铿】课后习题解答

.
解：(i)
(ii) 10 当
时，显然
20 假设当
时，满足
成立； ，则
这就是说当 综上 10,20 可知 3.4 证明：
时，满足 对于任意
；
；
；
. 的整数恒成立.
. 证：1)
由角动量与坐标算符的对易子
，知
同理有
，
即
6
量子力学(第二版)【苏汝铿】课后习题解答
角动量算符与动量算符的对易子 2)
，同上可证
式中 是坐标， , 是相应于 态和 态的能量，求和对一切可能的状态进行. (注：由于质量 与态 字母一样，故将质量 改为 ,避免混淆)
解：
,
,
故
4.6 证明两个厄米矩阵能用同一个幺正变换对角化的充要条件是它们彼此对易.
证:(充分性)
.设使 对角化的幺正变换 ,则
.
的变换矩阵元
即
于是
即时
,
时
故
是对角矩阵的元素，
的两个不可穿透的同心球面之间运动，不存在其他势
径向波函数所满足的边界条件是 径向部分的薛定谔方程
. .
5
引入变换 的解是
量子力学(第二版)【苏汝铿】课后习题解答
,
,基态
,代入边界条件有
,可化为
即 而 归一化 即 基态波函数 归一化
粒子的基态能量
基态波函数
3.1 若算符 、 满足
,求证:
（i）
；
（ii）用数学归纳法证明：
(必要性) 能同时将 对角化,即
的变换矩阵元
是对角矩阵， 能用同一个幺正变换 对角化. , (同充分性)
4.7 已知在和的共同表象中，算符和的矩阵分别为：

量子力学答案(第二版)苏汝铿第2章课后答案2#01

量子力学答案(第二版)苏汝铿第2章课后答案2#01
（2） 、当
U, z U new ， , z
即
U, 0 U new , 0
时，方程（1）中的方程①、②均不变，因此其本征值 E1n , E2 n 不变，方程③变为
2 1 d 2T1 B 2 E3 , 0 2 ， T1 0, 0 ……④ 2m T1 d T 0 0 1
2
……①
2 d 2S 1 (1 ) Av 2 E2 2 2m S dv 2
2
……②

1 d 2T B 2 E3 2m T d 2
2
……③
其中 E1 E2 E3 B 2 E 0 对于一维谐振子有
2 d2 1 m 2 x 2 x E x 2 2m dx 2
第一组： 第二章 2.24 一 个 质 量 为 m 的 非 相 对 论 性 粒 子 在 一 势 场 中 运 动 ， 势 场 是
U ( x, y, z )
的，求：
2
A ( x2பைடு நூலகம் y 2
x) y2 (B，其中 z 2 A )0 z ， B 0 ， 1 ， 是任意
(1) 能量的本征值；
E001 1 2
3 3 B 2 （ n1 n2 0, n3 1 ） 2
2.25
一个刚体具有惯性矩 I z ， 可以自由地在 x y 平面中转动， 令 为 x 轴与转动轴之间的夹角， 求： （1）能量本征值和相应的本征函数； （2）若在 t 0 时，转子由波包 (0) A sin 2 描述，求在 t 0 时的 (t ) .
(t )
1 1 (e2i ei 2 3 2 3

第二章[波函数及薛定谔方程]

第二章[波函数及薛定谔方程]
则微观粒子在 t 时刻出现在 r 处体积元 dτ 内的几率
dW = Aψ (rr, t) 2 dτ
设衍射波波幅用 ψ (rr, t) 描述，则衍射花样的强度分布 用 ψ (rr, t) 2 描述。但这里波的强度 ψ (rr, t) 2 的意义与经典波 的根本不同，它是用来刻画电子出现在点附近几率大小的一 个量。
如水波，声波，由物质的分子密度疏密变化而形成的一种 分布。这种看法是与实验矛盾的，它不能解释长时间单个电子 衍射实验。
电子一个一个的通过小孔，但只要时间足够长，底片上仍 可呈现出衍射花纹。这说明电子的波动性并不是许多电子在空 间聚集在一起时才有的现象，单个电子就具有波动性。
事实上，正是由于单个电子具有波动性，才能理解氢原子 （只含一个电子！）中电子运动的稳定性以及能量量子化这样 一些量子现象。
这个波不再是经典概念的波，粒子也不是经典概念中的粒子。
经典概念中 1. 有一定质量、电荷等“颗粒性”的属性; 粒子意味着 2 .有确定的运动轨道，每一时刻有一定位置和速度。
经典概念中 1. 实在的物理量的空间分布作周期性的变化; 波意味着 2 .干涉、衍射现象，即相干叠加性。
几率波
(一). 几率波
将粒子性与波动性统一起来，更确切地说：把微观粒子的 “原子性”与波的“叠加性”统一起来的是波恩（Born）1926年提出 的几率波。
波恩认为：德布罗意提出的“物质波”或“薛定谔方程中的波 函数所描述的”，并不像经典波那样代表什么实在的物理量的波 动，只不过是刻画粒子在空间的几率分布的几率波而已。
几率波
波函数的统计解释 The Wave function and its statistic explanation 态叠加原理 The principle of superposition 薛定谔方程 The Schrödinger equation 粒子流密度和粒子数守恒定律 The current density of particles and conservation laws 定态薛定谔方程 Time independent Schrödinger equation

量子力学讲义 第二章(2)

量子力学讲义 第二章(2)

•
在讨论了状态或波函数随时间变化的规律后
， 进一步讨论粒子在一定空间区域内出现的概 率将 怎样随时间变化。
设描写粒子状态的波函数是： (r , t ) 在时刻t 在r点周围单位体积内粒子出现的概率（概 2 率密度）： ( r , t ) ( r , t ) ( r , t ) | ( r , t ) | （1）
将（2）代入 （1）式中：
一、定态薛定谔方程
i [ 2 U r ] 2m t
（2）
2
2
（1）
i (r )
d f (t ) f (t )[ 2 U r ] 2 m dt 上式两边除以 ( r ) f (t )
（3）
2 i df 1 [ 2 U r ] f dt 2m
j k 其中 i x y z
（称为动量算符）
（向量算符）
问：p x
?
p x i

x
利用关系式(8)、(9)来建立在力场 中粒子波函数所满足的微分方程。 设粒子在力场中的势能为 U r ，则：
2、薛定谔方程：
三、薛定谔方程
2 p 两边乘以 p U r （10） E E U r 2m r , t 2m 2 E i t 代入上式得 i 2 U r 将 t 2m p i （11）
定态的特点 1）粒子的概率密度和概率流密度
与时间无关 因为
2 Et ( r , t ) ( r )e
t
i 2
一、定态薛定谔方程
2 (r )
显然， 0
2）能量具有确定的值 3）各力学量的平均值不随时间变化

量子力学第二章波函数

量子力学第二章波函数

第二章波函数和薛定谔方程2.1 波函数的统计解释与态叠加原理1、波函数的统计解释上一章已说到，为了表示粒子的波粒二象性，可以用复数形式的平面波束描写自由粒子。

自由粒子是不受力场作用的，它的能量与动量都是常量。

如果粒子受到随时间及位置等变化的力场的作用，它的能量和动量就不再是常量，或者不再都是常量。

这时，粒子就不能用平面波来描写，设这时描写粒子的波是某一个函数，这个函数就称为波函数。

它描写粒子所处的状态，所以也称为态函数，它通常是一个复数。

究竟怎样理解波函数和它所描写的粒子之间的关系呢？对于这个问题，曾经有过各种不同的看法。

例如，将波看作是由它所描写的粒子构成的，这种看法是不对的。

我们知道，衍射现象是由波的干涉而产生的，如果波果真是由它所描写的粒子构成，则粒子流的衍射现象应当是由于构成波的这些粒子相互作用而形成的。

但事实证明，在粒子流的衍射实验中，照片上所显示出来的衍射图形与入射粒子流的强度无关，如果减少入射粒子流强度，即使粒子是一个一个地被衍射，虽然一开始照片上的点子看起来是毫无规则的，但当足够长的时间后，如果落在照片上的粒子数基本上保持不变，则所得到的衍射图形是相同的。

这说明每一个粒子被衍射的现象与其他粒子无关，衍射图形不是由粒子之间的相互作用而产生的。

除了上面的看法外，还有其他一些企图解释波函数的尝试，但都因与实验事实不符而被否定。

为人们所普遍接受的对波函数的解释，是由玻恩（Born）首先提出的统计解释：波函数在空间某一点的强度（振幅绝对值的平方）和在该点找到粒子的几率成比例。

按照这种解释，描写粒子的波及是几率波。

按照波函数的几率解释，很容易理解衍射实验：每一个粒子都具有波性，所以每一个粒子都被衍射。

但如果粒子数很少，则统计性质显示不出来，所以在照片上的点子看起来好象是毫无规则的；如果粒子数目足够大，则在波的强度最大的地方，粒子投射在这里的几率也最大，便出现衍射极大，在波的强度最小的地方，粒子投射在这里的几率也最小，便出现衍射极小。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢ 建立方程的启示 自由粒子
已知解=>方程式(不唯一)
编辑ppt
23
§2.3 薛定谔方程
➢ 已知解=>方程式(不唯一)
编辑ppt
24
§2.3 薛定谔方程
一般情况:
编辑ppt
25
§2.3 薛定谔方程
➢ 说明: a)波动力学的基本假定,表征量子体系特征的量h 进入了方程式,薛定谔方程在量子力学中的地位与 牛顿方程在经典力学中的地位相当 b)算符形式
• 将势能为零的区间放大或者缩小一倍(分是 足够缓慢的变还是突变两种情况)时,波函数 和能级怎么变?
• 将势场曲线正题右移a,波函数和能级怎么变?
编辑ppt
42
§2.4 一维方势阱
➢ 一维方势阱
编辑ppt
43
§2.4 一维方势阱
➢ 一维方势阱
编辑ppt
44
§2.4 一维方势阱
➢ 一维方势阱
编辑ppt
§2.1 波函数的统计解释
➢ 处在
的粒子,动量无确定值
➢ 相当于晶体衍射
➢ 如若 则
编辑ppt
12
§2.1 波函数的统计解释
➢ 坐标表象和动量表象
编辑ppt
13
§2.2 态叠加原理
➢ 波叠加 经典 合成的波中有各种成分 相干性 量子 相干性 新特点
编辑ppt
14
§2.2 态叠加原理
新特点 • 可能性和概率 • 干涉项的概率性 • 是粒子运动状态概率波自身的干涉,不是不
• 要求: • 线性方程(态叠加原理的直接要求) • 系数也不含状态参数 • t与x,y,z均为变量=>只能是偏微分方程 • 解的唯一性=>两阶正规方程
编辑ppt
21
§2.3 薛定谔方程
➢ 量子力学
• 进入方程式,体现微观世界的特点(量子化) • ->0,过渡到牛顿方程
编辑ppt
22
§2.3 薛定谔方程
编辑ppt
26
§2.3 薛定谔方程
➢ 力学量用算符表示 ➢ 两个惯例
1)只在直角坐标中适用,因为微商不协变 例:二维极坐标下的薛定谔方程
编辑ppt
27
§2.3 薛定谔方程
➢ 两个惯例 2)将H分成三部分: i)与坐标无关的动量二次式 ii)只依赖于坐标的函数 iii)
编辑ppt
28
§2.3 薛定谔方程
45
§2.4 一维方势阱
a)偶宇称 波函数为 cos(kx)
关键:用
在
连续以代替波函数
以及导数的连续.好处在于去掉波函数中常数的影响
编辑ppt
46
§2.4 一维方势阱
结论:无论Ua^2取何值,都有解(见下一页图)
编辑ppt
47
一维方势阱偶宇称能谱图
➢ 一维无限深势阱
编辑ppt
36
§2.4 一维方势阱
➢ 一维无限深势阱
编辑ppt
37
§2.4 一维方势阱
➢ 一维无限深势阱
编辑ppt
38
§2.4 一维方势阱
➢ 一维无限深势阱
编辑ppt
39
一维方势阱波函数图象
编辑ppt
40
一维方势阱波函数图象
编辑ppt
41
§2.4 一维方势阱
➢ 思考题:
=>概率相干
编辑ppt
18
§2.2 态叠加原理
➢ 讨论 c)线性叠加 d)叠加次序并不重要
编辑ppt
19
§2.3 薛定谔方程
➢ 经典力学
• 牛顿方程特点: • 线性方程 • 二阶全微分方程,只有一个独立变量t • 唯一性 • 方程系数不含状态参数,有普适性
编辑ppt
20
§2.3 薛定谔方程
➢ 量子力学
第二章 波函数和Schroinger方程
▪
质子在钯中的波函数
▪
/groups/materials%20characterisation/hydrogen%20in%20palladium.s
html
编辑ppt
1
薛定谔 ERWIN SCHRODINGER
➢ 因为有波函数统计解释,因此概率流守恒定律自动 包含在薛定谔方程中
编辑ppt
29
§2.3 薛定谔方程
编辑ppt
30
§2.3 薛定谔方程
➢ 为什么
而与t无关?
编辑ppt
31
§2.3 薛定谔方程
➢ 定态U=U(r), 不显含t
编辑ppt
32
§2.3 薛定谔方程
=> 几率流密度变不变?
编辑ppt
➢ 多粒子体系的推广
编辑ppt
8
§2.1 波函数的统计解释
▪ 动量几率分布函数 =>Fourier变换频谱 展开
编辑ppt
9
§2.1 波函数的统计解释
➢
可描写体系状态,
也可描写体系状态
是同一个态,不同自变量
编辑ppt
10
§2.1 波函数的统计解释
➢
代表在
出现单色平面波
态中,
的几率
编辑ppt
11
33
§2.3 薛定谔方程
➢ 本征值方程
编辑ppt
34
§2.3 薛定谔方程
➢ 边界条件的讨论:
• U连续,波函数及其一阶导数连续
• U不连续,波函数及其一阶导数连续
• U趋向无穷大 (一阶)波函数连续,一阶导数不 连续
• U趋向无穷大(二阶及以上)波函数不连续,一 阶导数亦不连续
编辑ppt
35
§2.4 一维方势阱
编Hale Waihona Puke ppt6§2.1 波函数的统计解释
▪ 波函数的讨论
➢
的平方可积
➢ 除了个别孤立奇点外,波函数单值,有界,连续
➢ 不确定性:
i)
表示同一个态->归一化
ii)相角不确定性(常数相角)
➢ 经典,态确定性
量子:几率性=>可用以计算平均值
编辑ppt
7
§2.1 波函数的统计解释
▪ 波函数的讨论 ➢ 平面波
群速度:
相速度: 必有色散->粒子解体
编辑ppt
4
§2.1 波函数的统计解释
➢ 粒子性 颗粒性(V) 轨道(X)
➢ 波动性 物理量周期分布(V and X) 将”粒子分布”视为物理量 叠加性->干涉,衍射(V)
编辑ppt
5
§2.1 波函数的统计解释
▪ 波函数的统计解释
时间为t时刻,粒子出在 位置r的几率
同粒子之间的干涉
编辑ppt
15
§2.2 态叠加原理
➢ 波叠加原理的表述 a)如果
是可能态
则
也是一个可能态
b)在 中,体系出现
的几率是
编辑ppt
16
§2.2 态叠加原理
➢ 讨论 a)
b)光子偏整态:Malus定律
编辑ppt
17
§2.2 态叠加原理
➢ 讨论
但任何时候观测到的都是一整个光子,
而不是
个光子
(1887-1961)
编辑ppt
2
§2.1 波函数的统计解释
▪ 波粒二象性的矛盾和解释 1. 波和粒子的关系
➢ 波由粒子组成,波是大量粒子运动的表现 与减少入射粒子流密度,让粒子近似地一 个个从粒子源射出后仍有波动性的实验不符
➢ 粒子由波组成,粒子=波包
编辑ppt
3
§2.1 波函数的统计解释
➢ 反例:i)自由粒子平 面波,占据整个空间 ii)色散