波动方程与波速

波的运动方程与波速波是指能够在介质中传播的一种物理现象。

波的运动方程描述了波在空间和时间上的变化规律，而波速则表示波在介质中传播的速度。

本文将探讨波的运动方程及其与波速之间的关系。

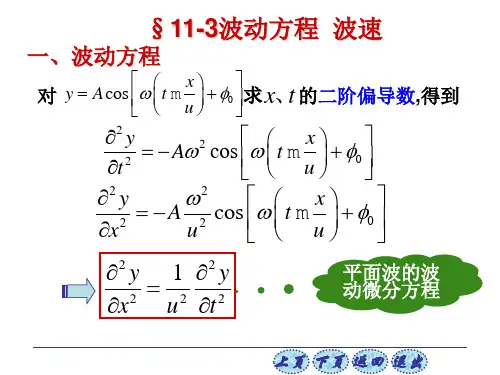
一、波动方程波的运动方程是描述波随时间和空间变化的数学表达式。

不同类型的波具有不同的运动方程。

下面以机械波为例，讨论波动方程的一般形式。

对于机械波，其运动方程可以用以下泛定的形式表示：y = A sin(kx - ωt + φ)其中，y表示波的振幅，A表示振幅的最大值，k表示波数，x表示位置坐标，ω表示角频率，t表示时间，φ表示初相位。

波动方程中的每一项都具有特定的物理意义。

振幅A表示波的振动幅度，反映了波的能量大小。

波数k表示波的空间频率，描述了波的周期性。

角频率ω则表示波的频率，与波的周期倒数成正比。

初相位φ表示波动的起始相位。

二、波速的计算波速是指波在介质中的传播速度。

对于机械波，波速可以由波动方程中的波长和周期来计算。

波长λ表示波的一个完整周期所对应的空间距离。

周期T表示波完成一个振动周期所需的时间。

波速v定义为波长和周期的商：v = λ / T波速的计算与波的性质和介质有关。

例如，在弹性介质中传播的横波和纵波的波速分别由介质的弹性模量和密度决定。

在真空中，电磁波的波速等于光速。

三、波速的影响因素波速的大小受多种因素影响，包括介质性质、温度、压力等。

以下介绍一些常见的影响因素：1. 介质性质：不同介质具有不同的质量和弹性特性，因此波速会因介质而异。

例如，声音在不同材料中的传播速度会有所不同。

2. 温度：温度的变化也会影响波速。

一般来说，温度升高会导致介质的分子和原子振动加剧，使波速增加。

3. 压力：在气体中传播的声波受压力的影响。

随着压力的增加，气体的密度增加，分子之间的相互作用也会增强，导致波速增加。

除了以上因素，波速还可受到介质中存在的其他波或障碍物的干扰而发生变化。

四、应用与意义波动方程和波速的研究对于物理学和工程学领域具有重要的意义。

波动方程通解
波动方程是研究波的传播与变化规律的重要方程，其通解可以通过偏微分方程的求解得到。

波动方程的一般形式为：
^2u/t^2 = c^2 ^2u/x^2
其中u表示波函数，t表示时间，x表示空间位置，c表示波速。

解波动方程需要使用分离变量法，即假设u(x,t)可以分解为两个函数的乘积，即u(x,t) = X(x) × T(t)。

将u(x,t)带入波动方程中，得到：
X(x) × T''(t) = c^2 X''(x) × T(t)
两边同时除以X(x) × T(t)，得到：
T''(t) / T(t) = c^2 X''(x) / X(x)
由于左边只与t有关，右边只与x有关，所以等式两边必须相等，即：
T''(t) / T(t) = c^2 X''(x) / X(x) = -ω^2
其中ω为常数，可表示波的频率或角频率。

根据上述等式，我们可以分别求解出X(x)和T(t)的通解：
X(x) = A sin( kx + φ)
其中A、k、φ为常数，k = ω / c。

T(t) = B cos( ωt + α)
其中B、α为常数。

因此，波动方程的通解为：
u(x,t) = A sin( kx + φ) × B cos( ωt + α)
其中A、B、φ、α为常数，k = ω / c。

该通解可以表示任意形式的波函数，包括机械波、电磁波等。

在具体求解时，需要根据实际问题进行边界条件的约束，从而确定待定常数的具体取值。

波动学中的波速与波动方程知识点总结波动学是物理学中一个重要的分支，研究波的传播和性质。

在波动学中，波速以及波动方程是两个关键的知识点。

本文将对波速和波动方程进行总结介绍，以帮助读者更好地理解波动学的基本概念和原理。

一、波速波速是指波沿介质传播的速度。

根据波速的不同，波动可以分为机械波和电磁波两种类型。

1. 机械波的波速机械波是指需要介质传播的波动，例如水波和声波。

机械波的波速可以通过介质的性质来确定。

在同一介质中，波速与介质的密度以及弹性有关。

一般情况下，密度越大，波速越小，弹性越大，波速越大。

波速的确定可以通过实验测量，例如在绷紧的绳子上传播波动，可以通过测量绳子的质量和拉伸力来确定波速。

2. 电磁波的波速电磁波是指不需要介质传播的波动，例如光波和无线电波。

电磁波的波速与空气中的光速相等，约为3×10^8米/秒。

这是一个常数，与电磁波所处的媒质无关。

二、波动方程波动方程是用来描述波动传播的数学方程，可以根据波动的性质和场景的不同而有所差异。

常见的波动方程包括一维波动方程、二维波动方程和三维波动方程。

1. 一维波动方程一维波动方程描述沿着一个维度传播的波动。

一维波动方程可用以下形式表示：∂^2u/∂t^2 = v^2 ∂^2u/∂x^2其中，u表示波函数，t表示时间，x表示空间坐标，v表示波速。

这个方程说明了波函数在时间和空间上的二阶导数与波速的平方成正比。

2. 二维和三维波动方程二维和三维波动方程描述沿着两个或三个维度传播的波动。

以二维波动方程为例，可用以下形式表示：∂^2u/∂t^2 = v^2 (∂^2u/∂x^2 + ∂^2u/∂y^2)其中，u表示波函数，t表示时间，x和y表示空间坐标，v表示波速。

这个方程说明了波函数在时间和空间上的二阶导数与波速的平方成正比。

三、波动学中的应用波速和波动方程在波动学中具有广泛的应用。

以下是一些常见的应用领域：1. 声学声波是一种机械波，其传播速度取决于介质的性质。

人教版高中物理知识点解析机械波中的波动方程与波速人教版高中物理知识点解析——机械波中的波动方程与波速机械波是一种通过物质粒子之间的振动传递能量的波动现象。

在机械波的研究中，波动方程和波速是非常重要的概念。

本文将对人教版高中物理中关于机械波的波动方程和波速进行详细解析，帮助学生更好地理解和掌握这些知识点。

1. 机械波的波动方程机械波的波动方程描述了波的传播过程中粒子的振动状态。

在一维情况下，机械波的波动方程可以表示为：y(x, t) = A*sin(kx - ωt + φ)其中，y表示波的振幅；x表示波传播的位置；t表示时间；A表示振幅的最大值；k表示波数，它与波长λ之间的关系为k = 2π/λ；ω表示角频率，它与周期T之间的关系为ω = 2π/T；φ表示相位差。

通过波动方程，我们可以描述出不同位置和不同时刻波的振动状态。

波动方程中的k和ω都与波的性质相关，它们可以通过波的频率f和周期T来计算，其中 f = 1/T。

2. 机械波的波速机械波的波速是指波沿着介质传播的速度。

在弹性介质中，波速的大小与介质的性质有关。

一维机械波的波速v可以通过介质的弹性模量E和密度ρ来计算，公式如下：v = √(E/ρ)其中，E表示介质的弹性模量，单位为帕斯卡(Pa)；ρ表示介质的密度，单位为千克/立方米(kg/m³)。

三. 波动方程与波速的应用波动方程和波速是研究机械波传播和振动性质的重要工具。

它们在各个领域中都有广泛的应用。

首先，波动方程和波速可以用于解释声波的传播和声学现象。

声波是一种机械波，通过媒质传播而产生的压力波动。

通过对波动方程和波速的理解，我们可以解释声波的特性，如音量大小、音调高低等。

其次，波动方程和波速也可以用于解释光的传播和光学现象。

光是一种电磁波，通过介质或真空传播而产生的辐射。

光的传播速度是万亿倍的光速，它的波动方程和波速可以帮助我们理解光的折射、反射等现象。

此外，波动方程和波速还可以应用于地震波、海洋波、地下水波等自然现象的研究。