当前位置：文档之家 › 第五章 相平衡

第五章 相平衡

  • 格式：pdf
  • 大小：239.77 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

第五章 相平衡

第五章 相平衡

衡时的p－x相图如右图
g
A
xB
B
三、二组分气－液平衡系统
例题二：在p=101.3 kPa，85℃时，由甲苯(A)及苯(B)组成的 二组分液态混合物即达到沸腾。该液态混合物可视为理想液 态混合物。试计算该理想液态混合物在101.3 kPa及85℃沸腾 时的液相组成及气相组成。已知85℃时纯甲苯和纯苯的饱和 蒸气压分别为46.00 kPa和116.9 kPa。
b、具有最低会溶温度的系统 如H2O－(C2H5)3N系统 TB＝291K
c、具有两种会溶温度的系统 如H2O－(C2H5)3N系统 曲线内为两相共存 曲线外是互溶单相区
d、不具有两种会溶温度的系统 如H2O－乙醚系统
T/K
291
H2O x
481
T/K
(C2H5)3N
333
H2O x
烟碱
五、二组分液－固平衡系统
pA*
p pA pB pA* xA pB* xB
pA* (1 xB) pB* xB
pB* pA* xB pA*
A
xB
B
压力与液相组成图（T一定）
设A在气相中的摩尔分数为yA，B为yB，则有
yA
pA p
pA* xA p
yB
pB p
pB* xB p
yA pA* xA yB pB* xB
继续降低压力至D，气液达到平衡
此时，液相组成为C点
p T一定 a
气相组成为E点
C点和E点称为相点 CE称为联结线
继续降低压力至F
pA*
CN
D
F
pB*
EM
此时，液相已经全部蒸发
气相组成为F点 继续降低压力
气相的简单状态变化

第05章 相平衡

第05章 相平衡

第五章相平衡§5.1 引言相平衡是热力学在化学领域中的重要应用之一。

化工中很多分离提纯过程，例如精馏、吸收、结晶、萃取等，都涉及到物质在不同相中的分配，它们主要利用物质的挥发性或溶解度等方面的差异，以达到分离提纯的目的，相平衡亦可为此提供理论依据。

因此研究相平衡有着重要现实意义。

一、相（phase）体系内部物理和化学性质完全均匀的部分称为相。

相与相之间在指定条件下有明显的界面。

（1）气体，不论有多少种气体混合，只有一个气相。

（2）液体，按其互溶程度可以组成一相、两相或三相共存。

（3）固体，一般有一种固体便有一个相。

两种固体粉末无论混合得多么均匀，仍是两个相（固体溶液除外，它是单相）。

体系中相的总数用Φ表示。

二、相变物质从一个相流动到另一个相的过程，称为相变化，简称相变。

相变包括气化（boil）、冷凝（condensation）、熔化（melt）、凝固（freeze）、升华（sublimation）、凝华以及晶型转化等。

三、相图（phase diagram）将多相体系的状态随组成、温度、压力等强度性质的改变而发生的过程用图形表示，称为相图。

根据组成相的物态不同分为气-液相图、液-液相图和液-固相图。

根据用途不同可将相图分为温度-蒸汽压图（T－p图，P314 图5.1）、蒸汽压－组成图（p－x图，P318 图5.3）:恒定温度，研究P-x，y之间的关系。

称为压力组成图。

温度－组成图（T －x 图，P321 图5.5）:在恒定压力下表示二组分系统气-液平衡时温度与组成关系的相图。

研究T-x ，y 之间的关系。

和温度－蒸汽压－组成图（T －p －x 图，P322 图5.6），T-x-y ,x-y ,p-x-y 相图等。

四、自由度（degrees of freedom ）确定平衡体系的状态所必须的压力、温度和浓度等独立强度性质的数目称为自由度，用字母f 表示。

如果已指定某个强度性质，除该性质以外的其它强度性质数称为条件自由度，用*f 表示。

第五章 相平衡

第五章 相平衡

b.同一相内物质间有浓度限制条件R′
5.3 相律
相律
例如：合成氨时系统内有N2,H2,NH3 N2+3H2=2NH3
Kp p p p
2 NH 3 3 N2 H 2
C= S-R C =S-R-R´ 5.3 相律
相律
C = S - R - R'
注意： (1)R---表示独立的化学平衡数。有时系统中可以 存在很多化学平衡，但是独立的并不多。
5.3 相律
相律
自由度(degree of freedom) 系统内独立可变因素的数目称为自由度，用字母f 表示。独立可变因素包括压力、温度和浓度等。
独立可变因素是指在一定范围内这些可变因素变 化时，不会引起相的改变，既不会使原有相消失， 也不会增加新的相。
5.3 相律
相律
相律(phase rule)
Φmin=1
fmin=0
(3)可求系统中最多相数Φ
max
5.3 相律
相律
例题(P336，习题4)：已知Na2CO3(s)和 H2O(l)可以生成三种水合物： Na2CO3· H2O(s)， Na2CO3· 7H2O(s)和 Na2CO3· 10H2O(s)，试求： (1) 在大气压力下，与Na2CO3水溶液和冰 平衡共存的水合盐的最大值； (2) 在298K时，与水蒸气平衡共存的水合 盐的最大值。
单组分系统的两相平衡
解：
p2 vap H m 1 1 (1) ln p1 R T1 T2 p2 34170J m ol1 1 1 ln 1 1 10.02kPa 8.314J m ol K 293K 303K p2 15.91kPa
5.1 引言

化工热力学 第五章 相平衡

化工热力学 第五章 相平衡

A）汽相为理想气体混合物，液相为理想溶液。 B）汽相和液相都是理想溶液。 C）汽相是理想气体混合物，而液相是非理想溶液。 D）两相都是非理想溶液。 5.2.1、相平衡的处理方法 状态方程法：用状态方程来解决相平衡中的逸度系数
ˆ iv yi P li xi P ˆ
活度系数法：液相的逸度用活度系数来计算
s s i i
5.3.2.2） 泡点温度和组成的计算（BUBLT）
已知：平衡压力P，液相组成xi，求 平衡温度T，汽相组成 yi 假设T，确定Pis 计算yi 否
y
i
1
是
园整
5.3.2.3 露点压力和组成计算（DEWP）
已知 平衡温度T，汽相组成yi ， 求平衡压力 P，液相组成xi 假设 P 计算Pis及xi
第5章
相 平 衡
在化工生产中，原料由于含有各种杂质，需要提纯进入反 应器；反应又常常是不完全的并伴有副产物，因而产物也是不 纯的，也需要进一步处理，才能得到产品。所有这些都离不开 分离操作，典型的分离操作有精馏（VLE）、吸收（GLE）、 萃取（LLE）、结晶（SLE）等，他们的投资常达整个工厂投 资的一半以上，对有些行业如石油和煤焦油加工等，甚至达到 80%--90%，这些分离都需要相平衡数据。 5.1 相平衡基础 5.1.1、相平衡的判据 何谓相平衡：
例：乙醇（1）----苯（2）溶液，含乙醇80%（mol%），求该溶液在 750mmHg时，的沸点及饱和蒸汽组成。已知乙醇---苯系统有一恒沸 混合物，此混合物含44.8%乙醇，在760mmHg时的沸点为68.24oC （忽略温度对活度系数的影响。 乙醇
苯
lg P1S 8.04494
1554 .3 222 .65 t

化工热力学第五章 相平衡 ppt课件

化工热力学第五章 相平衡 ppt课件

汽液平衡计算类型
计算类型 泡点压力计算
(bubble point pres.)
泡点温度计算 (bubble point temp.)
露点压力计算 (dew point pres.)
均已被确定，但描述系统的平衡状态无须使用全部的变量，只要由相律 求得的自由度数的变量即可。因此相平衡问题在数学上是完全可解的， 这也是气液相平衡计算的主要任务，并进而进行各相的其它热力学性质 计算。
【例5-1】 试确定下述系统到达相平衡时的自 由度
（1）水的三相点， （2）水－水蒸汽平衡， （3）水－水蒸汽－惰性气体， （4）乙醇－水汽液平衡， （5）戊醇－水汽液平衡（液相分层）。
由此可见，对于一个典型的化工生产车间，无论是原料（混 合物）的预处理、物料的反应，还是产物与副产物的分 离，都需要用平衡性质来确定分离方法及其设备的结构 尺寸。
5.1 相平衡基础 5.2互溶体系的汽液平衡计算通式 5.3汽液平衡 5.4 汽液平衡数据的热力学一致性检验 5.5平衡、稳定性与液液平衡 5.6 其他类型的相平衡
解：根据相律的表达式，分别计算各个特定相平衡条件下的 自由度
(1) 对于水的三相点体系 C＝1（水）
＝3（三相－汽、
液、固）
自由度: F ＝1－3＋2＝0 这说明水的三相点是一
个无变量平衡状态。
(2) 对于水－水蒸汽平衡体系 C＝1（水）
＝2（两相－汽、液）
则自由度为 F ＝1－2＋2＝1
fˆi L

fi
0
L i
xi
i 1,2,3,L N
5.2.1 状态方程法（EOS法）
yiˆiV xiˆiL i 1,2,3,L N
5.2.2 活度系数（ i 法）

物理化学 第五章 相平衡

物理化学 第五章 相平衡
第五章 相平衡
一、基本概念和公式 （一）几个基本概念 1. 相和相数 （1）相 (phase) 系统内部物理和化学性质完全均匀的部分称为相。 特点 相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。 （2）相数 (number of phase) 系统中相的总数称为相数，用 表示。 气体:
（三）二组分系统的相图及应用
(3) 同时具有最高、最低会溶温度 （4） 不具有会溶温度
（三）二组分系统的相图及应用
4. 不互溶双液系 (1) 特点 如果A，B 两种液体彼此互溶程度极小，以致可忽略 不计。则A与B共存时，各组分的蒸气压与单独存在时一 样，液面上的总蒸气压等于两纯组分饱和蒸气压之和。 * * 即： p pA pB 当两种液体共存时，不管其相对数量如何，其 总蒸气压恒大于任一组分的蒸气压，而沸点则恒低 于任一组分的沸点。 (2) 水蒸气蒸馏
CaF2 ( A)
0 .6
0 .8
1 .0 CaCl2 ( B)
（三）二组分系统的相图及应用
(3) 相合熔点 A和B形成的化合物有确定的熔点，完全熔化时不 分解，在熔点时液相和固相的组成相同，所以稳定化 合物的熔点称为相合熔点。 (4) 不相合熔点 因为C没有自己的熔点，将C加热，到O点温 度时分解成 CaF2 (s) 和组成为B的熔液，所以将O点 的温度称为转熔温度（peritectic temperature）也 叫异成分熔点或不相合熔点。
（四）三组分系统的相图及其应用
(d) 如果代表两个三个组分 系统的D点和E点，混合成新 系统的物系点O必定落在DE 连线上。哪个物系含量多， O点就靠近哪个物系点。 O点的位置可用 杠杆规则求算。
mD OD mE OE

第5章- 相平衡

第5章- 相平衡
(1) CO H2O CO2 H2
1 (2) CO O 2 CO 2 2 1 (3) H 2 O 2 H 2O 2
这三个反应中只有两个是独立的，所以 R=2
独立组分数：C＝ S – R – R′
浓度限制条件：R′ 例如，在真空容器中发生如下反应：
2NH3 (g) N2 (g) 3H2 (g)
第五章
相平衡
相数的确定
系统中相的总数称为相数，用 表示。
气体，不论有多少种气体混合，只有一个气相； 液体，按其互溶程度可以组成一相、两相或三相共存；
固体，一般有一种固体便有一个相。两种固体粉末无论混 合得多么均匀，仍是两个相（固溶体除外，它是单相）；
自由度
确定平衡系统的状态（既不产生新相也不消失
* nA (g) pA * nB (g) pB
2、 工业应用：水蒸气蒸馏
简单的低共熔二元相图
1.0Bi
a
A
0.4Cd 1.0Cd 0.2Cd 0.7Cd b c d e H A'
F
p
A
H 596
熔化物（单相）
546
C
F
T /K
C
B
413
D D' E
G
M
熔化物+Cd(s)
G E 413 Bi(s)+熔化物 D BBi
0.2
0.4
0.6
0.8
wCd
1 Cd
Cd-Bi二元相图的绘制
Cd-Bi二元相图的绘制
w(Cd) 0.2
的步冷曲线
b
T /K
f* 2
C
D
f * 1
1. 加热到b点,Bi-Cd全部熔化 Φ 1 f * 2 1 Φ 2 温度可以下降,组成也可变 2. 冷至C点,固体Bi开始析出 Φ 2 f * 2 1 Φ 1 温度可以下降 3.D点固体Bi、Cd同时析出

第五章相平衡

第五章相平衡

第五章相平衡（Phase equilibrium）相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用，也是化学热力学的主要研究对象。

相平衡研究对生产和科学研究具有重大的实际意义。

例如在化学研究和化学生产过程的分离操作中，经常会遇到各种相变化过程，如蒸发、冷凝、升华、溶解、结晶和萃取等，这些过程及到不同相之间的物质传递。

相平衡研究是选择分离方法、设计分离装置以及实现最佳操作的理论基础。

除了分离以外，相平衡及其基本理论还广泛应用于冶金、材料科学、地质矿物学、晶体生长等学科中，对这些部门的科研和生产有着重要的指导意义。

相平衡研究多相体系相变化规律，是热力学基本原理在化学领域中的重要应用。

“相律”是根据热力学原理推导出来的，以统一观点处理各种类型多相平衡的理论方法十分严谨明确。

它表明一个多相平衡体系的组分数、相数以及自由度之间的关系，可以帮助我们确定体系的平衡性质以及达平衡的必要条件。

然而，相律也有其局限性，它只能对多相平衡作定性描述。

可指明特定条件下平衡体系至多的相数以及为保持这些相数所必具的独立变量数。

但究竟是哪些相共存？哪些性质可作为独立变量以及它们之间的定量关系如何等问题，相律均无能为力。

这方面知识仍有待从实验中确定。

本章着重讨论各种相平衡体系所遵守的一个普遍规律----相律，以及各种基本类型的相图，具体分析体系的相平衡情况与温度、压力和组成等因素的关系，并举例说明其实际应用§5.1相律一、基本术语1、相：体系中物理性质和化学性质完全均匀的一部分称为相物质从一个相转移到另一个相的过程称为相变化过程，而相平衡状态就是相变化过程的极限，此时宏观上投有任何物质在相间传递。

此处“完全均匀”，是指体系中的物质在分子水平上的均匀混合的状态，此时即便是由多种物质构成的体系，但其物理性质和化学性质都达到了完全均匀的程度，用一般的仪器已分不出其界面了，形成一个均相体系。

多相体系中，相与相之间存在明显的界面，称为相界面。

物理化学第5章相平衡

物理化学第5章相平衡
（3） 保持组成不变，得 T-p 图 不常用。
（2） 保持压力不变，得 T-x 图 常用
这三个变量通常是T，p 和组成 x。所以要表示二组分系统状态图，需用三个坐标的立体图表示。
一. 合金体系 1、相图绘制—— 热分析法 §5.7 具有简单低共熔混合物的固液二组分系统 Cd-Bi二元相图
①对拉乌尔定律有较大正偏差：
在T-x图上就有最低点，这最低点称为最低恒沸点
最低恒沸混合物是混合物而不是化合物，它的组成在定压下有定值。
在标准压力下， 的最低恒沸点温度为351.28 K，含乙醇 95.57 。
改变压力，最低恒沸点的温度也改变，它的组成也随之改变。
属于此类的系统有：
5.8 有化合物生成的固液二组分系统
5.4 完全互溶的双液系统
5.2 单组分系统的克-克方程
5.9 三组分系统
5.7 具有简单低共熔混合物的固液二组分系统
5.1 相律
5.3 水的相图
第五章 相平衡
相平衡是热力学在化学领域中的重要应用之一 研究多相系统的平衡在化学、化工的科研和生产中有重要的意义，例如：溶解、蒸馏、重结晶、萃取、提纯及金相分析等方面都要用到相平衡的知识 相律（phase rule）；相图（phase diagram）
2、分析相图
区：图上有4个相区 （ 1） AEH线之上， 熔液(l)单相区 （2） ABE之内， Bi(s)+ l 两相区 （3） HEM之内， Cd(s)+ l 两相区 （4）BEM线以下， Bi(s)+Cd(s)两相区
线：有三条多相平衡曲线
（1)ACE线，Bi(s)+熔液 共存时的熔液组成线。
组成为F的气体冷到E
有组成为x1的液体出现

第五章 相平衡

第五章 相平衡

二元凝聚系统相图表示法：T－x图
一、二元凝聚系统相图的基本类型
1.具有一个低共熔点的简单二元系统相图
特点：两组分在液态时完全互溶，形成单相溶液； 固态时完全不互溶，二组分各自从液相中分别结 晶，组分间无化学作用，不生成新化合物。
⑴
相
图
分
析
G
H
相区：
aEb : 高温熔体的单相区 (液相区)
bEH : L B 两相平衡共存区
熔体(1600℃) 熔体 (1670℃)
α－石英
870℃
1470℃
α－鳞石英
α－方石英
1723℃ 熔融石英
573℃
163℃
180～270℃
急
冷
β－石英
β－鳞石英
β－方石英
石英玻璃
117℃ γ－鳞石英 同 级 转 变(慢)
同
类 转
(快)
变
SiO2相图
1、在573℃以下的低温，SiO2的稳定晶型为－石英，加热至573℃转变为高温型 的－石英，这种转变较快；冷却时在同一温度下以同样的速度发生逆转变。如 果加热速度过快，则－石英过热而在1600℃时熔融。如果加热速度很慢，则在 870℃转变为－鳞石英。
以 忽略压强的影响，相律中的“2”应为“1”。
3. 必须正确判断独立组分数、独立化学反应式、相数以及限 制条件数，才能正确应用相律。
4. 自由度只取“0”以上的正值。如果出现负值，则说明体系可 能处于非平衡态。
第二节 单元系统相图
单元系统中， c = 1
f=c–p+2=3–p
pmin=1 pmax=3
2. 介稳态 即热力学非平衡态，经常出现于硅酸盐系统中。
如： α－石英 870α℃－鳞石英 1470℃α－方石英

物理化学-第五章 相平衡

物理化学-第五章 相平衡
•理想液态混合物的蒸气压介于两纯组分蒸气压之间
* p* p p A B
1. 压力-组成图—p-x（y）
(3) 气相线的制作 气相线：液相蒸气总压与蒸气组成关系线。
* pB pB xB yB p p
* * p p* ( p p A B A ) xB
* pB xB yB * * p A +( pB p* A ) xB
讨论组分数（C）与物 种数（S）的关系： 例1：液态水 S=1=C 例2：任意量的PCl5（g）、PCl3（g）和 Cl2（g）构成的平衡系统。 1指的是系统存在一个化学平衡方程式 S=3 C=3-1
PCl5（g）= PCl3（g）+ Cl2（g）
0 vB B
5.1 相律
3.独立组分数（number of independent component） 在平衡系统所处的条件下，能够确保各相组 成所需的最少独立物种数称为独立组分数，用 字母C表示。
在平衡系统所处的条件下，能够确保各相组 成所需的最少独立物种数称为独立组分数，用 字母C表示。
讨论组分数（C）与物 种数（S）的关系： 例1：液态水 S=1 = C
5.1
相律
3.独立组分数（number of independent component） 在平衡系统所处的条件下，能够确保各相组 成所需的最少独立物种数称为独立组分数，用 字母C表示。
5.1
自由度(f)= 系统总变量 -关联方程式数
热力学 平衡系统 S种物种
ф个相
假设S种物种都可 溶于ф个相中
2通常指T， P两个变量
1）系统总变量
1
2
3 … … S系统总变量= NhomakorabeaS-1）ф +2

物理化学 第5章 相平衡

物理化学 第5章 相平衡
水的相图是根据实验绘制的。 图上有： 1、三个单相区 在气、液、固三 个单相区内， φ=1, f =2，温 度和压力独立地有限度地变化不会 引起相的改变。 COA以上区域——单一液相区“水” BOA以下区域——单一气相区“水蒸气” BOC以左区域——单一固相区“冰”
2、三条两相平衡线, φ=2 , f =1 ，压力与温度只能 改变一个，指定了压力，则温度随之而定。 OA 是气-液两相平衡线，即水的蒸气压曲线。它 不能任意延长，终止于临界点。临界点 T 647 K , p 2.2107 Pa ，这时气-液界面消失。 高于临界温度，不能用加压的方法 使气体液化。 OB 是气-固两相平衡线，即 冰的升华曲线，理论上可延长 至0 K附近。 OC 是液-固两相平衡线，当C点延长至压力大于 2 108 Pa 时，相图变得复杂，有不同结构的冰生成。
OD 是AO的延长线，是过冷水和水蒸气的介稳平衡 线。因为在相同温度下，过冷水的蒸气压大于冰的蒸 气压，所以OD线在OB线之上。过冷水处于不稳定状 态，一旦有凝聚中心出现，就立即全部变成冰。 3、一个三相点 （triple point）， O点 是气-液-固三 相共存点， φ=3，f=0 三相 点的温度和压力皆由系统自 定。
dp S m dT Vm
由于 因此:
H m S m T dp H m dT T Vm
克拉佩龙方程
适用于纯物质的任意两相平衡
(1)对气-液两相平衡
dp H m dT T Vm
RT Vm Vg Vl Vg p
d ln p vap H m 2 dT RT
T T TF
(2)压力平衡条件：达到平衡时各相的压力相等
p p pF
（3） 相平衡条件： 任一物质B在各相中的化学 势相等，相变达到平衡

第五章 相平衡(10个)

第五章 相平衡(10个)

第五章 相平衡一、本章基本要求1．掌握相、组分数和自由度的意义。

2．了解相律的推导过程及其在相图中的应用。

3．了解克劳修斯-克拉珀龙方程式的推导，掌握其在单组分两相平衡系统中的应用。

4．掌握各种相图中点、线及面的意义。

5．根据相图能够画出步冷曲线，或由一系列步冷曲线绘制相图。

6．掌握杠杆规则在相图中的应用。

7．结合二组分气液平衡相图，了解蒸馏与精馏的原理。

8．对三组分系统，了解水盐系统的应用，相图在萃取过程中的应用及分配定律的应用。

二、 基本公式和内容提要（一）基本公式相律的普遍形式：f K n =-Φ+ 克拉珀龙方程：mm d ln d V T H T p ∆∆= 克劳修斯-克拉珀龙方程的各种形式：微分式： 2m vap d ln d RT H T p ∆= vap m H ∆与温度无关或温度变化范围较小vap m H ∆可视为常数， 定积分：vap m 211211ln ()H p p R T T ∆=- 不定积分式：vap mln H p C RT ∆=-+ 特鲁顿规则：K)J/(mol 88b mvap ⋅≈∆T H杠杆规则：以系统点为支点，与之对应的两个相点为作用点，有如下关系：1122()()n x x n x x -=-其中n 1 、n 2 分别表示平衡两相的摩尔数，x 、x 1、x 2分别表示系统的组成及其对应的平衡两相的组成。

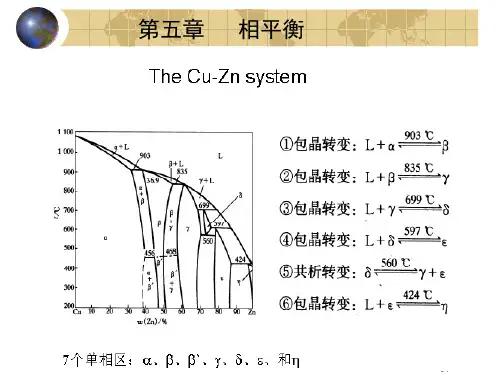
（二）内容提要1．单组分系统 单组分系统相律的一般表达式为：f =1－Φ+2=3－Φ图5-1 水的相图可见单组分系统最多只能有三相平衡共存，并且最多有两个独立变量，一般可选择温度和压力。

水的相图为单组分系统中的最简单相图之一。

图5-1中三条曲线将平面划分成固、液及气相三个区。

单相区内f =2。

AB 、AD 和AE 分别表示气液、气固和固液两相平衡线。

两相共存时f =1。

虚线AC表示应该结冰而未结冰的过冷水与水蒸气平衡共存。

A 点为三相点，这时f =0，水以气、液、固三相共存。

聊城大学《材料物理化学》第五章相平衡

聊城大学《材料物理化学》第五章相平衡
生物医学
相平衡在生物医学领域也有重要应用，如研究生物膜的相变、药 物释放等过程。
THANKS
感谢观看
相界面
不同相之间接触的界面， 界面两侧的物质传递过程 达到动态平衡。
相平衡条件
温度、压力和组成是影响 相平衡的主要因素，只有 在一定条件下各相才能达 到相对静止状态。
02
相平衡的热力学基础
热力学基本概念
热力学系统
一个与周围环境既没有物 质交换也没有能量交换的 系统。
热力学状态
系统在某一时刻所呈现的 宏观物理状态。
平衡，优化土壤污染修复工艺和效果。
06
相平衡的未来发展与挑战
相平衡理论的发展趋势
计算方法的改进
随着计算机技术的进步，相平衡理论计算方法将更加精确和高效，Байду номын сангаас能够模拟更复杂的系统和过程。
多尺度模型的发展
将不同尺度的模型结合起来，从微观到宏观多尺度描述相平衡现象， 提高预测的准确性和应用范围。
人工智能和机器学习的应用
在能源科学中的应用
1 2
燃料电池的相平衡研究
燃料电池在运行过程中，涉及多相反应和相平衡 问题，通过研究相平衡，优化燃料电池的性能和 稳定性。
核能利用中的相平衡问题
核反应过程中，涉及多相流动和相平衡问题，通 过研究相平衡，优化核反应过程的效率和安全性。
3
太阳能利用中的相平衡研究
太阳能电池在运行过程中，涉及光吸收和热转换 等多相过程，通过研究相平衡，提高太阳能的转 换效率和稳定性。
直接观测物质在相平衡状态下的 性质和行为，数据准确可靠；缺 点：实验条件要求较高，有时难
以实现。
间接法优点
实验操作简便，适用范围广；缺 点：推算结果受测量精度和模型
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章相平衡(Chapter 5 Phase Equilibrium)New Words and ExpressionsPhase diagrams 相图Number of phase 相数Number of substance 物种数Number of components 组分数Number of degree of freedom 自由度数Phase rule 相律Full miscible system 完全互溶体系Partially miscible system 部分互溶体系Full immiscible system 完全不互溶体系Conjugate Solutions 共轭溶液Lever rule 杠杆定律Cooling curve 步冷曲线Simple Eutectic 简单低共熔congruent melting 同成分熔融incongruent melting 异成分熔融基本公式和内容提要独立组分(Number of Components)：C＝S—R一R，相律(The Phase Rule)：f+Φ＝C+n相平衡是通过图形来描述多相平衡体系的宏观状态与温度、压力、组成的关系，具有重要的生产实践意义。

相律是多相平衡体系的一个重要规律，可由热力学基本原理推导而得，也可以从实践经验规律归纳而得，在相律指导下，本章讨论几种典型的相图(包括单组分、二组分体系)及其应用。

相变是一个连续的质的飞跃。

相平衡时物质在各相中的化学势相等，相变时某些物理性质有突变。

几个基本概念1．相(phase)：在体系内部宏观的物理性质和化学性质完全均匀的那一部称为相。

相与相之间有明显的界面，常温常压下，任何气体都能均匀混合。

体系内无论有多少种气体，都只有一个相。

多组分液体视其互溶度大小，可以是一相、两相或三相共存。

固体一般是一种固体一个相，但固态溶液是一个相。

2．组分(Number of Components ) 足以确定平衡体系中所有各相组成所需要的最少数目的独立物质数，称为独立组分数，简称组分数。

用符号c表示。

组分数C和体系中的物种数S之间的关系为：C二S一R一R，式中R为体系内各物种之间存在的独立的化学平衡的数目，R，为浓度限制条件数。

体系中的物种数-与考虑问题的方法有关，但体系中的组分数与考虑问题的方法无关。

3．自由度(Degrees of Freedom) 保持相平衡体系中相的数目不变时，体系独立可变的强度因素的数目(The number of degrees of freedom is the number of intensive variables, such as temperature, pressure, and concentration that can be independently varied without changing the number of phases.)。

相律是一个定性规律，它可以指示相平衡体系中有几个相，但不能指出是哪些相。

相律可以指导如何去识别由实验绘制的相图。

单组分体系相图二组分体系相图1．气液相图2．固液相图例 题例1. 指出下列平衡体系中的物种数、组分数、相数和自由度：(1)Ca(OH)2(s)与CaO(s)和H2O(g)呈平衡。

(2)I2在液态水和CCl4中分配达平衡(无固体存在)。

(3)将固体NH4HCO3(s)放入真空中恒温至400K，NH4HCO3(s)按下式分解达平衡：NH4HCO3(s) NH3(g) + H2O(g) +CO2(g)(4)Na＋、Cl－、K＋、NO3－、H2O(l)达平衡。

(5)含有CaCO3(s)、CaO(s)、CO2(s)的体系与CO2(g)和N2(g)的混合物达渗透平衡。

解：(1) Ca(OH)2(s)CaO(s) + H2O(g)S = 3, R = 1, R’ = 0, C = S－R－R’＝3－1－0＝2Φ = 3(二固，一气)f = C－Φ＋2＝2－3＋2＝1(2) S = 3, R = 0, R’ = 0, C = S－R－R’＝3－0－0＝3Φ = 2(二液)f = C－Φ＋2＝3－2＋2＝3(3) NH4HCO3(s) NH3(g) + H2O(g) +CO2(g)S = 4, R = 1, R’ = 2, C = S－R－R’＝4－1－2＝1Φ = 2f*= C－Φ＋1＝1－2＋1＝0(4) S = 5 [Na＋、Cl－、K＋、NO3－、H2O], R = 0溶液保持电中性，正负离子之间必定存在浓度关系:[Na＋]＋[K＋]＝[Cl－]＋[NO3－], 即R’ = 1C = S－R－R’＝5－0－1＝4Φ = 1f = C－Φ＋2＝4－1＋2＝5(5)CO2(g) CaO(s) CaCO3(s)CO2(g) N2(g)CaCO3(s)CaO(s) + CO2(g)S = 4, R = 1, R’ = 0, C = S－R－R’＝4－1－0＝3由于是渗透平衡，气体不能完全混合成一相，而是两侧各有一气相，所以系统的相数Φ = 4(二固、二气)f = C－Φ＋3＝3－4＋3＝2注意：在渗透平衡中，原来的相律f =C－Φ＋2不能用了，因为在该相律的推导过程中，假设了各相压力均相等。

相律公式中的2表示温度和压力。

在渗透平衡中二侧上方压力不等，p1≠p2, 原来相律应改为f = C－Φ＋3例2. 在熔点附近的温度范围内，TaBr5固体和液体的蒸气压方程分别为lg p＝14.696－5650/ T(固体) (1)lg p＝10.296－3265/ T(液体) (2)p的单位为Pa(a)求TaBr5的正常沸点及三相点的温度、压力。

(b)计算TaBr5在三相点的摩尔气化热、熔化热、升华热和摩尔气化熵、熔化熵和升华熵。

解：(a) 由式(2), 当p＝101325Pa时lg (101325)＝10.296－3265/ T bT b＝617.2K三相点时三个相有共同的平衡温度和蒸气压，所以式(1)与式(2)应相等，即：14.696－5650/ T3＝10.296－3265/ T3T3＝542.0K，代入式(1), 得：P3＝18.77kPa(b) 根据克劳修斯－克拉贝龙方程：ln p＝－ΔH m/ RT＋C对比 lg p＝14.696－5650/ T(固体) (1)lg p＝10.296－3265/ T(液体) (2)可得：Δsub H m＝5650×ln10×R＝5650×ln10×8.314＝108.2kJ·mol-1Δvap H m＝3265×ln10×R＝3265×ln10×8.314＝62.5kJ·mol-1摩尔熔化热Δfus H m＝Δsub H m－Δvap H m＝108.2－62.5＝45.7 kJ·mol-1摩尔升华熵Δsub S m＝Δsub H m/T3＝108.2×1000/54＝199.6 J·mol-1·K-1摩尔气化熵Δvap S m＝Δvap H m/T3＝62.5×1000/54＝115.4 J·mol-1·K-1摩尔熔化熵Δfus S m＝Δfus H m/T3＝45.7×1000/54＝84.3 J·mol-1·K-1例3. 指出下面a ，b 两图中所形成的化合物的经验式，并说明各相区是由哪些相组成的。

解：(a)图中，化合物C 的经验式为:AB 2各相区存在的相为：1区：A(s) +l 2区：C(s)＋l 3区：A(s)＋C(s)4区：C(s) +l 5区：B(s)＋l 6区：C(s)＋B(s)(b)图中，化合物C 1和C 2的经验式分别为：A 2B 和AB各相区存在的相为：1区：固溶体α 2区：α+l 3区：C s l 1()+4区：α+C s 1() 5区：C s l 2()+ 6区：C s C s 12()()+7区：C s l 2()+ 8区：B s l ()+ 9区：C s B s 2()()+例4. A 和B 能形成两种化合物A 2B 和AB 2，A 的熔点比B 低，A 2B 的相合熔点介于A 和B之间，AB 2的不相合熔点介于A 和A 2B 的熔点之间，请画出T -x 示意图，并注明各区相态。

解：由题意知A 的熔点比B 低，所以**A BT T <，A 2B 具有相合熔点为稳定化合物，在A 2B 的熔点两旁为凝固点下降曲线。

AB 2具有不相合熔点，即为不稳定化合物。

不稳定化合物在熔点处分解为一液相和另一固相。

题中没有给出液相组成，故该相图有两种可能。

不稳定化合物分解时液相组成为：(1)在AB 2与B 之间, (2)在A 2B 与AB 2之间，绘制图形如下：A A2B AB2 B A A2B AB2 B(a) (b)图(a) 图(b)相区相态相区相态1 L(熔化物) 1 L(熔化物)A(s)+L2 A(s)+L 23 L+A2B(s) 3 L+A2B(s)4 A2B(s)+L 4 A2B(s)+L5 AB2(s)+L 5 AB2(s)+LL+B(s)6 L+B(s) 67 A(s)+AB2(s) 7 A(s)+AB2(s)8 A2B(s)+AB2(s) 8 A2B(s)+AB2(s)9 AB2(s)+B(s) 9 AB2(s)+B(s)例5. 根据下列事实粗略地绘出HAc(醋酸)的相图，并指出图中各部分存在的相平衡。

(a)醋酸在蒸气压等于1213Pa时的熔点为289.8K。

(b)固态醋酸有两种晶型α、β，两者均较液态醋酸重，且α在低压下稳定。

(c)在2.03×108Pa、328.4K时，α、β和液相共存。

(d)α变成β的转换温度随压力的降低而下降。

(e)醋酸的正常沸点为391.2Κ。

解：1. 根据题意(a)，HAc的三相点为1213Pa、289.8K，见图中A点。

2. 根据题意(c)，α、β和液相共存的三相点为2.03×108Pa、328.4K，见图中B点。

3. 连AB线，此线为α固相与液相的固液平衡线，BC为β固相与液相的固液平衡线。

因为根据题意(b)，α在低压下稳定, 且两种晶型的密度均较液相大，即V m(s) < V m(l), 由克拉贝龙方程得d p/d T > 0，所以AB线和BC线的d p/d T为正值。

4. 过B点作一斜线BD，此线为α晶型与β晶型的两相平衡线。

从题意(d)可知，此线的d p/d T >0。

5. 根据题意(e)，F点为沸点(p∅, 391.2Κ)，连AF线为HAc的气液平衡线。