伍德里奇计量经济学第6章计算机习题详解STATA

第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★1计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。

2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。

根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。

(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。

②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。

③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。

考点二:经济数据★★★1经济数据的结构(见表1-3)2面板数据与混合横截面数据的比较(见表1-4)考点三:因果关系和其他条件不变★★1因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之计量分析虽然能发现变量之间的相关关系,但是如果想要解释因果关系,还要排除模型本身存在因果互逆的可能,否则很难让人信服。

2其他条件不变其他条件不变是指在经济分析中,保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

1.2课后习题详解一、习题1.假设让你指挥一项研究，以确定较小的班级规模是否会提高四年级学生的成绩。

(i)如果你能指挥你想做的任何实验，你想做些什么?请具体说明。

(ii)更现实地，假设你能搜集到某个州几千名四年级学生的观测数据。

你能得到它们四年级班级规模和四年级末的标准化考试分数。

你为什么预计班级规模与考试成绩成负相关关系?(iii)负相关关系一定意味着较小的班级规模会导致更好的成绩吗?请解释。

答:(i)假定能够随机的分配学生们去不同规模的班级，也就是说，在不考虑学生诸如能力和家庭背景等特征的前提下，每个学生被随机的分配到不同的班级。

第5章多元回归分析：OLS 的渐近性5.1复习笔记考点一：一致性★★★★1．定理5.1：OLS 的一致性（1）一致性的证明当假定MLR.1～MLR.4成立时，对所有的j＝0，1，2，…，k，OLS 估计量∧βj 是βj 的一致估计。

证明过程如下：将y i ＝β0＋β1x i1＋u i 代入∧β1的表达式中，便可以得到：()()()()11111111122111111ˆnni ii i i i n ni i i i xx y n x x u xxnxx ββ-==-==--==+--∑∑∑∑根据大数定律可知上式等式右边第二项中的分子和分母分别依概率收敛于总体值Cov （x 1，u）和Var（x 1）。

假定Var（x 1）≠0，因为Cov（x 1，u）＝0，利用概率极限的性质可得：plim ∧β1＝β1＋Cov（x 1，u）/Var（x 1）＝β1。

这就说明了OLS 估计量∧βj 具有一致性。

前面的论证表明，如果假定只有零相关，那么OLS 在简单回归情形中就是一致的。

在一般情形中也是这样，可以将这一点表述成一个假定。

即假定MLR.4′（零均值与零相关）：对所有的j＝1，2，…，k，都有E（u）＝0和Cov（x j1，u）＝0。

（2）MLR.4′与MLR.4的比较①MLR.4要求解释变量的任何函数都与u 无关，而MLR.4′仅要求每个x j 与u 无关（且u 在总体中均值为0）。

②在MLR.4假定下，有E（y｜x 1，x 2，…，x k ）＝β0＋β1x 1＋β2x 2＋…＋βk x k ，可以得到解释变量对y 的平均值或期望值的偏效应；而在假定MLR.4′下，β0＋β1x 1＋β2x 2＋…＋βk x k 不一定能够代表总体回归函数，存在x j 的某些非线性函数与误差项相关的可能性。

2．推导OLS 的不一致性当误差项和x 1，x 2，…，x k 中的任何一个相关时，通常会导致所有的OLS 估计量都失去一致性，即使样本量增加也不会改善。

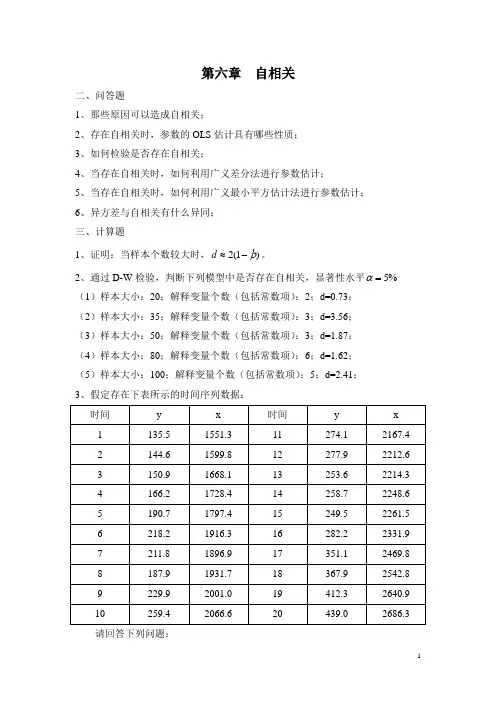
第六章自相关二、问答题1、那些原因可以造成自相关；2、存在自相关时，参数的OLS估计具有哪些性质；3、如何检验是否存在自相关；4、当存在自相关时，如何利用广义差分法进行参数估计；5、当存在自相关时，如何利用广义最小平方估计法进行参数估计；6、异方差与自相关有什么异同；三、计算题1、证明：当样本个数较大时，)d。

≈-1(2ρα2、通过D-W检验，判断下列模型中是否存在自相关，显著性水平%5=（1）样本大小：20；解释变量个数（包括常数项）：2；d=0.73；（2）样本大小：35；解释变量个数（包括常数项）：3；d=3.56；（3）样本大小：50；解释变量个数（包括常数项）：3；d=1.87；（4）样本大小：80；解释变量个数（包括常数项）：6；d=1.62；（5）样本大小：100；解释变量个数（包括常数项）：5；d=2.41；3、假定存在下表所示的时间序列数据：请回答下列问题：（1）利用表中数据估计模型：t t t x y εββ++=10；（2）利用D-W 检验是否存在自相关？如果存在请用d 值计算估计自相关系数ρ；（3）利用广义差分法重新估计模型：'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。

第三部分 参考答案二、问答题1、那些原因可以造成自相关？答：造成自相关的原因大致包括以下六个方面：（1）经济变量的变化具有一定的倾向性。

在实际的经济现象中，许多经济变量的现值依赖于他的前期值。

也就是说，许多经济时间序列都有一个明显的相依性特点，这种现象称作经济变量所具有的惯性。

（2）缺乏应有变量的设定偏差。

（3）不正确的函数形式的设定错误。

（4）蛛网现象和滞后效应。

（5）随机误差项的特征。

（6）数据拟合方法造成的影响。

2、存在自相关时，参数的OLS 估计具有哪些性质？答：当存在自相关，即I D ≠ΩΩ=,)(2σε时，OLS 估计的性质有：（1）βˆ是观察值Y 和X 的线性函数；（2）βˆ是β的无偏估计；（3）βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ；（4）βˆ不是β的最小方差线性无偏估计；（5）如果nX X n Ω'∞→lim存在，那么βˆ是β的一致估计；（6）2σ 不是2σ的无偏估计；（7）2σ不是2σ的一致估计。

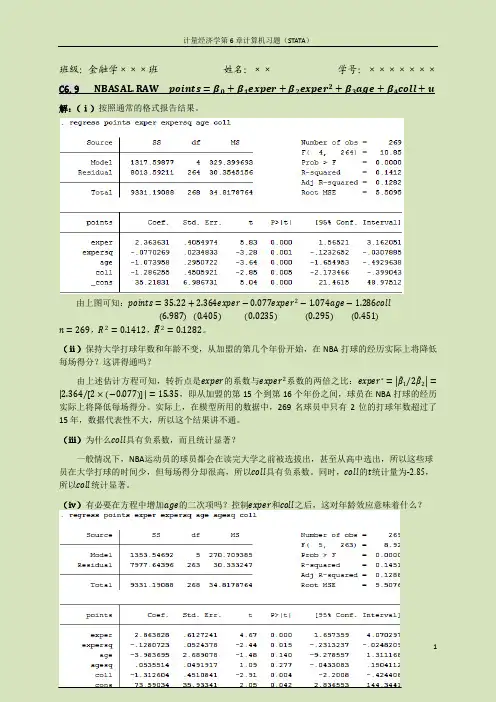
班级：金融学×××班姓名：××学号：×××××××C6.9 NBASAL.RAW points=β0+β1exper+β2exper2+β3age+β4coll+u 解：（ⅰ）按照通常的格式报告结果。

由上图可知：points=35.22+2.364exper−0.077exper2−1.074age−1.286coll6.9870.4050.02350.295 (0.451)n=269，R2=0.1412，R2=0.1282。

（ⅱ）保持大学打球年数和年龄不变，从加盟的第几个年份开始，在NBA打球的经历实际上将降低每场得分？这讲得通吗？由上述估计方程可知，转折点是exper的系数与exper2系数的两倍之比：exper∗= β12β2= 2.364[2×−0.077]=15.35，即从加盟的第15个到第16个年份之间，球员在NBA打球的经历实际上将降低每场得分。

实际上，在模型所用的数据中，269名球员中只有2位的打球年数超过了15年，数据代表性不大，所以这个结果讲不通。

（ⅲ）为什么coll具有负系数，而且统计显著？一般情况下，NBA运动员的球员都会在读完大学之前被选拔出，甚至从高中选出，所以这些球员在大学打球的时间少，但每场得分却很高，所以coll具有负系数。

同时，coll的t统计量为-2.85，所以coll统计显著。

（ⅳ）有必要在方程中增加age的二次项吗？控制exper和coll之后，这对年龄效应意味着什么？增加age的二次项后，原估计模型变成：points=73.59+2.864exper−0.128exper2−3.984age+0.054age2−1.313coll35.930.610.05 2.690.05 (0.45)n=269，R2=0.1451，R2=0.1288。

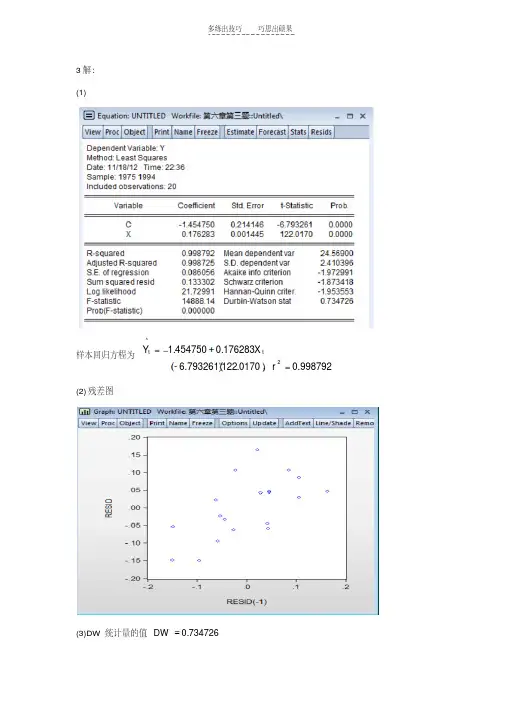
3解:(1)样本回归方程为998792.00170.1226.793261-176283.0454750.12^t r X Y t，(2)残差图(3)DW 统计量的值734726.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tX e e 000420.0060923.0638831.01因为84.3998223.7,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。

首先估计自相关系数^，得632637.02734726.0121^DW 对原变量做广义差分变换。

令1t 632637.0t t Y Y GDY ，1t 632637.0t t X X GDX 以年1994~1975,,t t GDX GDY 为样本再次回归，得tGDX GDY 173740.0391490.0t 回归方程拟合的效果仍然比较好,651914.1DW 对于给定05.0，查表得，。

43.1,24.1U L d d 因为75.243.11651914.1DW ,依据判别规则，误差项已消除自相关。

由391490.0^*0，得06568.1632637.01/391490.01/^^*0^0则原模型的广义最小二乘估计结果是t X Y 173470.006568.1^t 。

4解：（1）样本回归方程为tGDP Y 694454.0674.2816^t（2）残差图(3)3397.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tGDP e e 029062.07871.334985257.01因为84.309615.30,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。

首先估计自相关系数^，得83015.023397.0121^DW对原变量做广义差分变换。

令1t 83015.0t t Y Y GDY ，183015.0t t tGDGDP GDP GDGDP ，以年1994~1975,,t t GDGDP GDY 为样本再次回归，得。

伍德里奇计量经济学导论第6版笔记和课后习题详解伍德里奇所著的《计量经济学导论》（第6版）是我国许多高校采用的计量经济学优秀教材，也被部分高校指定为“经济类”专业考研考博参考书目。

作为该教材的学习辅导书，（1）整理名校笔记，浓缩内容精华。

每章的复习笔记以伍德里奇所著的《计量经济学导论》（第6版）为主，并结合国内外其他计量经济学经典教材对各章的重难点进行了整理，因此，（2）解析课后习题，提供详尽答案。

（3）补充相关要点，强化专业知识。

一般来说，国外英文教材的中译本不太符合中国学生的思维习惯，有些语言的表述不清或条理性不强而给学习带来了不便，因此，对每章复习笔记的一些重要知识点和一些习题的解答，我们在不违背原书原意的基础上结合其他相关经典教材进行了必要的整理和分析。

第1章计量经济学的性质与经济数据1.1复习笔记考点一：计量经济学★||计量经济学的含义计量经济学，又称经济计量学，是由经济理论、统计学和数学结合而成的一门经济学的分支学科，其研究内容是分析经济现象中客观存在的数量关系。

计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。

根据描述和模拟办法的不同，对模型进行分类，如表1-1所示。

表1-1模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系，计量经济学模型的研究内容是经济现象各因素之间的定量关系。

②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式，计量经济学模型的描述和模拟办法主要是随机性的数学形式。

③位置和作用不同数理经济模型可用于对研究对象的初步研究，计量经济学模型可用于对研究对象的深入研究。

拓展: 计量经济模型的检验(见表1・2)表1-2计量经济模型的检验考点二：经济数据★★★经济数据的结构(见表1-3)表1-3经济数据的结构面板数据与混合横截面数据的比较（见表1-4）表1-4面板数据与混合横截面数据的比较考点三：因果关系和其他条件不变★★因果关系因果关系是指一个变量的变动将引起另一个变量的变动，这是经济分析中的重要目标之一。

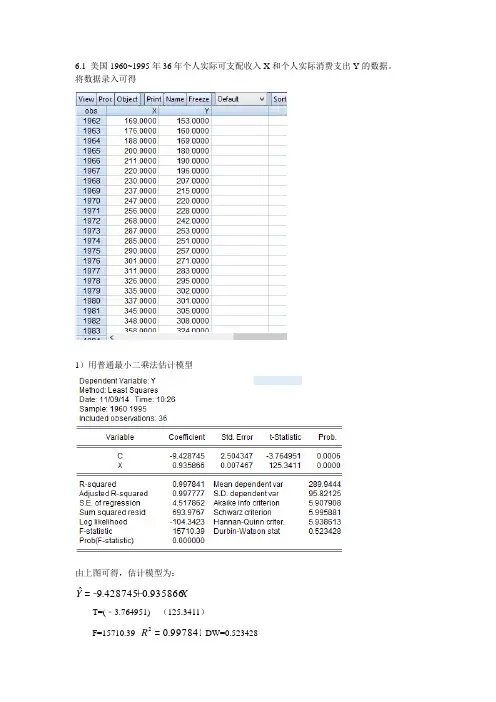
6.1 美国1960~1995年36年个人实际可支配收入X 和个人实际消费支出Y 的数据。

将数据录入可得1）用普通最小二乘法估计模型由上图可得，估计模型为：X Y 935866.0428745.9ˆ＋﹣=T=(﹣3.764951) （125.3411）F=15710.39 997841.02=R DW=0.5234282）检验自相关问题-------DW 检验根据DW=0.523428<411.1=L d ，可知此回归模型中误差项1μ，2μ......n μ间存在正相关关系。

3）用适当的方法消除模型中的问题----------广义差分法 首先得到t e 和1-t e 的回归结果。

如下图所示：由上图回归结果可知，回归方程为1721594.0ˆ﹣t t e e =故721594.0ρˆ=，对原模型进行广义差分，得到广义差分方差为 t t t t t X X Y Y υβ721594.01β1211）＋－（）＋－（－－－= 对广义差分方程进行回归，。

可得以下回归结果：可得回归方程为：••=t t X Y 948215.0858791.3ˆ＋﹣Se= (1.868548) (0.018453)t= (﹣2.065129) (51.38528)987656.02=R F=2640.445 DW=2.082177通过查表可知DW=1.255999>1.195，故可以判断不存在自相关关系。

画出t e 和1-t e 的散点图由图形可知，随机误差项之间不存在相关性。

6.3北京市连续19年城镇居民家庭人均收入与人均支出的数据1）为了消除价格变动因素对城镇居民人均收入和人均支出的影响，不宜直接采用现价的人均纯收入和现价的人均消费支出的数据，而需要采用经消费价格指数进行调整后的基期的可比价格计的人均纯收入和人居消费支出的数据作回归分析。

根据表中的数据，使用普通最小二乘法估计消费模型得：根据上图分析结果可知：21690488.093004.79ˆX X ＋= Se= (12.39919) (0.012877) t= (6.446390) (53.62068)994122.02=R 178.2875=F 574663.0=DW该方程的可决系数较高，回归系数显著，对于样本容量为19、一个解释变量的模型、1%的显著性水平，查DW 统计表可得，928.0=L d ，132.1=U d ，模型中DW<928.0=L d ，显然模型中存在自相关。

伍德⾥奇《计量经济学导论》（第6版）复习笔记和课后习题详解-多元回归分析：推断【圣才出品】第4章多元回归分析：推断4.1复习笔记考点⼀：OLS估计量的抽样分布★★★1．假定MLR.6（正态性）假定总体误差项u独⽴于所有解释变量，且服从均值为零和⽅差为σ2的正态分布，即：u～Normal（0，σ2）。

对于横截⾯回归中的应⽤来说，假定MLR.1～MLR.6被称为经典线性模型假定。

假定下对应的模型称为经典线性模型（CLM）。

2．⽤中⼼极限定理（CLT）在样本量较⼤时，u近似服从于正态分布。

正态分布的近似效果取决于u中包含多少因素以及因素分布的差异。

但是CLT的前提假定是所有不可观测的因素都以独⽴可加的⽅式影响Y。

当u是关于不可观测因素的⼀个复杂函数时，CLT论证可能并不适⽤。

3．OLS估计量的正态抽样分布定理4.1（正态抽样分布）：在CLM假定MLR.1～MLR.6下，以⾃变量的样本值为条件，有：∧βj～Normal（βj，Var（∧βj））。

将正态分布函数标准化可得：（∧βj－βj）/sd（∧βj）～Normal（0，1）。

注：∧β1，∧β2，…，∧βk的任何线性组合也都符合正态分布，且∧βj的任何⼀个⼦集也都具有⼀个联合正态分布。

考点⼆：单个总体参数检验：t检验★★★★1．总体回归函数总体模型的形式为：y＝β0＋β1x1＋…＋βk x k＋u。

假定该模型满⾜CLM假定，βj的OLS 量是⽆偏的。

2．定理4.2：标准化估计量的t分布在CLM假定MLR.1～MLR.6下，（∧βj－βj）/se（∧βj）～t n－k－1，其中，k＋1是总体模型中未知参数的个数（即k个斜率参数和截距β0）。

t统计量服从t分布⽽不是标准正态分布的原因是se（∧βj）中的常数σ已经被随机变量∧σ所取代。

t统计量的计算公式可写成标准正态随机变量（∧βj－βj）/sd（∧βj）与∧σ2/σ2的平⽅根之⽐，可以证明⼆者是独⽴的；⽽且（n－k－1）∧σ2/σ2～χ2n－k－1。

伍德里奇计量经济学导论课后题计算机操作下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!伍德里奇计量经济学导论课后题计算机操作简介伍德里奇计量经济学导论课程提供了对计量经济学基础概念和方法的全面介绍。

计量经济学导论第六版课后答案知识伍德里奇第一章：计量经济学介绍1. 为什么需要计量经济学？计量经济学的主要目标是提供一种科学的方法来解决经济问题。

经济学家需要使用数据来验证经济理论的有效性，并预测经济变量的发展趋势。

计量经济学提供了一种框架，使得经济学家能够使用数学和统计方法来分析经济问题。

2. 计量经济学的基本概念•因果推断：计量经济学的核心是通过观察数据来推断出变量之间的因果关系。

通过使用统计方法，我们可以分析出某个变量对另一个变量的影响。

•数据类型：计量经济学研究的数据可以是时间序列数据或截面数据。

时间序列数据是沿着时间轴观测到的数据，而截面数据是在某一时间点上观测到的数据。

•数据偏差：在计量经济学中，数据偏差是指由于样本选择问题、观测误差等原因导致数据与真实值之间的差异。

3. 计量经济学的方法计量经济学使用了许多统计和经济学方法来分析数据。

以下是一些常用的计量经济学方法：•最小二乘法（OLS）：在计量经济学中，最小二乘法是一种常用的回归方法。

它通过最小化观测值和预测值之间的平方差来估计未知参数。

•时间序列分析：时间序列分析是通过对时间序列数据进行模型化和预测来研究经济变量的变化趋势。

•面板数据分析：面板数据是同时包含时间序列和截面数据的数据集。

面板数据分析可以用于研究个体和时间的变化，以及它们之间的关系。

4. 计量经济学应用领域计量经济学广泛应用于经济学研究和实践中的各个领域。

以下是一些计量经济学的应用领域：•劳动经济学：计量经济学可以用来研究劳动力市场的供求关系、工资决定因素等问题。

•金融经济学：计量经济学可以用来研究证券价格、金融市场的波动等问题。

•产业组织经济学：计量经济学可以用来研究市场竞争、垄断力量等问题。

•发展经济学：计量经济学可以用来研究发展中国家的经济增长、贫困问题等。

第二章：统计学回顾1. 统计学基本概念•总体和样本：总体是指我们想要研究的全部个体或事物的集合，而样本是从总体中选取的一部分个体或事物。

第三篇高级专题第13章跨时横截面的混合：简单面板数据方法13.1复习笔记考点一：跨时独立横截面的混合★★★★★1．独立混合横截面数据的定义独立混合横截面数据是指在不同时点从一个大总体中随机抽样得到的随机样本。

这种数据的重要特征在于：都是由独立抽取的观测所构成的。

在保持其他条件不变时，该数据排除了不同观测误差项的相关性。

区别于单独的随机样本，当在不同时点上进行抽样时，样本的性质可能与时间相关，从而导致观测点不再是同分布的。

2．使用独立混合横截面的理由（见表13-1）表13-1使用独立混合横截面的理由3．对跨时结构性变化的邹至庄检验（1）用邹至庄检验来检验多元回归函数在两组数据之间是否存在差别（见表13-2）表13-2用邹至庄检验来检验多元回归函数在两组数据之间是否存在差别（2）对多个时期计算邹至庄检验统计量的办法①使用所有时期虚拟变量与一个（或几个、所有）解释变量的交互项，并检验这些交互项的联合显著性，一般总能检验斜率系数的恒定性。

②做一个容许不同时期有不同截距的混合回归来估计约束模型，得到SSR r。

然后，对T个时期都分别做一个回归，并得到相应的残差平方和，有：SSR ur＝SSR1＋SSR2＋…＋SSR T。

若有k个解释变量（不包括截距和时期虚拟变量）和T个时期，则需检验（T－1）k个约束。

而无约束模型中有T＋Tk个待估计参数。

所以，F检验的df为（T－1）k和n－T－Tk，其中n为总观测次数。

F统计量计算公式为：[（SSR r－SSR ur）/SSR ur][（n－T－Tk）/（Tk－k）]。

但该检验不能对异方差性保持稳健，为了得到异方差-稳健的检验，必须构造交互项并做一个混合回归。

4．利用混合横截面作政策分析（1）自然实验与真实实验当某些外生事件改变了个人、家庭、企业或城市运行的环境时，便产生了自然实验（准实验）。

一个自然实验总有一个不受政策变化影响的对照组和一个受政策变化影响的处理组。

自然实验中，政策发生后才能确定处理组和对照组。

伍德里奇计量经济学导论摘要：一、伍德里奇《计量经济学导论》概述二、伍德里奇对计量经济学的定义与应用三、伍德里奇《计量经济学导论》的主要内容四、伍德里奇《计量经济学导论》的课后习题及其答案五、伍德里奇《计量经济学导论》的参考价值正文：一、伍德里奇《计量经济学导论》概述伍德里奇所著的《计量经济学导论》是一本广泛应用于经济学领域的经典教材，受到了全球范围内众多学者和学生的欢迎。

本书旨在介绍计量经济学的基本概念、方法和应用，帮助读者理解和掌握计量经济学的基本理论和实证分析技巧。

二、伍德里奇对计量经济学的定义与应用在《计量经济学导论》中，伍德里奇对计量经济学进行了明确的定义，认为计量经济学是一门在经济理论基础上，运用数学和统计学方法，通过建立计量经济模型对经济变量之间的关系进行定量分析的学科。

计量经济学的应用范围广泛，包括政策分析、市场预测、数据分析等诸多领域。

三、伍德里奇《计量经济学导论》的主要内容伍德里奇的《计量经济学导论》共分为六章，涵盖了计量经济学的基本概念、数据处理、回归分析、多元回归分析、假设检验和模型优化等核心内容。

具体来说，书中内容包括：1.计量经济学的性质与经济数据：介绍了计量经济学的基本概念，经济数据的来源和特点，以及如何利用经济数据进行计量分析。

2.简单回归模型：阐述了简单回归模型的基本原理，包括线性回归、最小二乘法、参数估计等。

3.多元回归分析：介绍了多元回归分析的基本概念，包括多元线性回归、多元逻辑回归等，以及如何进行多元回归模型的估计和检验。

4.假设检验：介绍了计量经济学中的假设检验原理，包括t 检验、F 检验等。

5.模型优化：探讨了如何优化计量经济模型，提高模型的预测能力和解释能力。

6.横截面数据的回归分析：介绍了横截面数据的回归分析方法，包括生产函数估计、需求函数估计等。

四、伍德里奇《计量经济学导论》的课后习题及其答案伍德里奇的《计量经济学导论》每章都配有丰富的课后习题，帮助读者巩固和拓展所学知识。

计量经济学伍德里奇课后题stata的命令计量经济学是经济学中一种重要的研究方法，它将统计学的理论与经济学的实践相结合，旨在通过收集和分析数据来解决经济问题。

而伍德里奇是计量经济学中的重要书籍之一，该书的作者是英国经济学家大卫·伍德里奇，该书系统介绍了计量经济学的基本理论和实践方法，被广泛应用于经济学研究中。

在学习计量经济学的过程中，除了理论知识外，掌握数据处理和分析工具也是必不可少的。

而Stata就是计量经济学研究中非常常用的数据处理和分析软件之一，下面将介绍伍德里奇书中的一些课后题，并介绍如何使用Stata进行数据处理和分析。

课后题1在Stata中，运行以下命令将数据集mydata.dta导入到Stata中:import delimited "mydata.csv", clear该命令将csv格式的数据文件mydata.csv导入到Stata中，clear选项表示在导入数据之前，清除当前Stata工作区中的所有数据。

课后题2有一个包含两个变量y和x的数据集，其中y是连续的，x是二元的，值为0或1。

请使用Stata计算x=1时 y的平均值与x=0时y的平均值，并解释结果的意义。

运行以下命令，我们可以计算x=1时y的平均值：summarize y if x==1运行以下命令，我们可以计算x=0时y的平均值：summarize y if x==0这里的if表示只对满足条件的数据进行求和，其中x==1表示筛选x等于1的数据，x==0表示筛选x等于0的数据。

通过求和之后，我们初步得到y的平均值，进一步对结果进行解释和分析，可以了解x为二元变量时，y的平均值在x=0和x=1时的差异情况。

课后题3有一个包含3个变量y，x和z的数据集，请使用Stata分别计算y关于x的回归系数和y关于x和z的回归系数，并解释两者之间的差异。

对于y关于x的回归系数，我们可以使用以下命令：regress y x该命令运行回归模型regress，将x作为自变量，y作为因变量。

伍德里奇计量经济学导论计算机习题第六章第13题c_6.13clear,clc;% c6.13 by% 打开文字文件和数据文件importdata('meap00_01.des');data=xlsread('meap00_01');% 检验所用数据是否为非空Isnan=isnan(data(:,[3,5,8,9]));a=sum(Isnan')';b=find(a==0);data1=data(b,:);% 变量命名math4=data1(:,3);lunch=data1(:,5);lenroll=data1(:,8);lexppp=data1(:,9);% OLS估计result1=ols(math4,[ones(length(math4),1),lunch,lenroll,lexp pp]);vnames=char('math4','constant','lunch','lenroll','lexppp');prt(result1,vnames)% 回归结果% Ordinary Least-squares Estimates% Dependent Variable = math4% R-squared = 0.3729% Rbar-squared = 0.3718% sigma^2 = 234.1638% Durbin-Watson = 1.7006% Nobs, Nvars = 1692, 4%*************************************************************** % Variable Coefficient t-statistic t-probability% constant 91.932484 4.605444 0.000004% lunch -0.448743 -30.647631 0.000000% lenroll -5.399153 -5.741265 0.000000% lexppp 3.524742 1.680172 0.093109% 由回归结果中的p值发现lunch,lenroll是在5%的水平上显著的,而lexppp在5%水平上不显著,% 但在10%的显著水平上是显著的.% 求出回归的拟合值及其取值范围yhat=result1.yhat;std_yhat=std(yhat);mean_yhat=mean(yhat);yhat_qujian=[mean_yhat-2*std_yhat,mean_yhat+2*std_yhat] % yhat的取值范围是(49.1090 ,96.2665)% 求出math4的实际取值范围math4_qujian=[min(math4),max(math4)]% math4的实际取值范围是(0 ,100),可见拟合值的取值范围要比实际范围窄% 求出回归残差resid=result1.resid;max_resid=max(resid);row=find(resid==max_resid)school_code=data1(row,2)% 学校类型是school_code=1141,说明该学校的实际数学考试通过率要比估计的数学考试通% 过率高很多,也就这所学校的数学教学质量较高% 求取解释变量数据的平方项lenroll2=lenroll.^2;lexppp2=lexppp.^2;lunch2=lunch.^2;%在方程中加入所有解释变量的平方项进行回归result2=ols(math4,[ones(length(math4),1),lunch,lenroll,lexp pp,lunch2,lenroll2,lexppp2]);vnames=char('math4','constant','lunch','lenroll','lexppp','lunch2', 'lenroll2','lexppp2');prt(result2,vnames)% 检验联合显著性rsqr1=result1.rsqr;rsqr2=result2.rsqr;F=((rsqr2-rsqr1)/3)/((1-rsqr2)/(1692-6-1))p=1-fcdf(F,3,1685)% F =0.5180% p =0.6699% 所以这几个解释变量的平方项是联合不显著的,所以不应该把他们放到模型中% 求所用数据值除以其标准差lenroll_new=lenroll/std(lenroll);lunch_new=lunch/std(lunch);lexppp_new=lexppp/std(lexppp);math4_new=math4/std(math4);% 重新进行回归result3=ols(math4_new,[ones(length(math4_new),1),lunch_n ew,lenroll_new,lexppp_new]);vnames=char('math4_new','constant','lunch_new','lenroll_new','l exppp_new');prt(result3,vnames)% 回归结果% Ordinary Least-squares Estimates% Dependent Variable = math4_new% R-squared = 0.3729% Rbar-squared = 0.3718% sigma^2 = 0.6282% Durbin-Watson = 1.7006% Nobs, Nvars = 1692, 4%*************************************************************** % Variable Coefficient t-statistic t-probability% constant 4.761759 4.605444 0.000004% lunch_new -0.612853 -30.647631 0.000000% lenroll_new -0.114620 -5.741265 0.000000% lexppp_new 0.034743 1.680172 0.093109% 由结果lunch,lenroll和lexppp分别提高一倍,会使数学通过率分别变化0.613,0.115和% 0.035个标准差,所以lunch对数学考试通过率影响最大。