【创新方案】(浙江专版)2014届高考数学一轮复习 3.6 简单的三角恒等变换限时集训 理

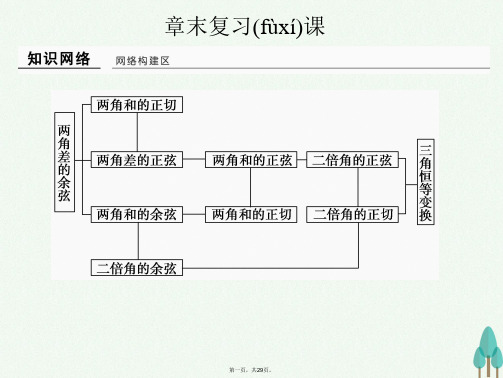
第二讲 三角变换与解三角形1．两角和与差的正弦、余弦、正切公式(1)sin(α±β)＝sin αcos β±cos αsin β. (2)cos(α±β)＝cos αcos β∓sin αsin β.(3)tan(α±β)＝tan α±tan β1∓tan αtan β.2．二倍角的正弦、余弦、正切公式(1)sin 2α＝2sin αcos α.(2)cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α.(3)tan 2α＝2tan α1－tan 2α. 3．三角恒等变换的基本思路(1)“化异为同”，“切化弦”，“1”的代换是三角恒等变换的常用技巧． “化异为同”是指“化异名为同名”，“化异次为同次”，“化异角为同角”． (2)角的变换是三角变换的核心，如β＝(α＋β)－α，2α＝(α＋β)＋(α－β)等． 4．正弦定理a sin A ＝b sin B ＝csin C＝2R (2R 为△ABC 外接圆的直径)． 变形：a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C . sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R.a ∶b ∶c ＝sin A ∶sin B ∶sin C .5．余弦定理a 2＝b 2＋c 2－2bc cos A ，b 2＝a 2＋c 2－2ac cos B ， c 2＝a 2＋b 2－2ab cos C .推论：cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac，cos C ＝a 2＋b 2－c 22ab.6．面积公式S △ABC ＝12bc sin A ＝12ac sin B ＝12ab sin C .7．三角形中的常用结论(1)三角形内角和定理：A ＋B ＋C ＝π. (2)A >B >C ⇔a >b >c ⇔sin A >sin B >sin C . (3)a ＝b cos C ＋c cos B .1．(2013·某某)已知α∈R ，sin α＋2cos α＝102，则tan 2α等于( ) A.43B.34C ．－34D ．－43 答案 C解析 ∵sin α＋2cos α＝102， ∴sin 2α＋4sin α·cos α＋4cos 2α＝52.用降幂公式化简得：4sin 2α＝－3cos 2α，∴tan 2α＝sin 2αcos 2α＝－34.故选C.2．(2013·某某)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若a sin B cos C ＋c sin B cosA ＝12b ，且a ＞b ，则B 的大小为( ) A.π6B.π3C.2π3D.5π6答案 A解析 由条件得a b sin B cos C ＋c b sin B cos A ＝12，由正弦定理，得sin A cos C ＋sin C cos A ＝12，∴sin(A ＋C )＝12，从而sin B ＝12，又a ＞b ，且B ∈(0，π)，因此B ＝π6.3．(2013·某某)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若b cos C ＋c cos B ＝a sinA ，则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定 答案 B解析 由b cos C ＋c cos B ＝a sin A ，得sin B cos C ＋sin C cos B ＝sin 2A ，即sin(B ＋C )＝sin 2A ，所以sin A ＝1，由0<A <π，得A ＝π2，所以△ABC 为直角三角形．4．(2012·某某)在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝32，则AC 等于( )A ．43B ．23C.3D.32答案 B解析 利用正弦定理解三角形．在△ABC 中，AC sin B ＝BCsin A ，∴AC ＝BC ·sin Bsin A ＝32×2232＝2 3.5．(2013·某某)设△ABC 的内角A ，B ，C 所对边的长分别为a ，b ，c .若b ＋c ＝2a,3sin A ＝5sin B ，则角C ＝________.答案 2π3解析 由已知条件和正弦定理得：3a ＝5b ，且b ＋c ＝2a ，则a ＝5b 3，c ＝2a －b ＝7b 3cos C ＝a 2＋b 2－c 22ab ＝－12，又0<C <π，因此角C ＝2π3.题型一 三角恒等变换例1 (1)若α∈⎝⎛⎭⎪⎫0，π2，且sin 2α＋cos 2α＝14，则tan α的值等于( )A.22B.33C.2D. 3 (2)已知α，β ∈⎝ ⎛⎭⎪⎫3π4，π，sin(α＋β)＝－35，sin ⎝ ⎛⎭⎪⎫β－π4＝1213，则cos ⎝ ⎛⎭⎪⎫α＋π4＝________.审题破题 (1)利用同角三角函数关系式先求sin α或cos α，再求tan α；(2)注意角之间的关系⎝ ⎛⎭⎪⎫α＋π4＝(α＋β)－⎝ ⎛⎭⎪⎫β－π4. 答案 (1)D (2)－5665解析 (1)∵α∈⎝⎛⎭⎪⎫0，π2，且sin 2α＋cos 2α＝14，∴sin 2α＋cos 2α－sin 2α＝14，∴cos 2α＝14，∴cos α＝12或－12(舍去)，∴α＝π3，∴tan α＝ 3.(2)因为α，β∈⎝ ⎛⎭⎪⎫3π4，π，所以α＋β＝⎝ ⎛⎭⎪⎫3π2，2π，所以cos(α＋β)>0.易得cos(α＋β)＝45.又π2<β－π4<3π4，所以cos ⎝⎛⎭⎪⎫β－π4<0， 易得cos ⎝⎛⎭⎪⎫β－π4＝－513.故cos ⎝⎛⎭⎪⎫α＋π4＝cos[(α＋β)－(β－π4)] ＝cos(α＋β)cos ⎝ ⎛⎭⎪⎫β－π4＋sin(α＋β)sin ⎝⎛⎭⎪⎫β－π4 ＝45×⎝ ⎛⎭⎪⎫－513＋⎝ ⎛⎭⎪⎫－35×1213＝－5665. 反思归纳 (1)公式应用技巧：①直接应用公式，包括公式的正用、逆用和变形用；②常用切化弦、异名化同名、异角化同角等．(2)化简常用技巧：①注意特殊角的三角函数与特殊值的互化；②注意利用角与角之间的隐含关系，如2α＝(α＋β)＋(α－β)，θ＝(θ－φ)＋φ等；③注意利用“1”的恒等变形，如tan 45°＝1，sin 2α＋cos 2α＝1等．变式训练1 (1)若0<α<π2，－π2<β<0，cos ⎝ ⎛⎭⎪⎫π4＋α＝13，cos ⎝ ⎛⎭⎪⎫π4－β2＝33，则cos ⎝ ⎛⎭⎪⎫α＋β2等于( )A.33B ．－33C.539D ．－69答案 C解析 ∵cos ⎝ ⎛⎭⎪⎫π4＋α＝13，0<α<π2，∴sin ⎝ ⎛⎭⎪⎫π4＋α＝223.又∵cos ⎝ ⎛⎭⎪⎫π4－β2＝33，－π2<β<0，∴sin ⎝ ⎛⎭⎪⎫π4－β2＝63，∴cos ⎝ ⎛⎭⎪⎫α＋β2＝cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫π4＋α－⎝ ⎛⎭⎪⎫π4－β2 ＝cos ⎝ ⎛⎭⎪⎫π4＋αcos ⎝ ⎛⎭⎪⎫π4－β2＋sin ⎝ ⎛⎭⎪⎫π4＋αsin ⎝ ⎛⎭⎪⎫π4－β2 ＝13×33＋223×63＝539. (2)已知sin α＝12＋cos α，且α∈⎝ ⎛⎭⎪⎫0，π2，则cos 2αsin ⎝ ⎛⎭⎪⎫α－π4的值为________．答案 －142解析 cos 2αsin ⎝⎛⎭⎪⎫α－π4＝cos 2α－sin 2α22sin α－cos α＝cos α＋sin αcos α－sin α22sin α－cos α＝－2(cos α＋sin α)．∵sin α＝12＋cos α，∴cos α－sin α＝－12，两边平方得1－2sin αcos α＝14，∴2sin αcos α＝34.∵α∈⎝ ⎛⎭⎪⎫0，π2，∴cos α＋sin α＝cos α＋sin α2＝1＋34＝72， ∴cos 2αsin ⎝⎛⎭⎪⎫α－π4＝－142. 题型二 解三角形例2 △ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a .(1)求b a；(2)若c 2＝b 2＋3a 2，求B .审题破题 (1)利用正弦定理，化去角B 的三角函数，再化简求值；(2)由条件结构特征，联想到余弦定理，求cos B 的值，进而求出角B . 解 (1)由正弦定理，得a sin B ＝b sin A ， 又a sin A sin B ＋b cos 2A ＝2a ，所以b sin 2A ＋b cos 2A ＝2a ，即b ＝2a .所以b a＝ 2. (2)由余弦定理和c 2＝b 2＋3a 2，又0°<B <180°，得cos B ＝1＋3a2c .由(1)知b 2＝2a 2，故c 2＝(2＋3)a 2.可得cos 2B ＝12.又cos B >0，故cos B ＝22，又0°<B <180°，所以B ＝45°. 反思归纳 关于解三角形问题，一般要用到三角形的内角和定理，正、余弦定理及有关三角形的性质，常见的三角变换方法和原则都适用，同时要注意“三统一”，即“统一角、统一函数、统一结构”，这是使问题获得解决的突破口．变式训练2 (2013·某某)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＋c ＝6，b＝2，cos B ＝79.(1)求a ，c 的值； (2)求sin(A －B )的值．解 (1)由余弦定理得：cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－42ac ＝79，即a 2＋c 2－4＝149ac .∴(a ＋c )2－2ac －4＝149ac ，∴ac ＝9.由⎩⎪⎨⎪⎧a ＋c ＝6，ac ＝9得a ＝c ＝3.(2)在△ABC 中，cos B ＝79，∴sin B ＝1－cos 2B ＝1－⎝ ⎛⎭⎪⎫792＝429. 由正弦定理得：asin A ＝bsin B，∴sin A ＝a sin B b ＝3×4292＝223.又A ＝C ，∴0<A <π2，∴cos A ＝1－sin 2A ＝13，∴sin (A －B )＝sin A cos B －cos A sin B ＝223×79－13×429＝10227.题型三 解三角形的实际应用例3 某城市有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC 、△ABD ，经测量AD ＝BD ＝14，BC ＝10，AC ＝16，∠C ＝∠D .(1)求AB 的长度；(2)若建造环境标志的费用与用地面积成正比，不考虑其他因素，小李、小王谁的设计使建造费用较低，请说明理由．审题破题 首先借助余弦定理列式，通过等量关系求出角C 的大小，进而求AB 的长度；然后借助正弦定理比较三角形的面积大小，并作出判断． 解 (1)在△ABC 中，由余弦定理得，AB 2＝AC 2＋BC 2－2AC ·BC cos C＝162＋102－2×16×10cos C ．①在△ABD 中，由余弦定理及∠C ＝∠D 整理得，AB 2＝AD 2＋BD 2－2AD ·BD cos D＝142＋142－2×142cos C ．② 由①②得：142＋142－2×142cos C ＝162＋102－2×16×10cos C ，整理可得cos C ＝12，又∠C 为三角形的内角，所以∠C ＝60°. 又∠C ＝∠D ，AD ＝BD ，所以△ABD 是等边三角形，即AB 的长度是14.(2)小李的设计符合要求．理由如下：S △ABD ＝12AD ·BD sin D ，S △ABC ＝12AC ·BC sin C ，因为AD ·BD >AC ·BC ，∠C ＝∠D ，所以S △ABD >S △ABC .又已知建造费用与用地面积成正比，故选择△ABC 建造环境标志费用较低． 即小李的设计使建造费用较低．反思归纳 应用解三角形知识解决实际问题需要下列四步：(1)分析题意，准确理解题意，分清已知与所求，尤其要理解题中的有关名词、术语，如坡度、仰角、俯角、视角、方位角等；(2)根据题意画出示意图，并将已知条件在图形中标出；(3)将所求问题归结到一个或几个三角形中，通过合理运用正、余弦定理等有关知识正确求解；(4)检验解出的结果是否具有实际意义，对结果进行取舍，得出正确答案．变式训练3 (2013·某某)如图，游客从某旅游景区的景点A 处下山至C 处有两种路径．一种是从A 沿直线步行到C ，另一种是先从A 沿索道乘缆车到B ，然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山，甲沿AC 匀速步行，速度为50 m/min.在甲出发2 min后，乙从A 乘缆车到B ，在B 处停留1 min 后，再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ，山路AC 长为1 260 m ，经测量cos A ＝1213，cos C ＝35.(1)求索道AB 的长；(2)问：乙出发多少分钟后，乙在缆车上与甲的距离最短？(3)为使两位游客在C 处互相等待的时间不超过3分钟，乙步行的速度应控制在什么X 围内？解 (1)在△ABC 中，因为cos A ＝1213，cos C ＝35，所以sin A ＝513，sin C ＝45.从而sin B ＝sin[π－(A ＋C )]＝sin(A ＋C ) ＝sin A cos C ＋cos A sin C＝513×35＋1213×45＝6365. 由正弦定理AB sin C ＝ACsin B ，得AB ＝AC sin B ×sin C ＝1 2606365×45＝1 040(m)．所以索道AB 的长为1 040 m.(2)假设乙出发t 分钟后，甲、乙两游客距离为d ，此时，甲行走了(100＋50t )m ，乙距离A 处130t m ， 所以由余弦定理得d 2＝(100＋50t )2＋(130t )2－2×130t ×(100＋50t )×1213＝200(37t 2－70t ＋50)，由于0≤t ≤1 040130，即0≤t ≤8，故当t ＝3537 min 时，甲、乙两游客距离最短．(3)由正弦定理BC sin A ＝ACsin B ，得BC ＝AC sin B ×sin A ＝1 2606365×513＝500(m)．乙从B 出发时，甲已走了50×(2＋8＋1)＝550(m)，还需走710 m 才能到达C .设乙步行的速度为v m/min ，由题意得－3≤500v －71050≤3，解得1 25043≤v ≤62514，所以为使两位游客在C 处互相等待的时间不超过 3 min ，乙步行的速度应控制在⎣⎢⎡⎦⎥⎤1 25043，62514(单位：m/min)X 围内．典例 (14分)已知向量a ＝(cos ωx ，sin ωx )，b ＝(cos ωx ，3cos ωx )，其中0<ω<2.函数f (x )＝a ·b －12，其图象的一条对称轴为x ＝π6.(1)求函数f (x )的表达式及单调递增区间；(2)在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，S 为其面积，若f ⎝ ⎛⎭⎪⎫A 2＝1，b ＝1，S △ABC＝3，求a 的值． 规X 解答解 (1)f (x )＝a ·b －12＝cos 2ωx ＋3sin ωx cos ωx －12＝1＋cos 2ωx 2＋32sin 2ωx －12＝sin ⎝⎛⎭⎪⎫2ωx ＋π6.[3分] 当x ＝π6时，sin ⎝ ⎛⎭⎪⎫ωπ3＋π6＝±1，即ωπ3＋π6＝k π＋π2，k ∈Z . ∵0<ω<2，∴ω＝1.[5分]∴f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π6. 令－π2＋2k π≤2x ＋π6≤π2＋2k π，k ∈Z ，∴k π－π3≤x ≤k π＋π6，k ∈Z ，∴函数f (x )的单调递增区间为[k π－π3，k π＋π6]，k ∈Z .[8分](2)f ⎝ ⎛⎭⎪⎫A 2＝sin ⎝⎛⎭⎪⎫A ＋π6＝1，在△ABC 中，0<A <π，π6<A ＋π6<76π，∴A ＋π6＝π2，A ＝π3.由S △ABC ＝12bc sin A ＝3，b ＝1，得c ＝4.[10分]由余弦定理得a 2＝42＋12－2×4×1×cos π3＝13，故a ＝13.[14分]评分细则 (1)f (x )没有化成sin ⎝⎛⎭⎪⎫2ωx ＋π6的得1分；(2)k ∈Z 没写的扣1分；(3)得出A ＝π3的给1分．阅卷老师提醒 (1)三角形和三角函数的结合是高考命题的热点，灵活考查分析、解决问题的能力．(2)此类问题的一般解法是先将三角函数化成y ＝A sin(ωx ＋φ)的形式，利用三角函数求值确定三角形的一个角，然后和正、余弦定理相结合解题． (3)解题中要充分注意在三角形中这个条件，重视角的X 围．1．已知cos π－2αsin α－π4＝－22，则sin α＋cos α等于( )A ．－72B.72C.12D ．－12答案 D解析 cos π－2αsin α－π4＝－cos 2αsin α－π4＝sin 2α－π2sin α－π4＝2cos(α－π4)＝2cos α＋2sin α＝－22，∴sin α＋cos α＝－12，故选D.2．(2012·某某)已知f (x )＝sin 2⎝ ⎛⎭⎪⎫x ＋π4，若a ＝f (lg 5)，b ＝f ⎝ ⎛⎭⎪⎫lg 15，则( ) A ．a ＋b ＝0 B ．a －b ＝0 C ．a ＋b ＝1 D ．a －b ＝1 答案 C解析 将函数整理，利用奇函数性质求解．由题意知f (x )＝sin 2⎝⎛⎭⎪⎫x ＋π4＝1－cos ⎝ ⎛⎭⎪⎫2x ＋π22＝1＋sin 2x 2，令g (x )＝12sin 2x ，则g (x )为奇函数，且f (x )＝g (x )＋12，a ＝f (lg 5)＝g (lg 5)＋12，b ＝f ⎝ ⎛⎭⎪⎫lg 15＝g ⎝ ⎛⎭⎪⎫lg 15＋12，则a ＋b ＝g (lg 5)＋g ⎝ ⎛⎭⎪⎫lg 15＋1＝g (lg 5)＋g (－lg 5)＋1＝1，故a ＋b ＝1. 3．(2013·某某)在△ABC 中，∠ABC ＝π4，AB ＝2，BC ＝3，则sin ∠BAC 等于( )A.1010B.105 C.31010 D.55答案 C解析 在△ABC 中，由余弦定理得AC 2＝BA 2＋BC 2－2BA ·BC cos∠ABC ＝(2)2＋32－2×2×3cos π4＝5.∴AC ＝5，由正弦定理BC sin ∠BAC ＝ACsin ∠ABC 得sin∠BAC ＝BC ·sin∠ABCAC ＝3×sin π45＝3×225＝31010.4．设α、β均为锐角，且cos(α＋β)＝sin(α－β)，则tan α的值为( )A ．2 B.3C ．1 D.33答案 C解析 由已知得cos αcos β－sin αsin β＝sin αcos β－cos αsin β，即cosα(cos β＋sin β)＝sin α(sin β＋cos β)，∵β为锐角，∴cos β＋sin β≠0，因此有cos α＝sin α， 从而tan α＝1.5．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若(a 2＋c 2－b 2)tan B ＝3ac ，则角B 的值为( )A.π6B.π3C.π6或5π6D.π3或2π3答案 D解析 由(a 2＋c 2－b 2)tan B ＝3ac ，得a 2＋c 2－b 22ac ＝32·cos B sin B ，即cos B ＝32·cos B sin B， ∴sin B ＝32.又∵0＜B ＜π，∴角B 为π3或2π3.故选D. 6．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c 且满足c sin A ＝a cos C ．当3sin A－cos ⎝⎛⎭⎪⎫B ＋π4取最大值时，A 的大小为( ) A.π3B.π4C.π6D.2π3答案 A解析 由正弦定理得sin C sin A ＝sin A cos C .因为0<A <π，所以sin A >0，从而sin C ＝cos C .又cos C ≠0，所以tan C ＝1，则C ＝π4，所以B ＝3π4－A . 于是3sin A －cos ⎝⎛⎭⎪⎫B ＋π4＝3sin A －cos(π－A ) ＝3sin A ＋cos A ＝2sin ⎝⎛⎭⎪⎫A ＋π6. ∵0<A <3π4，∴π6<A ＋π6<11π12，从而当A ＋π6＝π2， 即A ＝π3时，2sin ⎝⎛⎭⎪⎫A ＋π6取最大值2.故选A. 专题限时规X 训练一、选择题1．已知cos ⎝ ⎛⎭⎪⎫α－π6＋sin α＝435，则sin ⎝⎛⎭⎪⎫α＋7π6的值是( ) A ．－235 B.235C ．－45D.45答案 C解析 cos ⎝ ⎛⎭⎪⎫α－π6＋sin α＝435⇒32sin α＋32cos α＝435⇒sin ⎝⎛⎭⎪⎫α＋π6＝45， 所以sin ⎝ ⎛⎭⎪⎫α＋7π6＝－sin ⎝⎛⎭⎪⎫α＋π6＝－45. 2．(2013·某某改编)设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是( ) A.3B ．23C.32D.12答案 A 解析 ∵sin 2α＝－sin α，∴sin α(2cos α＋1)＝0，又α∈⎝ ⎛⎭⎪⎫π2，π，∴sin α≠0,2cos α＋1＝0即cos α＝－12，sin α＝32，tan α＝－3，∴tan 2α＝2tan α1－tan 2α＝－231－－32＝ 3.3．已知锐角△ABC 的面积为33，BC ＝4，CA ＝3，则角C 的大小为( )A ．75° B．60° C．45° D．30°答案 B解析 由题意知，12×4×3×sin C ＝33，∴sin C ＝32. 又0°<C <90°，∴C ＝60°.4．在△ABC 中，若0<tan A ·tan B <1，那么△ABC 一定是( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．形状不确定答案 B解析 由0<tan A ·tan B <1，可知tan A >0，tan B >0，即A ，B 为锐角，tan(A ＋B )＝tan A ＋tan B 1－tan A tan B>0，即tan(π－C )＝－tan C >0，所以tan C <0，所以C 为钝角，所以△ABC 为钝角三角形，选B.5．已知tan ⎝ ⎛⎭⎪⎫α＋π4＝12，且－π2<α<0，则2sin 2α＋sin 2αcos ⎝⎛⎭⎪⎫α－π4等于( ) A ．－255B ．－3510C ．－31010D ．255答案 A解析 由tan ⎝⎛⎭⎪⎫α＋π4＝tan α＋11－tan α＝12， 得tan α＝－13. 又－π2<α<0，可得sin α＝－1010. 故2sin 2α＋sin 2αcos ⎝ ⎛⎭⎪⎫α－π4＝2sin αsin α＋cos α22sin α＋cos α ＝22sin α＝－255. 6．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝2A ，cos A ＝34，b ＝5，则 △ABC 的面积为( )A.1574B.1572C.574D.572答案 A解析 cos A ＝34，cos C ＝2cos 2A －1＝18， sin C ＝378，tan C ＝37， 如图，设AD ＝3x ，AB ＝4x ，CD ＝5－3x ，BD ＝7x .在Rt△DBC 中，tan C ＝BD CD ＝7x 5－3x＝37， 解之得：BD ＝7x ＝327，S △ABC ＝12BD ·AC ＝1574. 7．函数f (x )＝sin 2x －4sin 3x cos x (x ∈R )的最小正周期为( ) A.π8B.π4C.π2D ．π 答案 C解析 f (x )＝sin 2x －2sin 2x sin 2x＝sin 2x (1－2sin 2x )＝sin 2x cos 2x ＝12sin 4x ， 所以函数的周期为T ＝2πω＝2π4＝π2，选C. 8．在△ABC 中，AC ＝7，BC ＝2，B ＝60°，则BC 边上的高等于( )A.32B.332C.3＋62D.3＋394 答案 B解析 设AB ＝a ，则由AC 2＝AB 2＋BC 2－2AB ·BC cos B 知7＝a 2＋4－2a ，即a 2－2a －3＝0，∴a ＝3(负值舍去)．∴BC 边上的高为AB ·sin B ＝3×32＝332. 二、填空题9．在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若b ＝2，B ＝π3且sin 2A ＋sin(A －C )＝sin B ，则△ABC 的面积为________．答案 3 解析 ∵sin 2A ＝sin B －sin(A －C )，∴2sin A cos A ＝sin(A ＋C )－sin(A －C )，∴2sin A cos A ＝2cos A sin C .∵△ABC 是锐角三角形，∴cos A ≠0，∴sin A ＝sin C ，即A ＝C ＝B ＝π3， ∴S △ABC ＝12×2×2×32＝ 3. 10．设π3<α<3π4，sin ⎝⎛⎭⎪⎫α－π4＝35，则sin α－cos 2α＋1tan α的值为________． 答案 14＋5250解析 方法一 由π3<α<3π4， 得π12<α－π4<π2，又sin ⎝⎛⎭⎪⎫α－π4＝35， 所以cos ⎝⎛⎭⎪⎫α－π4＝45. 所以cos α＝cos[(α－π4)＋π4] ＝cos ⎝ ⎛⎭⎪⎫α－π4cos π4－sin ⎝⎛⎭⎪⎫α－π4sin π4＝210， 所以sin α＝7210. 故原式＝sin α＋2sin 2αsin αcos α＝cos α(1＋2sin α)＝14＋5250. 方法二 由sin ⎝⎛⎭⎪⎫α－π4＝35，得sin α－cos α＝325， 两边平方，得1－2sin αcos α＝1825， 即2sin αcos α＝725>0. 由于π3<α<3π4，故π3<α<π2. 因为(sin α＋cos α)2＝1＋2sin αcos α＝3225， 故sin α＋cos α＝425， 解得sin α＝7210，cos α＝210. 故原式＝sin α＋2sin 2αsin αcos α＝cos α(1＋2sin α)＝14＋5250. 11．(2012·某某)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .若(a ＋b －c )(a ＋b ＋c )＝ab ，则角C ＝________.答案 2π3解析 应用余弦定理求角．由(a ＋b －c )(a ＋b ＋c )＝ab ，得a 2＋b 2－c 2＝－ab ，则cos C ＝a 2＋b 2－c 22ab ＝－12. 又因为角C 为△ABC 的内角，所以C ＝2π3. 12．给出下列四个命题：①f (x )＝sin ⎝⎛⎭⎪⎫2x －π4的对称轴为x ＝k π2＋3π8，k ∈Z ； ②函数f (x )＝sin x ＋3cos x 的最大值为2；③函数f (x )＝sin x cos x －1的周期为2π；④函数f (x )＝sin ⎝⎛⎭⎪⎫x ＋π4在⎣⎢⎡⎦⎥⎤－π2，π2上是增函数． 其中正确命题的个数是________．答案 2解析 ①由2x －π4＝k π＋π2，k ∈Z ， 得x ＝k π2＋3π8(k ∈Z )， 即f (x )＝sin ⎝⎛⎭⎪⎫2x －π4的对称轴为x ＝k π2＋3π8，k ∈Z ，正确； ②由f (x )＝sin x ＋3cos x ＝2sin ⎝⎛⎭⎪⎫x ＋π3知，函数的最大值为2，正确； ③f (x )＝sin x cos x －1＝12sin 2x －1，函数的周期为π，故③错误； ④函数f (x )＝sin ⎝⎛⎭⎪⎫x ＋π4的图象是由f (x )＝sin x 的图象向左平移π4个单位得到的，故④错误．三、解答题13．(2013·某某)已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎪⎫ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的单调性． 解 (1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎪⎫ωx ＋π4 ＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin 2ωx ＋cos 2ωx )＋ 2＝2sin ⎝⎛⎭⎪⎫2ωx ＋π4＋ 2. 因为f (x )的最小正周期为π，且ω>0.从而有2π2ω＝π，故ω＝1. (2)由(1)知，f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4＋ 2.若0≤x ≤π2，则π4≤2x ＋π4≤5π4. 当π4≤2x ＋π4≤π2， 即0≤x ≤π8时，f (x )单调递增； 当π2≤2x ＋π4≤5π4， 即π8≤x ≤π2时，f (x )单调递减． 综上可知，f (x )在区间⎣⎢⎡⎦⎥⎤0，π8上单调递增， 在区间⎣⎢⎡⎦⎥⎤π8，π2上单调递减． 14．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，a 2＋b 2＝4ab cos C ，且c 2＝3ab .(1)求角C 的大小；(2)设函数f (x )＝sin(ωx －C )－cos ωx (ω>0)，且直线y ＝3与函数y ＝f (x )图象相邻两交点间的距离为π，求f (A )的取值X 围．解 (1)由余弦定理知a 2＋b 2－c 2＝2ab cos C ，∵a 2＋b 2＝4ab cos C ，c 2＝3ab ，∴4ab cos C －3ab ＝2ab cos C ，cos C ＝32. 又∵0<C <π，∴C ＝π6. (2)f (x )＝sin ⎝⎛⎭⎪⎫ωx －π6－cos ωx ＝32sin ωx －32cos ωx ＝3sin(ωx －π3)． 由已知2πω＝π⇒ω＝2，则f (A )＝3sin(2A －π3)， ∵C ＝π6，∴0<A <5π6，－π3<2A －π3<4π3. ∴根据正弦函数图象知－32<sin ⎝⎛⎭⎪⎫2A －π3≤1， ∴－32<f (A )≤ 3.。

第六节 简单的三角恒等变换[备考方向要明了][归纳²知识整合]1．半角公式 (1)用cos α表示sin 2α2，cos 2α2，tan 2α2. sin2α2＝1－cos α2；cos 2α2＝1＋cos α2；tan 2α2＝1－cos α1＋cos α. (2)用cos α表示sin α2，cos α2，tan α2.sin α2＝±1－cos α2； cos α2＝±1＋cos α2； tan α2＝±1－cos α1＋cos α.(3)用sin α，cos α表示tan α2.tan α2＝sin α1＋cos α＝1－cos αsin α.[探究] 如何用tan α表示sin 2α与cos 2α？ 提示：sin 2α＝2sin αcos α＝2sin αcos αsin 2 α＋cos 2α＝2tan αtan 2α＋1；cos 2α＝cos 2α－sin 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α. 2．形如a sin x ＋b cos x 的化简a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)，其中tan φ＝ba.[自测²牛刀小试]1．(教材习题改编)化简2＋cos 2－sin 21的结果是( ) A ．－cos 1 B ．cos 1 C.3cos 1 D ．－3cos 1解析：选C2＋cos 2－sin 21＝1＋cos 2＋1－sin 21＝2cos 21＋cos 21＝3cos 1.2.sin 235°－12sin 20°的值为( )A.12 B ．－12C ．－1D ．1解析：选B sin 235°－12sin 20°＝2sin 235°－12sin 20°＝－cos 70°2sin 20°＝－sin 20°2sin 20°＝－12.3．若f (x )＝2tan x －2sin 2x2－1sin x 2cos x 2，则f ⎝ ⎛⎭⎪⎫π12的值为( ) A ．－43 3B ．8C ．4 3D ．－4 3解析：选B ∵f (x )＝2tan x ＋1－2sin2x212sin x ＝2tan x ＋2cos x sin x ＝2sin x cos x ＝4sin2x ，∴f ⎝ ⎛⎭⎪⎫π12＝4sinπ6＝8.4．(教材习题改编)函数y ＝3cos 4x ＋sin 4x 的最小正周期为________． 解析：y ＝3cos 4x ＋sin 4x ＝2⎝⎛⎭⎪⎫32cos 4x ＋12sin 4x＝2⎝ ⎛⎭⎪⎫cos π6cos 4x ＋sin π6sin 4x ＝2cos ⎝ ⎛⎭⎪⎫4x －π6，故T ＝2π4＝π2.答案：π25．若cos α＝－45，α是第三象限角，则1＋tanα21－tanα2＝________.解析：∵cos α＝－45，且α是第三象限角，∴sin α＝－35，∴1＋tan α21－tan α2＝cos α2＋sinα2cos α2cos α2－sin α2cosα2＝cos α2＋sinα2cos α2－sinα2＝⎝ ⎛⎭⎪⎫cos α2＋sin α22⎝ ⎛⎭⎪⎫cos α2－sin α2⎝ ⎛⎭⎪⎫cos α2＋sin α2＝1＋sin αcos 2α2－sin 2α2＝1＋sin αcos α＝1－35－45＝－12.答案：－12[例1] (1)化简：sin 2α－2cos 2αsin ⎝ ⎛⎭⎪⎫α－π4＝________；(2)已知0＜x ＜π2，化简：lg ⎝ ⎛⎭⎪⎫cos x ²tan x ＋1－2sin 2x 2＋lg ⎣⎢⎡⎦⎥⎤2cos ⎝⎛⎭⎪⎫x －π4－lg(1＋sin 2x )． [自主解答] (1)原式＝2sin αcos α－2cos 2α22sin α－cos α＝22²cos α.(2)原式＝lg(sin x ＋cos x )＋lg(sin x ＋cos x )－lg(1＋sin 2x ) ＝lgsin x ＋cos x 21＋sin 2x＝lg 1＋sin 2x 1＋sin 2x＝lg 1＝0.[答案] (1)22cos α ———————————————————1.三角函数式的化简原则一是统一角，二是统一函数名，能求值的求值，必要时切化弦，更易通分、约分. 2.三角函数式化简的要求 1能求出值的应求出值； 2尽量使三角函数种数最少； 3尽量使项数最少； 4尽量使分母不含三角函数； 5尽量使被开方数不含三角函数. 3.三角函数化简的方法化简的方法主要有弦切互化，异名化同名，异角化同角，降幂或升幂.1．化简：⎝ ⎛⎭⎪⎪⎫1tan α2－tan α2²⎝ ⎛⎭⎪⎫1＋tan α²tan α2. 解：原式＝⎝ ⎛⎭⎪⎫cos α2sin α2－sin α2cos α2²⎝ ⎛⎭⎪⎫1＋sin αcos α²sinα2cosα2＝cos αsin α2cosα2²⎝ ⎛⎭⎪⎫1＋sin αcos α²sin α2cos α2 ＝2cos αsin α＋2cos αsin α²sin αcos α²sinα2cosα2＝2cos αsin α＋2sin α2cosα2＝2cos αsin α＋4sin2α2sin α＝2cos α＋4sin 2α2sin α＝2⎝ ⎛⎭⎪⎫1－2sin 2α2＋4sin2α2sin α＝2sin α.[例2] 已知3π4<α<π，tan α＋1tan α＝－103.(1)求tan α的值；(2)求5sin 2α2＋8sin α2cos α2＋11cos 2α2－82sin ⎝ ⎛⎭⎪⎫α－π4的值．[自主解答] (1)∵tan α＋1tan α＝－103， ∴3tan 2α＋10tan α＋3＝0， 解得tan α＝－13或tan α＝－3.∵3π4<α<π，∴－1<tan α<0. ∴tan α＝－13.(2)∵tan α＝－13，∴5sin 2α2＋8sin α2cos α2＋11cos 2α2－82sin ⎝⎛⎭⎪⎫α－π4＝5⎝⎛⎭⎪⎫sin 2α2＋cos 2α2＋4sin α＋6²1＋cos α2－8sin α－cos α＝5＋4sin α＋3＋3cos α－8sin α－cos α＝4sin α＋3cos αsin α－cos α＝4tan α＋3tan α－1＝－54.保持本例条件不变，求1－cos 2α－sin 2α1＋cos 2α－sin 2α的值．解：1－cos 2α－sin 2α1＋cos 2α－sin 2α＝2sin 2α－2sin αcos α2cos 2α －2sin αcos α ＝2sin αsin α－cos α2cos αcos α－sin α＝－tan α＝13.———————————————————已知三角函数式的值，求其他三角函数式值的一般思路 1先化简所求式子；2观察已知条件与所求式子之间的联系从三角函数名及角入手； 3将已知条件代入所求式子，化简求值.2．已知sin(2α－β)＝35，sin β＝－1213，且α∈⎝ ⎛⎭⎪⎫π2，π，β∈⎝ ⎛⎭⎪⎫－π2，0，求sin α的值．解：∵π2＜α＜π，∴π＜2α＜2π.∵－π2＜β＜0，∴0＜－β＜π2，π＜2α－β＜5π2，而sin(2α－β)＝35＞0，∴2π＜2α－β＜5π2，cos(2α－β)＝45.又－π2＜β＜0且sin β ＝－1213，∴cos β＝513，∴cos 2α＝cos[(2α－β)＋β]＝cos(2α－β)cos β－sin(2α－β)sin β ＝45³513－35³⎝ ⎛⎭⎪⎫－1213＝5665. 又cos 2α＝1－2sin 2α，∴sin 2α＝9130.又α∈⎝ ⎛⎭⎪⎫π2，π，∴sin α＝3130130.[例3] (2013²西域模拟)已知函数f (x )＝3sin 2x ＋sin x cos x ，x ∈⎣⎢⎡⎦⎥⎤π2，π.(1)求f (x )的零点；(2)求f (x )的最大值和最小值． [自主解答] (1)令f (x )＝0，得 sin x ²(3sin x ＋cos x )＝0， 所以sin x ＝0或tan x ＝－33. 由sin x ＝0，x ∈⎣⎢⎡⎦⎥⎤π2，π，得x ＝π； 由tan x ＝－33，x ∈⎣⎢⎡⎦⎥⎤π2，π，得x ＝5π6. 综上，函数f (x )的零点为5π6或π.(2)f (x )＝32(1－co s 2x )＋12sin 2x ＝sin ⎝⎛⎭⎪⎫2x －π3＋32. 因为x ∈⎣⎢⎡⎦⎥⎤π2，π，所以2x －π3∈⎣⎢⎡⎦⎥⎤2π3，5π3.所以当2x －π3＝2π3，即x ＝π2时，f (x )的最大值为3；当2x －π3＝3π2，即x ＝11π12时，f (x )的最小值为－1＋32. ———————————————————公式a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)的应用及注意事项(1)利用a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)把形如y ＝a sin x ＋b cos x ＋k 的函数化为一个角的某种函数的一次式，可以求三角函数的周期、单调区间、值域和最值、对称轴等．(2)该公式是逆用两角和的正弦公式得到的．当φ为特殊角即a b的值为1或3⎝ ⎛⎭⎪⎫33时要熟练掌握．对φ是非特殊角时，只要求会求最值即可．3．(2013²银川模拟)已知函数f (x )＝sin 2x －23sin 2x ＋3＋1. (1)求f (x )的最小正周期及其单调递增区间；(2)当x ∈⎣⎢⎡⎦⎥⎤－π6，π6时，求f (x )的值域． 解：f (x )＝sin 2x ＋3(1－2s in 2x )＋1＝sin 2x ＋3cos 2x ＋1＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＋1.(1)函数f (x )的最小正周期T ＝2π2＝π.由正弦函数的性质知，当2k π－π2≤2x ＋π3≤2k π＋π2，即k π－5π12≤x ≤k π＋π12(k ∈Z )时，函数y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3为单调递增函数，故函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－5π12，k π＋π12(k ∈Z )．(2)∵x ∈⎣⎢⎡⎦⎥⎤－π6，π6，∴2x ＋π3∈⎣⎢⎡⎦⎥⎤0，2π3，∴sin ⎝⎛⎭⎪⎫2x ＋π3∈[0,1]，∴f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＋1∈[1,3]．∴f (x )的值域为[1,3]．1个公式——辅助角公式可利用辅助角公式求最值、单调区间、周期．y ＝a sin α＋b cos α＝a 2＋b 2sin(α＋φ)其中tan φ＝ba有a 2＋b 2≥|y |.2个方向——三角恒等变换的基本方向三角函数求值、化简的基本思路是“变换”、通过适当的变换达到由此及彼的目的．变换的基本方向有两个：一是变换函数名称，可以使用诱导公式、同角三角函数关系、二倍角的余弦公式等；二是变换角的形式，可以使用两角和与差的三角函数公式、倍角公式、对角进行代数形式的变换等．3个步骤——三角恒等变换的步骤 三角恒等变换可以归纳为以下三步：创新交汇——三角恒等变换与函数性质的交汇问题1．三角恒等变换作为高考命题的重点内容之一，主要与三角函数的求值、化简以及三角函数的性质相结合命题，有时也与向量等其他知识交汇命题．2．解决此类问题时，一要重视三角变化中的诸多公式，熟悉它们之间的内在联系；二要熟悉三角变换中各方面的技巧，特别是切化弦、降幂和升幂、角的变换等技巧．[典例] (2012²安徽高考)设函数f (x )＝22cos ⎝⎛⎭⎪⎫2x ＋π4＋sin 2x .(1)求f (x )的最小正周期；(2)设函数g (x )对任意x ∈R ，有g ⎝ ⎛⎭⎪⎫x ＋π2＝g (x )，且当x ∈⎣⎢⎡⎦⎥⎤0，π2时，g (x )＝12－f (x )．求g (x )在区间[－π，0]上的解析式．[解] (1)f (x )＝22cos ⎝⎛⎭⎪⎫2x ＋π4＋sin 2x＝22⎝ ⎛⎭⎪⎫cos 2x cos π4－sin 2x sin π4＋1－cos 2x2＝12－12sin 2x ， 故f (x )的最小正周期为π.(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，g (x )＝12－f (x )＝12sin 2x ，故①当x ∈⎣⎢⎡⎦⎥⎤－π2，0时，x ＋π2∈⎣⎢⎡⎦⎥⎤0，π2.由于对任意x ∈R ，g ⎝ ⎛⎭⎪⎫x ＋π2＝g (x )，从而g (x )＝g ⎝⎛⎭⎪⎫x ＋π2＝12sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π2＝12sin(π＋2x )＝－12sin 2x . ②当x ∈⎣⎢⎡⎭⎪⎫－π，－π2时，x ＋π∈⎣⎢⎡⎭⎪⎫0，π2，从而g (x )＝g (x ＋π)＝12sin[2(x ＋π)]＝12sin 2x .综合①②得g (x )在[－π，0]上的解析式为 g (x )＝⎩⎪⎨⎪⎧12sin 2x ，x ∈⎣⎢⎡⎭⎪⎫－π，－π2，－12sin 2x ，x ∈⎣⎢⎡⎦⎥⎤－π2，0.[名师点评]1．本题具有以下创新点(1)命题方式：本题突破以往依据函数图象确定三角函数解析式的传统，而是将抽象函数与函数的周期性等相结合，考查函数解析式的求法．(2)考查内容的创新：本题考查了函数周期性及分类讨论思想在求抽象函数及分段函数解析式中的应用，考查了考生分析问题、解决问题的能力以及逻辑推理能力．2．解决本题的关键有以下几点 (1)准确识别函数g (x )的周期T ＝π2；(2)根据周期恰当地将区间[－π，0]分成⎣⎢⎡⎦⎥⎤－π，－π2和⎣⎢⎡⎦⎥⎤－π2，0两部分，并正确求出相应的解析式；(3)具备较强的逻辑推理能力和运算能力． [变式训练]1．设△ABC 的三个内角为A ，B ，C ，向量m ＝(3sin A ，sin B )，n ＝(cos B ，3cos A )，若n²m ＝1＋cos(A ＋B )，则C 的值为________．解析：m²n ＝3sin A cos B ＋3cos A sin B ＝3sin(A ＋B )＝3sin(π－C )＝3sin C ，又cos(A ＋B )＝cos(π－C )＝－cos C ，故3sin C ＝1－cos C ，即3sin C ＋cos C ＝1，即2sin ⎝ ⎛⎭⎪⎫C ＋π6＝1，即sin ⎝⎛⎭⎪⎫C ＋π6＝12，由于π6＜C ＋π6＜7π6，故只有C ＋π6＝5π6，即C ＝2π3.答案：23π2．(2013²江南十校联考)已知函数f (x )＝sin x ＋cos x . (1)若f (x )＝2f (－x )，求cos 2x －sin x cos x1＋sin 2x的值；(2)求函数F (x )＝f (x )²f (－x )＋f 2(x )的最大值和单调递增区间． 解：(1)∵f (x )＝sin x ＋cos x ，∴f (－x )＝cos x －sin x . 又∵f (x )＝2f (－x )，∴sin x ＋cos x ＝2(cos x －sin x )，且cos x ≠0， ∴tan x ＝13，∴cos 2x －sin x cos x 1＋sin 2x ＝cos 2x －sin x cos x 2sin 2x ＋cos 2x ＝1－tan x 2tan 2x ＋1＝611. (2)由题知F (x )＝cos 2x －sin 2x ＋1＋2sin x cos x ， ∴F (x )＝cos 2x ＋sin 2x ＋1， 即F (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1.当sin ⎝⎛⎭⎪⎫2x ＋π4＝1时，[F (x )]max ＝2＋1.由－π2＋2k π≤2x ＋π4≤π2＋2k π(k ∈Z )得－3π8＋k π≤x ≤π8＋k π(k ∈Z )，故所求函数F (x )的单调递增区间为⎣⎢⎡⎦⎥⎤－3π8＋k π，π8＋k π(k ∈Z ).一、选择题(本大题共6小题，每小题5分，共30分)1．(2013²济南模拟)函数y ＝sin x sin ⎝ ⎛⎭⎪⎫π2＋x 的最小正周期是( ) A.π2B ．πC ．2πD ．4π解析：选B ∵y ＝sin x cos x ＝12sin 2x ，∴T ＝2π2＝π.2．(2013²沈阳四校联考)若1＋cos 2αsin 2α＝12，则tan 2α等于( )A.54 B ．－54C.43D ．－43解析：选D ∵1＋cos 2αsin 2α＝2cos 2α2sin αcos α＝cos αsin α＝12，∴tan α＝2，∴tan 2α＝2tan α1－tan 2α＝41－4＝－43. 3．已知α∈(－π，0)，tan(3π＋α)＝a log a 13(a ＞0，且a ≠1)，则cos ⎝ ⎛⎭⎪⎫32π＋α的值为( )A.1010 B ．－1010C.31010D ．－31010解析：选B ∵由题意可知tan(3π＋α)＝13，∴tan α＝13.又∵cos ⎝ ⎛⎭⎪⎫32π＋α＝cos ⎝ ⎛⎭⎪⎫π2－α＝sin α， ∴cos ⎝⎛⎭⎪⎫3π2＋α＝－1010.∵α∈(－π，0)， ∴sin α＝－1010. 4．已知x ∈⎝ ⎛⎭⎪⎫π2，π，cos 2x ＝a ，则cos x ＝( ) A. 1－a 2 B ．－ 1－a2 C.1＋a2D ．－1＋a2解析：选D 依题意得cos 2x ＝1＋cos 2x 2＝1＋a 2；又x ∈⎝⎛⎭⎪⎫π2，π，因此cos x ＝－1＋a2. 5．已知cos ⎝ ⎛⎭⎪⎫α－π6＋sin α＝435，则sin ⎝ ⎛⎭⎪⎫α＋7π6的值是( ) A ．－235B.235C ．－45D.45解析：选C cos ⎝ ⎛⎭⎪⎫α－π6＋sin α＝435⇒32sin α＋32cos α＝435⇒sin ⎝⎛⎭⎪⎫α＋π6＝5则sin ⎝ ⎛⎭⎪⎫α＋7π6＝－sin ⎝⎛⎭⎪⎫α＋π6＝－45. 6．设α∈⎝ ⎛⎭⎪⎫0，π2，则sin 3αcos α＋cos 3αsin α的最小值为( ) A.2764 B.325C.536D ．1解析：选D sin 3αcos α＋cos 3αsin α＝sin 4α＋cos 4αsin αcos α＝sin 2α＋cos 2α2－2sin 2αcos 2αsin αcos α＝1sin αcos α－2sin αcos α.令sin αcos α＝t ，则t ＝12sin 2α.∵α∈⎝ ⎛⎭⎪⎫0，π2，∴t ∈⎝ ⎛⎦⎥⎤0，12.令g (t )＝1t －2t ，g (t )在⎝ ⎛⎦⎥⎤0，12上是减函数， ∴当t ＝12时，g (t )min ＝2－1＝1.二、填空题(本大题共3小题，每小题5分，共15分)7．若α、β是锐角，且sin α－sin β＝－12，cos α－cos β＝12，则tan(α－β)＝________.解析：∵sin α－sin β＝－12，cos α－cos β＝12，两式平方相加得：2－2cos αcos β－2sin αsin β＝12，即2－2cos(α－β)＝12，∴cos(α－β)＝34.∵α、β是锐角，且sin α－sin β＝－12<0，∴0<α<β<π2.∴－π2<α－β<0.∴sin(α－β)＝－1－cos 2α－β＝－74.∴tan(α－β)＝sin α－βcos α－β＝－3答案：－738．设α是第二象限角，tan α＝－43，且sin α2<cos α2，则cos α2＝________.解析：∵α是第二象限角，∴α2可能在第一或第三象限．又sin α2<cos α2，∴α2为第三象限角，∴cos α2<0.∵tan α＝－43，∴cos α＝－35，∴cos α2＝－1＋cos α2＝－ 55. 答案：－559．(2012²江苏高考)设α为锐角，若cos ⎝ ⎛⎭⎪⎫α＋π6＝45，则sin ⎝ ⎛⎭⎪⎫2α＋π12的值为________．解析：因为α为锐角，cos ⎝ ⎛⎭⎪⎫α＋π6＝45，所以sin ⎝ ⎛⎭⎪⎫α＋π6＝35，sin 2⎝ ⎛⎭⎪⎫α＋π6＝2425，cos 2⎝ ⎛⎭⎪⎫α＋π6＝725，所以sin ⎝ ⎛⎭⎪⎫2α＋π12＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α＋π6－π4＝sin 2⎝ ⎛⎭⎪⎫α＋π6cos π4－cos2⎝⎛⎭⎪⎫α＋π6sin π4＝17250.答案：17250三、解答题(本大题共3小题，每小题12分，共36分) 10．(1)化简4cos 4x －2cos 2x －1tan ⎝ ⎛⎭⎪⎫π4＋x sin 2⎝ ⎛⎭⎪⎫π4－x ；(2)化简[2sin 50°＋sin 10°(1＋3tan 10°)]²2sin 280°. 解：(1)原式＝1＋cos 2x 2－2cos 2x －1tan ⎝ ⎛⎭⎪⎫π4＋x cos 2⎝ ⎛⎭⎪⎫π4＋x ＝cos 22x sin ⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4＋x ＝2cos 22xsin ⎝ ⎛⎭⎪⎫π2＋2x ＝2cos 22xcos 2x＝2cos 2x .(2)原式＝⎝ ⎛⎭⎪⎫2sin 50°＋sin 10°²cos 10°＋3sin 10°cos 10°²2²sin 80°＝⎝⎛⎭⎪⎪⎫2sin 50°＋2sin 10°²12cos 10°＋32sin 10°cos 10°²2cos 10° ＝22[sin 50°²cos 10°＋sin 10°²cos(60°－10°)] ＝22sin(50°＋10°)＝22³32＝ 6. 11．已知函数f (x )＝sin x ＋cos x ，f ′(x )是f (x )的导函数． (1)求f ′(x )及函数y ＝f ′(x )的最小正周期；(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，求函数F (x )＝f (x )f ′(x )＋f 2(x )的值域．解：(1)由题意可知，f ′(x )＝cos x －sin x ＝－2²sin ⎝ ⎛⎭⎪⎫x －π4，所以y ＝f ′(x )的最小正周期为T ＝2π. (2)F (x )＝cos 2x －sin 2x ＋1＋2sin x cos x ＝1＋sin 2x ＋cos 2x ＝1＋2sin ⎝⎛⎭⎪⎫2x ＋π4.∵x ∈⎣⎢⎡⎦⎥⎤0，π2，∴2x ＋π4∈⎣⎢⎡⎦⎥⎤π4，5π4，∴sin ⎝ ⎛⎭⎪⎫2x ＋π4∈⎣⎢⎡⎦⎥⎤－22，1. ∴函数F (x )的值域为[0,1＋ 2 ]．12．已知函数f (x )＝3cos(ωx ＋φ)⎝ ⎛⎭⎪⎫－π2＜φ＜0的最小正周期为π，且其图象经过点⎝⎛⎭⎪⎫5π12，0.(1)求函数f (x )的解析式；(2)若函数g (x )＝f ⎝ ⎛⎭⎪⎫x 2＋π6，α，β∈⎝⎛⎭⎪⎫0，π2，且g (α)＝1，g (β)＝324，求g (α－β)的值．解：(1)依题意函数的最小正周期T ＝2πω＝π，解得ω＝2，所以f (x )＝3cos(2x ＋φ)．因为函数f (x )的图象经过点⎝⎛⎭⎪⎫5π12，0，所以3cos ⎝ ⎛⎭⎪⎫2³5π12＋φ＝0，得到2³5π12＋φ＝k π＋π2，k ∈Z ，即φ＝k π－π3，k ∈Z .由－π2＜φ＜0得φ＝－π3.故函数f (x )的解析式为f (x )＝3cos ⎝⎛⎭⎪⎫2x －π3.(2)依题意有g (x )＝3cos ⎣⎢⎡⎦⎥⎤2³⎝ ⎛⎭⎪⎫x 2＋π6－π3＝3cos x ，由g (α)＝3cos α＝1，得cos α＝13，同理g (β)＝3cos β＝324，得cos β＝24.而α，β∈⎝⎛⎭⎪⎫0，π2，所以sin α＝1－⎝ ⎛⎭⎪⎫132＝223， sin β＝1－⎝⎛⎭⎪⎫242＝144， 所以g (α－β)＝3cos(α－β)＝3(cos αcos β＋sin αsin β)＝3³⎝ ⎛⎭⎪⎫13³24＋223³144＝2＋474.1．求值：(1)sin 10°sin 30°sin 50°sin 70°； (2)2cos 10°－sin 20°cos 20°.解：(1)原式＝sin 10°cos 10°sin 50°sin 70°2cos 10°＝sin 20°sin 50°sin 70°4cos 10°＝sin 20°cos 20°sin 50°4cos 10°＝sin 40°sin 50°8cos 10°＝sin 80°16cos 10°＝116.(2)原式＝2cos 30°－20°－sin 20°cos 20°＝2cos 30°cos 20°＋2sin 30°sin 20°－sin 20°cos 20°＝2cos 30°cos 20°cos 20°＝ 3.2．已知sin(2α＋β)＝3sin β，设tan α＝x ，tan β＝y ，记y ＝f (x )． (1)求f (x )的解析式；(2)若角α是一个三角形的最小内角，试求函数f (x )的值域． 解：(1)∵由sin(2α＋β)＝3sin β， 得sin[(α＋β)＋α]＝3sin[(α＋β)－α]，即sin(α＋β)cos α＋cos(α＋β)sin α＝3sin(α＋β)²cos α－3cos(α＋β)sin α，∴sin(α＋β)cos α＝2cos(α＋β)²s in α，∴tan(α＋β)＝2tan α，于是tan α＋tan β1－tan αtan β＝2tan α，即x ＋y 1－xy ＝2x ，∴y ＝x 1＋2x 2，即f (x )＝x1＋2x2. (2)∵角α是一个三角形的最小内角， ∴0＜α≤π3，则0＜x ≤ 3，f (x )＝x 1＋2x 2＝11x＋2x ≤121x²2x＝24⎝ ⎛⎭⎪⎫当且仅当x ＝22时取“＝”，故函数f (x )的值域为⎝ ⎛⎦⎥⎤0，24. 3．已知sin θ和cos θ是关于x 的方程x 2－2x sin α＋sin 2β＝0的两个根． 求证：2cos 2α＝cos 2β.证明：因为sin θ，cos θ是方程x 2－2x sin α＋sin 2β＝0的两根，所以sin θ＋cos θ＝2sin α，sin θ²cos θ＝sin 2β.因为(sin θ＋cos θ)2＝1＋2sin θcos θ，所以(2sin α)2＝1＋2sin 2β，即4sin 2α＝1＋2sin 2β，所以2(1－cos 2α)＝1＋1－cos 2β，所以2cos 2α＝cos 2β.4．A 是单位圆与x 轴正半轴的交点，点P 在单位圆上，∠AOP ＝θ(0＜θ＜π)，OQ＝OA ＋OP，四边形OAQP 的面积为S .(1)求OA ²OQ＋S 的最大值及此时θ的值θ0；(2)设点B 的坐标为⎝ ⎛⎭⎪⎫－35，45，∠AOB ＝α，在(1)的条件下，求cos(α＋θ0)． 解：(1)由已知，A ，P 的坐标分别为(1,0)，(cos θ，sin θ)．则OQ＝(1＋cos θ，sin θ)，OA ²OQ ＝1＋cos θ.又S ＝2³12|OP |²|OA |²sin θ＝sin θ，所以OA ²OQ ＋S ＝cos θ＋1＋sin θ＝2²sin ⎝⎛⎭⎪⎫θ＋π4＋1(0＜θ＜π)．故OA ²OQ ＋S 的最大值是2＋1，此时θ0＝π4.(2)∵cos α＝－35，sin α＝45，且sin θ0＝cos θ0＝22，∴cos(θ0＋α)＝cos θ0cos α－sin θ0sin α＝－7210.。

第2课时简单的三角恒等变换【课程标准】能运用两角和与差的正弦、余弦、正切公式推导二倍角的正弦、余弦、正切公式,并进行简单的恒等变换(包括推导出积化和差、和差化积、半角公式,这三组公式不要求记忆).【考情分析】考点考法:高考命题常以角为载体,考查二倍角公式、升幂降幂公式、半角公式;三角函数求值是高考热点,常以选择题或填空题的形式出现.核心素养:数学抽象、数学运算【必备知识·逐点夯实】【知识梳理·归纳】1.二倍角的正弦、余弦、正切公式(1)公式S2α:sin2α=2sinαcosα.(2)公式C2α:cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α.(3)公式T2α:tan2α=2tan1-tan2.2.常用的部分三角公式(1)1-cosα=2sin22,1+cosα=2cos22.(升幂公式) (2)1±sinα=(sin2±cos2)2.(升幂公式) (3)sin2α=1-cos22,cos2α=1+cos22,tan2α=1-cos21+cos2.(降幂公式)3.半角公式sin2=±cos2=±tan2=±=sin 1+cos=1-cos sin.【基础小题·自测】类型辨析改编易错高考题号12431.(多维辨析)(多选题)下列说法正确的是()A .半角的正弦、余弦公式实质就是将倍角的余弦公式逆求而得来的B .存在实数α,使tan 2α=2tan αC .cos 22=1-cos2D .tan 2=sin 1+cos =1-cos sin【解析】选ABD .由半角公式、二倍角公式可知,选项A 正确;因为当α=0时,tan 2α=2tan α=0,所以选项B 正确;因为由二倍角公式可知:cos θ=2cos 22-1,所以cos 22=1+cos2,因此选项C 错误;因为tan2=sin2cos 2=2sin2cos22cos 22=sin 1+cos ,tan 2=sin2cos 2=2sin2cos22cos 22=1-cossin ,所以选项D 正确.2.(必修第一册P223练习5改条件)cos 2π12-cos 25π12=()A .12B .33C .22D .32【解析】选D .因为cos5π12=sin(π2-5π12)=sin π12,所以cos 2π12-cos 25π12=cos 2π12-sin 2π12=cos(2×π12)=cos π6=32.3.(2023·新高考Ⅱ卷)已知α为锐角,cos α=1+54,则sin2=()A .3-58B .-1+58C .3-54D .-1+54【解析】选D .cos α=1+54,则cos α=1-2sin 22,故2sin 22=1-cos α=3-54,即sin 22=3-58=(5)2+12-2516=(5-1)216,因为α为锐角,所以sin2>0,所以sin 2=-1+54.4.(忽视隐含条件)已知2sin α=1+cos α,则tan2=()A .2B .12C .2或不存在D .12或不存在【解析】选D .当α=2k π+π(k ∈Z )时,满足2sin α=1+cos α,此时tan 2不存在;当α≠2k π+π(k ∈Z )时,tan2=sin1+cos =12.【核心考点·分类突破】考点一三角函数式的化简[例1](1)函数f (x )=sin 2x +3sin x cos x -12可以化简为()A .f (x )=sin(2x -π3)B .f (x )=sin(2x -π6)C .f (x )=sin(2x +π3)D .f (x )=sin(2x +π6)【解析】选B .f (x )=sin 2x +3sin x cos x -12=1-cos22+32sin 2x -12=32sin 2x -12cos 2x =sin(2x -π6).(2)已知0<θ<π,(1+sinrcos )(sin 2-cos 2)________.【解析】由θ∈(0,π)得0<2<π2,所以cos2>0,所以2+2cos =2.又(1+sin θ+cos θ)(sin 2-cos 2)=(2sin 2cos2+2cos 22)(sin 2-cos2)=2cos2(sin 22-cos 22)=-2cos2cos θ.故原式=-2cos2cos 2cos2=-cos θ.答案:-cos θ【解题技法】三角函数式化简的解题策略(1)从三角函数名、角以及幂的差异三方面入手进行适当变形,结合所给的“形”的特征求解;(2)注意弦切互化、异名化同名、异角化同角、降幂升幂.【对点训练】1.化简:2cos 4-2cos 2r122tan(π4-psin 2(π4+p =__________.【解析】原式=12(4cos 4-4cos 2r1)2×sin(π4-pcos(π4-p ·cos 2(π4-p =(2cos 2-1)24sin(π4-pcos(π4-p =cos 222sin(π2-2p =cos 222cos2=12cos 2x.答案:12cos 2x2.化简:sin 2αsin 2β+cos 2αcos 2β-12cos 2αcos 2β=________.【解析】原式=1-cos22·1-cos22+1+cos22·1+cos22-12cos 2αcos 2β=1-cos2-cos2rcos2vos24+1+cos2rcos2rcos2vos24-12cos 2α·cos 2β=12+12cos 2αcos 2β-12cos 2αcos 2β=12.答案:12【加练备选】化简:2sin (π-)+sin2cos 22=________.【解析】2sin (π-)+sin2cos 22=2sinr2sinvos 12(1+cos )=2sin (1+cos )12(1+cos )=4sin α.答案:4sin α考点二三角函数式的求值角度1给值求值[例2](2023·新高考Ⅰ卷)已知sin(α-β)=13,cos αsin β=16,则cos(2α+2β)=()A .79B .19C .-19D .-79【解析】选B.因为sin(α-β)=sinαcosβ-cosαsinβ=13,cosαsinβ=16,所以sinαcosβ=12,所以sin(α+β)=sinαcosβ+cosαsinβ=23,所以cos(2α+2β)=cos2(α+β)=1-2sin2(α+β)=1-2×(23)2=19.【解题技法】给值求值解题的两点注意(1)注意“变角”,使其角相同或具有某种关系.(2)注意公式的选择及其公式的逆应用.角度2给角求值[例3](2023·淄博模拟______.【解析】=14sin48°2sin48°=18.答案:18【解题技法】给角求值的解题策略(1)该问题一般所给出的角都是非特殊角,解题时一定要注意非特殊角与特殊角的关系;(2)要利用观察得到的关系,结合三角函数公式转化为特殊角的三角函数.角度3给值求角[例4]若sin2α=55,sin(β-α)=1010,且α,π,β∈π则α+β的值是() A.7π4B.9π4C.5π4或7π4D.5π4或9π4【解析】选A.因为α4π,所以2α2π,因为sin2α=55,所以2α,π.所以αcos2α=-255,又因为sin(β-α)=1010,β∈π,所以β-α(β-α)=-31010,所以cos(α+β)=cos[(β-α)+2α]=cos(β-α)cos2α-sin(β-α)sin2α=---1010×55=22,又α+β2π,所以α+β=7π4.【解题技法】给值求角的方法依条件求出所求角的范围,选择一个在角的范围内严格单调的三角函数求值.【对点训练】1.(2023·保定模拟)已知sin(θ-π4)=223,则sin2θ的值为()A.79B.-79C.29D.-29【解析】选B.由sin(θ-π4)=223,得sin(θ-π4)=sinθcosπ4-cosθsinπ4=22(sinθ-cosθ)=223,即sinθ-cosθ=43,等式两边同时平方,得1-sin2θ=169,所以sin2θ=-79.2.(2023·枣庄模拟)在平面直角坐标系xOy中,已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边经过点(-3,4),则tan2=()A.-12或2B.2C.-13或3D.3【解析】选B.因为角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边经过点(-3,4),所以sinα=45,cosα=-35,所以tan2=sin1+cos=451-35=2.3.已知sin(α-2)=55,sin(β-2)=1010,且α-2∈(0,π2),β-2∈(0,π2),则r2=__________.【解析】因为α-2∈(0,π2),β-2∈(0,π2),所以0<r2<π,cos(α-2)=255,cos(β-2)=31010.因为cos r2=cos[(α-2)+(β-2)]=cos(α-2)cos(β-2)-sin(α-2)sin(β-2)=255×31010-55×1010=22,所以r2=π4.答案:π44.化简求值:3-4sin20°+8sin320°2sin20°sin480°.【解析】原式=3-4sin20°(1-2sin 220°)2sin20°sin480°=3-4sin20°cos40°2sin20°sin480°=2sin (20°+40°)-4sin20°cos40°2sin20°sin480°=2sin (40°-20°)2sin20°sin480°=1sin480°=1sin120°=233.【加练备选】若tan 2α=-34,则sin2rcos 21+2sin 2=()A .-14或14B .34或14C .34D .14【解析】选D .由tan 2α=2tan1-tan 2=-34,可得tan α=3或tan α=-13.故sin2rcos 21+2sin 2=2sinvosrcos 23sin 2rcos 2=2tanr13tan 2r1,当tan α=3时,2×3+13×32+1=728=14;当tan α=-13时,2×(-13)+13×(-13)2+1=1343=14.考点三三角恒等变换的应用教考衔接教材情境·研习·典题类[例5](必修第一册P227·例10)如图,在扇形OPQ 中,半径OP =1,圆心角∠POQ =π3,C 是扇形弧上的动点,矩形ABCD 内接于扇形.记∠POC =α,求当角α取何值时,矩形ABCD 的面积最大?并求出这个最大面积.【解题导思】看问题三角恒等变换中的最值问题提信息半径OP =1,圆心角∠POQ =3,矩形ABCD 内接于扇形,∠POC =α定思路借助角α并利用三角函数,把矩形ABCD 的长和宽表示出来,确定矩形ABCD面积的表达式,最后利用三角恒等变换和三角函数的性质确定最大面积【解析】在Rt△OBC中,OB=cosα,BC=sinα.在Rt△OAD中,D D=tanπ3=3.OA=33DA=33BC=33sinα,AB=OB-OA=cosα-33sinα.设矩形ABCD的面积为S,则S=AB·BC=(cosα-33sinα)sinα=sinαcosα-33sin2α=12sin2α-36(1-cos2α)=12sin2α+36cos2α-36(32sin2α+12cos2α)-36=α+π6)-36.由0<α<π3,得π6<2α+π6<5π6,所以当2α+π6=π2,即α=π6时,S最大-36=36.因此,当α=π6时,矩形ABCD的面积最大,最大面积为36.【高考链接】(2024·保定模拟)已知扇形POQ的半径为2,∠POQ=π3,如图所示,在此扇形中截出一个内接矩形ABCD(点B,C在弧P 上),则矩形ABCD面积的最大值为__________.【解析】作∠POQ的平分线OE,交AD于F,BC于E,连接OC,根据题意可知△AOD为等边三角形,则E为BC的中点,F为AD的中点,设∠COE=α,α∈(0,π6),CE=OC sinα=2sinα,则AD=BC=2CE=4sinα,则OF=32AD=23sinα,OE=OC cosα=2cosα,则AB=2cosα-23sinα,所以矩形ABCD的面积S=BC·AB=4sinα(2cosα-23sinα)=4sin2α+43cos2α-43=8sin(2α+π3)-43,当2α+π3=π2,即α=π12时,S取得最大值8-43,所以矩形ABCD面积的最大值为8-43.答案:8-43[溯源点评]两题的区别在于扇形内接矩形ABCD的方式不同,考虑该问题是否能转化为更简单的、熟悉的问题来解决.根据图形的对称性,作∠POQ的平分线,分别交AD,BC于点F,E,从而使整个问题又回到教材中的问题.。