2016-2017学年七年级数学上册 1.4 从三个方向看物体的形状练习试题 (新版)北师大版

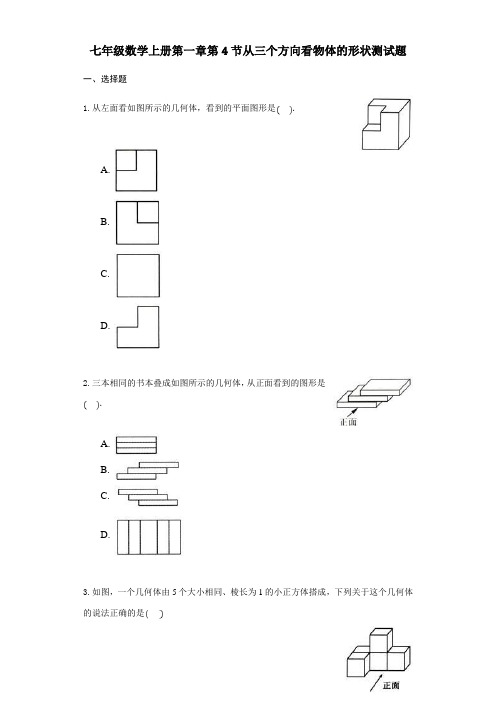
七年级数学上册第一章第4节从三个方向看物体的形状测试题一、选择题1.从左面看如图所示的几何体，看到的平面图形是．A.B.C.D.2.三本相同的书本叠成如图所示的几何体，从正面看到的图形是．A.B.C.D.3.如图，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列关于这个几何体的说法正确的是A. 从正面看到的图形的面积为5B. 从左面看到的图形的面积为3C. 从上面看到的图形的面积为3D. 从三个方向看到的图形的面积都是44.如图所示为由4个大小相同的正方体组成的几何体，则从正面看到的平面图形是．A.B.C.D.5.由若干个相同的小正方体搭成的一个几何体如图所示，从上面看到的图形为．A.B.C.D.6.如图2所示的三幅图分别是从不同方向看如图1所示的工件立体图得到的平面图形不考虑尺寸，其中正确的是．A. B. C. D.7.如图是由8个完全相同的小正方体组成的几何体，则从正面看得到的形状图是A.B.C.D.8.如图所示为由6个相同的小正方体搭成的几何体，那么从上面看到的平面图形是．A. B.C. D.9.下面几何体中，全是由曲面围成的是A. 圆柱B. 圆锥C. 球D. 正方体10.如图所示是某正方体的展开图，在顶点处标有数字，当把它折成正方体时，与13重合的数字是A. 1和9B. 1和10C. 1和12D. 1和811.一个几何体是由一些大小相同的小立方块摆成的，其主视图和俯视图如图所示，则组成这个几何体的小立方块最少有A. 3个B. 4个C. 5个D. 6个12.一个几何体的主视图和俯视图如图所示，若这个几何体最多由a个小正方体组成，最少由b个小正方体组成，则等于A. 10B. 11C. 12D. 1313.桌面上放置的几何体中，从正面和左面看可能不同的是A. 圆柱B. 正方体C. 球D. 直立圆锥14.下列所列举的物体，与圆锥的形状类似的是A. 足球B. 字典C. 易拉罐D. 标枪的尖头15.已知图1是图2中正方体的表面的展开图，其中有五个面内标注了数字，则图2中涂有阴影的面在图1中标注的数字是A. 2B. 3C. 4D. 5二、填空题16.图中的三个图形分别是从________、________、________看图中的物体得到的形状图．填“正面”“左面”或“上面”17.一个几何体是由一些完全相同的小立方块搭成的，从三个不同的方向看到的图形如图所示，则搭成这个几何体共需这样的小方块________个．18.如图所示为由6个棱长均为1的正方体组成的几何体，从正面看到的平面图形的面积为________．19.如图所示为由10个完全相同的小正方体搭成的立体图形．若现在你还有若干个相同的小正方体，在保证该立体图形从正面、上面、左面看到的图形不变的情况下，最多还能放________个小正方体．20.一个几何体由若干个相同的小立方体搭成，从正面和上面看到的图形分别如图所示，从上面看到的图形中，方格中的字母和数字表示该位置上小立方体的个数，求________，________．三、解答题21.如图是由几个相同的小立方块搭成的几何体从上面看的形状图，小正方形中的数字表示在该位置的小立方块的个数．请画出这个几何体从正面看和从左面看的形状图；已知小立方块的棱长为1，求该几何体的表面积．22.将棱长为a的小正方体摆成如图所示的形状．求该物体的表面积；依图中摆放方法类推，如果该物体摆放了20层，求该物体的表面积．答案1.【答案】B2.【答案】B3.【答案】B4.【答案】B5.【答案】A6.【答案】D7.【答案】D8.【答案】A9.【答案】C10.【答案】A11.【答案】B12.【答案】C13.【答案】A14.【答案】D15.【答案】D16.【解答】解：观察题图发现，从正面看共3列2行，第一列有两层；从左面看共2列，左边一列有2层，右边一列有1层；从上面看共3列2行．故答案为上面；正面；左面．17.【解答】解：综合主视图，俯视图，左视图可知，底层有4个正方体，第二层有1个正方体，所以搭成这个几何体所用的小立方块的个数是5，故答案为5．18.【解答】解：题中的几何体从正面看到的平面图形如图所示，该几何体是由6个棱长均为1的正方体组成的，从正面看到的平面图形的面积为，故答案为5．19.【解答】解：主视图是第一层三个小正方形，第二层是左边一个小正方形，中间一个小正方形，第三层是左边一个小正方形，俯视图是第一层三个小正方形，第二层三个小正方形，左视图是第一层两个小正方形，第二层两个小正方形，第三层左边一个小正方形，不改变三视图，只能在中间第二层加一个，故答案为：1．20.【解答】解：由俯视图可知，该组合体有两行两列，左边一列前一行有两个正方体，结合主视图可知左边一列最高叠有2个正方体，故或2；由主视图右边一列可知，右边一列最高可以叠3个正方体，故．故答案为：1或2；3．21.【答案】解：如图所示：表面积．22.【答案】解：．答：该物体的表面积是；从上到下第一层为1个，第二层为个，、第20层为个，俯视面，左视面，主视面，右视面，底面，后面各有210个正方形，该物体的表面积共包含个正方形，该物体的表面积为：．答：该物体的表面积是．。

1.4 从三个方向看物体的形状
准备好上节课用到的自制的正方体、长方体、棱锥、圆锥等用具.
阅读教材完成下列问题：
1.说出每一幅图都是从什么方向看到的？两人小组交流.
2.在议一议中，说出每一幅图都是从什么方向看到的？描述你看到的平面图形的形状.
3. 一般地我们把从上面往下看到的图叫_________；从正面看到的图叫___________；从左面看到的图叫__________。

4. 假如我们用“长、宽、高”来描述几何体的大小，三视图分别体现了几何体长高宽中的什么？主视图体现了物体的_______和_______；左视图体现了物体的_______和_______；俯视图体现了物体的_______和_______.
5.一个球、正方体、圆柱、圆锥的三视图分别是什么？展示给大家.
1. 观察下图①②③分别得它的主视图、左视图和俯视图，请写在对应图的下边.
2.画出下图所示几何体的主视图,左视图与俯视图.
3.如图两个图形分别是某个几何体的俯视图和主视图，则该几何体是________．
4.下面是用五个小正方体搭成的四种几何体，分别画出它们的三视图。

参考答案
1.俯视图，主视图，左视图；左视图，俯视图，主视图；
俯视图，左视图，主视图；
2.略，
3.圆柱.
4.略.。

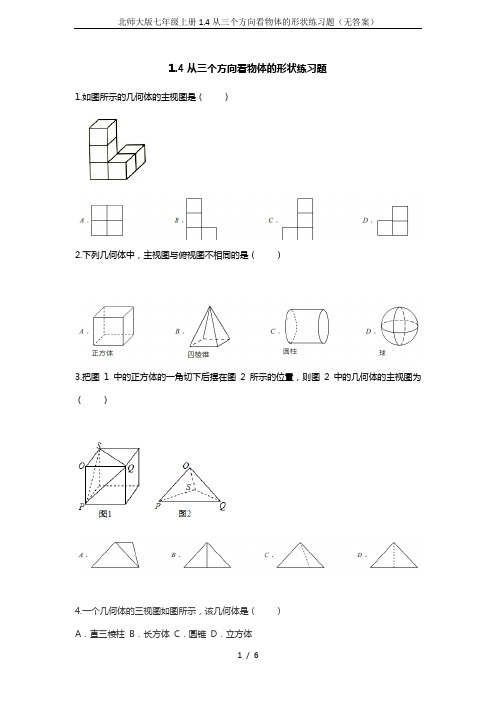
1.4从三个方向看物体的形状练习题1.如图所示的几何体的主视图是（）2.下列几何体中，主视图与俯视图不相同的是（）3.把图1中的正方体的一角切下后摆在图2所示的位置，则图2中的几何体的主视图为（）4.一个几何体的三视图如图所示，该几何体是（）A．直三棱柱B．长方体C．圆锥D．立方体5.小明从正面观察下图所示的两个物体，看到的是（）6．如图，是一个几何体的主视图、左视图和俯视图，则这个几何体是（）7.如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是。

8.图是某圆锥的主视图和左视图，该圆锥的侧面积是。

BA C D正面9.在一个仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱从三个方面观察到的图画了出来．如图所示，则这堆正方体货箱共有______个．10.用小立方体搭一个几何体，使得它的从正面和上面看到的图形如图所示，这样的几何体有种，最少需要个小正方体，最多需要个小正方体11. 用小立方块搭一几何体，使得它从正面看和从上面看如图所示，这样的几何体最少要_____个立方块，最多要____个立方块。

12.如图是由一些相同的小正方体构成的几何体的三视图，那么构成这个几何体的小正方体的个数为______13.5个正方体的六个面上分别写着1、2、3、4、5、6六个数，并且它们任意两个相对的面上所写的两个数的和都等于7．现在把五个这样的正方体一个挨着一个地连接起来（如图），在紧挨着的两个面上的两个数之和都等于8，那么，图中打“？”的这个面上所写的数．14. 已知一个几何体从上面看到的形状如图所示，请画出这个几何体从正面和左面看到的形状（小正方形中的数字表示在该位置中小立方体的个数）．15.画出下面几何体从三个不同的方向看的图形．(1) 从正面看从左面看从上面看(2) 从正面看：从左面看：从上面看：16.如图是由小正方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小正方形的个数，请画出它的主视图和左视图。

最新北师版七年级上册数学精品习题 1.4从三个方向看物体的形状同步练习1最新北师版七年级上册数学精品习题-1.4从三个方向看物体的形状同步练习1初中最新高质量数学课程的毕业设计4.从三个方向看物体的形状一、多项选择题1．如图，其主视图是（）2.如图所示，② 是…的（）吗①a．主视图b．左视图c．俯视图d．无法确定3.如图所示，如果是几何图形的前视图、左视图和俯视图，则几何图形为(4．如图，是一个四棱柱和圆柱的摆放组合，则其俯视图是（）5.如图所示，（）视图① 和② 都一样最新初中数学精品整理设计1）最新初中数学精品整理设计a、前视图B.左视图C.俯视图D.左视图和俯视图6．如图，是由若干相同小正方体组成的几何体的主观图和左视图，则这个几何体有（）种可能的形状．a、 1b.2c.3d.47．如图是由一些相同的小正方体构成的立体图形的三种视图：组成这个三维图形的小立方体的数量是（）a．5b．6c．7d．8二、填空8．如图，①的主视图是_____、左视图是________、俯视图是________.9.如果几何体的前视图和左视图为矩形，顶视图为圆形，则几何体为__10。

如图所示，它是由几个长度、宽度和高度相等的小立方体组成的几何体的前视图、左视图和俯视图，这些几何体由该几何体的组成部分共享最新初中数学精品整理设计2初中最新高质量数学课程的毕业设计三、解答题11.指出右图中物体的三个视图中的哪一个是下图中左边的三个平面图？12．如果正对一个长方体每个面观察所得的视图都是相同的图形，那么，这个长方体一定是正方体吗？说明你的理由。

13.绘制以下几何图形的前视图、左视图和俯视图。

14．如图，是一个几何体的主视图和左视图，请把这个几何体的可能形状画出来．最新初中数学精品整理设计3最新初中数学精品整理设计参考答案一、1.B2。

A3。

补体第四成份。

D5。

D6。

C7。

D II8．③、④、②9．圆柱体10．6三、11.（1）主（左）视图；（2）俯视图；（3）左（前）视图。

1.4 从三个方向看物体的形状一、单选题1．如图，从左面看如图所示的几何体得到的平面图形是（）A．B．C．D．【答案】B【解析】【分析】直接根据三视图进行排除选项即可．【详解】由立体图形的三视图可直接排除A、C、D，只有B符合该立体图形的左视图；故选B．【点睛】本题主要考查三视图，熟练掌握三视图的方法是解题的关键．2．有一种圆柱体茶叶简如右图所示，则它的主视图是（）A．B．C．D．【答案】D【解析】【分析】根据主视图的定义判断即可．【详解】茶叶盒是圆柱体,主视图应是矩形,故选D．【点睛】本题考查主视图的定义,关键在于牢记基本概念．3．下列几何体中，其俯视图与主视图完全相同的是（）A．B．C．D．【答案】C【解析】【分析】俯视图是指从上面往下看，主视图是指从前面往后面看，根据定义逐一分析即可求解．【详解】解：选项A：俯视图是圆，主视图是三角形，故选项A错误；选项B：俯视图是圆，主视图是长方形，故选项B错误；选项C：俯视图是正方形，主视图是正方形，故选项C正确；选项D：俯视图是三角形，主视图是长方形，故选项D错误．故答案为：C．【点睛】本题考查了视图，主视图是指从前面往后面看，俯视图是指从上面往下看，左视图是指从左边往右边看，熟练三视图的概念即可求解.4．下列立体图形中，俯视图是圆的是（）A．①①①B．①①①C．①①①D．①①①【答案】D【解析】【分析】俯视图是从几何体的上面看物体，所得到的图形，分析每个几何体，解答出即可．【详解】解：①圆柱的俯视图是圆，符合题意；①圆锥的俯视图是圆，符合题意；①六棱柱的俯视图是六边形，不符合题意；①球的俯视图是圆，符合题意．故选：D．【点睛】本题主要考查了简单几何体的俯视图，具有一定的空间想象能力是解决本题的关键．5．某几何体的三视图如下所示，则该几何体可以是（）A．B．C．D．【答案】A【解析】【分析】【详解】解：根据主视图、左视图、俯视图的平面图形，可以判断该几何体为A．故选：A6．如图是由几个大小相同的小正方体搭成的几何体从不同方向看到的平面图形，则搭成这个几何体的小正方体有（）A．3个B．4个C．5个D．6个【答案】B【解析】【分析】根据给出的几何体，通过动手操作，观察可得答案为4，也可以根据画三视图的方法，发挥空间想象能力，直接想象出每个位置正方体的数目，再加上来解答即可.【详解】由三视图可得，需要的小正方体的数目：1＋2＋1＝4．故选：B．【点睛】本题考查了几何体的三视图及空间想象能力．根据“俯视图打地基，正视图疯狂盖，左视图拆违章”很容易就知道小正方体的个数．7．如图，模块①由15个棱长为1的小正方体构成，模块①-①均由4个棱长为1的小正方体构成．现在从模块①-①中选出三个模块放到模块①上，与模块①组成一个棱长为3的大正方体．下列四个方案中，符合上述要求的是（）A．模块①，①，①B．模块①，①，①C．模块①，①，①D．模块①，①，①【答案】C【解析】【分析】观察模块①可知，模块①补到模块①上面的左边，模块①补到模块①上面的右上角，模块①补模块①上面的右下角，使得模块①成为一个棱长为3的大正方体.【详解】由图形可知模块①补模块①上面的左边，模块①补模块①上面的右上角，模块①补模块①上面的右下角，使得模块①成为一个棱长为3的大正方体，故能够完成任务的是模块①，①，①，故选C.【点睛】此题主要考察简单组合体的三视图.8．从不同方向看一只茶壶，你认为是俯视效果图的是（）A．B．C．D．【答案】A【解析】俯视图是从上面看到的平面图形，也是在水平投影面上的正投影. 易判断选A.9．一个几何体的三视图如图所示，则该几何体外接球的表面积为（）A ．43πB ．83πC ．163πD ．3π 【答案】C【解析】【分析】根据主视图、左视图以及俯视图，即可判定这个几何体是圆锥，求出外接球的半径，即可求出球的表面积．【详解】由三视图可知，这个几何体是圆锥，其外接球的球心恰好是正三角形的外心，因为这个圆锥外接球的半径为23=① 所以这个球的表面积为：S =4πr 2=163π. 故选C.【点睛】本题考查了利用三视图求几何体的表面积.理解外接球的球心就是正三角形的外心是解题的关键. 10．如图，是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图，则组成这个几何体的小正方体的个数是( )A．3个或4个或5个B．4个或5个C．5个或6个D．6个或7个【答案】A【解析】根据主视图①左视图①画出俯视图可能情况.所以选A.二、填空题11．从正面、左面、上面看一个几何体，三个面看到的图形大小、形状完全相同的是__.（写出一个这样的几何体即可）．【答案】正方体【解析】【分析】分别根据所看位置写出每个几何体的三视图形状，即可得到答案．【详解】解：正方体从正面看是正方形、从左面看是正方形、从上面看正方，符合题意，故答案为正方体.【点睛】本题考查三视图相关，从不同的方向观察几何体，即可分析得到答案.12．如图是一个由一些相同的小正方体搭成的立体图形，图(1)～(3)是它的三视图，试标出各个视图的名称________，______，_________.【答案】(1)左视图(2)俯视图(3)主视图【解析】【分析】根据从正面看到的图叫做主视图，从左面看到的图叫做左视图，从上面看到的图叫做俯视图，可得答案．【详解】解：根据题意可知，主视图是（3），左视图是（1），俯视图是（2），故答案为：(1)左视图，(2)俯视图，(3)主视图.【点睛】本题考查了简单组合体的三视图，从上边看到的图是俯视图，从左边看到的图是左视图，从正面看到的图是主视图．13．一个几何体分别从上面看、从左面看、从正面看，得到的平面图形如图所示，则这个几何体是________．【答案】圆柱【解析】【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．【详解】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是圆可判断出这个几何体应该是圆柱．故答案为：圆柱．【点睛】本题由物体的三种视图推出原来几何体的形状，考查了学生的思考能力和对几何体三种视图的空间想象能力和综合能力．14．已知一个物体由x个相同的正方体堆成，它的三视图如图，那么x ________．【答案】8【解析】【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，求出总个数即可．【详解】综合三视图，这个物体共有3层，第一层有6个，第二层2个，一共有6+2=8（个），则x=8，故答案是：8．【点睛】考查了由三视图判断几何体，考查了对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．15．若干桶方便面摆放在桌面上，如图所给出的是从不同方向看到的图形，从图形上可以看出这堆方便面共有_______桶．【答案】6【解析】【分析】从俯视图中可以看出最底层方便面的个数及摆放的形状，从主视图可以看出每一层方便面的层数和个数，从左视图可看出每一行方便面的层数和个数，从而算出总的个数．【详解】三摞方便面是桶数之和为：3+1+2=6．故答案是：6．【点睛】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．16．一个由若干个小正方体搭建而成的几何体的三视图如下，则搭建这个几何体的小正方体有_______个。

北师大版七年级数学上册1.4《从三个方向看物体的形状》同步训练一、选择题1.如图，是由三个相同的小正方体组成的几何体，该几何体的左视图是( )A. B. C. D.2.如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是( )A. B. C. D.3.圆锥的三视图是（）A. 主视图和俯视图是三角形，侧视图是圆。

B. 主视图和侧视图是三角形，俯视图是圆。

C. 主视图和侧视图是三角形，俯视图是圆和圆心。

D. 主视图和俯视图是三角形，侧视图是圆和圆心。

4.如图是某几何题的三视图，下列判断正确的是（）A. 几何体是圆柱体，高为2B. 几何体是圆锥体，高为2C. 几何体是圆柱体，半径为2D. 几何体是圆锥体，半径为25.一个几何体是由若干个相同的立方体组成，其主视图和左视图如图所示，则组成这个几何体的立方体个数不可能的是（）A. 15个B. 13个C. 11个D. 5个二、填空题6.观察图1中的几何体，指出图2的三幅图分别是从哪个方向看到的．甲是从________ 看到的，乙是从________ 看到的，丙是从________ 看到的．7.某个立体图形的三视图的形状都相同，请你写出一种这样的几何体________．8.如图是一个几何体的三视图，若这个几何体的体积是36，则它的表面积是________.9.如图两个图形分别是某个几何体的俯视图和主视图，则该几何体是________．10.如图，在一次数学活动课上，张明用17个边长为1的小正方形搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要________个小立方体，王亮所搭几何体的表面积为________．三、解答题11.如图是一个由若干个小正方体搭成的几何体从上面看到的形状图，其中小正方形内的数字是该位置小正方体的个数，请你画出它从正面和从左面看到的形状图．12.如图是一个几何体的三视图．（1）写出这个几何体的名称；（2）求此几何体表面展开图的面积．13.如图是用几个小正方体搭成的几何体，画出它的三视图。

1.4 从三个方向看物体的形状
一、选择题（共13小题；共52分）
1. 某几何体的三视图如图所示，则这个几何体是
A. 圆柱
B. 正方体
C. 球
D. 圆锥
2. 桌面上放着个长方体和个圆柱体，按如图所示的方式摆放在一起，其左视图
是
A. B.
C. D.
3. 如图是由五个相同的小正方体组成的几何体，则它的左视图是
A. B.
C. D.
4. 如图是一个三视图，则此三视图所对应的直观图是
A. B.
C. D.
5. 如图，由两个相同的正方体和一个圆锥体组成一个立体图形，其俯视图是
A. B.
C. D.
6. 图中的三视图所对应的几何体是
A. B.
C. D.
7. 由个相同的小正方体堆成的几何体，其主视图、俯视图如下所示，则的最大
值是
A. B. C. D.
8. 由若干个边长为的正方体堆积成一个几何体，它的三视图如图，则这个几何
体的表面积是
A. B. C. D.
9. 一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其
中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是。

1.4 从三个方向看物体的形状练习题一、选择题1．如图，从正面看是（）2．如图，其中②是从①的（）方向看。

A．正面B．左面C．上面D．无法确定3．如图，从三个方向看这个几何体，则这个几何体是（）4．如图，是一个四棱柱和圆柱的摆放组合，则从上面看是（）5．如图，从①和②的（）方向看是一样的．A．正面 B．左面 C．上面 D．左面、上面6．如图，从正面看和从左面看，由若干相同小正方体组成的几何体，，则这个几何体有（）种可能的形状．A．2 B．3 C．4 D．57．如图，从三个方向看，由一些相同的小正方体构成的立体图形：构成这个立体图形的小正方体的个数是（）．A．5 B．6 C．7 D．88．图中三视图所对应的直观图是（）第8题图二、填空题1．如图，①从正面看是_____、从左面看是________、从上面看是________.2．一个几何体从其正面看，左面看都是长方形，从上面看是圆．则这个几何体是________．3．如图，从一个由若干个长、宽、高相等的小正方体摆成的几何体的正面、左面和上面看，则组成这个几何体共用了________个小正方体．4．一个几何体从正面看和左面看都是三角形，而上面看是圆，则这个几何体是_______．5．如图，从一个由若干个小正方体组成的几何体的正面和左面看，则这个几何体至少由______个小正方体组成，最多由______个小正方体组成．6．一个球体从正面，左面，上面看都是__________．三、解答题1．指出下图中左面三个平面图形分别是从右面这个物体的哪个方向看？2．如果正对一个长方体每个面观察所得的视图都是相同的图形，那么，这个长方体一定是正方体吗？说明你的理由。

3．画出下列几何体从正面看，从左面看，从上面看到的形状图。

4．如图是一个几何体的主视图和左视图，构成这个立体图形的小正方体的个数有哪些情况？参考答案：一、1． B 2． A 3． C 4．A 5． D 6． D 7． D二、1．③、④、② 2．圆柱体 3．6 4．圆锥 5． 5、9 6．圆三、1．（1）主（左）视图；（2）俯视图；（3）左（主）视图．2．是．3.4．答如图，4个或者5个。