五年级高斯奥数之包含与排除含答案

第4讲包含与排除内容概述有重叠部分的若干对象的计数问题。

能利用文氏图进行辅助分析，弄清文氏图中每部分的含以；结合文氏图理解两个对象和三个对象的容斥原理；灵活处理具有一些不确定性的计数问题，以及其他形式的重复计数问题。

兴趣篇1．某次练习共有2道题，做对第一题的有40人，这40人中有13人第2题做错了，那么第1题第2题全对的共有多少人？答案：27人解析：40-13=27人。

2．暑假里，萱萱和小高一起讨论“金陵十八景”。

他们发现十八景中的每一处都有人去过，而且有五处是两人都去过的。

如果萱萱去过其中的十二景，那么小高去过其中的几景？答案：11景解析：方法一：画文氏图：圆A是萱萱去过的地方，圆B是小高去过的地方。

这样①号部分表示的是只有萱萱去过的地方，②号部分表示的是两个人都去过的地方，③号部分表示的是只有小高去过的地方。

根据条件知：萱萱去过12景，也就是圆A共12景；他们一共去了18景，所以圆A与圆B一共包括18景；于是③有18-12=6景。

两人都去过的有5景，也就是说②有5景。

小高去过的是②和③，共5+6=11景。

方法二：运用容斥原理：对于两个对象A和B，有这样的公式：A与B的总数=A+B-A和B的重叠。

因此小高去过的有18+5-12=11景。

3．在一群小朋友中，有12人看过动画片《黑猫警长》，有21人看过动画片《大闹天宫》，并且有8人两部动画片都看过。

请问：至少看过其中一部的小朋友有多少人？答案：25人解析：方法一：画文氏图：圆A表示看过《黑猫警长》的人，圆B表示看过《大闹天宫》的人，这样②是两个都看过的人，有8人。

有12人看过《黑猫警长》，①②共12人；有21人看过《大闹天宫》，②③共21人；只看过《大闹天宫》的人是③，它有21-8=13人。

因此，①②③加起来共有12+13=25人。

方法二：根据容斥原理，得12+21-8=25人。

4．一群小朋友共有40人，他们都喜欢吃馒头或者米饭中的一种或者两种，喜欢吃馒头的有30人，两种都喜欢吃的有7人，那么喜欢吃米饭的有多少人？答案：17人解析：方法一：画出文氏图解答（图略，可参考前两题）．只喜欢吃馒头的有30-7=23人；喜欢吃米饭的有40-23=17人．方法二：根据容斥原理，得40+7-30=17人。

第33讲包含与排除（容斥原理）一、专题简析：集合是指具有某种属性的事物的全体，它是数学中的最基本的概念之一。

如某班全体学生可以看作是一个集合，0、1、2、3、4、5、6、7、8、9便组成一个数字集合。

组成集合的每个事物称为这个集合的元素。

如某班全体学生组成一个集合，每一个学生都是这个集合的元素，数字集合中有10个元素。

两个集合中可以做加法运算，把两个集合A、B合并在一起，就组成了一个新的集合C。

计算集合C的元素的个数的思考方法主要是包含与排除：先把A、B的一切元素都“包含”进来加在一起，再“排除”A、B两集合的公共元素的个数，减去加了两次的元素，即：C=A＋B－AB。

在解包含与排除问题时，要善于使用形象的图示帮助理解题意，搞清数量关系的逻辑关系。

有些语言不易表达清楚的关系，用了适当的图形就显得很直观、很清楚，因而容易进行计算。

二、精讲精练例1五年级96名学生都订了报纸，有64人订了少年报，有48人订了小学生报。

两种报纸都订的有多少人？练习一1、一个班的52人都在做语文和数学作业。

有32人做完了语文作业，有35人做完了数学作业。

语文、数学作业都做完的有多少人？2、五年级有122人参加语文、数学考试，每人至少有一门功课得优。

其中语文得优的有65人，数学得优的有87人。

语文、数学都得优的有多少人？例2：某校教师至少懂得英语和日语中的一种语言。

已知有35人懂英语，34人懂日语，两种语言都懂的有21人。

这个学校共有多少名教师？练习二1、某校的每个学生至少爱体育和文娱中的一种活动。

已知有900人爱好体育活动，有850人爱好文娱活动，其中260人两种活动都爱好。

这个学校共有学生多少人？2、某班在一次测验中有26人语文获优，有30人数学获优，其中语文、数学双优的有12人，另外还有8人语文、数学均未获优。

这个班共有多少人？例3：学校开展课外活动，共有250人参加。

其中参加象棋组和乒乓球组的同学不同时活动，参加象棋组的有83人，参加乒乓球组的有86人，这两个小组都参加的有25人。

第4讲包含与排除内容概念：有重叠部分的若干对象的计数问题，能利用文氏图进行辅助分析，弄清文氏图中每部分的含义；结合文氏图理解两个对象和三个对象的容斥原理；灵活处理具有一些不确定性的计数问题，以及其他形式的重复计数问题。

典型问题：兴趣篇：1.暑假里，小悦和冬冬一起讨论“金陵十八景”。

他们发现十八景中的每一处都有人去过，而且有五处是两人都去过的。

如果小悦去过其中的十二景，那么冬冬去过其中的几景？2.在一群小朋友中，有12人看过动画片《黑猫警长》，有21人看过动画片《大闹天宫》，并且有8人两部动画片都看过。

请问：至少看过其中一部的小朋友有多少人？3、五年级一班45个学生参加期末考试。

成绩公布后，数学得满分的有10人，数学及语文均得满分的有3人，这两科都没有得满分的有29人。

请问：语文成绩得满分的有多少人？4.某餐馆有27道招牌菜。

小悦吃过其中的13道，冬冬吃过其中的7道，而且有2道菜是两人都吃过的。

请问：有多少道招牌菜是两人都没有吃过的？5.如图4-1，已知甲、乙、丙三个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6、8、5，同时被这三个圆覆盖的部分的面积为2。

请问：（1）只被甲或乙覆盖，却不被丙覆盖的部分的面积是多少？（2）只被这3个圆中某一个圆覆盖的部分的面积是多少？6.在一个由30人组成的合唱队中，每个人都爱喝红茶、绿茶、花茶中的一种或者几种。

其中有10个人爱喝红茶，12人不爱喝红茶却爱喝绿茶。

请问：只爱喝花茶的有多少人？7.光明小学五年级课外活动有体育、音乐、书法三个小组，参加的人数分别是54人、46人、36人。

同时参加体育小组和音乐小组的有4人，同时参加体育小组和书法小组的有7人，同时参加音乐小组和书法小组的有10人，三组都参加的有2人。

光明小学五年级参加课外活动的一共有多少人？8.卫生部对120种食物是否含有维生素A、C、E进行调查，结果发现：含维生素A的有62种，含维生素C的有90种，含维生素E的有68种，同时含维生素A和C的有48种，同时含维生素A和E的有36种，同时含维生素C和E的有50种，同时含这三种维生素的有25种。

五年级奥数－包含与排除1.某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组都参加。

那么有多少人两个小组都不参加？2.50名同学面向老师站成一行，老师先让大家从左至右按1，2，3， (49)50依次报数；再让报数是4的倍数的同学向后转，接着又让报数是6的倍数的同学向后转。

问：现在面向老师的同学还有多少名？3.在从1至100的自然数中，既不能被5除尽也不能被7除尽的数有多少个？4.在前1000个自然数（不包括0）中，既不是平方数也不是立方数的自然数有多少个？5.有三个面积各为20平方厘米的圆纸片放在桌上，见下图。

三个纸片共同重叠的面积是8平方厘米，三个纸片盖住桌面的总面积是36平方厘米。

问：图中阴影部分的面积之和是多少？五年级奥数－包含与排除答案1.解析：40=--人。

(+)171015182.解析：面向老师的学生包括报数既不是4的倍数也不是6的倍数、报数既是4的倍数也是6的倍数即12的倍数的同学，共计38+[=-+50-人。

)]44812(3.解析：1000=(-+-个。

142686200)284.解析：前1000个自然数中，平方数有：1，4，9，16，25，36， (900)961，共计31个；立方数有1，8，27，64，125，216，343，521，729，1000，共计10个；既是平方数又是立方数的有1，64，729，共计3个。

所以既不是平方数也不是立方数的有9621000=+-个。

-)3(10315.解析：2⨯-=-⨯。

88236320cm。

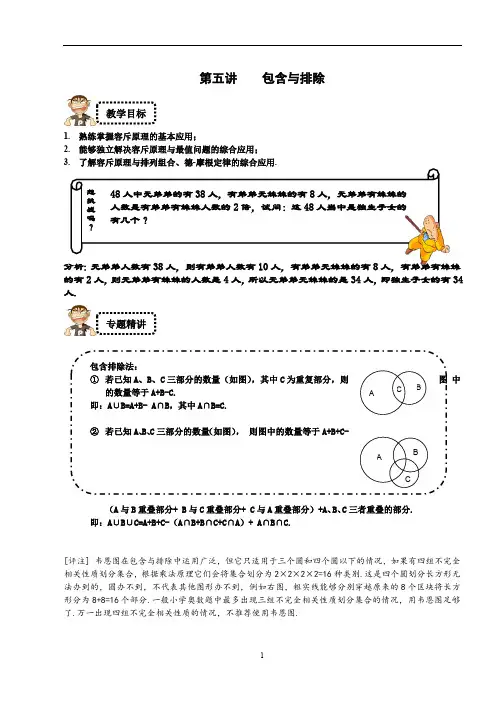
第五讲 包含与排除教学目标1. 熟练掌握容斥原理的基本应用；2. 能够独立解决容斥原理与最值问题的综合应用；3. 了解容斥原理与排列组合、德-摩根定律的综合应用.分析：无弟弟人数有38人，则有弟弟人数有10人，有弟弟无妹妹的有8人，有弟弟有妹妹的有2人，则无弟弟有妹妹的人数是4人，所以无弟弟无妹妹的是34人，即独生子女的有34人.包含排除法：① 若已知A 、B 、C 三部分的数量（如图），其中C 为重复部分，则图中的数量等于A+B-C.即：A ∪B=A+B- A ∩B ，其中A ∩B=C.② 若已知A 、B 、C 三部分的数量（如图）， 则图中的数量等于A+B+C-（A 与B 重叠部分+ B 与C 重叠部分+ C 与A 重叠部分）+A 、B 、C 三者重叠的部分. 即：A ∪B ∪C=A+B+C-（A ∩B+B ∩C+C ∩A ）+ A ∩B ∩C.[评注] 韦恩图在包含与排除中运用广泛，但它只适用于三个圆和四个圆以下的情况，如果有四组不完全相关性质划分集合，根据乘法原理它们会将集合划分为2×2×2×2=16种类别.这是四个圆划分长方形无法办到的，圆办不到，不代表其他图形办不到，例如右图，粗实线能够分别穿越原来的8个区块将长方形分为8+8=16个部分.一般小学奥数题中最多出现三组不完全相关性质划分集合的情况，用韦恩图足够了.万一出现四组不完全相关性质的情况，不推荐使用韦恩图. C B A C B A 想挑战吗？48人中无弟弟的有38人，有弟弟无妹妹的有8人，无弟弟有妹妹的人数是有弟弟有妹妹人数的2倍，试问：这48人当中是独生子女的有几个？专题精讲（一）容斥原理的基本应用【例1】（2004年中央A类公务员考题）在桌面上放置着三个面积相等的纸片A、B、C，A和B的重叠面积为16 cm2，B和C重叠的面积为12 cm2，C和A重叠的面积为10 cm2，三张纸片共同重叠的面积为6 cm2，已知三张纸片一共覆盖了160 cm2，那么每张纸片的面积为多少？分析：将各种重叠、部分重叠的各部分凑成三张纸片的的面积和.可以由公式推倒，也可以靠对各部分面积的容斥关系和数量关系的理解，三张纸片的面积和=覆盖面积+重叠了两次部分的面积+2×重叠了三次部分的面积=覆盖面积+两两相互重叠的面积之和-重叠了三次的部分=160+16+12+10-6=192，所以每张纸片的面积为64cm2.[前铺] 在桌面上放置着三个两两重叠的近圆形纸片（如图，三个纸片等大），它们的面积都是100cm2，并知A、B两圆重叠的面积是20cm2，A、C两圆重叠的面积为45cm2，B、C两圆重叠的面积为31cm2,三个圆共同重叠的面积为15cm2，求盖住桌子的总面积．分析：（法1）直接套用公式：100×3-20-45-31+15=219cm2.套用公式的前提必须建立在对公式的理解的基础上，A、B、C三个圆的面积各包含了四块面积，例如A覆盖的部分包括，A与B 共有而C没有的；A与C共有的而B没有的，A、B、C三圆共有的；A独有的.这样如果将A、B、C的面积简单相加，A与B共有而B没有的；A与C共有的而B没有的；B与C共有的而A没有的；A、B、C三个部分的共有部分则被计算了3次，如果再将A、C两圆重叠的；B、C两圆重叠的；A、B两圆重叠的三部分各减去一遍，那么同时A、B、C三个部分的共有部分则被减了3次，此时得到的结果中A、B、C三个部分的共有部分没有被计算过，所以最后还要将这一部分加上.（法2）分别计算各区块的面积，A与B共有而C没有的=20-15=5，B与C共有的而A没有的=31-15=16，A与C共有的而B没有的=45-15=30.A独有的=100-5-30-15=50，B独有的=100-16-5-15=64，C独有的100-30-16-15=39.盖住桌子的总面积=15+5+16+30+50+64+39=219，事实上如果我们实现没有将各个区块算出来的话，盖住桌子的总面积=15+（20-15）+（31-15）+（45-15）+（100-15-（20-15）-（45-15））+（100-15-（20-15）-（31-15））+（100-15-（36-15）-（45-15））=100×3-20-45-31+15=219.[拓展] 将1～13这13个数字分别填入如图所示的由四个大小相同的圆分割成的13个区域中，然后把每个圆内的7个数相加，最后把四个圆的和相加，问：和最大是多少？分析：越是中间，被重复计算的越多，最中心的区域被重复计算四次，将数字案从大到小依次填写于被重复计算多的区格中，最大和为：13×4+（12+11+10+9）×3+（8+7+6+5）×2+（4+3+2+1）=240.【例2】（奥数网原创题）学而思学校有46名学生参加三项课外活动，其中24人参加了绘画小组，20人参加了合唱小组，参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍，又是三项活动都参加人数的7倍，既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍，既参加绘画小组又参加合唱小组的有10人，求参加朗诵小组的人数．分析：设三项都参加的人数有X人，则参加朗诵小组的人数为7X人，参加绘画小组又参加朗诵小组的人数为2X人，参加朗诵小组又参加合唱小组的人数为2X人.有46-24-20-7X+2X+2X+10-X=0，解得X=3，所以参与朗诵小组的人数为21人．[前铺] 学而思举行各年级学生画展，其中18幅不是六年级的，20幅不是五年级的，现在知道五、六年级共展出22幅画，问：其他年级共展出多少幅画？分析：（法1）其他年级与五年级共展出18幅画，其他年级与六年级共展出20幅画，五年级六年级共展出22幅画，其他年级共展出（18+20-22）÷2=8幅.（法2）把五年级的画看成一个集合A，六年级的画看成一个集合B，其他年级的画看成一个集合C，它们的画加起来是集合I，那么我们知道：n(I)－n(A)=20,n(I)－n(B)=18,n(A)＋n(B)=22,其他年级展出的画n(C)=n(I)-n(A)-n(B).把n(I)－n(A)=20,n(I)－n(B)=18两个式子相加得到：2n(I)－n(A)－n(B)=38,即2n(I)=n(A)＋n(B)＋38=22＋38=60,n(I)=30.所以，n(C)=n(I)―n(A)―n(B)=30―22=8幅．[拓展] 五一班有28位同学，每人至少参加数学、语文、自然课外小组中的一个．其中仅参加数学与语文小组的人数等于仅参加数学小组的人数，没有同学仅参加语文或仅参加自然小组，恰有6个同学参加数学与自然小组但不参加语文小组，仅参加语文与自然小组的人数是3个小组全参加的人数的5倍，并且知道3个小组全参加的人数是一个不为0的偶数，那么仅参加数学和语文小组的人有多少人？分析：参加3个小组的人数是一个不为0的偶数，如果该数大于或等于4，那么仅参加语文与自然小组的人数则大于等于20，而仅参加数学与自然小组的人有6个，这样至少应有30人，与题意矛盾，所以参加3个小组的人数为2．仅参加语文与自然小组的人数为10，于是仅参加语文与自然、仅参加数学与自然和参加3个小组的认识一共是18人，剩下的10人是仅参加数学与语文以及仅参加数学的．由于这两个人数相等，所以仅参加数学和语文小组的有5人．【例3】（奥数网原创题）求不超过120的合数的个数分析：从120中去掉质数，再去掉“1”，剩下的即是合数．（法1）120以内：①既不是素数又不是合数的数有一个，即“1”；②素数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97、101、103、107、109、113、共30个．所以不超过120的合数有120－1－30＝89(个)筛法：从小到大按顺序写出1－120的所有自然数：先划掉1，保留2，然后划掉2的所有倍数4,6，…120等；保留3，再划掉所有3的倍数6,9…117、120等；保留5，再划掉5的所有倍数10,15，…120；保留7，再划掉7的所有倍数，…这样，上面数表中剩下的数就是120以内的所有素数，这种方法是最古老的寻找素数的方法，叫做“埃斯托拉‘筛法’”) 当n 不很大时，计算1－n 中的合数的个数困难不大；但当n 很大时，利用筛法就很困难、很费时了，必须另觅他途．（法2）如果能找出1－n 中质数的个数m ，则n －1－m 就是不超过n 的合数的个数．由初等数论中定理：a 是大于1的整数．如果所有不大于√a 的质数都不能整除a ，那么a 是质数．因为120<121＝112，√120<11，所以不超过120的合数必是2或3或5或7的倍数，所以只要分别计算出不超过120的2、3、5、7的倍数，再利用“容斥原理”即可，所以不超过120的合数共有89个．[前铺1] 求1至100的自然数中能被3或7整除的数的个数.分析：记 A ：1到100中3的倍数，100÷3=33……1，有33个；B ：1到100中7的倍数，100÷7=14……2，有14个；A ∩B:1到100中3和7的倍数，即21的倍数，100÷21=4……16，有4个．依据公式，1到100中3的倍数或7的倍数共有33+14-4=43个，则能被3或7整除的数的个数为43个.[前铺2]（07年我爱数学夏令营）在1到2004的所有自然数中，既不是2的倍数，也不是3、5的倍数的数有多少个？分析：1到2004中是2的倍数的有1002个，3的倍数有668个，5的倍数有[2004/5]=400个,6的倍数有334个，10的倍数有[2004/10]=200个，15的倍数有[2004/15]=133个，30的倍数有[2004/30]=66个.所以不是2、3、5的倍数有2004-1002-668-400+334+200+133-66=535个.[巩固] 求在1～100的自然数中不是5的倍数也不是6的倍数的数有多少个？分析：“既不是5的倍数也不是6的倍数”的反面情况就是“是5的倍数或者是6的倍数”．记 A ：1～100中5的倍数，，有20个；100520÷=B ：1～100中6的倍数，，有16个；4166100 =÷：1～100中5和6的公倍数，即30的倍数，，有3个．B A 10330100 =÷依据公式，1～100中5的倍数或6的倍数共有个，则既不是5的倍数也不是6的3331620=-+倍数的数有个．6733100=-[拓展1] 不超过201的自然数中，至少有两个数字相同的奇数有多少个？分析：10～99中符合条件的数有5个（11、33、55、77、99），100～199中有三个数字都不同的有9×8=72个，偶数有50个，有三个数字都不同的偶数有5×8=40个，因此至少有两个数字相同的不同的奇数有100-72-50+40=18个，200和201都不符合条件．一共有23个符合条件．[拓展2] 有2000盏亮着的电灯，各有一个拉线开关控制着，现按其顺序编号为1，2，3，…，2000，然后将编号为2的倍数的灯线拉一下，再将编号为3的倍数的灯线拉一下，最后将编号为5的倍数的灯线拉一下，三次拉完后，亮着的灯有多少盏？分析：教师可以先讲解前铺，但要区分例题与前铺的区别.三次拉完后，亮着的灯包括不是2、3、5的倍数的数以及是6、10、15的倍数但不是30的倍数的数．1～2000这2000个正整数中，2的倍数有1000个，3的倍数有666个，5的倍数有400个，6的倍数有333个，10的倍数有200个，15的倍数有133个，30的倍数有66个，亮着的灯一共有2000-1000-666-400+2×（333+200+133）-4×66=1002盏．【例4】 学而思举行数学擂台赛，共出A 、B 、C 三道题，有110人参加，每个人都至少答对一道题，已知答对A 题的有52人，只答对A 题的有16人；答对B 题的有61人，只答对B 题的有15人；答对C 题的有63人，只答对C 题的有21人，问三道题都答对的有多少人？分析：结合题的条件，设仅答对AB 的有X 人，BC 的有Z 人，AC 的有Y 人，全答对的有W 人，可得以下等式： 16+X+Z+W=52……①15+X+Y+W=61……②21+Y+Z+W=63……③16+15+21+X+Y+Z+W=110…④②+①+③-④×2：解得W=8，即三道题都答对的人数为8．【例5】 （2007中央B 类公务员考题）某次考试有52人参加，共考5题，每题做错的人数统计如表：已知每人都至少做对一道题，做对一道题的有7人，5道题全对的有6人，做对2道题和3道题的人数一样多，那么做对4道题的人数是多少？分析：设做对2道题的和3道题的人数为X ，做对4道题的人数有Y 人．则根据人数和错题数的相关等量关系有以下两条等式：7+2X+Y+6=524×7+3X+2X+Y=4+6+10+20+39X=4Y=31 所以做对4道题的有31人．（二） 容斥原理与最值问题的综合应用题号 一 二 三 四 五 做错人数 4 6 10 20 39容斥原理与最值问题的结合往往是小学生的难点，不仅是因为不等式的出现，还有分数、倍数关系的融合都会使题目复杂易错，更重要的是注意“至少”“最多”等所隐含的数学关系.【例6】 1～100这100个自然数，A 、B 、C 三个人都分别从某一个数开始按顺序往后数，已知A 数了75个数，B 数了60个数，C 数了52个数，那么三个人共同数到的数最少有多少个？分析：三个人共同数到的数也必然是一段连续的数，这段数有X 个．A,B,C 三人中至多有一个人既数了小于这段数的数，又数了大于这段数的数．否则如果有两个人既数了小于这段数的数，又数了大于这段数的数，则第三人无论数了小于这段数的数，还是大于这段数的数，三人共同数的数都不止这X 个．对于另外两个数数区间没有跨越这段数的人有不等式Y+Z-X ≤100（Y 和Z 分别为两人所数的个数）X ≥Y+Z-100≥60+52-100=12.[前铺] 学校组织一次数学竞赛，共出了一、二、三共三道大题，至少做对一道题的有40人，其中做对第一题的有15人，做对第二题的有20人，做对第三题的有25人，如果三道题都做对的只有2人，那么只对两道题的有多少人？只做对一道题的又有多少人？分析：假设只答对两道题的有X 人，根据一、二、三道题总人数中扣去重复计算的人员数乘以被重复计算的次数等于做对一道题的人数，则有15+20+25-X-2×2=40，解得X=16，即只作对一道题的人数为15+20+25-2×16-3×2=22人．【例7】 （人大附中考题）一次数学考试，小明答错题目占总数的，小军答对7道题，两人都答对的19题目是总数的，问：小明答对多少道题？ 16分析：设两人都答对的题的数目是X ，由条件可知一共有6X 道题，小明至少有（7-X ）道题没答，又因为小明答错题目占总数的，所以，小明没答的题有X 道．X ≤（7-X ），得到X ≥，且X 为3192323215的倍数，所以只能为6，一共有题36道，小明答题36-36÷9=32题．[前铺] 某班在体育课上进行了成绩考核，这个班在100米自由泳、跳远、铅球三项测试中获优秀等级的人数分类统计如下：100米自由泳获得优秀的有21人，跳远获得优秀的有19人，铅球获得优秀的有20人．100米自由泳和跳远都获得优秀的有9人，跳远和铅球都获得优秀的有7人，铅球和100米自由泳都获得优秀的有8人．有5人没有获得任何一项优秀．试判断这个班的人数的取值范围．分析：该班人数表达为5+21+19+20-9-7-8+X ，X 为三项测试都优秀的人．考虑X 的取值范围，0≤X ≤7，即该班人数最多能有48人，最少有41人．[小笑话]1. 公共汽车上老太太怕坐过站逢站必问．汽车到一站她就一个劲地用雨伞捅司机：＂这是展览中心吗？＂＂不是，这是排骨！＂2. 护士看到肝病病人在病房喝酒，就上前走过去叮嘱说：＂小心肝！＂病人微笑道：＂小宝贝．＂【例8】 （仁华考题）60人中有的人会打乒乓球，的人会打羽毛球，的人会打排球，这三项运动233445都会的人有22人，问：这三项运动都不会的最多有多少人？分析：设只会打乒乓球和羽毛球的人有X ，只会打乒乓球和排球的有Y 人，只会打羽毛球和排球的有Z 人．则X 、Y 、Z 有如下关系： 40-(X+Y+22)≥045-(X+Z+22)≥048-(Y+Z+22)≥0将三条关系式相加，得到X+Y+Z ≤33，而60人当中会至少一项运动的人数有40+45+48-（X+Y+Z ）-2×22≥56人．60人当中三项都不会的人数最多4人．（当X 、Y 、Z 分别取7、10、15时，不等式组成立）．【例9】 希望小学的音乐兴趣小组有37人，其中有20人会手风琴，16人会钢琴，24人会电子琴，其中既会手风琴又会钢琴的有8人，既会电子琴又会钢琴的有10人，既会手风琴又会电子琴的有8人．请问：这三种琴都不会的人至多有多少人？分析：三种琴都不会的人有37-20-16-24+8+10+8-X 人，其中X 为三种琴都会的人数，考虑X 的取值范围, X 必须满足会指定乐器的学生人数必须为非负整数．于是有不等式组：X ≥08-X ≥010-X ≥08-X ≥020-8-8+X ≥016-8-10+X ≥024-8-10+X ≥037-20-16-24+8+10+8-X ≥0得到的X 取值范围为2≤X ≤3．当X 取2时三种琴都不会的人数得到最小值1.[前铺] 图书室有100本书，借阅者要在借书证上签名，已知这100本书中有甲签名的33本，有乙签名的44本，有丙签名的55本，其中同时有甲、乙签名的图书有29本，同时有甲、丙签名的图书有25本，同时有乙、丙签名的图书有36本，问：这批图书中有多少本没有被这三个人中的任何一个人借阅过？分析：设这批图书中被这三个人同时借阅过的有x 本，则有33+44+55-29-25-36+x=42+x 本书被人借过，因为同时有甲、丙签名的图书才有25本，所以x 的最大值是25，42+x 的最大值是67，100-67=33（本），即没有被这三个人中的任何一个人借阅过的至少有33本.[小笑话]1. 南非有一位渔民，有一件很烦心的心事：每当他停车离开后，总有野生狒狒把他的汽车后视镜和雨刷掰下来．后来，他想到一条妙计：狒狒很怕蛇，何不在车上放几条橡胶蛇吓唬吓唬它们呢？第二天一早，他就到玩具店买了12条长长的蛇，放在引擎盖和车顶上，几个小时后，他回到车边，发现车身上全是凹坑：一群狒狒正在一边怒气冲冲的朝那些“蛇”扔石头！2. 沙僧参加数学考试，监考老师盯着他脖子上的珠子看了半天，冷笑道：“嘿嘿，把算盘伪装成这样了！休想作弊，快摘下来！”（三） 容斥原理与排列组合、德·摩根定律的综合应用（本部分例题根据近两年全国高中数学联赛改编）[信息提示] 集合的基本概念某些指定的对象集在一起就成为一个集合，也简称集，集合常常用大写字母表示，比如A ，B ，C 等等，在平面上集合也常用一个圆表示，集合中的每个对象叫做这个集合的元素，元素与集合只有两种关系，即元素属于集合或者不属于集合，元素一般用小写字母表示．元素属于集合记作．a A a A ∈元素不属于集合记作或．a A a A ∉a A ∈由所有属于集合且属于集合的元素所构成的集合，叫做与的交集，记作：（读作“A B A B A B A 交”）．B由所有属于集合或属于集合的元素所构成的集合，叫做与的并集，记作：（读作“A B A B A B A 并”）．B已知全集，集合，由于中所有不属于的元素组成的集合，叫做集合在集合中的补集，I A I A A I 记作：（读作“补”）．A A如果我们用（）表示集合中元素的个数，那么可以叙述容斥原理如下：n A A （1），若是非空集合，称，两个集合是相容的，则()()()()n A B n A n B n A B =+- A B A B ，从而，特别地，若（是空集，称，两个集合()0n A B > ()()()n A B n A n B <+ A B =∅ ∅A B 是不相容的即相斥的），则，这时有()0n A B = ()()()n A B n A n B =+ （2）（是全集，，是的子集）．()(I)()()()n A B n n A n B n A B =--+ I A B I（3）()()()()()()()()n A B C n A n B n C n A B n B C n C A n A B C =++---+ （4）()()()()()()()n A B C n I n A n B n C n A B n B C =---++()()n CA n A B C +-【例10】 从6名运动员中选出4名参加4x100m 接力赛，如果甲不跑第一棒，乙不跑第四棒，共有多少种不同的参赛方法?分析：设全集U ＝｛6人中任取4人参赛的排列｝，A={甲跑第一棒的排列，B={乙跑第四棒的排列}，根据容斥原理得参赛方法共有：252)()()()(24353546=+--=+--A A A A B A B n A n n (种).【例11】 学而思五年级竞赛班的学生中，参加课外语文小组的有20人，参加数学小组的有22人，既参加语文又参加数学小组的有10人，既未参加语文又未参加数学小组的有15人，问共有多少学生? 分析：设U={学而思五年级竞赛班的学生}，A={学而思五年级竞赛班参加语文小组的学生}，B={学而思五年级竞赛班参加数学小组的学生}，由容斥原理及德·摩根定律：)(4710222015)()()())(()()]([)(人=-++=-++=+=B A n B n A n B A C n B A n B A C n U n【例12】 由数字1、2、3、4、5可以组成多少个无重复数字且2、3都与4不相邻的五位数． 分析：设A={2与4相邻的五位数}，B={3与4相邻的五位数}，则原题即求)(B C A C n ，由容斥原理及德·摩根定律：.36)()()()()()()]([)(33224422442255=⋅+⋅-⋅-=+--=-==A A A A A A A B A n B n A n n B A n n B A C n B C A C n注：)(B A n 表示2与4相邻且3与4相邻的五位数的个数，那么4一定排在2与3之间，且2、3、4相邻，故有3322A A ⋅种排法．[字谜及脑筋急转弯]1. 十个人打架，八个人拉，六个人进屋把门叉（打一个字）——答案：校2. 乌龟和豆子赛跑，遇到一条河，乌龟游过去赢了.（猜一种蔬菜名）——答案：荷兰豆3. 一个小人，带个小帽，过个小桥，看着月亮，哼着小曲，吃着小豆（打一个繁体字）——答案：體（体）专题展望因为容斥原理的相关内容我们会在六年级继续学习.练习五1. （例1）边长为6、5、2的三个正方形，如图所示，求它们的盖住部分的面积．分析：边长为5的正方形与边长为6的正方形，共同盖住的部分面积为9；边长为5的正方形与边长为2的正方形，共同盖住的部分面积为2；边长为2的正方形与边长为6的正方形，共同盖住的部分面积为2；三个正方形共同盖住的面积为1．它们一共盖住面积为25+36+4-9-2-2+1=53.2. （例3）求在1～100的自然数中不是5的倍数也不是6的倍数的数有多少个？分析：“既不是5的倍数也不是6的倍数”的反面情况就是“是5的倍数或者是6的倍数”．记 A ：1～100中5的倍数，，有20个；100520÷=B ：1～100中6的倍数，，有16个；4166100 =÷：1～100中5和6的公倍数，即30的倍数，，有3个．B A 10330100 =÷依据公式，1～100中5的倍数或6的倍数共有个，则既不是5的倍数也不是6的3331620=-+倍数的数有个．6733100=-3. （例3）以105为分母的最简真分数共有多少个？分析：105=3×5×7，105以内的3的倍数有35个，5的倍数有21个，7的倍数有15个，3×5的倍数有7个，3×7的倍数有5个，5×7的倍数有3个，只有105是3、5、7的倍数，105以内与105互质的数一共有105-35-21-15+7+5+3-1=48个.4. （例4）在所有的三位自然数中，组成数字的三个数字既有大于5的数字，又有小于5的数字的自然数共有多少个？分析：所有三位的自然树中仅仅由不大于五的数字组成的数有5×6×6=180个数字，仅仅由不小于5的数字组成的数有5×5×5=125个，其中555各位书即不大于5，也不小于5，因此符合条件的三位数共有999-99-（180+125-1）=596个.5. （例8）某校有28名学生参加市运动会，参加跑步类项目的有15人，参加跳类项目的有13人，参加投掷类项目的有14人，既参加跑又参加跳项目的有4人，既参加跑又参加投掷项目的有6人，既参加跳又参加投掷项目的有5人，三种项目都参加的有2人，试说明，这个报名表有误．分析：按照赞加各个项目的详细人数，该校参加市运动会的人数为15+13+14-4-6-5+2=29人，与实际参加人数不符，所以这个报名表有误．6. （例9）某班有45人，其中35人会中国象棋，30人会国际象棋，38人会围棋，40人会跳棋，那么这个班至少有多少人四项都会？分析：由题可知该班10人不会中国象棋，15人不会国际象棋，7人不会围棋，5人不会跳棋，所以最多可以有37人不全都会，至少有45-37=8人四项都会．成长故事好学不倦在一个漆黑的晚上，老鼠首领带领着小老鼠出外觅食，在一家人的厨房内，垃圾桶之中有很多剩余的饭菜，对于老鼠来说，就好像人类发现了宝藏． 正当一大群老鼠在垃圾桶及附近范围大挖一顿之际，突然传来了一阵令它们肝胆俱裂的声音，那就是一头大花猫的叫声．它们震惊之余，更各自四处逃命，但大花猫绝不留情，不断穷追不舍，终于有两只小老鼠走避不及，被大花猫捉到，正要向它们吞噬之际，突然传来一连串凶恶的狗吠声，令大花猫手足无措，狼狈逃命． 大花猫走后，老鼠首领施施然从垃圾桶后面走出来说："我早就对你们说，多学一种语言有利无害，这次我就因而救了你们一命．" 温馨提示："多一门技艺，多一条路．"不断学习实在是成功人士的终身承诺11。

五年级奥数：包含与排除五年级奥数：包含与排除1、某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组都参加。

那么有多少人两个小组都不参加？解：两个小组共有（15+18）-10=23（人），都不参加的有40-23=17（人）答：有17人两个小组都不参加。

解：45-29-10+3=9（人）答：语文成绩得满分的有9人。

解：4的倍数有50/4商12个，6的倍数有50/6商8个，既是4又是6的倍数有50/12商4个。

4的倍数向后转人数=12，6的倍数向后转共8人，其中4人向后，4人从后转回。

面向老师的人数=50-12=38（人）答：现在面向老师的同学还有38名。

解：2的倍数有100/2商50个，3的倍数有100/3商33个，2和3人倍数有100/6商16个。

领2支的共准备（50-16）*2=68，领3支的共准备（33-16）*3=51，重复领的共准备16*（2+3）=80，其余准备100-（50+33-16）*1=33共需要68+51+80+33=232（支）答：游艺会为该项活动准备的奖品铅笔共有232支。

5、有一根长为180厘米的绳子，从一端开始每隔3厘米作一记号，每隔4厘米也作一记号，然后将标有记号的地方剪断。

问绳子共被剪成了多少段？解：3厘米的记号：180/3=60，最后到头了不划，60-1=59个4厘米记号：180/4=45，45-1=44个，重复的记号：180/12=15，15-1=14个，所以绳子中间实际有记号59+44-14=89个。

剪89次，变成89+1=90段答：绳子共被剪成了90段。

解：1，2，3，4，5年级共有16，1，2，3，4，6年级共有15，5，6年级共有25所以总共有（16+15+25）/2=28（幅），1，2，3，4年级共有28-25=3（幅）答：其他年级的画共有3幅。

7、有若干卡片，每张卡片上写着一个数，它是3的倍数或4的倍数，其中标有3的倍数的卡片占2/3，标有4的倍数的卡片占3/4，标有12的倍数的卡片有15张。

包含与排除（一） 包含与排除问题也叫容斥原理。

“容”是容纳、包含的意思，“斥”是排斥、排除的意思，从题目名称上看，比较抽象，下面我们结合具体实例来说明这种问题的思考方法。

【典型例题】例1：如下图，桌面上放着两个正方形，求盖住桌面的面积。

（单位：厘米） 分析与解：这是一个组合图形，是由两个正方形组成的，中间重合部分是一个长方形，要想求出盖住桌面的面积，可以有三种不同方法：方法一：75256422+-⨯=（平方厘米）方法二：72556422-⨯+=（平方厘米）方法三：52576422-⨯+=（平方厘米）答：盖住桌面的面积是64平方厘米。

例2：四（1）班同学中有37人喜欢打乒乓球，26人喜欢打羽毛球，21人既爱打乒乓球又爱打羽毛球。

问全班喜欢打乒乓球或羽毛球活动的有多少人？分析与解：根据题意可画图如下此类问题画集合图比画线段图更直观，更形象一些。

方法一：37 + 26—21 = 42（人）方法二：37—21 + 26 = 42（人）方法三：37 +（26—21）= 42（人）以上三种方法是紧密联系的，都是要从中减去重叠部分，可以从其中一部分中减去，再与另一部分合并，也可以从两部分之和中减去重叠部分。

三种方法比较，你喜欢哪一种解法呢？我们根据以上两个例题可以得出这样的数量关系：第一部分 + 第二部分 — 重叠部分 = 两部分之和例3：四年级一班在期末考试中，语文得“优”的有15人，数学得“优”的有17人，老师请得“优”的同学都站起来，数了数有24人。

两科都得“优”的有几人？ 分析与解：根据“第一部分 + 第二部分 — 重叠部分 = 两部分之和”可以求出两科都得“优”的人数。

15 + 17—24 = 8（人）另外，从下图中我们还能得出两种不同方法方法二：17—（24—15）= 8（人）15—（24—17）= 8（人）答：两科都得优的有8人。

例4：图新小学四年级二班有24人参加了美术小组，有18人参加了音乐小组，其中11人两个小组都参加，还有5人什么组都没参加。

第4讲包含与排除容概述有重叠部分酌若干对象的计数问题．能利用文氏图进行辅助分析，弄清文氏图中每部分的含义；结合文氏图理解两个对象和三个对象酌容斥原理；灵活处理具有一些不确定性酌计数问题，以及其他形式的重复计数问题．典型问题兴趣篇1．暑假里，小悦和冬冬一起讨论“金陵十八景”．他们发现十八景中的每一处都有人去过，而且有五处是两人都去过的．如果小悦去过其中的卜二景，那么冬冬去过其中的几景？2．在一群小朋友中，有12人看过动画片《黑猫警长》，有21人看过动画片《大闹天宫》，并且有8人两部动画片都看过．请问：至少看过其中一部的小朋友有多少人？3．五年级一班45个学生参加期末考试，成绩公布后，数学得满分的有10人，数学及语文均得满分的有3人，这两科都没有得满分的有29人．请问：语文成绩得满分的有多少人？4．某餐馆有27道招牌菜．小悦吃过其中的13道，冬冬吃过其中的7道，而且有2道菜是两人都吃过的．请问：有多少道招牌菜是两人都没有吃过的？5．如图4-I，已知甲、乙、丙三个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6、8、5，同时被这三个圆覆盖的部分的面积为2．请问：(1)只被甲或乙覆盖，却不被丙覆盖的部分的面积是多少？(2)只被这3个圆中某一个圆覆盖的部分的面积是多少？6．在一个由30人组成的合唱队中，每个人都爱喝红茶、绿茶、花茶中的一种或者几种，其中有10个人爱喝红茶，12个人不爱喝红茶却爱喝绿茶，请问：只爱喝花茶的有多少人？7．光明小学五年级课外活动有体育、音乐、书法三个小组，参加的人数分别是54人、46人、36人．同时参加体育小组和音乐小组的有4人，同时参加体育小组和书法小组的有7人，同时参加音乐小组和书法小组的有10人，三组都参加的有2人．光明小学五年级参加课外活动的一共有多少人？8．卫生部对120种食物是否含有维生素A、C、E进行调查，结果发现：含维生素A的有62种，含维生素C的有90种，含维生素E的有68种，同时含维生素A和C的有48种，同时含维生素A和E的有36种，同时含维生素C和E的有50种，同时含这三种维生素的有25种．请问：(1)这三种维生素都不含的食物有多少种？(2)仅含维生素A的食物有多少种？9．操场上有50名同学在跑步或跳绳，其中女生有18名，跳绳的同学有31名，跑步的男生有14名．跳绳的女生有多少名？10．学校举行棋类比赛，分为象棋、围棋和军棋三项，每人最多参加其中两项．根据报名的人数，学校决定对象棋的前9名、围棋的前10名和军棋的前11名发放奖品．请问：最少有几人获得奖品？拓展篇1．在一个办公室中，有7个人爱喝茶，10个人爱喝咖啡，3个人既爱喝茶又爱喝咖啡，如果每个人都至少爱喝茶或咖啡中的一种，那么这个办公室里共有多少人？2．五年级二班有40名同学，其中有25:人没参加数学小组，有18人参加航模小组，有10人两个小组都参加．那么只参加了这两个小组之一的学生共有多少人？3．在1至100这100个自然数中，既不能被2整除也不能被3整除的数有多少个？4．渔乡小学举行长跑和游泳比赛，共305人参加．参加长跑比赛的有150名男生和90名女生，参加游泳比赛的有120名男生和70名女生，有110名男生两项比赛都参加了，请问：只参加游泳比赛而没有参加长跑比赛的女生有多少人？5．森林里住着一群小白兔，每只小白兔都爱吃萝卜、白菜和青草中的一种或者几种．爱吃萝卜的小白兔中有12只不爱吃白菜；爱吃白菜的小白兔中有23只不爱吃青草；爱吃青草的小白兔中有34只不爱吃萝卜．如果三种食物都爱吃的小白兔有5只，那么这群小白兔一共有多少只？6．三位基金经理投资若干只股票．经理买过其中66只，王经理买过其中40只，经理买过其中23只．经理和王经理都买过的有17只，王经理和经理都买过的有13只，经理和经理都买过的有9只，三个人都买过的有6只．请问：这三位经理一共买过多少只股票？7．唐僧西天取经共经历了81难，其中单独渡过了3难，与悟空一起渡过了77难，与猪八戒一起渡过了65难，与沙和尚一起渡过了62难，同时与悟空和猪八戒一起渡过了64难，同时与悟空和沙和尚一起渡过了61难，同时与猪八戒和沙和尚一起渡过了60难．请问：师徒四人共同渡过的有多少难？8．培英学校有学生1000人，其中有500人订阅了《中国少年报》，有350人订阅了《少年文艺》，有250人订阅了《数学报》，至少订阅两种报刊的有400人，订阅了三种报刊的有100人．请问：培英学校有多少人没有订报？9．五年级一班有46名学生参加数学、语文、文艺三项课外小组．其中有24人参加了数学小组，20人参加了语文小组，既参加数学小组又参加语文小组的有10人．参加文艺小组的人数是既参加数学小组又参加文艺小组人数的3.5倍，还是三项小组都参加的人数的7倍，既参加文艺小组也参加语文小组的人数等于三项小组都参加的人数的2倍．求参加文艺小组的人数．10．图书室有100本书，借阅图书者需在图书上签名．已知这100本书中有甲、乙、丙三人签名的分别有33本、44本和55本，其中同时有甲、乙签名的图书为29本，同时有甲、丙签名的图书为25本，同时有乙、丙签名的图书为36本，问：这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过？11五年级三班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有22人，参加英语竞赛的有20人．如果每人最多参加两科竞赛，那么该班未参加竞赛人数最多可能有多少人？12．甲、乙、丙三人都在读同一本故事书，书中有100个故事．已知甲读了85个故事，乙读了70个故事，丙读了62个故事．请问：(1)甲、乙、丙三人共同读过的故事最少有多少个？(2)如果每个人都是从某一个故事开始，按顺序连续往后读，那么甲、乙、丙三人共同读过的故事最少有多少个？超越篇1．森林里住着100只小白兔，凡是不爱吃萝卜的小白兔都爱吃白菜．其中爱吃萝卜的小白兔数量是爱吃白菜的小白兔数量的2倍，而不爱吃白菜的小白兔数量是不爱吃萝卜的小白兔数量的3倍，它们当中有多少只小白兔既爱吃萝卜又爱吃白菜？2．育才小学匦展上展出了许多幅画，其中有16幅画不是六年级的，有15幅画不是五年级的，五、六年级共展出25幅画．其他年级的画共有多少幅？3．巨人学校有105名男生和75名女生参加数学竞赛，有95名女生和85名男生参加作文竞赛．已知该校一共有280名学生参加了竞赛，其中只参加数学竞赛的男生人数与只参加作文竞赛的女生人数相同．请问：只参加数学竞赛的女生有多少人？4．冬冬和爸爸妈妈去芬兰旅游，他们照了很多照片．回家后，冬冬先把所有有自己像的照片放到自己的相册里，再把剩下的有妈妈像的照片放到妈妈的相册里，最后把剩下的照片放到爸爸的相册里，爸爸认为应该把所有有自己像的照片都放到自己相册里，于是从冬冬和妈妈的相册里一共拿出了37照片放到了自己的相册，妈妈不同意，又把放在冬冬和爸爸的相册里所有有自己像的45照片都拿出来放到了自己的相册．请问：究竟是妈妈和冬冬的合影多，还是爸爸和冬冬的合影多？多几？5．一次测验共有5道试题．测试后统计如下：有81%的同学做对第1题，有85%的同学做对第2题，有91%的同学做对第3题，有74%的同学做对第4题，有79%的同学做对第5题．如果做对3道或3道以上试题的同学为考试合格，请问：这次考试的合格率最多达百分之几？最少达百分之几？6．五年级一班有22人参加语文竞赛，32人参加数学竞赛，27人参加英语竞赛，其中同时参加语文竞赛和数学竞赛的有12人，同时参加语文竞赛和英语竞赛的有14人，同时参加数学竞赛和英语竞赛的有15人．请问：五年级一班参加竞赛的总人数最少是多少？7．在明媚的一天下午，甲、乙、丙、丁四人给100盆花浇水，已知甲浇了30盆，乙浇了75盆，丙浇了80盆，丁浇了90盆，请问：(1)恰好被3个人浇过的花最少有多少盆？(2)恰好被1个人浇过的花最多有多少盆？8．一根1.8米长的木棍，从左端开始每隔2厘米划一个刻度，每隔3厘米划一个刻度，每隔5厘米划一个刻度，每隔7厘米划一个刻度，如果按刻度把木棍截断，一共可以截成多少段小木棍？。

“包含与排除” 学生姓名授课日期 教师姓名授课时长包含与排除是小学奥数中一个非常重要的知识点，很多杯赛和小升初选拔考试中都会有相关考察内容，是考察学生逻辑思维能力，以及理解利用新知识的一个非常重要的方面，其中容斥原理更是最关键的点，而且与数论和几何的综合性题目是历年考察的重点。

一、容斥原理公式1、若已知A 、B 、C 三部分的数量（如图），其中C 为重复部分，则图中的数量等于A+B-C. 即：A ∪B=A+B- A ∩B ，其中A ∩B=C.2、若已知A 、B 、C 三部分的数量（如图）， 则图中的数量等于A+B+C-（A 与B 重叠部分+ B 与C 重叠部分+ C 与A 重叠部分）+A 、B 、C 三者重叠的部分.即：A ∪B ∪C=A+B+C-（A ∩B+B ∩C+C ∩A ）+ A ∩B ∩C.以上概念中符号解释：“∪”表示并集，“A ∪B ”表示A 并B ，通俗的讲表示所有或属于A 、或属于B 的元素的数量（集合），“A ∪B ∪C ” 通俗的讲表示所有或属于A 、或属于B 、或属于C 的元素数量.“∩”表示交集，“A ∪B ”表示A 交B ，通俗的讲表示所有即属于A 、又属于B 的元素的数量（集合），“A ∩B ∩C ”通俗的讲表示所有即属于A ，又属于B ，还属于C 的元素数量C B A C B A【试题来源】【题目】某小学三年级四班，参加语文兴趣小组的有28人，参加数学兴趣小组的有29人，有12人两个小组都参加。

这个班有多少人参加了语文或数学兴趣小组？【试题来源】【题目】在桌面上放置着三个两两重叠的圆纸片（如图，三个圆等大），它们的面积都是100cm2，并知A、B两圆重叠的面积是20cm2，A、C两圆重叠的面积为45cm2，B、C两圆重叠的面积为31cm2,三个圆共同重叠的面积为15cm2，求盖住桌子的总面积。

【试题来源】【题目】东方大学有外语老师120名，其中教英语的有50名，教日语的45名，教法语的有40名，有15名教师既教英语又教日语，有10名教师既教英语又教法语，有8名教师既教日语又教法语，有4名教师会教英语、日语和法语三门课，求不教这三门课的外教有多少名？【试题来源】【题目】五年级三班有46名学生参加三项课外活动，其中24人参加了绘画小组，20人参加了合唱小组，参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍，又是三项活动都参加人数的7倍，既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍，既参加绘画小组又参加合唱小组的有10人，求参加朗诵小组的人数。

学科培优 数学 “包含与排除” 学生姓名授课日期 教师姓名授课时长 知识定位 包含与排除是小学奥数中一个非常重要的知识点,很多杯赛和小升初选拔考试中都会有相关考察内容,是考察学生逻辑思维能力,以及理解利用新知识的一个非常重要的方面,其中容斥原理更是最关键的点,而且与数论和几何的综合性题目是历年考察的重点。

知识梳理一、容斥原理公式1、若已知A 、B 、C 三部分的数量（如图）,其中C 为重复部分,则图中的数量等于A+B-C. 即：A ∪B=A+B- A ∩B,其中A ∩B=C.2、若已知A 、B 、C 三部分的数量（如图）, 则图中的数量等于A+B+C-（A 与B 重叠部分+ B 与C 重叠部分+ C 与A 重叠部分）+A 、B 、C 三者重叠的部分.即：A ∪B ∪C=A+B+C-（A ∩B+B ∩C+C ∩A ）+ A ∩B ∩C.以上概念中符号解释：“∪”表示并集,“A ∪B ”表示A 并B,通俗的讲表示所有或属于A 、或属于B 的元素的数量（集合）,“A ∪B ∪C ” 通俗的讲表示所有或属于A 、或属于B 、或属于C 的元素数量.“∩”表示交集,“A ∪B ”表示A 交B,通俗的讲表示所有即属于A 、又属于B 的元素的数量（集合）,“A ∩B ∩C ”通俗的讲表示所有即属于A,又属于B,还属于C 的元素数量C B A C B A例题精讲【试题来源】【题目】某小学三年级四班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。

这个班有多少人参加了语文或数学兴趣小组？【试题来源】【题目】在桌面上放置着三个两两重叠的圆纸片（如图,三个圆等大）,它们的面积都是100cm2,并知A、B两圆重叠的面积是20cm2,A、C两圆重叠的面积为45cm2,B、C两圆重叠的面积为31cm2,三个圆共同重叠的面积为15cm2,求盖住桌子的总面积。

【试题来源】【题目】东方大学有外语老师120名,其中教英语的有50名,教日语的45名,教法语的有40名,有15名教师既教英语又教日语,有10名教师既教英语又教法语,有8名教师既教日语又教法语,有4名教师会教英语、日语和法语三门课,求不教这三门课的外教有多少名？【试题来源】【题目】五年级三班有46名学生参加三项课外活动,其中24人参加了绘画小组,20人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的 3.5倍,又是三项活动都参加人数的7倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗诵小组的人数。

第十二讲几何计数漫画，共一格一群古代的人在田地中劳作，田地中阡陌交错。

旁边文字描述：西周时期，道路和渠道纵横交错，把土地分隔成方块，形状像“井”字，因此称做“井田”。

分割田地大概有3条横线、4条竖线左右，可适当增减。

人的耕作情况要符合西周时的实际情况，比如不能有拖拉机，不能有牛耕。

后面给出问题：在图中，有多少个“井”字？几何计数，同学们一看这一讲的名字就知道了，我们学习的内容就是专门数几何图形的个数．可能会有同学觉得这类问题很简单，数数嘛，一个一个数就能数清楚了，而且图都画好了，一边看图一边数，肯定不会数错的．真的是这么简单吗？数图形有没有更好的办法呢？学完这一讲后，大家就知道答案了．三角形应该是很简单的几何图形了，我们先从三角形数起吧．例题1．下列图形中各有多少个三角形？「分析」对于一般的几何计数问题，最简单也最常用的方法是枚举法，但注意枚举不是漫无目的的举例，一定要注意按照一定的顺序来枚举，并注意寻找规律．那么，本题应该按照怎样的顺序去枚举呢？下图中有多少个三角形？例题2．右图中共有多少个三角形？「分析」对于这道题目，我们也首先想到枚举法．应该按照怎样的顺序去枚举呢？你能发现其中的规律吗？练习2:．请数出这个图形中有多少个三角形．下面我们来学习数正方形和长方形，同学们要学会在观察、思考、分析中总结归纳出解决问题的规律和方法.例题3．下列图形中，分别有多少个正方形？「分析」同上一题，在枚举的时候要注意顺序，这样才能做到不重不漏．围棋棋盘是由19条横线和19条竖线组成的正方形方阵，其中有多少个正方形呢？例题4．在右图中（下列各小题中，长方形均包括正方形）（1）一共有多少个长方形？（2）包含“★”的长方形共多少个？（3）包含“☆”的长方形共多少个？（4）两个五角星都包含的长方形共多少个？（5）至少包含一个五角星的长方形共多少个？（6）两个五角星都不包含的长方形共多少个？★☆「分析」如果还用枚举法处理这道题目，就会越数越复杂．那有没有好一点的方法？我们换一个角度来思考这个问题．同学们可以想想看，怎样才能在图中画出一个长方形来？当然很简单，只需要画出它的两条长和两条宽就可以了，也就是只需要画出两条横线和两条竖线．如右图所示．因此，长方形的个数就是选择两条横线和两条竖线的所有方法数．下图中是一个长为9，宽为4的长方形网格，每一个小格都是一个正方形．那么：（1）从中可以数出多少个长方形？（2）从中可以数出包含黑点的长方形有多少个？通过上面的学习我们可以知道，几何计数与我们之前学过的有序思考、分类枚举、乘法原理以及排列组合都有着密切的关系．同学们在学习过程中要勤于观察，勤于思考，这样才能发现和总结出更好的方法．例题5．右图中共有多少个长方形？（注意：长方形包括正方形）「分析」我们可以考虑下方3×5的长方形和右边6×2的长方形，分别计算出两部分中长方形的个数，这样所有的长方形都考虑到了，但是其中有重复计算的．哪些重复计算了？容易看出来重复计算的是右下角重叠的3×2的部分，那么把这部分中的长方形减去就能得到最后答案．例题6．右图中有多少个平行四边形？「分析」题目中要求数出平行四边形的个数，那么你能发现图中有几类平行四边形吗？如何数出每一种的数量呢？数学家的墓志铭一些数学家生前献身于数学，死后在他们的墓碑上，刻着代表着他们生平业绩的标志．古希腊学者阿基米德死于进攻西西里岛的罗马敌兵之手（死前他还在叮嘱：“不要弄坏我的圆”．）后，人们为纪念他便在其墓碑上刻上球内切于圆柱的图形，以纪念他发现球的体积和表面积均为其外切圆柱体积和表面积的三分之二．德国数学家高斯在他研究发现了正十七边形的尺规作法后，便放弃原来立志学文的打算而献身于数学，以至在数学上作出许多重大贡献．甚至他在遗嘱中曾建议为他建造正十七边形的棱柱为底座的墓碑．16世纪德国数学家鲁道夫，花了毕生精力，把圆周率算到小数点后35位，后人称之为鲁道夫数，他死后别人便把这个数刻到他的墓碑上．瑞士数学家雅谷·伯努利，生前对螺线（被誉为生命之线）有研究，他死之后，墓碑上就刻着一条对数螺线，同时碑文上还写着：“我虽然改变了，但却和原来一样”．这是一句既刻划螺线性质又象征他对数学热爱的双关语．阿基米德（公元前287年—公元前212年）作业1. 右图中共有多少个三角形？作业2. 右图中共有多少个三角形？作业3. 右图是由12个11⨯的小正方形组成的，数一数图中一共有多少个正方形．作业4. 右图是由15个11⨯的小正方形组成的，数一数图中一共有多少个长方形．（长方形包括正方形．）作业5. 在右图中（下列各小题中，长方形均包括正方形）（1）包含“★”的长方形共多少个？ （2）包含“☆”的长方形共多少个？ （3）两个五角星都包含的长方形共多少个？第十二讲几何计数例题1.答案：16；15详解：注意有序枚举：（1）左图中由一部分组成的三角形有6个，由两部分组成的三角形有3个，由三部分组成的三角形有6个，由六部分组成的三角形有1个，共计16个．（2）右图中由一部分组成的三角形有4个，由两部分组成的三角形有6个，由三部分组成的三角形有2个，由四部分组成的三角形有2个，由六部分组成的三角形有1个，共计15个．例题2.答案：78详解：恰当分类，有序枚举．图中的三角形可以分为两类，一类是尖朝上的，一类是尖朝下的．设最小的三角形边长为1．（1）尖朝上的：边长为1的三角形有123410+++=个；边长为2的三角形有1236++=个；边长为3的三角形有123410+++=个；边长为4的三角形有1236++=个；边长为5的三角形有123+=个；边长为6的三角形有1个．共计56个．（2）尖朝下的：边长为1的三角形有1234515++++=个；边长为2的三角形有1236++=个；边长为3的三角形有1个．共计22个．图中一共有78个三角形．例题3.答案：91，112详解：分别考虑边长为1、2、3、4、5、6的正方形各有多少个即可．左图有66554433221191⨯+⨯+⨯+⨯+⨯+⨯=个，右图有766554433221112⨯+⨯+⨯+⨯+⨯+⨯=个．例题4.答案：（1）756；（2）216；（3）240；（4）108；（5）348；（6）408详解：（1）7条横线选2条作为长，9条竖线选2条作为宽，有22792136756C C⨯=⨯=个．（2）含★的长方形上下左右边分别有3、4、3、6种选法，这样长方形有3436216⨯⨯⨯=个．（3）含☆的长方形上下左右边分别有4、3、5、4种选法，这样长方形有4354240⨯⨯⨯=个．（4）两个五角星都含的长方形上下左右边分别有3、3、3、4种选法，长方形有3334108⨯⨯⨯=个．（5）根据容斥原理，至少包含一个五角星的长方形有216240108348+-=个．（6）用排除法，两个五角星都不包含的长方形有756348408-=个．例题5.答案：135个详解：如图，下方阴影部分中一共有长方形224690C C⨯=个；右方阴影部分中一共有长方形227363C C⨯=个．其中右下方3×2长方形中的长方形被重复计算了，共有224318C C⨯=个．所以图中一共包含长方形906318135+-=个．例题6.答案：45个．详解：所有平行四边形一共有三种不同的方向：尖朝右、尖朝左和尖朝上，如图：这就提示我们可以按这个特点来分类，因为根据图形的对称性，这三种平行四边形的个数是一样多的．只需数出其中的一种，就能算出最后的答案了．下面我们来数尖朝上的平行四边形．所有这种平行四边形的边都是斜的，没有横线，所以要数它们的个数，可以把图中的所有横线都去掉，变成如下图形：这样一来图形就简单了，这个图里的平行四边形很容易数出来：最小的平行四边形有10个，两个小平行四边形拼成的有12个，三个小平行四边形拼成的有6个，四个小平行四边形拼成的有5个，六个小平行四边形拼成的有2个，共35个．而对于另外两种平行四边形，也可根据同样的方法数出，都是35个．因此原来图形中一共有353105⨯=个平行四边形．练习1.答案：8个；12个简答：（1）左图中由一部分组成的三角形有3个，由两部分组成的三角形有4个，由四部分组成的三角形有1个，共计8个．（2）右图中由一部分组成的三角形有5个，由两部分组成的三角形有4个，由三部分组成的三角形有2个，由五部分组成的三角形有1个，共计12个．练习2.答案：48个简答：由1个小三角形组成的三角形有151025+=个；由4个小三角形组成的三角形有10313+=个；由9个小三角形组成的三角形有6个；由16个小三角形组成的三角形有3个；由25个小三角形组成的三角形有1个；共有48个．练习3.答案：2470个简答：按正方形的大小分类，共有2222191817119203962470++++=⨯⨯÷=个．练习4.答案：（1）450；（2）144简答：（1）5条横线选2条作为长，10条竖线选2条作为宽，有225101045450C C⨯=⨯=个．（2）含黑点的长方形上下左右边分别有2、3、6、4种选法，这样长方形有2364144⨯⨯⨯=个．作业1.答案：10个简答：由一个部分组成的三角形有5个，由两个部分组成的三角形有4个，由三个部分组成的三角形有1个，共计10个．作业2.答案：14个简答：边长为1的有10个，边长为2的有4个，共计14个．作业3.答案：20个简答：正方形数目：边长为1的12个，边长为2的6个，边长为3的2个，共计20个．作业4. 答案：90个简答：长方形有2246C C 90⨯=个．作业5. 答案：（1）180个；（2）192个；（2）108个简答：（1）3354180⨯⨯⨯=个；（2）4443192⨯⨯⨯=个；（3）3343108⨯⨯⨯=个．。

第4讲包含与排除内容概述有重叠部分酌若干对象的计数问题．能利用文氏图进行辅助分析，弄清文氏图中每部分的含义；结合文氏图理解两个对象和三个对象酌容斥原理；灵活处理具有一些不确定性酌计数问题，以及其他形式的重复计数问题．典型问题兴趣篇1．暑假里，小悦和冬冬一起讨论“金陵十八景”．他们发现十八景中的每一处都有人去过，而且有五处是两人都去过的．如果小悦去过其中的卜二景，那么冬冬去过其中的几景？2．在一群小朋友中，有12人看过动画片《黑猫警长》，有21人看过动画片《大闹天宫》，并且有8人两部动画片都看过．请问：至少看过其中一部的小朋友有多少人？3．五年级一班45个学生参加期末考试，成绩公布后，数学得满分的有10人，数学及语文均得满分的有3人，这两科都没有得满分的有29人．请问：语文成绩得满分的有多少人？4．某餐馆有27道招牌菜．小悦吃过其中的13道，冬冬吃过其中的7道，而且有2道菜是两人都吃过的．请问：有多少道招牌菜是两人都没有吃过的？5．如图4-I，已知甲、乙、丙三个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6、8、5，同时被这三个圆覆盖的部分的面积为2．请问：(1)只被甲或乙覆盖，却不被丙覆盖的部分的面积是多少？(2)只被这3个圆中某一个圆覆盖的部分的面积是多少？6．在一个由30人组成的合唱队中，每个人都爱喝红茶、绿茶、花茶中的一种或者几种，其中有10个人爱喝红茶，12个人不爱喝红茶却爱喝绿茶，请问：只爱喝花茶的有多少人？7．光明小学五年级课外活动有体育、音乐、书法三个小组，参加的人数分别是54人、46人、36人．同时参加体育小组和音乐小组的有4人，同时参加体育小组和书法小组的有7人，同时参加音乐小组和书法小组的有10人，三组都参加的有2人．光明小学五年级参加课外活动的一共有多少人？8．卫生部对120种食物是否含有维生素A、C、E进行调查，结果发现：含维生素A的有62种，含维生素C的有90种，含维生素E的有68种，同时含维生素A和C的有48种，同时含维生素A和E的有36种，同时含维生素C和E的有50种，同时含这三种维生素的有25种．请问：(1)这三种维生素都不含的食物有多少种？(2)仅含维生素A的食物有多少种？9．操场上有50名同学在跑步或跳绳，其中女生有18名，跳绳的同学有31名，跑步的男生有14名．跳绳的女生有多少名？10．学校举行棋类比赛，分为象棋、围棋和军棋三项，每人最多参加其中两项．根据报名的人数，学校决定对象棋的前9名、围棋的前10名和军棋的前11名发放奖品．请问：最少有几人获得奖品？拓展篇1．在一个办公室中，有7个人爱喝茶，10个人爱喝咖啡，3个人既爱喝茶又爱喝咖啡，如果每个人都至少爱喝茶或咖啡中的一种，那么这个办公室里共有多少人？2．五年级二班有40名同学，其中有25:人没参加数学小组，有18人参加航模小组，有10人两个小组都参加．那么只参加了这两个小组之一的学生共有多少人？3．在1至100这100个自然数中，既不能被2整除也不能被3整除的数有多少个？4．渔乡小学举行长跑和游泳比赛，共305人参加．参加长跑比赛的有150名男生和90名女生，参加游泳比赛的有120名男生和70名女生，有110名男生两项比赛都参加了，请问：只参加游泳比赛而没有参加长跑比赛的女生有多少人？5．森林里住着一群小白兔，每只小白兔都爱吃萝卜、白菜和青草中的一种或者几种．爱吃萝卜的小白兔中有12只不爱吃白菜；爱吃白菜的小白兔中有23只不爱吃青草；爱吃青草的小白兔中有34只不爱吃萝卜．如果三种食物都爱吃的小白兔有5只，那么这群小白兔一共有多少只？6．三位基金经理投资若干只股票．张经理买过其中66只，王经理买过其中40只，李经理买过其中23只．张经理和王经理都买过的有17只，王经理和李经理都买过的有13只，李经理和张经理都买过的有9只，三个人都买过的有6只．请问：这三位经理一共买过多少只股票？7．唐僧西天取经共经历了81难，其中单独渡过了3难，与孙悟空一起渡过了77难，与猪八戒一起渡过了65难，与沙和尚一起渡过了62难，同时与孙悟空和猪八戒一起渡过了64难，同时与孙悟空和沙和尚一起渡过了61难，同时与猪八戒和沙和尚一起渡过了60难．请问：师徒四人共同渡过的有多少难？8．培英学校有学生1000人，其中有500人订阅了《中国少年报》，有350人订阅了《少年文艺》，有250人订阅了《数学报》，至少订阅两种报刊的有400人，订阅了三种报刊的有100人．请问：培英学校有多少人没有订报？9．五年级一班有46名学生参加数学、语文、文艺三项课外小组．其中有24人参加了数学小组，20人参加了语文小组，既参加数学小组又参加语文小组的有10人．参加文艺小组的人数是既参加数学小组又参加文艺小组人数的3.5倍，还是三项小组都参加的人数的7倍，既参加文艺小组也参加语文小组的人数等于三项小组都参加的人数的2倍．求参加文艺小组的人数．10．图书室有100本书，借阅图书者需在图书上签名．已知这100本书中有甲、乙、丙三人签名的分别有33本、44本和55本，其中同时有甲、乙签名的图书为29本，同时有甲、丙签名的图书为25本，同时有乙、丙签名的图书为36本，问：这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过？11五年级三班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有22人，参加英语竞赛的有20人．如果每人最多参加两科竞赛，那么该班未参加竞赛人数最多可能有多少人？12．甲、乙、丙三人都在读同一本故事书，书中有100个故事．已知甲读了85个故事，乙读了70个故事，丙读了62个故事．请问：(1)甲、乙、丙三人共同读过的故事最少有多少个？(2)如果每个人都是从某一个故事开始，按顺序连续往后读，那么甲、乙、丙三人共同读过的故事最少有多少个？超越篇1．森林里住着100只小白兔，凡是不爱吃萝卜的小白兔都爱吃白菜．其中爱吃萝卜的小白兔数量是爱吃白菜的小白兔数量的2倍，而不爱吃白菜的小白兔数量是不爱吃萝卜的小白兔数量的3倍，它们当中有多少只小白兔既爱吃萝卜又爱吃白菜？2．育才小学匦展上展出了许多幅画，其中有16幅画不是六年级的，有15幅画不是五年级的，五、六年级共展出25幅画．其他年级的画共有多少幅？3．巨人学校有105名男生和75名女生参加数学竞赛，有95名女生和85名男生参加作文竞赛．已知该校一共有280名学生参加了竞赛，其中只参加数学竞赛的男生人数与只参加作文竞赛的女生人数相同．请问：只参加数学竞赛的女生有多少人？4．冬冬和爸爸妈妈去芬兰旅游，他们照了很多照片．回家后，冬冬先把所有有自己像的照片放到自己的相册里，再把剩下的有妈妈像的照片放到妈妈的相册里，最后把剩下的照片放到爸爸的相册里，爸爸认为应该把所有有自己像的照片都放到自己相册里，于是从冬冬和妈妈的相册里一共拿出了37张照片放到了自己的相册，妈妈不同意，又把放在冬冬和爸爸的相册里所有有自己像的45张照片都拿出来放到了自己的相册．请问：究竟是妈妈和冬冬的合影多，还是爸爸和冬冬的合影多？多几张？5．一次测验共有5道试题．测试后统计如下：有81%的同学做对第1题，有85%的同学做对第2题，有91%的同学做对第3题，有74%的同学做对第4题，有79%的同学做对第5题．如果做对3道或3道以上试题的同学为考试合格，请问：这次考试的合格率最多达百分之几？最少达百分之几？6．五年级一班有22人参加语文竞赛，32人参加数学竞赛，27人参加英语竞赛，其中同时参加语文竞赛和数学竞赛的有12人，同时参加语文竞赛和英语竞赛的有14人，同时参加数学竞赛和英语竞赛的有15人．请问：五年级一班参加竞赛的总人数最少是多少？7．在阳光明媚的一天下午，甲、乙、丙、丁四人给100盆花浇水，已知甲浇了30盆，乙浇了75盆，丙浇了80盆，丁浇了90盆，请问：(1)恰好被3个人浇过的花最少有多少盆？(2)恰好被1个人浇过的花最多有多少盆？8．一根1.8米长的木棍，从左端开始每隔2厘米划一个刻度，每隔3厘米划一个刻度，每隔5厘米划一个刻度，每隔7厘米划一个刻度，如果按刻度把木棍截断，一共可以截成多少段小木棍？。

五年级奥数集训专题讲座（七）——包含与排除包含与排除问题其实也叫容斥问题。

即当两个计数部分有重复包含时，为了不重复的计数，应从他们的和中排除重复部分。

如：集合A加集合B组成一个新的集合C，再计算C的元素时为：C=A+B-ABA AB B （韦恩图）例1：一个班有 48 人，班主任在班会上问：“谁做完语文作业？请举手！”有 37 人举手。

又问：‘谁做完数学作业？请举手！”有 42 人举手。

最后问：“谁语文、数学作业没有做完？”没有人举手。

求这个班语文、数学作业都完成的人数。

【思路导航】如图所示，完成语文作业的有 37 人，完成数学作业的有 42 人，一共有 37 + 42 = 79 （人），多于全班人数，这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次，在统计做完数学作业的人数时又算了一次，这样就多算了一次。

所以，这个班语文、数学作业都完成的有： 79－48 = 31（人）37 + 42－48=31（人）答：语文、数学作业都完成的有 31 人。

想一想：下面算式有何道理？( l ) 37－（48 －42 ) = 31 （人）( 2 ) 42 －（ 48 － 37 ）= 31 （人）【疯狂操练】：(1）五年级有 122 名学生参加语文、数学考试，每人至少有一门功课取得优秀成绩。

其中语文成绩优秀的有 65 人，数学优秀的有 87 人。

语文、数学都优秀的有多少人？解：语文成绩优秀的有 65 人，数学优秀的有 87 人，那么总人数是：65+87=152（人）其中有一部分是语文数都优秀的，所以语文数学都优秀的有：152－122=30（人）答：语文数学都优秀的有30人。

( 2）四年级一班有 54 人，订阅《小学生优秀作文》和《数学大世界》两种读物的有 13 人，订《小学生优秀作文》的有 45 人，每人至少订一种读物，订《数学大世界》的有多少人？解：根据两种读物的有 13 人，订《小学生优秀作文》的有 45 人，每人至少订一种读物，可知只订了《数学大世界》的有：54-45=9（人），而两种读物都订了的有13人，所以订了《数学大世界》的有：13+9=22（人）答：订《数学大世界》的有22人。

包含与排除涉及互相重复的两类或三类对象的计数问题．解题可利用计算所有对象总个数的容斥原理，以及图示包含与排除关系．1．某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组都参加．那么有多少人两个小组都不参加?【分析与解】至少参加一个小组的同学有15+18-10=23人，所以有40-23=17人两个小组都不参加．2．某班45个学生参加期末考试，成绩公布后，数学得满分的有10人，数学及语文均得满分的有3人，这两科都没有得满分的有29人．那么语文成绩得满分的有多少人?【分析与解】数学、语文至少有一门得满分的学生有45-29=16人．所以语文成绩得满分的有16-10+3=9人．3．50名同学面向老师站成一行．老师先让大家从左至右按1，2，3，…，49，50依次报数；再让报数是4的倍数的同学向后转，接着又让报数是6的倍数的同学向后转．问：现在面向老师的同学还有多少名?【分析与解】在转过两次后，面向老师的同学分成两类：第一类是标号既不是4的倍数，又不是6的倍数；第二类是标号既是4的倍数又是6的倍数．150之间，4的倍数有504⎡⎤⎢⎥⎣⎦=12,6的倍数有506⎡⎤⎢⎥⎣⎦=8，即是4的倍数又是6的倍数的数一定是12的倍数，所以有5012⎡⎤⎢⎥⎣⎦=4．于是，第一类同学有50-12-8+4=34人，第二类同学有4人，所以现在共有34+4=38名同学面向老师．4．在游艺会上，有100名同学抽到了标签分别为1至100的奖券．按奖券标签号发放奖品的规则如下：①标签号为2的倍数，奖2支铅笔；②标签号为3的倍数，奖3支铅笔；③标签号既是2的倍数，又是3的倍数可重复领奖；④其他标签号均奖1支铅笔．那么游艺会为该项活动准备的奖品铅笔共有多少支?【分析与解】 1～100，2的倍数有1002⎡⎤⎢⎥⎣⎦=50，3的倍数有1003⎡⎤⎢⎥⎣⎦=33个，因为既是2的倍数，又是3的倍数的数一定是6的倍数，所以标签为这样的数有1006⎡⎤⎢⎥⎣⎦=16个． 于是，既不是2的倍数，又不是3的倍数的数在1～100中有100-50-33+16=33． 所以，游艺会为该项活动准备的奖品铅笔共有：50×2+33×3+33×1=232支.5.有一根长为180厘M 的绳子，从一端开始每隔3厘M 作一记号，每隔4厘M 也作一记号，然后将标有记号的地方剪断．问绳子共被剪成了多少段?【分析与解】 只需先计算剪了多少刀，再加上1即为剪成的段数．从一端开始，将绳上距离这个端点整数厘M 数的点编号，并将距离长度作为编号．有1～180，3的倍数有1803⎡⎤⎢⎥⎣⎦=60个，4的倍数有1804⎡⎤⎢⎥⎣⎦=45个，而既是3的倍数，又是4的倍数的数一定是12的倍数，所以这样的数有18012⎡⎤⎢⎥⎣⎦=15个． 注意到180厘M 处的无法标上记号，所以剪了(60-1)+(45-1)-(15-1)=89，所以绳子被剪成89+1=90段．6.东河小学画展上展出了许多幅画，其中有16幅画不是六年级的，有15幅画不是五年级的．现知道五、六年级共有25幅画，那么其他年级的画共有多少幅?【分析与解】 将东河小学分成3个部分，六年级、五年级、其他年级，那么有五年级和其他年级共作画16幅，六年级和其他年级共作画15幅．而五、六年级共作画25幅，所以其他年级的画共有(16+15-25)÷2=3幅．7．有若干卡片，每张卡片上写着一个数，它是3的倍数或4的倍数，其中标有3的倍数的卡片占23，标有4的倍数的卡片占34，标有12的倍数的卡片有15张．那么，这些卡片一共有多少张?【分析与解】 设这些卡片的总数为“1”，而标有12的倍数的卡片既属于3的倍数又属于4的倍数．所以有"2""3"15"1"34+-=，解得“1”对应36张．即这些卡片一共有36张．8．在从1至1000的自然数中，既不能被5除尽，又不能被7除尽的数有多少个?【分析与解】 l～1000之间，5的倍数有10005⎡⎤⎢⎥⎣⎦=200个，7的倍数有10007⎡⎤⎢⎥⎣⎦=142个，因为既是5的倍数，又是7的倍数的数一定是35的倍数，所以这样的数有100035⎡⎤⎢⎥⎣⎦=28个．所以既不能被5除尽，又不能被7除尽的数有1000-200-142+-28=686个．9．五年级三班学生参加课外兴趣小组，每人至少参加一项．其中有25人参加自然兴趣小组，35人参加美术兴趣小组，27人参加语文兴趣小组，参加语文同时又参加美术兴趣小组的有12人，参加自然同时又参加美术兴趣小组的有8人，参加自然同时又参加语文兴趣小组的有9人，语文、美术、自然3科兴趣小组都参加的有4人．求这个班的学生人数．【分析与解】设参加自然兴趣小组的人组成集合A，参加美术兴趣小组的人组成集合日，参加语文兴趣小组的人组成集合C．A=25，B=35，C=27，B C=12，A B =8，A C=9，A B C=4.A B C=A B C A B A C B C A B C++---+.所以，这个班中至少参加一项活动的人有25+35+27-12-8-9+4=62，而这个班每人至少参加一项．即这个班有62人．10．如图8-1，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【分析与解】设甲圆组成集合A，乙圆组成集合B，丙圆组成集合C．===30，A B=6，B C=8，A C=5，A B C=73，A B C而A B C=A B C+--A B B C A C A B C--+.有73=30×3-6-8-5+A B C，即A B C=2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．11．四年级一班有46名学生参加3项课外活动．其中有24人参加了数学小组，20人参加了语文小组，参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3．5倍，又是3项活动都参加人数的7倍，既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍，既参加数学小组又参加语文小组的有10人．求参加文艺小组的人数．【分析与解】设参加数学小组的学生组成集合A，参加语文小组的学生组成集合B，参加文艺小组的学生组成集合G．三者都参加的学生有z人．有A B C=46，A=24，B=20，C=3.5，A C=7A B C，B C=2A B C，A B=10．=++---+，所以46=24+20+7x-因为A B C A B C A B A C B C A B C10-2x-2x+x，解得x=3，即三者的都参加的有3人．那么参加文艺小组的有3⨯7=21人．12．图书室有100本书，借阅图书者需在图书上签名．已知这100本书中有甲、乙、丙签名的分别有33，44和55本，其中同时有甲、乙签名的图书为29本，同时有甲、丙签名的图书为25本，同时有乙、丙签名的图书为36本．问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?【分析与解】设甲借过的书组成集合A，乙借过的书组成集合B，丙借过的书组成集合C．A=33, B=44，C=55，A B=29，A C=25，B C=36．本题只需算出甲、乙、丙中至少有一人借过的书的最大值，再将其与100作差即可．=++---+,当A B C最大时，A B C A B C A B A C B C A B CA B C有最大值.也就是说当三人都借过的书最多时，甲、乙、丙中至少有一人借过的书最多．而A B C最大不超过A、B、C、A B、B C、A C 6个数中的最小值，所以A B C最大为25．此时A B C=33+44+55-29-25-36+25=67，即三者至少有一人借过的书最多为67本，所以这批图书中最少有33本没有被甲、乙、丙中的任何一人借阅过．13．如图8-2，5条同样长的线段拼成了一个五角星．如果每条线段上恰有1994个点被染成红色，那么在这个五角星上红色点最少有多少个?【分析与解】如下图，下图中“”位置均有两条线段通过，也就是交点，如果这些交点所对应的线段都在“”位置恰有红色点，那么在五角星上重叠的红色点最多，所以此时显现的红色点最少，有1994×5-(2-1)×10=9960个．14．甲、乙、丙同时给100盆花浇水．已知甲浇了78盆，乙浇了68盆，丙浇了58盆，那么3人都浇过的花最少有多少盆?【分析与解】只考虑甲乙两人情况，有甲、乙都浇过的最少为：78+68-100=46盆，此时甲单独浇过的为78-46=32盆，乙单独浇过的为68-46=22盆；欲使甲、乙、丙三人都浇过的花最少时，应将丙浇过的花尽量分散在两端。

包含与排除【专题导引】两个集合中可以做加法运算，把两个集合A、B合并在一起，就组成了一个新的集合C。

计算集合C的元素的个数的思考方法主要是包含与排除：先把A、B的一切元素都“包含”进来加在一起，再“排除”A、B两集合的公共元素的个数，减去加了两次的元素，即：C=A+B-AB。

在解包含与排除问题时，要善于使用形象的图示帮助理解题意，搞清楚数量关系和逻辑关系。

有些语言不易表达清楚的关系，用了适当的图形就显得很直观、很清楚，因而容易进行计算。

【典型例题】【例1】五年级96名学生都订了刊物，有64人订了少年报，有48人订了小学生报，问两种刊物都订的有多少人？【试一试】1、一个班的52人都在做语文和数学作业，有32人做完了语文作业，有35人做完了数学作业，这个班语文、数学作业都做完的有多少人？2、五年级有112人参加语文、数学考试，每人至少有一门功课得优，其中，语文得优的有65人，数学得优的有87人，问语文、数学都得优的有多少人？【例2】某地区的外语教师中，每人至少懂得英语和日语中的一种语言。

已知有35人懂英语，34人懂日语，两种语言都懂的有21人，这个地区有多少个外语教师？【试一试】1、某校的每个学生至少爱好体育和文娱中的一种活动，已知有900人爱好体育活动，有850人爱好文娱活动，其中260人两种活动都爱好。

这个学校共有学生多少人？2、某班在一次测验中有26人语文获优，有30人数学获优，其中语、数双优的有12人，另外还有8人语、数均未获优，这个班共有多少个学生？【例3】在100个外语教师中，懂英语的75人，懂日语的45人，其中必然有既懂英语又懂日语的老师，问：只懂英语的老师有多少人？【试一试】1、40人都在做加试的两道题，并且至少做对了其中的一题，已知做对第一题的有30人，做对第二题的有21人，问：只做对第一题的有多少人？2、五年级122名同学参加语文、数学考试，每人至少有一门得优，已知语文65人得优，数学78人得优，求只有语文一门得优的人数。

第二讲包含与排除——容斥原理生活中我们常常会遇到清点某种事物数目的事，有的只要直接相加就可以得到结果，但是，有的问题，却并不能直接相加得到，而是需要用到容斥原理。

包含与排除问题也叫容斥原理。

“容”是容纳、包含的意思，“斥”是排斥、排除的意思。

从题目名称上看，比较抽象，下面我们结合具体实例来说明这种问题的思考方法。

典型例题【例1】：如下图，桌面上放着两个正方形，求盖住桌面的面积。

（单位：厘米）752【例2】：学校组织体育活动，某班级参加乒乓球比赛的有32人，参加跳绳比赛的有26人，乒乓球、跳绳两项都参加的有8人.全班同学每人至少参加一项，问这个班有多少人？【例3】：四年级一班在期末考试中，语文得“优”的有15人，数学得“优”的有17人，老师请得“优”的同学都站起来，数了数有24人。

两科都得“优”的有几人？【例4】：某小学四年级二班有24人参加了美术小组，有18人参加了音乐小组，其中11人两个小组都参加，还有5人什么组都没参加。

这个班共有学生多少人？【例5】：某班学生参加音乐组的有11人，参加美术组的有8人，参加英语组的有12人，既参加音乐组又参加美术组的有5人，既参加音乐组又参加英语组的有3人，既参加美术组又参加英语组的有4人，三个组都参加的只有1人，问：至少参加一个组的有多少人？小结：在解答包含与排除--容斥原理问题时，首先要确定采用哪些分类标准，然后根据题意画出图示，找到哪些是重复的，重复了几次？仔细审题，明确求的是哪部分，再根据原理进行解题。

【模拟试题】1. 两个边长分别为5厘米、3厘米的正方形重叠在一起，重叠部分面积为1平方厘米（如图），求这个图形所能够覆盖的面积？2. 某班订阅《少年文摘》的有19人，订阅《学与玩》的有24人，两种都订的有13人。

全班同学每人至少订阅一项，问这个班有多少人？3. 幼儿园有58人学钢琴，43人学画画，37人既学钢琴又学画画，问只学钢琴和只学画画的分别有多少人？4. 某班数学、英语期中考试的成绩统计如下：英语得100分的有12人，数学得100分的有10人，两门功课都得100分的有3人，两门功课都未得100分的有26人。

小学五年级数学思维专题训练—包含与排除1、某山区的村落有人口2476人，全村落的人都会说普通话或广东话，调查所得，会说普通话的有1765人，会说广东话的有987人，问：会说普通话和广东话两种语言的有多少人？2、从1到100的正整数中，不含数字1的数有多少个？3、为了做科展，小丁观察一段期间里的天气，共写出4个数据：（1）上午和下午共下雨7次；（2）有5天下午未下雨；（3）有6天上午未下雨；（4）下午下雨的那几天，上午都未下雨。

请问在这段期间里有多少天全天未下雨？4、某个班的全体学生进行了短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优秀，其余每人至少有一个项目达到优秀，这部分学生达到优秀的项目、人数如下表：短跑游泳篮球短跑、游泳游泳、篮球篮球、短跑短跑、游泳、篮球、1718156652求这个班的学生数。

5、在1～209这209个自然数中，与209互质的自然数共有多少个？6、在不大于1000的自然数中，不能被3、5、7中任何一个整除的数共有多少个？7、体育课上，60名学生面向老师站成一行，按老师口令，从左到右报数：1，2，3， (60)然后，老师让所报的数是4的倍数的同学向后转，接着又让所报的数是5的倍数的同学身后转，然后让所报的数是6的倍数的同学向后转，现在面向老师的学生有多少人？8、甲、乙、丙三个共解出100道数学题，每人都解出了其中60道题，现将其中只有一人能解出的题叫做难题，三人都能解出的题叫做容易题，容易题与难题相差多少题？9、有100种食品，其中含钙的有68种，含铁的有43种，含锌的有15种，那么，其中既含钙又含铁的食品最少有种？同时含钙、铁、锌的食品最多有种？10、某公司针对A,B,C三种岗位招聘了35人，其中只能上B岗位的人数等于只能上C岗位人数的2倍，而只能上A岗位的人数比能兼职别的岗位的多1人，在只能上一个岗位的人群中，有一半不能上A岗位，则招聘的35人中能兼职别的岗位的有多少人？11、2010盏灯排成一排，开始都亮着，第一次从左边第一盏灯开始，每隔一盏灯拉一下开关（即拉左数第1，3，5，…，2009盏），第二次从右边第一盏灯开始，每隔两盏拉一下开关，第三次又从左边第一盏灯开始，每隔3盏灯拉一下开关，三次都拉到的灯有多少盏？亮着的还有多少盏？12、某玩具城有一楼梯，大约有几十级，但肯定不到一百级。