数学符号 (中英文对照)

+ plus 加号；正号- minus 减号；负号± plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号＝is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于≈ is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号≮is not less than 不小于号≯is not more than 不大于号≤ is less than or equal to 小于或等于号≥ is more than or equal to 大于或等于号% per cent 百分之…‰ per mill 千分之…∞ infinity 无限大号∝varies as 与…成比例√ (square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于,成比例∠angle 角⌒semicircle 半圆⊙circle 圆○ circumference 圆周π pi 圆周率△ triangle 三角形⊥perpendicular to 垂直于∪union of 并,合集∩ intersection of 交,通集∫ the integral of …的积分∑ (sigma) summation of 总和° degree 度′ minute 分〃second 秒℃Celsius system 摄氏度{ open brace, open curly 左花括号} close brace, close curly 右花括号( open parenthesis, open paren 左圆括号) close parenthesis, close paren 右圆括号() brakets/ parentheses 括号[ open bracket 左方括号] close bracket 右方括号[] square brackets 方括号. period, dot 句号,点| vertical bar, vertical virgule 竖线& ampersand, and, reference, ref 和,引用* asterisk, multiply, star, pointer 星号,乘号,星,指针/ slash, divide, oblique 斜线,斜杠,除号// slash-slash, comment 双斜线,注释符# pound 井号\ backslash, sometimes escape 反斜线转义符,有时表示转义符或续行符~ tilde 波浪符. full stop 句号, comma 逗号: colon 冒号; semicolon 分号? question mark 问号! exclamation mark (英式) exclamation point (美式)' apostrophe 撇号- hyphen 连字号-- dash 破折号... dots/ ellipsis 省略号" single quotation marks 单引号"" double quotation marks 双引号‖ par allel 双线号& ampersand = and～swung dash 代字号§ section; division 分节号→ arrow 箭号；参见号。

×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbol Symbol Name Meaning / definition Example ∠angle formed by two rays ∠ABC = 30°measuredABC = 30°anglespherical angle AOB = 30°∟right angle = 90°α = 90°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExample[a,b] closed interval [a,b] ={x | a≤x≤b}x∈[2,6]∆delta change /difference∆t = t1 - t0∆discriminant Δ =b2 - 4ac∑sigma summation -sum of allvalues in rangeof series∑ x i= x1+x2+...+x n∑∑sigma doublesummation∏capital pi product -product of allvalues in rangeof series∏ x i=x1∙x2∙...∙x ne e constant / Euler's number e =2.718281828...e = lim (1+1/x)x , x→∞γEuler-Mascheroni constantγ =0.527721566...φgolden ratio golden ratioconstantπpi constant π =3.141592654...is the ratiobetween thecircumference anddiameter of acirclec = π·d = 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example ·dot scalar product a · b×cross vector product a × bA⊗B tensor product tensor product of A and B A⊗B inner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose (A T)ij = (A)jiA†Hermitian matrix matrix conjugate transpose (A†)ij = (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij = (A)ji A-1inverse matrix A A-1 = Irank(A) matrix rank rank of matrix A rank(A) = 3 dim(U) dimension dimension of matrix A rank(U) = 3 Probability and statistics symbolsSymbol Symbol Name Meaning / definition ExampleP(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A∪B) = 0.5P(A | B) conditionalprobabilityfunctionprobability of event Agiven event BoccuredP(A | B) = 0.3f (x) probabilitydensity function(pdf)P(a ≤ x ≤ b) = ∫f (x) dxF(x) cumulative F(x) = P(X≤ x)distribution function (cdf)μpopulationmean mean of populationvaluesμ = 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σX standarddeviation standard deviationvalue of randomvariable XσX=2median middle value of random variable xcov(X,Y) covariance covariance ofrandom variables Xand Ycov(X,Y) = 4corr(X,Y) correlation correlation ofrandom variables Xand Ycorr(X,Y) = 0.6ρX,Y correlation correlation ofrandom variables Xand YρX,Y = 0.6∑summation summation - sum of all values in range of series∑∑doublesummationdouble summationBin(n,p) binomialdistributionf (k) = n C k p k(1-p)n-kPoisson(λ)Poissondistributionf (k)= λk e-λ / k!Geom(p) geometricdistributionf (k) = p(1-p) kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionCombinatorics SymbolsSymbol Symbol Name Meaning / definition Examplen! factorial n! = 1·2·3·...·n5! = 1·2·3·4·5 = 120 n P k permutation 5P3 = 5! / (5-3)! = 60 n C kcombination 5C3 = 5!/[3!(5-3)!]=10Set theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strict subset has fewer elements than {9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2A power set all subsets of A power set all subsets of AA =B equality both sets have the same members A={3,9,14}, B={3,9,14}, A=BA c complement all the objects that do not belong to set AA \B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A -B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A ∆B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A andB|A| cardinality the number of elements of set A A={3,9,14},|A|=3#A cardinality the number of elements of set A A={3,9,14},#A=3aleph-null infinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { } C = {Ø} universal set set of all possible values0natural numbers / wholenumbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈01natural numbers / wholenumbers set (withoutzero)1= {1,2,3,4,5,...} 6 ∈1 integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set = {x | x=a/b, a,b∈} 2/6 ∈real numbers set = {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a+bi,-∞<a<∞,-∞<b<∞}6+2i∈Logic symbolsSymbol Symbol Name Meaning / definition Example ·and and x·y^ caret / circumflex and x ^ y& ampersand and x & y+ plus or x + y∨reversed caret or x∨y | vertical line or x | yx' single quote not - negation x'x bar not - negation x¬not not - negation ¬x! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Example limit limit value of a functionεepsilon represents a very small number,ε→0near zeroe e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18 derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z) vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。

数学符号及读法大全常用数学输入符号：≈ ≡ ≠ ＝≤≥ ＜＞≮≯∷±＋－× ÷／∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴⊥‖ ∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙‖α β γ δ ε ζ η θ Δ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin yacos x y，余弦函数反函数在x处的值，即x = cos yatan x y，正切函数反函数在x处的值，即x = tan yacot x y，余切函数反函数在x处的值，即x = cot yasec x y，正割函数反函数在x处的值，即x = sec yacsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值∑表示求和，通常是某项指数。

常用数学符号大全[标签：数学]1 几何符号↌ⅷⅶ↍↋ↆↄ△2 代数符号ⅴⅸⅹ～ⅼↅↇↈↃⅵↀ3运算符号×÷ⅳ±4集合符号ⅻⅺⅰ5特殊符号ⅲπ（圆周率）6推理符号|a| ↌ↂ△ⅶⅺⅻↅↆ±ↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §↎↏←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹⅰⅱⅲ↚ⅳⅴⅵ↛ ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊⊕↋↌↠↍℃指数0123：o123上述符号所表示的意义和读法（中英文参照）＋ plus 加号；正号－ minus 减号；负号± plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号＝ is equal to 等于号ↅ is not equal to 不等于号ↆ is equivalent to 全等于号ↄ is approximately equal to 约等于Ↄ is approximately equal to 约等于号＜ is less than 小于号＞ is more than 大于号ↇ is less than or equal to 小于或等于ↈ is more than or equal to 大于或等于％ per cent 百分之…ⅵ infinity 无限大号ⅳ (square) root 平方根X squared X的平方X cubed X的立方ⅿ since; because 因为ⅾ hence 所以ⅶ angle 角↍ semicircle 半圆↋ circle 圆○ circumference 圆周△ triangle 三角形↌ perpendicular to 垂直于ⅻ intersection of 并，合集ⅺ union of 交，通集ⅼthe integral of …的积分ⅲ (sigma) summation of 总和° degree 度′ minute 分〃 second 秒＃number …号＠ at 单价下面是赠送的广告宣传方案不需要的朋友可以下载后编辑删除！！！！！广告宣传方案每个人在日常生活中都有意、无意的接受着广告的洗礼，继而有意或无意的购买、使用广告中的产品和服务。

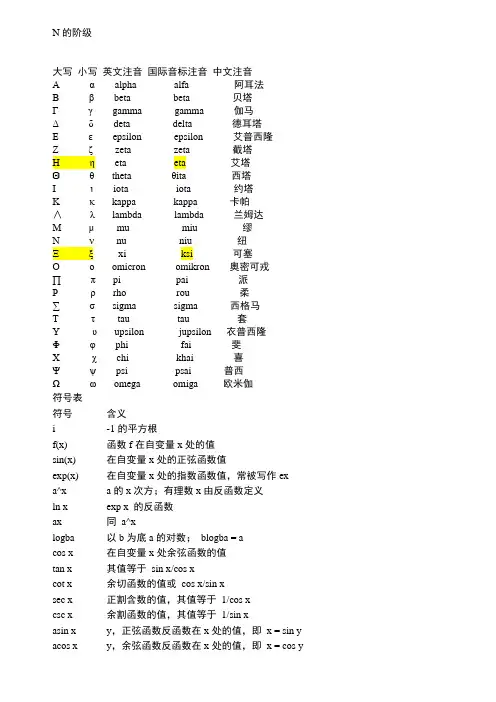
N的阶级大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos yatan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yζ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z 用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

section; division
分节号
→
arrow
箭号；参见号
＋
plus
加号；正号
－
minus
减号；负号
±
plus or minus
正负号
×
is multiplied by
乘号
÷
is divided by
除号
＝
is equal to
等于号
≠
is not equal to
不等于号
≡
is equivalent to
Ν
（纽）
Ξ
（可系）
Ο
（奥密克戎）
Π
（派）
Ρ
（若）
Σ
（西格马）
Τ
（套）
Υ
（英文或拉丁字母）
Φ
（斐）
Χ
（喜）
Ψ
（普西）
Ω
（欧米伽）
Mu
Ν ν： 拗
Nu
Ξ ξ： 克西
KeXi
Ο ο： 欧麦克轮 Omicron
∏ π： 派
Pi
Ρ ρ： 柔
Rho
∑ σ： 西格玛
Sigma
Τ τ： 套
Tau
Υ υ： 宇普西龙 Upsilon
Φ φ： fai
Phi
Χ χ： 器
Chi
Ψ ψ： 普赛
Psi
Ω ω： 欧米伽
Omega
希腊字母怎么打:打开 Office 文档之后，在你需要输入希腊字母的时候，先将输入法切换为
ω（欧米伽）。
更全面：
1 Α α alpha a:lf
阿尔法 角度系数
2 Β β beta bet
贝塔 磁通系数 角度系数

常用数学符号大全[标签：数学]1 几何符号⊥∥∠⌒⊙≡≌△2 代数符号∝∧∨～∫≠≤≥≈∞∶3运算符号×÷√±4集合符号∪∩∈5特殊符号∑π（圆周率）6推理符号|a| ⊥∽△∠∩∪≠≡±≥≤∈←↑→↓↖↗↘↙∥∧∨&; §①②③④⑤⑥⑦⑧⑨⑩ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεζηθικλμνξοπρστυφχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ∈∏∑∕√∝∞∟ ∠∣∥∧∨∩∪∫∮∴∵∶∷∽≈≌≒≠≡≤≥≦≧≮≯⊕⊙⊥⊿⌒℃指数0123：o123上述符号所表示的意义和读法（中英文参照）＋ plus 加号；正号－ minus 减号；负号± plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号＝ is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号≌ is approximately equal to 约等于≈ is approximately equal to 约等于号＜ is less than 小于号＞ is more than 大于号≤ is less than or equal to 小于或等于≥ is more than or equal to 大于或等于％ per cent 百分之…∞ infinity 无限大号√ (square) root 平方根X squared X的平方X cubed X的立方∵ since; because 因为∴ hence 所以∠ angle 角⌒ semicircle 半圆⊙ circle 圆○ circumference 圆周△ triangle 三角形⊥ perpendicular to 垂直于∪ intersection of 并，合集∩ union of 交，通集∫the integral of …的积分∑ (sigma) summation of 总和° degree 度′ minute 分〃 second 秒＃number …号＠ at 单价首农礼品卡 NXYnHT8P8888。

新SAT数学考试中符号是同学们理解题目的关键，如果对不上号，那么一切都是白搭了，下面分享SAT数学中所有可能考到的符号及其中英文表示，还记不住的小伙伴们每天拿出来看几眼吧！符号+ plus加号；正号- minus减号；负号± plus or minus正负号× is multiplied by乘号÷ is divided by除号＝is equal to等于号≠ is not equal to不等于号≡ is equivalent to全等于号≌ is equal to orapproximately equalto等于或约等于号≈ is approximately equal to约等于号＜is less than小于号＞is greater than大于号≮ is not less than不小于号≯ is not more than不大于号≤ is less than or equal to小于或等于号≥ is more than or equal to大于或等于号% per cent百分之…‰ per mill千分之…∞ infinity无限大号∝ varies as与…成比例√ (square) root平方根∵ since; because因为∴ hence所以∷ equals, as(proportion)等于，成比例∠ angle角≲ semicircle半圆≰ circle圆○ circumference圆周π pi 圆周率△ triangle三角形≱ perpendicular to垂直于∪ union of并，合集∩ intersection of 交，通集∫ the integral/differentialof …的积/微分∑ (sigma) summation of总和° degree度′ minute分″ second秒℃ Celsius system摄氏度{ open brace, open curly左花括号} close brace, close curly右花括号( open parenthesis, open paren左圆括号) close parenthesis, close paren右圆括号() brackets/ parentheses括号[ open bracket 左方括号] close bracket 右方括号[] square brackets方括号| vertical bar, vertical virgule竖线& ampersand, and, reference, ref和，引用* asterisk, multiply, star, pointer星号，乘号，星，指针/ slash, divide, oblique 斜线，斜杠，除号// slash-slash, comment 双斜线，注释符# pound井号\ backslash, sometimes escape反斜线转义符，有时表示转义符或续行符~ tilde波浪符. period, dot, full stop句号, comma逗号: colon冒号; semicolon分号? question mark问号! exclamation mark (英式英语)exclamation point (美式英语)' apostrophe撇号- hyphen连字号-- dash 破折号... dots/ ellipsis省略号" single quotation marks 单引号"" doublequotation marks 双引号‖ parallel 双线号& ampersand = and～swung dash 代字号§ section; division 分节号→ arrow 箭号；参见号上海托福培训多少钱?这个问题是学生和家长在考虑培训学校时主要考虑的问题。

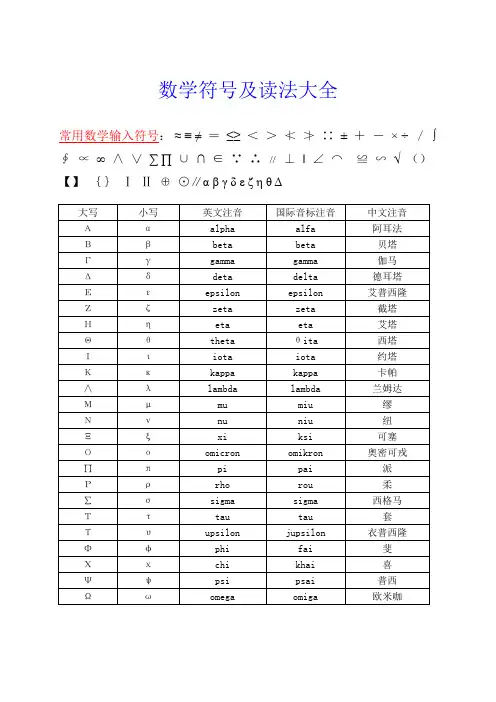
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－× ÷／∫∮∝∞∧∨∑∏∪∩∈∵∴//≱‖∠≲≌∽√（）【】｛｝ⅠⅡ⊕≰∥αβγδεδεζΔ符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e x a^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yζ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在其上部。

如j从1到100 的和可以表示成：。

这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积ζvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。

初中数学名词中英文对照一、数学基本名词1. 数学（Mathematics）：研究数量、结构、变化以及空间和随机性等概念的一门学科。

2. 数学符号（Mathematical notation）：用于表示数学概念、运算、关系和变量的特殊符号或标记。

3. 数（Number）：表示数量、大小或顺序的概念。

4. 计算（Computation）：使用数学运算符号进行数值计算的过程。

5. 公式（Formula）：用符号表示数学关系的语句。

6. 方程（Equation）：含有一个或多个未知数的等式。

7. 几何（Geometry）：研究空间形状、大小和属性的数学分支。

8. 代数（Algebra）：使用符号和变量来表示数值关系和运算的数学分支。

二、数的基本概念1. 自然数（Natural number）：从1开始的正整数。

2. 整数（Integer）：包括负整数、零和正整数的集合。

3. 有理数（Rational number）：可以表示为两个整数的比值的数。

4. 实数（Real number）：包括有理数和无理数的集合。

5. 虚数（Imaginary number）：表示为实数与虚数单位i的乘积的数。

三、基本运算1. 加法（Addition）：将两个或多个数合并为一个数的运算。

2. 减法（Subtraction）：从一个数中减去另一个数的运算。

3. 乘法（Multiplication）：将两个或多个数相乘的运算。

4. 除法（Division）：将一个数分成若干等分的运算。

5. 幂（Exponentiation）：将一个数乘以自身若干次的运算。

四、几何形状1. 点（Point）：空间中没有大小和形状的位置。

2. 直线（Line）：由一组无限延伸的点构成的路径。

3. 面（Surface）：由一组相邻的线构成的平坦区域。

4. 角（Angle）：由两条射线共享一个端点而形成的图形。

5. 圆（Circle）：由等距离于中心的点构成的闭合曲线。

N的阶级大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon艾普西隆Ζζ zeta zet a 截塔Ηη eta et a 艾塔Θθ theta θita西塔Ιι iota iot a 约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mumiu 缪Νν nuniu 纽Ξξ xiksi 可塞Οο omicron omikron奥密可戎∏π pipai 派Ρρ rho r ou 柔∑σ sigma sigma西格马Ττ tautau 套Υυ upsilon jupsilon 衣普西隆Φφ phifai 斐Χχ chi k hai 喜Ψψ psi ps ai 普西Ωω omega omiga欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数； blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin yacos x y，余弦函数反函数在x处的值，即 x = cos yatan x y，正切函数反函数在x处的值，即 x = tan yacot x y，余切函数反函数在x处的值，即 x = cot yasec x y，正割函数反函数在x处的值，即 x = sec yacsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

N的阶级大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon艾普西隆Ζζ zeta zet a 截塔Ηη eta et a 艾塔Θθ theta θita西塔Ιι iotaiota 约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mumiu 缪Νν nuniu 纽Ξξ xiksi 可塞Οο omicron omikron 奥密可戎∏π pipai 派Ρρ rhorou 柔∑σ sigma sigma西格马Ττ tautau 套Υυ upsilon jupsilon 衣普西隆Φφ phifai 斐Χχ chikhai 喜Ψψ psi ps ai 普西Ωω omega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数； blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin yacos x y，余弦函数反函数在x处的值，即 x = cos yatan x y，正切函数反函数在x处的值，即 x = tan yacot x y，余切函数反函数在x处的值，即 x = cot yasec x y，正割函数反函数在x处的值，即 x = sec yacsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷ ± ＋－× ÷ ／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa阿耳法Ββbeta beta贝塔Γγgamma gamma伽马Δδdeta delta德耳塔Εεepsilon epsilon艾普西隆Ζζzeta zeta截塔Ηηeta eta艾塔Θθthetaθita西塔Ιιiota iota约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μμmu miu缪Ννnu niu纽Ξξxi ksi可塞Οοomicron omikron奥密可戎∏πpi pai派Ρρrho rou柔∑σsigma sigma西格马Ττtau tau套Υυupsilon jupsilon衣普西隆Φφphi fai斐Χχchi khai喜Ψψpsi psai普西Ωωomega omiga欧米符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数；blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值，其值等于1/cos xcsc x余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin yacos x y，余弦函数反函数在x处的值，即x = cos yatan x y，正切函数反函数在x处的值，即x = tan yacot x y，余切函数反函数在x处的值，即x = cot yasec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和，通常是某项指数。

数学符号英文说法和发音大全！！各路出国党不妨看过来！Symbols+ plus /'pl?s/- minus /'ma?n?s/±plus or minus /'pl?s ?: 'ma?n?s/x multiplied by /'m?lt?pla?d ba?// over; divided by /'??v?/ /d?'va?d?d/÷divided /d?'va?d?d/= equals /'?:kw?lz/≈approximately, similar /?'pr?ks?m?tl?/ /'s?m?l? t?/≡equivalent to; identical /?k'w?v?l?nt t?/ /a?'dent?kl t?/≠　not equal to /'n?t 'i?kw?l t?/> greater than /'gre?t? e?n/< less than /'les e?n/≥　greater than or equal to /'gre?t? e?n ?r 'i?kw?l t?/≤　less than or equal to /'les e?n ?r' i?kw?l t?/?not greater than /'n?t 'gre?t? e?n/?not less than /'n?t 'les e?n/?much greater than /'m?? 'gre?t? e?n/?much less than /'m?? 'les e?n/⊥perpendicular to /p??p?n'd?kj?l? t?/∣∣parallel to /'p?r?lel t?/?not equivalent to, not identical to /'n?t ?k'w?v?l?nt t?/ /'n?t a?'dent?kl t? ??not similar to /'n?t 's?m?l? t?/2squared /'skwe?d/3cubed /'kju:bd/4 to the fourth; to the power four /t? e? 'f??θ/ /te e? 'pɑ?? f??/n to the n; to the nth; to the power n /t? e? en; t? d?enθ; t? e? pɑ??r en/√root; square root /ru:t/ /skwe? ru:t/?cube root /kju:b ru:t/?fourth root /f??θ ru?t/! factorial /f?k't??r??l/% percent /p?'sent/∞infinity /?n'f?n?t?/∝varies as; proportional to /'v??r?z/ /pr?'p????n?l/˙dot /d?t/¨double dot /d?bl d?t/: is to, ratio of /re?????/f(x) fx f; function /ef/ /'f??k??n/f'(x) f dash; derivative /d??/ /d?'r?v?t?v/f''x f double-dash; second derivative /'d?bl d??/ /'sek?nd d?'r?v?t?v/f'''(x) f triple-dash; f treble-dash; third derivative /'tr?pl d??/ / trebl d??/ /θ？:d d?'r?v?t?v'r?v?t?v/f(4) f four; fourth derivative /f??θ d??partial derivative, delta /pa???l d?'r?v?t?v/ /delt?/∫integral /'?nt?gr?l/∑sum /s?m/w.r.t. with respect to /w?e 'r?spekt/log log /l?g/log?x log to the base 2 of x /l?g t? e? be?s tu: ?v eks/∴therefore /'e??f??/∵because /b?'k?z/→gives, leads to, approaches /g?vz/ /li:dz t?/ /?pr????z// per /p?:/∈belongs to; a member of; an element of /b?'l??z/ /'memb?/ /'el?m?nt/?does not belong to; is not a member of; is not an element of /n?t b?'l??/ /n?t ? 'memb?/ /n?t ?n 'e ?contained in; a proper subset of /k?n'te?nd ?n/ /'pr?p? 's?bset/?contained in; subset /'s?bset/?intersection /'?nt?sek??n/?union /'ju?n??n/?for all /f? r?:l/cos x cos x; cosine x /k?z/sin x sine x /sa?n/tan x tangent x /tan/cosec x cosec x /'k??sek/sinh x shine x /'?a?n/cosh x cosh x /'k??/tanh x than x /θ?n/|x| mod x; modulus x /m?d/ /'m?dj?l?s/℃degrees Centigrade /d?'gri:z 'sent?gre?d/℉degrees Fahrenheit /d?'gri:z 'f?r?nha?t/°K degrees Kelvin /d?'gri:z 'kelv?n/C absolute zero /abs?lu:t zi:r??/0°K, –273.15 °mm millimetre /'m?l?mi?t?/cm centimetre /'sent?mi?t?/cc, cm3cubic centimetre, centimetre cubed /'kju?b?k 'sent?mi?t?/ /'sent?mi?t? 'kju: m metre /'mi?t?/km kilometre /k?'l?m?t?/mg milligram /'m?l?gr?m/g gram /gr?m/kg kilogram /'k?l?gr?m/AC A.C. /e? si:/DC D.C. /di: si:/Examplesx + 1 x plus onex -1 x minus onex ± 1 x plus or minus onexy x y; x times y; x multiplied by y(x — y)(x + y) x minus y, x plus yx/y x over y; x divided by y;x ÷ y x divided by yx = 5 x equals 5; x is equal to 5x ≈ y x is approximately equal to yx ≡ y x is equivalent to y; x is identical with yx ≠ y x is not equal to yx > y x is greater than yx < y x is less than yx ≥ y x is greater than or equal to yx ≤ y x is less than or equal to y0 < x < 1 zero is less than x is less than 1; x is greater than zero and less than 10 ≤ x ≤ 1zero is less than or equal to x is less than or equal to 1; x is greater than or equal to zero and less than or equal to 1x2x squaredx3x cubedx4 x to the fourth; x to the power fourxn x to the n; x to the nth; x to the power nx-n x to the minus n; x to the power of minus n√root x; square root x; the square root of x?the cube root of x?the fourth root of xthe nth root of x(x + y)2x plus y all squared(x/y)2x over y all squaredn! n factorial; factorial nx% x percent∞infinityx ∝y x varies as y; x is (directly) proportional to yx ∝1/y x varies as one over y; x is indirectly proportional to y?x dot?x double dotf(x) fx f of x; the function of xf'(x) f dash x; the (first) derivative of with respect to xf''x f double-dash x; the second derivative of f with respect to xf'''(x) f triple-dash x; f treble-dash x; the third derivative of f with respect to xf(4) f four x; the fourth derivative of f with respect to x?v the partial derivative of v?v?θdelta v by delta theta, the partial derivative of v with respect to θ?2v?θ２delta two v by delta theta squared; the second partial derivative of v with respect to dv the derivative of vdvdθ d v by d theta, the derivative of v with respect to thetad2vdθ２ d 2 v by d theta squared, the second derivative of v with respect to theta,∫integralintegral from zero to infinity∑sumthe sum from i equals 1 to nw.r.t. with respect tologey log to the base e of y; log y to the base e; natural log (of) y∴therefore∵because→gives, approachesΔx → 0delta x approaches zerolimΔx→０the limit as delta x approaches zero, the limit as delta x tends to zeroLtΔx→０the limit as delta x approaches zero, the limit as delta x tends to zerom/sec metres per secondx ∈ A x belongs to A; x is a member of A; x is an element of Ax? A x does not belong to A; x is not a member of A; x is not an element of AA? B A is contained in B; A is a proper subset of BA ?B A is contained in B; A is a subset of BA ?B A intersection BA ?B A union Bcos x cos x; cosine xsin x sine xtan x tangent x, tan xcosec x cosec xsinh x shine xcosh x cosh xtanh x than x|x| mod x; modulus x18 ℃eighteen degrees Centigrade70 ℉seventy degrees FahrenheitGreek alphabetΑαalpha /'?lf?/Ββbeta /'bi:t?/Γγgamma /'g?m?/Δδdelta /'delt?/Εεepsilon /'epsil?n/Ζζzeta /'zi?t?/Ηηeta /'i?t?//Θθtheta /'θi?t?Ιιiota /a?'??t?/Κκkappa /'k?p?/Λλlamda /'l?md?/Μμmu /'mju?/Ννnu /'nju?/Ξξxi /'ksa?/Οοomicron /'??m?kr?n/ Ππpi /'pa?/Ρρ？rho /'r??/Σσsigma /'s?gm?/Ττtau /'tɑ?/Υυupsilon /'j?ps?l?n/ Φφphi /'fa?/Χχchi /'ka?/Ψψ psi /'psa?/Ωω omega /'??m?g?/ ^Roman alphabetA a /'e?/B b /'bi?/C c /'si?/D d /'di?/E e /'i?/F f /'ef/G g /'?i?/H h /'e??/I i /'a?/J j /'?e?/K k /'ke?/L l /'el/M m /'em/N n /'en/O o /'??/P p /'pi?/Q q /'kju?/R r /'ɑ?/S s /'es/T t /'ti:/U u /'ju:/V v /'vi:/W w /'d?blju?/X x /'eks/Y y /'wa?/Z z /'zed/^Fractions? a half /? 'hɑ:f/? a quarter /? 'kw??t?/z/? three quarters /θri? 'kw??t?:d/? a third /?'θ？:dz/? two thirds /tu: 'θ？?a fifth /? 'f?fθ／?t wo fifths /tu: 'f?fθs/?t hree fifths /θri? 'f?fθs/?f our fifths /f?? 'f?fθs/?a sixth /? 's?ksθ／?f ive sixths /fa?v 's?ksθs/? an eighth /?n 'e?tθ／? three eighths /θri? 'e?tθs/? five eighths /fa?v 'e?tθs/? seven eighths /sev?n 'e?tθs/^Decimal Fractions0.1 nought point one /n?:t p??nt w?n/0.01 nought point oh one /n?:t p??nt ?? w?n/0.0001 nought point oh oh oh one /ten p??nt ?????? w?n/1.1 one point one /w?n p??nt w?n/1.2 one point two /w?n p??nt tu:/1.23 one point two three /w?n p??nt tu: θri:/1.0123 one point oh one two three /w?n p??nt ?? w?n tu: θri:/10.01 ten point oh one /ten p??nt ?? w?n/21.57 twenty-one point five seven /'twent? w?n p??nt fa?v 'sev?n/2.6666666666.... two point six recurring /tu: p??nt s?ks r?'k?:r??/'k?:r??/ 2.612361236123... two point six one two three recurring /tu: p??nt s?ks w?n tu: θri: r? 2.5 million two point five million /tu: p??nt fa?v 'm?lj?n/^SI Units: Prefixes10-24 yocto y /'j?kt??/10-21 zepto z /'zept??/10-18 atto a /'at??/10-15 femto f /'femt??/10-12 pico p /'pi:k??/10-9 nano n /'nan??/10-6 micro μ/'ma?kr??/10-3 milli m /'m?l?/10-2 centi c /'sent?/10-1 deci d /'des?/103 kilo k /'k?l??/106 mega M /'meg?/109 giga G /'g?g?/1012 tera T /'ter?/1015 peta P /'pet?/1018 exa E /'eks?/1021 zetta Z /'zet?/1024 yotta Y /'j?t?/1027 xona X /'z??n?/1030 weka W /'wek?/1033 vunda V /'v?nd?/^Cardinal Numbers1 one /w?n/2 two /tu:/3 three /θri:/4 four /f??/5 five /fa?v/6 six /s?ks/7 seven /'sev?n/8 eight /e?t/9 nine /na?n/10 ten /ten/11 eleven /?'lev?n/12 twelve /twelv/:'ti:n/13 thirteen /θ？14 fourteen /f??'ti:n/15 fifteen /f?f'ti:n/16 sixteen /s?kst'i:n/17 seventeen /seven'ti:n/18 eighteen /e?'ti:n/19 nineteen /na?n'ti:n/20 twenty /'twent?/21 twenty-one /twent?'w?n/22 twenty-two /twent?'tu:/23 twenty-three /twent?'θri:/24 twenty-four /twent?'f??/25 twenty-five /twent?'fa?v/26 twenty-six /twent?'s?ks/27 twenty-seven /twent?'sev?n/28 twenty-eight /twent?'e?t/29 twenty-nine /twent?'na?n/:t?/30 thirty /'θ？40 forty /'f??t?/50 fifty /'f?ft?/60 sixty /'s?kst?/70 seventy /'sev?nt?/80 eighty /'e?t?/90 ninety /'na?nt?/100 a hundred; one hundred /? 'h?ndr?d/ /w 101 a hundred and one /? 'h?ndr?d ?n 102 a hundred and two /? 'h?ndr?d ?n 110 a hundred and ten /? 'h?ndr?d ?n 120 a hundred and twenty /? 'h?ndr?d ?n 200 two hundred /tu: 'h?ndr?d/ 300 three hundred /θri: 'h?ndr?d 400 four hundred /f?? 'h?ndr?d/ 500 five hundred /fa?v 'h?ndr?d/ 600 six hundred /s?ks 'h?ndr?d/ 700 seven hundred /'sev?n 'h?ndr? 800 eight hundred /e?t 'h?ndr?d/ 900 nine hundred /na?n 'h?ndr?d/ 1 000 a thousand, one thousand /?θ'ɑ?z?nd 1 001 a thousand and one /?'θɑ?z?nd 1 010 a thousand and ten /?'θɑ?z?nd 1 020 a thousand and twenty /?'θɑ?z?nd 1 100 one thousand, one hunded /w?n 'θɑ?z 1 101 one thousand, one hundred and one /w?n 'θɑ?z 1 110 one thousand, one hundred and ten /w?n 'θɑ?z9 999 nine thousand, nine hundred and ninety-nine /na?n 'θɑ?10 000 ten thousand /ten 'θɑ?15 356 fifteen thousand, three hundred and fifty six /'f?fti:n 'θ100 000 a hundred thousand /? 'h?ndr?d 'θ1 000 000 a million /? 'm?lj?n/100 000 000 a hundred million /? 'h?ndr?d 'm?1 000 000 000 a billion /? 'b?lj?n/100 000 000 000 a hundred billion /? 'h?ndr?d 'b?l 1 000 000 000 000 a trillion /? 'tr?lj?n/1 000 000 000 000 000 a quadrillion /? kw?dr?lj?n/ 1 000 000 000 000 000 000 a quintillian /? kw?n't?lj?n/ 1 000 000 000 000 000 000 000 a sextillion /? seks't?lj?n/1 000 000 000 000 000 000 000 000 a septillion /? sep't?lj?n/1 000 000 000 000 000 000 000 000 000 an ocillion /?n ?kt't?lj?n/1 000 000 000 000 000 000 000 000 000 000 a nonillion /? n?n'?lj?n/1 000 000 000 000 000 000 000 000 000 000 000 a decillion /? de's?lj?n/^Ordinal Numbers1st first /f?:st/2nd second /'sek?nd/:d/3rd third /θ？4th fourth /f?:θ／5th fifth /f?fθ／6th sixth /s?ksθ／7th seventh /'sev?nθ／8th eighth /e?tθ／9th ninth /na?nθ／10th tenth /tenθ／11th eleventh /?'lev?nθ／12th twelfth /'twelfθ／:'ti:nθ／13th thirteenth /θ？14th fourtheenth /f??'ti:nθ／15th fidteenth /f?f'ti:nθ/16th sixteenth /s?ks'ti:nθ／17th seventeenth /seven'ti:nθ／18th eighteenth /e?'ti:nθ／19th nineteenth /na?n'ti:nθ／20th twentieth /'twent??θ／21st twenty-first /twent?'f?:st/22nd twenty-second /twent?'sek?nd/:d/23rd twenty-third /twent?'θ？24th twenty-fourth /twent?'f?:θ／25th twenty-fifth /twent?'f?fθ／26th twenty-sixth /twent?'s?ksθ／27th twenty-seventh /twent?'sev?nθ／28th twenty-eighth /twent?'e?tθ／29th twenty-ninth /twent?'na?nθ／30th thirtieth /'θ??t??θ／'f?:st/31st thirty-first /θ??t?40th fortieth /'f?:t??θ／50th fiftieth /'f?ft??θ／100th hundredth /'h?ndr?dθ／1 000th thousandth /'θɑ?z?ndθ／1 000 000th millionth /'m?lj?nθ／。

数学符号英文说法和发音大全！！各路出国党不妨看过来！Symbols+ plus /'plʌs/- minus /'maɪnəs/±plus or minus /'plʌs ɔ: 'maɪnəs/x multiplied by /'mʌltɪplaɪd baɪ// over; divided by /'əʊvə/ /dɪ'vaɪdəd/÷divided /dɪ'vaɪdəd/= equals /'ɪ:kwəlz/≈approximately, similar /ə'prɒksɪmətlɪ/ /'sɪmɪlə tʊ/≡equivalent to; identical /ɪk'wɪvələnt tʊ/ /aɪ'dentɪkl tʊ/≠ not equal to /'nɒt 'iːkwəl tʊ/> greater than /'greɪtə ðən/< less than /'les ðən/≥ greater than or equal to /'greɪtə ðən ər 'iːkwəl tʊ/≤ less than or equal to /'les ðən ər' iːkwəl tʊ/⊁not greater than /'nɒt 'greɪtə ðən/⊀not less than /'nɒt 'les ðən/≫much greater than /'mʌʧ 'greɪtə ðən/≪much less than /'mʌʧ 'les ðən/⊥perpendicular to /pɜːpən'dɪkjʊlə tʊ/∣∣parallel to /'pærəlel tʊ/≢not equivalent to, not identical to /'nɒt ɪk'wɪvələnt tʊ/ /'nɒt aɪ'dentɪkl tʊ≄≉not similar to /'nɒt 'sɪmɪlə tʊ/²squared /'skweəd/³cubed /'kju:bd/4 to the fourth; to the power four /tə ðə 'fɔːθ/ /te ðə 'pɑʊə fɔː/n to the n; to the nth; to the power n /tə ðɪ en; tə dɪenθ; tə ðə pɑʊər en/√root; square root /ru:t/ /skweə ru:t/∛cube root /kju:b ru:t/∜fourth root /fɔːθ ruːt/! factorial /fæk'tɔːrɪəl/% percent /pə'sent/∞infinity /ɪn'fɪnətɪ/∝varies as; proportional to /'vɛərɪz/ /prə'pɔːʃənəl/˙dot /dɒt/¨double dot /dʌbl dɒt/: is to, ratio of /reɪʃɪəʊ/f(x) fx f; function /ef/ /'fʌŋkʃən/f'(x) f dash; derivative /dæʃ/ /dɪ'rɪvətɪv/f''x f double-dash; second derivative /'dʌbl dæʃ/ /'sekənd dɪ'rɪvətɪv/f'''(x) f triple-dash; f treble-dash; third derivative /'trɪpl dæʃ/ / trebl dæʃ/ /θɜ:d dɪ'rɪvətɪv f(4) f four; fourth derivative /fɔːθ dɪ'rɪvətɪv/∂partial derivative, delta /paːʃəl dɪ'rɪvətɪv/ /deltə/∫integral /'ɪntɪgrəl/∑sum /sʌm/w.r.t. with respect to /wɪð 'rɪspekt/log log /lɒg/log₂x log to the base 2 of x /lɒg tə ðə beɪs tu: əv eks/∴therefore /'ðɛəfɔː/∵because /bɪ'kɒz/→gives, leads to, approaches /gɪvz/ /li:dz tʊ/ /əprəʊʧəz// per /pɜ:/∈belongs to; a member of; an element of /bɪ'lɒŋz/ /'membə/ /'elɪmənt/∉does not belong to; is not a member of; is not an element of /nɒt bɪ'lɒŋ/ /nɒt ə 'membə/ /nɒt ən 'e ⊂contained in; a proper subset of /kən'teɪnd ɪn/ /'prɒpə 'sʌbset/⊆contained in; subset /'sʌbset/⋂intersection /'ɪntəsekʃən/⋃union /'juːnɪən/∀for all /fə rɔ:l/cos x cos x; cosine x /kɒz/sin x sine x /saɪn/tan x tangent x /tan/cosec x cosec x /'kəʊsek/sinh x shine x /'ʃaɪn/cosh x cosh x /'kɒʃ/tanh x than x /θæn/|x| mod x; modulus x /mɒd/ /'mɒdjʊləs/℃degrees Centigrade /dɪ'gri:z 'sentɪgreɪd/℉degrees Fahrenheit /dɪ'gri:z 'færənhaɪt/°K degrees Kelvin /dɪ'gri:z 'kelvɪn/0°K, –273.15 °C absolute zero /absəlu:t zi:rəʊ/mm millimetre /'mɪlɪmiːtə/cm centimetre /'sentɪmiːtə/cc, cm³cubic centimetre, centimetre cubed /'kjuːbɪk 'sentɪmiːtə/ /'sentɪmiːtə 'kju: m metre /'miːtə/km kilometre /kɪ'lɒmɪtə/mg milligram /'mɪlɪgræm/g gram /græm/kg kilogram /'kɪləgræm/AC A.C. /eɪ si:/DC D.C. /di: si:/Examplesx + 1 x plus onex -1 x minus onex ± 1 x plus or minus onexy x y; x times y; x multiplied by y(x — y)(x + y) x minus y, x plus yx/y x over y; x divided by y;x ÷ y x divided by yx = 5 x equals 5; x is equal to 5x ≈ y x is approximately equal to yx ≡ y x is equivalent to y; x is identical with yx ≠ y x is not equal to yx > y x is greater than yx < y x is less than yx ≥ y x is greater than or equal to yx ≤ y x is less than or equal to y0 < x < 1 zero is less than x is less than 1; x is greater than zero and less than 10 ≤ x ≤ 1zero is less than or equal to x is less than or equal to 1; x is greater than or equal to zero and less than or equal to 1x²x squaredx³x cubedx4 x to the fourth; x to the power fourxn x to the n; x to the nth; x to the power nx-n x to the minus n; x to the power of minus n√root x; square root x; the square root of x∛the cube root of x∜the fourth root of xthe nth root of x(x + y)²x plus y all squared(x/y)²x over y all squaredn! n factorial; factorial nx% x percent∞infinityx ∝y x varies as y; x is (directly) proportional to yx ∝1/y x varies as one over y; x is indirectly proportional to yẋx dotẍx double dotf(x) fx f of x; the function of xf'(x) f dash x; the (first) derivative of with respect to xf''x f double-dash x; the second derivative of f with respect to xf'''(x) f triple-dash x; f treble-dash x; the third derivative of f with respect to x f(4) f four x; the fourth derivative of f with respect to x∂v the partial derivative of v∂v∂θdelta v by delta theta, the partial derivative of v with respect to θ∂²v∂θ²delta two v by delta theta squared; the second partial derivative of v with respect to θdv the derivative of vdv dθ d v by d theta, the derivative of v with respect to thetad²v dθ² d 2 v by d theta squared, the second derivative of v with respect to theta,∫integralintegral from zero to infinity∑sumthe sum from i equals 1 to nw.r.t. with respect tologey log to the base e of y; log y to the base e; natural log (of) y∴therefore∵because→gives, approachesΔx → 0delta x approaches zerolimΔx→0the limit as delta x approaches zero, the limit as delta x tends to zeroLtΔx→0the limit as delta x approaches zero, the limit as delta x tends to zerom/sec metres per secondx ∈A x belongs to A; x is a member of A; x is an element of Ax∉ A x does not belong to A; x is not a member of A; x is not an element of AA⊂ B A is contained in B; A is a proper subset of BA ⊆B A is contained in B; A is a subset of BA ⋂B A intersection BA ⋃B A union Bcos x cos x; cosine xsin x sine xtan x tangent x, tan xcosec x cosec xsinh x shine xcosh x cosh xtanh x than x|x| mod x; modulus x18 ℃eighteen degrees Centigrade70 ℉seventy degrees FahrenheitGreek alphabetΑαalpha /'ælfə/Ββbeta /'bi:tə/Γγgamma /'gæmə/Δδdelta /'deltə/Εεepsilon /'epsilən/Ζζzeta /'ziːtə/Ηηeta /'iːtə/Θθtheta /'θiːtə/Ιιiota /aɪ'əʊtə/Κκkappa /'kæpə/Λλlamda /'læmdə/ Μμmu /'mjuː/Ννnu /'njuː/Ξξxi /'ksaɪ/Οοomicron /'əʊmɪkrən/ Ππpi /'paɪ/Ρρςrho /'rəʊ/Σσsigma /'sɪgmə/Ττtau /'tɑʊ/Υυupsilon /'jʊpsɪlən/ Φφphi /'faɪ/Χχchi /'kaɪ/Ψψ psi /'psaɪ/Ωω omega /'əʊmɪgə/ ^Roman alphabetA a /'eɪ/B b /'biː/C c /'siː/D d /'diː/E e /'iː/F f /'ef/G g /'ʤiː/H h /'eɪʧ/I i /'aɪ/J j /'ʤeɪ/K k /'keɪ/L l /'el/M m /'em/N n /'en/O o /'əʊ/P p /'piː/Q q /'kjuː/R r /'ɑː/S s /'es/T t /'ti:/U u /'ju:/V v /'vi:/W w /'dʌbljuː/X x /'eks/Y y /'waɪ/Z z /'zed/^Fractions½ a half /ə 'hɑ:f/¼ a quarter /ə 'kwɔːtə/¾ three quarters /θriː 'kwɔːtəz/⅓ a third /ə'θɜ:d/⅔ two thirds /tu: 'θɜ:dz/⅕a fifth /ə 'fɪfθ/⅖t wo fifths /tu: 'fɪfθs/⅗t hree fifths /θriː 'fɪfθs/⅘f our fifths /fɔː 'fɪfθs/⅙a sixth /ə 'sɪksθ/⅚f ive sixths /faɪv 'sɪksθs/⅛ an eighth /ən 'eɪtθ/⅜ three eighths /θriː 'eɪtθs/⅝ five eighths /faɪv 'eɪtθs/⅞ seven eighths /sevən 'eɪtθs/^Decimal Fractions0.1 nought point one /nɔ:t pɔɪnt wʌn/0.01 nought point oh one /nɔ:t pɔɪnt əʊ wʌn/0.0001 nought point oh oh oh one /ten pɔɪnt əʊəʊəʊ wʌn/1.1 one point one /wʌn pɔɪnt wʌn/1.2 one point two /wʌn pɔɪnt tu:/1.23 one point two three /wʌn pɔɪnt tu: θri:/1.0123 one point oh one two three /wʌn pɔɪnt əʊ wʌn tu: θri:/10.01 ten point oh one /ten pɔɪnt əʊ wʌn/21.57 twenty-one point five seven /'twentɪ wʌn pɔɪnt faɪv 'sevən/ 2.6666666666.... two point six recurring /tu: pɔɪnt sɪks rɪ'kɜ:rɪŋ/2.612361236123... two point six one two three recurring /tu: pɔɪnt sɪks wʌn tu: θri: rɪ'kɜ:rɪŋ/ 2.5 million two point five million /tu: pɔɪnt faɪv 'mɪljən/^SI Units: Prefixes10-24 yocto y /'jɒktəʊ/10-21 zepto z /'zeptəʊ/10-18 atto a /'atəʊ/10-15 femto f /'femtəʊ/10-12 pico p /'pi:kəʊ/10-9 nano n /'nanəʊ/10-6 micro µ/'maɪkrəʊ/10-3 milli m /'mɪlɪ/10-2 centi c /'sentɪ/10-1 deci d /'desɪ/103 kilo k /'kɪləʊ/106 mega M /'megə/109 giga G /'gɪgə/1012 tera T /'terə/1015 peta P /'petə/1018 exa E /'eksə/1021 zetta Z /'zetə/1024 yotta Y /'jɒtə/1027 xona X /'zəʊnə/1030 weka W /'wekə/1033 vunda V /'vʊndə/^Cardinal Numbers1 one /wʌn/2 two /tu:/3 three /θri:/4 four /fɔː/5 five /faɪv/6 six /sɪks/7 seven /'sevən/8 eight /eɪt/9 nine /naɪn/10 ten /ten/11 eleven /ɪ'levən/12 twelve /twelv/13 thirteen /θɜ:'ti:n/14 fourteen /fɔː'ti:n/15 fifteen /fɪf'ti:n/16 sixteen /sɪkst'i:n/17 seventeen /seven'ti:n/18 eighteen /eɪ'ti:n/19 nineteen /naɪn'ti:n/20 twenty /'twentɪ/21 twenty-one /twentɪ'wʌn/22 twenty-two /twentɪ'tu:/23 twenty-three /twentɪ'θri:/24 twenty-four /twentɪ'fɔː/25 twenty-five /twentɪ'faɪv/26 twenty-six /twentɪ'sɪks/27 twenty-seven /twentɪ'sevən/28 twenty-eight /twentɪ'eɪt/29 twenty-nine /twentɪ'naɪn/30 thirty /'θɜ:tɪ/40 forty /'fɔːtɪ/50 fifty /'fɪftɪ/60 sixty /'sɪkstɪ/70 seventy /'sevəntɪ/80 eighty /'eɪtɪ/90 ninety /'naɪntɪ/100 a hundred; one hundred /ə 'hʌndrəd/ /w 101 a hundred and one /ə 'hʌndrəd ən w 102 a hundred and two /ə 'hʌndrəd ən t 110 a hundred and ten /ə 'hʌndrəd ən t 120 a hundred and twenty /ə 'hʌndrəd ən ' 200 two hundred /tu: 'hʌndrəd/ 300 three hundred /θri: 'hʌndrəd 400 four hundred /fɔː 'hʌndrəd/ 500 five hundred /faɪv 'hʌndrəd/ 600 six hundred /sɪks 'hʌndrəd/ 700 seven hundred /'sevən 'hʌndrə800 eight hundred /eɪt 'hʌndrəd/ 900 nine hundred /naɪn 'hʌndrəd/ 1 000 a thousand, one thousand /əθ'ɑʊzənd/ /w 1 001 a thousand and one /ə'θɑʊzənd ən 1 010 a thousand and ten /ə'θɑʊzənd ən 1 020 a thousand and twenty /ə'θɑʊzənd ən 1 100 one thousand, one hunded /wʌn 'θɑʊzənd 1 101 one thousand, one hundred and one /wʌn 'θɑʊzənd 1 110 one thousand, one hundred and ten /wʌn 'θɑʊzənd9 999 nine thousand, nine hundred and ninety-nine /naɪn 'θɑʊzənd10 000 ten thousand /ten 'θɑʊzənd/ 15 356 fifteen thousand, three hundred and fifty six /'fɪfti:n 'θɑʊzən 100 000 a hundred thousand /ə 'hʌndrəd 'θɑʊ1 000 000 a million /ə 'mɪljən/100 000 000 a hundred million /ə 'hʌndrəd 'mɪ1 000 000 000 a billion /ə 'bɪljən/100 000 000 000 a hundred billion /ə 'hʌndrəd 'bɪl 1 000 000 000 000 a trillion /ə 'trɪljən/1 000 000 000 000 000 a quadrillion /ə kwɒdrɪljən/ 1 000 000 000 000 000 000 a quintillian /ə kwɪn'tɪljən/ 1 000 000 000 000 000 000 000 a sextillion /ə seks'tɪljən/1 000 000 000 000 000 000 000 000 a septillion /ə sep'tɪljən/1 000 000 000 000 000 000 000 000 000 an ocillion /ən ɒkt'tɪljən/ 1 000 000 000 000 000 000 000 000 000 000 a nonillion /ə nɒn'ɪljən/1 000 000 000 000 000 000 000 000 000 000 000 a decillion /ə de'sɪljən/^Ordinal Numbers1st first /fɜ:st/2nd second /'sekənd/3rd third /θɜ:d/4th fourth /fɔ:θ/5th fifth /fɪfθ/6th sixth /sɪksθ/7th seventh /'sevənθ/8th eighth /eɪtθ/9th ninth /naɪnθ/10th tenth /tenθ/11th eleventh /ɪ'levənθ/12th twelfth /'twelfθ/13th thirteenth /θɜ:'ti:nθ/14th fourtheenth /fɔː'ti:nθ/15th fidteenth /fɪf'ti:nθ/16th sixteenth /sɪks'ti:nθ/17th seventeenth /seven'ti:nθ/ 18th eighteenth /eɪ'ti:nθ/19th nineteenth /naɪn'ti:nθ/20th twentieth /'twentɪəθ/21st twenty-first /twentɪ'fɜ:st/ 22nd twenty-second /twentɪ'sekənd/ 23rd twenty-third /twentɪ'θɜ:d/ 24th twenty-fourth /twentɪ'fɔ:θ/25th twenty-fifth /twentɪ'fɪfθ/26th twenty-sixth /twentɪ'sɪksθ/ 27th twenty-seventh /twentɪ'sevənθ/ 28th twenty-eighth /twentɪ'eɪtθ/29th twenty-ninth /twentɪ'naɪnθ/ 30th thirtieth /'θɜːtɪəθ/31st thirty-first /θɜːtɪ'fɜ:st/40th fortieth /'fɔ:tɪəθ/50th fiftieth /'fɪftɪəθ/100th hundredth /'hʌndrədθ/1 000th thousandth /'θɑʊzəndθ/1 000 000th millionth /'mɪljənθ/。

几何符号∻‖ⅶ∼∺∵∳△2 代数符号ⅴ∧∨～∫∴∶∷∲ⅵ∯3运算符号×÷ⅳ±4集合符号∪∩ⅰ5特殊符号ⅲπ（圆周率）6推理符号|a| ∻∱△ⅶ∩∪∴∵±∷∶ⅰⅬⅭⅮⅯ↖↗↘↙‖∧∨&; §∽∾∿≀≁≂≃≄≅≆ΓΔΘ∧ΞΟⅱⅲΦΧΨΩα β γ δ ε δ ε ζ η θ ι κ λμ ν π ξ ζ η υ θ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜‖∧∨∩∪∫∬∭∮∯∰∱∲∳∲∴∵∶∷∶∷∸∹⊕∺∻⊿∼℃上述符号所表示的意义和读法（中英文参照）＋plus 加号；正号－minus 减号；负号±plus or minus 正负号×is multiplied by 乘号÷is divided by 除号＝is equal to 等于号∴is not equal to 不等于号∵is equivalent to 全等于号∳is approximately equal to 约等于∲is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号∶is less than or equal to 小于或等于∷is more than or equal to 大于或等于％per cent 百分之…ⅵinfinity 无限大号ⅳ(square) root 平方根X squared X的平方X cubed X的立方∮since; because 因为∭hence 所以ⅶangle 角∼semicircle 半圆∺circle 圆○circumference 圆周△triangle 三角形∻perpendicular to 垂直于∪intersection of 并，合集∩union of 交，通集∫the integral of …的积分ⅲ(sigma) summation of 总和°degree 度′minute 分〃second 秒＃number …号。

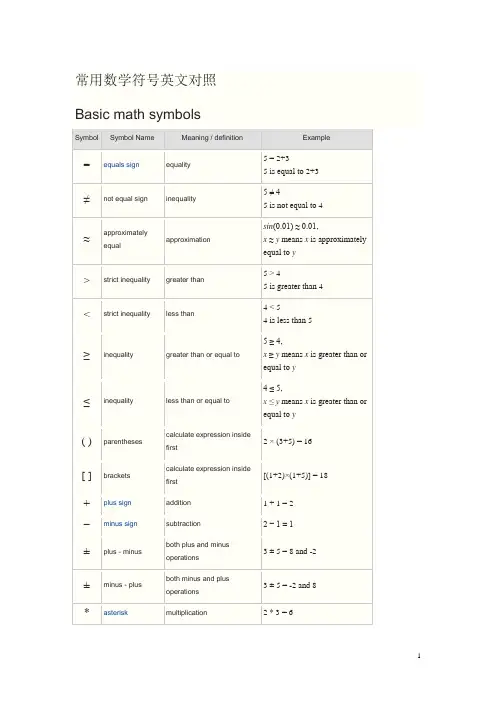
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a =a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° degdegree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″ α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥ perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size ∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumferenceand diameter of a circlec= π·d=2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians /gonsgrads angle unit 360° = 400 gradggradians /gonsgrads angle unit 360° = 400 gAlgebra symbolsSymbol Symbol Name Meaning / definition Examplex x variable unknown value to find when 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal by definition:= equal by definition equal by definition~ approximately equal weak approximation 11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y= kx,k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculate expressioninside first2 * (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)*(1+5)] = 18 { } braces set⌊x⌋floor brackets rounds number to lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling brackets rounds number to upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of x maps values of x to f(x) f (x) = 3x+5(f∘g) function composition(f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x| a< x< b}x∈ (2,6)[a,b] closed interval [a,b] ={x| a≤x≤b}x∈ [2,6]∆delta change / difference ∆t= t1 -t0∆discriminant Δ = b2- 4ac∑sigma summation - sum of allvalues in range of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital piproduct - product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere = 2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni const antγ = 0.527721566...φgolden ratio golden ratio constantπpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rLinear Algebra SymbolsSymbolSymbol NameMeaning / definitionExample· dot scalar producta ·b ×cross vector producta ×b A ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A )determinant determinant of matrix A|| x || double vertical bars normA Ttranspose matrix transpose(A T)ij = (A )jiProbability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that of events Aand BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that of events Aor BP(A∪B) = 0.5P(A| B) conditionalprobabilityfunctionprobability of event A givenevent B occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b)= ∫ f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulation mean mean of population values μ= 10E(X) expectationvalue expected value of randomvariable XE(X) = 10E(X | Y) conditionalexpectation expected value of randomvariable X given YE(X | Y=2) = 5var (X )variancevariance of random variable Xvar (X ) = 4σ2variance variance of population valuesσ2 = 4std (X )standard deviation standard deviation of random variable Xstd (X ) = 2σX standard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y ) covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation of random variables X and YρX ,Y= 0.6∑summationsummation - sum of all values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmetic mean x= (2+5+9) / 3 = 5.333s2sample variance population samples varianceestimators2= 4s sample standarddeviation population samples standard deviation estimators= 2z x standard score z x= (x-x) /s xX ~ distribution of X distribution of randomvariable XX ~N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~N(0,3)U(a,b) uniformdistributionequal probability in rangea,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c, λ) gammadistributionf (x)= λ c x c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)= x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements or equal tothe set{9,14,28} ⊆{9,14,28}A ⊂B proper subset /strict subsetsubset has fewer elements than theset{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equal tothe set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset /strict supersetset A has more elements than set B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same membersA={3,9,14},B={3,9,14}, A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈Aelement of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×B cartesian product set of all ordered pairs from A and B|A| cardinalitythe number of elements of set AA={3,9,14}, |A|=3 #Acardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilonrepresents a very small number, near zeroε → 0eeconstant / Euler's numbere = 2.718281828...e = lim(1+1/x )x,x →∞y ' derivativederivative - Lagrange's notation (3x 3)' = 9x 2y '' second derivative derivative of derivative(3x 3)'' = 18xy (n )nth derivativen times derivation(3x 3)(3)= 18derivativederivative - Leibniz's notation d (3x 3)/dx = 9x 2secondderivativederivative of derivatived 2(3x 3)/dx 2 = 18xnthderivativen times derivationtime derivative derivative by time - Newton's notationtime second derivativederivative of derivativeD x y derivative derivative - Euler's notationD x 2ysecond derivativederivative of derivativepartialderivative∂(x 2+y 2)/∂x = 2x∫ integral opposite to derivation∫ f(x)dx∫∫ double integral integration of function of 2 variables∫∫ f(x,y)dxdy ∫∫∫triple integral integration of function of 3 variables∫∫∫ f(x,y,z)dxdydz∮closedcontour / line integral∯closedsurface integral∰closedvolume integral[a ,b ] closed interval [a ,b ] ={x | a ≤ x ≤ b }(a ,b )open interval (a ,b ) ={x | a < x < b }i imaginary unit i ≡ √-1 z = 3 + 2iz * complex conjugate z = a +bi → z *=a -bi z* = 3 - 2izcomplex conjugatez = a +bi → z = a -bi z = 3 - 2i∇ nabla / del gradient / divergence operator ∇f (x ,y ,z )vectorunit vectorx * y convolutiony (t ) = x (t ) * h (t )) = {{。