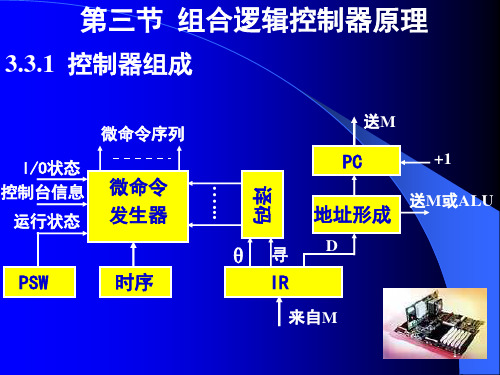
第三节组合逻辑控制器原理
- 格式:ppt
- 大小:346.00 KB
- 文档页数:20


组合逻辑电路原理概述及作用分析
组合逻辑电路概述:
数字电路根据逻辑功能的不同特点,可以分成两大类,一类叫组合逻辑电路(简称组合电路),另一类叫做时序逻辑电路(简称时序电路)。
组合逻辑电路在逻辑功能上的特点是任意时刻的输出仅仅取决于该时刻的输入,与电路原来的状态无关。
而时序逻辑电路在逻辑功能上的特点是任意时刻的输出不仅取决于当时的输入信号,而且还取决于电路原来的状态,或者说,还与以前的输入有关。
1.半加器与全加器
①半加器
两个数A、B相加,只求本位之和,暂不管低位送来的进位数,称之为半加。
完成半加功能的逻辑电路叫半加器。
实际作二进制加法时,两个加数一般都不会是一位,因而不考虑低位进位的半加器是不能解决问题的。
②全加器
两数相加,不仅考虑本位之和,而且也考虑低位来的进位数,称为全加。
实现这一功能的逻辑电路叫全加器。
2.加法器
实现多位二进制数相加的电路称为加法器。
根据进位方式不同,有串行进位加法器和超前进位加法器两种。
①四位串行加法器:如T692。
优点:电路简单、连接方便。
缺点:运算速度不高。
最高位的计算,必须等到所有低位依此运算结束,送来进位信号之后才能进行。
为了提高运算速度,可以采用超前进位方式。

组合逻辑电路设计的基本原理
组合逻辑电路是由多个逻辑门组成的电路,其输出仅取决于输入信号的状态,而不受电路历史状态的影响。
组合逻辑电路的设计是数字电路设计的基础,其设计原理包括以下几个方面。
1. 布尔代数
布尔代数是一种逻辑代数,用于描述逻辑运算的规则和性质。
布尔代数的基本运算包括与、或、非、异或等,这些运算可以用逻辑门实现。
在组合逻辑电路设计中,布尔代数是设计的基础,通过对输入和输出信号的逻辑关系进行分析,可以确定电路的逻辑功能。
2. 真值表
真值表是一种用于描述逻辑运算结果的表格,其中列出了所有可能的输入组合和对应的输出结果。
通过真值表可以直观地了解电路的逻辑功能,从而进行电路设计和优化。
3. 卡诺图
卡诺图是一种用于简化布尔代数表达式的图形化方法。
通过将真值表中相邻的1或0用方格表示,可以得到卡诺图。
在卡诺图中,相邻的方格表示只有一个变量不同的项,通过对方格进行合并,可以得到最简布尔代数表达式,从而实现电路的最小化设计。
4. 逻辑门
逻辑门是实现逻辑运算的基本元件,包括与门、或门、非门、异或门等。
通过逻辑门的组合可以实现各种逻辑功能,从而实现电路的设计。
5. 时序逻辑电路
时序逻辑电路是一种受电路历史状态影响的电路,其输出不仅取决于当前输入信号的状态,还受到电路之前的状态影响。
时序逻辑电路的设计需要考虑时序逻辑的特性,包括时钟信号、触发器等。
组合逻辑电路设计的基本原理包括布尔代数、真值表、卡诺图、逻辑门和时序逻辑电路等。
通过对这些原理的理解和应用,可以实现电路的设计和优化,从而满足不同的应用需求。

组合逻辑控制原理
组合逻辑控制原理,是指利用逻辑门(包括与门、或门、非门等)来实现逻辑运算和逻辑函数的一种电路设计方法。
它将多个逻辑门按照一定的组合方式连接在一起,以实现复杂的逻辑功能。
在组合逻辑控制原理中,逻辑门的输入和输出只受当前输入信号的影响,与过去的输入信号无关。
这种控制方式可以通过真值表、卡诺图等方法进行逻辑函数的化简和分析,从而设计出所需的电路。
组合逻辑控制原理的主要特点是无记忆性和无反馈性。
无记忆性是指输出仅与当前输入有关,无法通过当前的输出来控制过去的输入;无反馈性是指输出不会作为输入再次输入到逻辑门中,避免了回路的产生。
组合逻辑控制原理的应用非常广泛,常见于各类数字电路、计算机设计、自动化控制、数字信号处理等领域。
通过合理设计和组合不同的逻辑门,可以实现各种逻辑运算、逻辑函数和逻辑操作,满足不同应用需求。
总之,组合逻辑控制原理是一种利用逻辑门进行逻辑运算和逻辑函数设计的方法,通过组合逻辑门的输入和输出关系,实现复杂的逻辑功能。
它具有无记忆性和无反馈性的特点,被广泛应用于各种电子领域。

常用组合逻辑器件的原理及集成电路在数字集成产品中有许多具有特定组合逻辑功能的数字集成器件,称为组合逻辑器件(或组合逻辑部件)。
本节主要介绍这些组合器件,以及这些组合部件的应用。
1. 编码器和译码器(1)编码器组合逻辑部件中的编码器是对输入赋予一定的二进制代码,给定输入就有相应的二进制码输出。
常用的编码器有二进制编码器和二—十进制编码器等。
所谓二进制编码器是指输入变量数(m )和输出变量数(n )成2n 倍关系的编码器,如有4线/2线,8线/3线,16线/4线的集成二进制编码器;二—十进制编码器是输入十进制数(十个输入分别代表0~9十个数)输出相应BCD 码的10线/4线编码器。
1)二进制编码器二进制编码器是对2n 个输入进行二进制编码的组合逻辑器件,按输出二进制位数称为n 位二进制编码器。
二线―四线编码器编码器有4个输入(I 0,I 1,I 2,I 3分别表示0~3四个数或四个事件),给定一个数(或出现某一事件)以该输入为1表示,编码器输出对应二位二进制码(Y 1Y 0),其真值表如表3-1所示。
根据真值表可得最小项表达式∑=)4,1()I ,I ,I ,(I Y 32100m ,()∑=)2,1(I ,I ,I ,I Y 32101m 。
进一步分析表3-1,若限定输入中只能有一个为“1”,那么,除表3-6所列最小项和m 0外都是禁止项,则输出表达式可以用下式表示:31310I I I I Y =+= 32321I I I I Y =+= 。
图3-2 2线/4线编码器 由此输出函数表达式可得与非门组成的,如图3-2所示的2线/4线编码器逻辑图。
2)优先编码器由上述编码器真值表可以知道,4个输入中只允许一个输入有信号(输入高电平)。
若I 1和I 2同时为1,则输出Y 1Y 0为11,此二进制码是I 3有输入时的输出编码。
即此编码器在多个输入有效时会出现逻辑错误,这是其一。
其二,在无输入时,即输入全0时,输出Y 1Y 0为00,与I 0为1时相同。