第五讲时间序列数据描述712105314

统计学时间数列分析笔记
时间序列数据用于描述现象随时间发展变化的特征。

时间序列（timesseries）是同一现象在不同时间的相继观察值
排列而形成的序列。

经济数据大多数以时间序列的形式给出。

时间序列可以分为平稳序列和非平稳序列两大类。

平稳序列是基本上不存在趋势的序列。

这类序列中的各观察值基本上在某个固定的水平上波动，虽然在不同的时间段波动的程度不同，但并不存在某种规律，波动可以看成是随机的。

时间序列的成分可以分为四种：
趋势（T）、季节性或季节变动（S）、周期性或循环波动（C）、随机性或不规则波动（I）。

构成要素：长期趋势，季节变动，循环变动，不规则变动。

1）长期趋势（T）现象在较长时期内受某种根本性因素作用而形成的总的变动趋势。

2）季节变动（S）现象在一年内随着季节的变化而发生的有规律的周期性变动。

3）循环变动（C）现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动。

4）不规则变动（I）是一种无规律可循的变动，包括严格的随机变动和不规则的突发性影响很大的变动两种类型。

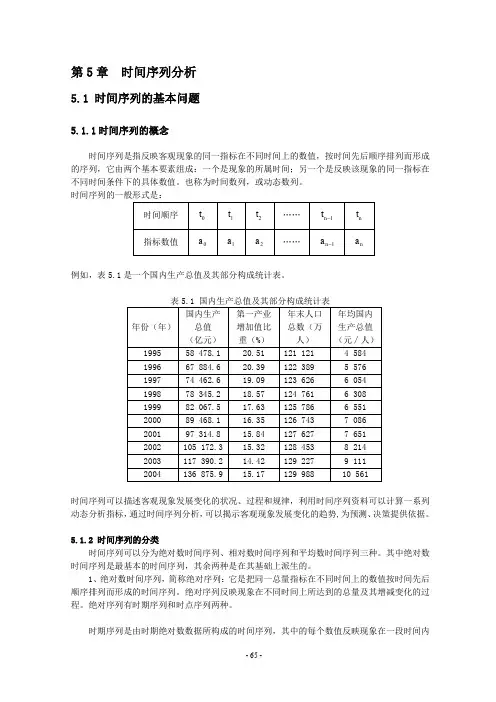
第5章时间序列分析5.1 时间序列的基本问题5.1.1时间序列的概念时间序列是指反映客观现象的同一指标在不同时间上的数值，按时间先后顺序排列而形成的序列，它由两个基本要素组成：一个是现象的所属时间；另一个是反映该现象的同一指标在不同时间条件下的具体数值。

也称为时间数列，或动态数列。

例如，表5.1是一个国内生产总值及其部分构成统计表。

时间序列可以描述客观现象发展变化的状况、过程和规律，利用时间序列资料可以计算一系列动态分析指标，通过时间序列分析，可以揭示客观现象发展变化的趋势,为预测、决策提供依据。

5.1.2 时间序列的分类时间序列可以分为绝对数时间序列、相对数时间序列和平均数时间序列三种。

其中绝对数时间序列是最基本的时间序列，其余两种是在其基础上派生的。

1、绝对数时间序列，简称绝对序列：它是把同一总量指标在不同时间上的数值按时间先后顺序排列而形成的时间序列。

绝对序列反映现象在不同时间上所达到的总量及其增减变化的过程。

绝对序列有时期序列和时点序列两种。

时期序列是由时期绝对数数据所构成的时间序列，其中的每个数值反映现象在一段时间内发展过程的总量。

时点序列是由时点绝对数数据所构成的时间序列，其中的每个数值反映现象在某一时点上所达到的水平。

时期序列中的各个数数值可以相加，各个数数值的和表示了在所对应的时期之内事物及其现象的发展总量。

而时点序列中各个数数值相加通常没有明确的意义；时期序列中各项数值的大小与所包括的时期长短有直接关系，时点序列中各数数值与其时点间隔长短没有直接关系。

2、相对数时间序列：它是把一系列同类的统计相对数按照时间先后顺序排列起来而形成的时间序列，反映事物之间对比关系的变化情况。

3、平均数时间序列：它是把一系列同类的统计平均数按照时间先后顺序排列起来而形成的时间序列，表现事物一般水平的变化过程的发展趋势。

参看上表格。

5.1.3编制时间序列的原则编制时间序列的目的是要通过对序列中各个时期指标值进行比较，以达到研究客观现象的发展变化状况、过程及其规律。

时间序列的概述时间序列是一种基于时间顺序排列的数据集合，用来描述过去一定时间内发生的事件或现象的变化。

它是统计学与经济学中的一个重要分析工具，被广泛应用于各个领域，如经济预测、股票市场分析、气象预报、交通流量等。

时间序列的数据可以是连续或离散的。

连续时间序列是在连续时间间隔内收集到的数据，例如每分钟、每小时或每天的数据。

离散时间序列则是在固定的时间点上收集到的数据，例如每年一次的问卷调查。

时间序列的特点是随时间变化而变化。

数据的变化可以是趋势性的，即随着时间的推移，数据呈现出持续上升或下降的趋势。

数据的变化还可以是周期性的，即在一定时间范围内，数据会周期性地波动。

此外，时间序列中还存在着随机性的变化，即数据在一段时间内没有明显的趋势或周期，呈现出随机波动的特征。

为了对时间序列进行分析，常常采用统计学中的方法。

其中最常用的是建立模型来描述时间序列的变化规律。

常见的时间序列模型包括平稳模型、非平稳模型、季节性模型和自回归移动平均模型等。

通过拟合模型，我们可以获得对时间序列的预测，从而做出相应的决策。

通过时间序列分析，我们可以提取出其中所包含的有用信息。

例如，我们可以根据过去的股票价格数据预测未来的价格趋势，或者根据过去的气温数据来预测未来的气候变化。

同时，时间序列分析还可以帮助我们检测异常值或异常事件，从而及时采取措施进行调整或干预。

总而言之，时间序列是一种重要的数据分析方法，通过对事件或现象在时间上的变化进行建模和预测，可以帮助我们理解和解释数据的规律，为决策提供有力的支持。

时间序列的应用范围广泛，几乎涵盖了所有需要对时间变化进行分析的领域。

时间序列分析是统计学中一个重要的分析方法，可以帮助我们理解数据的趋势、周期和随机波动，并预测未来的发展趋势。

时间序列分析的方法和技术有很多种，下面将介绍一些常用的时间序列分析方法。

首先，时间序列分析中最常用的方法是平滑法。

平滑法的基本思想是通过对数据进行加权平均来降低数据的波动，从而显示出数据背后的趋势。

第五讲描述性时间序列分析11 时间序列成分分析1.1 时间序列的构成因素时间序列中的数据（也称为观测值），总是由各种不同的影响因素共同作用所至；换一句话说，时间序列中的数据，总是包含着不同的影响因素。

我们可以将这些影响因素合并归类为几种不同的类型，并对各种类型因素的影响作用加以测定。

对时间序列影响因素的归类，最常见的是归为3类：21、长期趋势T（SPSS的名称为Smoothed Trend-Cycle，缩写stc），长期趋势是一种对事物的发展普遍和长期起作用的基本因素。

受长期趋势因素的影响，事物表现出在一段相当长的时期内沿着某一方向的持续发展变化。

2、季节周期因子S（SPSS的名称为Season Factors Component）, 缩写saf，季节周期也称为季节变动，是一种现象以一定时期（如一年、一月、一周等）为一周期呈3现较有规律的上升、下降交替运动的影响因素。

3、不规则变动因子I（SPSS的名称为Irregular Component, 缩写err）。

不规则变动是一种偶然性、随机性、突发性因素。

受这种因素影响，现象呈现时大时小、时起时伏、方向不定、难以把握的变动。

这种变动不同于前三种变动，它完全无规律可循，无法控制和消除，例如战争、自然灾害等。

【例】1993年1月至2000年12月社会消费品月零售4总额的各成分图如下。

图1 1993年1月至2000年12月社会消费品月零售总额曲线图5图2 长期趋势成分6图3 不规则变动因子图7图4 季节因子图81.2 时间序列的组合模型若以Y代表时间序列中的数据（观测值），则Y由上述四类因素所决定的组合模型为：=++（加法模型）Y T S I在加法模型中，各种影响因素是相互独立的，均为与Y同计量单位的绝对量。

加法模型中，各因素的分解是根据减法进行（如Y T S I-=+）。

Y T S I=⨯⨯（乘法模型）9在乘法模型中，只有长期趋势是与Y同计量单位的绝对量；其余因素均为以长期趋势为基础的比率，表现为对于长期趋势的一种相对变化幅度，通常以百分数表示。

时间序列分析教材本教材将介绍时间序列分析的基本概念、常用方法和应用示例，帮助读者了解和掌握时间序列分析的基本原理和操作方法。

一、时间序列分析的基本概念1、时间序列的特点：时间序列数据具有趋势性、季节性和周期性等特点，可以通过分析这些特征来预测未来的数据变化。

2、平稳时间序列：平稳时间序列是指时间序列数据的统计特性在时间上保持恒定，如均值、方差和自相关系数等。

平稳时间序列可以使用各种统计方法进行分析和预测。

3、非平稳时间序列：非平稳时间序列是指时间序列数据的统计特性在时间上发生变化，如趋势变化、季节变化和周期变化等。

非平稳时间序列需要进行差分或转化处理，使其变为平稳时间序列再进行分析。

二、时间序列分析的基本方法1、时间序列的图形表示：通过绘制时间序列的折线图、散点图和自相关图等，可以观察数据的分布、趋势和季节性等特征。

2、时间序列的分解：时间序列的分解是将时间序列数据分解为趋势、季节和随机成分三个部分，以便更好地对数据进行分析和预测。

3、时间序列的平滑方法：平滑方法包括移动平均法和指数平滑法，可以减少数据的随机波动，更好地揭示数据的趋势性。

4、时间序列的预测方法：预测方法包括线性回归模型、ARIMA模型和季节性ARIMA模型等，可以基于历史数据对未来数据进行预测。

5、时间序列的评估方法：评估方法包括残差分析、均方误差和平均绝对误差等，可以评估预测模型的准确性和可靠性。

三、时间序列分析的应用示例1、经济学中的时间序列分析：时间序列分析可以应用于宏观经济指标的预测和监测，如国内生产总值、通货膨胀率和失业率等。

2、金融学中的时间序列分析：时间序列分析可以应用于股票价格、汇率和利率等金融数据的分析和预测，帮助投资者进行投资决策。

3、气象学中的时间序列分析：时间序列分析可以应用于气象数据的分析和预测，如气温、降雨量和风速等，帮助预测天气变化和灾害风险。

四、时间序列分析的实际案例1、某股票价格的时间序列分析：通过对某只股票价格的时间序列数据进行分析，预测未来股票价格的走势，指导投资决策。

第5章时间序列的描述性分析5.1 时间序列及其分解5.2 时间序列的描述性分析学习目标1.时间序列及其分解原理2.时间序列的图形描述及增长率的分析5.1 时间序列及其分解5.1.1 时间序列的构成要素5.1.2 时间序列的分解方法时间序列(times series)1.同一现象在不同时间上的相继观察值排列而成的数列2.形式上由现象所属的时间和现象在不同时间上的观察值两部分组成3.排列的时间可以是年份、季度、月份或其他任何时间形式时间序列分析目的一是为了描述事物在过去时间的状态、分析其发展趋势。

二是为了揭示事物发展变化的规律性。

三是预测事物在未来时间的数量。

时间序列的分类时间序列的分类平稳序列(stationary series)基本上不存在趋势的序列，各观察值基本上在某个固定的水平上波动或虽有波动，但并不存在某种规律，而其波动可以看成是随机的非平稳序列 (non-stationary series)有趋势的序列线性的，非线性的有趋势、<a name=baidusnap0></a>季节</B>性和周期性的复合型序列时间序列的构成要素趋势、季节</B>、周期、随机性趋势(trend)呈现出某种持续向上或持续下降的状态或规律季节</B>性(seasonality)也称季节</B>变动(Seasonal fluctuation)时间序列在一年内重复出现的周期性波动周期性(cyclity)也称循环波动(Cyclical fluctuation)围绕长期趋势的一种波浪形或振荡式变动随机性(random)也称不规则波动(Irregular variations)除去趋势、周期性和季节</B>性之后的偶然性波动含有不同要素的时间序列平稳趋势季节</B>季节</B>与趋势时间序列的构成模型时间序列的构成要素分为四种，即趋势(T)、季节</B>性或季节</B>变动(S)、周期性或循环波动(C)、随机性或不规则波动(I)非平稳序列时间序列的分解模型乘法模型Yi=Ti×Si×Ci×Ii加法模型Yi=Ti+Si+Ci+Ii组合模型的解释乘法模型是假定四个成分对发展对象的影响是相互的，长期趋势成分取与时间序列原始指标数值Y相同计量单位的绝对量，以长期趋势为基础，其余成分则均以比率（相对量）表示加法模型是假定四个因素的影响相互独立的，每个成分均以与时间序列原始指标数值Y相同计量单位的绝对量来表示。