当前位置：文档之家 › 计量经济学 第八章 分布滞后模型

计量经济学 第八章 分布滞后模型

  • 格式：ppt
  • 大小：855.00 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

计量学分布滞后模型演讲概要

计量学分布滞后模型演讲概要

1 递减滞后结构 假定权数是递减的，认为滞后解释变量对被解释变量 的影响随着时间的推移越来越小。如消费函数 2 不变滞后结构 假定权数是相等的，认为滞后解释变量对被解释变量 的影响不随时间而变化。 3 A型滞后结构 权数先递增后递减。这类滞后结构适合于前后期滞后 解释变量对被解释变量的影响不大，而中期滞后解释变量 对被解释变量的影响较大的分布滞后模型。如投资对产出 的影响。
0.4,0,3,0.2,0.1）的分布滞后方程。即:
Yt - 1486.159 1.339518Z 1t
Yt 1486 .159 0.5358072 Ct 0.4018554 Ct - 1 0.2679036 Ct - 2 0.1339518 Ct - 3
2018/11/9
则式（5）可变换为
Yt 0 Z 0t 1 Z1t 2 Z 2t ut
2018/11/9
25
3、阿尔蒙（Almon）多项式滞后模型
利用样本数据对式（5）进行最小二乘估计，可得到式 （5）各个参数的估计值，分别记为
ˆ, ˆ0 , ˆ1 , ˆ2
将之代入式（4）可得原模型（3）参数的估计值为
艾特—丁伯根（Alt-Tinbergen)法
经验加权估计法
2018/11/9
8
第二节 分布滞后模型的参数估计
一、经验加权估计法
概念：根据实际经济问题的特点及经验判断，形成相 应的约束，对解释变量的系数赋予一定的权数，利用这些 权数构成各滞后变量的线性组合，以形成新的变量。再应 用最小二乘法进行估计。
2018/11/9 21
第二节 分布滞后模型的参数估计
3、阿尔蒙（Almon）多项式滞后模型
阿尔蒙多项式滞后模型的基本思想是：针对 有限滞后期模型，通过阿尔蒙变换，定义新变 量，以减少解释变量个数，然后用OLS法估计参 数。 如果有限分布滞后模型中的参数 i i 0,1,2,, k 的分布可以近似用一个关于i 的低阶多项式表 示就可以利用多项式减少模型中的参数。
分布滞后模型的估计

分布滞后模型的估计

分布滞后模型的估计建立总量消费函数是进行宏观经济管理的重要手段。

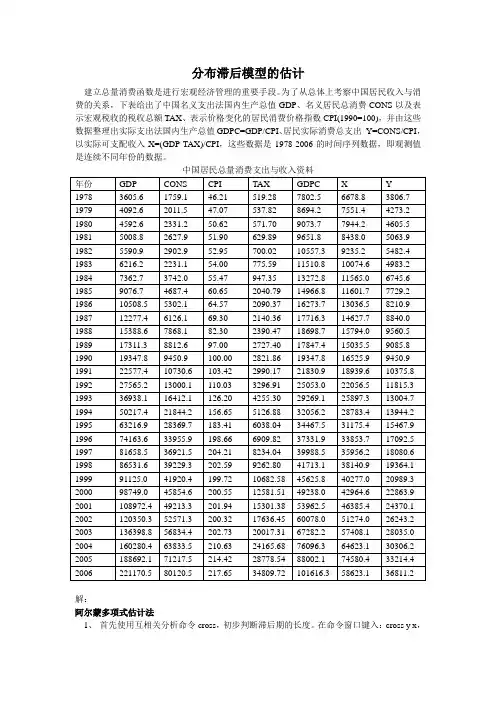
为了从总体上考察中国居民收入与消费的关系，下表给出了中国名义支出法国内生产总值GDP、名义居民总消费CONS以及表示宏观税收的税收总额TAX、表示价格变化的居民消费价格指数CPI(1990=100)，并由这些数据整理出实际支出法国内生产总值GDPC=GDP/CPI、居民实际消费总支出Y=CONS/CPI，以实际可支配收入X=(GDP-TAX)/CPI，这些数据是1978-2006的时间序列数据，即观测值是连续不同年份的数据。

中国居民总量消费支出与收入资料解：阿尔蒙多项式估计法1、首先使用互相关分析命令cross，初步判断滞后期的长度。

在命令窗口键入：cross y x，输出结果如下图所示：x与y各期滞后值的相关系数从上图中可以看出，消费总支出y与当年和前四年的实际可支配收入相关，因此，利用阿尔蒙多项式估计法估计模型时，解释变量滞后阶数为5.利用EViews软件，输入样本数据，在命令窗口键入：LS y c pdl(x,5,2)得到以下回归分析结果：估计结果：xx x x x x yt t t t t t t5432104497.010270.013208.013311.010580.005015.0192.1794-----∧+++---= t = (2.07755) (6.63411) (6.51267) (7.90985) (6.26776) (0.99479)997444.02=R，250.2471=F ，955959.0..=W D其中括号内的数为相应参数的T 检验，R2是可决系数，F 和D.W.是有关的两个检验统计量。

2、模型检验从回归估计和残差图可以看出模型的拟合程度较好。

从截距项与斜率项的t 检验值看，均大于5%显著性水平下自由度为n-2=27的临界值052.2)27(025,0 t，认为中国总量消费与支出以及与各滞后消费间线性相关性显著，并且解释变量间不存在多重共线性。

分布滞后模型

分布滞后模型


S.E. of regression
21.88962 Akaike info criterion
Sum squared resid
7187.333 Schwarz criterion
Log likelihood
-75.52028 F-statistic
Durbin-Watson stat
1.438436 Prob(F-statistic)
8.2 有限分布滞后模型及其估计
如果有限分布滞后模型
yt a b0 xt b1xt1 ...... bk xtk ut
中的参数bi（i＝0，1，2，…，k）的分布可以 近似地用一个关于i的低阶多项式表示，就可以利 用多项式减少模型中的参数。
8.2 有限分布滞后模型及其估计
8.2 有限分布滞后模型及其估计
8.2.2 有限分布滞后模型的估计方法 1．经验加权估计法 根据实际经济问题的特点及经验判断，对滞后 变量赋予一定的权数，利用这些权数构成各滞后变 量的线性组合，以形成新的变量，再应用最小二乘 法进行估计。
8.2 有限分布滞后模型及其估计
基本思路是设法减少模型中被估计的参数个数。 模型中参数的个数主要由解释变量的个数来决定， 要减少模型中被估计的参数个数，就要对解释变量 进行归并，并通过解释变量的归并，消除或削弱多 重共线性问题。
Prob. 0.0023 0.0000 818.6959 279.9181 9.120033 9.218058 2601.407 0.000000
8.2 有限分布滞后模型及其估计
Dependent Variable: Y
Method: Least Squares
Sample(adjusted): 1958 1974
计量经济学 第八章 分布滞后模型汇编

计量经济学 第八章 分布滞后模型汇编


2018/12/9
11
计量经济学 Econometrics
估计问题
Yt Yt 1 X t t
* *
局部调整模型：满足古典假定，可用OLS估计 Koyck模型和适应预期模型： 误差项存在自相关，且与 Yt 1 相关 可以采用工具变量法或最大似然估计来估计参数
2018/12/9
双对数模型中系数为弹性，这样Q关于P的 短期弹性 长期弹性
C1
C1 1 C2
2018/12/9
10
计量经济学 Econometrics
三个模型关系
最终形式都为一阶自回归模型 区别： 1. 导出模型的经济背景与思想不同。 Koyck模 型是在无限分布滞后模型的基础上根据 Koyck几何分布滞后假定导出的；适应预期 模型是由解释变量的自适应过程而得到的； 局部调整模型则是对因变量的局部调整而得 到的。 2. 随机误差项的结构不同
Yt 1 0 X t 1 0 X t 2 0 2 X t 3 t 1
Yt Yt 1 1 0 X t t t 1
Yt * Yt 1 0 X t t
此时长期乘数是？
2018/12/9
Year
1980 1981 1982 1983
imp
585.6 584.2 537.4 547.8
GDP
19603.6 20083.7 19677.5 20529.4
Year
1990 1991 1992 1993
imp
877.3 819.2 829.6 873.8
GDP
26831.6 26705.7 27520.4 28250.6
12
计量经济学 Econometrics
分布滞后模型及其估计

分布滞后模型及其估计


将（2）代入（1），得
从而估计多项式的系数，再由多项式的系数与模型参数间
的
关系Yt，最 后 得0到X t分（布滞0 后 模1 型 。2）即X t1 （0 21 42）X t2 （0 31 92）X t3 ut
3
3
3
0 X ti 1 iX ti 2 i2 X ti ut (3)
权和Zt (各滞后变量的线性组合），把 Zt 作为新解释变量拟合一 元线性回归模型
Y Z u
t
0
1t
i
问题：不同时间的解释变量应该给多大的权数？
“经验加权法” 包括：
（1） 递减滞后结构
Xt
Xt-1
Xt-2
Xt-3
1/2
1/4
1/6
1/8
(令0 1 2 ) (令1 1 4 ) (令 2 1 6 ) (令 3 1 8 )
例 消费滞后模型
Yˆt 0.735 0.886Xt 0.012Xt1 0.010Xt2
t = （8.16）
（4.23）
（0.51）
（0.52）
R2 0.997
由于解释变量之间高度线性相关，由OLS估计的结果分析： 滞后收入对消费没有显著性影响（造成了一种假象）。
（三） 滞后长度难以确定 在大对数情况下，有限分布滞后模型的最大滞后长度S是未
j 1
例如 Yt 0 X t 1X t1 2 X t2 3 X t3 ut （1）
设 m 2 i 0 1i 2i2
(总约束）
i 0 0 0 1 0 2 0 0
i 1 1 0 1 2 i 2 2 0 21 42
(2)
(先验约束）
i 3 3 0 31 92
i0
i 1
计量经济学-中-4-分布滞后模型

计量经济学-中-4-分布滞后模型

在某时期的一个事件冲击后，从原来的均衡经过充分的调整达 到新的均衡之间的变化。
度的是以前不同时期Ｘ变化一个单位对Ｙ均值的滞后影响。
• 当然，分布滞后模型可以不仅含有两个 时间序列。这里主要是为了简化起见， 实际上，在有多个时间序列的情形，方 法是类似的。
二、滞后的原因
• 1. 归纳起来，产生滞后影响的原因有： 心理上的原因。作为一种习惯势力（或惰性）的结果，人 们在收入增加或价格上升后，并不马上改变他们的消费习 惯，甚至生活方式。
解决办法：
• 对于问题（3），一般通过引入被解释变量的滞后值 （AR项）作为解释变量，或引入随机误差项的滞后 值（MA项）来解决，即建立自回归分布滞后 （ADL：Auto-regressive Distributed Lag）模型：
Y
t
k Y Y Y X 1 t 1 2 t 2 p t p i 0 i t i
茨准则（Schwarz Criterion，简称为SC准则）来确
定适当的滞后长度k：
– 用这两个准则确定滞后长度k时，都要求使所计算的统计 量（AIC值或SC值）达到最小。 – 参见[美]乔治· 贾奇等《经济计量学理论与实践引论》 G·
P434。
对于无约束有限分布滞后模型，采用OLS
法估计所面临的特殊问题
达到最大的滞后长度 k；或者采用 AIC 准则或 SC 准 则，选择使 AIC 值或 SC 值达到最小的滞后长度 k ） 之外，还可以根据有关的经济理论确定。
确定多项式的次数p，可以按以下程序进行：先给p 一个较大的值（ 但p最大不得超过滞后长度k ），然
后用t检验逐步降低多项式的次数，直到模型中的所
2 i 0 1 2 p
p
（i=0，1，2，…，k） （3.4）
分布滞后模型2

分布滞后模型2


L β α
ˆ = ˆ + kα + k2α ˆ1 ˆ2 k 0
2.应用阿尔蒙模型之前需要解决的问题
(1)如何确定滞后长度 k 可以结合统计量来检验 如何确定滞后长度 结合相关系数分析，计算因变量和自变量的各期相关 计 量 经 济 学 系 数，可以大致判断滞后期长度； 利用调整后的修正系数 R2 ，在模型中逐期增加滞 后变量，扩大滞后期长度，直到模型的修正拟合系数不 再增加为止；或者先取一个较长的滞后期，再逐渐剔除 滞后变量，缩短滞后期长度，直到模型修正的拟合系数 明显下降为止；
Yt = α + β0 Xt + β1Xt−1 +L+ βk Xt−k + εt = α + ∑βi Xt−i + εt
i=0 k
计 量 经 济 学
根据数学中的维尔斯特拉斯定理，阿尔蒙假定估计参数β可 用滞后长度i的一个适当高次的多项式逼近
根据数学中的维尔斯特拉斯定理，阿尔蒙假定βi可用i的 一个适当高次的多项式逼近
i=0
3
估计上面的方程，有下面的结果
ˆ Yt = −9152.012 + 0.5825Z0t +1.2231Z1t − 0.5446Z2t
t=
(3.4431) (2.4112)
(-3.1145)
3.进一步得到βi的系数
ˆ ˆ β0 = α0 = 0.5825
计 量 经 济 学
ˆ ˆ ˆ ˆ β1 = α0 +α1 +α2 = 0.5825 +1.2231− 0.5446 = 1.261 ˆ ˆ ˆ ˆ β2 = α0 + 2α1 + 4α2 = 0.5825 + 2 ×1.2231− 4 ×0.5446 = 0.8503
计量经济学 滞后变量模型.详解

计量经济学 滞后变量模型.详解


克模型与自适应预期模型不满足古典假定，如果用最小二乘法直接进 行估计，则估计是有偏的，而且不是一致估计。
8.4.2 工具变量法
所谓工具变量法，就是在进行参数估计的过程中选择适当的替代
变量，代替回归模型中同随机误差项存在相关性的解释变量。工具变 量的选择应满足如下条件：
(1)与随机误差项不相关，这是最基本的要求；
(2)与所代替的解释变量高度相关，这样的工具变量与替代的解 释变量才有足够的代表性； (3)与其他解释变量不相关，以免出现多重共线性。
8.5 案例分析
表8.5.1给出了某地区消费总额y(亿元)和货币收入总额x(亿元)的 年度资料，试分析消费同收入的关系。 表8.5.1 某地区消费总额和货币收入总额年度资料
2．自回归模型
如果滞后变量模型的解释变量仅包括自变量x的当期值和因变量的若干期 滞后值，即模型形如
例8.1.1
消费滞后
消费者的消费水平，不仅依赖于当年的收入，还同以前的消费水平有关。 其消费模型可以表示为
边际消费倾向：增加的消费和增加的收入之间的比率，也就是 增加的1单位的收入中用于增加的消费部分的比率，用公式表示就 是：MPC=ΔC/ΔY。 例如，收入增加到3万亿元（增加了1万亿元），消费增加到2万 亿元（增加了0.5万亿元），边际消费倾向就是0.5(0.5/1)。 国际上大致的划分是： 通 货 （M0）=银行体系外的纸币或铸币 狭义货币（M1）=流通中的现金+支票存款（以及转账信用卡 存款） 广义货币（M2）=M1+储蓄存款（包括活期和定期储蓄存款） 另外还有M3=M2+其他短期流动资产（如国库券、银行承兑汇 票、商业票据等）
CROSS
y
x
例8.2.2
表8.2.3给出了某行业1975-1994年的库存额y和销售额x的
计量经济学第8章

计量经济学第8章


6443.33 8631.94 1
最高收入户
7593.95 10962.1 0
8262.42 12083.79 1
表 回归结果
这表明1998年、1999年我国城镇居民消费函数并没有显著差 异。因此，可以将两年的样本数据合并成一个样本，估计城镇居 民的消费函数，结果如下:
回归结果
虚拟变量的特殊应用
0
1
0
1988.1
3929.8 25 0
0
0
1984.4
4270.6 12
1
0
0
1988.2
4126.2 26 0
0
1
1985.1
3044.1 13
0
0
0
1988.3
4015.1 27 0
1
0
1985.2
3078.8 14 0
0
1
1988.4
4904.2 28 1
0
0
由于受取暖用煤的影响，每年第四季度的销售量大大高于其
设根据同一总体两个样本估计的回归模型分别为
为“相异回归”(Dissimilar regressions)。 上述情况中，只有第(1)种情况模型结构是稳定的，其余情况都表明模 型结构不稳定。
3．分段回归
回归系数反映了奖金的提高程度。使用虚拟变量既能如实描述不同阶段 的经济关系，又未减少估计模型时的样本容量，保证了模型的估计精度。
后期变动一个单位对Y的影响，即x的滞后影响。 如果 b = bi 存在，i=0,1,2…,k
b 称为长期分布或总分布乘数。表示X 变动一个单
位时，由于滞后效应而形成的对Y值的总的影响。
分布滞后模型的参数估计
对分布滞后模型直接采用OLS不适宜 • 没有先验准则确定滞后期长度；
计量经济学-分布滞后模型与自回归模型

计量经济学-分布滞后模型与自回归模型

分布滞后模型与自回归模型实验目的：设定模型，按照一定的处理方法估计模型参数，并解释模型的经济意义，探测模型扰动项的一阶自相关性。

实验要求：（1）设定模型t tu tXY ++=βα*运用局部调整假定（其中Yt*为预期最佳值）。

（2）设定模型e X Yu tttβα=*运用局部调整假定（其中Yt*为预期最佳值）。

（3）设定模型u X Yttt++=*βα运用自适应预期假定（其中Xt*为预期值）。

（4）运用阿尔蒙多项式变换法，估计分布滞后模型u XX Yt t tt++⋯+++=-X4-t 411βββα实验原理：最小二乘估计 实验步骤：一、在局部调整假定下，先估计回归模型：*1*1*0*t t t t u Y X Y +++=-ββα得到以下回归结果：Dependent Variable: YMethod: Least Squares Date: 11/16/10 Time: 19:39 Sample (adjusted): 1981 2001 Included observations: 21 after adjustmentsVariable Coefficien t Std. Error t-StatisticProb. C -15.10403 4.729450 -3.193613 0.0050 X 0.629273 0.097819 6.433031 0.0000 Y(-1) 0.271676 0.114858 2.365315 0.0294R-squared 0.987125 Mean dependent var109.2167 Adjusted R-squared 0.985695 S.D. dependent var 51.78550 S.E. of regression 6.193728 Akaike info criterion 6.616515 Sum squared resid 690.5208 Schwarz criterion 6.765733 Log likelihood -66.47341 F-statistic 690.0561 Durbin-Watson stat 1.518595 Prob(F-statistic)0.000000t Y ^=-15.10403+0.629273Xt+0.271676Yt 1-（4.729450）（0.097819） （0.114858） t=（-3.193613）（6.433031）（2.365315）R2=0.9871252R -=0.985695F=690.0561 DW=1.518595由局部调整模型的参数关系，有：α*=δα，δββ=*0，δβ-=1*1，u u t t δ=*将上述估计结果代入得到：βδ*11-==1-0.271676=0.728324δαα*==-20.738064δββ*0==0.864001故局部调整模型的估计结果为：=Yt* -20.738064+0.864001X t模型的经济意义：该地区的销售额每增加一亿元，其预期最佳固定资产投资将增加0.864001亿元。

计量教案(8分布滞后)

计量教案(8分布滞后)

第六章分布滞后模型在回归分析中，被解释变量的变化，除了受当期解释变量的影响外，还经常会受以前时期解释变量的变动影响，这是因为许多的经济现象的滞后影响作用所造成的结果。

这些滞后影响的问题，在经济计量分析中，也是一个重要的内容之一。

描述经济现象滞后影响的计量经济模型就是本章将要介绍的分布滞后模型。

本章的目的与要求通过本章学习，学生应充分理解各种滞后分布模型的有关概念、表现形式，重点掌握有限多项式滞后模型和几何分布滞后模型的特点及其变换，了解自回归模型的估计方法。

本章内容（计划学时）一、分布滞后模型的概念及其估计二、有限多项式滞后模型阿尔蒙多项式法的意义及具体操作步骤三、几何分布滞后模型1、几何分布滞后模型的概念2、Koyck（柯依克）变换模型3、以经济理论为基础的几何分布滞后模型四、自回归模型的估计1、部分调整模型的估计2、自适应预期模型的估计3、自相关的检验学习重点一、分布滞后模型的有关基本概念二、阿尔蒙多项式法的基本操作步骤三、几何分布滞后模型及其变换方法四、自回归模型的估计学习难点一、几何分布滞后模型及其变换方法二、自回归模型的估计第一节分布滞后模型的概念103104一、什么是分布滞后模型 （一）滞后变量模型1、概念：含有滞后变量的回归模型，称作滞后模型。

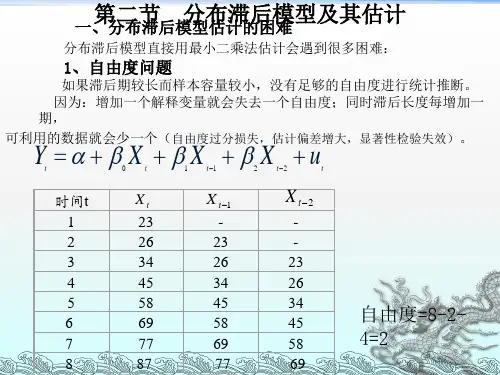
2、滞后模型的一般形式Yt ＝α + β0X t + β1X t -1 + … + βk X t-k + γ1Y t -1 + γ2Y t -2 + … + γp Y t -p + u t式中：k 和p 分别为解释变量与被解释变量的滞后长度，通常是有限的，故此模型称为有限滞后模型。

若最大滞后期k 和p 的长度是无限的，则模型为无限滞后模型。

（二）分布滞后模型： 1、概念：只有解释变量含有滞后变量的回归模型，称作分布滞后模型。

什么是分布滞后模型☆居民的消费需求除受同期居民收入的影响外，还同时与以前各期的收入有关； ☆农业生产者决定种植某种农产品、种植多少？经常要考虑前几期的农产品市场价格因素；☆固定资产的形成，往往是一个较长时期的投资过程。

第八章 分布滞后模型

第八章分布滞后模型第一节 引言从现在开始，我们用连续三章的篇幅对经济时间序列进行简明正式的讨论。

在本书的开始，就已经介绍了数据可分为横截面数据和时间序列数据两个基本类型。

注意到两个数据类型的一个基本区别在于数据的顺序性，这种顺序性给我们利用数据对经济问题做模型分析带来了许多问题。

例如。

在第五章自相关部分，我们提到时间序列的自相关性从本质上就是由于“顺序性”引起的。

另一方面，许多经济理论也都涉及到了时间问题。

如价格粘性、经济惯性等。

对此，将在本章许多例子中具体的连续看到。

所以，在时间序列的分析中，有必要对时间以及变量之间穿越时间的关系给以特别重视。

在以后的讨论中，我们将发现，着在给估计带来新问题的同时，也给模型赋予了许多令人感兴趣的新的特征和优势。

先在本章讨论分布滞后模型。

这类模型包括回归量的当前值，也包括早期自变量。

同以前的讨论类似，这类模型的构造基本上是经济理论要求的结果或直接来源于经济理论，而不是为了克服自相关等问题。

更直接地说这类模型与以前的不同仅在于引入了滞后变量而已。

所以，这一章的内容，仍然是在许多古典假定下进行的。

本章详细讨论了三种分布滞后模型：无约束有限滞后模型，有限多项式滞后模型和几何滞后模型，这没有穷尽所以可能的模型，但它们是最常用和最基本的分布滞后模型。

时间序列的时间顺序性和经济运动的内政逻辑性，使时间序列具有自己的数据特征，如强烈的序列相关性，于是，下一章，将不再依据经济理论，而从时序读有的数据特征的角度出发构造模型（如AR ，MA ，ARMA 模型等），对时间序列的生成作出解释。

第十章，进一步研究时间序列的性质，讨论非平稳时间序列及其建模问题。

第二节 分布滞后模型一、分布滞后模型的概念许多事件在时间上具有持久的影响，一个适当的模型将包括滞后变量。

例1消费函数。

假定某消费者每年的收入增加2000元，那么该消费者各年的消费支出会有什么变化呢？按照一般的经验，人们并不会马上化完增加的收入。

分布滞后模型

9
第三年的消费支出不仅取决于当 年的收入;还与第一年和第二年的收入 有关 当然;还可以和前面更多期有关
10
第一年 10000元
第二年 10000元
第三年
10000元 t
消费增加 消费增加
4000元
7000元
消费增加 9000元
消费追加 3000元
消费追加 2000元
11
于是;由该例可以得到以下消费函数关系式
１ 产生多重共线问题 对于时间序列的各期变量之间往往是 高度相关的;因而分布滞后模型常常产生多 重共线性问题
22
２ 损失自由度问题 由于样本容量有限;当滞后变量数目增 加时;必然使得自由度减少 由于经济数据 的收集常常受到各种条件的限制;估计这 类模型时经常会遇到数据不足的困难
23
３ 对于有限分布滞后模型;最大滞后
34
将阿尔蒙多项式方法推广到阶分布滞后 模型;即:
Y t 0 X t 1 X t 1 k X t k的最高阶数为m;则可
将阿尔蒙多项式法的步骤概括如下：
1 将项用一个m 次多项式近似表示：
i 0 1 i 2 i2 m im
i=0;1;2;…;k
69
式中;项为待定系数；m 为多项式次数;可 以预先给定
36
式6 9可写为
0 0
1 0 1 m 20 21 2 mm
k 0 k1 k 22 k m m
37
把 0,1, ,k 代入式6 8中有
Yt 0Xt (01 m)Xt1 (021 2mm)Xt2
0k1k22 kmm Xtk ut
i 01i2i2 i=0;1;2;3 6 5
其中; 0,1,2是待估计的参数
30
将式6 5代入式6 4并整理得:

计量经济学第八章分布滞后模型

(1)经验加权法
根据实际问题的特点、实际经验给各滞后变 量指定权数，滞后变量按权数线性组合，构成新 的变量。权数据的类型有：
•递减型： 即认为权数是递减的， X 的近期值对 Y 的 影响较远期值大。 如消费函数中，收入的近期值对消费的影 响作用显然大于远期值的影响。 例如：滞后期为 3的一组权数可取值如下： 1/2， 1/4， 1/6， 1/8
1.
滞后效应与与产生滞后效应的原因
因变量受到自身或另一解释变量的前几期值 影响的现象称为滞后效应。 表示前几期值的变量称为滞后变量。 如：消费函数 通常认为，本期的消费除了受本期的收入影 响之外，还受前1期，或前2期收入的影响： Ct=0+1Yt+2Yt-1+3Yt-2+t Yt-1，Yt-2为滞后变量。
该模型可用OLS法估计。假如参数估计结果为：
ˆ0
=0.5
ˆ 1 =0.8
则原模型的估计结果为：
0 .8 0 .8 Yˆ t 0 . 5 Xt X 2 4
t 1

0 .8 6
X
t2

0 .8 8
X
t3
0 .5 0 .4 X t 0 .2 X
t 1
0 . 133 X
①在解释变量x之后必须指定k和m的值，d为可选项， 不指定时取默认值0；1强制b0趋于0；2强制bk趋于0； 3强制两端趋于0。
②如果有多个具有滞后效应的解释变量，则分别用几 个PDL项表示；例如： LS Y C PDL(x1，4，2) PDL(x2，3，2，2) ③在估计分布滞后模型之前，最好使用互相关分析命 令CROSS初步判断滞后期的长度k； 命令格式为： CROSS Y X 接着输入滞后期 p 之后，将输出 yt 与 xt ， xt-1…xt-p的各期相关系数，以判断较为合适的滞后 期长度k。 例 表给出了中国电力基本建设投资X与发电 量Y的相关资料，拟建立一多项式分布滞后模型 来考察两者的关系。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2013-11-27
20
计量经济学 Econometrics
Almon模型

create a 1975 1994 read F:\Econometrics13\data\data82.xls 2 cross(12) y x 初步判断p的大小 ls y c PDL(x,3,2) 注：PDL和括号中间不留空格
2013-11-27
11
计量经济学 Econometrics
估计问题
Yt Yt 1 X t t
* *
局部调整模型：满足古典假定，可用OLS估计 Koyck模型和适应预期模型： 误差项存在自相关，且与 Yt 1 相关 可以采用工具变量法或最大似然估计来估计参数
2013-11-27
1984
1985 1986 1987 1988
663.3
656.4 703.8 766.1 827.3
22020.5
22868.1 23649.6 24453 25473.2
1994
1995 1996 1997 1998
988.4
1102.9 1159 1269.2 1321.9
29390.9
30175.3 31252.5 32638 34062.6
Year
1980 1981 1982 1983
imp
585.6 584.2 537.4 547.8
GDP
19603.6 20083.7 19677.5 20529.4
Year
1990 1991 1992 1993
imp
877.3 819.2 829.6 873.8
GDP
26831.6 26705.7 27520.4 28250.6
81.97653 27.85539 4.321154 4.517204 1145.160 0.000000
*
Std. Error t-Statistic 3.51797 5.90452 4.27495 -2.17104
1.99398 0.06785 29.3877
2013-11-27
22
计量经济学 Econometrics
得长期乘数为：
0 1 p
2013-11-27 3
计量经济学 Econometrics
分布滞后模型作用
更加全面客观的描述经济现象，提高模型的 拟合优度 反映经济活动的动态行为 可以用来模拟分析经济系统的变化和调整过 程
2013-11-27
4
计量经济学 Econometrics
模型估计问题
损失自由度 产生多重共线性 滞后长度难以确定
2013-11-27
5
计量经济学 Econometrics
几何滞后模型
2013-11-27
6
计量经济学 Econometrics
几何滞后模型(Koyck滞后模型)
假设 i i1,0 1
Yt 0 X t 0 X t 1 0 2 X t 2 t
p r
ˆ Yt 6.469601 0.63208 X t 1.15686 X t 1 0.76178 X t 2 0.55495 X t 3
genr z1=x+x(-1)+x(-2)+x(-3) genr z2=x(-1)+2*x(-2)+3*x(-3) genr z3=x(-1)+4*x(-2)+9*x(-3) equation eq1.ls y c z1 z2 z3 2013-11-27 show eq1
12
计量经济学 Econometrics
工具变量法
工具变量：与误差项不相关，与所替代的解释 变量高度相关，与其他解释变量不相关。
ˆ 用 Yt 1 替代 Yt 1
估计模型
ˆ Yt * Yt 1 * X t t
ˆ ˆ ˆ ˆ ˆ Yt 0 X t 1 X t 1 p X t p
ˆ Yt 1 是
ˆ Yt 的滞后值
13
2013-11-27
计量经济学 Econometrics
例
表中数据为某国1980年至1999年进口额(imp) 和GDP(单位是十亿元)，要求拟合下列分布滞后 模型(Koyck滞后模型) (data81.xls)
impt 1 0GDPt impt 1 t
2013-11-27 15
计量经济学 Econometrics
多项式分布滞后模型
2013-11-27
16
计量经济学 Econometrics
多项式分布滞后模型(Almon模型)
Yt 0 X t 1 X t 1 p X t p t
i f i 0 1i 2i 2 r i r , i 0,1,, p
Yt 1 0 X t 1 0 X t 2 0 2 X t 3 t 1
Yt Yt 1 1 0 X t t t 1
Yt * Yt 1 0 X t t
此时长期乘数是？
ˆ 0.576342
ˆ ˆ -329.9945 1- =-778.9172

create a 1980 1999 read F:\Econometrics13\data\data81.xls 2 equation eq1.ls imp c gdp imp(-1) eq1.results
2013-11-27
7
计量经济学 Econometrics
适应期望(Adaptive Expectation)模型
Yt X t* t
X t* Yt t
Y的变化与X期望水平的变化有关
X t* X t*1 X t X t*1
21
计量经济学 Econometrics
i
Variable Coefficient Std. Error t-Statistic Prob. C -6.419601 2.130157 -3.013675 0.0100 PDL01 1.156862 0.195928 5.904516 0.0001 PDL02 0.065752 0.176055 0.373472 0.7148 PDL03 -0.460829 0.181199 -2.543216 0.0245 R-squared 0.996230 Mean dependent var Adjusted R-squared 0.995360 S.D. dependent var S.E. of regression 1.897384 Akaike info criterion Sum squared resid 46.80087 Schwarz criterion Log likelihood -32.72981 F-statistic Durbin-Watson stat 1.513212 Prob(F-statistic) Lag Distribution of X . * | . *| . * | . | Sum of Lags i 0 1 2 3 Coefficient 0.63028 0.17916 1.15686 0.19593 0.76178 0.17820 -0.55495 0.25562
计量经济学 Econometrics
第八章 分布滞后模型
☆ ☆ ☆ ☆
几何滞后模型 多项式分布滞后模型 滞后项数选择 因果关系检验
2013-11-27
1
计量经济学 Econometrics
滞后变量产生原因
1. 经济变量自身的原因 2. 决策者心理上的原因：经济转型变革时期， 人们往往由于心理定势不能及时适应变化， 表现为行为决策滞后 3. 技术上的原因：投入产出常有滞后性 4. 制度方面的原因：契约因素和管理因素
局部调整模型的实践意义
需求函数
ln Qt C0 C1 ln Pt C2 ln Qt 1 t
双对数模型中系数为弹性，这样Q关于P的 短期弹性 长期弹性
C1
C1 1 C2
2013-11-27
10
计量经济学 Econometrics
三个模型关系
最终形式都为一阶自回归模型 区别： 1. 导出模型的经济背景与思想不同。 Koyck模 型是在无限分布滞后模型的基础上根据 Koyck几何分布滞后假定导出的；适应预期 模型是由解释变量的自适应过程而得到的； 局部调整模型则是对因变量的局部调整而得 到的。 2. 随机误差项的结构不同
SSR p SC ln ln T T T
SSR 2 p AIC ln T T
其中：SSR是残差平方和，p为滞后期长度，T为观测 值个数
2013-11-27 19
计量经济学 Econometrics
例
已知某行业1975-1994年的库存额y和销售额 x的资料。利用Almon法建立库存函数模型。 数据：data82.xls
t* t 1 t 1
长期乘数 1 1
2013-11-27 8
计量经济学 Econometrics
局部调整(Partial Adjustment)模型
Yt* X t t
Yt Yt 1 Yt* Yt 1
1989
2013-11-27
866.2
26367.3
1999
1446.5
35503.1
14
计量经济学 Econometrics
估计结果
imp t 329.9945 0.027393 GDPt 0.576342 impt 1 3.171215 2.953212 3.145555