安徽大学高数期末考试试卷及答案解析 (1)
- 格式:pdf
- 大小:158.49 KB
- 文档页数:3

安徽大学2009-2010学年第二学期《高等数学A (二)、B (二)》考试试卷(A 卷)参考答案与评分标准一、填空题(本大题共五小题,每小题2分,共10分)12、0;3、;4、1 /20 arcsin d (,y y f x y π∫∫)d x 32;5、53二、选择题(本大题共五小题,每小题2分,共10分)6、 A ;7、D ;8、D ;9、A ; 10、A.三、计算题(本大题共五小题,其中第11、12、13题每小题10分,第14、15题每小题12分,共54分)11.解. 设。
则曲面在点处的法向量为22(,,)F x y z x y z =+−S (1,1,2)(1,1,2)(1,1,2)(,,)(2,2,1)(2,2,1)x y z F F F x y =−=−由题设可知,平面Π通过法线L ,故12a b 0,+−+=(1,,1)(2,2,1)0a −⋅−=即,由此解得123a b a +=⎧⎨+=⎩035,.22a b =−=12.解:令222(,),(,)2y xP x y Q x y x y x y−==++,则d d L I P x Q y =+∫v ,当时,220x y +≠22222()Q x y Px x y y∂−==∂+∂∂2。
取一小圆周22:C x y εε+=,0ε>充分小,使得C ε完全位于L 所围成的区域内,取逆时针方向。
设D ε为由L 与C ε所围成的区域,则由Green 公式得d d (d L C D Q PP x Q y x y x yεε+∂∂+=−=∂∂∫∫∫0, 所以d d d d LC P x Q y P x Q yε+=−+∫∫22(sin )(sin )(cos )(cos )d πεθεθεθεθθε−−=−∫20d 2πθπ==∫13.解:设cos ,sin ,x R u y R u z ==v =,则Σ对应于:02,0D u v h π≤≤≤≤。





2024学年安徽省安大附中高三数学第一学期期末统考试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“20,(1)(1)∀>+>-x x x x ”的否定为( )A .20,(1)(1)∀>+>-x x x xB .20,(1)(1)∀+>-x x x xC .20,(1)(1)∃>+-x x x xD .20,(1)(1)∃+>-x x x x2.如图,某几何体的三视图是由三个边长为2的正方形和其内部的一些虚线构成的,则该几何体的体积为( )A .23B .163C .6D .与点O 的位置有关3.已知复数z 满足()11z i i +=-(i 为虚数单位),则z 的虚部为( ) A .i -B .iC .1D .1-4.已知集合M ={y |y =,x >0},N ={x |y =lg (2x -)},则M∩N 为( ) A .(1,+∞)B .(1,2)C .[2,+∞)D .[1,+∞)5.若[]0,1x ∈时,|2|0xe x a --≥,则a 的取值范围为( ) A .[]1,1-B .[]2,2e e --C .[]2e,1-D .[]2ln 22,1-6.若向量(1,5),(2,1)a b ==-,则(2)a a b ⋅+=( ) A .30 B .31 C .32 D .337.已知圆224210x y x y +-++=关于双曲线()2222:10,0x y C a b a b-=>>的一条渐近线对称,则双曲线C 的离心率为( ) A 5B .5C 5D .548.复数z 满足()11z i -=-,则复数z 等于() A .1i -B .1i +C .2D .-29.已知定义在R 上的函数()2xf x x =⋅,3(log a f =,31(log )2b f =-,(ln 3)c f =,则a ,b ,c 的大小关系为( ) A .c b a >>B .b c a >>C .a b c >>D .c a b >>10.已知集合A {x x 0}︱=>,2B {x x x b 0}=-+=︱,若{3}A B ⋂=,则b =( ) A .6- B .6C .5D .5-11.设10(){2,0xx f x x ≥=<,则((2))f f -=( )A .1-B .14C .12D .3212.已知AB 是过抛物线24y x =焦点F 的弦,O 是原点,则OA OB ⋅=( ) A .-2B .-4C .3D .-3二、填空题:本题共4小题,每小题5分,共20分。


第一学期期末高等数学试卷一、解答下列各题(本大题共16小题,总计80分)1、(本小题5分)求极限 lim x x x x x x →-+-+-23321216291242、(本小题5分) .d )1(22x x x ⎰+求3、(本小题5分) 求极限limarctan arcsinx x x →∞⋅14、(本小题5分)⎰-.d 1x x x 求5、(本小题5分) .求dt t dx d x ⎰+2021 6、(本小题5分)⎰⋅.d csc cot 46x x x 求7、(本小题5分) .求⎰ππ2121cos 1dx x x8、(本小题5分) 设确定了函数求.x e t y e ty y x dy dx t t ==⎧⎨⎪⎩⎪=cos sin (),229、(本小题5分) .求dx x x ⎰+301 10、(本小题5分)求函数 的单调区间y x x =+-42211、(本小题5分) .求⎰π+202sin 8sin dx x x 12、(本小题5分).,求设 dx t t e t x kt )sin 4cos 3()(ωω+=-13、(本小题5分) 设函数由方程所确定求.y y x y y x dy dx =+=()ln ,226 14、(本小题5分)求函数的极值y e e x x =+-215、(本小题5分) 求极限lim ()()()()()()x x x x x x x →∞++++++++--121311011011112222Λ16、(本小题5分) .d cos sin 12cos x x x x ⎰+求二、解答下列各题(本大题共2小题,总计14分)1、(本小题7分),,512沿一边可用原来的石条围平方米的矩形的晒谷场某农场需建一个面积为.,,才能使材料最省多少时问晒谷场的长和宽各为另三边需砌新石条围沿2、(本小题7分) .8232体积轴旋转所得的旋转体的所围成的平面图形绕和求由曲线ox x y x y ==三、解答下列各题 ( 本 大 题6分 )设证明有且仅有三个实根f x x x x x f x ()()()(),().=---'=1230一学期期末高数考试(答案)一、解答下列各题(本大题共16小题,总计77分)1、(本小题3分)解原式:lim =--+→x x x x 22231261812 =-→lim x x x 261218 =22、(本小题3分) ⎰+x x x d )1(22 ⎰++=222)1()1d(21x x =-++12112x c .3、(本小题3分) 因为arctan x <π2而limarcsin x x →∞=10故limarctan arcsin x x x →∞⋅=10 4、(本小题3分) ⎰-x x x d 1 x x x d 111⎰----= ⎰⎰-+-=x x x 1d d =---+x x c ln .1 5、(本小题3分)原式=+214x x6、(本小题4分) ⎰⋅x x x d csc cot 46⎰+-=)d(cot )cot 1(cot 26x x x=--+171979cot cot .x x c7、(本小题4分) 原式=-⎰cos ()1112x d x ππ=-sin 112x ππ=-1 8、(本小题4分) 解: dy dx e t t e t t t t t =+-22222(sin cos )(cos sin ) =+-e t t t t t t (sin cos )(cos sin )2222 9、(本小题4分)令 1+=x u 原式=-⎰24122()u u du=-2535312()u u =11615 10、(本小题5分) ),(+∞-∞函数定义域 01)1(222='=-=-='y x x x y ,当 (][)+∞<'>∞->'<,1011,01函数的单调减区间为,当函数单调增区间为, 当y x y x 11、(本小题5分)原式=--⎰d x x cos cos 9202π=-+-163302ln cos cos x x π=162ln12、(本小题6分) dx x t dt ='()[]dt t k t k e kt ωωωωsin )34(cos )34(+--=- 13、(本小题6分) 2265yy y y x '+'='=+y yx y 315214、(本小题6分) 定义域,且连续(),-∞+∞ '=--y e e x x 2122()驻点:x =1212ln 由于''=+>-y e e x x 20 22)21ln 21(,,=y 故函数有极小值 15、(本小题8分) 原式=++++++++--→∞lim ()()()()()()x x x x x x x 1121311011011112222Λ =⨯⨯⨯⨯=101121610117216、(本小题10分) dx x x dx x x x ⎰⎰+=+2sin 2112cos cos sin 12cos :解⎰++=x x d 2sin 211)12sin 21(=++ln sin 1122x c 二、解答下列各题(本大题共2小题,总计13分)1、(本小题5分)设晒谷场宽为则长为米新砌石条围沿的总长为 x xL x x x ,,()51225120=+> '=-=L x x 2512162 唯一驻点 ''=>=L x x 10240163 即为极小值点 故晒谷场宽为米长为米时可使新砌石条围沿所用材料最省165121632,,= 2、(本小题8分)解 :,,.x x x x x x 232311288204====V x x dx x x dx x =-⎡⎣⎢⎤⎦⎥=-⎰⎰ππ()()()223204460428464=⋅-⋅π()1415164175704x x π=-π=35512)7151(44三、解答下列各题( 本 大 题10分 ) 证明在连续可导从而在连续可导:()(,),,[,];,.f x -∞+∞03又f f f f ()()()()01230====则分别在上对应用罗尔定理得至少存在[,],[,],[,](),011223f x ξξξξξξ1231230112230∈∈∈'='='=(,),(,),(,)()()()使f f f 即至少有三个实根'=f x (),0,,,0)(它至多有三个实根是三次方程又='x f由上述有且仅有三个实根'f x ()高等数学(上)试题及答案一、 填空题(每小题3分,本题共15分)1、.______)31(lim 20=+→x x x 。


第一学期期末考试试卷(1)课程名称: 高等数学(上) 考试方式: 闭卷 完成时限:120分钟班级: 学号: 姓名: 得分: . 一、填空(每小题3分,满分15分)1、xx x x 2sin 3553lim 2++∞→ 2、设A f =-'')1(,则=--'--'→hh f f h )12()1(lim 0 3、曲线⎩⎨⎧==-t tey e x 2在0=t 处切线方程的斜率为4、已知)(x f 连续可导,且2)2(,)1(,1)0(,0)(e f e f f x f ===>,='⎰10)2()2(dx x f x f5、已知21)(xe xf x+=,则='')0(f 二、单项选择(每小题3分,满分15分)1、函数x x x f sin )(=,则 ( )A 、当∞→x 时为无穷大B 、当∞→x 时有极限C 、在),(+∞-∞内无界D 、在),(+∞-∞内有界2、已知⎩⎨⎧≥<=1,ln 1,)(x x x e x f x ,则)(x f 在1=x 处的导数( )A 、等于0B 、等于1C 、等于eD 、不存在3、曲线xxe y -=的拐点是( )A 、1=xB 、2=xC 、),1(1-eD 、)2,2(2-e 4、下列广义积分中发散的是( )A 、⎰10sin x dxB 、⎰-101xdx C 、⎰+∞+02/31x dx D 、⎰+∞22ln xx dx5、若)(x f 与)(x g 在),(+∞-∞内可导,)()(x g x f <,则必有( ) A 、)()(x g x f -<- B 、)()(x g x f '<'C 、)(lim )(lim 0x g x f xx xx →→< D 、⎰⎰<0000)()(x x dx x g dx x f三、计算题(每小题7分,共56分)答题要求:写出详细计算过程1、求xx e e x x x x sin )cos 1()(lim 220---→2、求)arcsin(lim 2x x x x -++∞→3、设)(x y y =由03=-+xyy x 确定,求0|=x dy 。
填空題(每小题3分,共15分)1 02・设A 是4x3矩阵,且A 的秩R(A)=2,而3 = 02 1 03・已知三阶矩阵/啲特征值为1, 2,-l,B = A 3-5A 2,则卜_288 _________________2 x ( + x 2 + x3 = 04-齐次线性方程组《 X, + 2X 2 + x 3 = 0,只有零解,贝!J 兄满足一耳赵 -----------------------------兀]+兀2 +兀3 = °5.当死元二次型正定时,二次型的秩为 n 二. 选择题(每小题3分,共15分)1.设A 为兀阶方阵,则|內"的必要条件是(B )(a) A 的两行(或列)元素对应成比例 (b) A 中必有一行为其余行的线性组合 (c) A 中有一行元素全为零 (d) 任一行为其余行的线性组合 2.设 n 维行向量矩阵A = E — 刃a ,B= E + 2a la.其中E 为〃阶单位矩阵,则AB = ( B )(a) 0(b) E(c) -E(d)a3. 设4』为〃阶方阵,满足等式AB = 0,则必有(c )(a) A = 0 或〃 =0 (b) A + B =() (c)间=0或|B = 0(a) |A|-f- B =04. S 维向量组少,硯,…,乞(3<n<s)线性无关的充分必婆条件是(c )(a)存在一组不全为零的数冏,氐2,…,龟I'使得k }(X } 4- k 2CC 2 d ------- &0“兴05兀 1 2 3 1.设CXX 12 D =12X3X 1 2 2x则工4的系数二(b )a 、。
空…o”中存在一个向量,它不能由其余向量线性表出(c )任意一个向量都不能山•其余向量线性表出(d ) ©,•••,%中任意两个向量都线性无关 5.设A 为n 阶方阵,且秩R (A ) = 〃一1, $,还是A 兀=0的两个不同的解, 则Ax = 0的通解为(AB )3.设力为刀阶方阵,且人2 +人-5£: = 0。
高等数学(下)试卷一一、 填空题(每空3分,共15分)(1)函数z =的定义域为 (2)已知函数arctany z x =,则zx ∂=∂(3)交换积分次序,2220(,)y y dy f x y dx⎰⎰=(4)已知L 是连接(0,1),(1,0)两点的直线段,则()Lx y ds +=⎰(5)已知微分方程230y y y '''+-=,则其通解为 二、选择题(每空3分,共15分)(1)设直线L 为321021030x y z x y z +++=⎧⎨--+=⎩,平面π为4220x y z -+-=,则( ) A. L 平行于π B. L 在π上 C. L 垂直于π D. L 与π斜交(2)设是由方程xyz =(1,0,1)-处的dz =( )A.dx dy +B.dx ++D.dx (3)已知Ω是由曲面222425()z x y =+及平面5z =所围成的闭区域,将22()x y dv Ω+⎰⎰⎰在柱面坐标系下化成三次积分为( ) A.2253d r dr dzπθ⎰⎰⎰ B.2453d r dr dzπθ⎰⎰⎰ C.2253502rd r dr dzπθ⎰⎰⎰ D. 22520d r dr dzπθ⎰⎰⎰(4)已知幂级数,则其收敛半径( )A. 2B. 1C. 12D.(5)微分方程3232x y y y x e '''-+=-的特解y *的形式为y *=( )A.B.()x ax b xe +C.()xax b ce ++D.()xax b cxe ++三、计算题(每题8分,共48分)1、 求过直线1L :123101x y z ---==-且平行于直线2L :21211x y z+-==的平面方程 2、 已知22(,)z f xy x y =,求zx ∂∂, z y ∂∂3、 设22{(,)4}D x y x y =+≤,利用极坐标求2Dx dxdy ⎰⎰4、 求函数22(,)(2)x f x y e x y y =++的极值5、计算曲线积分2(23sin )()yL xy x dx x e dy ++-⎰, 其中L 为摆线sin 1cos x t t y t =-⎧⎨=-⎩从点(0,0)O 到(,2)A π的一段弧6、求微分方程 xxy y xe '+=满足 11x y ==的特解四.解答题(共22分)1、利用高斯公式计算22xzdydz yzdzdx z dxdy ∑+-⎰⎰,其中∑由圆锥面z =与上半球面z =所围成的立体表面的外侧 (10)' 2、(1)判别级数111(1)3n n n n∞--=-∑的敛散性,若收敛,判别是绝对收敛还是条件收敛;(6')(2)在(1,1)x ∈-求幂级数1nn nx∞=∑的和函数(6')高等数学(下)试卷二一.填空题(每空3分,共15分)(1)函数z =的定义域为 ; (2)已知函数xyz e =,则在(2,1)处的全微分dz = ;(3)交换积分次序,ln 1(,)e x dx f x y dy⎰⎰= ;(4)已知L 是抛物线2y x =上点(0,0)O 与点(1,1)B 之间的一段弧,则=⎰;(5)已知微分方程20y y y '''-+=,则其通解为 .二.选择题(每空3分,共15分)(1)设直线L 为300x y z x y z ++=⎧⎨--=⎩,平面π为10x y z --+=,则L 与π的夹角为( );A. 0B. 2πC. 3πD. 4π(2)设是由方程333z xyz a -=确定,则z x ∂=∂( );A. 2yz xy z -B. 2yz z xy -C. 2xz xy z -D. 2xy z xy -(3)微分方程256x y y y xe '''-+=的特解y *的形式为y *=( );A.2()x ax b e +B.2()x ax b xe +C.2()x ax b ce ++D.2()xax b cxe ++ (4)已知Ω是由球面2222x y z a++=所围成的闭区域, 将dv Ω⎰⎰⎰在球面坐标系下化成三次积分为( ); A222sin ad d r drππθϕϕ⎰⎰⎰ B.220ad d rdrππθϕ⎰⎰⎰C.20ad d rdrππθϕ⎰⎰⎰ D.220sin a d d r drππθϕϕ⎰⎰⎰(5)已知幂级数1212nnn n x ∞=-∑,则其收敛半径( ).B. 1C. 12 D.三.计算题(每题8分,共48分)5、 求过(0,2,4)A 且与两平面1:21x z π+=和2:32y z π-=平行的直线方程 .6、 已知(sin cos ,)x yz f x y e +=,求zx ∂∂, z y ∂∂ .7、 设22{(,)1,0}D x y x y y x =+≤≤≤,利用极坐标计算arctanDydxdy x ⎰⎰ .8、 求函数22(,)56106f x y x y x y =+-++的极值. 9、 利用格林公式计算(sin 2)(cos 2)xx Ley y dx e y dy-+-⎰,其中L 为沿上半圆周222(),0x a y a y -+=≥、从(2,0)A a 到(0,0)O 的弧段.6、求微分方程 32(1)1y y x x '-=++的通解.四.解答题(共22分)1、(1)(6')判别级数11(1)2sin3n n n n π∞-=-∑的敛散性,若收敛,判别是绝对收敛还是条件收敛;(2)(4')在区间(1,1)-内求幂级数1nn x n ∞=∑的和函数 .2、(12)'利用高斯公式计算2xdydz ydzdx zdxdy∑++⎰⎰,∑为抛物面22z x y =+(01)z ≤≤的下侧高等数学(下)模拟试卷三一. 填空题(每空3分,共15分)1、 函数arcsin(3)y x =-的定义域为 .2、22(2)lim 332n n n n →∞++-= .3、已知2ln(1)y x =+,在1x =处的微分dy = . 4、定积分1200621(sin )x x x dx -+=⎰.5、求由方程57230y y x x +--=所确定的隐函数的导数dydx =.二.选择题(每空3分,共15分)1、2x =是函数22132x y x x -=-+的 间断点 (A )可去 (B )跳跃 (C )无穷 (D )振荡2、积分1⎰= .(A) ∞ (B)-∞(C) 0 (D) 13、函数1xy e x =-+在(,0]-∞内的单调性是 。
安徽大学2011—2012学年第一学期《高等数学A (三)》考试试卷(A 卷)院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------(闭卷 时间120分钟)考场登记表序号题 号 一 二 三 四 五 总分 得 分阅卷人得分 一、选择题(每小题2分,共10分)1.设A 为阶可逆矩阵,则下列各式正确的是( )。
n (A); (B)1(2)2A −=1A −11(2)(2)T T A A −−=; (C); (D)。
1111(())(())T T A A −−−−=11(())(())T T T A A −−−=12.若向量组12,,,r αα α可由另一向量组12,,,s ββ β线性表示,则下列说法正确的是( )。
(A); (B)r ;r s ≤s ≥(C)秩(12,,,r ααα )≤秩(12,,,s ββ β); (D)秩(12,,,r ααα ≥)秩(12,,,s ββ β)。
3.设,A B 为阶矩阵,且n A 与B 相似,E 为阶单位矩阵,则下列说法正确的是( )。
n (A)E A E B λλ−=−;(B)A 与B 有相同的特征值和特征向量; (C)A 与B 都相似于一个对角矩阵;(D)对任意常数,与k kE A −kE B −相似。
4.设123,,ααα为3R 的一组基,则下列向量组中,( )可作为3R 的另一组基。
(A)11212,,3ααααα−−; (B)1212,,2αααα+; (C)12231,,3αααααα++−; (D)12231,,3αααααα+++。
安徽大学2019—2020学年第二学期高等数学A 二卷(二)(闭卷时间120分钟)考场登记表序号一、填空题(每空2分,共10分)1.绕y 轴旋转而成的椭球面1323222=++z y x 的曲线是______________.2.设()=∂∂=x u xy x z 则,ln _______________________.3.设)(x f 是周期为π2的周期函数,它在区间],ππ-(上的定义为:⎩⎨⎧≤<≤<-=πππx x x x f 0,0,)(,则)(x f 的傅立叶级数在π2=x 收敛于.4.以()()dy y y x dx xy x 42234564-++为全微分的函数是.5.函数()22ln z y x u ++=在点A (1,0,1)处由A 指向B (3,-2,2)的方向的方向导数是.二、选择题(每小题2分,共10分)6.方程()()[()x y x dt t y t t y x ⋅=++⎰0222是().(A)齐次方程;(B)一阶线性方程;(C)伯努利(Bernoulli )方程;(D)可分离变量方程.题号一二三四五总分得分阅卷人得分院/系年级专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分7.已知,7,3,2=-==b a b a 则,a b 的夹角为().(A)12;(B)12-;(C)3π;(D)3π-.8.设().arcsin ,yx y x f =则(),1x f x =().)(A ()121+x x ;)B (221x x -;)(C x ;)D (x11+.9.设L 为曲线2x y =上从A(1,1)到B(0,0)的一段弧,则⎰=L xdy ().)(A dx x ⎰1022;)B (dy x ⎰10;)(C dx x ⎰0122;)D (dy y ⎰10.10.幂级数n n n x n212∑∞=的收敛半径为().)(A 2;2)B (;)(C 21;)D (21.三、计算题(每小题9分,共54分)11.求螺旋线θθθb z a y a x ===,sin ,cos 在点()0,0,a 处的切线方程与法平面方程.12.计算⎰Γ+-ydz dy dx ,其中Γ是有向闭折线ABCA ,这里A (1,0,0),B (0,1,0),C (0,0,1).得分13.求0324223=-+dy y x y dx y x 的通解.14.计算第一类曲面积分()⎰⎰∑+dS y x 22,其中∑为锥面()2223y x z +=被平面0=z 和3=z 所截得的部分值.15.利用Gauss 公式计算第二类曲面积分()()zdydz x y dxdy y x -+-⎰⎰∑,其中∑为柱面122=+y x 及平面0=z 和3=z 所围成的空间闭区域V 的整个边界曲面的外侧.16.求级数()()n n x n 111-+∑∞=的收敛域及和函数.院/系年级专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------四、应用题(每小题10分,共20分)17.将周长为p 2的矩形绕它的一边旋转构成一个圆柱体。
大一高等数学期末考试一试卷一、选择题(共12 分)1.( 3 分)若 f ( x)2e x , x 0,为连续函数 , 则a的值为 ().a x, x0(A)1 (B)2 (C)3 (D)-12.( 3 分)已知f(3) 2, 则lim f (3 h) f (3) 的值为().h02h(A)1 (B)3 (C)-1(D)1 23.( 3 分)定积分212xdx 的值为().cos2(A)0 (B)-2 (C)1(D)24.(3分)若f (x)在x x0处不连续,则 f ( x) 在该点处().(A)必不行导 (B) 必定可导 (C) 可能可导 (D) 必无极限二、填空题(共 12 分)1.(3 分)平面上过点(0,1) ,且在任意一点 ( x, y) 处的切线斜率为 3x2的曲线方程为.2.( 31x4 sin x) dx.分)( x213.( 3分) lim x2 sin1=.x0x4.( 3分) y2x33x2的极大值为.三、计算题(共42 分)1.( 6x ln(15x).分)求 limsin 3x2x02.(6 分)设ye xx2, 求 y .13.( 6分)求不定积分x ln(1 x2 )dx.x 4.( 63f ( x 1)dx, 此中f (x) 1, x 1,分)求cosxe x1,x 1.5. ( 6 分)设函数 yy x f ( x) 由方程e t dtcostdt 0 所确立 , 求 dy.6. ( 6 分)设 f ( x)dxsin x 2 C, 求 f (2 x 3)dx.3 n7. ( 6 分)求极限 lim 1 .2nn四、解答题(共 28 分)1. ( 7 分)设 f (ln x) 1 x, 且 f (0)1, 求 f ( x). 2. ( 7 分)求由曲线 ycos x2x与 x 轴所围成图形绕着 x 轴旋转一周2所得旋转体的体积 .3. ( 7 分)求曲线 y x 3 3x 2 24x 19 在拐点处的切线方程 .4. ( 7 分)求函数 yx1 x 在 [ 5,1] 上的最小值和最大值 .五、证明题 (6 分)设 f ( x) 在区间 [ a, b] 上连续 , 证明b b a1 bf (x)dx[ f (a) f (b)]( x a)( x b) f ( x) dx.a22 a标准答案一、 1 B;2C; 3D; 4 A.二、 1y x31;22 ;3 0;40.3三、 1解 原式limx5x 5 分x 03x 251 分32 解Q ln y lne x x ln( x 2 1),2 分x 2 12y e x[12x] 4 分x 21 2x 2 13 解原式1ln(1 x 2 ) d (1 x 2 )3 分21[(12)ln(12 (12) 12xdx]2xx )xx 22 分1[(1 x 2 )ln(1 x 2 )x 2 ] C1 分24解令 x1 t, 则2 分320 f ( x)dx1 f (t )dt1t2 t11 costdt1 (e 1)dt0 [ e tt ]12e 2 e 15两边求导得 eyy cosx 0,cosxQ ye ycosxsin x 1dycosx dxsin x 16 解f (2 x 3) dx1 f (2 x2 1sin(2 x 3)2 C21 分1 分1 分 1 分2 分1 分1 分2 分3)d(2 x 2)2 分4 分32 n 37 解原式 = lim3 24 分1n2n3= e22 分四、 1 解令 ln xt, 则 xe t ,f (t) 1 e t ,3 分f (t )(1 e t )dt = t e tC.2 分Q f (0)1, C 0,2 分f (x) xe x .1 分2 解V x2 23 分cos xdx222cos 2 xdx2 分2.2 分23 解 y3x 2 6x 24, y6x 6,1 分令 y 0, 得 x 1.1 分当x 1时 , y0; 当 1 x时 , y0,2 分(1,3) 为拐点 ,1 分该点处的切线为 y 3 21(x 1).2 分4 解 y 11x2 1 x 1, 2 分2 12 1 x令 y0, 得 x3 . 1 分4y( 5)56,2.55,y3 5, y(1) 1,2 分44最小值为 y(5)56, 最大值为 y35 . 2 分44五、证明ba)( x b) f(x) ba)( x b) df ( x)1 分(x( xaabb[( x a)( x b) f (x)] aaf ( x)[2 x ( a b)dx1分ba [2 x (a b)df ( x)1分[2 x (a b)] f ( x)(b a)[ f ( a) f (b)]移项即得所证 .b ba2 a f ( x)dx1分b2 a f ( x)dx,1分1分。
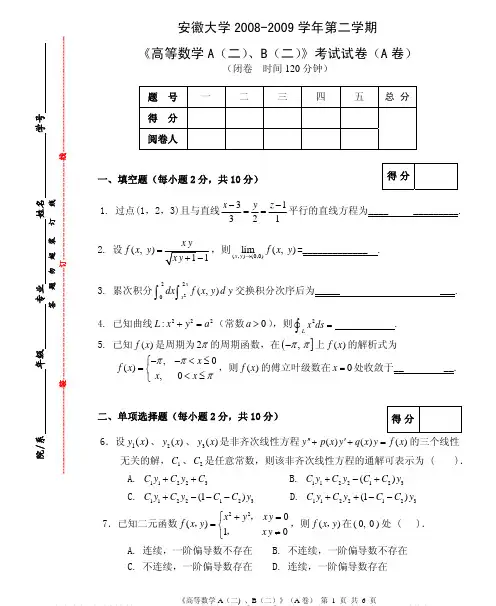
安徽大学2009-2010学年第二学期《高等数学A (二)、B (二)》
考试试卷(A 卷)参考答案与评分标准
一、填空题(本大题共五小题,每小题2分,共10分)
1
2、0;
3、;
4、1 /20 arcsin d (,y y f x y π∫∫)d x 3
2;
5、
53
二、选择题(本大题共五小题,每小题2分,共10分)
6、 A ;
7、D ;
8、D ;
9、A ; 10、A.
三、计算题(本大题共五小题,其中第11、12、13题每小题10分,第14、15题每小题12分,共54分)
11.解. 设。
则曲面在点处的法向量为
22(,,)F x y z x y z =+−S (1,1,2)(1,1,2)(1,1,2)(,,)(2,2,1)(2,2,1)
x y z F F F x y =−=−由题设可知,平面Π通过法线L ,故
12a b 0,+−+=(1,,1)(2,2,1)0a −⋅−=
即,由此解得123a b a +=⎧⎨+=⎩035,.
22a b =−=12.解:令222(,),(,)2y x
P x y Q x y x y x y
−=
=++,则d d L I P x Q y =+∫v ,当时,2
2
0x y +≠22222()Q x y P
x x y y
∂−==∂+∂∂2。
取一小圆周22:C x y εε+=,0ε>充分小,使得C ε完全位于L 所围成的区域内,取逆时针方向。
设D ε为由L 与C ε所围成的区域,则由Green 公式得
d d (
d L C D Q P
P x Q y x y x y
ε
ε
+∂∂+=−=∂∂∫
∫∫0, 所以d d d d L
C P x Q y P x Q y
ε
+=−+∫∫22
(sin )(sin )(cos )(cos )
d π
εθεθεθεθθε−−=−∫
20
d 2π
θπ
==∫13.解:设cos ,sin ,x R u y R u z ==v =,则Σ对应于:02,0D u v h π≤≤≤≤。
sin ,cos ,0u u x R u y R u z u =−==,0,0,1v v v x y z ===1=
故
2,0,E R F G ==R =. 于是,原式22
d d D
v
R u v R v
=+∫∫
222022
1d d 2ln(2h
h
v R u v R R v )|R v
π
π==⋅⋅+∫∫
+2
2
[ln()2ln ]2ln R R h R R R
ππ=+−=。
14.解:由题设,222
00
1()(1)()(1)1n n
n n n n f x x x ∞∞
==′==−=−+∑∑x 。
所以0
()()d (0)x
f x f t t f ′=+∫
200
(1)d x n
n
n t t ∞
==−∑∫21
0(1)21n n
n x n +∞
==−+∑,
上述级数的收敛域为[1,又因为,1]−()f x 在1x =处连续,故令1x =,可得
1(1)
(1).214
n
n f n π
∞
=−==+∑ 15.解:(1)
'()'()sin ,'()'()cos x x z u z u
f u f u e y f u f u e x x y y ∂∂∂∂====∂∂∂∂y 222
2
()sin '()sin ,x x z f u e y f u e y x
∂′′=+∂2222
()cos '()sin .x x
z f u e y f u e y y
∂′′=−∂(2)将(1)中结果代人方程,得2222x
22''()x z z
e z
f u e x y
∂∂=+=∂∂''()()0
f u f u −=,即这是一个齐次线性常系数方程,相应的特征方程为210λ−=,特征根为
121,1λλ==−
故12()u u f u C e C e −=+,其中为任意常数。
12,C C 四、应用题(本大题共两小题,其中第16题10分,第17题6分,共16分) 16.解:设所围成的圆的半径为x ,长方形的长、宽分别为,y z 。
原问题转化为求函数在条件2S x y π=+z 22()x y z l π++=下的最大值。
为此,构造Lagrange 函数2(,,,)(222)L x y z x yz x y z l λπλπ=+−++−。
220,x L x ππλ=−=20y L z λ=−=,20z L y λ=−=,222L x y z l λ0π=++−=。
得,x y z 2λλ===,代入得0L λ=28
l
λπ=+。
即,.284
l l
x y z ππ=
==++ 17.解:由质量公式得
(,)d L
M x y s
ρ=
∫1
x
=
∫3
21
2011(14)|1).1212
x =+=−五、证明题(本大题共两小题,其中第18题6分,第19题4分,共10分) 18.证明:11ln ln(1n n n +=+为的单调递减,且n 1
lim ln(1)0n n →+∞+=。
故由Leibniz 判别法可知,11
(1)ln
n n n n
∞
=+−∑收敛。
但1
ln
1lim
lim ln 11n n n n n n n n
→+∞
→+∞++==,且11n n ∞=∑发散,故由比较判别法的可知,1
1ln n n n ∞
=+∑发散。
综上所述,原级数条件收敛。
19.证明:设,则0()()d x
F x f t t =∫'()().
F x f x =左边110
d d ()()()d y
x
x
x y f x f y f z =∫∫∫z
11
d ()()()|
d z y z x
x
x f x f y F z y ===∫∫11
d ()()[()()]d x
x f x f y F y F x y
=−∫∫121
01()[()()]|d 2y y x f x F y F x x ===−∫1201()[(1)()]d 2
f x F F x x =−∫1313
300
111[()(1)]|[(1)](()d )666F x F F f t t =−==∫=右边。