《材料力学》第6章简单超静定问题习题解复习过程
- 格式:doc
- 大小:1.37 MB
- 文档页数:27









第 1 页/共 3 页第六章 容易的超静定问题6-1 一次超静定解除A 端约束,加反力F A 变形协调 0=∆=∆L A 补充方程 0])3()2(2[1=-+-+=∆a F F a F F a F EAL A A A 解得 F F A 47=轴力图: 6-4 一次超静定解除杆2约束,加反力F E 变形协调 EAl F EA lF C C E E C E =∆=∆∆=∆,,2 补充方程 C E F F 2=平衡 F F F M C E A 320=+⇒=∑ 解得 kN F F kN F F C E 30536056====, 从而可得轴力 kN F kN F N N 603021==,应力 MPa AFMPa A F N N 60302211====σσ, 6-9 若杆未碰到支座B ,计算δ>∆L ,则杆必碰到支座B ,一次超静定解除下端支座B ,加反力F B变形协调 δ=∆=∆L B 补充方程 []δ=-++-+-=∆a F F F a F F EAEA a F L B D C B C B )()(221解得 kN aEAF F F D C B 155253=-+=δ (其中a =1.2m ,A =300mm 2)kN F F F F B D C A 85=-+= 轴力图:6-11 一次超静定解除B 端约束,加反力偶M B 变形协调 0=BA ϕ 补充方程 0)(221=-+=p e B p B BA GI aM M GI a M ϕ 解得 e B M M 331=,从而e A M M 3332= 扭矩图:6-14 拉杆EF 与GH 相同,且变形同为C 端位移,故两杆拉力相等 一次超静定第 3 页/共 3 页解除两杆约束,加反力F C 变形协调 ,,2122/EA L F L d LC CA =∆∆=ϕ []L d F M l d F GI C e C p CA )(1111-+-=ϕ (其中L =1m ) 补充方程21114)2(EA F d F M GI d C C e p =- 解得 kN d M F eC 1071==从而AB 段 m kN M T e ⋅==676max 最大切应力 MPa d T W T p 6.3016/31maxmax max ===πτ 6-15(a) 一次超静定解除B 端约束,加反力F B 变形协调 0==∆B B w补充方程 0931433=-=EIa F EI Fa w B B 解得 F F B 2714= 6-16 一次超静定基础梁AB 与CD 间的约束,加互相作使劲F C 变形协调 C B w w =补充方程 23213133)(EI l F EI l F F C C =- 解得 FF C 167135=。

材料力学(土)笔记第六章超静定问题及其解法1.超静定问题及其解法约束反力或构件内力都能通过静力学的平衡方程求解,称为静定问题不能单凭静力学平衡方程求解的问题,称为超静定问题在超静定问题中,都存在多于维持平衡所必需的支座或杆件,习惯上称其为“多余”约束由于多余约束的存在,未知力的数目必然多于独立平衡方程的数目未知力数超过独立平衡方程的数目,称为超静定次数与多余约束相应的支反力或内力,习惯上称为多余未知力因此,超静定的次数就等于多余约束或多余未知力的数目未知力数超过独立的静力平衡方程数因此,除了静力平衡方程外,还必须寻求补充方程有“多余”约束存在,杆件(或结构)的变形受到了多于静定结构的附加限制根据变形的几何相容条件,可建立附加的变形几何相容方程而变形(或位移)与力(或其他产生变形的因素)间具有一定的物理关系将物理关系代入变形几何相容方程,即可得补充方程将静力平衡方程与补充方程联立求解,就可以解出全部未知力着就是综合运用变形的几何相容条件、物理关系和静力学平衡条件三方面求解超静定问题的方法在求解由于约束多于维持平衡所必需的数目而形成的超静定结构时可设想将某一处的约束当作“多余”约束予以解除并在该处施加于所解除的约束相对应的支反力(多余未知力)从而得到一个作用有荷载和多余未知力的静定结构称为原超静定结构的基本静定系或相当系统为使得基本静定系等同于原超静定结构基本静定系在多余未知力作用处相应的位移满足原超静定结构的约束条件即变形相容条件将力与位移间的物理关系代入变形相容方程,即可得多余未知力求得多余未知力后,基本静定系就等同于原超静定结构其余的支反力,以及构件内力、应力或变形(位移)均可按基本静定系进行计算2.拉压超静定问题2.1 拉压超静定问题解法对于拉压超静定问题可综合运用变形的几何相容条件、力-变形间的物理关系和静力学的平衡条件三方面来求解在超静定杆系问题中,各杆的轴力应与该杆本身的刚度和其他杆的刚度之比有关对于高一次的超静定问题,总可以找到必要的变形几何相同条件从而得到相应的补充方程其补充方程和静力学平衡方程联立即可求解静定问题中的全部未知力2.2 装配应力·温度应力①装配应力杆件在制成后,其尺寸有微小误差往往是难免的在静定结构中,这种误差仅略为改变结构的几何形状,而不会引起附加的内力但在超静定结构中,由于有了多余约束,就将产生附加的内力这种附加的内力称为装配内力,与之相应的应力则称为装配应力装配应力是结构在荷载作用以前已经具有的应力,称为初应力计算装配应力的关键仍然是根据变形相容条件列出变形相容方程在超静定结构中,杆件尺寸的微小误差,将产生相当可观的装配应力 ②温度应力在工程实际中,结构物或其部分杆件往往会遇到温度变化 若杆的同一截面上各点处的温度变化相同,则杆将仅发生伸长或缩短变形在静定结构中,由于杆能自由变形,由温度所引起的变形不会在杆中产生内力 在超静定结构中,由于存在多余约束杆由温度变化所引起的变形受到限制,从而将在杆中产生内力这种内力称为温度内力,与之相应的应力则称为温度应力 计算温度应力的关键同样是根据问题的变形相容条件列出变形几何相容条件 不同的是,杆的变形包括两部分即由温度变化所引起的变形,以及与温度内力相应的弹性变形杆件的线膨胀系数为α(单位为01()C -),温度差为t ∆,杆件原长为l 则杆变形长度为l t l α∆=⋅∆⋅在超静定结构中,温度应力是个不容忽视的因素3.扭转超静定问题扭转超静定问题的解法同样是综合考虑静力、几何、物理三个方面4.简单超静定梁4.1 超静定梁的解法求解超静定梁同样是综合考虑静力、几何、物理三个方面对于约束多余维持平衡所必需的数目而形成的超静定问题根据选取的多余约束(基本静定系)由变形几何相容方程和力-变形(位移)物理关系所得的补充方程即可解得多余未知力,解得多余未知力后其余的支反力以及杆件的内力、应力和变形(位移)均可按基本静定系求解 大多数的超静定梁是由约束多余维持平衡所必需的数目而形成的因此,按上述方法主要求解其多余未知力若梁具有一个或更多的中间支座,称为连续梁4.2 支座沉陷和温度变化对超静定梁的影响①支座沉陷的影响②梁上、下表面温度变化不同的影响。
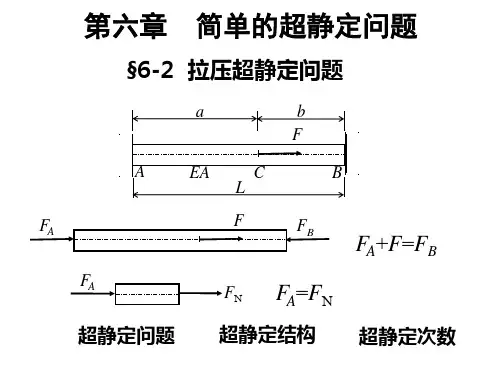
轴力图1234-5-4-3-2-11234567N(F/4)x(a)第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
[习题6-3] 一刚性板由四根支柱支撑,四根支柱的长度和截面都相同,如图所示。
如果荷载F 作用在A 点,试求这四根支柱各受多少力。
解:以刚性板为研究对象,则四根柱子对它对作用力均铅垂向上。
分别用4321,,,N N N N 表示。
由其平衡条件可列三个方程:0=∑Z04321=-+++F N N N N F N N N N =+++4321 (1)0=∑xM0222242=-⋅a N a N 42N N = (2)0=∑yM0222231=⋅-⋅+⋅a N e F a N aFeN N 231-=-…………(3) 由变形协调条件建立补充方程EAN EA l N EA l N 2312=+2312N N N =+。
(4)(1)、(2)、(3)、(4)联立,解得:442F N N == F a e N )241(1-=F ae N )241(3+=[习题6-4] 刚性杆AB 的左端铰支,两根长度相等、横截面面积相同的钢杆CD 和EF 使该刚性杆处于水平位置,如所示。
如已知kN F 50=,两根钢杆的横截面面积21000mm A =,试求两杆的轴力和应力。
解:以AB 杆为研究对象,则:0=∑AM0350221=⨯-⋅+⋅a a N a N150221=+N N (1)变形协调条件:122l l ∆=∆ EAlN EA l N 122= 122N N = (2)(1)、(2)联立,解得:kN N 301= kN N 602=MPa mm NA N 30100030000211===σ MPa mm NA N 60100060000222===σ[习题6-5] 图示刚性梁受均布荷载作用,梁在A 端铰支,在B 点和C 点由两根钢杆BD 和CE 支承。
已知钢杆BD 和CE 的横截面面积22200mm A =和21400mm A =,钢杆的许用应力MPa 170][=σ,试校核该钢杆的强度。
解:以AB 杆为研究对象,则:0=∑AM023)330(3121=⨯⨯-⨯+⨯N N 135321=+N N (1)变形协调条件:3121=∆∆l l 123l l ∆=∆112238.1EA lN EA l N ⨯=⋅40032008.112N N =⋅ 212.1N N = (2)(1)、(2)联立,解得:kN N 571.381=(压);kN N 143.322=(拉)故可记作:kN N 571.381-=;kN N 143.322= 强度校核: MPa MPa mmNA N 170][4275.9640038571||||2111=<===σσ,符合强度条件。
MPa MPa mm N A N 170][715.160200321432122=<===σσ,符合强度条件。
[习题6-6] 试求图示结构的许可荷载[F]。
已知杆AD ,CE ,BF 的横截面面积均为A ,杆材料的许用应力为][σ,梁AB 可视为刚体。
解:以AB 杆为研究对象,则:∑=0Y0321=-++F N N NF N N N =++321 (1)∑=0AM0232=⋅-⋅+⋅a F a N a N F N N =+322 (2)变形协调条件: 2132l l l ∆+∆=∆EAlN EA l N EA l N 21322+=⋅ 2134N N N += (3)(1)(2)(3)联立,解得: 5221F N N ==;53FN = 强度条件: ][5221σσσ≤==AFA A F ][5.22][5σσ=≤][53σσ≤=AF][5σA F ≤故:A F ][5.2][σ=[习题6-7] 横截面积为mm mm 250250⨯的短木柱,用四根mm mm mm 54040⨯⨯的等边角钢加固,并承受压力F ,如图所示。
已知角钢的许用应力MPa s 160][=σ,弹性模量GPa E s 200=;木材的许用应力MPa w 12][=σ,弹性模量GPa E w 10=。
试求短木柱的许可荷载[F]。
解:(1)木柱与角钢的轴力由盖板的静力平衡条件:(1)由木柱与角钢间的变形相容条件,有(2)由物理关系:(3)式(3)代入式(2),得(4)解得:代入式(1),得:(2)许可载荷 由角钢强度条件由木柱强度条件:故许可载荷为:[习题6-8] 水平刚性横梁AB 上部由于某1杆和2杆悬挂,下部由铰支座C 支承,如图所示。
由于制造误差,杆1和长度短了mm 5.1=δ。
已知两杆的材料和横截面面积均相同,且GPa E E 20021==,A A A ==21。
试求装配后两杆的应力。
解:以AB 梁为研究对象,则:0=∑CM0145sin 2021=⨯+⋅-N N2142N N =…………(1) 变形协调条件: 11AA l -=∆δ 1222BB l =∆2111212l l BB AA ∆∆-==δ 2122l l ∆=∆-δEAl N EA l N 22221⋅=-δEAlN EA l N 214=-δ………...(2) (1)、(2)联立,解得:l EA N )162(21+=δ;lEA N )162(42+=δMPa mm mm MPa l E 242.161500)162(5.1102002)162(231=⨯+⨯⨯⨯=+=δσMPa mmmm MPa lE 939.451500)162(5.1102004)162(432=⨯+⨯⨯⨯=+=δσ[习题6-9] 图示阶梯状杆,其上端固定,下端与支座距离mm 1=δ。
已知上、下两段杆的横截面面积分别为2600mm 和2300mm ,材料的弹性模量GPa E 210=。
试作图示荷载作用下杆的轴力图。
解:设装配后,支座B 的反力为B R (↓),则: B BC R N =40+=B CD R N (D 为60kN 集中力的作用点)100+=B AD R N变形协调条件:δ=∑=ni il1m R R m m kN m kN R B B B 36666262610110600102102.1)100(10600102104.2)40(10300/102102.1----⨯=⨯⨯⨯⋅++⨯⨯⨯⋅++⨯⨯⨯⋅1261202.1964.24.2=++++B B B R R R 906-=B R)(15kN R B -=。
故:轴力图0.81.62.43.244.8-15-10-50510152025303540455055606570758085N(kN)x(m)kN N BC 15-= ; kN N CD 25= ; kN N AD 85=。
轴力图如下图所示。
[习题6-10] 两端固定的阶梯状杆如图所示。
已知AC 段和BD 段的横截面面积为A ,CD 段的横截面面积为2A ;杆的弹性模量为GPa E 210=,线膨胀系数106)(1012--⨯=C l α。
试求当温度升高C 030后,该杆各部分产生的应力。
解:变形协调条件:0=∆l0=∆+∆t N l l04)2(22=⋅∆⋅++a t A E aN EA Na l α 043=⋅∆⋅+a t EANal α 043=⋅∆⋅+t EANl α )(100800/1021030)(101234342260106kN A Am m kN C c tEA N l -=⋅⨯⨯⨯⨯⨯-=∆-=--α MPa kPa ANBD AC 8.100)(100800-=-===σσ MPa kPa ANCD 4.50)(504002-=-==σ[习题6-11] 图示为一两端固定的阶梯状圆轴,在截面突变处承受外力偶矩e M 。
若212d d =,试求固定端的支反力偶矩A M 和B M ,并作扭矩图。
解:把B 支座去掉,代之以约束反力偶 ,其矩为B M ,转向为逆时针方向,则:B BC M T = e B CA M M T -=变形协调条件:A 、B 为两固定端支座,不允许其发生转动,故:0=+=CB AC AB ϕϕϕ02)(21=+-P B P e B GI aM GI a M M0221=+-P BP e B I M I M M式中,241414111632116)2(321321P P I d d d I =⋅===πππ,故: 021622=+-P B P e B I M I M M0216=+-B eB M M M33eB M M =333233ee e A M M M M -=-=(顺时针方向转动) 33eB BC M M T == 3332ee B CA M M M T -=-=扭矩图-33-32-31-30-29-28-27-26-25-24-23-22-21-20-19-18-17-16-15-14-13-12-11-10-9-8-7-6-5-4-3-2-101200.511.522.53x(a)T(Me/33)AB 轴的轴力图如下:[习题6-12] 图示一两端固定的钢圆轴,其直径mm d 60=。