高中数学培优班专题资料(含答案)

高一年段数学培优教材--平面向量（1）一、 基础知识： 1．向量的运算：①加法运算：;AB BC AC +=设1122(,),(,)a x y b x y ==则1212(,)a b x x y y +=++ ②减法运算：;AB AC CB -=设1122(,),(,)a x y b x y ==则1212(,)a b x x y y -=-- ③实数与向量的积运算： 向量a λ与a 的关系；设(,),a x y =则(,)()a x y R λλλλ=∈ 22||,||||||a x y a a λλ=+=⋅ 22||a a a a =⋅= ④向量的数量积运算： ||||cos (a b a b θθ⋅=⋅⋅是a 与b 的夹角）； 设1122(,),(,)a x y b x y ==则1212a b x x y y ⋅=+2．向量的关系：①不等关系： ||||||||||||a b a b a b -≤±≤+ ||||||a b a b ⋅≤⋅ （注意等号的条件） ②设1122(,),(,),0a x y b x y b ==≠ 则a b ⇔,a b λ=12210a b x y x y ⇔-=12120;0a b a b a b x x y y ⊥⇔⋅=⊥⇔+=3．平面向量的基本定理：如果12,e e 是同一平面内的不共线向量，那么对于这个平面内的任一向量a ，有且只有一对实数,λμ，使12a e e λμ=+。

相关结论：如果12,e e 是同一平面内的不共线向量，且120e e λμ+=，则0λμ== 点O 、A 、B 、C 在同一平面内，A 、B 、C 共线的充要条件是：(1)OA xOB yOC x y =++=4．常用公式： 22222()2()()a b a a b b a b a b a b±=±⋅++⋅-=- ABC ∆中，M 为BC 边的中点，G 为重心， 则10;();02AB BC CA AM AB AC GA GB GC ++==+++=二、综合应用：例1：求证：三角形的三条中线交于一点。

高二数学培优辅导资料 函数（二）一，选择题 1.函数)2,(21-∞-+=在x ax y 上为增函数,则实数a 的取值范围是（） A.21->a B.21>a C.21<a D.21-<a2.已知函数0)(,)1,1(213)(00=--+=x f x a ax x f 使得上存在在,则a 的取值范围是（） A.511<<-aB.51>a C.1-<a 或51>a D.1-<a3.设21,,x x R k ∈是方程01222=-+-k kx x 的两根,则2221x x +的最小值为（ ）A.－2B.0C.1D.24、设函数2()21f x ax ax =+-对于满足13x <<的一切()0f x <，则a 的取值范围 是（ ） A 、10,15⎡⎫⎪⎢⎣⎭ B 、(],0-∞ C 、()1,00,15⎛⎫-∞ ⎪⎝⎭ D 、1,15⎛⎫-∞ ⎪⎝⎭ 5. 已知函数224)(2-+-=x x x f ，则它是（）A ．偶函数B ．既是奇函数又是偶函数C ．奇函数D ．既不是奇函数又不是偶函数 6．函数xx xx x x f cos 22)4sin(2)(22++++=π的最大与最小值分别为M, N ， 则( ) A 、4=-N M B 、4=+N M C 、2=-N M D 、2=+N M7. 对于任意实数x ，若不等式34(0)x x a a -+->>恒成立，则实数a 应满足（） A. 01a << B. 01a <≤ C. 1a > D. 1a ≥ 8设2(0)()(1)(0)x a x f x f x x -⎧-≤=⎨->⎩，若()f x x =有且仅有两个实数解，则实数a 的取值范围是（ ）A ．(),2-∞B ．[)1,2C ．[)1,+∞D ．(],1-∞ 9．设函数,0x ,10x ,1)x (f ⎩⎨⎧<>-= 则)b a (2)b a (f )b a ()b a (≠-⋅--+ 的值为 （ ） A ．aB ．bC ．a, b 中较小的数D ．a, b 中较大的数10.如果23()1log 2log 9log 64x x x f x =-+-，则使()0f x <的x 的取值范围为（）A. 01x <<B. 813x << C. 1x <<+∞ D. 83x <<+∞ 11.函数y=f(x+1)与y=f(1－x)的图象关于( )A.y 轴对称B.原点对称C.直线x=1对称D.关于y 轴对称且关于直线x=1对称 12.函数f(x)=⎪⎩⎪⎨⎧>≤-)1|(|||)1|(|12x x x x ，如果方程f(x)=a 有且只有一个实根，那么a 满足( )A.a<0B.0≤a<1C.a=1D.a>1 13．如果100,0,log log 3x y x y y x >>+=， 144xy =，那么x y +的值是（ ）ABCD 14. 设函数)10()(||≠>=-a a a x f x 且，f （－2）＝9，则 （ ） A. f （－2）＞f （－1） B. f （－1）＞f （－2） C. f （1）＞f （2） D. f （－2）＞f （2） 152007=的正整数解(,)x y 的组数是（ ） A ．1组 B. 2 组 C. 4组 D. 8组16．.已知⎪⎩⎪⎨⎧≤+≥-≥03030y x y x y ,则x 2+y 2的最大值是17. 若2|1||1|2x ax -≤+--≤对x ∈R 恒成立，则实数a 的个数为 （） （A ）0 （B ）1 （C ）2 （D ）无数个 解: 只有1a =±时，原不等式恒成立. 选C. 18．函数4218y x x =--+的部分图象是（）ABC D 19、设)(n f 为正整数n （十进制）的各数位上的数字的平方之和，比如14321)123(222=++=f ，记)()(1n f n f =，))(()(1n f f n f k k =+，，⋯=,3,2,1k 则)2006(2006f ＝（ ） A.20 B. 4 C. 42 D. 145 二，填空题20．对于任意实数t ，不等式212sin 212()2t t x -+≥恒成立，则x 的取值范围是__________。

高一K1409班数学培训资料一1．已知a ∈R ，b ∈R ，若⎩⎨⎧⎭⎬⎫a ，b a ，1＝{a 2，a ＋b,0}，则a 2 014＋b 2 014＝________. 解析 由已知得b a ＝0及a ≠0，所以b ＝0，于是a 2＝1，即a ＝1或a ＝－1，又根据集合中元素的互异性可知a ＝1应舍去，因此a ＝－1，故a 2 014＋b 2 014＝1. 答案 12．(2014·金华第二次统练)已知M ，N 为集合I 的非空真子集，且M ，N 不相等，若∁I (M ∩N )＝∁I N ，则M ∪N ＝________.解析 由Venn 图可知N ⊆M ，∴M ∪N ＝M .答案 M3．函数y ＝x －3x ＋1的值域为________． y ＝x －3x ＋1＝x ＋1－4x ＋1＝1－4x ＋1，因为4x ＋1≠0， 所以1－4x ＋1≠1.即函数的值域是{y |y ≠1}． 4．已知实数a ≠0，函数f (x )＝⎩⎨⎧2x ＋a ，x ＜1，－x －2a ，x ≥1.若f (1－a )＝f (1＋a )，则a 的值为________．解：当a ＞0时，1－a ＜1,1＋a ＞1.此时f (1－a )＝2(1－a )＋a ＝2－a ，f (1＋a )＝－(1＋a )－2a ＝－1－3a .由f (1－a )＝f (1＋a )，得2－a ＝－1－3a ，解得a ＝－32.不合题意，舍去．当a ＜0时，1－a ＞1,1＋a ＜1，此时f (1－a )＝－(1－a )－2a ＝－1－a ，f (1＋a )＝2(1＋a )＋a ＝2＋3a .由f (1－a )＝f (1＋a )，得－1－a ＝2＋3a ，解得a ＝－34.综上可知，a 的值为－34.5．定义在R 上的函数f (x )满足f (x ＋1)＝2f (x )．若当0≤x ≤1时，f (x )＝x (1－x )，则当－1≤x ≤0时，f (x )＝________.解析 当－1≤x ≤0时，有0≤x ＋1≤1，所以f (1＋x )＝(1＋x )[1－(1＋x )]＝－x (1＋x )，又f (x ＋1)＝2f (x )，所以f (x )＝12f (1＋x )＝－x (x ＋1)2.答案 －x (x ＋1)26．函数f (x )＝cx 2x ＋3(x ≠－32)满足f (f (x ))＝x ，则常数c 等于( )．A ．3B ．－3C ．3或－3D ．5或－3解析 f (f (x ))＝c ⎝ ⎛⎭⎪⎫cx 2x ＋32⎝ ⎛⎭⎪⎫cx 2x ＋3＋3＝c 2x 2cx ＋6x ＋9＝x ，即x [(2c ＋6)x ＋9－c 2]＝0， 所以⎩⎨⎧2c ＋6＝0，9－c 2＝0，解得c ＝－3. 答案 B7．．已知f ⎝ ⎛⎭⎪⎫1－x 1＋x ＝1－x 21＋x 2，则f (x )的解析式为________． 解析 令t ＝1－x 1＋x ，由此得x ＝1－t 1＋t(t ≠－1)， 所以f (t )＝1－⎝ ⎛⎭⎪⎫1－t 1＋t 21＋⎝ ⎛⎭⎪⎫1－t 1＋t 2＝2t 1＋t 2， 从而f (x )的解析式为f (x )＝2x 1＋x 2(x ≠－1)． 答案 f (x )＝2x 1＋x 2(x ≠－1) 8．设二次函数f (x )满足f (2＋x )＝f (2－x )，且f (x )＝0的两个实根的平方和为10，f (x )的图象过点(0,3)，求f (x )的解析式．解 ∵f (2＋x )＝f (2－x )，∴f (x )的图象关于直线x ＝2对称．于是，设f (x )＝a (x －2)2＋k (a ≠0)，则由f (0)＝3，可得k ＝3－4a ，∴f (x )＝a (x －2)2＋3－4a ＝ax 2－4ax ＋3.∵ax 2－4ax ＋3＝0的两实根的平方和为10，∴10＝x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝16－16a ，∴a ＝1.∴f (x )＝x 2－4x ＋3.9．已知函数y ＝f (x )的图象关于直线x ＝－1对称，且当x ∈(0，＋∞)时，有f (x )＝1x ，则当x ∈(－∞，－2)时，f (x )的解析式为( )．A ．f (x )＝－1xB ．f (x )＝－1x －2C ．f (x )＝1x ＋2D ．f (x )＝－1x ＋2解析 当x ∈(－∞，－2)时，则－2－x ∈(0，＋∞)，∴f (x )＝－1x ＋2.答案 D10．若函数f (x )＝12x 2－x ＋a 的定义域和值域均为[1，b ](b >1)，求a ，b 的值．解 ∵f (x )＝12(x －1)2＋a －12，∴其对称轴为x ＝1，即函数f (x )在[1，b ]上单调递增．∴f (x )min ＝f (1)＝a －12＝1，①f (x )max ＝f (b )＝12b 2－b ＋a ＝b ，②又b >1，由①②解得⎩⎪⎨⎪⎧a ＝32，b ＝3，∴a ，b 的值分别为32，3. 11．判断函数f (x )＝x ＋k x (k ＞0)在(0，＋∞)上的单调性．解 (1)法一 任意取x 1＞x 2＞0，则f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫x 1＋k x 1－⎝ ⎛⎭⎪⎫x 2＋k x 2＝(x 1－x 2)＋⎝ ⎛⎭⎪⎫k x 1－k x 2＝(x 1－x 2)＋k (x 2－x 1)x 1x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1－k x 1x 2. 当k ≥x 1＞x 2＞0时，x 1－x 2＞0,1－k x 1x 2＜0， 有f (x 1)－f (x 2)＜0，即f (x 1)＜f (x 2)，此时，函数f (x )＝x ＋k x (k ＞0)在(0，k ]上为减函数；当x 1＞x 2≥k 时，x 1－x 2＞0,1－k x 1x 2＞0， 有f (x 1)－f (x 2)＞0，即f (x 1)＞f (x 2)，此时，函数f (x )＝x ＋k x (k ＞0)在[k ，＋∞)上为增函数；综上可知，函数f (x )＝x ＋k x(k ＞0)在(0，k ]上为减函数；在[k ，＋∞)上为增函数． 12．试讨论函数f (x )＝ax x 2－1，x ∈(－1,1)的单调性(其中a ≠0)． 解 (定义法)任取－1＜x 1＜x 2＜1，则f (x 1)－f (x 2)＝ax 1x 21－1－ax 2x 22－1＝a (x 2－x 1)(x 1x 2＋1)(x 21－1)(x 22－1)， ∵－1＜x 1＜x 2＜1，∴|x 1|＜1，|x 2|＜1，x 2－x 1＞0，x 21－1＜0，x 22－1＜0，|x 1x 2|＜1，即－1＜x 1x 2＜1，∴x 1x 2＋1＞0，∴(x 2－x 1)(x 1x 2＋1)(x 21－1)(x 22－1)＞0， 因此，当a ＞0时，f (x 1)－f (x 2)＞0，即f (x 1)＞f (x 2)，此时函数在(－1,1)为减函数；当a ＜0时，f (x 1)－f (x 2)＜0，即f (x 1)＜f (x 2)，此时函数在(－1,1)为增函数．13．已知函数f (x )＝ax －1x ＋1. (1)若a ＝－2，试证f (x )在(－∞，－2)上单调递减．(2)函数f (x )在(－∞，－1)上单调递减，求实数a 的取值范围．(1)证明 任设x 1＜x 2＜－2，则f (x 1)－f (x 2)＝－2x 1－1x 1＋1－－2x 2－1x 2＋1＝－(x 1－x 2)(x 1＋1)(x 2＋1). ∵(x 1＋1)(x 2＋1)＞0，x 1－x 2＜0，∴f (x 1)－f (x 2)＞0，∴f (x 1)＞f (x 2)，∴f (x )在(－∞，－2)上单调递减．(2)解 f (x )＝ax －1x ＋1＝a －a ＋1x ＋1，设x 1<x 2<－1， 则f (x 1)－f (x 2)＝⎝⎛⎭⎪⎫a －a ＋1x 1＋1－⎝ ⎛⎭⎪⎫a －a ＋1x 2＋1＝a ＋1x 2＋1－a ＋1x 1＋1＝(a ＋1)(x 1－x 2)(x 1＋1)(x 2＋1)， 又函数f (x )在(－∞，－1)上是减函数，所以f (x 1)－f (x 2)>0.由于x 1<x 2<－1，∴x 1－x 2<0，x 1＋1<0，x 2＋1<0，∴a ＋1<0，即a <－1.故a 的取值范围是(－∞，－1)．14． (1)函数y ＝x －5x －a －2在(－1，＋∞)上单调递增，则a 的取值范围是( )． A ．{－3} B ．(－∞，3)C ．(－∞，－3]D ．[－3，＋∞)(2)(2014·日照模拟)若f (x )＝－x 2＋2ax 与g (x )＝a x ＋1在区间[1,2]上都是减函数，则a 的取值范围是( )．A ．(－1,0)∪(0,1)B ．(－1,0)∪(0,1]C ．(0,1)D ．(0,1]解析 (1)y ＝x －5x －a －2＝1＋a －3x －(a ＋2)，由函数在(－1，＋∞)上单调递增，有⎩⎨⎧ a －3＜0，a ＋2≤－1，解得a ≤－3. (2)f (x )在[a ，＋∞)上是减函数，对于g (x )，只有当a >0时，它有两个减区间为(－∞，－1)和(－1，＋∞)，故只需区间[1,2]是f (x )和g (x )的减区间的子集即可，则a 的取值范围是0<a ≤1.15．已知f (x )＝x 2＋2x ＋a x ，x ∈[1，＋∞)． (1)当a ＝12时，求函数f (x )的最小值；(2)若对任意x ∈[1，＋∞)，f (x )＞0恒成立，试求实数a 的取值范围．审题路线 (1)当a ＝12时，f (x )为具体函数→求出f (x )的单调性，利用单调性求最值．(2)当x ∈[1，＋∞)时，f (x )＞0恒成立→转化为x 2＋2x ＋a ＞0恒成立．解 (1)当a ＝12时，f (x )＝x ＋12x ＋2，联想到g (x )＝x ＋1x 的单调性，猜想到求f (x )的最值可先证明f (x )的单调性．任取1≤x 1＜x 2，则f (x 1)－f (x 2)＝(x 1－x 2)＋⎝ ⎛⎭⎪⎫12x 1－12x 2＝(x 1－x 2)(2x 1x 2－1)2x 1x 2， ∵1≤x 1＜x 2，∴x 1x 2＞1，∴2x 1x 2－1＞0.又x 1－x 2＜0，∴f (x 1)＜f (x 2)，∴f (x )在[1，＋∞)上是增函数，∴f (x )在[1，＋∞)上的最小值为f (1)＝72.(2)在区间[1，＋∞)上，f (x )＝x 2＋2x ＋a x＞0恒成立， 则⎩⎨⎧ x 2＋2x ＋a ＞0，x ≥1⇔⎩⎨⎧ a ＞－(x 2＋2x )，x ≥1，等价于a 大于函数φ(x )＝－(x 2＋2x )在[1，＋∞)上的最大值．只需求函数φ(x )＝－(x 2＋2x )在[1，＋∞)上的最大值．φ(x )＝－(x ＋1)2＋1在[1，＋∞)上递减，∴当x ＝1时，φ(x )最大值为φ(1)＝－3.∴a ＞－3，故实数a 的取值范围是(－3，＋∞)．16． 对任意两个实数x 1，x 2，定义max(x 1，x 2)＝⎩⎨⎧ x 1，x 1≥x 2，x 2，x 1＜x 2，若f (x )＝x 2－2，g (x )＝－x ，则max(f (x )，g (x ))的最小值为________．解析 f (x )－g (x )＝x 2－2－(－x )＝x 2＋x －2，当x 2－2－(－x )＝x 2＋x －2≥0时，x ≥1或x ≤－2；当－2＜x ＜1时，x 2＋x －2＜0，即f (x )＜g (x )，所以max(f (x )，g (x ))＝⎩⎨⎧－x ，－2＜x ＜1，x 2－2，x ≥1或x ≤－2，作出图象如图所示，由图象可知函数的最小值在A 处取得，所以最小值为f (1)＝－1.答案 －117．用min{a ，b ，c }表示a ，b ，c 三个数中的最小值．设f (x )＝min{2x ，x ＋2,10－x }(x ≥0)，则f (x )的最大值为( )．A ．4B ．5C ．6D ．7解析 由f (x )＝min{2x ，x ＋2，10－x }(x ≥0)画出图象，最大值在A处取到，联立⎩⎨⎧ y ＝x ＋2，y ＝10－x ，得y ＝6. 答案 C18．(2014·黄冈中学适应性考试)定义在R 上的偶函数f (x )满足：f (x ＋1)＝－f (x )，且在[－1,0]上是增函数，下列关于f (x )的判断：①f (x )是周期函数；②f (x )的图象关于直线x ＝2对称；③f (x )在[0,1]上是增函数；④f (x )在[1,2]上是减函数；⑤f (4)＝f (0)．其中判断正确的序号是________．解析 f (x ＋1)＝－f (x )⇒f (x ＋2)＝f (x )，故f (x )是周期函数．又f (x )＝f (－x )，所以f (x ＋2)＝f (－x )，故f (x )的图象关于直线x ＝1对称．同理，f (x ＋4)＝f (x )＝f (－x )，所以f (x )的图象关于直线x ＝2对称．由f (x )在[－1,0]上是增函数，得f (x )在[0,1]上是减函数，在[1,2]上是增函数．因此可得①②⑤正确．答案 ①②⑤19．已知二次函数f (x )＝ax 2＋bx ＋1(a >0)，F (x )＝⎩⎨⎧ f (x )，x >0，－f (x )，x <0.若f (－1)＝0，且对任意实数x 均有f (x )≥0成立．(1)求F (x )的表达式；(2)当x ∈[－2,2]时，g (x )＝f (x )－kx 是单调函数，求k 的取值范围．解 (1)∵f (－1)＝0，∴a －b ＋1＝0，∴b ＝a ＋1，∴f (x )＝ax 2＋(a ＋1)x ＋1.∵对任意实数x 均有f (x )≥0恒成立，∴⎩⎨⎧a ＞0，Δ＝(a ＋1)2－4a ≤0， ∴⎩⎨⎧ a ＞0，(a －1)2≤0.∴a ＝1，从而b ＝2，∴f (x )＝x 2＋2x ＋1，∴F (x )＝⎩⎨⎧x 2＋2x ＋1，x ＞0，－x 2－2x －1，x ＜0.(2)g (x )＝x 2＋2x ＋1－kx ＝x 2＋(2－k )x ＋1.∵g (x )在[－2,2]上是单调函数，∴k －22≤－2或k －22≥2，解得k ≤－2或k ≥6.故k 的取值范围是(－∞，－2]∪[6，＋∞).20．函数f (x )是周期为4的偶函数，当x ∈[0,2]时，f (x )＝x －1，则不等式xf (x )>0在[－1,3]上的解集为( )．A ．(1,3)B ．(－1,1)C ．(－1,0)∪(1,3)D ．(－1,0)∪(0,1) 解析 f (x )的图象如图．当x ∈(－1,0)时，由xf (x )>0，得x ∈(－1,0)；当x ∈(0,1)时，由xf (x )>0，得x ∈∅；当x ∈(1,3)时，由xf (x )>0，得x ∈(1,3)．∴x ∈(－1,0)∪(1,3)，故选C.答案 C21．设定义在[－2,2]上的偶函数f (x )在区间[0,2]上单调递减，若f (1－m )＜f (m )，则实数m 的取值范围是________．解析 ∵f (x )是偶函数，∴f (－x )＝f (x )＝f (|x |)．∴不等式f (1－m )＜f (m )⇔f (|1－m |)＜f (|m |)．又当x ∈[0,2]时，f (x )是减函数．∴⎩⎨⎧ |1－m |＞|m |，－2≤1－m ≤2，－2≤m ≤2，解得－1≤m ＜12.答案 ⎣⎢⎡⎭⎪⎫－1，12 22．设f (x )是定义域为R 的周期函数，最小正周期为2，且f (1＋x )＝f (1－x )，当－1≤x ≤0时，f (x )＝－x .(1)判定f (x )的奇偶性；(2)试求出函数f (x )在区间[－1,2]上的表达式．解 (1)∵f (1＋x )＝f (1－x )，∴f (－x )＝f (2＋x )．又f (x ＋2)＝f (x )，∴f (－x )＝f (x )，∴f (x )是偶函数．(2)当x ∈[0,1]时，－x ∈[－1,0]，则f (x )＝f (－x )＝x ；进而当1≤x ≤2时，－1≤x －2≤0，f (x )＝f (x －2)＝－(x －2)＝－x ＋2.故f (x )＝⎩⎨⎧ －x ，x ∈[－1，0)，x ，x ∈[0，1)，－x ＋2，x ∈[1，2].。

专题5.3.1 函数的单调性知识储备1.函数的单调性与导数的关系 函数y ＝f (x )在区间(a ，b )内可导，(1)若f ′(x )>0，则f (x )在区间(a ，b )内是单调递增函数； (2)若f ′(x )<0，则f (x )在区间(a ，b )内是单调递减函数； (3)若恒有f ′(x )＝0，则f (x )在区间(a ，b )内是常数函数．讨论函数的单调性或求函数的单调区间的实质是解不等式，求解时，要坚持“定义域优先”原则.2.常用结论汇总——规律多一点(1)在某区间内f ′(x )>0(f ′(x )<0)是函数f (x )在此区间上为增(减)函数的充分不必要条件．(2)可导函数f (x )在(a ，b )上是增(减)函数的充要条件是对∀x ∈(a ，b )，都有f ′(x )≥0(f ′(x )≤0)且f ′(x )在(a ，b )上的任何子区间内都不恒为零．能力检测注意事项：本试卷满分100分，考试时间45分钟，试题共16题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置． 一、单选题1．（2020·全国高二课时练习）设函数()f x 的图象如图所示，则导函数()f x 的图象可能为（ ）A ．B ．C ．D ．【答案】C【解析】∵()f x 在(,1)-∞，(4,)+∞上为减函数，在(1,4)上为增函数， ∴当1x <或4x >时，()0f x '<；当14x <<时，()0f x '>．故选：C ．2．（2020·全国高二专题练习）设奇函数()f x 在R 上存在导函数()'f x ，且在(0,)+∞上2()f x x '<，若331(1)()(1)3f m f m m m ⎡⎤--≥--⎣⎦，则实数m 的取值范围为（ ） A ．11,22⎡⎤-⎢⎥⎣⎦B ．11,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C ．1,2⎛⎤-∞- ⎥⎝⎦D ．1,2⎡⎫+∞⎪⎢⎣⎭【答案】D【解析】331(1)()(1)3f m f m m m ⎡⎤--≥--⎣⎦， 即3311(1)(1)()33f m m f m m ≥----，构造函数31()()3g x f x x =-，由题意知：在(0,)+∞上，2()()0g x f x x '=-<'， 故()g x 在(0,)+∞上单调递减，()f x 为奇函数，()()()3311()33g x f x x f x x g x ∴-=-+=-+=-，即()g x 为奇函数， 故()g x 在R 上单调递减，因此原不等式可化为：()()1g m g m -≥，即1m m -≤，解得12m ≥.故选：D ．3．（2020·全国高二课时练习）函数()sin 2,()3f x x xf f x π''⎛⎫=+⎪⎝⎭为()f x 的导函数，令31,log 22a b ==，则下列关系正确的是（ ）A ．()()f a f b <B ．()()f a f b >C ．()()f a f b =D ．()()f a f b ≤【答案】B【解析】由题意得，()cos 23f x x f π''⎛⎫=+⎪⎝⎭，cos 2333f f πππ''⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，解得132f π⎛⎫'=-⎪⎝⎭，所以()sin f x x x =-． 所以()cos 10f x x '=-≤，所以()f x 为减函数．因为331log 2log 2b a =>==，所以()()f a f b >，故选：B ． 4．（2020·全国高二课时练习）若函数()y f x =的导函数()y f x '=的图象如图所示，则函数()y f x =的图象可能是（ ）A ．B ．C ．D ．【答案】D【解析】设导函数()y f x '=的图象与x 轴交点的横坐标从左到右依次为123,,x x x ，其中1320,0x x x <>>，故()y f x =在()1,x -∞上单调递减，在()12,x x 上单调递增，在()23,x x 上单调递减，在()3,x +∞单调递增．故选：D ．5．（2020·全国高二课时练习）若函数()()3230,f x ax x x b a b =+++>∈R 恰好有三个不同的单调区间，则实数a 的取值范围是（ ） A ．()()0,33,+∞ B ．[)3,+∞ C ．(]0,3 D ．()0,3【答案】D【解析】由题意得()()23610f x ax x a '=++>，函数()f x 恰好有三个不同的单调区间，()f x '∴有两个不同的零点，所以，361200a a ∆=->⎧⎨>⎩，解得0<<3a .因此，实数a 的取值范围是()0,3.故选：D.6．（2020·全国高二课时练习）函数2()ln f x x x =的单调递减区间为（ ）A ．B ．⎫+∞⎪⎪⎝⎭C ．)+∞D ．0,e ⎛ ⎝⎭【答案】D【解析】由题意得，函数()f x 的定义域为(0,)+∞，21()2ln 2ln (2ln 1)f x x x x x x x x x x=⋅+⋅=+=+'．令()0f x '<，得2ln 10x ，解得0x <<，故函数2()ln f x x x =的单调递减区间为0,e ⎛ ⎝⎭．故选：D 7．（2020·江苏南通市·高三期中）设()f x 是定义在R 上的函数，其导函数为()f x '，若()()1f x f x '+>，()02020f =，则不等式()20191x f x e ->+（其中e 为自然对数的底数）的解集为（ ） A ．()(),00,-∞⋃+∞ B ．()(),02019,-∞+∞C ．()0,∞+D ．()2019,+∞【答案】C【解析】因为()f x 满足()()1f x f x '+>，， 令()()1xg x e f x =-⎡⎤⎣⎦，则()()()10xg x e f x f x ''=+->⎡⎤⎣⎦，所以()g x 在R 上是增函数， 又()02020f =，则()02019g =，不等式()20191xf x e ->+可化为()12019x e f x ->⎡⎤⎣⎦，即()()0g x g >， 所以0x >，所不等式的解集是()0,∞+，故选：C8．（2020·洛阳理工学院附属中学高三月考（理））已知奇函数()f x 的定义域为ππ,22⎛⎫- ⎪⎝⎭，其图象是一段连续不断的曲线，当π02x -<<时，有()()cos sin 0f x x f x x '+>成立，则关于x 的不等式()π2cos 3f x f x ⎛⎫<⎪⎝⎭的解集为（ ） A ．ππ23⎛⎫-⎪⎝⎭， B ．ππ23⎛⎫-- ⎪⎝⎭，C ．ππππ2332⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，， D ．πππ0332⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，， 【答案】A【解析】设()()cos f x g x x= ，则()()()2cos sin cos f x x f x xg x x'+'=当π02x -<<时，有()()cos sin 0f x x f x x '+>成立，此时()0g x '> 所以()()cos f x g x x=在02π⎛⎫-⎪⎝⎭，上单调递增. 又()f x 为奇函数，则()00f =，则()()cos f x g x x=为奇函数，又()00g =则()()cos f x g x x=在02，上单调递增，所以()g x 在ππ,22⎛⎫-⎪⎝⎭上单调递增.当ππ,22x ⎛⎫∈-⎪⎝⎭，恒有cos 0x >()π2cos 3f x f x ⎛⎫< ⎪⎝⎭可化为()π3πcos cos 3f f x x ⎛⎫⎪⎝⎭<，即()3g x g π⎛⎫< ⎪⎝⎭，由()()cos f x g x x=在ππ,22⎛⎫-⎪⎝⎭上单调递增，所以23x ππ-<<故选：A二、多选题9．（2020·全国高二课时练习）（多选）已知函数()f x 的定义域为R ，其导函数()'f x 的图象如图所示，则对于任意()1212,x x x x ∈≠R ，下列结论正确的是（ ）A ．()()()12120x x f x f x --<⎡⎤⎣⎦B ．()()()12120x x f x f x -->⎡⎤⎣⎦C ．()()121222f x f x x x f ++⎛⎫>⎪⎝⎭D ．()()121222f x f x x x f ++⎛⎫<⎪⎝⎭【答案】AD【解析】由题中图象可知，导函数()'f x 的图象在x 轴下方，即()0f x '<，且其绝对值越来越小，因此过函数()f x 图象上任一点的切线的斜率为负，并且从左到右切线的倾斜角是越来越大的钝角，由此可得()f x 的大致图象如图所示．A 选项表示12x x -与()()12f x f x -异号，即()f x 图象的割线斜率()()1212f x f x x x --为负，故A 正确；B 选项表示12x x -与()()12f x f x -同号，即()f x 图象的割线斜率()()1212f x f x x x --为正，故B 不正确；122x x f +⎛⎫⎪⎝⎭表示122x x +对应的函数值，即图中点B 的纵坐标，()()122f x f x +表示当1x x =和2x x =时所对应的函数值的平均值，即图中点A 的纵坐标，显然有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭，故C 不正确，D 正确．故选:AD ．10．（2020·全国高二课时练习）（多选）如图是函数()y f x =的导函数()'f x 的图象，则下面判断正确的是（ ）A ．()f x 在(3,1)-上是增函数B ．()f x 在(1,3)上是减函数C ．()f x 在(1,2)上是增函数D ．当4x =时，()f x 取得极小值【答案】CD【解析】()'f x 的图象在(3,1)-上先小于0，后大于0，故()f x 在(3,1)-上先减后增，因此A 错误；()'f x 的图象在(1,3)上先大于0，后小于0，故()f x 在(1,3)上先增后减，因此B 错误；由图可知，当(1,2)x ∈时，()0f x '>，所以()f x 在(1,2)上单调递增，因此C 正确；当(2,4)x ∈时，()0f x '<，当(4,5)x ∈时，()0f x '>，所以当4x =时，()f x 取得极小值，因此D 正确．故选：CD ．11．（2020·全国高二课时练习）(多选)已知函数2()(ln )f x x x a a =-+，则下列结论正确的是（ ）A ．0,0,()0a x f x ∃>∀>B ．0,0,()0a x f x ∃>∃>C ．0,0,()0a x f x ∀>∀>D ．0,0,()0a x f x ∀>∃>【答案】ABD 【解析】当12a =时，211()ln 22f x x x ⎛⎫=-+ ⎪⎝⎭，函数的定义域为(0,)+∞，211()2ln 2ln 2ln 2f x x x x x x x x x x x ⎛⎫=-+⋅=-+= ⎪⎝'⎭，令()0f x '=，得1x =，当1x >时，()0f x '>，此时函数单调递增， 当01x <<时，()0f x '<，此时函数单调递减，故当1x =时，函数()f x 取得极小值，也是最小值，11(1)022f =-+=， 则0,()(1)0x f x f ∀>=，故选项A 正确； 当5a =时，2()(ln 5)5f x x x =-+， 则22()(ln 5)5450f e e e e =-+=-+<，故0,0,()0a x f x ∃>∃>，故选项B 正确，选项C 错误；因为2(1)1(ln1)0f a a a a =-+=-+=，所以0,10a x ∀>∃=>，使()0f x 成立，因此选项D正确.故选：ABD.12．（2020·广东揭阳市·高三期中）下列函数在其定义域上既是奇函数又是减函数的是（ ） A ．()2x f x = B ．()sin f x x x =- C ．()x x f x e e -=- D ．()||f x x x =-【答案】BCD【解析】对于A ，()2x f x =既不是奇函数也不是偶函数，且单调递增，故A 错误；对于B ，()f x 的定义域为R ，且()()()()sin sin f x x x x x f x -=-+=--=-，()f x ∴是奇函数，又()cos 10f x x '=-≤恒成立，故()f x 是减函数，故B 正确； 对于C ，()f x 的定义域为R ，且()()xxf x e f x e--=-=-，()f x ∴是奇函数，)0(x x f x e e -'--<=，故()f x 是减函数，故C 正确；对于D ，()f x 的定义域为R ，且()()||||f x x x x x f x -=-==-，()f x ∴是奇函数，又22,0(),0x x f x x x x x ⎧<=-=⎨-≥⎩是减函数，故D 正确.故选：BCD.三、填空题13．（2020·全国高二课时练习）已知函数()f x 与()f x '的图象如图所示，则函数()()xf xg x e =的单调递减区间为___________．【答案】()0,1、()4,+∞【解析】由图象可知，不等式()()0f x f x '-<的解集为()()0,14,+∞，()()x f x g x e =，()()()()()()()2x x x x f x e f x e f x f x g x e e ''-⋅'-=='， 由()0g x '<，可得()()0f x f x '-<，解得()()0,14,x ∈+∞.因此，函数()()x f x g x e=的单调递减区间为()0,1、()4,+∞． 故答案为：()0,1、()4,+∞.14．（2020·山西高三期中（理））已知()3216132m f x x x x =-++在()1,1-单调递减，则m 的取值范围为______． 【答案】[]5,5- 【解析】()f x 在()1,1-单调递减，∴2()60f x x mx '=+-≤在()1,1-恒成立，又2()6f x x mx '=+-是开口向上的二次函数，为使()0f x '≤在()1,1-恒成立，只需(1)0(1)0f f ''-≤⎧⎨≤⎩，即160160m m --≤⎧⎨+-≤⎩，则[]5,5m ∈-.故答案为：[]5,5-.15．（2020·全国高二单元测试）设()'f x 是函数()f x 在R 的导函数，对x R ∀∈，2()()f x f x x -+=，且[0x ∀∈，)+∞，()f x x '>．若()()2f a f a --22a -，则实数a 的取值范围为__．【答案】(-∞，1] 【解析】2()()f x f x x -+=，2211()()022f x x f x x ∴-+--=，令21()()2g x f x x =-， 2211()()()()022g x g x f x x f x x -+=--+-=， ∴函数()g x 为奇函数．(0,)x ∈+∞时，()f x x '>．(0,)x ∴∈+∞时，()()0g x f x x '='->，故函数()g x 在(0,)+∞上是增函数， 故函数()g x 在(,0)-∞上也是增函数， 由(0)0f =，可得()g x 在R 上是增函数．()()2f a f a --22a -，等价于()()()2222a f a f a ---22a -，即()()2g a g a -，2a a ∴-，解得1a ．故答案为：(-∞，1]． 四、双空题16．（2020·江苏省太湖高级中学高二期中）已知函数()(0)bf x ax b x=+>的图象在点()()1,1P f 处的切线与直线210x y +-=垂直，则a 与b 的关系为_______(用b 表示)，若函数()y f x =在区间1[,)2+∞上单调递增，则b 的最大值等于______. 【答案】2b + 23【解析】由题意，函数()(0)b f x ax b x=+>，可得2()b f x a x '=-，所以(1)f a b '=-， 即函数()f x 的图象在点()()1,1P f 处的切线的斜率为k a b =-又由函数()f x 的图象在点()()1,1P f 处的切线与直线210x y +-=垂直， 所以()1()12a b -⨯-=-，可得2a b -=，即a 与b 的关系为2a b -=；又由函数()y f x =在区间1[,)2+∞上单调递增， 可得2()0b f x a x '=-≥在区间1[,)2+∞上恒成立， 即22b b x +≥在区间1[,)2+∞上恒成立，整理得22b x b ≤+在区间1[,)2+∞上恒成立， 又由2min 1()4x =，所以124b b ≤+，解得203b <≤， 所以b 的最大值等于23.故答案为：2a b -=，23.。

高一年级数学培优教材---二次函数一、基础知识：1．二次函数的解析式（1）一般式：2()(0)f x ax bx c a =++≠ （2）顶点式：2()()f x a x h k =-+，顶点为(,)h k （3）两根式：12()()()f x a x x x x =-- （4）三点式：132312321313221231213()()()()()()()()()()()()()()()()x x x x x x x x x x x x f x f x f x f x x x x x x x x x x x x x ------=++------2．二次函数的图像和性质（1）2()(0)f x ax bx c a =++≠的图像是一条抛物线，顶点坐标是24(,)24b ac b a a --，对称轴方程为2bx a=-，开口与a 有关。

（2）单调性：当0a >时，()f x 在(,]2b a -∞-上为减函数，在[,)2ba-+∞上为增函数；0a <时相反。

（3）奇偶性：当0b =时，()f x 为偶函数；若()()f a x f a x +=-对x R ∈恒成立，则x a =为()f x 的对称轴。

（4）最值：当x R ∈时，()f x 的最值为244ac b a-，当[,],[,]2b x m n m n a ∈-∈时，()f x 的最值可从(),(),()2bf m f n f a -中选取； 当[,],[,]2bx m n m n a∈-∉时，()f x 的最值可从(),()f m f n 中选取。

常依对称轴与区间[,]m n 的位置分类讨论。

3．三个二次之间的关联及根的分布理论：二次方程2()0(0)f x ax bx c a =++=≠的区间根问题，一般情况需要从三个方面考虑：判别式、区间端点函数值的符号；对称轴与区间端点的关系。

二、 综合应用：例1：已知二次函数()f x 的图像经过三点(1,6),(1,0),(2.5,0)A B C --，求()f x 的解析式。

例题解答第一讲例1.解：，，，因此，例2解：表明.①若，则.②若，则.①和②的范围并在一起得到的范围为（，）.例3.解：例4. 解：（1）证明：显然B中任意元素均为奇数，因此.任取中一个元素，设，若为偶数，则；若n为奇数，则.因此，所以. （2）证明：中必然都是偶数，故又任取中一个元素，设，.故因此所以.例5. 解：，最小元素为，所以，或.，因此是完全平方数，结合知，故，，因为或注意的元素和等于A的元素和加B的元素和减去的元素和.即.若，则，无自然数满足它，矛盾.若则又因为，又，所以.所以，，，，. 例6. 解：（1），，不具有，因为和都不属于该集合.，，，具有.直接验证即可.（2）证明：考虑，由于所以故当时，，即对，，，均成立，且因此，，，，，，.所以即例7.解：我们把奇子集以外的子集叫做偶子集。

含1的奇子集数目和不含1的偶子集数目相等。

不含1的奇子集和含1的偶子集数目相等。

因此奇子集和偶子集数目相等，各占总子集数的一半，即256.例8.解：我们把这100个数中，存在3倍关系的数依次排成一条链。

例如1-3-9-27-81.则每个数都恰好出现在某条链中。

每条链中相邻的数不可取，不同链上的数互不影响。

长度为5的链仅有一条，可取3数。

长度为4的链仅有一条，可取2数。

长度为3的链有6条，可取6x2=12个数长度为2的链有14条，可取14个数长度为1的链有45条，可取45个数总共可取3+2+12+14+45=76个数例9解：单元素集显然符合要求.当时，设，则有又所以①时，，若，矛盾若，则矛盾②时，.所以，故，，代入得. 综上，符合要求的有，，和任意单元正整数集例10解：（1）当k不为完全平方数时，共有个，当或2时，有，，，，，，，，共个.所以P中元素个数为个.（2）先说明时不能办到.，，.表明1只能和6分在一起，3和10分在一起.这时15不论分在那边都矛盾：1，.时可以划分.只需要考虑中有理元素的划分.将分为和；将，，划分为，，，和，，；将，，，，，，，，，划分为，，，和，，，，. 将上述划分集各取1个组成并集A,则和它的补集符合要求例11.证明：可举例整数集.①若和存在包含关系，不妨设，由于是的真子集，故必存在，且，这时②若、不存在包含关系，设，，，，考虑.若则，矛盾若，则，矛盾.所以满足.第二讲例1.解：由，得，.解不等式，得定义域为：（，）（，）例2解：由得解不等式得的定义域为：例3 解：符合要求.例4 解设令，有，即.令，有，即.令，有，即.得出，，，因此.例5解：，用代替有，继续用代替有；三式联立，解出例 6.解：设，则.故.设，则，.例7.解：（1），故值域为，，；（2）所以，故值域为，，，；（3），令，则，且.故值域为（，；（4），令，.值域为，（，）；（5）这表示x轴上一点，到点，和，的距离之和做对称即可知故值域为，；（6）其几何意义是数轴上的一点到，，三点距离之和，所以，值域为，）；（7），，故值域为，第三讲例 1.解：令，则，（），且当，是递减，，时递增.即，时，，为递减区间，，为递增区间，最小值为.此题也可用导函数解出.例2.证明：由条件，，有和成立.于是.所以是周期函数.例3.解：，考虑函数，于是有，又是R上的增函数，故.例4.解：为了使在时的表达式有意义，则在上恒大于0.又是奇函数，值域要是R，只需在上能取到。

专题4.1 数列的概念与简单表示法知识储备知识点一数列及其有关概念思考1数列1,2,3与数列3,2,1是同一个数列吗？【答案】不是.顺序不一样.思考2根据你对于数列的定义的理解，看看能不能回答下面的问题：(1)按照一定顺序排列的一列数称为数列，数列中的每一个数叫做这个数列的项.数列中的每一项都和它的序号有关，排在第一位的数称为这个数列的第1项(通常也叫做首项)，排在第二位的数称为这个数列的第2项，……，排在第n位的数称为这个数列的第n项.(2) 数列的一般形式可以写成a1，a2，…，a n，…，简记为{a n}.思考3数列的记法和集合有些相似，那么数列与集合的区别在哪儿？【答案】数列中的数讲究顺序，集合中的元素具有无序性；数列中可以出现相同的数，集合中的元素具有互异性.知识点二通项公式思考1数列1,2,3,4，…的第100项是多少？你是如何猜的？【答案】100.由前四项与它们的序号相同，猜第n项a n＝n，从而第100项应为100.思考2上例中的a n＝n当序号n取不同的值，就可得到不同的项，所以可以把a n＝n当作数列1,2,3,4，…的项的通用公式，这个公式就叫通项公式.你能把通项公式推广到一般数列吗？【答案】如果数列{a n}的第n项a n与序号n之间的关系可以用一个式子a n＝f(n)来表示，那么这个公式叫做这个数列的通项公式.思考3数列的通项公式a n＝f(n)与函数解析式y＝f(x)有什么异同？【答案】如图，数列可以看成以正整数集N*(或它的有限子集{1,2,3，…，n})为定义域的函数a n＝f(n)当自变量按照从小到大的顺序依次取值时所对应的一列函数值.不同之处是定义域，数列中的n必须是从1开始且连续的正整数，函数的定义域可以是任意非空数集.知识点三数列的分类(1)按项数分类，项数有限的数列叫做有穷数列，项数无限的数列叫做无穷数列.(2)按项的增减趋势分类，从第二项起，每一项都大于它的前一项的数列叫做递增数列；从第二项起，每一项都小于它的前一项的数列叫做递减数列；各项相等的数列叫做常数列；从第二项起，有些项大于它的前一项，有些项小于它的前一项的数列叫做摆动数列. 知识点四 递推公式思考1 (1)已知数列{a n }的首项a 1＝1，且有a n ＝3a n －1＋2(n >1)，则a 4＝________. (2) 已知数列{a n }中，a 1＝a 2＝1，且有a n ＋2＝a n ＋a n ＋1(n ∈N *)，则a 4＝________. 【答案】(1)53 (2)3思考2 上例是一种给出数列的方法，叫递推公式.你能概括一下什么叫递推公式吗？【答案】如果数列{a n }的第1项或前几项已知，并且数列{a n }的任一项a n 与它的前一项a n －1(或前几项)间的关系可以用一个式子来表示，那么这个式子就叫做这个数列的递推公式.思考3 我们已经知道通项公式和递推公式都能给出数列.那么通项公式和递推公式有什么不同？ 【答案】通项公式和递推公式都是给出数列的方法.已知数列的通项公式，可以直接求出任意一项；已知递推公式，要求某一项，则必须依次求出该项前面所有的项. 知识点五 数列的表示方法思考1 以数列2,4,6,8,10,12，…为例，你能用几种方法表示这个数列？ 【答案】(1)解析法、列表法、图象法.数列可以用通项公式、图象、列表等方法来表示. (2)对数列2,4,6,8,10,12，…可用以下几种方法表示： ①通项公式法：a n ＝2n .②递推公式法：⎩⎪⎨⎪⎧a 1＝2，a n ＋1＝a n ＋2，n ∈N *.③列表法：④图象法：思考2 归纳一下数列的表示方法.【答案】数列的表示方法有通项公式法、图象法、列表法、递推公式法.能力检测注意事项：本试卷满分100分，考试时间45分钟，试题共16题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置． 一、单选题1．下列说法正确的是( )A ．数列1,3,5,7与数集{1,3,5,7}是一样的B ．数列1,2,3与数列3,2,1是相同的C ．数列11n ⎧⎫+⎨⎬⎩⎭是递增数列 D ．数列()11nn ⎧⎫-⎪⎪+⎨⎬⎪⎪⎩⎭是摆动数列【答案】D【解析】数列是有序的，而数集是无序的，所以A ，B 不正确；选项C 中的数列是递减数列；选项D 中的数列是摆动数列． 2．已知数列12，23，34，…，1n n +，则0.96是该数列的( ) A ．第20项 B ．第22项 C ．第24项 D ．第26项【答案】C 【解析】由1nn +＝0.96，解得n ＝24. 3．在数列1,1,2,3,5,8，x,21,34,55中，x 等于( ) A ．11 B ．12 C ．13 D ．14 【答案】C【解析】观察数列可知，后一项是前两项的和，故x ＝5＋8＝13.4．已知数列{a n }的通项公式a n ＝log (n ＋1)(n ＋2)，则它的前30项之积是( ) A.15B ．5C ．6D ．231log 3log 325+【答案】B【解析】a1·a2·a3·…·a30＝log23×log34×log45×…×log3132＝log232＝log225＝5. 5．已知递减数列{a n}中，a n＝kn(k为常数)，则实数k的取值范围是() A．R B．(0，＋∞)C．(－∞，0) D．(－∞，0]【答案】C【解析】a n＋1－a n＝k(n＋1)－kn＝k<0.6．数列{a n}中，a n＝－n2＋11n，则此数列最大项是()A．第4项B．第6项C．第5项D．第5项和第6项【答案】D【解析】a n＝－n2＋11n＝－2112n⎛⎫-⎪⎝⎭＋1214，∵n∈N＋，∴当n＝5或n＝6时，a n取最大值．故选D.7．我国古代数学名著《九章算术》中，有已知长方形面积求一边的算法，其方法的前两步为：第一步：构造数列1，12，13，14，…，1n.①第二步：将数列①的各项乘n，得到数列(记为)a1，a2，a3，…，a n.则n≥2时，a1a2＋a2a3＋…＋a n－1a n＝()A．n2B．(n－1)2 C．n(n－1) D．n(n＋1)【答案】C【解析】由题意得a k＝nk.k≥2时，a k－1a k＝2211(1)1nnk k k k⎛⎫=-⎪--⎝⎭.∴n≥2时，a1a2＋a2a3＋…＋a n－1a n＝n21111112231n n⎡⎤⎛⎫⎛⎫⎛⎫-+-++-⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦＝n211n⎛⎫-⎪⎝⎭＝n(n－1)．故选C.8．由1,3,5，…，2n－1，…构成数列{a n}，数列{b n}满足b1＝2，当n≥2时，b n＝a b n－1，则b6的值是()A．9 B．17C．33 D．65【答案】C【解析】∵b n＝a b n－1，∴b2＝a b1＝a2＝3，b3＝a b2＝a3＝5，b4＝a b3＝a5＝9，b5＝a b4＝a9＝17，b6＝a b5＝a17＝33.二、多选题9．(多选)一个无穷数列{a n }的前三项是1,2,3，下列可以作为其通项公式的是( ) A ．a n ＝nB ．a n ＝n 3－6n 2－12n －6C ．a n ＝12n 2－12n ＋1 D ．a n ＝26611n n -+ 【答案】AD【解析】对于A ，若a n ＝n ，则a 1＝1，a 2＝2，a 3＝3，符合题意；对于B ，若a n ＝n 3－6n 2－12n ＋6，则a 1＝－11，不符合题意；对于C ，若a n ＝12n 2－12n ＋1，当n ＝3时，a 3＝4≠3，不符合题意；对于D ，若a n ＝26611n n -+，则a 1＝1，a 2＝2，a 3＝3，符合题意．故选A 、D. 10．(多选)数列{F n }：1,1,2,3,5,8,13,21,34，…称为斐波那契数列，是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入的，故又称为“兔子数列”．该数列从第三项开始，每项等于其前相邻两项之和．记数列{F n }的前n 项和为S n ，则下列结论正确的是( ) A ．S 5＝F 7－1 B ．S 5＝S 6－1 C ．S 2 019＝F 2 021－1 D ．S 2 019＝F 2 020－1【答案】AC【解析】根据题意有F n ＝F n －1＋F n －2(n ≥3)，所以S 3＝F 1＋F 2＋F 3＝1＋F 1＋F 2＋F 3－1＝F 3＋F 2＋F 3－1＝F 4＋F 3－1＝F 5－1，S 4＝F 4＋S 3＝F 4＋F 5－1＝F 6－1，S 5＝F 5＋S 4＝F 5＋F 6－1＝F 7－1，…，所以S 2 019＝F 2 021－1.故选A 、C.11．已知数列{}n a 的前4项为2，0，2，0，则该数列的通项公式可能为（ ） A ．0,2,n n a n ⎧=⎨⎩为奇数为偶数B ．1(1)1n n a -=-+C ．2sin 2n n a π= D ．cos(1)1n a n π=-+【答案】BD【解析】因为数列{}n a 的前4项为2，0，2，0， 选项A ：不符合题设；选项B ：01(1)12,a =-+=12(1)10,a =-+=23(1)12,a =-+=34(1)10a =-+=，符合题设；选项C ：，12sin2,2a π==22sin 0,a π==332sin22a π==-不符合题设； 选项D ：1cos 012,a =+=2cos 10,a π=+=3cos 212,a π=+=4cos310a π=+=，符合题设.故选：BD.12．“太极生两仪，两仪生四象，四象生八卦……”大衍数列，来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理，是中华传统文化中隐藏着的世界数学史上第一道数列题．大衍数列中的每一项都代表太极衍生过程中，曾经经历过的两仪数量总和，从第一项起依次为0，2，4，8，12，18，24，32，40，50，……．记大衍数列为{}n a ，其前n 项和为*,n S n ∈N ，则（ ）A ．20220a =B ．357202111115051011a a a a ++++=C ．232156S =D ．246489800a a a a ++++=【答案】BCD【解析】根据数列前10项依次是0,2,4,8,12,18,24,32,40,50,，则奇数项为：2112-，2312-，2512-，2712-，2912-，，偶数项为：222，242，262，282，2102，，所以通项公式为221,(2,(2n n n a n n ⎧-⎪⎪=⎨⎪⎪⎩为奇数）为偶数），对于A ， 22020020==2a ，故A 错误；对于B ，35720211111a a a a ++++22222222=++++31517120211----1111224466820202022⎛⎫=++++⎪⨯⨯⨯⨯⎝⎭111111*********20202505100222202211⎛⎫=⨯-+-++-=-= ⎪⎝⎭，故B 正确； 对于C ，()()2313232422S a a a a a a =++++++222212323122+++-=，由()()22221211236n n n n +++++=，所以()()2323231461112215626S ++⎛⎫=-= ⎪⎝⎭，故C 正确；对于D ，24648a a a a ++++()222221242922421224=⨯+⨯+⨯++⨯=++()()242412241298006+⨯+=⋅=，故D 正确.故选：BCD三、填空题13．已知数列{a n }的通项公式a n ＝19－2n ，则使a n >0成立的最大正整数n 的值为________． 【答案】9【解析】由a n ＝19－2n >0，得n <192.∵n ∈N *，∴n ≤9.14．已知数列{a n }的通项公式a n ＝1nn +，则a n ·a n ＋1·a n ＋2＝________. 【答案】3n n + 【解析】a n ·a n ＋1·a n ＋2＝1n n +·12n n ++·23n n ++＝3n n +. 15.数列{a n }的前n 项和为S n ，若S n ＋S n －1＝2n －1(n ≥2)，且S 2＝3，则a 1＋a 3的值为________． 【答案】-1【解析】∵S n ＋S n －1＝2n －1(n ≥2)，令n ＝2， 得S 2＋S 1＝3，由S 2＝3得a 1＝S 1＝0， 令n ＝3，得S 3＋S 2＝5，所以S 3＝2，则a 3＝S 3－S 2＝－1，所以a 1＋a 3＝0＋(－1)＝－1.16.如图(1)是第七届国际数学教育大会(简称ICME­7)的会徽图案，会徽的主体图案是由如图(2)的一连串直角三角形演化而成的，其中OA 1＝A 1A 2＝A 2A 3＝…＝A 7A 8＝1，如果把图(2)中的直角三角形继续作下去，记OA 1，OA 2，…，OA n ，…的长度构成数列{a n }，则此数列的通项公式为a n ＝________.【解析】因为OA 1＝1，OA 2，OA 3…，OA n ，…，所以a 1＝1，a 2，a 3…，a n . 四、解答题17．已知数列{}n a 的前n 项和2321n S n n =-+，（1）求数列{}n a 的通项公式； （2）求数列{}n a 的前多少项和最大．【解析】（1）当1n =时，11321132a S ==-+=；当2n ≥时，()()()22132132111n n n a S S n n n n -⎡⎤=-=-+----+⎣⎦332n =-；所以：32,1332,2n n a n n =⎧=⎨-≥⎩；（2）因为()22321321n S n n n n =-+=--+()216257n =--+；所以前16项的和最大．18．在数列{}n a 中，2293n a n n =-++.（1）-107是不是该数列中的某一项？若是，其为第几项？ （2）求数列中的最大项.【解析】（1）令22107,293107,291100n a n n n n =--++=---=，解得10n =或112n =-（舍去）.所以10107a =- （2）229105293248n a n n n ⎛⎫=-++=--+ ⎪⎝⎭， 由于*n ∈N ，所以最大项为213a = 19．数列{a n }满足a 1= 1 ,a n +1 +2a n a n +1- a n =0. （1）写出数列的前5项；（2）由（1）写出数列{a n }的一个通项公式；（3）实数199是否为这个数列中的一项？若是,应为第几项？ 【答案】(1)见解析（2）121n a n =-（3）50【解析】（1）由已知可得11a =，213a =，315a =，417a =，519a =.（2）由（1）可得数列的每一项的分子均为1，分母分别为1，3，5，7，9，…，所以它的一个通项公式为121n a n =-. （3）令119921n =-，解得50n =，故199是这个数列的第50项.20．已知数列2299291n n n ⎧⎫-+⎨⎬-⎩⎭. (1)求这个数列的第10项； (2)98101是不是该数列中的项，为什么？ (3)求证：数列中的各项都在区间(0,1)内；(4)在区间1233⎛⎫ ⎪⎝⎭，内有无数列中的项？若有，是第几项？若没有，说明理由．【解析】(1)设a n ＝f (n )＝2299291n n n -+-＝(31)(32)(31)(31)n n n n ---+＝3231n n -+.令n ＝10，得第10项a 10＝f (10)＝2831. (2)令3231n n -+＝98101，得9n ＝300. 此方程无正整数解，所以98101不是该数列中的项． (3)证明：∵a n ＝3231n n -+＝1－331n +， 且n ∈N *，∴0<1－331n +<1， ∴0<a n <1.∴数列中的各项都在区间(0,1)内． (4)令13<a n ＝3231n n -+<23， ∴3196,9662,n n n n +<-⎧⎨-<+⎩∴7,68,3n n ⎧>⎪⎪⎨⎪<⎪⎩∴当且仅当n ＝2时，上式成立，故在区间1233⎛⎫⎪⎝⎭，内有数列中的项，且只有一项为a 2＝47. 21．已知函数f (x )＝x －1x.数列{a n }满足f (a n )＝－2n ，且a n >0.求数列{a n }的通项公式． 【解析】∵f (x )＝x －1x，∴f (a n )＝a n －1n a ，∵f (a n )＝－2n .∴a n －1na ＝－2n ，即2n a ＋2na n －1＝0. ∴a n ＝－n.∵a n >0，∴a n－n .22．已知数列{a n }的通项公式为a n ＝22n n (n ∈N *)，则这个数列是否存在最大项？若存在，请求出最大项；若不存在，请说明理由．【解析】存在最大项．理由：a 1＝12，a 2＝2222＝1，a 3＝2332＝98，a 4＝2442＝1，a 5＝2552＝2532，….∵当n≥3时，221122(1)2(1)22nnnna n na n n++++=⨯=＝1211n⎛⎫+⎪⎝⎭2<1，∴a n＋1<a n，即n≥3时，{a n}是递减数列．又∵a1<a3，a2<a3，∴a n≤a3＝9 8 .∴当n＝3时，a3＝98为这个数列的最大项．。

第三单元 三角函数、解三角形第01讲 三角函数的图像与性质【课前双基巩固】 知识聚焦1.[-1,1] [-1,1] R 奇函数 偶函数 2k π+π2,2k π+3π2[2k π-π,2k π] (k π,0) x=k π对点演练1.π [解析] 最小正周期T=2πω=2π2=π.2.-1 [解析] 依题意得A+1=3,所以A=2,所以函数y=2sin x+1的最小值为1-2=-1.3.增 减 [解析] 由余弦函数的单调性,得函数y=2cos x 在[-π,0]上是增函数,在[0,π]上是减函数.4.[π4+kπ,π2+kπ)(k ∈Z ) [解析] 由题意知tan x ≥1,所以π4+k π≤x<π2+k π(k ∈Z ).5.[2k π-π,2k π](k ∈Z ) [解析] 函数y=1-2cos x 的单调递减区间即函数y=-cos x 的单调递减区间,即函数y=cos x 的单调递增区间,即为[2k π-π,2k π](k ∈Z ).6.(-1,1) [解析] ∵x ≠π2+k π(k ∈Z ),y=cos x tan x=sin x ,∴y=sin x ∈(-1,1),即函数y=cos x tan x 的值域是(-1,1).7.1 [解析] 设t=cos x ,则-1≤t ≤1,所以y=-t 2+3t-1=-t-322+54,当t=1时,函数取得最大值1.8.(kπ2-π4,0)(k ∈Z ) [解析] 由x+π4=kπ2(k ∈Z ),得x=kπ2-π4(k ∈Z ),所以函数y=tan (x +π4)图像的对称中心为(kπ2-π4,0)(k ∈Z ). 【课堂考点探究】例1 [思路点拨] 根据偶次根式和对数函数的性质以及正切函数、正弦函数、余弦函数的性质列出关于x 的不等式组求解. (1)x 0<x ≤4且x ≠π6且x ≠7π6(2)x2k π≤x<2k π+2π3,k ∈Z[解析] (1)依题意得{2−log 2x ≥0,x +π3≠kπ+π2,k ∈Z,得0<x ≤4且x ≠k π+π6,k ∈Z ,所以函数f (x )的定义域是x 0<x ≤4且x ≠π6且x ≠7π6.(2)由题意得{2cosx +1>0,sinx ≥0,即{cosx >−12,sinx ≥0,解得{2kπ-2π3<x <2kπ+2π3,k ∈Z,2kπ≤x ≤2kπ+π,k ∈Z,所以2k π≤x<2k π+2π3,k ∈Z ,所以函数的定义域为x 2k π≤x<2k π+2π3,k ∈Z . 变式题 (1)x 2k π+π4≤x ≤2k π+5π4,k ∈Z (2)x 2k π-π3<x<2k π+4π3,k ∈Z[解析] (1)由题意知sin x-cos x ≥0.作出函数y=sin x 和y=cos x 的图像,如图所示.在[0,2π]内,满足sin x=cos x 的x 的值为π4,5π4,再结合正弦、余弦函数的周期是2π,得原函数的定义域为x 2k π+π4≤x ≤2k π+5π4,k ∈Z .(2)依题意知,√3+2sin x>0,即sin x>-√32,结合函数y=sin x 的图像(图略),可得函数f (x )的定义域为x 2k π-π3<x<2k π+4π3,k ∈Z .例2[思路点拨](1)将函数转化为以sin x为自变量的二次函数求最值;(2)将函数化为f(x)=A sin(ωx+φ)+k的形式,再利用函数的单调性求最值.(1)4916(2)1[解析](1)由题知,y=2cos 2x-sin x+1=2-4sin2x-sin x+1=-4(sinx+18)2+4916,当sin x=-18时,函数取得最大值,最大值为4916.(2)由题可知,f(x)=2cos x(sinxcosπ3+cosxsinπ3)-√3sin2x+sin x cos x=2sin x cos x+√3cos2x-√3sin2x=sin 2x+√3cos2x=2sin(2x+π3).因为x∈[-π4,π6],所以2x+π3∈[-π6,2π3],所以当2x+π3=π2,即x=π12时,函数取得最大值,即为2sinπ2=2;当2x+π3=-π6,即x=-π4时,函数取得最小值,即为2sin(-π6)=-1.所以最大值与最小值之和为2-1=1.变式题(1)B(2)[-2-√2,178][解析](1)∵f(x)=sin(x-π4)-cos(x-π4)=√2sin x-π4-π4=√2sin x-π2=-√2cos x,∴当x=(2k+1)π(k∈Z)时,f(x)取得最大值√2.(2)令t=cos x-sin x,则t=√2cos(x+π4)∈[-√2,√2],又t2=1-2sin x cos x,所以sin x cos x=1−t22,所以y=t+4·1−t 22=-2t2+t+2=-2(t-14)2+178.因为t∈[-√2,√2],所以当t=14时,y取得最大值178;当t=-√2时,y取得最小值-2-√2.所以函数的值域是[-2-√2,178].例3[思路点拨](1)根据三角函数的周期性,求出各个函数的最小正周期,从而得出结论;(2)首先求出参数a,再求最小正周期.(1)A(2)π[解析](1)对于①,y=cos|2x|=cos 2x,则它的最小正周期为2π2=π;对于②,y=|cos x|的最小正周期为12×2π1=π;对于③,y=cos(2x+π6)的最小正周期为2π2=π;对于④,y=tan(2x-π4)的最小正周期为π2.故选A.(2)∵函数f(x)=1+a sin(ax+π6)(a>0)的最大值为1+a,∴1+a=3,∴a=2,因此f(x)的最小正周期为2πa=π.例4[思路点拨](1)函数f(x)的图像的对称轴为直线x=1,逐一验证各选项,可得符合条件的函数;(2)由周期求出ω=2,再由图像关于直线x=π3对称,求得φ=-π6,进而可求得f(x)的图像的对称中心.(1)D(2)B[解析](1)易知f(x)=12x2-x的图像关于直线x=1对称.对于选项A,函数g(x)的图像的对称轴为直线x=12+kπ2(k∈Z);对于选项B,函数g(x)的图像的对称轴为直线x=12+k(k∈Z);对于选项C,函数g(x)的图像不存在对称轴;对于选项D,函数g(x)的图像的对称轴为直线x=k(k∈Z),当k=1时,其中有一条对称轴为直线x=1,符合题意.故选D.(2)由题意可得2πω=π,∴ω=2,∴f (x )=A sin (2x+φ).∵函数f (x )的图像关于直线x=π3对称,∴f (π3)=A sin (2π3+φ)=±A ,即sin (2π3+φ)=±1.∵|φ|<π2,∴φ=-π6,故函数f (x )=A sin (2x -π6).令2x-π6=k π,k ∈Z ,可得x=kπ2+π12,k ∈Z ,故函数f (x )的图像的对称中心为kπ2+π12,0,k ∈Z .结合选项可知,函数f (x )的图像的一个对称中心是(π12,0).故选B .例5 [思路点拨] (1)由条件求出φ,根据正弦函数的单调性求解;(2)先求出函数f (x )的单调递增区间,由(π3,π2)是所求单调递增区间的子集得出ω的取值范围.(1)C (2)C [解析] (1)∵π3为函数f (x )=sin (2x+φ)0<φ<π2的一个零点,∴f (π3)=sin (2π3+φ)=0,∴2π3+φ=k π(k ∈Z ),解得φ=k π-2π3(k ∈Z ). ∵0<φ<π2,∴φ=π3,∴f (x )=sin (2x +π3),令-π2+2k π≤2x+π3≤π2+2k π(k ∈Z ),则k π-5π12≤x ≤k π+π12(k ∈Z ), 故选C .(2)令2k π-π≤ωx+π3≤2k π,k ∈Z ,∵ω>0,∴2kπω-4π3ω≤x ≤2kπω-π3ω,k ∈Z , ∴函数f (x )=cos (ωx +π3)的单调递增区间为[2kπω-4π3ω,2kπω-π3ω],k ∈Z . ∵f (x )在(π3,π2)上单调递增,∴{π2≤2kπω-π3ω,π3≥2kπω-4π3ω,k ∈Z , 解得6k-4≤ω≤4k-23,k ∈Z .由题意知,π2-π3≤12×2πω,∴0<ω≤6,∴2≤ω≤103. 应用演练1.A [解析] ∵函数f (x )=cos (x+θ)(0<θ<π)在x=π3处取得最小值,∴cos (π3+θ)=-1,∴π3+θ=π+2k π,k ∈Z ,又∵0<θ<π,∴θ=2π3,即f (x )=cos (x +2π3).令-π+2k π≤x+2π3≤2k π,k ∈Z ,解得-5π3+2k π≤x ≤-2π3+2k π,k ∈Z ,又∵x ∈[0,π],∴k=1,∴f (x )在[0,π]上的单调递增区间是[π3,π],故选A .2.C [解析] 因为函数f (x )=cos x 是偶函数,所以c=f (ln 13)=f (ln 3).因为0<ln 2<ln 3<ln π<π,且函数f (x )在[0,π]上单调递减,所以f (ln 2)>f (ln 3)>f (ln π),即a>c>b.故选C .3.C [解析] 由题可知,函数的最小正周期T=2×2=4,所以ω=2π4=π2.令π2x+π6=k π+π2,k ∈Z ,解得x=2k+23,k ∈Z ,结合选项可知,x=23满足条件.故选C .4.π [解析] 易知T=2π2=π第20讲 函数y=A sin (ωx+φ)的图像及三角函数模型的简单应用【课前双基巩固】 知识聚焦 1.2πωω2πωx+φ φ2.-φω π2-φω π-φω3π2-φω2π-φωπ2π3π22π3.|φ| |φω| 对点演练1.y=2sin x [解析] 根据函数图像变换法则可得.2.y=sin (x +3π4) [解析] 函数y=sin (x +π4)的图像向左平移π2个单位长度后得到y=sin (x +π2+π4)=sin (x +3π4)的图像,即原函数的解析式为y=sin x+3π4.3.π [-π4+kπ,π4+kπ](k ∈Z ) [解析] y=cos (2x -π2)=sin 2x ,所以函数的周期T=2π2=π.由-π2+2k π≤2x ≤π2+2k π(k ∈Z ),得-π4+k π≤x ≤π4+k π(k ∈Z ),故函数的单调递增区间为[-π4+kπ,π4+kπ](k ∈Z ).4.π6[解析] 将点(0,1)代入函数解析式,可得2sin φ=1,即sin φ=12.∵|φ|<π2,∴φ=π6.5.左 5π12[解析] y=cos (2x +π3)=sinπ2+(2x +π3)=sin (2x +5π6). 故要得到y=sin (2x +5π6)=sin 2(x +5π12)的图像,只需将函数y=sin 2x 的图像向左平移5π12个单位长度.6.(0,1] [解析] 因为函数f (x )=12sin ωx 在区间[-π2,π2]上单调递增,所以T 2=πω≥π2+π2=π,所以ω≤1,又因为ω>0,所以ω∈(0,1]. 7.-5或-1 [解析] 由f (π8+t)=f (π8-t)得,函数f (x )的图像的对称轴为直线x=π8.故当x=π8时,函数取得最大值或最小值,于是有-2+m=-3或2+m=-3,即m=-1或m=-5.8.-π6[解析] 由图像可知,T=4×7π12-π3=π,所以ω=2ππ=2.因为f (π3)=sin2π3+φ=1,所以2π3+φ=π2+2k π(k ∈Z ),即φ=-π6+2k π(k ∈Z ),又|φ|<π2,所以φ=-π6. 【课堂考点探究】例1 [思路点拨] 根据图像平移“左加右减”的规则以及平移量确定结果.(1)A (2)A [解析] (1)由题意知,将f (x )=sin (2x +π4)的图像向左平移π8个单位长度后,得到y=sin [2(x +π8)+π4]=sin (2x +π2)=cos 2x 的图像,故选A .(2)把y=sin (2x +π2)图像上所有点的横坐标变为原来的4倍,得到函数y=sin (x 2+π2)的图像,再把所得图像沿x 轴向右平移π3个单位长度,可以得到y=sin [12(x -π3)+π2]=sin (12x +π3)的图像.故选A .变式题 (1)C (2)A [解析] (1)将函数y=sin (x -π6)的图像向右平移π4个单位长度,得到y=sin (x -5π12)的图像,再把所得图像上各点的横坐标扩大到原来的2倍(纵坐标不变),得到y=sin (x 2-5π12)的图像,故选C .(2)由题意知,y=cos 3x=sin (3x +π2)=sin 3(x +π6),将函数y=sin 3(x +π6)的图像向右平移π6个单位长度,得到y=sin 3(x +π6-π6)=sin 3x 的图像,故选A .例2 [思路点拨] (1)先根据图像确定A ,T ,ω,θ,再根据平移得函数g (x )的解析式;(2)结合函数的图像首先确定ω的值,然后确定φ的值即可.(1)D (2)9π10[解析] (1)由题图得,A=2,T=7π8-(-π8)=π,∴ω=2πT=2.∵当x=3π8-π82=π8时,y=2,∴2×π8+θ=π2+2k π(k ∈Z ),∴θ=π4+2k π(k ∈Z ),又∵|θ|<π,∴θ=π4,∴f (x )=2sin (2x +π4),∴g (x )=2sin [2(x -π4)+π4]=2sin (2x -π4),故选D . (2)由题意可知,函数的最小正周期T=2×(2π-34π)=52π, 则ω=2πT =2π52π=45.当x=2π时,ωx+φ=45×2π+φ=2k π+π2(k ∈Z ), 则φ=2k π-1110π(k ∈Z ),由于-π≤φ<π,故φ=9π10.变式题 -5π6[解析] 根据函数f (x )=2sin (ωx+φ)(ω>0,|φ|<π)的图像,且Aπ2,1,B (π,-1),可得从点A 到点B 正好经过了半个周期,即12×2πω=π-π2,∴ω=2.再把点A ,B 的坐标代入函数解析式,可得2sin 2×π2+φ=-2sin φ=1,2sin (2×π+φ )=2sinφ=-1,∴sin φ=-12,∴φ=2k π-π6或φ=2k π-5π6,k ∈Z .再结合“五点作图法”,可得φ=-5π6.例3 [思路点拨] (1)根据已知求得ω的值,然后求出φ的值,从而可求出f (x )的解析式,进而得到g (x )的解析式;(2)确定g (x )的单调性,然后求出最值. 解:(1)由题意可知,T 2=11π12-5π12=π2,∴ω=2,又sin (2×5π12+φ)=1,|φ|<π2,∴φ=-π3, ∴f (x )=sin (2x -π3), ∴g (x )=sin (4x +π6). (2)由(1)可知,g (x )在[0,π12]上为增函数,在[π12,π4]上为减函数,∴g (x )max =g (π12)=1,又∵g (0)=12,g (π4)=-12,∴g (x )min =g (π4)=-12,故函数g (x )在[0,π4]上的最大值和最小值分别为1和-12.变式题 (1)A (2)B [解析] (1)由题意知,g (x )=cos 2(x -π3)+θ=cos 2x-2π3+θ,令2x-2π3+θ=k π(k ∈Z ),则函数g (x )的图像的对称轴为直线x=π3-θ2+kπ2(k ∈Z ),令π3-θ2+kπ2=π4(k ∈Z ),则θ=π6+k π(k ∈Z ),又|θ|<π2,所以θ=π6.故选A .(2)观察图像可得,函数的最小值为-2,所以A=2.由图像可知函数过点(0,√3),所以√3=2sin φ,又因为π2<φ<π,所以φ=2π3.由图像可知,5π4·ω+2π3=3π2+2k π,k ∈Z ,解得ω=23+85k ,k ∈Z ,又T 2=πω>5π4,所以0<ω<45,所以ω=23,则f (x )=2sin (23x +2π3).显然A 选项错误;对于B ,f (x-π)=2sin23(x-π)+2π3=2sin 23x ,是奇函数,故B 选项正确;对于C ,观察图像可知,f (x )在[-π,π2]上不单调,故C 选项错误;对于D ,f (3π4)=2sin 23×3π4+2π3=2sin 7π6≠0,故D 选项错误.故选B .例4 [思路点拨] (1)注意到BA 1=AA 1,AH 1=H 1H ,从而知△AA 1H 1的周长为4,设AH 1=x ,从而可求得S △AA 1H 1;(2)令t=sin α+cos α,用t 表示S △AA 1H 1,根据t ∈(1,√2]可求得最大值. 解:(1)设AH 1=x ,由题意知,x+x sinα+x tanα=4, ∴x=4sinαsinα+cosα+1,∴S △AA 1H 1=12·x 2tanα=8sinαcosα(sinα+cosα+1)2,α∈(0,π2).(2)令t=sin α+cos α,∵α∈(0,π2),∴t ∈(1,√2].当八角形所覆盖的面积最大时,S △AA 1H 1取得最大值.由(1)可知,S △AA 1H 1=4(t 2-1)(t+1)2=4-8t+1,∴当t=√2,即α=π4时,S △AA 1H 1取得最大值,此时八角形所覆盖的面积最大,设为S ,则S=16+4×(4√2+1=64-32√2,∴八角形所覆盖面积的最大值为64-32√2.变式题 20.5 [解析] 因为当x=6时,y=a+A=28,当x=12时,y=a-A=18,所以a=23,A=5, 所以y=23+5cos π6(x-6),所以当x=10时,y=23+5cos (π6×4)=23-5×12=20.5.第21讲 两角和与差的正弦、余弦和正切考试说明 1.会用向量的数量积推导出两角差的余弦公式. 2.能利用两角差的余弦公式导出两角差的正弦、正切公式.3.会用两角差的余弦公式导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式,了解它们的内在联系.【课前双基巩固】 知识聚焦(1)sin αcos β±cos αsin β (2)cos αcos β∓sin αsin β (3)tanα±tanβ1∓tanαtanβ对点演练 1.√6+√24[解析] sin 75°=sin (45°+30°)=sin 45°cos 30°+cos 45°sin 30°=√22×√32+√22×12=√6+√24. 2.4−3√310[解析] ∵cos α=-35,α∈(π2,π),∴sin α=45,∴sin (α+π3)=sin αcos π3+cos αsin π3=45×12+(-35)×√32=4−3√310.3.-1 [解析] 原式=cos 65°cos 115°-sin 65°sin 115°=cos (65°+115°)=cos 180°=-1.4.7 [解析] tan (α-β)=tanα-tanβ1+tanαtanβ=7.5.-45 [解析] 因为tan5π4+α=tanπ4+α=17,所以1+tanα1−tanα=17,所以tan α=-34,又α∈π2,π,所以cos α=-4√3+(−4)=-45.6.sin (x -π3) [解析] 12sin x-√32cos x=cos π3sin x-sin π3cos x=sin (x -π3).7.√33[解析]1−tan15°1+tan15°=tan45°−tan15°1+tan45°tan15°=tan (45°-15°)=tan 30°=√33.8.2 [解析] 因为α+β=3π4,所以tan (α+β)=-1,即tanα+tanβ1−tanαtanβ=-1,整理得(1-tan α)(1-tan β)=2,所以[1+tan (π-α)](1-tanβ)=(1-tan α)(1-tan β)=2. 【课堂考点探究】例1 [思路点拨] (1)利用两角和与差的正弦公式展开已知条件,进而求解;(2)先利用已知条件求出tan α,再根据两角和的正切公式求解.(1)B (2)-√33[解析] (1)由sin (2α-β)=16,sin (2α+β)=12,可得sin 2αcos β-cos 2αsin β=16①, sin 2αcos β+cos 2αsin β=12②,由①+②得2sin 2αcos β=23,所以sin 2αcos β=13.故选B . (2)∵cos (α+π6)=√32cos α-12sin α=√3cos α,∴-sin α=√3cos α,故tan α=-√3,∴tan (α+β)=tanα+tanβ1−tanαtanβ=√3+√331+√3×√33=-2√332=-√33.变式题 (1)D (2)D[解析] (1)∵cos α=17,α∈(0,π2),∴sin α=√1−cos 2α=√1−(17)2=4√37, ∴cos (α-π3)=cos αcos π3+sin αsin π3=17×12+4√37×√32=1314.故选D .(2)由题意知,tan (α-π6)=tan [(α+π6)-π3]=tan (α+π6)-tan π31+tan (α+π6)tan π3=√31+√3=-2+√3.故选D .例2 [思路点拨] (1)首先利用两角差的余弦公式展开cos (x -π3),整理后再逆用两角差的余弦公式即可;(2)将两个条件等式分别平方相加即可.(1)B (2)-5972 [解析] (1)由题可知,cos x+cos (x -π3)=cos x+cos x cos π3+sin x sin π3=32cos x+√32sin x=√3(√32cosx +12sinx)=√3cos (x -π6)=√3×√33=1.故选B .(2)∵sin α+cos β=13,sin β-cos α=12,∴(sin α+cos β)2=19,(sin β-cos α)2=14,即sin 2α+2sin αcosβ+cos 2β=19①,sin 2β-2sin βcos α+cos 2α=14②,由①+②得sin 2α+2sin αcos β+cos 2β+sin 2β-2sin βcos α+cos 2α=(sin 2α+cos 2α)+(cos 2β+sin 2β)+2(sin αcos β-sinβcos α)=1+1+2sin (α-β)=2+2sin (α-β)=1336,则sin (α-β)=-5972.变式题 (1)A (2)4 [解析] (1)√22cos 375°+√22sin 375°=√22cos 15°+√22sin 15°=cos (45°-15°)=cos 30°=√32.故选A .(2)(1+tan 20°)(1+tan 25°)=1+tan 20°+tan 25°+tan 20°tan 25°=1+tan (20°+25°)(1-tan 20°tan 25°)+tan 20°tan 25°=2,同理可得(1+tan 21°)(1+tan 24°)=2,所以原式=4.例3 [思路点拨] (1)对条件整理可得cos (α+π3)=45,又α+π12=(α+π3)-π4,利用两角差的正弦公式求解;(2)根据角的变换得β=α+(β-α),利用已知条件先求出sin β的值,再求角β. (1)B (2)C [解析] (1)由cos (α+π6)-sin α=4√35, 得cos αcos π6-sin αsin π6-sin α=4√35,即√32cos α-32sin α=4√35, ∴12cos α-√32sin α=45,即cos (α+π3)=45. ∵α∈(-π3,0),∴α+π3∈(0,π3), ∴sin (α+π3)=√1−cos 2(α+π3)=35,∴sin (α+π12)=sin [(α+π3)-π4]=√22sin (α+π3)-√22cos (α+π3)=√22×(35-45)=-√210,故选B . (2)因为sin α=2√55,sin (β-α)=-√1010,且α,β均为锐角,所以cos α=√55,cos (β-α)=3√1010,所以sin β=sin [α+(β-α)]=sinαcos (β-α)+cos αsin (β-α)=2√55×3√1010+√55×(-√1010)=25√250=√22,所以β=π4.故选C .变式题 (1)A (2)B [解析] (1)由题可知,0<π4+α<π2,π4<π4-β2<π2,所以sin (π4+α)=2√23,sin (π4-β2)=√63, 所以cos (α+β2)=cos (π4+α)-(π4-β2)=cos (π4+α)cos (π4-β2)+sin (π4+α)sin (π4-β2)=13×√33+2√23×√63=5√39.故选A .(2)因为π2<β<α<3π4,所以0<α-β<π4,π<α+β<3π2,由cos (α-β)=1213,得sin (α-β)=513,由sin (α+β)=-35,得cos (α+β)=-45,则sin 2α=sin [(α-β)+(α+β)]=sin (α-β)cos (α+β)+cos (α-β)sin (α+β)=513×(-45)+1213×(-35)=-5665,故选B .【备选理由】 例1考查两角差的正切公式、基本不等式、正切函数的单调性,考查综合分析与运算的能力;例2主要考查三角函数中的恒等变换的应用,熟练运用相关公式和特殊角的关系是解题的关键;例3考查两角和与差的正弦公式的运用,关键是角的配凑,然后化简求值.例1 [配合例1使用] [2018·南充模拟] 若tan α=3tan β(0<β<α<π2),则α-β的最大值为 .[答案] π6[解析] ∵tan α=3tan β(0<β<α<π2),∴tan β>0,∴tan (α-β)=tanα-tanβ1+tanαtanβ=2tanβ1+3tan 2β=21tanβ+3tanβ. ∵tan β>0,∴1tanβ+3tan β≥2√1tanβ·3tanβ=2√3,∴tan (α-β)≤√33,当且仅当3tan 2β=1,即tan β=√33时取等号,此时β=π6,tan α=3tan β,即tan α=√3,α=π3. 又0<β<α<π2,∴0<α-β<π2,∴0<tan (α-β)≤√33,又y=tan x 在(0,π2)上单调递增,∴当tan (α-β)取得最大值时,α-β的值最大,∴当α=π3,β=π6时,α-β的值最大,∴α-β的最大值为π3-π6=π6.例2 [配合例3使用] [2018·安徽皖江八校联考]2cos55°−√3sin5°cos5°的值为 .[答案] 1 [解析]2cos55°−√3sin5°cos5°=2cos(60°−5°)−√3sin5°cos5°=cos5°+√3sin5°−√3sin5°cos5°=1.例3 [配合例3使用] [2018·安阳模拟] 已知m=tan(α+β+γ)tan(α-β+γ),若sin 2(α+γ)=3sin 2β,则m=( )A .12B .34C .32 D .2[解析] D ∵sin 2(α+γ)=3sin 2β,∴sin [(α+β+γ)+(α+γ-β)]=3sin [(α+β+γ)-(α+γ-β)], ∴sin (α+β+γ)cos (α+γ-β)+cos (α+β+γ)sin (α+γ-β) =3sin (α+β+γ)cos (α+γ-β)-3cos (α+β+γ)sin (α+γ-β), ∴-2sin (α+β+γ)cos (α+γ-β)=-4cos (α+β+γ)sin (α+γ-β), 即sin(α+β+γ)cos(α+γ-β)cos(α+β+γ)sin(α+γ-β)=tan(α+β+γ)tan(α-β+γ)=2,∴m=2.故选D .第22讲 二倍角公式与简单的三角恒等变换考试说明 能运用两角和与差的正弦、余弦、正切公式以及二倍角的正弦、余弦、正切公式,进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).【课前双基巩固】 知识聚焦1.(1)2sin αcos α (2)cos 2α-sin 2α 2cos 2α-1 1-2sin 2α (3)2tanα1−tan 2α2.(1)2sin 2α22cos 2α2(2)sin α2±cosα22(3)1−cos2α2 1+cos2α21−cos2α1+cos2α (4)1−tan 2α21+tan 2α22tan α21−tan 2α2(5)√a 2+b 2sin (α+φ)对点演练1.-√2 [解析] sin 15°-√3cos 15°=212sin 15°-√32cos 15°=2(sin 30°sin 15°-cos 30°cos15°)=-2cos (30°+15°)=-2cos 45°=-√2. 2.π [解析] f (x )=sin 2x-12=-cos2x2,故f (x )的最小正周期T=2π2=π.3.-14[解析] 由cos (α+β)=13,cos (α-β)=15,得{cosαcosβ-sinαsinβ=13,cosαcosβ+sinαsinβ=15, 解得{cosαcosβ=415,sinαsinβ=−115, 所以tan αtan β=sinαsinβcosαcosβ=-14. 4.-2425 [解析] ∵sin θ=35,θ为第二象限角,∴cos θ=-45,∴sin 2θ=2sin θcos θ=2×35×(-45)=-2425. 5.79 [解析] 由题意知,cos (π3-2α)=1-2sin 2(π6-α)=1-29=79.6.3π4[解析] tan (α+β)=tanα+tanβ1−tanαtanβ=7+431−7×43=-1,又0<α+β<π,所以α+β=3π4.7.2k π-π4,k ∈Z [解析] sin α-cos α=√2√22sin α-√22cos α,则cos φ=√22,sin φ=-√22,所以φ=2k π-π4,k ∈Z .8.-12[解析] 因为2α∈0,π2,所以α∈0,π4,所以sin α-cos α<0,所以sin α-cosα=-√(sinα-cosα)2=-√1−2sinαcosα=-√1−34=-12. 【课堂考点探究】例1 [思路点拨] (1)先根据余弦的二倍角公式降幂,再根据两角和与差的余弦公式化简得结果;(2)先化切为弦,再通分,然后利用两角差的余弦公式求解. (1)B (2)C [解析] (1)cos 2(x -π12)+sin 2(x+π12)=1+cos (2x -π6)2+1−cos (2x+π6)2=1+12cos 2x cos π6+sin 2x sinπ6-cos 2x cos π6-sin2x sinπ6=1+sin 2x sin π6=1+12sin 2x ,故选B .(2)tan α+1tan (π4+α2)=sinαcosα+cos (π4+α2)sin (π4+α2)=sinαsin (π4+α2)+cosαcos (π4+α2)cosαsin (π4+α2)=cos (π4+α2-α)cosαsin (π4+α2)=cos (π4-α2)cosαsin (π4+α2)=sin (π4+α2)cosαsin (π4+α2)=1cosα.故选C .变式题 D [解析]√1+sin6+√1−sin6=√(√1+sin6+√1−sin6)2=√1+sin6+1−sin6+2√(1+sin6)(1-sin6)=√2+2cos6=√2+2(2cos 23−1)=√4cos 23=-2cos 3.例2 [思路点拨] (1)根据两角差的正弦公式进行化简,求得sin β的值,再根据二倍角公式,即可得到答案;(2)由已知条件求得sin θcos θ的值,再由二倍角的正、余弦公式及诱导公式求值.(1)A (2)B [解析] (1)由题意得sin (α-β)cos α-cos (α-β)sin α=sin (-β)=-sin β=35, 所以sin β=-35,所以cos 2β=1-2sin 2β=725,故选A . (2)由tan θ+1tanθ=4, 得sinθcosθ+cosθsinθ=4,即sin 2θ+cos 2θsinθcosθ=4, ∴sin θcos θ=14, ∴cos 2(θ+π4)=1+cos (2θ+π2)2=1−sin2θ2=1−2sinθcosθ2=1−2×142=14. 变式题 (1)A (2)B [解析] (1)∵α∈(3π2,2π),sin (π2+α)=cos α=13,∴sin α=-2√23,tan α=-2√2, ∴tan (π+2α)=tan 2α=2tanα1−tan 2α=-4√2-7=4√27. (2)cos (2π3+2α)=cos [π-(π3-2α)]=-cos (π3-2α)=-cos 2(π6-α)=-1-2sin 2(π6-α)=-(1−2×19)=-79.例3 [思路点拨] 首先利用同角三角函数关系式,将切化弦,之后利用诱导公式化简,借助于两角差的正弦公式及辅助角公式求得结果. C[解析] 2cos10°sin70°-tan 20°=2cos10°sin70°-sin20°cos20°=2cos10°−sin(30°−10°)sin70°=32cos10°+√32sin10°sin70°=√3sin(10°+60°)sin70°=√3,故选C .变式题 C [解析] 原式=sin70°cos70°·cos 10°(√3·sin20°cos20°-1)=cos20°cos10°sin20°·(√3sin20°−cos20°cos20°)=cos10°sin20°×2sin (20°-30°)=-sin20°sin20°=-1. 例4 [思路点拨] 转化为求cos (α+β)的值,再求角α+β的值. A [解析] ∵α∈[π4,π],∴2α∈[π2,2π], 又0<sin 2α=√55<12,∴2α∈(5π6,π),即α∈(5π12,π2),∴cos 2α=-√1−sin 22α=-2√55.∵β∈[π,3π2],∴β-α∈(π2,13π12), 又sin (β-α)=√1010,∴β-α∈(π2,π),∴cos (β-α)=-√1−sin 2(β-α)=-3√1010, ∴cos (α+β)=cos [2α+(β-α)]=cos 2αcos (β-α)-sin 2αsin (β-α)=-2√55×(-3√1010)-√55×√1010=√22. 又α∈(5π12,π2),β∈[π,3π2],∴α+β∈(17π12,2π),∴α+β=7π4,故选A .变式题-3π4[解析] ∵α∈(0,π),tan α=tan [(α-β)+β]=tan(α-β)+tanβ1−tan(α-β)tanβ=12-171+12×17=13>0,∴0<α<π2. 又∵tan 2α=2tanα1−tan 2α=2×131−(13)2=34>0,∴0<2α<π2,∴tan (2α-β)=tan2α-tanβ1+tan2αtanβ=34+171−34×17=1.∵β∈(0,π),tan β=-17<0,∴π2<β<π,∴-π<2α-β<0, ∴2α-β=-3π4.例5 [思路点拨] (1)利用两角差的正弦公式和倍角公式对函数解析式化简整理,利用函数的最大值求得a ,进而根据正弦函数的单调性得到f (x )的单调递减区间;(2)由题意易得sin (α-π6)=35,进而得到cos (α-π6)=45,利用配角法可得cos α=cos α-π6+π6,从而得到结果.解:(1)由题意知,f (x )=4cos x ·sin (x -π6)+a=4cos x ·(√32sinx -12cosx)+a=2√3sin x cos x-2cos 2x+a=√3sin 2x-cos2x-1+a=2sin (2x -π6)-1+a.当sin (2x -π6)=1时,f (x )取得最大值,此时f (x )=2-1+a=3,∴a=2. 由π2+2k π≤2x-π6≤3π2+2k π,k ∈Z ,得π3+k π≤x ≤5π6+k π,k ∈Z ,∴f (x )的单调递减区间为π3+k π,5π6+k π,k ∈Z .(2)由(1)可知,f (x )=2sin (2x -π6)+1,∵f (α2)=115,∴sin (α-π6)=35, 又α∈(0,π2),∴α-π6∈(-π6,π3),∴cos (α-π6)=45,∴cos α=cos [(α-π6)+π6]=√32cos (α-π6)-12sin (α-π6)=4√3-310. 变式题 解:(1)依题意得f (x )=sin x+√3cos x+1=2sin (x +π3)+1. 因为-2≤2sin (x +π3)≤2,所以-1≤2sin (x +π3)+1≤3, 即函数f (x )的值域是[-1,3].令-π2+2k π≤x+π3≤2k π+π2,k ∈Z ,解得-5π6+2k π≤x ≤π6+2k π,k ∈Z ,所以函数f (x )的单调递增区间为[-5π6+2kπ,π6+2kπ],k ∈Z . (2)由f (α)=2sin (α+π3)+1=135,得sin (α+π3)=45. 因为π6<α<2π3,所以π2<α+π3<π,所以cos (α+π3)=-35, 所以sin (2α+2π3)=sin 2(α+π3)=2sin (α+π3)cos (α+π3)=-2×45×35=-2425.【备选理由】 例1考查三角函数式的化简;例2是给值求值问题;例3是给角求值问题的补充,给出的是非特殊角;例4是给值求角问题,选择相应的三角函数求值是解题的关键.例1 [配合例1使用] 化简:sin (α+β)cos α-12[sin (2α+β)-sin β]= .[答案] sin β[解析] 原式=sin (α+β)cos α-12[sin (α+β+α)-sin β]=sin (α+β)cos α-12[sin (α+β)cos α+cos (α+β)sin α-sin β] =12[sin (α+β)cos α-cos (α+β)sin α]+12sin β =12sin β+12sin β=sin β.例2 [配合例2使用] [2018·资阳三诊] 已知角α的顶点与原点O 重合,始边与x 轴的正半轴重合,若它的终边经过点P (2,1),则tan (2α+π4)= ( )A .-7B .-17C .17D .7[解析] A 由角α的顶点与原点O 重合,始边与x 轴的正半轴重合,且它的终边经过点P (2,1),可得tan α=12,∴tan2α=2tanα1−tan 2α=11−14=43,∴tan (2α+π4)=tan2α+tan π41−tan2αtan π4=43+11−43×1=-7.故选A .例3 [配合例3使用] 若a=√2(cos 216°-sin 216°),b=sin 15°+cos 15°,c=√1+cos56°,则a ,b ,c 的大小关系为( )A .c<b<aB .b<c<aC .a<b<cD .b<a<c[解析] C a=√2(cos 216°-sin 216°)=√2cos 32°,b=sin 15°+cos 15°=√2cos 30°, c=√1+cos56°=√2cos 228°=√2cos 28°, 又∵y=cos x 在(0°,90°)上单调递减,∴cos 28°>cos 30°>cos 32°, ∴c>b>a.故选C .例4 [配合例4使用] 已知α,β均为锐角,且sin α=√55,cos β=√1010,则α-β的值为 .[答案] -π4[解析] ∵α,β均为锐角,sin α=√55,cos β=√1010,∴cos α=√1−sin 2α=2√55,sin β=√1−cos 2β=3√1010, ∴sin (α-β)=sin αcos β-cos αsin β=√55×√1010-2√55×3√1010=-√22.又∵-π2<α-β<π2,∴α-β=-π4.第23讲 正弦定理和余弦定理考试说明 1.通过对任意三角形边长和角度的探索,掌握正弦定理、余弦定理. 2.能利用正弦定理和余弦定理解决一些简单的三角形度量问题.【课前双基巩固】 知识聚焦 1.b sinBc sinCb 2+c 2-2bc cos A c 2+a 2-2ac cos B a 2+b 2-2ab cos C 2R sin B 2R sin C sin A∶sin B∶sin Cb 2+c 2-a 22bc a 2+c 2-b22caa 2+b 2-c 22ab2.一解 两解 一解 一解 对点演练 1.2√63[解析] 易知A=75°,角B 最小,所以边b 最短.由正弦定理b sinB =c sinC ,得b sin45°=2sin60°,解得b=2√63. 2.√7 [解析] 由余弦定理得c 2=a 2+b 2-2ab cos C=52+(2√3)2-2×5×2√3cos 30°=7,所以c=√7. 3.60° [解析] 因为cos C=a 2+b 2-c 22ab=12,所以C=60°.4.4√3 [解析] 因为sin C=√1−cos 2C =2√23,所以△ABC 的面积S=12ab sin C=4√3.5.A=B A>B [解析] 根据正弦定理知,在△ABC 中有sin A=sin B ⇔a=b ⇔A=B ,sin A>sin B ⇔a>b ⇔A>B.6.45° [解析] 由正弦定理知a sinA =bsinB,则sin B=bsinA a=√2×√324√3=√22.又a>b ,所以A>B ,所以B 为锐角,故B=45°.7.√73√32[解析] 易知c=√4+9−2×2×3×12=√7,△ABC 的面积等于12×2×3×√32=3√32.8.直角 [解析] ∵c cos A=b ,∴由正弦定理得sin C cos A=sin B=sin (A+C )=sin A cos C+cos A sin C , 整理得sin A cos C=0,∵sin A ≠0,∴cos C=0,即C=90°,则△ABC 为直角三角形. 【课堂考点探究】例1 [思路点拨] (1)由余弦定理可得出;(2)用正弦定理将b sin C 表示为关于C 的三角函数,再结合C 的取值范围求最大值. 解:(1)由a=√3,b 2+c 2=3+bc ,得b 2+c 2-a 22bc=3+bc -a 22bc =12, 即cos A=12,又∵A ∈(0,π),∴A=π3. (2)由正弦定理,得b=asinAsin B=2sin B , ∴b sin C=2sin C sin B=2sin C sin (2π3-C)=2sin C (12sinC +√32cosC)=sin 2C+√3sin C cos C=√32sin 2C-12cos2C+12=sin (2C -π6)+12.∵0<C<2π3,∴-π6<2C-π6<7π6,∴当sin (2C -π6)=1,即C=π3时,b sin C 取得最大值32. 变式题 (1)B (2)√10 [解析] (1)由1+tanA tanB =2cb得1+sinAcosB cosAsinB =2sinCsinB,整理得sin B cos A+sin A cos B=2sin C cos A ,所以sin (A+B )=sin C=2sin C cos A ,所以cos A=12. 又因为A ∈(0,π),所以sin A=√32.由正弦定理a sinA =csinC,得sin C=csinA a=√22,所以C=π4.故选B .(2)由正弦定理可得sinA sinB =BCAC,因为A+B+C=π,所以cos (A+B )=-cos C , 则由已知条件可知BC AC =-12cosC =√22,又BC ·AC=2√2,可得BC=√2,AC=2,由余弦定理得AB=√BC 2+AC 2-2·BC ·AC ·cosC =2)√10.例2 [思路点拨] 由b 2+c 2=a 2+bc 及余弦定理可得A=π3,由sin B ·sin C=sin 2A 及正弦定理可得bc=a 2,结合b 2+c 2=a 2+bc 可得b=c. C [解析] 在△ABC 中,∵b 2+c 2=a 2+bc ,∴cos A=b 2+c 2-a 22bc=bc 2bc =12. 又∵A ∈(0,π),∴A=π3.∵sin B ·sin C=sin 2A ,∴bc=a 2.又由b 2+c 2=a 2+bc ,得(b-c )2=a 2-bc=0,∴b=c , ∴△ABC 的形状是等边三角形.故选C . 变式题 D [解析] 由条件可得sinA a 2cosA=sinBb 2cosB,由正弦定理可得aa 2cosA=bb 2cosB,整理可得a cos A=b cos B ,所以sin A cos A=sin B cos B ,即sin 2A=sin 2B ,所以2A=2B 或2A=π-2B , 所以A=B 或A+B=π2,所以△ABC 是等腰三角形或直角三角形.例3 [思路点拨] (1)利用已知条件,结合正弦定理以及余弦定理即可求出角A 的大小;(2)利用正弦定理以及三角形的面积公式求解a.解:(1)由b sin B+(c-b )sin C=a sin A 及正弦定理得b 2+(c-b )c=a 2,即b 2+c 2-bc=a 2,由余弦定理得cos A=b 2+c 2-a 22bc=12,又∵A ∈(0,π),∴A=π3. (2)由正弦定理a sinA =b sinB =c sinC,可得b=asinB sinA ,c=asinCsinA ,∴S △ABC =12bc sin A=12·asinBsinA ·asinCsinA ·sin A=a 2sinBsinC2sinA=2√3, 又sin B sin C=38,sin A=√32,∴√38a 2=2√3,∴a=4.变式题 解:(1)由a 2-bc=(b-c )2可得b 2+c 2-a 2=bc ,∴cos A=12,又∵A ∈(0°,180°),∴sin A=√32,∴S △ABC =12bc sin A=√34.(2)∵cos A=-cos (B+C )=12,∴sin B sin C-cos B cos C=12,又cos B cos C=14,∴sin B sin C=34. 由正弦定理得(a sinA )2=bc sinBsinC =43,∴a=1, ∴b 2+c 2-a 2=(b+c )2-2bc-1=(b+c )2-3.又∵b 2+c 2-a 2=1,∴b+c=2,∴△ABC 的周长为a+b+c=1+2=3.【备选理由】 例1考查了利用正弦、余弦定理解三角形;例2考查了利用二倍角公式、余弦定理以及勾股定理判断三角形的形状;例3考查了求三角形的面积的最大值;例4考查了与三角形面积有关的问题,涉及三角形的中线以及利用基本不等式求解边的最值等问题.例1 [配合例1使用] [2018·莆田六中月考] 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且c (sin C-sin A )=(sin A+sinB )(b-a ).(1)求角B 的大小;(2)若c=8,点M ,N 是线段BC 的两个三等分点,且BM=13BC ,ANBM=2√3,求AM 的值.解:(1)∵c (sin C-sin A )=(sin A+sin B )(b-a ),∴由正弦定理得c 2-ca=b 2-a 2,∴a 2+c 2-b 2=ca ,∴cos B=a 2+c 2-b 22ca=12,又0<B<π,∴B=π3.(2)设BM=x ,则BN=2x ,AN=2√3x ,又B=π3,AB=8,∴在△ABN 中,由余弦定理得12x 2=64+4x 2-2×8×2x cos π3,解得x=2(负值舍去),即BM=2,∴在△ABM 中,由余弦定理得AM=√AB 2+BM 2-2·AB ·BM ·cos π3=√82+22-2×8×2×12=√52=2√13.例2 [配合例2使用] 已知在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且cos 2A 2=12+b2c ,则△ABC 为 ( )A .正三角形B .直角三角形C .等腰直角三角形D .等腰三角形[解析] B ∵cos 2A2=12+b 2c,∴1+cosA 2=12+b2c ,即cos A=b c,∴b 2+c 2-a 22bc =b c ,则c 2=a 2+b 2,故△ABC 为直角三角形,故选B .例3 [配合例3使用] [2018·三明一中月考] 如图所示,在平面四边形ABCD 中,AB=1,CB=2,△ACD 为正三角形,则△BCD 的面积的最大值为 .[答案] 1+√3[解析] 在△ABC 中,设∠ABC=α,∠ACB=β,由余弦定理可知AC 2=12+22-2×1×2cos α=5-4cos α.∵△ACD 为正三角形,∴CD 2=5-4cos α, 由正弦定理得1sinβ=AC sinα, ∴AC·sin β=sin α,∴CD·sin β=sin α.∵(CD ·cos β)2=CD 2(1-sin 2β)=CD 2-sin 2α=5-4cos α-sin 2α=(2-cos α)2,β<∠BAC , ∴β为锐角,CD ·cos β=2-cos α,∴S △BCD =12×2·CD sin (π3+β)=CD sin (π3+β)=√32CD ·cos β+12CD ·sin β=√32×(2-cos α)+12sin α=√3+sin (α-π3), ∴当α=5π6时,△BCD 的面积最大,最大值为1+√3.例4 [配合例3使用] [2018·三明一中月考] 已知△ABC 的内角A ,B ,C 所对的边分别为a ,b , c ,且△ABC 的面积为12c (a sin A+b sinB-c sin C ). (1)求角C 的大小;(2)若D 为AB 的中点,且c=2,求CD 的最大值.解:(1)依题意得,12ab sin C=12c (a sin A+b sin B-c sin C ), 由正弦定理得,abc=c (a 2+b 2-c 2),即a 2+b 2-c 2=ab ,由余弦定理得,cos C=a 2+b 2-c 22ab=ab 2ab =12,又因为C ∈(0,π),所以C=π3. (2)在△ACD 中,AC 2=AD 2+CD 2-2AD ·CD cos ∠ADC ,即b 2=1+CD 2-2CD cos ∠ADC , 在△BCD 中, BC 2=BD 2+CD 2-2BD ·CD cos ∠BDC ,即a 2=1+CD 2-2CD cos ∠BDC.因为∠ADC+∠BDC=π,所以cos ∠ADC=-cos ∠BDC ,所以CD 2=12(a 2+b 2)-1. 由(1)及c=2得,a 2+b 2-4=ab ≤12(a 2+b 2),当且仅当a=b=2时,等号成立, 所以12(a 2+b 2)≤4,所以CD 2=12(a 2+b 2)-1≤3,即CD ≤√3, 所以CD 的最大值为√3.第24讲 正弦定理和余弦定理的应用考试说明 能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.【课前双基巩固】 知识聚焦1.水平视线 上方 下方2.正北方向3.水平角4.水平面 水平长度 对点演练。

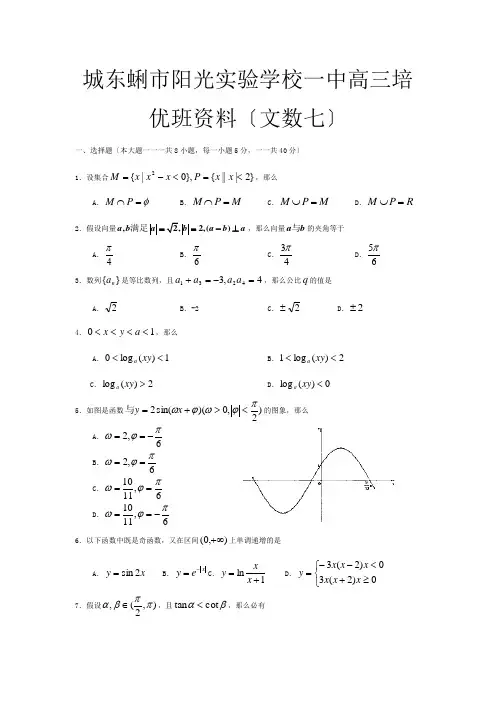
城东蜊市阳光实验学校一中高三培优班资料〔文数七〕一、选择题〔本大题一一一共8小题，每一小题5分，一一共40分〕 1．设集合}2|||{},0|{2<=<-=x x P x x x M，那么A ．φ=⋂P MB ．M P M=⋂C ．M P M =⋃D ．R P M =⋃2．假设向量,2,2,()满足a b a b a b a ==-⊥，那么向量与a b 的夹角等于A ．4πB ．6π C ．43π D ．65π 3．数列}{n a 是等比数列，且4,34231=-=+a a a a ，那么公比q 的值是A ．2B ．-2C ．2±D ．2±4．10<<<<a y x ，那么 A ．1)(log 0<<xy aB ．2)(log 1<<xy aC ．2)(log >xy aD ．0)(log <xy a5．如图是函数)2,0)(sin(2πϕωϕω<>+=x y与的图象，那么A ．6,2πϕω-==B ．6,2πϕω==C ．6,1110πϕω==D ．6,1110πϕω-==6．以下函数中既是奇函数，又在区间),0(+∞上单调递增的是A ．x y 2sin =B ．xey -=C ．1ln +=x xyD ．⎩⎨⎧≥+<--=0)2(30)2(3x x x x x x y7．假设),2(,ππβα∈，且βαcot tan <，那么必有A ．πβα23>+B ．πβα23<+C ．βα>D ．βα<8．在区间),0(+∞上函数)(x f 是减函数，且当b a x f x <<>>0,0)(,0若时，那么A ．)()(b af a bf <B ．)()(a bf b af <C ．)()(b f a af <D ．)()(a f b bf < 第二卷〔非选择题，一一共80分〕二、填空题：〔本大题一一一共6小题，每一小题5分，一一共30分。

高中数学培优讲义练习（人教A版2019必修一）专题1.3集合基本关系-重难点题型精讲1．子集的概念2．真子集的概念3．集合相等的概念如果集合A的任何一个元素是集合B的元素，同时集合B的任何一个元素都是集合A 的元素，那么，集合A与集合B相等，记作A＝B.也就是说，若A⊆B且B⊆A，则A＝B。

4．空集的概念【题型1子集、真子集的概念】【方法点拨】①集合A中的任何一个元素都是集合B中的元素，即由x∈A能推出x∈B，这是判断A⊆B的常用方法。

②不能简单地把“A⊆B”理解成“A是B中部分元素组成的集合”，因为若A＝∅时，则A中不含任何元素；若A＝B，则A中含有B中的所有元素。

③在真子集的定义中，A⫋B首先要满足A⊆B，其次至少有一个x∈B，但x∉A。

【例1】（2022•新疆模拟）已知集合A＝{x|﹣1＜x＜3，x∈N}，则A的子集共有（）A．3个B．4个C．8个D．16个【解题思路】化简集合A，再求子集个数即可。

【解答过程】解：∵A＝{x|﹣1＜x＜3，x∈N}＝{0，1，2}。

∴A的子集共有23＝8。

故选：C。

【变式1-1】（2022•新疆模拟）已知集合A＝{x|x2＜3，x∈N}，则A的真子集共有（）A．1个B．2个C．3个D．7个【解题思路】可得出集合A＝{0，1}，然后可得出集合A的真子集个数。

【解答过程】解：∵A＝{x|x2＜3，x∈N}＝{0，1}。

∴A有22﹣1个真子集，即3个真子集。

故选：C。

【变式1-2】（2022春•兖州区期中）设集合A＝{1，2，3，4，5，6}，则在集合A的子集中，有2个元素的子集个数为（）A．A62B．C62C．62D．26【解题思路】有2个元素，相当于从6个数中随机抽取2个。

【解答过程】解：从6个数中随机选取2个，即为C62。

故选：B。

【变式1-3】（2021秋•尚志市校级月考）已知集合A={x∈N|86−x∈N}，则集合A的所有非空子集．的个数为（）A．5个B．6个C．7个D．8个【解题思路】解出集合A，再由含有n个元素的集合，其真子集个数为2n﹣1个可得答案。

2021年高中数学《数列-含参数问题》专项复习一、选择题1.首项为－20的等差数列，从第10项起开始为正数，则公差d 的取值范围是( )A.d ＞920 B.d ≤25 C.920＜d ≤25 D.920≤d ＜25 2.已知数列{a n }的通项公式是a n =n 2＋kn ＋2，若对所有的n ∈N *，都有a n ＋1＞a n 成立，则实数k 的取值范围是( )A ．(0，＋∞)B ．(－1，＋∞)C ．(－2，＋∞)D ．(－3，＋∞)3.设数列{a n }的通项公式为a n =n 2－bn ，若数列{a n }是单调递增数列，则实数b 的取值范围为( )A ．(－∞，－1]B ．(－∞，2]C ．(－∞，3)D ．⎝ ⎛⎦⎥⎤－∞，92 4.一个等差数列的首项为251，从第10项起开始比1大，则这个等差数列的公差d 的取值范围是( ). A.d>758 B.d<253 C.758<d<253 D.758<d ≤253 5.已知{a n }是等比数列，a 2=2，a 5=14，则a 1a 2＋a 2a 3＋…＋a n a n ＋1(n ∈N *)的取值范围是( )A ．[12,16]B ．⎣⎢⎡⎦⎥⎤8，323 C.⎣⎢⎡⎭⎪⎫8，323 D ．⎣⎢⎡⎦⎥⎤163，3236.已知数列{a n }满足a n =⎩⎪⎨⎪⎧a n －2，n<4，6－a n －a ，n ≥4，若对任意的n ∈N *都有a n <a n ＋1成立，则实数a的取值范围为( )A ．(1,4)B ．(2,5)C ．(1,6)D ．(4,6)7.已知数列{a n }的通项公式为a n =2n 2＋tn ＋1，若{a n }是单调递增数列，则实数t 的取值范围是( )A ．(-6，＋∞)B ．(-∞，-6)C ．(-∞，-3)D ．(-3，＋∞)8.在数列{a n }中，已知a 1=3，且数列{a n ＋(－1)n }是公比为2的等比数列，对于任意的n ∈N *，不等式a 1＋a 2＋…＋a n ≥λa n ＋1恒成立，则实数λ的取值范围是( )A.⎝ ⎛⎦⎥⎤－∞，25B.⎝ ⎛⎦⎥⎤－∞，12C.⎝⎛⎦⎥⎤－∞，23 D.(－∞，1] 二、填空题9.已知{a n }是递增数列，且对任意的自然数n(n ≥1)，都有a n =n 2＋λn 恒成立，则实数λ的取值范围为________.10.在等差数列{a n }中,a 1=7,公差为d,前n 项和为S n ,当且仅当n=8时S n 取得最大值,则d 的取值范围为 .11.数列{a n }的通项为a n =⎩⎪⎨⎪⎧2n－1，n≤4，－n 2＋(a －1)n ，n≥5(n ∈N *)，若a 5是{a n }中的最大值，则a 的取值范围是________．12.已知数列{a n }的前n 项和S n =-12n，如果存在正整数n ，使得(m-a n )(m-a n ＋1)<0成立，那么实数m 的取值范围是________．13.等差数列的首项为125，且从第10项开始为比1大的项，则公差d 的取值范围是________．14.已知{a n }是递增数列,且对于任意的n ∈N *,a n =n 2+λn 恒成立,则实数λ的取值范围是 .三、解答题15.已知数列{a n }中，a n =1＋1a ＋2(n －1)(n ∈N *，a ∈R ，且a≠0)．(1)若a=-7，求数列{a n }中的最大项和最小项的值；(2)若对任意的n ∈N *，都有a n ≤a 6成立，求a 的取值范围． 16.已知数列{a n }满足a 1=1，前n 项和S n 满足()130n n nS n S +-+=（1）求{S n }的通项公式； （2）求{a n }的通项公式； （3）设2nn n n c a λ⎛⎫=-⎪⎝⎭，若数列{c n }是单调递减数列，求实数λ的取值范围.17.已知数列{a n }与{b n }满足a n+1-a n =2(b n+1-b n )(,n ∈N).(1)若a 1=1,b n =3n+5，求数列{a n }的通项公式；(2)若a 1=6，b n =2n (n ∈N *)且λa n >2n +n+2λ对一切n ∈N *恒成立，求λ的取值范围. 18.已知数列{a n }和{b n }满足a 1a 2a 3...a n =n b)2((n ∈N *)，若{a n }为等比数列，且a 1=2,b 3=b 2+6. (1)求a n 与b n ;(2)对于任意自然数n ，求使不等式232120...321λλ-<++++nb b b b n 恒成立的λ的取值范围.参考答案1.答案为：C ；解析：由题意知a 10>0,a 9≤0,即-20+9d>0,-20+8d ≤0即920＜d ≤25. 2.答案为：D.a n ＋1＞a n ，即(n ＋1)2＋k(n ＋1)＋2＞n 2＋kn ＋2，则k ＞－(2n ＋1)对所有的n ∈N *都成立， 而当n=1时，－(2n ＋1)取得最大值－3，所以k ＞－3. 3.答案为：C ；解析：因为数列{a n }是单调递增数列，所以a n ＋1－a n =2n ＋1－b>0(n ∈N *)，所以b<2n ＋1(n ∈N *)，所以b<(2n ＋1)min =3，即b<3. 4.答案为：D ；解析：由题意可得a 10>1,a 9≤1,得251+9d>1,251+8d ≤1,所以758<d ≤253.故选D. 5.答案为：C.解析：因为{a n }是等比数列，a 2=2，a 5=14，所以q 3=a 5a 2=18，q=12，a 1=4，故a 1a 2＋a 2a 3＋…＋a n a n ＋1=a 1a 21－q 2n1－q 2=323(1-q 2n)∈⎣⎢⎡⎭⎪⎫8，323，故选C. 6.答案为：A ；解析：因为对任意的n ∈N *都有a n <a n ＋1成立，所以数列{a n }是递增数列，因此⎩⎪⎨⎪⎧1<a ，6－a>0，a<6－a ×4－a ，解得1<a<4，故选A.7.答案为：A ；解析：因为{a n }是单调递增数列，所以对于任意的n ∈N *，都有a n ＋1>a n ，即2(n ＋1)2＋t(n ＋1)＋1>2n 2＋tn ＋1，化简得t>-4n-2，所以t>-4n-2对于任意的n ∈N *都成立，因为-4n-2≤-6，所以t>-6．故选A ． 8.答案为：C ；解析：由已知，a n ＋(－1)n =[3＋(－1)1]·2n －1=2n，∴a n =2n －(－1)n.当n 为偶数时，a 1＋a 2＋...＋a n =(2＋22＋ (2))－(－1＋1－…＋1) =2n ＋1－2，a n ＋1=2n ＋1－(－1)n ＋1=2n ＋1＋1，由a 1＋a 2＋…＋a n ≥λa n ＋1，得λ≤2n ＋1－22n ＋1＋1=1－32n ＋1＋1对n ∈N *恒成立，∴λ≤23；当n 为奇数时，a 1＋a 2＋…＋a n =(2＋22＋…＋2n )－(－1＋1－…＋1－1)=2n ＋1－1，a n ＋1=2n ＋1－(－1)n ＋1=2n ＋1－1，由a 1＋a 2＋…＋a n ≥λa n ＋1得，λ≤2n ＋1－12n ＋1－1=1对n ∈N *恒成立，综上可知λ≤23.9.答案为：λ>－3；解析：由{a n }为递增数列，得a n ＋1－a n =(n ＋1)2＋λ(n ＋1)－n 2－λn=2n ＋1＋λ>0恒成立， 即λ>－2n －1在n ≥1时恒成立，令f(n)=－2n －1，f(n)max =－3.只需λ>f(n)max =－3即可. 10.答案为：(-1,-87)；11.答案为：[9,12]；解析：当n≤4时，a n =2n -1单调递增，因此n=4时取最大值，a 4=24-1=15．当n≥5时，a n =-n 2＋(a-1)n=-n-a －122＋(a －1)24． ∵a 5是{a n }中的最大值，∴⎩⎪⎨⎪⎧a －12≤5.5，－25＋5(a －1)≥15，解得9≤a≤12．∴a 的取值范围是[9,12]．12.答案为：-12，34；解析：易得a 1=-12，n≥2时，有a n =S n -S n-1=-12n --12n-1=3×-12n．则有a 1<a 3<…<a 2k-1<0<a 2k <…<a 4<a 2(k ∈N *)．若存在正整数n ，使得(m-a n )(m-a n ＋1)<0成立，则只需满足a 1<m<a 2即可，即-12<m<34．13.答案为：875<d≤325；解析：由题意得⎩⎪⎨⎪⎧a 10>1，a 9≤1，∴⎩⎪⎨⎪⎧125＋9d>1，125＋8d≤1，∴875<d≤325. 14.答案为：(-3,+∞)；解析：∵对于任意的n ∈N *,a n =n 2+λn 恒成立,∴a n+1-a n =(n+1)2+λ(n+1)-n 2-λn=2n+1+λ.又∵{a n }是递增数列,∴a n+1-a n >0,且当n=1时,a n+1-a n 最小,∴a n+1-a n ≥a 2-a 1=3+λ>0,∴λ>-3. 15.解：(1)∵a n =1＋1a ＋2(n －1)(n ∈N *，a ∈R ，且a≠0)，a=-7，∴a n =1＋12n －9(n ∈N *)．结合函数f(x)=1＋12x －9的单调性，可知1>a 1>a 2>a 3>a 4，a 5>a 6>a 7>…>a n >1(n ∈N *)． ∴数列{a n }中的最大项为a 5=2，最小项为a 4=0．(2)a n =1＋1a ＋2(n －1)=1＋12n －2－a2．∵对任意的n ∈N *，都有a n ≤a 6成立，结合函数f(x)=1＋12x －2－a 2的单调性，∴5<2－a 2<6，∴-10<a<-8．16.解：17.解：18.解:。

高一下期数学期末培优题组一（含答案）（必修4：三角恒等变换，必修5：解三角形，数列，不等式；必修2：直线方程，圆的方程）1.已知向量，令u（x）=．（1）求函数u（x）的对称轴方程；（2）设，当时，求函数f（x）=4u（x）﹣2λv（x）+6λ+5（λ∈R）的最小值g（λ）；（3）在（2）的条件下，若对任意的实数a，b且a＞b＞0，不等式对任意的λ∈[0，5]恒成立，求实数t的取值范围．【解答】解：（1）向量，由u（x）==cos5x•2cos（x﹣）+2sin5x•sin（x﹣）=2cos（5x﹣x+）∴．由4x+=kπ，k∈Z．可得x=∴函数u（x）对称轴方程为．（2）函数f（x）=4u（x）﹣2λv（x）+6λ+5（λ∈R），∵u（x）=2cos（4x+）=2[2cos2（2x+）﹣1]=4cos2（2x+）﹣2∴令，∵，2x+∈[，]∴则f（x）=h（t）=16t2﹣8λt+6λ﹣3．对称轴t=λ．当时，可得t=，函数h（t）取得小值为2λ+1．当时，可得t=，函数h（t）取得小值为﹣λ2+6λ﹣3当时，可得t=1，函数h（t）取得小值为﹣2λ+13．∴…（7分）（3）当λ∈[0，5]时，由（2）g（λ）解析式可得：g（λ）max=6，g（λ）min=1．∴而∴解得：1≤t≤5．故得实数t的取值范围是[1，5]．2．已知函数f（x）=．（1）求f（x）的值域和最小正周期；（2）方程m[f（x）+]+2=0在内有解，求实数m的取值范围．【解答】解：（1）f（x）=2sin（2x+）﹣．∵﹣1≤sin（2x+）≤1．∴﹣2﹣≤2sin（2x+）﹣≤2﹣，T==π，即f（x）的值域为[﹣2﹣，2﹣]，最小正周期为π．…（7分）（2）当x∈[0，]时，2x+∈[]，故sin（2x+）∈[]，此时f（x）+=2sin（2x+）∈[，2]．由m[f（x）+]+2=0知，m≠0，∴f（x）+=﹣，即≤﹣≤2，即，解得﹣≤m≤﹣1．即实数m的取值范围是[﹣]．3．已知a，b，c分别为△ABC三个内角A，B，C的对边，S为△ABC的面积，sin（B+C）=．（Ⅰ）证明：A=2C；（Ⅱ）若b=2，且△ABC为锐角三角形，求S的取值范围．【解答】（Ⅰ）证明：由，即，∴，sinA≠0，∴a2﹣c2=bc，∵a2=b2+c2﹣2bccosA，∴a2﹣c2=b2﹣2bccosA，∴b2﹣2bccosA=bc，∴b﹣2ccosA=c，∴sinB﹣2sinCcosA=sinC，∴sin（A+C）﹣2sinCcosA=sinC，∴sinAcosC﹣cosAsinC=sinC，∴sin（A﹣C）=sinC，∵A，B，C∈（0，π），∴A=2C．（Ⅱ）解：∵A=2C，∴B=π﹣3C，∴sinB=sin3C．∵且b=2，∴，∴==，∵△ABC为锐角三角形，∴，∴，∴，∵为增函数，∴．4.（1）已知sin（2α+β）=5sinβ，求证：2tan（α+β）=3tanα．【解答】证明：∵2α+β=α+（α+β），β=（α+β）﹣α，∴sin（2α+β）=sin[（α+β）+α]=sin（α+β）cosα+cos（α+β）sinα，而5sinβ=5sin[（α+β）﹣α]=5sin（α+β）cosα﹣5cos（α+β）sinα．由已知得sin（α+β）cosα+cos（α+β）sinα=5sin（α+β）cosα﹣5cos（α+β）sinα．∴2sin（α+β）cosα=3cos（α+β）sinα，等式两边都除以cos（α+β）cosα，得2tan（α+β）=3tanα．4．（2）若tan（α+β）=2tanα，求证：3sinβ=sin（2α+β）．【解答】证明：由tan（α+β）=2tanα，得，即sin（α+β）cosα=2sinαcos （α+β）（*）另一方面，要证3sinβ=sin（2α+β），即证3sin[（α+β）﹣α]=sin[（α+β）+α]，即证3sin（α+β）cosα﹣3cos（α+β）sinα=sin（（α+β）cosα+cos（α+β）sinα，化简，得sin（α+β）cosα=2sinαcos（α+β）∵上式与（*）式相同．所以，命题成立．（3）求证：=tan2θ【解答】证明：左边====tan2θ=右边．（4）已知，a，b，c分别是△ABC中角A，B，C的对边，若a，b，c成等比数列，求证：+=．【解答】证明：因为a，b，c成等比数列，所以b2=ac由正弦定理得sin2B=sinAsinC，所以+===．5．若0，0，sin（）=，cos（）=．（I）求sinα的值；（II）求cos（）的值．【解答】解：（Ⅰ）∵0，∴，又sin（）=，∴cos（）=，∴sinα=sin[﹣（）]=sin cos（）﹣cos sin（）=；（Ⅱ）∵0，∴，又cos（）=，∴sin（）=．∴cos（）=cos[（）+（）]=cos（）cos（）﹣sin（）sin（）=．6.已知数列{a n}中，a1=a，a2=2，数列{a n}的前n项和为S n，且2S n=n（3a1+a n），n∈N*．（Ⅰ）求a的值；（Ⅱ）求数列{a n}的通项公式；（Ⅲ）若T n是数列{b n}的前n项和，且对一切n∈N*都成立，求实数m取值范围．【解答】解：（Ⅰ）∵2S n=n（3a1+a n），S1=a1=a，∴2a=4a，所以a=0．…..（3分）（Ⅱ）由（Ⅰ）知，∴．∴．=na n．∴（n﹣1）a n+1∴当n≥2时，．∴，…，，∴．∴a n=2（n﹣1），n≥2．∵a1=a=0满足上式，∴a n=2（n﹣1），n∈N*．…..（6分）（Ⅲ）当n≥2时，．…..（7分）又b1=2，∴T n=b1+b2+…+b n=…..（9分）==所以．…..（10分）因为对一切n∈N*都成立，即对一切n∈N*都成立．∴．…..（12分）∵，当且仅当，即n=1时等号成立．∴．∴∴．…..（14分）7．已知数列{a n}的前n项和为S n，且S n=n（n+1）（n∈N*）．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若数列{b n}满足：，求数列{b n}的通项公式；（Ⅲ）令（n∈N*），求数列{c n}的前n项和T n．【解答】解：（Ⅰ）当n=1时，a1=S1=2，当n≥2时，a n=S n﹣S n﹣1=n（n+1）﹣（n﹣1）n=2n，知a1=2满足该式，∴数列{a n}的通项公式为a n=2n．（2分）（Ⅱ）∵（n≥1）①∴②（4分）②﹣①得：，b n+1=2（3n+1+1），故b n=2（3n+1）（n∈N*）．（6分）（Ⅲ）=n（3n+1）=n•3n+n，∴T n=c1+c2+c3+…+c n=（1×3+2×32+3×33+…+n×3n）+（1+2+…+n）（8分）令H n=1×3+2×32+3×33+…+n×3n，①则3H n=1×32+2×33+3×34+…+n×3n+1②①﹣②得：﹣2H n=3+32+33+…+3n﹣n×3n+1=∴，…（10分）∴数列{c n}的前n项和…（12分）8.已知不等式|2x﹣3|＜x与不等式x2﹣mx+n＜0的解集相同．（Ⅰ）求m﹣n；（Ⅱ）若a、b、c∈（0，1），且ab+bc+ac=m﹣n，求a+b+c的最小值．【解答】解：（Ⅰ）当2x﹣3≥0，即x≥时，不等式|2x﹣3|＜x可化为2x﹣3＜x，解得x＜3，∴≤x＜3；当2x﹣3＜0，即x＜时，不等式|2x﹣3|＜x可化为3﹣2x＜x，解得x＞1，∴1＜x＜；综上，不等式的解集为{x|1＜x＜3}；∴不等式x2﹣mx+n＜0的解集为{x|1＜x＜3}，∴方程x2﹣mx+n=0的两实数根为1和3，∴，∴m﹣n=4﹣3=1；（Ⅱ）a、b、c∈（0，1），且ab+bc+ac=m﹣n=1，∴（a+b+c）2=a2+b2+c2+2（ab+bc+ca）≥（2ab+2bc+2ac）+2（ab+bc+ac）=3（ab+bc+ca）=3；∴a+b+c的最小值是．9．关于x的不等式ax2+（a﹣2）x﹣2≥0（a∈R）（1）已知不等式的解集为（﹣∞，﹣1]∪[2，+∞），求a的值；（2）解关于x的不等式ax2+（a﹣2）x﹣2≥0．【解答】解：（1）∵关于x的不等式ax2+（a﹣2）x﹣2≥0可变形为（ax﹣2）（x+1）≥0，且该不等式的解集为（﹣∞，﹣1]∪[2，+∞），∴a＞0；又不等式对应方程的两个实数根为﹣1和2；∴=2，解得a=1；（2）①a=0时，不等式可化为﹣2x﹣2≥0，它的解集为{x|x≤﹣1}；②a≠0时，不等式可化为（ax﹣2）（x+1）≥0，当a＞0时，原不等式化为（x﹣）（x+1）≥0，它对应的方程的两个实数根为和﹣1，且＞﹣1，∴不等式的解集为{x|x≥或x≤﹣1}；当a＜0时，不等式化为（x﹣）（x+1）≤0，不等式对应方程的两个实数根为和﹣1，在﹣2＜a＜0时，＜﹣1，∴不等式的解集为{x|≤x≤﹣1}；在a=﹣2时，=﹣1，不等式的解集为{x|x=﹣1}；在a＜﹣2时，＞﹣1，不等式的解集为{x|﹣1≤x≤}．综上，a=0时，不等式的解集为{x|x≤﹣1}，a＞0时，不等式的解集为{x|x≥或x≤﹣1}，﹣2＜a＜0时，不等式的解集为{x|≤x≤﹣1}，a=﹣2时，不等式的解集为{x|x=﹣1}，a＜﹣2时，不等式的解集为{x|﹣1≤x≤}．10.如图，在△ABC中，BC边上的高所在的直线方程为x﹣2y+1=0，∠A的平分线所在的直线方程为y=0，若点B的坐标为（1，2），求：（Ⅰ）点A和点C的坐标；（Ⅱ）△ABC的面积．【解答】解：（Ⅰ）由得顶点A（﹣1，0）．﹣﹣﹣﹣﹣﹣﹣（1分）又AB的斜率k AB==1．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）∵x轴是∠A的平分线，故AC的斜率为﹣1，AC所在直线的方程为y=﹣（x+1）①﹣﹣﹣﹣﹣﹣（4分）已知BC上的高所在直线的方程为x﹣2y+1=0，故BC的斜率为﹣2，BC所在的直线方程为y﹣2=﹣2（x﹣1）②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）解①，②得顶点C的坐标为（5，﹣6）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）（Ⅱ）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）又直线BC的方程是2x+y﹣4=0A到直线的距离﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）所以△ABC 的面积=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）高一下期数学期末培优题组二（含答案）（必修4：三角恒等变换，必修5：解三角形，数列，不等式；必修2：直线方程，圆的方程）1.在△ABC中，设角A、B、C的对边分别为a、b、c，已知cos2A=sin2B+cos2C+sinAsinB．（I）求角C的大小；（Ⅱ）若c=，求△ABC周长的取值范围．【解答】解：（I）∵cos2A=sin2B+cos2C+sinAsinB，∴1﹣sin2A=sin2B+1﹣sin2C+sinAsinB，∴sin2A+sin2B﹣sin2C=﹣sinAsinB，∴a2+b2﹣c2=﹣ab，∴=，又0＜C＜π，∴．（2）∵，∴a=2sinA，b=2sinB，则△ABC的周长L=a+b+c=2（sinA+sinB）+=2（sinA+）+=，∵，，∴，即，∴△ABC周长的取值范围是．2.已知函数，其中（1）若x∈[0，π]，求函数f（x）的单调递增区间和最小值；（2）在△ABC中，a、b、c分别是角A．B．C的对边，旦f（A）=﹣1，求的值；（3）在第二问的条件下，若，求△ABC面积的最大值．【解答】解：（1）f（x）=====，由解得，又x∈[0，π]，因此函数f（x）的单调递增区间为．其最小值为==﹣2+1=﹣1．（2）由f（A）=﹣1，可得，化为，∵A∈（0，π），∴，∴，解得．即A=60°．由正弦定理可得=== =2．（3）由（2）可知：A=60°．∴3=a2=b2+c2﹣2bccos60°≥2bc﹣bc=bc，当且仅当b=c=时取等号．∴△ABC面积==，即最大值为．3.设S n是正项数列{a n}的前n项和，且S n=a+a n﹣（Ⅰ）求数列{a n}的通项公式；（Ⅱ）是否存在等比数列{b n}，使a1b1+a2b2+…+a n b n=（2n﹣1）•2n+1+2对一切正整数n都成立？并证明你的结论．（Ⅲ）设=（n∈N*），且数列{C n}的前n项和为T n，试比较T n与的大小．【解答】解：（1）由S n=+a n﹣得S n+1=，相减并整理得（a n+1+a n）（a n+1﹣a n﹣2）=0又由于a n+1+a n＞0，则a n+1=a n+2，故{a n}是等差数列．∵+a12﹣，所以a1=3故a n=2n+1 …4分（2）当n=1，2时，a1b1=22（2×1﹣1）+2=6，a1b1+a2b2=23（2×2﹣1）+2=26，可解得b1=2，b2=4，猜想b n=2n，使a1b1+a2b2+…+a n b n=2n+1（2n﹣1）+2成立．证明：3•2+5•22+7•23+…+（2n+1）2n=2n+1（2n﹣1）+2恒成立．令S=3•2+5•22+7•23+…+（2n+1）2n①2S=3•22+5•23+7•24+…+（2n+1）2n+1②②﹣①得：S=（2n+1）2n+1﹣2•2n+1+2=（2n﹣1）2n+1+2，故存在等比数列{b n}符合题意…8分（3）C n=＜=（）则T n=c1+c2+…+c n（+…+）=（﹣）＜故…12分4.已知数列{a n}中，a2=2，前n项和为．（I）证明数列{a n+1﹣a n}是等差数列，并求出数列{a n}的通项公式；（II）设，数列{b n}的前n项和为T n，求使不等式对一切n∈N*都成立的最大正整数k的值．【解答】解：（I）由题意，当．a2=2，则a2﹣a1=1．当，，则，则（n﹣1）a n+1﹣2（n﹣1）a n+（n﹣1）a n﹣1=0，即a n+1﹣2a n+a n﹣1=0，即a n+1﹣a n=a n﹣a n﹣1．则数列{a n+1﹣a n}是首项为1，公差为0的等差数列．…（6分）从而a n﹣a n﹣1=1，则数列{a n}是首项为1，公差为1的等差数列．所以，a n=n（n∈N*）…（8分）（II）…（10分）所以，=．…（12分）由于．因此T n单调递增，故T n的最小值为…（14分）令，所以k的最大值为18．…（16分）5.已知数列{a n}的前n项和，数列{b n}的前n项和为B n．（1）求数列{a n}的通项公式；（2）设，求数列{c n}的前n项和C n；（3）证明：．【解答】（本小题满分13分）解：（I）当n≥2时，，，两式相减：a n=A n﹣A n﹣1=2n﹣1；当n=1时，a1=A1=1，也适合a n=2n﹣1，故数列{a n}的通项公式为a n=2n﹣1；．…（3分）（II）由题意知：，C n=c1+c2+…+c n，，，两式相减可得：，…（4分）即，，．…（7分）（III），显然，即b n＞2，B n=b1+b2+…+b n＞2n；…（9分）另一方面，，即，，…，，，即：2n＜B n＜2n+2．…（13分）6.已知二次函数f（x）=ax2+bx（a，b为常数，且a≠0）满足条件：f（2）=0，且方程f（x）=x有两个相等的实数根．（1）求f（x）的解析式；（2）求函数在区间[﹣3，3]上的最大值和最小值；（3）是否存在实数m，n（m＜n），使f（x）的定义域和值域分别为[m，n]和[2m，2n]，如果存在，求出m，n的值，如不存在，请说明理由．【解答】解：（1）∵f（2）=0∴4a+2b=0 ①又方程f（x）=x有等根，即ax2+bx﹣x=0的判别式为零∴（b﹣1）2=0∴b=1代入①a=﹣∴f（x）=（2）∴函数的对称轴为x=1∴当x=1时，函数取得最大值为；当x=﹣3时，函数取得最小值为；（3）∵，f（x）的定义域和值域分别为[m，n]和[2m，2n]，∴∴而f（x）=的对称轴为x=1，∴当n≤时，f（x）在[m，n]上为增函数．若满足题设条件的m，n存在，则即∴∵m＜n≤．∴m=﹣2，n=0，这时，定义域为[﹣2，0]，值域为[﹣4，0]．由以上知满足条件的m，n存在，m=﹣2，n=0．7.某公司为了变废为宝，节约资源，新上了一个从生活垃圾中提炼生物柴油的项目．经测算，该项目月处理成本y（元）与月处理量x（吨）之间的函数关系可以近似地表示为：y=，且每处理一吨生活垃圾，可得到能利用的生物柴油价值为200元，若该项目不获利，政府将给予补贴．（Ⅰ）当x∈[200，300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损？（Ⅱ）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？【解答】解：（Ⅰ）当x∈[200，300）时，该项目获利为S，则S=200x﹣（x2﹣200x+80000）=﹣（x﹣400）2，∴当x∈[200，300）时，S＜0，因此，该项目不会获利当x=300时，S取得最大值﹣5000，所以政府每月至少需要补贴5000元才能使该项目不亏损；（Ⅱ）由题意可知，生活垃圾每吨的平均处理成本为：=．当x∈[120，144）时，=（x﹣120）2+240所以当x=120时，取得最小值240；当x∈[144，500）时，=x+﹣200≥2﹣200=300当且仅当x=，即x=400时，取得最小值300因为240＜300，所以当每月处理量为120吨时，才能使每吨的平均处理成本最低．8.已知△ABC的顶点A（5，1），AB边上的中线CM所在直线方程为2x﹣y﹣5=0，AC边上的高BH所在直线方程为x﹣2y﹣5=0．（1）求AC边所在直线方程；（2）求顶点C的坐标；（3）求直线BC的方程．【解答】解：（1）由AC边上的高BH所在直线方程为x﹣2y﹣5=0可知k AC=﹣2，又A（5，1），AC边所在直线方程为y﹣1=﹣2（x﹣5），即AC边所在直线方程为2x+y﹣11=0．（2）由AC边所在直线方程为2x+y﹣11=0，AB边上的中线CM所在直线方程为2x﹣y﹣5=0，由，解得x=4，y=3，所以顶点C的坐标为（4，3）．（3）设点B的坐标为（x0，y0），且点B与点A关于直线2x﹣y﹣5=0对称，∴2•﹣﹣5=0，又点B在直线BH上，∴x0﹣2y0﹣5=0，∴x0=﹣1，y0=﹣3，所以，由两点式，得直线BC的方程为6x﹣5y﹣9=0．9.设数列{a n}的前n项和为S n，n∈N*．已知a1=1，a2=，a3=，且当n≥2时，4S n+5S n=8S n+1+S n﹣1．+2﹣a n}为等比数列；（3）求数列{a n}的通项公式．（1）求a4的值；（2）证明：{a n+1【分析】（1）直接在数列递推式中取n=2，求得；+5S n=8S n+1+S n﹣1（n≥2），变形得到4a n+2+a n=4a n+1（n≥2），进一步得到（2）由4S n+2，由此可得数列{}是以为首项，公比为的等比数列；（3）由{}是以为首项，公比为的等比数列，可得．进一步得到，说明{}是以为首项，4为公差的等差数列，由此可得数列{a n}的通项公式．10.已知函数f（x）的图象是由函数g（x）=cosx的图象经如下变换得到：先将g（x）图象上所有点的纵坐标伸长到原来的2倍，横坐标不变，再将所得到的图象向右平移个单位长度．（1）求函数f（x）的解析式，并求其图象的对称轴方程；（2）已知关于x的方程f（x）+g（x）=m在[0，2π）内有两个不同的解α，β（i）求实数m的取值范围；（ii）证明：cos（α﹣β）=﹣1．【分析】（1）由函数y=Asin（ωx+φ）的图象变换规律可得：f（x）=2sinx，从而可求对称轴方程．（2）（i）由三角函数中的恒等变换应用化简解析式可得f（x）+g（x）=sin（x+φ）（其中sinφ=，cosφ=），从而可求||＜1，即可得解．（ii）由题意可得sin（α+φ）=，sin（β+φ）=．当1≤m＜时，可求α﹣β=π﹣2（β+φ），当﹣＜m＜0时，可求α﹣β=3π﹣2（β+φ），由cos（α﹣β）=2sin2（β+φ）﹣1，从而得证．高一下期数学期末培优题组三（含答案）（必修4：三角恒等变换，必修5：解三角形，数列，不等式；必修2：直线方程，圆的方程）1．在△ABC中，角A，B，C对边分别是a，b，c，满足．（1）求角A的大小；（2）求sinA•sinB•sinC的最大值，并求取得最大值时角B，C的大小．【解答】解：（1）∵=cbcosA，．∴2bccosA=a2﹣（b+c）2，展开为：2bccosA=a2﹣b2﹣c2﹣2bc，∴2bccosA=﹣2bccosA﹣2bc，化为cosA=﹣，∵A∈（0，π）．∴．（2）∵，∴，．∴sinA•sinB•sinC===﹣==﹣=﹣，∵．∴，当=时，即时，sinA•sinB•sinC取得最大值，此时B=C=．2．在△ABC中，角A、B、C所对的边分别是a、b、c，已知a+b=m c（m＞0）．（1）当m=3时，①若A=B，求sinC；②若B=，求sin（A﹣C）的值．（2）当m=2时，若c=2，求△ABC面积的最大值．【解答】解：（1）①△ABC中，m=3时，a+b=c，∴sinA+sinB=sinC；又A=B，∴A+B=2A=2B=π﹣C，∴A=B=﹣，∴sin（﹣）+sin（﹣）=sinC，∴2cos=2sin cos，∴sin=，∴cos=，∴sinC=2sin cos=2××=；②∵B=，∴A+C=π﹣B=；又∵sinA+sinB=sinC，∴sinA+=sinC，∴sinA=sinC﹣；又sinA=sin（﹣C）=sin cosC﹣cos sinC=cosC+sinC，∴cosC+sinC=sinC﹣，∴cosC﹣sinC=﹣，∴sinC﹣cosC=，即sin（C﹣）=；∴C=，A=﹣=，∴sin（A﹣C）=sin（﹣）=sin=；（2）当m=c=2时，a+b=c=2，∴a2+2ab+b2=8；∴4ab≤a2+b2+2ab=8，∴ab≤2，此时a=b=；△ABC是等腰直角三角形，其面积最大值为S=ab=××=1．3．已知数列{a n}的前n项和S n=﹣a n﹣（）n﹣1+2（n为正整数）．（1）令b n=2n a n，求证数列{b n}是等差数列；（2）求数列{a n}的通项公式；（3）令c n=a n，T n=c1+c2+…+c n．是否存在最小的正整数m，使得对于n∈N×都有T n＜2m ﹣4恒成立，若存在，求出m的值；不存在，请说明理由．【解答】（1）证明：∵S n=﹣a n﹣（）n﹣1+2，∴S n=﹣a n+1﹣（）n+2，+1S n+1﹣S n=a n+1=﹣a n+1+a n+（）n，2a n+1=a n+（）n，2n+1a n+1=2n a n+1，∵b n=2n a n，∴b n+1=b n+1，∴数列{b n}是等差数列．（2）解：∵S n=﹣a n﹣（）n﹣1+2，∴a1=S1=﹣a1﹣（）0+2，解得，又b n=2n a n，b n+1=b n+1，∴b1=2×=1，∴b n=2n a n=n，∴．（3）解：∵c n=a n=，∴T n=c1+c2+…+c n=，①2T n=2+，②②﹣①，得：T n=2++…+﹣=2+﹣=3﹣﹣=3﹣．假设存在最小的正整数m，使得对于n∈N×都有T n＜3≤2m﹣4恒成立，则2m﹣4≥3，解得m≥，∴最小的正整数m=4．4．已知正项数列{a n}的前n项和为S n，数列{a n}满足，2S n=a n（a n+1）．（1）求数列{a n}的通项公式；（2）设数列{}的前n项和为A n，求证：对任意正整数n，都有A n＜成立；（3）数列{b n}满足b n=（）n a n，它的前n项和为T n，若存在正整数n，使得不等式（﹣2）n﹣1λ＜Tn+﹣2n﹣1成立，求实数λ的取值范围．【解答】解：（1），当n≥2时，，两式相减得：，所以（a n+a n﹣1）（a n﹣a n﹣1﹣1）=0．因为数列{a n}为正项数列，故a n+a n﹣1≠0，也即a n﹣a n﹣1=1，所以数列{a n}为以1为首项1为公差的等差数列，故通项公式为a n=n，n∈N*．（2）=，所以对任意正整数n，都有成立．（3）易知，则，①，，②①﹣②可得：．故，所以不等式成立，若n为偶数，则，所以．设，则y=﹣2t+t2+1=（t﹣1）2在单调递减，故当时，，所以；若n为奇数，则，所以．设，则y=2t﹣t2﹣1=﹣（t﹣1）2在（0，1]单调递增，故当t=1时，y max=0，所以λ＜0．综上所述，λ的取值范围λ＜0或．5．已知f（x）是二次函数，不等式f（x）＜0的解集是（0，5），且f（x）在区间[﹣1，4]上的最大值是12．（1）求f（x）的解析式；（2）设函数f（x）在x∈[t，t+1]上的最小值为g（t），求g（t）的表达式．【解答】解：（1）f（x）是二次函数，且f（x）＜0的解集是（0，5），∴可设f（x）=ax（x﹣5）（a＞0），可得在区间f（x）在区间[﹣1，]上函数是减函数，区间[，4]上函数是增函数∵f（﹣1）=6a，f（4）=﹣4a，f（﹣1）＞f（4）∴f（x）在区间[﹣1，4]上的最大值是f（﹣1）=6a=12，得a=2．因此，函数的表达式为f（x）=2x（x﹣5）=2x2﹣10x（x∈R）．（2）由（1）得f（x）=2（x﹣）2﹣，函数图象的开口向上，对称轴为x=①当t+1时，即t时，f（x）在[t，t+1]上单调递减，此时f（x）的最小值g（t）=f（t+1）=2（t+1）2﹣10（t+1）=2t2﹣6t﹣8；②当t时，f（x）在[t，t+1]上单调递增，此时f（x）的最小值g（t）=f（t）=2t2﹣10t；③当＜t＜时，函数y=f（x）在对称轴处取得最小值此时，g（t）=f（）=﹣综上所述，得g（t）的表达式为：g（t）=6．阅读：已知a、b∈（0，+∞），a+b=1，求y=+的最小值．解法如下：y=+=（+）（a+b）=++3≥3+2，当且仅当=，即a=﹣1，b=2﹣时取到等号，则y=+的最小值为3+2．应用上述解法，求解下列问题：（1）已知a，b，c∈（0，+∞），a+b+c=1，求y=++的最小值；（2）已知x∈（0，），求函数y=+的最小值；（3）已知正数a1、a2、a3，…，a n，a1+a2+a3+…+a n=1，求证：S=+++…+≥．【解答】解（1）∵a+b+c=1，∴y=++=（a+b+c）=3+++2=9，当且仅当a=b=c=时取等号．即的最小值为9．（2）==10+2，而，∴=8，当且仅当，即∈时取到等号，则y≥18，∴函数y=的最小值为18．（3）∵a1+a2+a3+…+a n=1，∴2S=（+++…+）[（a1+a2）+（a2+a3）+…+（a n+a1）]=+++…+++（2a1a2+2a2a3+…+2a n a1）==1．当且仅当a1=a2=…=a n=时取到等号，则．7．已知二次函数f（x）=x2+bx+c（b、c∈R），不论α、β为何实数，恒有f（sinα）≥0，f（2+cosβ）≤0．（1）求证：b+c=﹣1；（2）求证：c≥3；（3）若函数f（sinα）的最大值为8，求b、c的值．【解答】解：（1）证明：∵|sinα|≤1且f（sinα）≥0恒成立，可得f（1）≥0．又∵1≤2+cosβ≤3且f（2+cosβ）≤0恒成立，可得f（1）≤0，∴f（1）=0，∴1+b+c=0，∴b+c=﹣1．（2）证明：∵b+c=﹣1，∴b=﹣1﹣c，∴f（x）=x2﹣（1+c）x+c=（x﹣1）（x﹣c）．又∵1≤2+cosβ≤3且f（2+cosβ）≤0恒成立∴x﹣c≤0，即c≥x恒成立．∴c≥3．（3）∵f（sinα）=sin2α﹣（1+c）sinα+c=（sinα﹣）2+c﹣（）2，∵∴当sinα=﹣1时，f（sinα）的最大值为1﹣b+c．由1﹣b+c=8与b+c=﹣1联立，可得b=﹣4，c=3．即b=﹣4，c=3．8.已知直线l：kx﹣y+1+2k=0（k∈R）．（1）证明：直线l过定点；（2）若直线l不经过第四象限，求k的取值范围；（3）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．【分析】（1）直线l的方程可化为y=k（x+2）+1，直线l过定点（﹣2，1）．（2）要使直线l不经过第四象限，则直线的斜率和直线在y轴上的截距都是非负数，解出k 的取值范围．（3）先求出直线在两个坐标轴上的截距，代入三角形的面积公式，再使用基本不等式可求得面积的最小值．9.已知直线l过点P（4，1），且与x，y的正半轴交于点A，B，其中O为坐标原点．（1）求直线l的方程，使△OAB的面积最小；（2）求直线l的方程，是直线在两坐标上的截距之和最小；（3）求|PA|•|PB|最小时，直线l的方程．【分析】（1）设A（a，0），B（0，b），a，b＞0．则直线l的方程为：，由于直线l 过点P（4，1），可得=1．利用基本不等式的性质即可得出．（2）由（1）可得：=1，a，b＞0．a+b==5+，再利用基本不等式的性质即可得出．（3）由=1，a，b＞0．可得b=＞0，（a＞4）．设t=|PA|•|PB|，则t2=[（a﹣4）2+1]•[16+（b﹣1）2]=[（a﹣4）2+1]•，设（a﹣4）2=m＞0，则t2==32+，利用基本不等式的性质即可得出．。

2020-2021年高二数学选择性必修二尖子生同步培优题典4.1数列的概念 解析版学校:___________姓名：___________班级：___________考号：___________注意事项：本卷共16小题，6道单选题，3道多选题，3道填空题，4道解答题。

一、单选题1．已知数列{}n a 中，13=4a ，111n n a a -=-（,2n N n +∈≥），那么2020a 等于（ ）A ．13- B ．34C ．2D ．4【答案】B 【解析】 【分析】根据13=4a ，111n n a a -=-，计算数列的前几项，得到数列{}n a 是以3为周期的数列求解.【详解】因为13=4a ，111n n a a -=-，所以211113a a =-=-， 32114a a =-=， 431314a a =-=， …所以数列{}n a 是以3为周期的数列， 所以202067331134a a a ⨯+===， 故选：B 【点睛】本题主要考查数列的周期性的应用，还考查了运算求解的能力，属于基础题. 2．数列1、1、2、3、5、8、13、21、34、称为斐波那契数列，是意大利著名数学家斐波那契于1202年在他撰写的《算盘全书》中提出的，该数列的特点是：从第三项起，每一项都等于它前面两项的和.在该数列的前2020项中，偶数的个数为（ ） A ．505 B ．673C ．674D ．1010【答案】B 【解析】 【分析】由斐波那契数列的特点可知，该数列只有第()3k k *∈N 项为偶数，再由202036731=⨯+可求得结果. 【详解】由斐波那契数列的特点，可得此数列只有第()3k k *∈N项为偶数，由于202036731=⨯+，所以前2020项中偶数的个数为673． 故选：B. 【点睛】本题考查斐波那契数列的应用，考查推理能力，属于基础题.3．“干支纪法”是我国记年、月、日、时的序号的传统方法，天干地支简称“干支”，天干指：甲、乙、丙、丁、戊、己、庚、辛、壬、癸．“地支”指：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥．如，农历1861年为辛酉年，农历1862年为壬戌年，农历1863年为癸亥年，则农历2068年为（ ） A ．丁亥年 B ．丁丑年C ．戊寅年D ．戊子年【答案】D 【解析】 【分析】由题意得天干是以10为周期的数列，地支是以12为周期的数列，以1861为首项，即可得答案. 【详解】记1a =辛，1b =酉（1861）；2a =壬，2b =戌（1862）；3a =癸，3b =亥（1863）， 所以记天干为数列{}n a ，且最小正周期为10，记地支为数列{}n b ，且最小正周期为12， 故20688a a ==戊，20684b b ==子（2068）， 故选：D ． 【点睛】本题考查数列的周期性，难点在于需将题目信息转化为所学数列的知识，考查逻辑推理，归纳分析的能力，属中档题.4．原始的蚊香出现在宋代.根据宋代冒苏轼之名编写的《格物粗谈》记载：“端午时，贮浮萍，阴干，加雄黄，作纸缠香，烧之，能祛蚊虫.”如图，为某校数学兴趣小组用数学软件制作的“螺旋蚊香”，画法如下:在水平直线l上取长度为1的线段AB，做一个等边三角形ABC，然后以点B为圆心，AB 为半径逆时针画圆弧，交线段BC的延长线于点D，再以点C为圆心，CD为半径逆时针画圆弧，交线段AC的延长线于点E，以此类推，当得到的“螺旋蚊香”与直线l恰有21个交点时，“螺旋蚊香”的总长度的最小值为（）A．310πB．340πC．930πD．1020π【答案】A【解析】【分析】根据画圆弧的规律：分别以B，C，A 为圆心，抽象半径长度的数列，明确圆弧与直线的交点情况，再根据当“螺旋蚊香”与直线l恰有21个交点时，若使“螺旋蚊香”的总长度最小，确定数列的项数，求得最后圆弧的半径即可.【详解】如图所示：当以B为圆心，半径为：1，4，7，10，…除起点外，与直线无交点，①当以C为圆心，半径为：2，5，8，11，…与直线有一个点，②当以A为圆心，半径为：3，6，9，12，…除终点（即①的起点，点A 除外）外，与直线无交点，③所以当“螺旋蚊香”与直线l恰有21个交点时，若使“螺旋蚊香”的总长度最小，则完成整数个循环，所以以B 为圆心的弧与直线只有交点A ，以C 为圆心的弧与直线10个交点，以A 为圆心的弧与直线有10 个交点，即数列②有10项，数列③有10项，所以最后一个圆弧的半径为33(101)30r =+-= ，所以“螺旋蚊香”的总长度的最小值为()()30130112123 (302310332)l πππ+=⨯⨯++++=⨯= . 故选：A 【点睛】本题主要考查数列的抽象与等差数列的通项公式和前n 项和的应用，还考查了分析求解问题的能力，属于中档题.5．衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理，数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，它是中华传统文化中隐藏着的世界数学史上第一道数列题，该数列从第一项起依次是0，2，4，8，12，18，24，32，40，50…，则该数列第16项为（ ） A ．152 B ．134 C ．128 D ．102【答案】C 【解析】 【分析】根据数据找出规律,依次写出来即可. 【详解】前10项依次是0,2,4,8,12,18,24,32,40,50,偶数项分别为2,8,18,32,50,…,可得偶数项的通项公式: 222n a n =.所以该数列第16项为21628=128a =⨯. 故选:C. 【点睛】本题考查了数列递推关系、通项公式、归纳法,考查了推理能力与计算能力,属于中档题.6．公元前四世纪，毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形（或格点）来表示数，称为形数.形数是联系算术和几何的纽带.如图所示，数列1，6，15，28，45，…，从第二项起每一项都可以用六边形表示出来，故称它们为六边形数，那么该数列的第11项对应的六边形数为（ ）A ．153B ．190C ．231D ．276【答案】C 【解析】 【分析】根据题中所给图与对应的六边形数，记第n 个六边形数为n a ，找出规律，相邻两项差构成等差数列，累加求得22n a n n =-，将11n =代入求得结果.【详解】记第n 个六边形数为n a ，由题意知：11a =，215141a a -==+⨯，32142a a -=+⨯，43143a a -=+⨯，，114(1)n n a a n --=+-，累加得21(1)[543]59[14(1)]212n n n a a n n n -+--=++++-==--，即22n a n n =-，所以21121111231a =⨯-=，故选：C. 【点睛】该题考查的是有关数列的问题，涉及到的知识点有利用累加法求数列的通项公式，属于中档题目.二、多选题7．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，….，其中从第三项起，每个数等于它前面两个数的和，后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”，记n S 为数列{}n a 的前n 项和，则下列结论正确的是（ ） A ．68a =B ．733S =C ．135********a a a a a +++⋅⋅⋅+=D ．22212201920202019a a a a a ++⋅⋅⋅⋅⋅⋅+=【分析】由题意可得数列{}n a 满足递推关系12211,1,(3)n n n a a a a a n --===+≥，对照四个选项可得正确答案. 【详解】对A ，写出数列的前6项为1,1,2,3,5,8，故A 正确； 对B ，71123581333S =++++++=，故B 正确；对C ，由12a a =，342a a a =-，564a a a =-，……，201920202018a a a =-，可得：135********a a a a a +++⋅⋅⋅+=.故1352019a a a a +++⋅⋅⋅+是斐波那契数列中的第2020项.对D ，斐波那契数列总有21n n n a a a ++=+，则2121a a a =，()222312321a a a a a a a a =-=-，()233423423a a a a a a a a =-=-，……，()220182018201920172018201920172018a a a a a a a a =-=-，220192019202020192018a a a a a =-2222123201920192020a a a a a a +++⋅⋅⋅⋅⋅⋅+=，故D 正确；故选：ABCD. 【点睛】本题以“斐波那契数列”为背景，考查数列的递推关系及性质，考查方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意递推关系的灵活转换.8．斐波那契数列，又称黄金分割数列、兔子数列，是数学家列昂多·斐波那契于1202年提出的数列.斐波那契数列为1，1，2，3，5，8，13，21，……，此数列从第3项开始，每一项都等于前两项之和，记该数列为(){}F n ，则(){}F n 的通项公式为（ ）A ．(1)1()2n n F n -+=B ．()()()11,2F n F n F n n +=+-≥且()()11,21F F ==C ．()n nF n ⎡⎤⎥=-⎥⎝⎭⎝⎭⎦D ．()n nF n ⎡⎤⎥=+⎥⎝⎭⎝⎭⎦【分析】根据数列的前几项归纳出数列的通项公式，再验证即可； 【详解】解：斐波那契数列为1，1，2，3，5，8，13，21，……，显然()()11,21F F ==，()()()3122F F F =+=，()()()4233F F F =+=，，()()()11,2F n F n F n n +=+-≥，所以()()()11,2F n F n F n n +=+-≥且()()11,21F F ==，即B 满足条件；由()()()11,2F n F n F n n +=+-≥， 所以()()()()11F n n F n n ⎤+-=-⎥⎣⎦所以数列()()1F n n ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭为公比的等比数列， 所以()()1nF n n +=⎝⎭()11515()n F F n n -+=+， 令1nn n Fb -=⎝⎭，则11n n b +=+，所以1n n b b +-=， 所以n b⎧⎪⎨⎪⎪⎩⎭32为公比的等比数列，所以1n n b -=+，所以()11152n n n nF n --⎤⎤⎛⎫+⎥⎥=+=- ⎪ ⎪⎥⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦； 即C 满足条件； 故选：BC 【点睛】考查等比数列的性质和通项公式，数列递推公式的应用，本题运算量较大，难度较大，要求由较高的逻辑思维能力，属于中档题．9．对于数列{}n a ，若存在正整数k ()2k ≥，使得1k k a a -<，1k k a a +<，则称k a 是数列{}n a 的“谷值，k 是数列{}n a 的“谷值点”，在数列{}n a 中，若98n a n n=+-，则数列{}n a 的“谷值点”为( ) A ．2 B ．3C ．5D ．7【答案】AD 【解析】 【分析】由数列的通项公式求出前七项各项的值，然后根据题意进行求解即可, 【详解】 因为98n a n n =+-，所以123456783761292,,2,,,,,245278a a a a a a a a ========， 当7,n n N ≥∈，9998088n n a n n n n n+->∴=+-=+-，此时数列单调递增， 21a a <，23a a <，76a a <，78a a <，所以数列{}n a 的“谷值点”为2，7. 故选：AD 【点睛】本题考查了数学阅读能力，考查了数学运算能力，考查了数列的单调性，属于中档题.三、填空题10．在数列{}n a 中，11a =，()32122223n n a a a a a n n*++++=∈N ，则n a =______． 【答案】21nn + 【解析】 【分析】由已知得：当2n ≥时，()31211222231n n a a a a a n --++++=-，与原式相减得12n n n a a a n -=-，即11+1n n nn n a a n --=，递推可得答案. 【详解】由题意得：当2n ≥时，()31211222231n n a a a a a n --++++=-，所以12n n n a a a n -=-，即()2211n n na n a --=，也即是11+1n n n n n a a n --=，所以121+1221211n n n n n a n n n a a a n ---===-=-=， 所以21n na n =+，故答案为：21nn +. 【点睛】本题考查由数列的递推式求数列的通项，属于中档题. 11．已知数列{}n a 满足1133,2,n n a a a n +=-=则na n的最小值为__________. 【答案】212【解析】 【分析】先利用累加法求出a n ＝33+n 2﹣n ，所以331n a n n n =+-，设f （n ）331n n=+-，由此能导出n ＝5或6时f （n ）有最小值．借此能得到na n的最小值． 【详解】解：∵a n +1﹣a n ＝2n ，∴当n ≥2时，a n ＝（a n ﹣a n ﹣1）+（a n ﹣1﹣a n ﹣2）+…+（a 2﹣a 1）+a 1＝2[1+2+…+（n ﹣1）]+33＝n 2﹣n +33且对n ＝1也适合，所以a n ＝n 2﹣n +33．从而331n a n n n=+- 设f （n ）331n n =+-，令f ′（n ）23310n-=+＞，则f （n ）在)+∞上是单调递增，在(0上是递减的，因为n ∈N +，所以当n ＝5或6时f （n ）有最小值．又因为55355a =，66321662a ==， 所以n a n 的最小值为62162a =故答案为 212【点睛】本题考查了利用递推公式求数列的通项公式，考查了累加法．还考查函数的思想，构造函数利用导数判断函数单调性．12．已知数列{}n a 满足：12020a =，()2*11n n n a a a n N +=+-∈，若正整数k 使得2221212 (2) (2021)k k a a a a a a ++++=成立，则k =___________. 【答案】2019 【解析】 【分析】根据()2*11n n n a a a n N +=+-∈可得211n n n a a a +=-+且111n n n a a a ++=+，结合已知条件的等式成立，即可求k 的值； 【详解】()2*11n n n a a a n N +=+-∈知：211n n n a a a +=-+且111n n n a a a ++=+，则：22212213211...11...12020k k k k a a a a a a a a a a k +++++=-++-+++-+=-+， 311212121111......1112021k k k k a a a a a a a a a a ++++++=⋅⋅⋅=+++，而2221212...2 (2021)k k a a a a a a ++++=，∴112018120212021k k a k a +++-+=，即得2019k =.故答案为：2019 【点睛】本题考查了利用数列递推式，结合等式成立求数列的项数，注意结合已知等式中乘积形式、平方形式转化递推式求参数；四、解答题13．数列{}n a 中，254n a n n =-+.（1）18是数列中的第几项？（2）n 为何值时，n a 有最小值？并求最小值.【答案】（1）第7项；（2）2n =或3n =时，最小值为2- 【解析】【分析】（1）令25418n a n n =-+=且n *∈N ，解方程可得n 的值.（2）利用二次函数的单调性和最值可得n a 有最小值以及对应的n 的值.【详解】令25418n a n n =-+=，即25140n n --=，解得：7n =或2n =-（舍）（2）由254n a n n =-+，因为254y x x =-+，开口向上，对称轴52x =所以2n =或3n =时，n a 有最小值为2225242a =-⨯+=- . 【点睛】本题主要考查了判断数列中的项，以及求数列的最小项，属于基础题.14．下面图形都是由小正三角形构成的,设第n 个图形中的黑点总数为()f n .(1)求()()()()2,3,4,5f f f f 的值;(2)找出()f n 与()1f n +的关系,并求出()f n 的表达式.① ② ③ ④【答案】(1)见解析；(2)()23,*.f n n n N =∈ 【解析】【分析】（1）根据题意可直接写出结果；（2）分别计算出()()21f f -，()()32f f -，()()43f f -，()()54f f -，归纳出()()1f n f n +-，再由累加法即可求出()f n 的表达式.【详解】（1）由题意可得：()212f =，()327f =，()448f =，()575f =；（2）因为()()219f f -=； ()()3215f f -=； ()()4321f f -=； ()()5427f f -=； 观察猜想：()()1f n f n +-是一个首项为9公差为6的等差数列，即()()()191663f n f n n n +-=+-⨯=+．因为()()219f f -=；()()3215f f -=；()()4321f f -=；()()5427f f -=；()()163f n f n n --=-；把上述式子累加可得到：()()()()296311332n n f n f n +---==-； 又因为()13f =，所以()23f n n =. 【点睛】本题主要考查归纳推理以及累加法求数列的通项公式，属于常考题型.15．已知数列{}n a 中，11a =，214a =，且1(1))(2,3,4,n n n n a a n n a +-==-. （1）求3a 、4a 的值，（2）设*111()n n b n N a +=-∈试用n b 表示1n b +，并求{}n b 的通项公式； （3）设*1sin 3()cos cos n n n c n N b b +=∈⋅，求数列{}n c 的前n 项和n S . 【答案】（1）317a =，4110a =；（2）11n n n b b n++=，*n N ∈，3n b n =，*n N ∈；（3）()tan 33tan3n +-.【解析】【分析】（1）由数列{}n a 中，11a =，214a =，且1(1)(2,3,4,...)n n n n a n n a a +-==-，分别令2n =和3n =，求出3a 、4a 的值.（2）当2n ≥时，1(1)11111(1)(1)1n n n n n n n a n a n a n a n a n a +⎛⎫---=-==- ⎪---⎝⎭，即11n n n b b n -=-，则11n n n b b n++=，然后用累乘法求解.（3）由1sin 3tan(33)tan 3cos cos n n n c n n b b +==+-⋅，然后利用裂项相消法求解. 【详解】 （1）∵数列{}n a 中，11a =，214a =， 且1(1)(2,3,4,...)n n nn a n n a a +-==- ∴2321(21)1412724a a a -===--， 34312(31)17131037a a a ⨯-===--， ∴317a =，4110a =· （2）当2n ≥时，1(1)11111(1)(1)1n n n n n n n a n a n a n a n a n a +⎛⎫---=-==- ⎪---⎝⎭, ∴当2n ≥时，11n n n b b n -=-， 故11n n n b b n++=，*n N ∈， 累乘得111232...12341n n n n n b b nb n n n n ---=⨯⨯⨯⨯=----， ∵13b =，∴3n b n =，*n N ∈.（3）∵1sin 3cos cos n n n c b b +=⋅ sin(333)tan(33)tan 3cos(33)cos3n n n n n n+-==+-+⋅， ∴12n n S c c c =++⋯+()(tan6tan3)(tan9tan6)tan(33)tan3n n =-+-+++-()tan 33tan3n =+-·【点睛】本题主要考查数列的通项公式和前n 项和的求法以及累乘法和裂项求和法、两角差的正弦公式的应用，还考查了运算求解的能力，属于中档题..16．已知数列{}n a 满足1a t =，111n na a +=+，数列{}n a 可以是无穷数列，也可以是有穷数列，如取1t =时，可得无穷数列：1，2，32，53，...；取12t =-时，可得有穷数列：12-，1-，0. （1）若50a =，求t 的值； （2）若12n a <<对任意2n ≥，*n N ∈恒成立.求实数t 的取值范围；（3）设数列{}n b 满足11b =-，()*111n n b n N b +=-∈，求证：t 取数列{}n b 中的任何一个数，都可以得到一个有穷数列{}n a .【答案】（1）35t =-；（2）1t >；（3）证明见解析. 【解析】【分析】（1）根据题意，得到111n n a a +=-，逐项计算，求出1a ，即可得出结果； （2）根据()*122,n a n n N <<≥∈，得出131122n na a +<=+<，因此只需212a <<即可，由题中条件，求出2a ，得出不等式求解，即可得出结果；（3）由题意，得到111n n b b +=+，设1k a t b ==，()*k N ∈，逐项计算，得出10k a +=，即可证明结论成立.【详解】（1）由111n n a a +=+得111n n a a +=-， ∴41101a ==--，311112a ==---，2121312a ==---，1132513t a ===---； （2）若()*122,n a n n N <<≥∈，则1112n a <<，131122n n a a +<=+<，即112n a +<<，故只要212a <<即可，因为1a t =，所以21t a t +=，∴112t t+<<，解得1t >； （3）由111n n b b +=-得111n n b b +=+， 设1k a t b ==，()*k N ∈，则2111k ka b b -=+= 32111k k a b b --=+=，12111k a b b =+==-，11101k a +=+=-， 故{}n a 有1k +项，为有穷数列.即t 取数列{}n b 中的任何一个数，都可以得到一个有穷数列{}n a .【点睛】本题主要考查由递推公式求数列中的项，考查由数列不等式恒成立求参数的问题，考查有穷数列的证明，属于常考题型.。

专题05 直线的倾斜角与斜率一、单选题1．（2020·四川省高二期末（理））直线x =( ) A ．30B ．45C ．60D ．902．（2019·四川省仁寿一中高二期中（文））若直线1x =的倾斜角为α，则α=（ ） A ．0B ．3πC ．2π D ．π3．（2020·江苏省丹徒高中高一开学考试）直线10x y ++=的倾斜角为（ ）A ．4πB ．34π C ．54π D ．2π 4．（2019·江苏省扬州中学高一期中）如果()3,1A 、()2,B k -、()8,11C 在同一直线上，那么k 的值是( ) A ．-6B ．-7C ．-8D ．-95．（2019·山东省高二期中）若直线过点(2,4)，(1,4+，则此直线的倾斜角是（ ） A ．30︒B ．60︒C ．120︒D ．150︒6．（2019·浙江省高三期中）以下哪个点在倾斜角为45°且过点（1，2）的直线上（ ） A ．（﹣2，3）B ．（0，1）C ．（3，3）D ．（3，2）7．（2020·四川省高二期末（理））已知一直线经过两点(2,4)A ，(,5)B a ，且倾斜角为135°，则a 的值为（ ） A ．-1B ．-2C ．2D ．18．（2019·浙江省高二期中）直线x sin α＋y ＋2＝0的倾斜角的取值范围是( ) A ．[0，π) B ．3[0,][,)44πππ⋃ C ．[0,]4πD ．[0,][,)42πππ⋃9．（2019·内蒙古自治区高二期末（文））已知直线l 的倾斜角为α，若tan 3πα⎛⎫+= ⎪⎝⎭α=（ ）A ．0B ．2π C ．56π D ．π10．（2019·浙江省镇海中学高一期末）已知直线倾斜角的范围是,32ππα⎡⎫∈⎪⎢⎣⎭2,23ππ⎛⎤⎥⎝⎦，则此直线的斜率的取值范围是（ ） A．⎡⎣B．(,-∞)+∞ C．⎡⎢⎣⎦D．,⎛-∞ ⎝⎦⎫+∞⎪⎪⎣⎭二、多选题11．（2020·吴江汾湖高级中学高一月考）下列说法中正确的是( ) A ．若α是直线l 的倾斜角，则0180α≤< B ．若k 是直线l 的斜率，则k ∈RC ．任意一条直线都有倾斜角，但不一定有斜率D ．任意一条直线都有斜率，但不一定有倾斜角12．（2020·江苏省苏州实验中学高一月考）有下列命题：其中错误的是（ ） A ．若直线的斜率存在，则必有倾斜角与之对应； B ．若直线的倾斜角存在，则必有斜率与之对应； C ．坐标平面上所有的直线都有倾斜角； D ．坐标平面上所有的直线都有斜率．13．（2018·全国单元测试）已知直线1:10l x y --=，动直线2:(1)0()l k x ky k k R +++=∈，则下列结论错误．．的是（ ） A ．不存在k ，使得2l 的倾斜角为90° B ．对任意的k ，1l 与2l 都有公共点 C ．对任意的k ，1l 与2l 都不．重合 D ．对任意的k ，1l 与2l 都不垂直．．．三、填空题14．（2019·银川唐徕回民中学高三月考（理））已知点P (1)，点Q 在y 轴上，直线PQ 的倾斜角为120°，则点Q 的坐标为_____．15．（2020·浙江省温州中学高三月考）平面直角坐标系中，直线倾斜角的范围为______，一条直线可能经过______个象限.16．（2019·浙江省效实中学高一期中）若直线斜率k ∈(－1,1)，则直线倾斜角α∈________.17．（2018·山西省山西大附中高二期中（文））已知直线l 经过点()1,0P 且与以()2,1A ，()3,2B -为端点的线段AB 有公共点，则直线l 的倾斜角的取值范围为____． 四、解答题18．（2019·全国高一课时练习）已知点()1,2A ，在y 轴上求一点P ，使直线AP 的倾斜角为120︒． 19．（2019·全国高一课时练习）点(,)M x y 在函数28y x =-+的图像上，当[2,5]x ∈时，求11y x ++的取值范围.20．（2020·广东省恒大足球学校高三期末）已知直线l ：320x y +-=的倾斜角为角α. （1）求tan α；（2）求sin α，cos2α的值.21．（上海市七宝中学高二期中）已知直线l 的方程为320x my -+=，其倾斜角为α. （1）写出α关于m 的函数解析式； （2）若3,34ππα⎛⎫∈ ⎪⎝⎭，求m 的取值范围.22．（2019·全国高一课时练习）经过点(0,1)P -作直线l ，若直线l 与连接(1,2)(2,1)A B -、的线段总有公共点.（1）求直线l 斜率k 的范围； （2）直线l 倾斜角α的范围；23．（上海位育中学高二期中）直角坐标系xOy 中，点A 坐标为(-2,0)，点B 坐标为(4,3)，点C 坐标为(1,-3)，且AM t AB =（t ∈R ）.(1) 若CM ⊥AB ，求t 的值；(2) 当0≤ t ≤1时，求直线CM 的斜率k 和倾斜角θ的取值范围.专题05 直线的倾斜角与斜率一、单选题1．（2020·四川省高二期末（理））直线x =( ) A ．30 B ．45C ．60D ．90【答案】D 【解析】直线x ∴其倾斜角为90. 故选：D .2．（2019·四川省仁寿一中高二期中（文））若直线1x =的倾斜角为α，则α=（ ） A ．0 B ．3πC ．2π D ．π【答案】C 【解析】直线1x =与x 轴垂直，故倾斜角为2π. 故选：C.3．（2020·江苏省丹徒高中高一开学考试）直线10x y ++=的倾斜角为（ ） A ．4π B ．34π C ．54π D ．2π 【答案】B 【解析】由题意，直线10x y ++=的斜率为1k =- 故3tan 14k παα==-∴= 故选:B4．（2019·江苏省扬州中学高一期中）如果()3,1A 、()2,B k -、()8,11C 在同一直线上，那么k 的值是( ) A ．-6 B ．-7C ．-8D ．-9【答案】D 【解析】(3,1)A 、(2,)B k -、(8,11)C 三点在同一条直线上，∴直线AB 和直线AC 的斜率相等， ∴11112383k --=---，解得9k =-．故选：D ．5．（2019·山东省高二期中）若直线过点(2,4)，(1,4+，则此直线的倾斜角是（ ） A ．30︒ B ．60︒C ．120︒D ．150︒【答案】C 【解析】由题意知，直线的斜率k =即直线的倾斜角α满足tan α=， 又0180α︒︒≤<，120α︒∴=，故选：C6．（2019·浙江省高三期中）以下哪个点在倾斜角为45°且过点（1，2）的直线上（ ） A ．（﹣2，3） B ．（0，1）C ．（3，3）D ．（3，2）【答案】B 【解析】由直线的倾斜角为45°，则直线的斜率为tan 451k ==，则过点()2,3-与点（1，2）的直线的斜率为321213-=---，显然点()2,3-不满足题意；过点()0,1与点（1，2）的直线的斜率为12101-=-，显然点()0,1满足题意； 过点()3,3与点（1，2）的直线的斜率为321312-=-，显然点()3,3不满足题意； 过点()3,2与点（1，2）的直线的斜率为22031-=-，显然点()2,3-不满足题意； 即点()0,1在倾斜角为45°且过点（1，2）的直线上， 故选：B.7．（2020·四川省高二期末（理））已知一直线经过两点(2,4)A ，(,5)B a ，且倾斜角为135°，则a 的值为（ ）A ．-1B ．-2C ．2D ．1【答案】D 【解析】由直线斜率的定义知,tan1351AB k ==-, 由直线的斜率公式可得,542AB k a -=-， 所以5412a -=--,解得1a =. 故选:D8．（2019·浙江省高二期中）直线x sin α＋y ＋2＝0的倾斜角的取值范围是( ) A ．[0，π) B ．3[0,][,)44πππ⋃ C ．[0,]4πD ．[0,][,)42πππ⋃ 【答案】B 【解析】直线xsinα+y +2＝0的斜率为k ＝﹣sinα， ∵﹣1≤sinα≤1，∴﹣1≤k ≤1 ∴倾斜角的取值范围是[0，4π]∪[34π，π） 故选：B ．9．（2019·内蒙古自治区高二期末（文））已知直线l 的倾斜角为α，若tan 3πα⎛⎫+= ⎪⎝⎭α=（ ） A ．0 B ．2π C ．56π D ．π【答案】A 【解析】tan 3πα⎛⎫+== ⎪⎝⎭tan 0α=，0απ≤<，0α∴=.故选:A10．（2019·浙江省镇海中学高一期末）已知直线倾斜角的范围是,32ππα⎡⎫∈⎪⎢⎣⎭2,23ππ⎛⎤⎥⎝⎦，则此直线的斜率的取值范围是（ ） A．⎡⎣B．(,-∞)+∞ C．,33⎡-⎢⎣⎦D．,3⎛-∞-⎝⎦3⎫+∞⎪⎢⎪⎣⎭【答案】B 【解析】因为直线倾斜角的范围是,32ππα⎡⎫∈⎪⎢⎣⎭2,23ππ⎛⎤ ⎥⎝⎦,又直线的斜率tan k α=,,32ππα⎡⎫∈⎪⎢⎣⎭2,23ππ⎛⎤⎥⎝⎦.故tan tan3πα≥=2tan tan3πα≤=故(,k ∈-∞)+∞. 故选：B 二、多选题11．（2020·吴江汾湖高级中学高一月考）下列说法中正确的是( ) A ．若α是直线l 的倾斜角，则0180α≤< B ．若k 是直线l 的斜率，则k ∈RC ．任意一条直线都有倾斜角，但不一定有斜率D ．任意一条直线都有斜率，但不一定有倾斜角 【答案】ABC 【解析】A. 若α是直线l 的倾斜角，则0180α≤<,是正确的；B. 若k 是直线l 的斜率，则tan k α=∈R ，是正确的；C. 任意一条直线都有倾斜角，但不一定有斜率，倾斜角为90°的直线没有斜率，是正确的；D. 任意一条直线都有斜率，但不一定有倾斜角，是错误的，倾斜角为90°的直线没有斜率. 故选：ABC12．（2020·江苏省苏州实验中学高一月考）有下列命题：其中错误的是（ ） A ．若直线的斜率存在，则必有倾斜角与之对应； B ．若直线的倾斜角存在，则必有斜率与之对应； C ．坐标平面上所有的直线都有倾斜角；D ．坐标平面上所有的直线都有斜率． 【答案】BD 【解析】任何一条直线都有倾斜角，但不是任何一条直线都有斜率 当倾斜角为90︒时，斜率不存在 故选：BD13．（2018·全国单元测试）已知直线1:10l x y --=，动直线2:(1)0()l k x ky k k R +++=∈，则下列结论错误．．的是（ ） A ．不存在k ，使得2l 的倾斜角为90° B ．对任意的k ，1l 与2l 都有公共点 C ．对任意的k ，1l 与2l 都不．重合 D ．对任意的k ，1l 与2l 都不垂直．．．【答案】AC 【解析】逐一考查所给的选项：A .存在0k =，使得2l 的方程为0x =，其倾斜角为90°，故选项不正确．B 直线1:10l x y --=过定点()0,1-，直线()()()2:1010l k x ky k k R k x y x +++=∈⇒+++=过定点()0,1-，故B 是正确的．C .当12x =-时，直线2l 的方程为1110222x y --=，即10x y --=，1l 与2l 都重合，选项C 错误；D .两直线重合，则：()()1110k k ⨯++-⨯=，方程无解，故对任意的k ，1l 与2l 都不垂直，选项D 正确． 故选：AC. 三、填空题14．（2019·银川唐徕回民中学高三月考（理））已知点P (1)，点Q 在y 轴上，直线PQ 的倾斜角为120°，则点Q 的坐标为_____． 【答案】(0，－2) 【解析】因为Q 在y 轴上，所以可设Q 点坐标为()0,y ，又因为tan120︒==2y =-，因此()0,2Q -，故答案为()0,2-.15．（2020·浙江省温州中学高三月考）平面直角坐标系中，直线倾斜角的范围为______，一条直线可能经过______个象限. 【答案】0, 0，2，3【解析】平面直角坐标系中，直线倾斜角的范围为[)0,π，一条直线可能经过2个象限，如过原点，或平行于坐标轴； 也可能经过3个象限，如与坐标轴不平行且不过原点时； 也可能不经过任何象限，如坐标轴； 所以一条直线可能经过0或2或3个象限． 故答案为：[)0,π，0或2或3．16．（2019·浙江省效实中学高一期中）若直线斜率k ∈(－1,1)，则直线倾斜角α∈________. 【答案】[0°，45°)∪(135°，180°) 【解析】直线的斜率为负时，斜率也随着倾斜角的增大而增大由于斜率有正也有负，且直线的斜率为正时，斜率随着倾斜角的增大而增大，故α∈(0°，45°)；又直线的斜率为负时，斜率也随着倾斜角的增大而增大，故α∈(135°，180°)；斜率为0时，α＝0°.所以α∈[0°，45°)∪(135°，180°) 故答案为[0°，45°)∪(135°，180°) 17．（2018·山西省山西大附中高二期中（文））已知直线l 经过点()1,0P 且与以()2,1A ，()3,2B -为端点的线段AB 有公共点，则直线l 的倾斜角的取值范围为____． 【答案】3[0,][,)44πππ 【解析】当直线l 过B 时，设直线l 的倾斜角为α，则3tan 14παα=-⇒=当直线l 过A 时，设直线l 的倾斜角为β，则tan 14πββ=⇒=综合：直线l 经过点()P 1,0且与以()A 2,1，()B 3,2-为端点的线段AB 有公共点时，直线l 的倾斜角的取值范围为][30,,44πππ⎡⎫⋃⎪⎢⎣⎭四、解答题18．（2019·全国高一课时练习）已知点()1,2A ，在y 轴上求一点P ，使直线AP 的倾斜角为120︒．【答案】(0,2P 【解析】设(0,)P y ，201PA y k -=-，tan120︒∴＝201y --，2y ∴=P ∴点坐标为(0,2.19．（2019·全国高一课时练习）点(,)M x y 在函数28y x =-+的图像上，当[2,5]x ∈时，求11y x ++的取值范围. 【答案】15,63⎡⎤-⎢⎥⎣⎦【解析】1(1)1(1)y y x x +--=+--的几何意义是过(,),(1,1)M x y N --两点的直线的斜率，点M 在线段28,[2,5]y x x =-+∈上运动，易知当2x =时，4y =，此时(2,4)M 与(1,1)N --两项连线的斜率最大，为53； 当5x =时，2y =-，此时(5,2)M -与(1,1)N --两点连线的斜率最小，为16-.115613y x +∴-+,即HF 的取值范围为15,63⎡⎤-⎢⎥⎣⎦20．（2020·广东省恒大足球学校高三期末）已知直线l ：320x y +-=的倾斜角为角α.（1）求tan α；（2）求sin α，cos2α的值.【答案】（1）13-；（2）10；45 【解析】（1）因为直线320x y +-=的斜率为13-，且直线的倾斜角为角α， 所以1tan 3α=- （2）由（1）知1tan 3α=-， 22sin 1tan cos 3sin cos 1ααααα⎧==-⎪∴⎨⎪+=⎩解得sin 10cos αα⎧=⎪⎪⎨⎪=⎪⎩sin 10cos αα⎧=-⎪⎪⎨⎪=⎪⎩， 因为,2παπ⎛⎫∈ ⎪⎝⎭，所以sin cos αα⎧=⎪⎪⎨⎪=⎪⎩224cos 22cos 1215αα⎛∴=-=⨯-= ⎝⎭21．（上海市七宝中学高二期中）已知直线l 的方程为320x my -+=，其倾斜角为α.（1）写出α关于m 的函数解析式；（2）若3,34ππα⎛⎫∈ ⎪⎝⎭，求m 的取值范围. 【答案】（1）3arctan ,0,023arctan ,0m m m m m παπ⎧>⎪⎪⎪==⎨⎪⎪+<⎪⎩；（2）3,3m .【解析】（1）直线l 的方程为320x my -+=，其倾斜角为α，当0m =时，2πα=当0m >时，则斜率3tan k m α==，3arctan m α=， 当0m <时，则斜率3tan k m α==，3arctan mαπ=+， 所以3arctan ,0,023arctan ,0m m m m m παπ⎧>⎪⎪⎪==⎨⎪⎪+<⎪⎩； （2）当,32ππα时，33,,0,3k m m ，当2πα=时，0m =， 当3,24ππα时，3,1,3,0k m m ， 综上所述：3,3m .22．（2019·全国高一课时练习）经过点(0,1)P -作直线l ，若直线l 与连接(1,2)(2,1)A B -、的线段总有公共点.（1）求直线l 斜率k 的范围；（2）直线l 倾斜角α的范围；【答案】（1）11k -≤≤（2）3044ππααπ≤≤≤<或 【解析】（1）2(1)110pA k --==-- 1(1)120pB k --==- l 与线段AB 相交pA pB k k k ∴≤≤11k ∴-≤≤（2）由（1）知0tan 11tan 0αα≤≤-≤<或由于tan 0,2y x π⎡⎫=⎪⎢⎣⎭在及(,0)2π-均为减函数3044ππααπ∴≤≤≤<或 23．（上海位育中学高二期中）直角坐标系xOy 中，点A 坐标为(-2,0)，点B 坐标为(4,3)，点C 坐标为(1,-3)，且AM t AB =（t ∈R ）.(1) 若CM ⊥AB ，求t 的值；(2) 当0≤ t ≤1时，求直线CM 的斜率k 和倾斜角θ的取值范围.【答案】(1) 15t =；(2) k ∈(-∞.,-1]⋃[2,+∞]，3[arctan 2,]4πθ∈ 【解析】(1)由题意可得()42,30(6,3)AB =+-=，(6,3)AM t AB t t ==， ()12,30(3,3)AC =+--=-，所以(63,33)CM AM AC t t =-=-+， ∵CM AB ⊥，则CM AB ⊥，∴()()6633334590CM AB t t t ⋅=-++=-=， ∴解得15t =； (2)由01t ≤≤，AM t AB =，可得点M 在线段AB 上，由题中A 、B 、C 点坐标，可得经过A 、C 两点的直线的斜率11k =-，对应的倾斜角为34π，经过C 、B 两点的直线的斜率22k =，对应的倾斜角为2arctan ,则由图像可知(如图所示)，直线CM 的斜率k 的取值范围为：1k ≤-或2k ≥，倾斜角的范围为：3[arctan 2,]4πθ∈.。