当前位置：文档之家 › 双曲线与抛物线的参数方程 PPT课件

双曲线与抛物线的参数方程 PPT课件

  • 格式：ppt
  • 大小：168.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

椭圆双曲线抛物线的参数方程课件

椭圆双曲线抛物线的参数方程课件

y A
B O M N
φ
x
a b x a cos (为参数) 椭圆的参数方程: y b sin
椭圆的参数方程中参数φ的几何意义: 是∠AOX=φ,不是∠MOX=φ.
圆的标准方程: x2+y2=r2
y
P θ
x r cos 圆的参数方程: (为参数) y r sin θ的几何意义是 ∠AOP=θ
x a cos y b sin 是椭圆的参
另外, 称为离心角,规定参数 的取值范围是 [0, 2 )
x a cos , x b cos , 焦点在X 轴 焦点在Y 轴 y b sin . y a sin .
知识归纳 x2 y2 椭圆的标准方程: 2 2 1
AB (2 p( t t ), 2 p( t 2 t1 ))
2 2 2 1

因为 OA OB , 所以 OA OB 0, 即 (2 pt1t 2 )2 (2 p)2 t1t 2 0, 所以t1t 2 1...........(8)




因为 OM AB, 所以 OM OB 0, 即
2 sin( ) 4
所以当 =

4 这时点P的坐标为( 3 2 2 , 2)
时, d 有最大值, 面积最大
抛物线的参数方程
y
M(x,y)

o
(
x

, ) 2 2
设抛物线的普通方程为 y 2 2 px ...........(5) 因为点M 在的终边上，根据三角函数的 y 定义可得 tan ..................................(6) x 2p x tan 2 由(5),(6)解出x , y，得到 ( 为参数） y 2p tan 这就是抛物线(5)(不包括顶点)的参数方程

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

x2 y2 设椭圆a2＋b2＝1，∴a＝5，c＝4，b＝3. x2 y2 ∴方程为25＋ 9 ＝1. 设椭圆上一点 P(5cos θ，3sin θ)， 双曲线一渐近线为 3x－4y＝0， |3×5cos θ－12sin θ| ∴点 P 到直线的距离 d＝ 5 3| 41sin θ－φ| 5 ＝ (tan φ＝4)． 5 3 41 ∴dmax＝ 5 .
[通一类] 2．已知抛物线
x＝2t2 C： y＝2t
(t 为参数)，设 O 为坐标原点，点 M
在抛物线 C 上，且点 M 的纵坐标为 2，求点 M 到抛物线焦点 的距离．
x＝2t2 解：由 y＝2t
，得 y2＝2x，即抛物线的标准方程为 y2＝2x.
又∵M 点的纵坐标为 2，∴M 点的横坐标也为 2. 即 M(2,2)． 1 又∵抛物线的准线方程为 x＝－2. 1 1 5 ∴由抛物线的定义知|MF|＝2－(－2)＝2＋2＝2. 5 即点 M 到抛物线焦点的距离为2.
[研一题] [例 2] 连结原点 O 和抛物线 2y＝x2 上的动点 M，延长 OM
到 P 点，使|OM|＝|MP|，求 P 点的轨迹方程，并说明它是何曲线．
[精讲详析]

本题考查抛物线的参数方程的求法及其应用． 解
答本题需要先求出抛物线的参数方程并表示出 M、P 的坐标，然 后借助中点坐标公式求解．
[悟一法] 对于同一个方程，确定的参数不同， 所表示的曲线就不同， 当题目条件中出现多个字母时，一定要注明什么是参数，什么是 常量，这一点尤其重要．
[通一类]
x＝ 5cos 3．(2011· 广东高考)已知两曲线参数方程分别为 y＝sin θ
θ
5 x＝ t2 4 (0≤θ≤π)和 (t∈R)， 它们的交点坐标为___________． y＝t

参数方程双曲线与抛物线的参数方程

参数方程双曲线与抛物线的参数方程
• e = 1。 • 偏心率：双曲线的偏心率是e' = \sqrt{1 - \frac{b^2}{a^2}}，其中a
是长半轴长度，b是短半轴长度。对于抛物线，由于对称性，偏心率 不存在。
准线方程
双曲线
准线方程为<math>x = \pm \frac{a^2}{c}</math>。
抛物线
准线方程为<math>x = \pm \frac{p}{2}</math>或<math>y = \pm \frac{p}{2}</math>，取决于抛物线的形式
抛物线参数方程
抛物线的参数方程在几何作图中，可以用来绘制出各种 弧线、曲线和对称图形，为解决一些几何问题提供便利 。
在物理学中的应用
参数方程双曲线
在物理学中，双曲线的参数方程常常被用来描述一些物理现象，例如振动、 波动、粒子运动等。
抛物线参数方程
抛物线的参数方程在物理学中可以用来描述一些运动轨迹，例如斜抛、平抛 等运动。
参数方程双曲线与抛物线的 参数方程
2023-11-04
contents
目录
• 参数方程双曲线的参数方程 • 参数方程抛物线的参数方程 • 参数方程双曲线与抛物线的共性 • 参数方程双曲线与抛物线的特性 • 参数方程双曲线与抛物线的应用
01
参数方程双曲线的参数方 程
定义与标准形式
定义
参数方程双曲线是一种通过参数t表示的平面曲线。
参数t的几何意义
参数t
在抛物线的参数方程中，t是一个参数， 它表示从焦点到曲线上任意一点的距离。
VS
几何意义
当t增加时，表示从焦点到曲线上一点的 距离增加，这符合抛物线的几何特性。

椭圆、双曲线、抛物线PPT课件

椭圆、双曲线、抛物线PPT课件

(2)证明：设线段 AB 的中点坐标为 N(x0，y0)，A(x1， y1)，B(x2，y2)，因为 AB 不垂直于 x 轴， 则直线 MN 的斜率为x0y－0 4，直线 AB 的斜率为 4－x0，
y0 直线 AB 的方程为 y－y0＝4－y0x0(x－x0)，
联立方程y－y0＝4－y0x0x－x0， y2＝4x，
第13页/共50页
【解】 (1)由已知得 c＝2 2，ac＝ 36， 解得 a＝2 3. 又 b2＝a2－c2＝4， 所以椭圆 G 的方程为1x22＋y42＝1.
第14页/共50页
(2)设直线 l 的方程为 y＝x＋m.
y＝x＋m， 由1x22 ＋y42＝1，
得 4x2＋6mx＋3m2－12＝0.①
第31页/共50页
消去 x 得(1－x40)y2－y0y＋y20＋x0(x0－4)＝0， 所以 y1＋y2＝4－4y0x0， 因为 N 为 AB 的中点， 所以y1＋2 y2＝y0， 即4－2y0x0＝y0， 所以 x0＝2，即线段 AB 中点的横坐标为定值 2.
第32页/共50页
轨迹问题
例4 (1)若动圆 P 过点 N(－2,0)，且与另一圆 M： (x－2)2＋y2＝8 相外切，则动圆 P 的圆心的轨迹方 程是__________； (2)已知直线 l：2x＋4y＋3＝0，P 为 l 上的动点， O 为坐标原点．若 2O→Q＝Q→P，则点 Q 的轨迹方程 是__________．
第18页/共50页
变式训练 2 已知过抛物线 y2＝2px(p＞0)的焦点， 斜率为 2 2的直线交抛物线于 A(x1，y1)，B(x2， y2)(x1＜x2)两点，且|AB|＝9. (1)求该抛物线的方程； (2)O 为坐标原点，C 为抛物线上一点，若O→C＝O→A ＋λO→B，求 λ 的值．

2.2《双曲线的参数方程》课件(新人教选修4-4).ppt

2.2《双曲线的参数方程》课件(新人教选修4-4).ppt

o B A' x
⑴ 这里参数 叫做双曲线的离心角与直线OM的倾斜角不同.
⑵se双c2曲线的1参t数an方2 程相可比以较由而方得程到，ax22所以by22双曲1与线三的角参恒数等方式程
的实质是三角代换.
例2、如图，设M
为双曲线
x2 a2
y2 b2
1(a 0, b 0)任意一点，O为原点，
过点M 作双曲线两渐近线的平行线，分别与两渐近线交于A，B两点。
二、圆锥曲线的参数方程
2、双曲线的参数方程
双曲线的参数方程
设M (x, y)
y
a
B'
A
•M
在OAA'中，x
| OA' | | OA | b b • sec,
cos cos
b
o B A' x
在OBB '中，y | BB ' || OB | • tan b • tan.
所以M的轨迹方程是
x
①
A
M
O B
x
a
所以MAOB的面积为
S
MAOB =|OA|•|OB|sin2 =
xA
cos
•
xB
cos
sin2
=
a2(sec2 -tan2 4cos2
)
•
sin2
=
a2 2
•
tan
a2行四边形MAOB的面积恒为定值，与点M在双曲线上的位置无关。
探求平行四边形MAOB的面积，由此可以发现什么结论？
解：双曲线的渐近线方程为：y b x.
a 不妨设M为双曲线右支上一点，其坐标为（asec,btan）,
y
则直线MA的方程为：y b tan b (x a sec).

双曲线的参数方程.抛物线参数方程

双曲线的参数方程.抛物线参数方程
由此可见, 的面积恒为定值, 由此可见 平行四边形 MAOB 的面积恒为定值 与点 M 在双曲线上的位置无关 在双曲线上的位置无关.
备选例题
设P是双曲线b 2 x 2 − a 2 y 2 = a 2b 2 ( a > 0, b > 0)上任意一点, 过点P作双曲线两渐近线的平行线,分别与两渐近线相交 a 2 + b2 R,求 于点Q和R,求证: PQ PR = 4
(±2 15, 0)
x = 3sec ϕ 2、双曲线{ (ϕ为参数)的渐近线方程为 _______ y = tan ϕ
1 y=± x 3
例1、已知圆O : x + ( y − 2) = 1上一点 P 与双曲线
2 2ห้องสมุดไป่ตู้
x 2 − y 2 = 1上一点 Q ，求 P、Q 两点距离的最小值
解：设双曲线上点的坐标为Q(secθ , tan θ ) 先求圆心到双曲线上点的最小距离 OQ = sec 2 θ + (tan θ − 2) 2
二、圆锥曲线的参数方程
2、双曲线的参数方程
4
B′ A M
2
x
-5
O
B
5
A′
-2
-4
双曲线的参数方程
设M ( x , y )
| OA ' |=
在 ∆ OAA '中 ， x = a | OA |
cos ϕ =
在∆OBB '中，y = | BB ' |=| OB | ⋅ tan ϕ = b ⋅ tan ϕ .
同理, 得点B的横坐标为 同理 得点 的横坐标为
a xB = (sec ϕ − tan ϕ ). 2
设
∠AOx = α, 则

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

x＝ 5cos 解析：由 y＝sin θ
θ
x2 2 (0≤θ≤π)得 5 ＋y ＝1(y≥0)，
52 x＝ t 5 2 4 由 (t∈R)得 x＝4y . y＝t
2 x ＋y2＝1， 5 联立方程可得 x＝5y2 4
则 5y4＋16y2－16＝0，
4 5 2 2 解得 y ＝5或 y ＝－4(舍去)，则 x＝4y ＝1.
[悟一法] 对于同一个方程，确定的参数不同， 所表示的曲线就不同， 当题目条件中出现多个字母时，一定要注明什么是参数，什么是 常量，这一点尤其重要．
[通一类]
x＝ 5cos 3．(2011· 广东高考)已知两曲线参数方程分别为 y＝sin θ
θ
5 x＝ t2 4 (0≤θ≤π)和 (t∈R)， 它们的交点坐标为___________． y＝t
(t 为参
数)，其中 p>0，焦点为 F，准线为 l.过抛物线上一点 M 作 l 的垂 线， 垂足为 E.若|EF|＝|MF|， M 的横坐标是 3， p＝________. 点 则
[命题立意]
本题考查抛物线的参数方程与普通方程的互化
及抛物线定义的应用．
[解析]
由题意知，抛物线的普通方程为 y2＝2px(p>0)，焦点
[研一题] [例 2] 连结原点 O 和抛物线 2y＝x2 上的动点 M，延长 OM
到 P 点，使|OM|＝|MP|，求 P 点的轨迹方程，并说明它是何曲线．
[精讲详析]
本题考查抛物线的参数方程的求法及其应用． 解
答本题需要先求出抛物线的参数方程并表示出 M、P 的坐标，然 后借助中点坐标公式求解．
设 M(x、y)为抛物线上的动点，P(x0，y0)在抛物线的延长 线上， M 为线段 OP 且

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

提示：参数 α 表示抛物线上除顶点外的任意一点 M，以射线 OM 为终边的角．
[研一题] [例 1] 距离为 2. 在双曲线 x2－y2＝1 上求一点 P， P 到直线 y＝x 的 使
[精讲详析]
本题考查双曲线的参数方程的应用，解答本题
需要先求出双曲线的参数方程， 设出 P 点的坐标， 建立方程求解． 设 P 的坐标为(secφ， φ)， P 到直线 x－y＝0 的距离为 2 tan 由 |secφ－tan φ| 得 ＝ 2 2 1 sin φ 得|cos φ－cos φ|＝2，|1－sin φ|＝2|cos φ|
[读教材· 填要点] 1．双曲线的参数方程 x2 y2 (1)中心在原点， 焦点在 x 轴上的双曲线a2－b2＝1 的参数方程是 x＝asecφ π 3π φ∈[0,2π)且 φ≠2，φ≠ 2 y＝btan φ 规定参数 φ 的取值范围为 y2 x2 (2)中心在原点， 焦点在 y 轴上的双曲线a2－b2＝1 的参数方程是 x＝btan φ y＝asecφ .
x＝ 5cos 解析：由 y＝sin θ
θ
x2 2 (0≤θ≤π)得 5 ＋y ＝1(y≥0)，
52 x＝ t 5 2 4 由 (t∈R)得 x＝4y . y＝t
2 x ＋y2＝1， 5 联立方程可得 x＝5y2 4
则 5y4＋16y2－16＝0，
4 5 2 2 解得 y ＝5或 y ＝－4(舍去)，则 x＝4y ＝1.
2．抛物线的参数方程 (1)抛物线 y2＝2px 的参数方程为
x＝2pt2 y＝2pt
，t∈ R .
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与原点 连线的 斜率的倒数 ．
[小问题·大思维]

双曲线的参数方程抛物线的参数方程

双曲线的参数方程抛物线的参数方程

,
xQ
a cos 1 sin
所以 OP OQ xP xQ a2 为定值
3、证明：设等轴双曲线的普通方程为
x2 y2 a2 (a 0),则它的参数方程为
x {
a
sec
(为参数)
y a tan
设M (a sec, a tan )是双曲线上任意一点，则
点M 到两渐近线y x, 及y x的距离之积为
解: 双曲线的渐近线方程为 y b x . 不妨设M为双曲 a
线右支上一点, 其坐标为(a sec,b tan ) , 则直线MA的方
程为 y b tan b (x a sec)
将
y
b
x
a
代入上式, 解得点A的
a
横坐标为
xA
a 2
(sec
tan )
同理, 得点B的横坐标为
xB
a 2
(sec
x p pk 2
{
k2 p
(k为参数)
y pk
k
6.已知椭圆C1
:
x=m+2cos y= 3 sin
(为参数)及
抛物线C2
:
y2
6( x
3 2
).若C1
C2
,
求m的取值范围.
t2
(x
2
pt12 )
所以点D的坐标为(2 pt1t2 ,0)
直线AC的方程为y
2
pt1
t1
1
t2
(x
2
pt12
)
所以E的坐标为(2 pt1t2 ,0)
因为DE的中点为原点(0,0),所以抛物线的顶点
O平分线段DE。
5、解：直线OA的方程为y kx，直线OB的方程为y 1 x k

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

提示：参数 α 表示抛物线上除顶点外的任意一点 M，以射线 OM 为终边的角．
[研一题] [例 1] 距离为 2. 在双曲线 x2－y2＝1 上求一点 P， P 到直线 y＝x 的 使
[精讲详析]
本题考查双曲线的参数方程的应用，解答本题
需要先求出双曲线的参数方程， 设出 P 点的坐标， 建立方程求解． 设 P 的坐标为(secφ， φ)， P 到直线 x－y＝0 的距离为 2 tan 由 |secφ－tan φ| 得 ＝ 2 2 1 sin φ 得|cos φ－cos φ|＝2，|1－sin φ|＝2|cos φ|
[悟一法] 参数方程是用一个参数表示曲线上点的横纵坐标的，因而曲 线的参数方程具有消元的作用，利用它可以简化某些问题的求解 过程，特别是涉及到最值、定值等问题的计算时，用参数方程可 将代数问题转化为三角问题，然后利用三角知识处理．
[通一类] 1．求证：等轴双曲线平行于实轴的弦为直径的圆过双曲线的顶 点．
证明：设双曲线为 x2－y2＝a2，取顶点 A(a,0)， 弦 B′B∥Ox，B(asecα，atan α)，则 B′(－asecα，atan α)． atan α atan α ∵kB′A＝ ，kBA＝ ， －asecα－a asecα－a ∴kB′A·BA＝－1. k ∴以 BB′为直径的圆过双曲线的顶点.
2．抛物线的参数方程 (1)抛物线 y2＝2px 的参数方程为
x＝2pt2 y＝2pt
，t∈ R .
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与原点 连线的 斜率的倒数 ．
[小问题·大思维]
1．在双曲线的参数方程中，φ的几何意义是什么？ 提示：参数φ是点M所对应的圆的半径OA的旋转角(称为点 M的离心角)，而不是OM的旋转角．

高二数学双曲线的参数方程课件

高二数学双曲线的参数方程课件
设OA与OX所成的角为φ(φ ∈[0, 2π)且φ ≠ φ, ≠ )3,求点M的轨迹方程, 并说出点 M的2 轨迹。2
双曲线的参数方程 设M(x, y)
y
a
B'
A
•M
在 O AA'中 ， x
o B A' x
| OA' | | OA | c,
b
在 OBB'中 ， y|B B '| |O B |•tanb • tan.
所 以 M 的 轨 迹 方 程 是 x y a b s ta ec n (为 参 数 )
消 去 参 数 后 ， 得x2-y2=1, a2 b2
这 是 中 心 在 原 点 ， 焦 点 在 x轴 上 的 双 曲 线 。
双曲线的参数方程
y
x2-y2=1(a>0,b>0)的 参 数 方 程 为 ： a a2 b2
的实质是三角代换.
双曲线的参数方程(焦点在x轴上)
双曲线的参数方程(焦点在x轴上)
1.标准普通方程
x2 y2 a2 b2 1 (a 0,b 0)
标准参数方程
平 x a sec [0，2 )
移
y
b tan
2
,
3
2
双曲线的参数方程(焦点在x轴上)
1.标准普通方程
x2 y2 a2 b2 1 (a 0,b 0)
AB '
•M
通 常 xy规 ab定 stae nc [(o ,为 2 参 )且 数 )， 3 。 b
oB
A' x
22
说明：
⑴ 这里参数 叫做双曲线的离心角与直线OM的倾斜角不同.
⑵se双c2曲线的1 参t数an方2程相可比以较由而方得程到，ax 22所 以by 22双曲1 与线三的角参恒数等方式程

高中数学 第二讲 参数方程 2-2-2 双曲线与抛物线的参数方程课件 新人教A版选修4-4

高中数学 第二讲 参数方程 2-2-2 双曲线与抛物线的参数方程课件 新人教A版选修4-4

5．过抛物线 y2＝4ax(a>0)的顶点，引互相垂直的两条射线 OA、OB，求顶点 O 在 AB 上的射影 H 的轨迹方程．
解析 设抛物线上动点A、B的坐标为(at12，2at1)和(at22， 2at2)(t1，t2≠0)，则AB的方程为2x－(t1＋t2)y＋2at1t2＝0.
∵OA⊥OB，∴2aat1t21·2aat2t22＝－1即t1t2＝－4. ∴AB的方程为2x－(t1＋t2)y－8a＝0.① 过点O与AB垂直的直线OP的方程为 (t1＋t2)x＋2y＝0.② 由①②消去t1，t2，得x2＋y2－4ax＝0. 故所求轨迹为圆心为(2a，0)，半径为2|a|的圆．
π 当tanθ－1＝0即θ＝ 4 时，|M0M|2取最小值3，此时有|M0M|
＝ 3，即M0点到双曲线的最小距离为 3.
思考题2 设P为等轴双曲线x2－y2＝1上的一点，F1，F2
为两个焦点，证明：|F1P|·|F2P|＝|OP|2. 【解析】 如图所示，设双曲线上的动点为P(x，y)，焦点
F1(－ 2，0)，F2( 2，0)，
课时学案
题型一 写出圆锥曲线的参数方程 例1 写出下列圆锥曲线的参数方程： (1)x2－y2＝4； (2)y2＝4x. 【解析】 根据圆锥曲线参数方程的写法可直接写出． (1)xy＝ ＝22staencθθ，(θ∈[0，2π)且θ≠π2 ，θ≠3π 2 )；
x＝4t2， (2)y＝4t.
思考题1 写出下列圆锥曲线的参数方程：
(1)x42－y92＝1； (2)x2＝4y.
x＝2secθ，
π
【答案】 (1)y＝3tanθ (θ为参数，θ∈[0，2π)且θ≠ 2 ，
ቤተ መጻሕፍቲ ባይዱ
3π θ≠ 2 )

双曲线的参数方程、抛物线的参数方程

双曲线的参数方程、抛物线的参数方程

a2 (sec2 tan 2 ) sin 2 4 cos2
a2 tan a2 b ab .
2
2a 2
由此可见, 平行四边形 MAOB 的面积恒为定值, 与点
M 在双曲线上的位置无关.
例3.设P是双曲线b2 x2 a2 y2 a2b2 (a 0,b 0)上任意一点, 过点P作双曲线两渐近线的平行线,分别与两渐近线相交 于点Q和R,求证: PQ PR a2 b2
1、解：因为2a 15565，2b 15443,所以
a 7782.5,b 7721.5,所求的椭圆的参数
方程为
x {

7782.5 cos
(为参数)
y 7721.5sin
2、证明：设M (a cos, b sin ), P(xp , 0), Q(xQ , 0)，
因为P、Q分别为B1M , B2M 与x轴的交点， 所以 KB1P KB1M , KB2Q KB2M 由斜率公式计算得
(2 15, 0)
2、双曲线{x 3sec (为参数)的渐近线方程为_______ y tan y 1 x 3
例1、已知圆O : x2 ( y 2)2 1上一点P与双曲线 x2 y2 1上一点Q，求 P、Q 两点距离的最小值
解：设双曲线上点的坐标为Q(sec , tan )
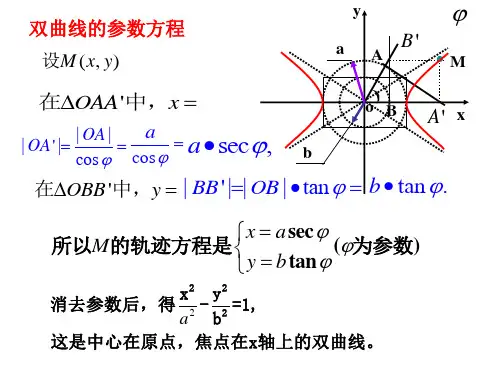
x

y

a sec b tan
(为参数)
消去参数后，得
x2 a2
-
y2 b2
=1,
这是中心在原点，焦点在x轴上的双曲线。
双曲线的参数方程
x2 a2
-
y2 b2
1(a
0,b

4-4第二讲双曲线、抛物线的参数方程经典课件

4-4第二讲双曲线、抛物线的参数方程经典课件

题组一： 写出下列双曲线的参数形式： 2 2 x y 1、 1 9 16 2 2 y x 2、 1 9 7 2 2 x y 3、 1 36 64 2 2 4、 3 x y 75
题组二： 已知双曲线的参数形式，写出普通式： 1
２
３
x 2sec y 3tan x 5sec y 7 tan 1 x sec 3 y tan
(0, )
y
x 2 py
2
o
x
令t tan
x 2 pt x 2 pt (t为参数) 2 y 2 pt (t R) y 2 pt2
﹒ ﹒ ﹒
y
图 形
o
焦
点
准
线
标准方程
x
y
o
x
y
o
x
y
﹒
o
x
例1：如图，O是直角坐标原点，A、B 是抛物线y2=2px (p>0)上异于顶点的两 动点，且OA⊥OB，OM ⊥AB并与AB 相交于点M，求点M的轨迹方程 y
x a sec 所以M的轨迹方程是 (为参数) y b tan
x2 y2 消去参数后，得 2 - 2 =1, a b 这是中心在原点，焦点在x轴上的双曲线。
双曲线的参数方程
x2 y2 - 2 =1(a>0,b>0)的参数方程为： 2 a b
a
y

A B' o B
•M
A' x
M
x
2 2 a2(sec2 -tan2 ) = sin2 = a tan a b ab . 4cos2 2 2 a 2
由此可见，平行四边形MAOB的面积恒为定值，(3) -----抛物线的参数方程
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可以互相讨论下，但要小声点
思考2：联立y2＝2px和y＝xtanα，可得 x，y分别等于什么？
xta2n2p,yta2np
思考3：参数方程
x
y
2p
t a n 2 （α为参数）
2p
ta n
是抛物线y2＝2px的参数方程吗？
思考4：用t替换
1 tan
，得
x 2 pt2
y
2
pt
x 2 pt2
探究（一）：双曲线的参数方程
思考1：由 1 sin 2
cos2
1
，得
1
cos2
tan2
1
记 1 sec ，则 sec2tan21
cos
类比建立椭圆参数方程的方法，双曲线
x2 a2
y2 b2
1(a0,b0)的参数方程是什么？
x a sec
y
b
tan
（φ为参数）
思考2：如图，以原点O为圆心，a，b
2.在研究圆锥曲线上的动点或未知点 的有关问题时，可利用其参数方程设出 点的坐标，从而拓广了解决问题的途径， 优化了解题思路.
3.利用圆锥曲线的参数方程解题时， 一般不考虑参数的几何意义，只利用参 数方程的外在形式.
那么参数方程
y
2
pt
（t为参数）是
抛物线y2＝2px的参数方程吗？参数t的
几何意义是什么？
参数t表示抛物线上除顶点外的任意一点 与原点连线的斜率的倒数.
思考5：设点M为抛物线y2＝2px(p＞0)上
任意一点，若以点M到抛物线准线的距离 t为参数，则该抛物线的参数方程是什么？
x
t
p 2
或
y
2 pt p2
双曲线与抛物线的 参数方程
复习提问：椭圆的参数方程
1、对于椭圆方程 x2 y2 1(ab0)
a2 b2
由此得到椭圆的参数方程是什么？
x a cos
y
b sin
（φ为参数）
2、类似地，椭圆
y2 a2
x2 b2
1(ab0)
的参数方程是什么？
x y
b a
cos sin
（φ为参数）
3、参数φ几何意义是什么？范围？
上异于顶点的两动点，O为原点，OA⊥OB，
OM⊥AB，并与AB相交于点M.
(1)求点M的轨迹方程；
（2）求△AOB面积的最小值.
x2＋y2－2px＝0 y A
4p2
(x≠0)
M
O
x
B
小结作业
1.对同一条曲线选取不同的参数，就 得到不同形式的参数方程，对圆锥曲线 的参数方程，只要求掌握上述几种形式.
(a＞0，b＞0)为半径分别作两个同心圆
C1，C2，设点A为圆C1上任意一点，点B为 圆C2与x轴的交点，设以Ox为始边，OA为 终边的角为φ，则asecφ和btanφ的几
何意义分别是什么？ y B′
A
asecφ是点A′
的横坐标，
φ
btanφ是点B′ O B
A′ x
的纵坐标.
思考3：设点M(asecφ，btanφ)，则点M 在双曲线上，如何根据点A′，B′的位 置确定点M的位置？
yt M
O
x
x
y
t
p 2 2 pt
p2
（t为参数）
例1 设点M为双曲线
x2
y2
1(a0,b0)上任意一点，
a2 b2
O为原点，过点M作双曲线两渐近线的平
行线，分别与两渐近线交于A，B两点，
试探求平行四边形MAOB的面积，由此可
以发现什么结论？
y
S ab 2
A M
OB
x
例2 设点A，B是抛物线y2＝2px(p＞0)
bx22
1(a0,b0)的参数方程是什么？
x b tan
y
a
sec
（φ为参数）
探究（二）：抛物线的参数方程
思考1：对于抛物线y2＝2px(p＞0)，设 点M(x，y)为抛物线上除顶点外的任意一 点，以Ox为始边，OM为终边的角为α， 则x，y，α三者关系是什么？
yM
y tan
x
α
O
x
大家有疑问的，可以询问和交流
过点A′作x轴的
y B′ A
M
垂线，过点B′作
x轴的平行线，其
φ
交点为M.
OB
A′ x
思考4：双曲线参数方程中参数φ叫做点
M的离心角，以Ox为始边，OM为终边的角
θ叫做点M的旋转角，怎样理解这两个角
的大小关系？
y B′
A
M
当φ和θ都为锐
角时，φ＞θ.
φ
A′ x
思考5：类似地，双曲线
y2 a2