当前位置：文档之家 › 齐次状态方程的解

齐次状态方程的解

  • 格式：ppt
  • 大小：1.38 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

浙大控制考研-现代控制理论(浙大)第二章

浙大控制考研-现代控制理论(浙大)第二章

1 A2t 2 2!
1 k
Aktk
)
b0
t 0 x(0) b0
x(t) (I At 1 A2t 2 1 Akt k )x(0)
2!
k
eAt I At 1 A2t 2 1 Akt k
2!
k
矩阵指数函数
Φ(t) 状态转移矩阵
x(t) eAtx(0) 描述了状态向量由初始状态x(0)向任意时 刻状态 x(t)转移的内在特性。
eAt I At 1 A2t 2 1 Akt k
2!
k
1）根据状态转移矩阵的定义求解：
eAt I At 1 A2t 2 1 Akt k
2!
k!
对所有有限的t值来说，这个无穷级数都是收敛的 。
求出的解不是解析形式，适合于计算机求解。
例：求解系统状态方程 解：
x1
x2
0 0
-11
6
-6 -11 5
试计算状态转移矩阵 eAt .
解: 1) 特征值
1 1
I A 6 -11 6 1 2 3 0
6 11 5
1 1,2 2,3 3
2) 计算特征向量：
1 1 1 p1 0, p2 2, p3 6
1 4 9
3) 构造变换阵P：
1 1 1 P 0 2 6
(A B)3 A3 B3 3A2B 3AB 2
(9) x Px Φ(t) P-1Φ(t)P P-1eAtP
证明：非奇异线性变换
x Px
n n非奇异矩阵 另一组状态变量
x Px
x P1AP x x(t) eP1AP x(0)
x Ax APx 新的系统矩阵 新的状态转移矩阵
Ax
eAt x(0) Φ(t)x(0)

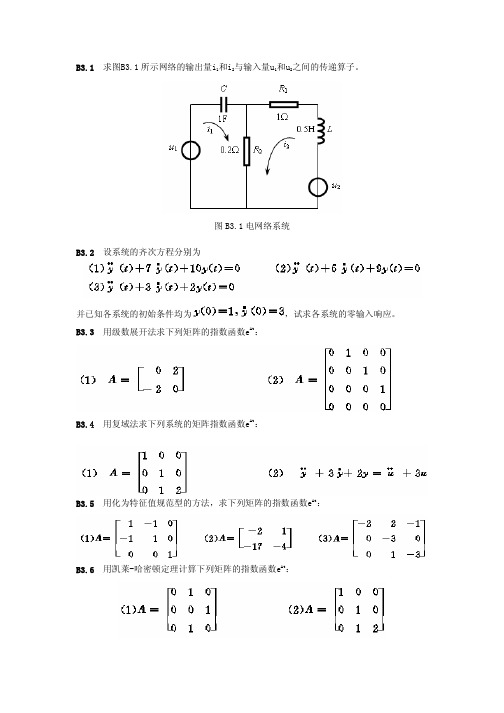
《自动控制原理》试题3

《自动控制原理》试题3

B3.1 求图B3.1所示网络的输出量i1和i2与输入量u1和u2之间的传递算子。

　图B3.1电网络系统B3.2 设系统的齐次方程分别为并已知各系统的初始条件均为，试求各系统的零输入响应。

B3.3 用级数展开法求下列矩阵的指数函数e At：B3.4 用复域法求下列系统的矩阵指数函数e At：B3.5 用化为特征值规范型的方法，求下列矩阵的指数函数e At：B3.6 用凯莱-哈密顿定理计算下列矩阵的指数函数e At：3.7 已知线性定常系统齐次状态方程的解为求系统的状态转移矩阵和状态矩阵A。

B3.8 判断下列矩阵是否是状态转移矩阵。

若是，求对应的状态矩阵A：B3.9 计算下列线性时变系统的状态转移矩阵Φ(t,0)及其逆矩阵Φ-1（t,0）：　B3.10 设系统的传递算子为已知试求这两个系统在单位阶跃信号作用下的时间响应。

B3.11 求下列系统在典型输入信号：(1)单位脉冲函数，(2)单位阶跃函数，(3)单位斜坡函数，(4)正弦函数sint，分别作用下系统的状态响应。

B3.12 若对图B3.12所示系统外施一幅值为10V持续时间为1s的矩形脉冲输入电压，且在第三秒时测得该系统的输出电压为0V。

试求输出电压的响应曲线u o(t)和电容器的初始电压u C(0)。

　图B3.12RC电路B3.13 已知系统的特征方程如下所列，试分别用劳斯判据和赫尔维茨判据分析系统的稳定性，并确定系统稳定时其可变参数K或T的取值范围。

　(1)s3+20s2+9s+100=0 (2)3s4+10s3+5s2+s+2=0　(3)s4+4s3+13s2＋36s+K=0 (4)s4+2s3+Ts2+10s+100=0B3.14 分析下列特征方程以及图B3.14(a)和(b)所示系统的稳定性，并求系统极点的分布：　(1)s6+3s5+5s4+9s3+8s2＋6s+4=0 (2)s6+s5-2s4-3s3-7s2-4s-4=0图B3.14题B3.14系统结构图B3.15 分析图B3.15所示的两个系统，引入与不引入反馈时系统的稳定性。

现代控制理论-状态方程的解

现代控制理论-状态方程的解

3、复频域上
非齐次状态方程的解
2、说明
e At 状态转移矩阵
一般用 t 表示，即 t e At
考虑初始条件拉氏变换
sX ( s ) X (0 ) AX ( s ) BU ( s ) 有 ( sI A) 1 X ( s ) X ( 0 ) BU ( s ) 即 1 X ( s ) ( sI A) X (0) ( sI A) 1 BU ( s ) 则
e
d At e Ae At e At A dt
At 1
e At
[5]、对于 n n的方阵 A、 B 当且仅当 AB BA时 有 e At e Bt e( A B)t , 而当AB BA, e At e Bt e( A B)t。
电气工程学院
几个特殊的矩阵指数eAt
设单变量系统的差分方程为：
y(k n) an1 y(k n 1) a0 y(k ) bnu(k n) bn1u(k n 1) b0u(k )
相应的系统脉冲传递函数为
bn z n bn 1 z n 1 b1 z b0 G( z ) n z an 1 z n 1 a1 z a0
有
d At At AX ] e X e [X dt e At Bu(t )
考虑初始条件 拉氏变换得 sX ( s ) X ( 0 ) AX ( s )
将上式积分有 t t X (t ) 1 ( sI A) 1 X (0) A d A e Bu( ) d d e X ( ) 0 0 d 1 显然 e At 1 t ( sI A) At A X ( 0 ) e X ( t ) e 可得 At Bu( )d

2-1 线性定常系统的解及转移矩阵

2-1 线性定常系统的解及转移矩阵

A(t t0 )
x(t0 )
（8）
将（8）式代入（1）式验证
x (t )
和
d x (t ) A e A(t t0 ) x (t0 ) Ax (t ) dt x (t ) t t e A(t0 t0 ) x (t0 ) x (t0 )
0
矩阵指数函数
e
A ( t t 0 )
即
(t ) A (t ) (t ) A
e A0 I
即
(0) I
3）可逆性 即 4）传递性
e
(t )
e
1
At 1
e At
1 (t ) (t )
A( t 2 t1 ) A( t1 t0 )
即
5）当且仅当
(t2 t1 ) (t1 t0 ) (t2 t0 )
根据凯莱-哈密顿定理
Δ( A) An an1 An1 a2 A2 a1 A a0 I 0 An an1 An1 a2 A2 a1 A - a0 I
例 解
3 9 用凯莱-哈密顿定理计算 2 6 λ 3 9 Δ( λ) det λ2 9λ 0 2 λ 6
1）A 的特征值互异 应用凯-哈定理， λi 和 A 都满足 A 的特征方程。因此， λi 也可以 满足（13）式。
e λit a0 (t ) a1 (t ) λi a2 (t ) λi2 an1 (t ) λin1
（其中，i 1,2,, n ） 写成矩阵形式 e λ1t 1 λ1 λ2t e 1 λ2 λnt e 1 λn 于是
2
100

现代控制理论第二章

现代控制理论第二章
（2）在e At 定义中，用（1 ）的方法可以消去 A的n及n以上的幂次项，即 e At = I + At + 1 2 2 1 1 A t +⋯+ An −1t n −1 + An t n + ⋯ 2! ( n − 1)! n!
= α n −1 (t ) An −1 + α n − 2 (t ) An − 2 + ⋯ + α1 (t ) A + α 0 (t ) I
【例2-5】见板书
（3）α i (t )的计算公式 A的特征值互异时 α 0 (t ) 1 λ1 α1 (t ) 1 λ2 ⋮ = ⋮ ⋮ α (t ) 1 λ n −1 n
λ λ λ
பைடு நூலகம்
2 1 2 2
⋮
2 n
⋯ λ e λ1t λ2 t ⋯ λ e ⋮ ⋮ λn t n −1 ⋯ λn e
At
2.变换A为约旦标准型 （1）A特征根互异 Λ = T −1 AT 有
例2-2 ，同例2-1
e At = Te ΛtT −1
（2）A特征值有重根
J = T AT e At = Te JtT −1
0 1 0 [例2 - 3]已知A = 0 0 1 , 求e At 2 - 5 4
若
σ ω A= −ω σ
则
cos ωt sin ωt σt e = Φ(t ) = e − sin ωt cos ωt
At
2.2.4 计算
1.根据 e At 或 Φ (t ) 的定义直接计算
1 2 2 1 33 1 n n e = I + At + A t + A t ⋯ A t + ⋯ 2! 3! k! 1 0 [例2 - 1]已知A = , 求e At − 2 − 3

现代控制理论课后答案

现代控制理论课后答案

前言
本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答，可帮助同学学习和理解教材的内容。由于习题数量较多，难易程度不同，虽然主要对象是研究型大学自动化专业本科学生，但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答；第4、7 章由井元伟教授组织编选和解答，第1、2章由郑艳副教授组织编选和解答。
+
若取 ，则有
（2）解 由（1）知
取 ，则有
若取 ，则有 ，
3.11 求下列系统在输入作用为：① 脉冲函数；② 单位阶跃函数；③ 单位斜坡函数下的状态响应。
(1)
(2)
图P2.2
解 这是一个物理系统，采用机理分析法求状态空间表达式会更为方便。令 为输入量，即 ， ， 的位移量 ， 为输出量，
选择状态变量 ， = ， = ， 。
根据牛顿定律对 有：
对 有：
经整理得：
状态方程为：
输出方程为：
写成矩阵形式为：
2.5 系统的结构如图P2.5所示。以图中所标记的 、 、 作为状态变量，推导其状态空间表达式。其中， 、 分别为系统的输入、输出， 、 、 均为标量。
图P2.5系统结构图
解 图P2.5给出了由积分器、放大器及加法器所描述的系统结构图，且图中每个积分器的输出即为状态变量，这种图形称为系统状态变量图。状态变量图即描述了系统状态变量之间的关系，又说明了状态变量的物理意义。由状态变量图可直接求得系统的状态空间表达式。
(2) 解 由已知得：
，
令： ，
得：
状态变量图如下：

《现代控制理论》课后习题答案2


( sI − A) −1 =
1 adj( sI − A) det( sI − A)
(1)
式（1）中的 adj( sI − A) 和 det( sI − A) 可分别写成以下形式：
adj( sI − A) = H n −1s n −1 + H n − 2 s n − 2 + " + H 0 det( sI − A) = s + an −1s
故
Φ (t ) = α 0 (t ) I + α1 (t ) A + α 2 (t ) A2
⎡ −2tet + e 2t ⎢ = ⎢ −2(1 + t )et + 2e 2t ⎢ −2(2 + t )et + 4e 2t ⎣
(3t + 2)et − 2e 2t (3t + 5)et − 4e 2t (3t + 8)et − 8e 2t
n n −1
(2) (3) (4)
+ " + a0
，可得 将式（1）两边分别左乘 det( sI − A)( sI − A) ，并利用式（2）和（3）
Is n + an −1 Is n −1 + " + a0 I = H n −1s n + ( H n − 2 − AH n−1 ) s n − 2 + " + ( H 0 − AH1 )s − AH 0
e jt = a0 (t ) + a1 (t ) j ， e − jt = a0 (t ) − a1 (t ) j
而
e jt = cos t + j sin t ， e− jt = cos t − j sin t 因此， a0 (t ) = cos t ， a1 (t ) = sin t 。由此得到状态转移矩阵 ⎡ cos t sin t ⎤ Φ (t ) = e At = a0 (0) I + a1 (t ) A = ⎢ ⎥ ⎣ − sin t cos t ⎦

现代控制理论基础第二章习题答案

第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ（t ）。

（1） ⎥⎦⎤⎢⎣⎡-=2010A （2） ⎥⎦⎤⎢⎣⎡-=0410A （3） ⎥⎦⎤⎢⎣⎡--=2110A （4） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A （5）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A （6）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】：（1） （2） （3） （4）特征值为：2,1321===λλλ。

由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为：（5）为结构四重根的约旦标准型。

（6）虽然特征值相同，但对应着两个约当块。

或}0100010000{])[()(1111----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-=Φλλλλs s s s L A sI L t 3-2-2 已知系统的状态方程和初始条件 （1）用laplace 法求状态转移矩阵； （2）用化标准型法求状态转移矩阵； （3）用化有限项法求状态转移矩阵； （4）求齐次状态方程的解。

【解】：（1） （2）特征方程为： 特征值为：2,1321===λλλ。

由于112==n n ，所以1λ对应的广义特征向量的阶数为1。

求满足0)(11=-P A I λ的解1P ，得：0110000000312111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--P P P ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011P 再根据0)(22=-P A I λ，且保证1P 、2P 线性无关，解得：对于当23=λ的特征向量，由0)(33=-P A I λ容易求得： 所以变换阵为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==110010001321P P P P ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1100100011P 线性变换后的系统矩阵为：（3）特征值为：2,1321===λλλ。

状态转移矩阵

)) 是 (A(t ), B(t ), C(t ), D(t 的一个基本矩阵；
解为
x(t ) e
y(t ) Ce
A ( t t0 )
x eA (t t ) Bu(t )d t
0 t0
t t0
t
A ( t t0 )
x CeA (t t ) Bu(t )d t Du(t )
0
通 常 假 定 t0=0， 这 时 则 有 t At x(t ) e x(0) eA (t t )Bu(t )d t
证明：反证法。若不然，设有t0，使得基本矩阵
Y (t 0 )为奇异阵。于是，存在非零实向量 ，使得
[Y 1 (t 0 ) Y 2 (t 0 )
由于
Y n (t 0 )]a ai Y i (t 0 ) 0
i 1
n
a Y (t
i i 1 i
n
0
) 0 是微分方程的一个解，故
i
由以上命题知
x A(t ) x B(t )u y C(t ) x D(t )u
x(t ) P(t )x(t )
(1 70)
称为(A(t), B(t), C(t), D(t)) 的代数等价动态方程， 当且仅当存在P(t)，使得
-1 A (t ) P ( t ) A ( t ) P ( t ) P (t )
例：试证明状态转移矩阵是唯一的，即状态转移 矩阵与基本矩阵的选取无关。
三、非齐次方程的解
1. 时变线性系统的解
x A(t )x B(t )u
令
(1 49)
x(t ) Φ t, t0 ξ(t )
(s 1)
则容易得到如下结论：

第2章 状态空间表达式求解


1 T 2. 若A能通过非奇异变换予以对角线化，即 AT
则
e1t e At (t ) T 0
e2t
0 T 1 n t e
证明：根据定义式
A2t 2 A3t 3 Ak t k e I At 2! 3! k 0 k! At
A2t 2 A3t 3 ( I At ) A e At A 信息与控制工程学院 2! 3!
5. 性质五
设有nxn矩阵A和B，当且仅当AB=BA 时，有eAteBt
= e(A+B)t ，而当AB≠BA 时，则eAteBt ≠ e(A+B)t 。
证明：根据定义式
e ( A B ) t ( A B ) 2 2 ( A B )3 3 I ( A B )t t t 2! 3! A2t 2 ABt2 BAt2 B 2t 2 I ( A B )t ( ) 2! 2! 2! 2! A3t 3 A2 Bt3 ABAt3 AB2t 3 BA2t 3 BABt3 ( 3! 3! 3! 3! 3! 3! B 2 At3 B 3t 3 ) 3! 3!
2 2 1 t 2! 1 1t 1 k k 2t At e At k 0 k! nt 1 0 0 k k 1 t k! k 0 0 2 2 2t 2!
(t )( ) (t ) (t )( t ) (t t ) I ( )(t ) ( t )
( t )(t ) ( t t ) I
从而证明了(t)与(-t)互为逆
信息与控制工程学院
4. 性质四
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

比较以上两式系数有：
b1 Ab0
32bb32

Ab1 Ab2


kb k Abk 1
b1 Ab0


b
2
b 3


1312AA2131!bb!A21A23bb00
b k

1
k
Ab1k k!
A1
k
b0
x(t) b0 b1 (t t0 ) b2 (t t0 )2 bk (t t0 )k
x(0)

ax(0)(t

t0 )

1 a2 x(0)(t 2!
t0 )2


1 ak x(0)(t k!
t0 )k

x(t) Ax(t)
向量
仿照标量 x(t) b0 b1(t t0 ) b2 (t t0 )2 微分方程：
bk (t t0 )k
代入微分方程： x(t) Ax(t) A(b0 b1(t t0 ) b2 (t t0 )2 bk (t t0 )k ) 对 x(t )求导： x(t) b1 2b2 (t t0 ) 3b3 (t t0 )2 kbk (t t0 )k 1
其解即为自由解。
x(t) |t t0 x(0)
非齐次状态方程：
x Ax Bu, x(t) |tt0 x(t0 )
其解为自由运动和强迫运动之和。
2.1.2、齐次状态方程的解：
状态方程
x (t) Ax(t)
求 x(t) ?
启发：一阶标量微分方程 x(t) ax(t), x(t0 ) x(0)
（4） Φ(t) AΦ(t) Φ(t)A Φ (0) A
eAt I At 1 A2t2 1 Aktk
2!
k!
（5）
AB BA e(AB)t eAteBt eBteAt
d eAt A 2 A2t k Akt k 1
dt
2!
Ak
(t

t0
)k

)x(t0)
x(t) eA(tt0 )x(t0 )
eA(tt0 )

I

A(t
t0 )
1 A2 (t 2!
t0 )2


1 k!
A矩k (阵t 指t0数)k函 数
结论：考虑齐次状态方程 x (t) Ax(t)，
若初始状态为x(t0 ) x0, 其解为：x(t) eA(tt0)x0,t t0,
dx
dx
ax dt

a dt x
ln x ln x(0) a(t t0 )
x(t) ea(t t0 ) x(0)
指数函数：
ea(t t0 )
1 a(t t0 )
1 a2 (t 2!
t0 )2


1 ak (t k!
t0 )k

x(t)


b0

Ab0
(t

t0
)

1 2!
A2b0
(t

t0
)2


1Байду номын сангаасk!
A
k
b0
(t
t0 )k


(I

A(t

t0
)

1 2!
A2
(t

t0
)2


1 k!
Ak
(t

t0
)k

) b0
t t0 x(t0 ) b0

x(t
)

(I

A(t

t0
)

1 2!
A2
(t

t0
)2


1 k!
第二章 控制系统状态空间表达式的解
本章主要内容：
• 线性定常齐次状态方程的解（自由解） • 矩阵指数函数——状态转移矩阵 • 线性定常系统非齐次状态方程的解
2.1 线性定常齐次状态方程的解
2.1.1 线性定常系统的运动
1）自由运动（零输入响应）：线性定常系统在没有控制作用，即u＝0时，
由初始状态引起的运动称自由运动。
可视为从 到0，再从 0到t 的组合，即：
(t 0)(0 ( )) (t ( )) (t )
（3）可逆性： Φ1(t) Φ(t)
由（1），(t t) I, 由（2），(t)(t) I.
可依此计算0时刻的状态值
x(t) Φ(t)x(0) x(0) Φ1(t)x(t) Φ(t)x(t)
x(t) eAtx0,t 0.
令：
eAt Φ(t)
e
A
(
t
t0
)
Φ(t
t0 )
则有：
状态转移矩阵
x(t) Φ(t)x(0) x(t) Φ(t t0 )x(t0 )
注1：对于线性定常系统来说，状态转移矩阵就是矩阵指数函数。
注2：状态转移矩阵的物理意义：
从时间角度看，状态转移矩阵使状态向量随着时间的推移不断地
在状态空间中作转移，故称为状态转移矩阵
x2
x(0)
x(t1 )
0
t1
x(t2 )
t t2
x1
(t1 0)
(t2 t1 )
x(t1) (t1 0)x(0)
x(t2) (t2 t1)x(t1)
x(t2) (t2 t1)(t1 0)x(0)
k!
=A(I+At 1 Akt k + ) k!
=(I+At 1 Akt k + )A k!
证明：
u0
x
( A, B)
x Ax , x(t) |t t0 x(0)
2）强迫运动（零初态响应）：线性定常系统在只有输入作用而无初始状态作用
下的运动，称为强迫运动。 u
x
( A, B)
x Ax Bu , x(t ) |tt0 x(t0 ) 0
齐次状态方程： x Ax ,
若 t0 0, 其解为x(t) eAtx0,t 0.
矩阵指数 eAt 把系统的状态 x(0)转移到 x(t)，也把它称为
状态转移矩阵，记为 (t) 。 (t) 是一般的表示形式
2.2 状态转移矩阵
2.2.1、状态转移矩阵的含义 线性定常系统的齐次状态方程的解：
x(t) eA(tt0)x0,t t0,
x(t2) (t2 0)x(0)
(t2 ) (t2 t1)(t1 0)
2.2.2、状态转移矩阵的性质
（1）状态转移矩阵初始条件：
Φ(0) I
也即： (t t) I
意为状态向量从时刻 t 转移到t ，显然保持不变。
（2）组合性： (t)( )=(t )