下载文档原格式
实验八、基于Excel的排队问题仿真排队问题常常连续地或并行地发生（例如在装配线和工作车间），通常无法用建立数学模型的方法解决。
然而，排队问题通常容易在计算机上进行仿真。
下面我们通过一个两阶段装配线的例子阐述如何借助于Excel建立一个排队问题的仿真模型。
一、实验目的1、掌握如何用Excel建立排队问题仿真模型；2、读懂Excel输出的运算结果，并用于指导实践。
二、实验内容两阶段装配线问题一条装配线所组装的产品体积可能很大，例如：冰箱、空调机、汽车、电视机或家具、图1表示的是一条装配线上的两个工作站。
产品的体积是装配线分析和设计所要考虑的一个重要因素，因为每个工作站上所能存放的产品数量将会影响工人的工作。
如果产品体积很大，那么相邻的工作站存在着相互依赖的关系。
如图1所示，鲍博和雷在一个两阶段装配线上工作，鲍博在工作站1上装配完的产品传递给工作站2上的雷，雷再进行加工。
如果两个工作站相连，中间没有存入半成品的地方，那么鲍博如果干得慢，雷就会被迫等待；相反，如果鲍博和干得快（或者说雷完成工作比鲍博用时长），那么鲍博就得等雷。
在这个仿真问题中，我们假设鲍博是组装线上的第一个工人，他能够在任何时候拿到需组装的半成品进行工作。
那么，我们把分析重点放在鲍博与雷彼此之间的相互影响上。
1、研究的目标：关于这条装配线，我们希望能通过研究解决一些问题。
下面是我们列出的部分待解决的问题：○每个工人的平均完工时间是多少？○这条组装线的生产率是多少？○鲍博等待雷的时间是多少？○雷等待鲍博的时间是多少？○如果两个工作站中间的空间加大，可以存储半成品，从而增加了工人的独立性，那么这对于生产率、等待时间等问题会有什么影响？2、数据的采集：进行系统仿真，我们需要鲍博和雷的装配时间数据。
要收集这些数据，一种方法就是将总装配时间分割成小段时间，在每段时间对工人进行单独观测。
对这些数据进行简单的汇总和分析，我们可以得到非常有用的直方图。
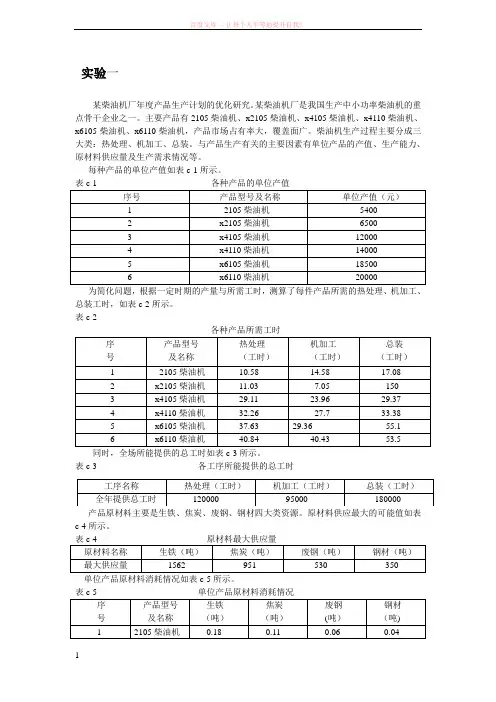
实验一某柴油机厂年度产品生产计划的优化研究。
某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。
主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机，产品市场占有率大，覆盖面广。
柴油机生产过程主要分成三大类：热处理、机加工、总装。
与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量及生产需求情况等。
每种产品的单位产值如表c-1所示。
序号 产品型号及名称 单位产值（元） 1 2105柴油机 5400 2 x2105柴油机 6500 3 x4105柴油机 12000 4 x4110柴油机 14000 5 x6105柴油机 18500 6x6110柴油机20000总装工时，如表c-2所示。
表c-2各种产品所需工时 同时，全场所能提供的总工时如表c-3所示。
表c-3 各工序所能提供的总工时 产品原材料主要是生铁、焦炭、废钢、钢材四大类资源。
原材料供应最大的可能值如表c-4所示。
表c-4 原材料最大供应量 原材料名称 生铁（吨） 焦炭（吨） 废钢（吨） 钢材（吨） 最大供应量1562951530350表c-5 单位产品原材料消耗情况 序 号 产品型号 及名称 生铁 （吨） 焦炭 （吨） 废钢 (吨） 钢材 （吨) 1 2105柴油机0.180.110.060.04序 号 产品型号 及名称 热处理 （工时） 机加工 （工时） 总装 （工时） 1 2105柴油机 10.5814.58 17.08 2 x2105柴油机 11.03 7.05 150 3 x4105柴油机 29.11 23.96 29.37 4 x4110柴油机 32.26 27.7 33.38 5 x6105柴油机 37.63 29.36 55.1 6x6110柴油机40.8440.4353.5工序名称 热处理（工时） 机加工（工时） 总装（工时） 全年提供总工时120000950001800002 x2105柴油机0.19 0.12 0.06 0.043 x4105柴油机0.35 0.22 0.12 0.084 x4110柴油机0.36 0.23 0.13 0.095 x6105柴油机0.54 0.33 0.18 0.120.19 0.136 x6110柴油机0.550.34依照历年销售情况、权威部门的市场预测及企业近期进行的生产调查结果，可以分别预测出各种型号柴油机今年的市场需求量，如表c-6所示。
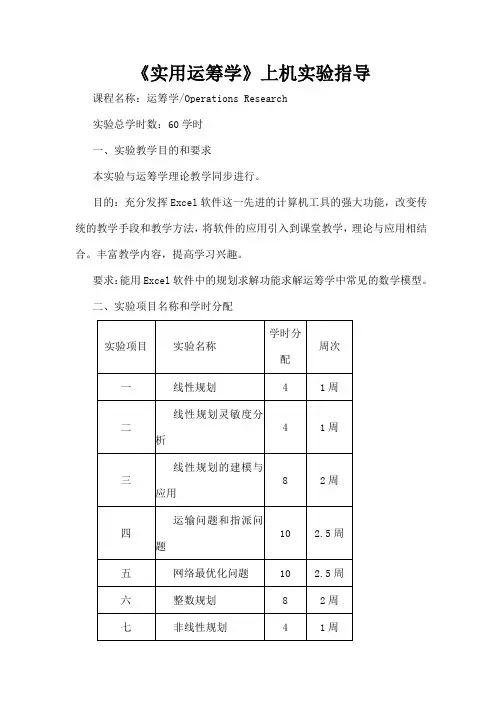
《实用运筹学》上机实验指导课程名称：运筹学/Operations Research实验总学时数：60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。
目的：充分发挥Excel软件这一先进的计算机工具的强大功能，改变传统的教学手段和教学方法，将软件的应用引入到课堂教学，理论与应用相结合。
丰富教学内容，提高学习兴趣。
要求：能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。
二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划（－）实验目的：安装Excel软件“规划求解”加载宏，用Excel软件求解线性规划问题。
（二）内容和要求：安装并启动软件，建立新问题，输入模型，求解模型，结果的简单分析。
（三）实例操作：求解习题1.1。
（1）建立电子表格模型：输入数据、给单元格命名、输入公式等；（2）使用Excel软件中的规划求解功能求解模型；（3）结果分析：如五种家具各生产多少？总利润是多少？哪些工序的时间有剩余，并对结果提出你的看法；（4）在Excel或Word文档中写实验报告，包括线性规划模型、电子表格模型和结果分析等。
案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。
某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。
主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机，产品市场占有率大，覆盖面广。
柴油机生产过程主要分成三大类：热处理、机加工、总装。
与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。
每种产品的单位产值如错误!未找到引用源。
所示。
表 C－1 各种产品的单位产值为简化问题，根据一定时期的产量与所需工时，测算了每件产品所需的热处理、机加工、总装工时，如表 C－2所示。
表 C－2 单位产品所需工时同时，全厂所能提供的总工时如表 C－3所示。
表 C－3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。
实验三、用Excel求解线性规划模型线性规划问题用手工求解工作量很大，而且没有较高的数学基础很难理解其计算过程和方法，但是借助Excel“规划求解”工具，就能轻而易举地求得结果。
Excel最多可解200个变量、600个约束条件的问题。
下面我们以一实例介绍利用Excel规划求解工具怎样快速解决具体的经济决策问题。
一、实验目的1、掌握如何建立线性规划模型。
2、掌握用Excel求解线性规划模型的方法。
3、掌握如何借助于Excel对线性规划模型进行灵敏度分析，以判断各种可能的变化对最优方案产生的影响。
4、读懂Excel求解线性规划问题输出的运算结果报告和敏感性报告。
二、实验内容1、[工具][规划求解]命令规划求解加载宏是Excel的一个可选安装模块，在安装Excel时，只有在选择“完全/定制安装”时才可选择装入这个模块。
在安装完成进入Excel后还要用[工具][加载宏]命令选中“规划求解”，以后在[工具]菜单下就增加了一条[规划求解]命令。
使用[规划求解]命令的一般步骤为：第一步：在选取[工具][规划求解]命令后，弹出图1所示“规划求解参数”对话框，其中各选项说明如表1。
图1“规划求解参数”对话框选项名说明设置目标单元格选取计算问题的目标函数，并含有计算公式的单元格等于按问题目标进行选择。
如利润问题，选取“最大值”可变单元格决策变量所在各单元格、不含公式，可以有多个区域或单元格约束增加、修改、删除各个约束等式或不等式，一个一个地与图2切换填入或修改添加选择后弹出图2所示对话框更改选择后弹出图3所示对话框删除删除所选定的约束条件选项决定采用线性模型还是非线性模型求解约束条件中的单元格引用位置，可从键盘直接录入，也可用鼠标拖放选取。
图2图3第二步：完成图1所示的一切填入项目后，单击“选项”按钮，在弹出的“规划求解选项”对话框中若是线性模型则选取“采用线性规模”选项按钮，再单击“确定”按钮回到图1。
图4第三步：在图1中单击“求解”按钮，经计算完成后弹出“规划求解结果”对话框（图5）。
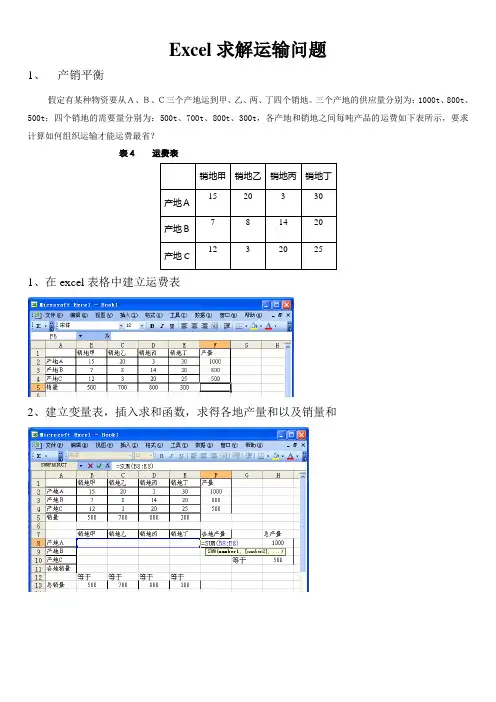
Excel求解运输问题1、产销平衡假定有某种物资要从Ａ、Ｂ、Ｃ三个产地运到甲、乙、两、丁四个销地。
三个产地的供应量分别为：1000t、800t、500t；四个销地的需要量分别为：500t、700t、800t、300t，各产地和销地之间每吨产品的运费如下表所示，要求计算如何组织运输才能运费最省？表4 运费表1、在excel表格中建立运费表2、建立变量表，插入求和函数，求得各地产量和以及销量和3、确定目标函数：运费最省4、规划求解，设置目标单元格、可变单元格，添加约束：各地产量和等于总产量，各地销量和等于总销量，变量非负5、得到最优解6、进行敏感性分析，得到极限值报告2、产销不平衡1、复制表格到excel，将不能到达的单元格设置一个很大的数字2、复制表格到下面单元格，将中间的数据清空，设置成可变单元格3、在相应的单元格插入求和函数（SUM），对可变单元格进行行和列求和4、输入“目标函数”，将后面空格作为目标单元格，输入“sumproduct”函数，对相应的行和列求和5、规划求解，在添加约束中销量等于，产量小于等于，所以变量非负，线性，求解得到最优解。
三个电视机厂供应四个地区某种型号电视机，各厂家的年产量、各地区的年销量及各厂到各地区的单位运价如下，求总运费最省的电视机调拨方案“不能到达”设置一个较大的数字；约束添加为5≤b1≤8；b2=12；6≤b3；b4≤7生产与储存问题（产销不平衡问题）某厂按合同规定须于当年每个季度末分别提供10、15、25、20台同一规格的柴油机。
已知该厂各季度的生产能力及生产每台柴油机的成本如右表。
如果生产出来的柴油机当季不交货，每台每积压一个季度需储存、维护等费用0.15万元。
试求在完成合同的情况下，使该厂全年生产总费用为最小的决策方案•解：设x ij为第i 季度生产的第j 季度交货的柴油机数目，那么应满足：•交货：x11 = 10 生产：x11 + x12 + x13 + x14 ≤25•x12 + x22 = 15 x22 + x23 + x24 ≤35x13 + x23 + x33 = 25 x33 + x34 ≤30x14 + x24 + x34 + x44 = 20 x44 ≤10把第i 季度生产的柴油机数目看作第i 个生产厂的产量；把第j 季度交货的柴油机数目看作第j 个销售点的销量；设cij是第i季度生产的第j季度交货的每台柴油机的实际成本，应该等于该季度单位成本加上储存、维护等费用。
