陕西省咸阳市兴平市西郊中学2019-2020学年高一数学上学期第一次月考试题【带解析】

陕西省高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共27分)1. （2分）设集合，则A .B .C .D .2. （2分）若全集，集合，，则（）A . {2}B . {1，2}C . {1，2，4}D . {1，3，4，5}3. （2分）已知集合，若，则实数a的取值范围为（）A .B .C .D .4. （2分） (2016高二上·晋江期中) 若A={x|2＜x＜3}，B={x|x2﹣4ax+3a2＜0}，且A⊆B则实数a的取值范围是（）A . 1＜a＜2B . 1≤a≤2C . 1＜a＜3D . 1≤a≤35. （2分） (2019高一上·南充期中) 下列各组函数中，表示同一个函数的是（）A . 与B . 与C . 与D . 与6. （2分） (2019高一上·江阴期中) 函数的定义域为（）A .B .C .D .7. （2分） (2019高三上·亳州月考) 函数y＝的定义域是（）A . [1，＋∞）B . （，＋∞）C . [ ，1]D . （，1]8. （2分） (2019高一上·兴平月考) 函数的定义域为，的定义域为，则A .B .C .D .9. （2分） (2019高二上·上海月考) 已知，则当时，数列的极限是（）A . 0B . 1C . 0或1D . 不存在10. （2分）已知集合，且，则实数a的取值范围是（）A .B .C .D .11. （2分） (2015高二下·赣州期中) 已知函数f（x）=ax3﹣x2+4x+3，若在区间[﹣2，1]上，f（x）≥0恒成立，则a的取值范围是（）A . [﹣6，﹣2]B .C . [﹣5，﹣3]D . [﹣4，﹣3]12. （5分）若命题“使得”为假命题，则实数m的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2018高一上·广东期中) 设集合，集合，则集合中有________个元素．14. （1分） (2019高一上·上海月考) 设集合，，若，则实数t的取值范围是________.15. （1分） (2016高一上·成都期中) 函数y=log0.5（x2+ax+1）的值域是R，则a的取值范围是________．16. （1分） (2019高二上·上杭期中) 已知，则的最小值为________．三、解答题 (共6题；共60分)17. （10分）(2019高一上·东至期中) 已知全集，集合，，．（1）求；（2）若，求实数的值．18. （5分） (2018高一上·四川月考) 若集合，．（1）若全集，求；（2）若，求实数的取值范围．19. （20分） (2018高一上·武汉月考) 已知集合，函数的定义域为集合 .(I)求集合 .(II)当时，若全集，求及；(III)若，求实数的取值范围.20. （10分） (2019高一上·大庆月考) 若二次函数满足，且（1）求的解析式；（2）设，求在上的最小值的解析式.21. （5分） (2019高一上·西湖月考) 若集合，，且，求实数的值.22. （10分）设f（x）=ax﹣1 ， g（x）=bx﹣1（a，b＞0），记h（x）=f（x）﹣g（x）（1）若h（2）=2，h（3）=12，当x∈[1，3]时，求h（x）的最大值（2） a=2，b=1，且方程有两个不相等实根m，n，求mn的取值范围（3）若a=2，h（x）=cx﹣1（x＞1，c＞0），且a，b，c是三角形的三边长，求出x的范围．参考答案一、单选题 (共12题；共27分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分) 17-1、答案：略17-2、答案：略18-1、答案：略18-2、答案：略19-1、20-1、答案：略20-2、21-1、22-1、22-2、22-3、。

2019-2020年高一上学期第一次月考试题 数学 含答案一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合，集合则为（ ） A. {0，2，4}B. {1，2，4}C.{2，3，4}D.{0，2，3，4}2．在下列各式中错误的个数是( )①1∈{0,1,2}；②{1}∈{0,1,2}；③{0,1,2}⊆{0,1,2}； ④{0,1,2}＝{2,0,1}；⑤{0,1}⊆{(0,1)}；⑥∅⊆{0} A ．1 B ．2 C ．3 D ．43．设全集，集合{|(3)0},{|1}A x x x B x x =+<=<-，则如图中阴影部分表示的集合为（ ） A ． B ． C ．D ．4．下列两个函数完全相同的是( )A ．y ＝与y ＝xB ．y ＝与y ＝xC ．y ＝与y ＝xD ．y ＝()2与y ＝x5．已知定义域为A={}, 值域为B={}, 下列各图中能表示从集合A 到集合B 的函数图像的是()6．已知＝()()()002010020x x x x >⎧⎪-=⎨⎪<⎩,则的值为( )A ．0B ．2 010C ．4 020D ．－4 0207．已知，，则M∩N=（ ） A . B. C. D.8．集合2{|1,}M y y x x R ==-∈,集合{|}N x y x R ==∈，则M∩N=( ) A. B ． C. D ．9．设，，若，则实数的取值范围是（ ） A. B. C. D.10．如果函数在区间上是减函数，那么实数的取值范围是( ) A ．B ．C ．D ．11．函数2,01()1,123,2x x f x x x ≤≤⎧⎪=<<⎨⎪≥⎩的值域是（ ）A ．RB ．C ．D ．12．已知函数的定义域为，求实数的取值范围是（ ） A ．B ．C ．D ．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13．函数的定义域为 ．14．已知2{|0}A x x x a =-+==∅，则实数的取值范围是________．15．已知集合M={1，2，3，4}，A ⊆M ，集合A 中所有元素的乘积称为集合A 的“累积值”，且规定：当集合A 只有一个元素时，其累积值即为该元素的数值，空集的累积值为0．设集合A 的累积值为n ．（1）若n=3，则这样的集合A 共有 个；（2）若n 为偶数，则这样的集合A 共有 个． 16．不等式的解集为，那么的值为 ．xx 高一年级第一次月考数学试卷答题卡13、14、15、16、三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. (12分)设，集合，求的值18. (12分)已知全集，集合{|41}{|312}A x x x B x x =<->=-≤-≤或，． （1）求； （2）求．19. (12分)已知函数（1）求函数的定义域； （2）求，当时，求；（3）判断点是否在的函数图像上.20.(12分)作出下列函数图像。

2019-2020学年度第一学期期中测试高一数学试卷（西郊中学）（本试卷满分150分考试时间120分钟）一、选择题（共12小题，每小题5分，共60分）1.已知全集{}1,2,3,4,5,6,7U =，{}3,4,5A =，{}1,3,6B =，那么集合{}2,7是（ ） A. A B U B. A B IC. ()U C A B ID. ()U C A B ⋃【答案】D 【解析】 【分析】分别求解A B I ,()U C A B I ,A B U ,()U C A B ⋃,即可得出答案. 【详解】Q {}1,2,3,4,5,6,7U =Q {}{}{}3,4,51,3,63A B ⋂=⋂=∴(){}1,2,4,5,6,7U C A B ⋂=Q {}{}{}3,4,51,3,6=1,3,4,5,6=A B ⋃⋃∴ (){}2,7U C A B ⋃=故选:D.【点睛】本题考查了集合的补集,并集和交集运算,掌握集合运算基本知识是解题关键,属于基础题. 2.设25a b m ==，且112a b+=，则m = ( )B. 10C. 20D. 100【答案】A 【解析】 【分析】将指数式化为对数值，然后利用对数运算公式化简112a b+=，由此求得m 的值.【详解】由25a b m ==得25log ,log a m b m ==，所以11log 2log 5log 102m m m a b+=+==，210,m m == A.【点睛】本小题主要考查指数式和对数式互化，考查对数运算，属于基础题. 【此处有视频，请去附件查看】3.若函数()f x 满足(32)98f x x +=+,则()f x 的解析式是( ) A. ()98f x x =+ B. ()32f x x =+C. ()34f x x =--D. ()32f x x =+或()34f x x =--【答案】B 【解析】【详解】试题分析：设()()232328323t t x x f t t t -=+∴=∴=-+=+ ()32f x x ∴=+,故选B.考点：换元法求解析式4.已知2()(1)33f x m x mx =-++为偶函数，则()f x 在区间(4,2)-上为（ ）A. 增函数B. 增函数C. 先增后减D. 先减后增【答案】C 【解析】 试题分析：因为为偶函数，所以，即，根据对应系数相等可得，，．函数的图像是开口向下对称轴为轴的抛物线，所以此函数在上单调递增，在上单调递减．故C 正确．考点：1偶函数；2二次函数的单调性．【方法点睛】本题重点考查偶函数和二次函数的单调性，难度一般．本题可以根据偶函数的定义由对应系数相等求得的值，也可以根据偶函数图像关于轴对称求得的值，但此方法前须验证时不满足题意．二次函数的单调性由图像的开口方向和对称轴决定，根据这两点即可求得二次函数的单调性．5.某企业去年销售收入1000万元，年成本为生产成本500万元与年广告成本200万元两部分．若年利润必须按p%纳税，且年广告费超出年销售收入2%的部分也按p%纳税，其他不纳税．已知该企业去年共纳税120万元．则税率p%为（）A. 10%B. 12%C. 20%D. 25%【答案】D【解析】【分析】欲求税率,只须求出去年的总收入即可,而总收入由两部分构成:去年的利润,广告费超支.根据税率公式计算即得答案.【详解】由题意得,去年的利润为:1000500200300--=(万元)广告费超支:200(10002%)180-⨯=(万元)税率为:12025% 300180=+故选:D.【点睛】根据题意列出利润,广告费超支和税率是解题关键,考查运算求解能力,解决实际问题的能力,属于基础题.6.已知5,6()(2),6x xf xf x x-≥⎧=⎨+<⎩，则(3)f为（）A. 2B. 3C. 4D. 5【答案】A【解析】根据自变量范围代入对应解析式，解得结果. 【详解】(3)(32)(52)752f f f =+=+=-= 故选：A【点睛】本题考查分段函数求值，考查基本分析求解能力，属基础题. 7.若()2lg 2lg lg x y x y -=+，则2log xy等于（ ） A. 0 B. 2或0C. 2D. -2或0【答案】B 【解析】 【分析】根据对数的运算性质,可将原方程化为22540x xy y -+=,通过换元法求解xy的值,即可得到答案.【详解】()2lg 2lg lg x y x y -=+Q2lg(2)lg()x y x y ∴-=⋅2(2)x y x y ∴-=⋅，22540x xy y -+=令,0xt t y=>，则2540t t -+= 解得:4t =或1t =22log log 42xy∴==或22log log 10x y ==故选:B.【点睛】解对数方程时,要将方程化为同底数对数形式,利用真数相等求解方程,这是解本题的关键. 8.函数f(x)＝log 3x －8＋2x 的零点一定位于区间 A. (5,6) B. (3,4)C. (2,3)D. (1,2)【答案】B试题分析：根据零点存在性定理，因为，所以函数零点在区间（3，4）内，故选择B 考点：零点存在性定理9.已知01a <<，则方程log xa a x=实数根个数是（ ）A. 2B. 3C. 4D. 与a 无关【答案】A 【解析】 【分析】画出||x y a =和log a y x =的函数图像,根据图像即可得出交点个数. 【详解】画出||x y a =和log a y x =的函数图像由图像可知两函数图像有两个交点,故方程log xa a x =有两个根.故选:A.【点睛】将求解log xa a x =实数根个数转化为求解||x y a =和log a y x =的函数交点个数,数形结合是解本题的关键.10.定义在R 上的偶函数在[0,7]上是增函数，在[7，＋∞)上是减函数，又f(7)＝6，则f(x)( ) A. 在[－7,0]上是增函数，且最大值是6 B. 在[－7,0]上是减函数，且最大值是6 C. 在[－7,0]上是增函数，且最小值是6 D. 在[－7,0]上是减函数，且最小值是 6的的【答案】B【解析】【详解】∵函数是偶函数，而且在[0，7]上为增函数，∴函数在[-7，0]上是减函数.又∵函数在x=7和x=-7的左边是增函数，右边是减函数，且f(7)=f(-7)，∴最大值为f(7)=f(-7)=6.故选B.11.已知y＝f（x）与y＝g（x）的图像如下图：则F（x）＝f（x）·g（x）的图像可能是下图中的（）A. B.C. D.【答案】A 【解析】 试题分析：在时，沿轴正方向f （x ）先为负值后为正值，而g （x ）恒为正值，所以F （x ）＝f （x ）·g（x ）也必须先为负值，后为正值，可能选项为A ，D ，同理在时，f （x ）先为负值后为正值，而g （x ）恒为负值，所以F （x ）＝f （x ）·g （x ）也必须先为正值，后为负值，可能选项为A ；综上所述，正确选项应该为A ．考点：函数的图象．【方法点睛】本题主要考查函数的图象，判断函数的大致图像是否正确，主要从以下几点取判断：1、函数的零点（多适用于某函数零点已知）；2、函数正负值所对区间（多适用于两函数相乘）；3、函数的单调性区间（适合于两函数求和或者求差）．本题为f （x ）·g （x ）所以选用函数正负值所对区间这一方法．12.若函数f(x)＝lg(10x＋1)＋ax 是偶函数，()42x xbg x -=是奇函数，则a ＋b 的值是 A. 12B. 1C. 12- D. －1【答案】A 【解析】 【分析】利用函数的奇偶性求得a ,b 的值，然后计算a +b 的值即可.【详解】偶函数满足()()11f f -=，即：()()1lg 101lg 101a a -+-=++，解得：12a =-， 奇函数满足()00f =，则00402b-=，解得：1b =，则11122a b +=-+=. 本题选择A 选项.【点睛】本题主要考查奇函数的性质，偶函数的性质等知识，意在考查学生的转化能力和计算求解能力.二、填空题（共4小题，每小题5分，共20分）13.若函数()y f x =的定义域为[0，2]，则函数(2)()1f xg x x =-的定义域是_______． 【答案】[0,1) 【解析】【详解】由10022x x -≠⎧⎨≤≤⎩，得0≤x<1，即定义域是[0，1)，故答案为[)0,1． 14.函数y =lnx 的反函数是__________.【答案】xy e = ()x R ∈【解析】 分析】由函数ln y x =解得y x e =,把x 与y 互换即可得出 【详解】Q 函数ln y x =∴ y x e =把x 与y 互换可得:xy e = ()x R ∈ 原函数的反函数为:xy e = ()x R ∈ 故答案为:xy e = ()x R ∈【点睛】在求解反函数时,要先求出原函数的值域,因为原函数的值域是反函数的定义域,这是解本题关键. 15.函数12log xy =的递增区间是__________.【答案】(,0)-∞ 【解析】 【分析】【令||t x =,当0x >,||t x =是增函数;当0x <,||t x =是减函数.对于12log y x =在定义域上是减函数, 根据复合函数单调性同增异减,即可得出函数12log xy =的递增区间.【详解】令||t x = 当0x > ||t x =是增函数 当0x < ||t x =是减函数 对于12log y x =在定义域上是减函数根据复合函数单调性同增异减∴ 12log xy =在0x <上是单调递增.故答案为:(,0)-∞.【点睛】对于复合函数单调性的判断要掌握同增异减,对函数的内层和外层分别判断,即可得出单调性. 16.函数y a =与函数21y x x =-+的图像有四个交点，则a 的取值范围是____________．【答案】3,14⎛⎫⎪⎝⎭【解析】试题分析：函数21y x x =-+的图象如下图所示，结合图象可得：当314a <<时，函数21y x x =-+与y a =的图象有四个交点，所以实数a 的取值范围是3,14⎛⎫⎪⎝⎭．考点：方程根的存性及根的个数的判定． 【方法点晴】本题主要考查了方程根存在性及根的个数的判定，着重考查了一元二次函数的图象与性质，函数与方程关系等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及转化思想和数形结合思想的应用，本题解答的关键在于作出函数21y x x =-+的图象，借助数形结合法求解．属于中档试题．三、解答题（共6小题，共70分）17.(1)计算：()112037272lg 5()964-⎛⎫++ ⎪⎝⎭(2)解方程3log (69)3x-= 【答案】(1) 4 (2) 2x = 【解析】 【分析】(1)利用指数的运算法则即可得出答案.(2)将3log (69)3x-=化简为33log (69)log 27x-=,即可得出答案. 【详解】(1) ()1123203112357272lg 5()4396413-⨯⨯⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎛⎫++ ⎪⎝⎭⎝⎭541433=++= (2)由方程3log (69)3x-= 得33log (69)log 27x-=,6927x ∴-= 26366x ∴==2x ∴=经检验,2x =是原方程的解,故原方程的解为2x =【点睛】本题考查了指数的运算和求解对数方程.解对数方程时,要将方程化为同底数对数形式,利用真数相等求解方程,这是解本题的关键,属于基础题.18.讨论函数()af x x x=+(a >0)在)x ∈+∞的单调性并证明. 【答案】答案见解析 【解析】 【分析】根据定义法证明函数单调性,即在函数的定义域内任取12,)x x ∈+∞,且12x x <,可通过作差法比较()1f x 和()2f x 大小,即可得到()f x 单调性【详解】在函数的定义域内任取12,)x x ∈+∞,且12x x <则()()()1212121212=1a a a f x f x x x x x x x x x ⎛⎫-=+---- ⎪⎝⎭Q12x x >故1201a x x << ∴ 1210->a x x ∴ ()()120f x f x -> 故()f x在)+∞上是单调增函数.【点睛】本题考查了用定义法证明函数单调性.在用定义法证明函数单调时要注意在所给定义内要任取两个自变量12,x x ,化简()()21f x f x -表达式, ()()21>0f x f x -时()f x 单调递增, ()()21<0f x f x -时()f x 单调递减.19.已知奇函数222,(0)()0,(0),(0)x x x f x x x mx x ⎧-+>⎪==⎨⎪+<⎩. （1）求实数m 的值；（2）做()y f x =的图象（不必写过程）；（3）若函数()f x 在区间[]1,2a --上单调递增，求a 的取值范围．【答案】（1）2；（2）图象见解析；（3）13a <?.【解析】【分析】（1）求出当x ＜0时，函数的解析式，即可求得m 的值；（2）分段作出函数的图象，即可得到y =f （x ）的图象；（3）根据图象，利用函数f （x ）在区间[﹣1，a ﹣2]上单调递增，建立不等式，即可求a 的取值范围．【详解】（1）设x ＜0，则﹣x ＞0，∴f （﹣x ）=﹣x 2﹣2x∵函数是奇函数，∴f （x ）=﹣f （﹣x ）=x 2+2x （x ＜0）∴m =2；（2）函数图象如图所示：（3）要使()f x 在区间[1,2]a --上单调递增，结合图象可知，﹣1＜a ﹣2≤1，∴1＜a ≤3．所以实数a 的取值范围是(1,3]．【考点】利用奇函数的定义求解析式，从而确定m 值；利用函数的单调性确定参数a 的取值范围．【点睛】利用数形结合的方法是解决本题的关键．20.已知函数()f x =的定义域为集合A ，函数22()31m x x g x +-=-的值域为集合B ，且A B B ⋃=，求实数m 的取值范围.【答案】0m ≥.【解析】【详解】试题分析：根据函数的定义域和指数函数的性质，得到集合,A B ，再利用A B B ⋃=，即可求解实数m 的取值范围.试题解析：由题意得{}(1|12,1,13m A x x B +⎤=<≤=--+⎦ 由A B B ⋃=，得A B ⊆即1132m +-+≥，133m +≥，11m +≥，得0m ≥考点：函数的定义域与值域；集合的运算.21.已知集合{}2|320,A x R ax x a R =∈-+=∈.（1）若A 是空集,求a 的取值范围；（2）若A 中只有一个元素,求a 的值,并把这个元素写出来.【答案】（1）98a >（2）0a =时,2{}3A =；98a =时，43A ⎧⎫=⎨⎬⎩⎭【解析】【详解】试题分析：（1）有由A 是空集,可得方程2320ax x -+=无解，故980a ∆=-<，由此解得a 的取值范围；（2）若A 中只有一个元素，则0a =或980a ∆=-=，求出a 的值，再把a 的值代入方程2320ax x -+=，解得x 的值，即为所求.试题解析：（1）要使A 为空集,方程应无实根,应满足0,0.a ≠⎧⎨∆<⎩解得98a >.（2）当0a =时,方程为一次方程,有一解23x =；当0a ≠,方程为一元二次方程,使集合A 只有一个元素的条件是0∆=,解得98a =,43x =.∴0a =时,23A ⎧⎫=⎨⎬⎩⎭，元素为：23；98a =时，43A ⎧⎫=⎨⎬⎩⎭.元素为：4322.若f (x )是定义在(0，+∞)上的增函数，且()()()xf f x f y y =-(1)求f (1)的值；(2)若f (6)=1，解不等式f (x +3)−f (1x )<2.【答案】(1) 0 (2) 3|02x x ⎧-+⎪<<⎨⎪⎪⎩⎭【解析】分析】(1)令1x y ==,即可求得(1)f .(2)利用()()x f f x f y y ⎛⎫=- ⎪⎝⎭和(6)1f =对1(3)2f x f x ⎛⎫+-< ⎪⎝⎭,结合单调性即可求出答案.【详解】(1)()()x f f x f y y ⎛⎫=- ⎪⎝⎭Q令1x y ==得:()1(1)(1)f f f =- 故:(1)0f =(2) ()()x f f x f y y ⎛⎫=- ⎪⎝⎭Q1(3)2f x f x ⎛⎫∴+-< ⎪⎝⎭ 化简为:()()32f x x +<即()()311f x x +-<又(6)1f =Q 可得: ()()3(6)(6)f x x f f +-<∴ ()3(6)6x x f f +⎛⎫< ⎪⎝⎭Q ()f x 是定义在(0，+∞)上的增函数∴则:()3010366x xx x⎧⎪+>⎪⎪>⎨⎪⎪+<⎪⎩┄①┄②┄③解①得3x >-解②得0x >解③:当2336=0x x +-得:32x -±=Q ()366x x+<(3)36x x ∴+⋅< 0x >23360x x ∴+-< 得方程的解为:302x -+<<综上所述,原不等式的解集为|0x x ⎧⎪<<⎨⎪⎪⎩⎭ .【点睛】利用函数单调性解函数不等式:首先根据函数的性质把不等式转化为(())(())f g x f h x 的形式,然后根据函数的单调性去掉"f ",转化为具体的不等式(组),此时要注意g()x 与()h x 的取值应在外层函数的定义域内.。

2019-2020学年陕西省咸阳实验中学高一（上）第一次月考数学试卷一、单选题（本大题共12小题，共60.0分） 1. 如果A ={x|x >−1}，那么( )A. 0⊊AB. {0}∈AC. ⌀∈AD. {0}⊆A2. 集合{y ∈N|y =−x 2+6,x ∈N}的真子集的个数是( )A. 9B. 8C. 7D. 63. 下列在法则f 的作用下，从集合A 到集合B 的对应中是映射的是( )A.B.C.D.4. 下列四个函数中，与y =x 表示同一函数的是( )A. y =(√x)2B. y = √x 33C. y = √x 2D. y = x2x5. 已知函数f(x)={x 2,x >0−x 2,x <0则f(x)是( )A. 奇函数B. 偶函数C. 既是奇函数又是偶函数D. 非奇非偶函数6. 已知函数f(x)=(m 2−m −1)x m2+m−3是幂函数，且当x ∈(0,+∞)时，f(x)是增加的，则m 的值为( )A. −1B. 2C. −1或2D. 37. 若函数f(x)=√2−x +√1x+1，则函数g(x)=f(2x)x−1的定义域是( )A. [−12,1]B. [−12,2]C. (−12,2] D. (−12,1)8. 给定下列函数：①f(x)=1x ②f(x)=−|x|③f(x)=−2x −1④f(x)=(x −1)2，满足“对任意x 1，x 2∈(0,+∞)，当x 1<x 2时，都有f(x 1)>f(x 2)”的条件是( )A. ①②③B. ②③④C. ①②④D. ①③④9. 已知g(x)=1−2x ，f[g(x)]=1−x 2x 2(x ≠0)，则f(12)等于( )A. 15B. 1C. 3D. 3010. A ={x|x 2+x −6=0}，B ={x|mx +1=0}且A ∪B =A ，则m 的取值范围( )A. {13,−12}B. {0,−13,−12}C. {0,13,−12}D. {13,12}11. 已知f(x)是定义在R 上的偶函数，它在(−∞,0]上单调递减，那么一定有( )A. f(34)<f(a 2−a +1) B. f(34)≤f(a 2−a +1) C. f(34)>f(a 2−a +1)D. f(34)≥f(a 2−a +1)12. 定义运算a ∗b ={a(a ≤b)b(a >b)，例如1∗2=1，则1∗a 的取值范围是( )A. (0,1)B. (−∞,1]C. [0,1]D. [1,+∞)二、单空题（本大题共3小题，共15.0分）13. 已知映射f ：N →N +,x →x 2+1，则17的原像是______．14. 有15人进了家电超市，其中有9人买了电视机，有7人买了电脑，两种均买了的有3人，则这两种均没买的有 人．15. 设函数f(x)=x|x|+bx +c ，给出下列四个命题：①当c =0时，f(−x)=−f(x)恒成立②当b =0，c >0时，方程f(x)=0只有一个实数根 ③函数y =f(x)的图象关于点(0,c)对称 ④方程f(x)=0至多有两个实数根． 其中正确例题的序号是______ ． 三、多空题（本大题共1小题，共5.0分） 16. 已知函数f(x)，g(x)分别由下表给出则f[g(1)]的值为 (1) ；满足f[g(x)]>g[f(x)]的x 的值是 (2) ．四、解答题（本大题共6小题，共70.0分）17.设全集为R，A={x|x<9}，B={x|x>3}．(1)求A∩(∁R B)和(∁R A)∩B；(2)若集合M={x|m<x<1+2m}，且M⊆(A∩B)，求实数m的取值范围．18.已知定义在R上的奇函数f(x)，当x>0时，f(x)=|x−1|．(Ⅰ)当x∈R时，求f(x)？并画出函数f(x)的图像；(Ⅱ)写出函数f(x)的值域，指出函数f(x)的单调增区间．19.已知函数f(x)定义在(−∞,+∞)上满足任意x，y∈R，都有f(x+y)=f(x)+f(y)成立，f(2)=1．(Ⅰ)求f(0)，f(1)的值；(Ⅱ)判断f(x)的奇偶性，并加以证明．20.A、B两城相距100km，在两地之间距A城xkm处D地建一核电站给A、B两城供电，为保证城市安全．核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比，比例系数λ=0.25.若A城供电量为20亿度/月，B城为10亿度/月．(Ⅰ)把月供电总费用y表示成x的函数，并求定义域；(Ⅱ)核电站建在距A城多远，才能使供电费用最小．21.已知函数f(x)=x+ax(常数a>0)．(Ⅰ)证明：函数f(x)在区间(0,√a]上是递减的；在区间[√a,+∞)上是递增的；(Ⅱ)若a=9，对任意的x∈[1,5]时，x的不等式f(x)≤2m+1都成立，求实数m 的范围．22.已知二次函数f(x)满足任意的x∈R，有f(12+x)=f(12−x)成立，且f(x)最小值为34，f(x)与y轴交点坐标为(0,1)．(Ⅰ)求f(x)的解析式；(Ⅱ)是否存在实数m，n(m<n)，使f(x)的定义域和值域分别为[m,n]和[32m,32n]，如果存在，求出m，n；如果不存在，请说明理由．答案和解析1.【答案】D【解析】解：A={x|x>−1}，由元素与集合的关系，集合与集合关系可知：{0}⊆A．故选：D．利用元素与集合的关系，集合与集合关系判断选项即可．本题考查元素与集合的关系，集合基本知识的应用，是基础题．2.【答案】C【解析】解：x=0时，y=6；x=1时，y=5；x=2时，y=2；x=3时，y=−3；∵函数y=−x2+6，x∈N，在[0,+∞)上是减函数；∴x≥3时，y<0；∴{y∈N|y=−x2+6,x∈N}={2,5，6}；∴该集合的所有真子集为：⌀，{2}，{5}，{6}，{2,5}，{2,6}，{5,6}；∴该集合的真子集个数为7．故选：C．根据条件，让x从0开始取值，求出对应的y值：x=0，y=6；x=1，y=5；x=2，y=2；x=3，y=−3，显然x往后取值对应的y值都小于0，所以集合{y∈N|y=−x2+ 6,x∈N}={2,5，6}，这样求出该集合的所有真子集即得到真子集的个数．考查描述法表示集合，自然数集N，以及真子集的概念．3.【答案】D【解析】解：根据映射的概念，两个非空集合A，B，对于集合A中的每一个元素，在集合B都有唯一的元素与之对应，选项A和选项C中出现一对多，选项B中，元素2没有对应元素，故只有选项D中的对应符合映射的定义．故选：D．利用映射的定义进行判断即可．本题考查了映射概念，考查了逻辑推理能力，属于基础题．4.【答案】B【解析】【分析】本题考查函数的基本概念，属于基础题．两函数相同，则定义域和对应关系相同，逐一分析判断即可．【解答】解：对于A，函数y=(√x)2的定义域为[0,+∞)，y=x的定义域为R，两函数不同，故排除选项A；3=x，定义域为R，与y=x是同一个函数，故选项B满足条件；对于B，函数y=√x3对于C，函数y=√x2=|x|，与y=x对应关系不同，两函数不同，故排除选项C；的定义域为{x|x≠0}，y=x的定义域为R，两函数不同，故排除选对于D，函数y=x2x项D；故选：B．5.【答案】A【解析】【分析】本题考查函数的奇偶性的判断，注意运用定义法，考查推理能力，属于基础题．根据函数奇偶性的定义，计算f(−x)是否等于−f(x)即可得到结论．【解答】解：当x>0时，−x<0，f(−x)=−(−x)2=−x2=−f(x)；当x<0时，−x>0，f(−x)=(−x)2=x2=−f(x)．综上可知，f(−x)=−f(x)，故f(x)为奇函数．故选A．6.【答案】B【解析】 【分析】根据幂函数的定义与性质，列出方程求出m 的值，再验证是否满足题意即可． 本题考查了幂函数的定义与性质的应用问题，也考查了解方程与不等式的应用问题，是基础题目． 【解答】解：∵函数f(x)=(m 2−m −1)x m 2+m−3是幂函数，∴m 2−m −1=1， 即m 2−m −2=0， 解得m =2或m =−1；当m =2时，m 2+m −3=3>0，f(x)在x ∈(0,+∞)上是增函数，满足题意； 当m =−1时，m 2+m −3=−3<0，f(x)在(0,+∞)上是减函数，不满足题意； 所以，m 的值为2． 故选：B ．7.【答案】D【解析】解：由{2−x ≥0x +1>0，解得−1<x ≤2．∴函数f(x)的定义域为(−1,2]， 由−1<2x ≤2，解得−12<x ≤1，则{−12<x ≤1x −1≠0，得−12<x <1． ∴函数g(x)=f(2x)x−1的定义域是(−12,1)． 故选：D ．求出函数f(x)的定义域，进一步得到f(2x)的定义域，再结合函数g(x)的分母不为0得答案．本题考查函数的定义域及其求法，关键是掌握该类问题的求解方法，是基础题．8.【答案】A【解析】解：因为对任意x 1，x 2∈(0,+∞)，当x 1<x 2时，都有f(x 1)>f(x 2)，故满足条件的函数是一个减函数．对于①，函数是反比例函数，其在(0,+∞)是一个减函数，满足题意； 对于②，f(x)=−|x|，其在(0,+∞)是一个减函数，满足题意； 对于③，函数是一次函数，其在(0,+∞)是一个减函数，满足题意；对于④，函数f(x)=(x −1)2在(0,1)是减函数，在(1,+∞)上是增函数，故不满足题意； 故选A ．对任意x 1，x 2∈(0,+∞)，当x 1<x 2时，都有f(x 1)>f(x 2)，说明对应的函数在(0,+∞)是一个减函数，故问题转化为判断四个函数单调性的问题，根据函数的解析式进行判断即可选出结论．本题考点是函数的单调性的判断与证明，考查根据已知的性质选择具有所给性质的函数的能力，在一些不要求证明函数单调性的函数单调性的判断中，常根据函数的解析式由那几个基本函数组成，综合利用这些基本函数的单调性来判断所研究函数的单调性．9.【答案】A【解析】解：令g(x)=12，得1−2x =12，解得x =14． ∴f(12)=f[g(14)]=1−(14)2(14)2=1516116=15．故选：A ．可令g(x)=12，得出x 的值，再代入可得答案． 本题主要考查已知函数解析式求函数值的问题．10.【答案】C【解析】 【分析】本题考查的知识点是集合关系中的参数取值问题，其中本题易忽略m =0的情况，而错选A ，属于基础题．根据已知中A ={x|x 2+x −6=0}，B ={x|mx +1=0}且A ∪B =A ，我们分m =0，m ≠0两种情况进行讨论，分别求出满足条件的m 的值，即可得到答案． 【解答】解：∵A ={x|x 2+x −6=0}={−3,2}， A ∪B =A ，则B ⊆A ，若m =0，则B =⌀，满足要求； 若m ≠0，则B ={x|x =−1m }， 则m =13，或m =−12，综上m 的取值范围组成的集合为{0,13,−12}， 故选：C ．11.【答案】B【解析】解：f(x)是定义在R 上的偶函数，它在(−∞,0]上单调递减 故f(x)在[0,+∞)上递增， ∵a 2−a +1=(a −12)2+34≥34， ∴f(34)≤f(a 2−a +1)， 故选：B ．由已知得f(x)在[0,+∞)上递增，结合a 2−a +1=(a −12)2+34≥34得到答案． 本题考查的知识点是抽象函数的应用，函数的单调性，利用配方法得到a 2−a +1≥34解答的关键．12.【答案】B【解析】解：由定义得1∗a ={1,1≤aa,1>a，当a ≥1时，1∗a =1，当a <1时，1∗a =a <1， 所以1∗a 的取值范围是(−∞,1]． 故选：B ．根据定义得到1∗a 的表达式为分段函数，由分段函数的性质即可求得范围． 本题考查分段函数值域问题，把各段函数范围求出再取并集即可．13.【答案】4【解析】解：根据映射的概念可得，{x 2+1=17x ∈N，解得x =4， 所以17的原像是4． 故答案为：4．根据映射的概念，列出{x 2+1=17x ∈N，求解即可．本题考查了映射概念的理解与应用，考查了逻辑推理能力，属于基础题．14.【答案】2【解析】 【分析】本题考查集合的实际应用．分别求出只买电脑和电视机的人数，然后进行计算即可． 【解答】解：有9人买了电视机，有7人买了电脑，两种都买的有3人， 则只买电视机的有9−3=6人，只买电脑的有7−3=4人， 则两种都没有买的有15−6−4−3=2人， 故答案为：2．15.【答案】①②③【解析】解：①当c =0时，函数f(x)=x|x|+bx 为奇函数，f(−x)=−f(x)恒成立，故①正确．②b =0，c >0时，得f(x)=x|x|+c 在R 上为单调增函数，且值域为R ，故方程f(x)=0，只有一个实数根，故②正确．③因为f(−x)=−x|x|−bx +c ，所以f(−x)+f(x)=2c ，可得函数f(x)的图象关于点(0,c)对称，故③正确．④当c =0，b =−2，f(x)=x|x|−2x =0的根有x =0，x =2，x =−2故④错误． 故答案为：①②③．①利用函数奇偶性的定义可判断．②当b =0时，得f(x)=x|x|+c 在R 上为单调增函数，方程f(x)=0只有一个实根．③利用函数图象关于点对称的定义，可证得函数f(x)图象关于点(0,c)对称．④举出反例如c=0，b=−2，可以判断．本题考查了函数奇偶性、对称性、单调性以及二次函数的图象和性质．对函数奇偶性和单调性的充分理解，并用于二次函数当中，是解决本题的关键．16.【答案】12【解析】解：f[g(1)]=f(3)=1当x=1时f[g(1)]=1，g[f(1)]=g(1)=3不满足f[g(x)]>g[f(x)]当x=2时，f[g(2)]=f(2)=3，g[f(2)]=g(3)=1满足f[g(x)]>g[f(x)]当x=3时f[g(3)]=f(1)=1，g[f(3)]=g(1)=3不满足f[g(x)]>g[f(x)]故满足f[g(x)]>g[f(x)]的x的值是2故答案为1；2结合表格，先求出内涵式的函数值，再求出外函数的函数值；分别将x=1，2，3代入f[g(x)]，g[f(x)]，判断出满足f[g(x)]>g[f(x)]的x．本题考查函数的表示法：表格法；结合表格求函数值：先求内函数的值，再求外函数的值．17.【答案】解：(1)∵全集为R，A={x|x<9}，B={x|x>3}．∴∁R B=x|x≤3}，∁R A={x|x≥9}，∴A∩(∁R B)={x|x≤3}，(∁R A)∩B={x|x≥9}．(2)集合M={x|m<x<1+2m}，且M⊆(A∩B)，A∩B={x|3<x<9}，∴当M=⌀时，m≥1+2m，解得m≤−1，当M≠⌀时，{m<1+2mm≥31+2m≤9，解得3≤m≤4．∴实数m的取值范围是(−∞,−1]∪[3,4]．【解析】(1)先求出∁R B =x|x ≤3}，∁R A ={x|x ≥9}，由此能求出A ∩(∁R B)，(∁R A)∩B ． (2)当M =⌀时，m ≥1+2m ，当M ≠⌀时，{m <1+2mm ≥31+2m ≤9，由此能求出实数m 的取值范围．本题考查补集、交集、实数的取值范围的求法，考查补集、交集定义、不等式的性质等基础知识，考查运算求解能力等数学核心素养，是基础题．18.【答案】解：(1)f(0)=0；当x <0时，−x >0，所以f(−x)=−f(x)=−|−x −1|=−|x +1|．所以f(x)={|x −1|,x >00,x =0−|x +1|,x <0.f(x)的图象如图． (2)结合图形，f(x)的值域为R ；单调增区间为(−∞,−1]，[1,+∞)．【解析】(1)利用奇函数的定义求出f(0)及当x <0时，f(x)的解析式即可；(2)结合图象求解．本题考查利用奇偶性求解析式，函数图象的应用，属于基础题．19.【答案】解：(Ⅰ)取x =y =0，得f(0)=f(0)+f(0)，∴f(0)=0，∵f(2)=f(1)+f(1)=1， ∴f(1)=12．(Ⅱ)f(x)是奇函数，证明如下：取y =−x ，得f(0)=f[x +(−x)]=f(x)+f(−x)=0， 可得f(−x)=−f(x) ∴函数f(x)是奇函数．【解析】(Ⅰ)令x =y =0代入函数满足的等式，即可求得f(0)，由f(2)=f(1)+f(1)=1即可求得f(1)；(Ⅱ)以−x 取代y ，代入函数满足的等式，可得f(x)+f(−x)=0，由此可得f(x)是奇函数．本题主要考查函数奇偶性的判断，抽象函数的应用，考查运算求解能力，属于基础题．20.【答案】解：(Ⅰ)A城供电费用为y1=0.25×20x2，B城供电费用y2=0.25×10(100−x)2；所以总费用为：y=y1+y2=7.5x2−500x+25000(其中10≤x≤90)；∵核电站距A城xkm，则距B城(100−x)km，∴x≥10，且100−x≥10，解得10≤x≤90；所以x的取值范围是{x|10≤x≤90}．(Ⅱ)因为函数y=7.5x2−500x+25000(其中10≤x≤90)，当x=−−5002×7.5=1003时，此函数取得最小值；所以，核电站建在距A城1003km处，能使A、B两城月供电总费用最小．【解析】(Ⅰ)A城供电费用y1=0.25×20x2，B城供电费用y2=0.25×10(100−x)2，总费用y=y1+y2，整理即可；因为核电站距A城xkm，则距B城(100−x)km，由x≥10，且100−x≥10，得x的范围；(Ⅱ)因为函数y=7.5x2−500x+25000是二次函数，由二次函数的性质可得，x=−b2a 时，函数y取得最小值．本题考查了二次函数模型的应用，二次函数求最值时，通常考虑是否取在对称轴x=−b2a 处，属于中档题．21.【答案】解：(I)设0<x1<x2，则f(x2)−f(x1)=x2−x1x2x1(x1x2−a)；当0<x1<x2<√a时，x1x2−a<0，所以f(x2)−f(x1)<0，即f(x2)<f(x1)；当√a<x1<x2时，x1x2−a>0，所以f(x2)−f(x1)>0，即f(x2)>f(x1)；所以，函数f(x)在区间(0,√a]上是递减的；在区间[√a,+∞)上是递增的；(II)当a=9时，由(1)知，f(x)在[1,3)上单调递减，(3,5]上单调递增，又f(1)=10，f(5)=345<10，所以f(x)的最大值为10，故10≤2m+1，解得m≥92．【解析】(I)利用单调性的定义证明即可；(II)求出f(x)的最大值，再列不等式[f(x)]max≤2m+1求解．本题考查函数的单调性及不等式的恒成立问题，属于基础题．22.【答案】解：(Ⅰ)由f(12+x)=f(12−x)，得x =12是二次函数f(x)的对称轴，由题意，可设f(x)=a(x −12)2+34，又f(x)与y 轴交点坐标为(0,1)，得f(0)=14a +34=1，解得a =1，所以f(x)=(x −12)2+34，即f(x)=x 2−x +1； (Ⅱ)假设存在m ，n(m <n)满足题意，由(Ⅰ)可知：f(x)在(−∞,12)上单调递减，在(12,+∞)上单调递增，若n ≤12，显然不符合题意；若m <12≤n ，则32m =34，即m =12，不符合题意， 若m ≥12，则{f(m)=32m f(n)=32n，即m ，n 是方程f(x)=32x 的两个实数根， 由f(x)=32x ，得x 2−x +1=32x ，即x 2−52x +1=0，解得x =12或x =2， 所以m =12，n =2．【解析】(Ⅰ)由f(12+x)=f(12−x)可得对称轴，根据题意可设出二次函数的顶点式，再代入已知点的坐标即可求解；(Ⅱ)根据对称轴与区间[m,n]的关系分类说明函数的值域，在m ≥12时，得{f(m)=32m f(n)=32n ，即m ，n 是方程f(x)=32x 的两个实数根，从而即可求出m ，n 的值．本题考查二次函数的解析式，考查二次函数的值域问题，考查学生的归纳推理和运算求解的能力，属于中档题．。

2019-2020学年度第一学期期中测试高一数学试卷（西郊中学）（本试卷满分150分 考试时间120分钟）一、选择题（共12小题，每小题5分，共60分）1.已知全集{}7,6,5,4,3,2,1=U ，{}5,4,3=A ，{}6,3,1=B ，那么集合{}7,2是（ ） A.B A Y B.B A I C.()B A C U I D.()B A C U Y3.若函数()x f 满足()8923+=+x x f ，则()x f 的解析式是（ ）A.()89+=x x fB.()23+=x x fC.()43--=x x fD.()23+=x x f 或()43--=x x f4.已知()()3312++-=mx x m x f 为偶函数，则()x f 在区间()2,4-上为（ ）A.增函数B.减函数C.先递增再递减D.先递减再递增5.某企业去年销售收入1000万元，年成本为生产成本500万元与年广告成本200万元两部分．若年利润必须按p %纳税，且年广告费超出年销售收入2%的部分也按p %纳税，其他不纳税．已知该企业去年共纳税120万元．则税率p %为（ ）A.10%B.12%C.20%D.25%6.已知()()()()⎩⎨⎧<+≥-=6265x x f x x x f ，则()3f 为（ ） A.2 B.3 C.4 D.57.若()y x y x lg lg 2lg 2+=-，则yx 2log 等于（ ） A.0 B.2或0 C.2 D.-2或08.函数x x 28log 3+-的零点一定位于区间（ ）A.()6,5B.()4,3C.()3,2D.()2,19.已知10<<a ，则方程x a a x log =的实数根个数是（ ）A.2B.3C.4D.与a 无关10.定义在R 上的偶函数在[0，7]上是增函数，在[]∞+，7上是减函数，又()67=f ，则有关()x f 的叙述正确的是（ ）A.在[]0,7-上是增函数，且最大值是6B.在[]0,7-上是减函数，且最大值是6C.在[]0,7-上是增函数，且最小值是6D.在[]0,7-上是减函数，且最小值是611.已知y =f (x )与y =g (x )的函数图像如下图：则F （x ）＝f （x ）·g （x ）的图像可能是下图中的（ ）12.若函数()()ax x f x ++=110lg 是偶函数，()x x b x g 24-=是奇函数，则b a +的值是（ ） A.-1 B.1 C.21- D.21二、填空题（共4小题，每小题5分，共20分）13、若函数 y =f (x )的定义域是[0，2] ，则函数1)2()(-=x x f x g 的定义域是 . 14、函数y =lnx 的反函数是 .15、函数x y 21log =的递增区间是 .16、若直线y =a 与曲线12+-=x x y 有四个交点，求a 的取值范围 .三、解答题（共6小题，共70分）17、（10分）(1)计算：31021)6427()5lg 972-++（）（ (2)解方程3)96(log 3=-x 18、（12分）讨论函数xa x x f +=)((a >0)在),[+∞∈a x 的单调性并证明.19、（12分）已知函数⎪⎩⎪⎨⎧<+=>+-=0,0,00,2)(22x mx x x x x x x f 是奇函数。

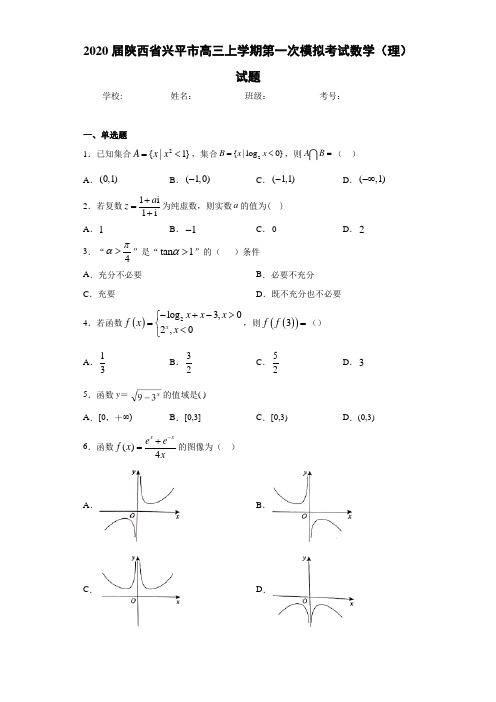
2020届陕西省兴平市高三上学期第一次模拟考试数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合2{|1}A x x =<，集合2{|log 0}B x x =<，则A B =（ ）A ．(0,1)B ．(1,0)-C ．(1,1)-D ．(,1)-∞2．若复数1i1ia z +=+为纯虚数，则实数a 的值为( ) A ．1 B ．1-C ．0D ．23．“4πα>”是“tan 1α>”的（ ）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要4．若函数()2log 3,02,0xx x x f x x -+->⎧=⎨<⎩，则()()3f f =（） A ．13 B ．32C ．52D ．35．函数y ＝的值域是( ) A ．[0，＋∞)B ．[0,3]C ．[0,3)D ．(0,3)6．函数()4x xe ef x x-+=的图像为（ ）A ．B ．C ．D ．7．要得到函数1sin2y x =的图象，只需将函数1sin 24y x π⎛⎫=+ ⎪⎝⎭的图象（ ）A ．向左平移4π个单位长度 B ．向右平移4π个单位长度 C ．向左平移2π个单位长度 D ．向右平移2π个单位长度 8．函数()23sin 23f x x π⎛⎫=-⎪⎝⎭的一个单调递减区间是（ ） A ．713,1212ππ⎡⎤⎢⎥⎣⎦ B ．7,1212ππ⎡⎤⎢⎥⎣⎦ C ．,22ππ⎡⎤-⎢⎥⎣⎦ D ．5,66ππ⎡⎤-⎢⎥⎣⎦ 9．在ABC ∆中，角,,A B C 对边分别是,,a b c ，满足22()6,3c a b C π=-+=，则ABC ∆的面积为（ ）A ．BCD ．3210．已知sin 45πα⎛⎫-=⎪⎝⎭，5,24ππα⎛⎫∈ ⎪⎝⎭，则sin α=（ ）A B ．10-C ．10±D ．10-11．若2log 3a =，5log 7b =，40.7c =，则实数a ，b ，c 的大小关系为（ ） A ．c b a >>B ．c a b >>C ．b a c >>D ．a b c >>12．定义在R 上的可导函数()f x 满足()11f =，且()2'1f x >，当3,22x ππ⎡⎤∈-⎢⎥⎣⎦时，不等式23(2cos )2sin22x f x +>的解集为( ) A ．4,33ππ⎛⎫⎪⎝⎭B ．4,33ππ⎛⎫- ⎪⎝⎭C ．0,3π⎛⎫⎪⎝⎭D ．,33ππ⎛⎫-⎪⎝⎭二、填空题13．命题“x ∀∈R ，210x ”的否定为_______14．定积分1()xx e dx +=⎰_______.15．函数()1x f x e-=在()1,1处切线方程是______．16．已知函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭的两条对称轴之间距离的最小值为4，将函数()f x 的图象向右平移1个单位长度后得到函数()g x 的图象，则()()()()1232019g g g g ++++=___________.三、解答题17．命题:p 关于x 的不等式2240,x ax x R ++>∈对一切恒成立；命题:q 函数()()32.xf x a =-是增函数 p q p q ∨∧若为真，为假，求实数a 的取值范围.18．已知函数()2cos 10cos f x x x x =-+. （1）求函数()f x 的最小正周期和单调递增区间； （2）将函数()f x 的图像向右平移6π个单位长度，得到函数()g x 的图像，求使得()0g x ≥的x 的取值范围.19．已知函数()11x af x e =++为奇函数. （1）判断()f x 的单调性并证明； （2）解不等式22(log )3)0f x f x +-≤.20．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c coscos CA=. （1）求角A 的值；（2）若6B π=，且ABC ∆的面积为BC 边上的中线AM 的大小.21．已知函数()()22xxaf x a R =-∈将()y f x =的图象向右平移两个单位，得到函数()yg x =的图象.（1）求函数()y g x =的解析式；（2）若方程()f x a =在[]0,1x ∈上有且仅有一个实根，求a 的取值范围.22．已知函数()sin (1)ln(1)f x x x x =-++；2()sin 12x g x x x =+-+.（1）判断()f x 在[0,)+∞上的单调性，并说明理由； （2）求()g x 的极值；（3）当(0,]x π∈时，sin (2)ln(1)x a x x >-+，求实数a 的取值范围.参考答案1．A 【解析】 【分析】先解不等式得集合A 与B ，再根据交集定义得结果. 【详解】根据题意：集合{|11}A x x =-<<，集合{|01}B x x =<<，(0,1)A B ∴=故选A ． 【点睛】本题考查一元二次不等式与对数不等式解法以及交集的定义，考查基本分析求解能力，属基础题. 2．B 【解析】 【分析】化简z 为a+bi(a,b ∈R)的形式利用纯虚数概念求解即可 【详解】()()()()()11111i 1i 112ai i a a i a z i i +-++-+===++-故10,10a a +=-≠ ，解1a =- 故选B 【点睛】本题考查复数的运算及基本概念，准确计算是关键，是基础题 3．D 【解析】 【分析】利用充分必要条件的定义，举反例进行说明． 【详解】 当α4π>时，不一定满足tan α1>，如3α4π=，当tan α1>时，不一定有α4π>，如5α8π=-∴“α4π>”是“tan α1>”的既不充分也不必要条件故选D ． 【点睛】本题主要考查充分不必要条件的定义，以及正切函数的函数值，是一道基础题． 4．A 【分析】首先计算()3f ，然后再计算()()3f f 的值.【详解】()223log 333log 30f =-+-=-<,()()()2log 3213log 323f f f -=-==.故选A. 【点睛】本题考查了分段函数求值，属于计算题型. 5．C 【解析】 试题分析：309393x x y >∴-<∴<，函数值域为[0，3）考点：函数值域 6．A 【解析】 【分析】由()()4x xe ef x f x x -+-=-=-，得()f x 的图象关于原点对称，当0x >时，得()0f x >，对选项分析判断即可. 【详解】由()()4x xe ef x f x x -+-=-=-，得()f x 的图象关于原点对称，排除C,D. 当0x >时，得()0f x >，排除B. 故选A本题考查了函数图像的识别，利用了函数的奇偶性等性质，属于基础题. 7．D 【分析】 将函数1sin 24y x π⎛⎫=+ ⎪⎝⎭表示为1sin 22y x π⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦，结合三角函数的变换规律可得出正确选项. 【详解】1sin 1s n 222i 4y x x ππ⎡⎤⎛⎫+ ⎛⎪⎢⎥⎝⎭⎫=+= ⎭⎣⎪⎝⎦，因此，为了得到函数1sin 2y x =的图象，只需将函数1sin 24y x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度，故选：D.【点睛】本题考查三角函数的平移变换，解决三角函数平移变换需要注意以下两个问题： （1）变换前后两个函数名称要保持一致；（2）平移变换指的是在自变量x 上变化了多少. 8．B 【分析】利用诱导公式化简函数的解析式，再利用余弦函数的单调性，求得()f x 的一个减区间． 【详解】解：对于函数2()3sin 23sin 23cos 23cos 232666f x x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=+-=-=-⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， 令2226k x k ππππ-+，k Z ∈，解得71212k x k ππππ++，k Z ∈，可得函数的单调递减区间为7,1212k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈， 令0k =，可得选项B 正确， 故选：B ． 【点睛】本题主要考查诱导公式、余弦函数的单调性，属于基础题． 9．B化简，再利用余弦定理即可求出ab 的值，代入三角形面积公式即可．【详解】，∴22226c a ab b =-++，又，由余弦定理可得： 222222cos c a b ab C a b ab =+-=+-∴ 222226a ab b a b ab -++=+-，解得：6ab =，由三角形面积公式可得1sin 22ABC S ab C ∆==故答案选B ． 【点睛】本题考查余弦定理、三角形的面积公式，考查学生化简、变形的能力，属于中档题． 10．B 【解析】分析：先根据sin 45πα⎛⎫-= ⎪⎝⎭得到54ππα<<，再求cos()4πα-=sin α的值. 详解：由题得11355(12sin cos ),sin cos 0,,2510244πππαααααπα-=∴=><<∴<<所以3,cos()444πππαπα<-<∴-=，所以sin sin[()](44ππαα=-+== 故答案为B点睛：（1）本题主要考查三角函数求值，意在考查学生对这些基础知识的掌握能力和分析转化能力. (2)解答本题的关键有两点，其一是根据已知求α的隐含范围，其二是通过变角求sin α的值，sin sin[()]44ππαα=-+.11．D 【分析】先判断出,a b 大于1，而c 小于1，得到最小为c .然后利用对数的运算和性质，比较,a b 两个数的大小. 【详解】2255log 3log 21,log 7log 51a b =>==>=，而400.71<<，故c 是最小的.由于542221log 7log 7log 7log log 32<==<，即52log 7log 3<，即b a <，故选D.【点睛】本小题主要考查指数式和对数式比较大小，考查对数函数的性质，考查比较大小的方法，属于中档题. 12．D 【分析】构造函数()()1122g x f x x =--，可得()g x 在定义域内R 上是增函数，且()10g =，进而根据23(2cos )2sin022x f x +->转化成()(2cos )1g x g >，进而可求得答案 【详解】令11()()22g x f x x =--，则1()'()0'2g x f x =->， ()g x ∴在定义域R 上是增函数，且11(1)(1)022g f =--=，1(2cos )(2cos )cos 2g x f x x ∴=--23=(2cos )2sin 22x f x +-，∴23(2cos )2sin 022x f x +->可转化成()(2cos )1g x g >，得到2cos 1x >，又3,22x ππ⎡⎤∈-⎢⎥⎣⎦，可以得到,33x ππ⎛⎫∴∈- ⎪⎝⎭故选D 【点睛】本题考查利用函数的单调性求取值范围，解题的难点在于如何合理的构造函数，属于中档题 13．x R ∃∈，210x +≤ 【解析】试题分析：本小题给出的命题是全称命题，它的否定是特称命题“x R ∃∈，210x +≤”. 考点：本小题主要考查含有一个量词的命题的否定.点评：对于此类问题，要主要特称命题的否定是全称命题，全称命题的否定是特称命题. 14．12e -【解析】分析：根据定积分，找到被积分函数的原函数，即可求解.详解：由12100111()()|()222xx x e dx x e e e e +=+=+-=-⎰. 点睛：本题主要考查了定积分的计算问题，其中解答中找到被积分函数的原函数是解答的关键，着重考查了推理与运算能力. 15．y x = 【分析】求得函数的导数1()x f x e-='，求得(1)1f '=，得到切线的斜率为1k =，利用直线的点斜式方程，即可求解切线的方程. 【详解】由题意，函数1()x f x e-=，则1()x f x e -='，则(1)1f '=，即在(1,1)处的切线的斜率为1k =，由直线的点斜式方程可得，切线的方程为11y x -=-，即y x =. 【点睛】本题主要考查了利用导数的几何意义求解曲线在某点处的切线方程，其中解答中熟记导数的几何意义的应用是解答的关键，着重考查了运算与求解能力，属于基础题. 161 【分析】由题意利用正弦函数的周期性求得ω，可得()f x 的解析式，再利用函数sin()y A x ωϕ=+的图象变换规律得到()g x 的解析式，再根据()g x 的周期性求出式子的结果． 【详解】 解：依题意，42T =，28T πω==，所以4πω=，故()sin 44f x x ππ⎛⎫=+ ⎪⎝⎭．将函数()f x 的图象向右平移1个单位长度后得到函数()g x 的图象，∴()(1)sin sin 4444g x f x x x ππππ⎛⎫=-=-+= ⎪⎝⎭．()1sin 4g π=，()2sin 12g π==，()33sin 4g π==，()4sin 0g π==，()55sin 4g π==()36sin 12g π==-，()77sin 4g π==()8sin 20g π== 因为()()()()12380g g g g ++++=， 所以()()()()()()()12320191231g g g g g g g ++++=++=，1．【点睛】本题主要考查正弦函数的周期性，函数sin()y A x ωϕ=+的图象变换规律，属于基础题． 17．12 2.a a ≤≤-＜或【分析】容易求出命题p 为真时，﹣2＜a ＜2，而q 为真时，a ＜1．由p ∨q 为真，p ∧q 为假便可得到p 真q 假，或p 假q 真两种情况，求出每种情况的a 的范围，再求并集即可得出实数a 的取值范围．【详解】①若命题p 为真，则：△=4a 2﹣16＜0，∴﹣2＜a ＜2；②若命题q 为真，则：3﹣2a ＞1，∴a ＜1；∴p ∨q 为真，p ∧q 为假，则p 真q 假，或p 假q 真；∴221a a -⎧⎨≥⎩＜＜，或221a a a ≤-≥⎧⎨⎩或＜； ∴1≤a ＜2，或a ≤﹣2；∴实数a 的取值范围为122a a ≤≤-＜或．【点睛】“p q ∨”，“p q ∧”“p ⌝”等形式命题真假的判断步骤：（1）确定命题的构成形式；（2）判断其中命题,p q 的真假；（3）确定“p q ∨”，“p q ∧”“p ⌝”等形式命题的真假.18．（1）最小正周期T=π，函数f （x ）在2,36k k ππππ⎡⎤--⎢⎥⎣⎦()k Z ∈上单调递增；（2）33x k x k ππππ⎡⎤∈-+≤≤+⎢⎥⎣⎦. 【解析】试题分析：（1）利用和与差以及二倍角公式，辅助角公式化简即可求函数f x （） 的最小正周期和单调减区间；（2）根据三角函数平移变换的规律求解g x （） 的解析式，利用预先函数的性质可求使得()0g x ≥的x 的取值范围.试题解析：（1）∵f（x ）=-10sinxcosx + 10cos 2x=5cos25x x -++ =10sin 526x π+（）+5. ∴所求函数f （x ）的最小正周期T=π5222262236k x k k x k πππππππππ-+≤+≤+-+≤≤-+ 所以函数f （x ）在2,36k k ππππ⎡⎤--⎢⎥⎣⎦()k Z ∈上单调递增 （2）将函数f （x ）的图象向右平移个单位长度后得到()510sin 2510cos25636g x f x x x πππ⎛⎫⎛⎫=-=-++=+ ⎪ ⎪⎝⎭⎝⎭的图象 所以当()10cos22g x x 时，≥≥-所以22222,3333k x k k x k ππππππππ-+≤≤+-+≤≤+ 所以33x k x k ππππ⎡⎤∈-+≤≤+⎢⎥⎣⎦()k Z ∈ 【点睛】本题考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键19．(1)答案见解析；(2)1[,2]8.【解析】 试题分析：(1)函数为奇函数，则()()f x f x -=-恒成立，据此得到关于实数a 的恒等式，整理可得2a =-，函数的解析式为()211x f x e -=++，利用导函数研究函数的单调性可得函数是单调递增函数； (2)结合函数的奇偶性和函数的单调性脱去f 符号，求解对数型二次不等式222230log x log x +-≤可得原不等式的解集为1,28⎡⎤⎢⎥⎣⎦. 试题解析：（1）由已知()()f x f x -=-，∴1111x x a a e e -⎛⎫+=-+ ⎪++⎝⎭∴22011x x x ae a a e e ++=+=++，2a =- ∵()2'01xx e f x e =>+，∴()211x f x e -=++为单调递增函数. （2）∵()()2230f log x f +-≤，∴()()223f log x f ≤--，而()f x 为奇函数，∴()()223f log x f ≤-+ ∵()f x 为单调递增函数，∴223log x ≤-+，∴222230log x log x +-≤，∴231log x -≤≤， ∴1,28x ⎡⎤∈⎢⎥⎣⎦.20．(1)6A π=；(2)AM =【解析】试题分析：（1）cosC cosA =，整理计算可得20sinBcosA =，则2cosA =，6A π=.（2）由题意可得6A π=，6B π=，12ABC S absinC ∆= 21223a sin π==4a =.在AMC ∆中应用余弦定理有2222120AM AC MC AC MCcos ︒=+-⋅，据此计算可得AM =试题解析：（1cosC cosA =，cosC cosA =，所以2sinBcosA =，所以()20sinBcosA A C +=，20sinBcosA =.又因为0sinB ≠，所以cosA =，又因为0A π<<，且2A π≠，所以6A π=.（2）据（1）求解知6A π=.若6B π=，则12ABC S absinC ∆= 21223a sin π==所以4a =，4a =-（舍）又在AMC ∆中，2222120AM AC MC AC MCcos ︒=+-⋅， 所以22211212022AM AC AC AC AC cos ︒⎛⎫=+-⋅⋅⋅ ⎪⎝⎭ 22142242282⎛⎫=+-⋅⋅⋅-= ⎪⎝⎭.所以AM =21．（1）()2222x x a g x --=-（2）1423a ≤≤ 【分析】(1)借助平移的知识可以直接求出函数解析式（2）先换元2x t =将问题转化为20t at a --=有且只有一个根，再运用函数方程思想建立不等式组分析求解．【详解】（1）()2222x x ag x --=-（2）设2x t =，则[]1,2t ∈，原方程可化为20t at a --=，于是只须20t at a --=在[]1,2t ∈上有且仅有一个实根.法1：设()2k t t at a =--，对称轴2a t =，则()()120k k ⋅≤①.或0122a ∆=⎧⎪⎨≤≤⎪⎩② 由①得()()12430a a --≤，即()()21340a a --≤，1423a ≤≤. 由②得24024a a a ⎧+=⎨≤≤⎩无解，则1423a ≤≤. 法2：由20t at a --=，[]1,2t ∈，因为a=0时，221110t at a a t t ⎛⎫--≠=+ ⎪⎝⎭，所以，[]1,2t ∈，设1u t =，则1,12u ⎡⎤∈⎢⎥⎣⎦，21u u a=+. 记()2g u u u =+，则()2g u u u =+在1,12⎡⎤⎢⎥⎣⎦上是单调递增函数，因为要使题设成立，只须()1112g g a⎛⎫≤≤ ⎪⎝⎭.即4123a ≤≤.从而1423a ≤≤. 【点睛】在解答指数函数的综合题目时可以采用换元法，转化为一元二次函数的问题，注意根据题目要求需要进行必要的分类讨论.22．（1）见解析（2）极小值(0)1g =.（3）10,2⎛⎤ ⎥⎝⎦【分析】（1）求导数，根据导函数符号确定单调性，（2）利用导数研究导函数单调性，根据单调性确定导函数符号变化规律，即得函数极值，（3）先根据特殊值得0a <，再由（1）得()()1ln 1sin x x x ++>，结合()()sin 2ln 1x a x x >-+得()21a x x -<+,因此102a <≤，最后利用（2）证明102a <≤满足条件. 【详解】解：（1）∵()()()sin 1ln 1f x x x x =-++，则()()'cos 1ln 1f x x x =--+.当0x ≥时，cos 10x -≤，()ln 10x -+≤，得()'0f x ≤，∴()f x 在[)0,+∞上单调递减. （2）∵()2sin 12x g x x x =+-+， 则()'cos 1g x x x =+-，令()()'g x m x =，则()'1sin 0m x x =-≥.∴()m x 即()'g x 在(),-∞+∞上单调递增.又()'00g =，∴当0x >时，()'0g x >，当0x <时，()'0g x <.∴()g x 在()0,+∞上单调递增，在(),0-∞上单调递减，∴()g x 有极小值()01g =.（3）令()()()sin 2ln 1F x x a x x =--+，即()0F x >对(]0,x π∈成立.①0a ≤时，()()()2ln 10F a πππ=--+≤与()0F x >矛盾，不成立. ②102a <≤时，当()0,2x ∈时， 令()()2ln 1h x x a x =-+，则()2'101a h x x =->+， ∴()h x 在()0,2上单调递增，又()00h =，∴()0h x >，即()ln 12x a x >+. 由（2）知()()()22sin 2ln 122x x x x x a x x ->-=>-+. 当[]2,x π∈时，sin 0x ≥，而()()2ln 10a x x -+≤，等号不同时成立，∴()()sin 2ln 1x a x x >-+.③12a >时，若210,1a x a -⎛⎫∈ ⎪+⎝⎭，则()21a x x ->+， 即()()()()2ln 11ln 1a x x x x -+>++，由（1）知()()sin 1ln 10x x x -++<，即()()1ln 1sin x x x ++>.∴()()2ln 1sin a x x x -+>，∴()0F x >不成立.综上，a 的取值范围为10,2⎛⎤ ⎥⎝⎦. 【点睛】本题考查利用导数研究函数单调性与函数极值以及不等式恒成立，考查综合分析求解能力，属难题.。

普集高中2019—2020学年度第一学期高一年级第1次月考（数学）试题（卷）一、选择题（本大题共10小题，每小题5分，共50分，在每小题的四个选项中，只有一个选项是符合题目要求的）1.设集合A ＝{1,2}，则满足A ∪B ＝{1,2,3}的集合B 的个数是( )A ．1B ．3C ．4D ．82. 设B A f →:是从集合A 到集合B 的映射,其中(){}R y R x y x B A ∈∈==,,,()()y x y x y x f -+→,,:,那么B 中元素()3,1的原像是（ ）A.()4,2-B.()4,2-C.()1,2-D.()1,2-3．设集合A =}3,2,1{，B =}5,4{，M =},,|{B b A a b a x x ∈∈+= ，则M 中元素的个数为（ ）A.3B.4C.5D.64．在下列四组函数中，表示同一函数的是（ ）.A ．f (x )＝0x ，g (x )＝1B ．()()f x g x ==C ．(1)(3)(),()31x x f x g x x x -+==+- D ．f (x )＝|x |， g (x )＝ 5．已知全集U ＝R ，集合A ＝{1,2,3,4,5}，B ＝{x ∈R |x ≥3}，图1中阴影部分所表示的集合为( )图1A ．{1}B ．{1,2}C ．{1,2,3}D ．{0,1,2}6. 函数y ＝x ＋|x |x 的图像是( )7. 定义在R 上的函数f (x ) 满足f (x ) =21,12,1x x x x⎧+≤⎪⎨>⎪⎩则f (f (3))的值为( A ) A. 139 B. 3 C. 23 D. 158．已知集合A ＝{x |x <a }，B ＝{x |1<x <2}，且A ∪(∁R B )＝R ，则实数a 的取值范围是( ) A ．a ≤2 B ．a <1 C ．a ≥2 D ．a >29．下列函数f (x )中，满足对任意x 1，x 2∈(0，＋∞)，当x 1<x 2时，都有f (x 1)>f (x 2)的是( ) A ．f (x )＝x 2B ．f (x )＝1xC ．f (x )＝|x |D ．f (x )＝2x ＋110．已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1<x <2m －1}，且B ≠∅，若A ∪B ＝A ，则( ) A ．－3≤m ≤4B ．－3<m <4C ．2<m <4D ． 2<m ≤4二、填空题（每小题4分，共20分，）11．若A ＝{x |y ＝x ＋1}，B ＝{y |y ＝x 2＋1}，则A ∩B ＝ .12. 函数y=的定义域为 . 13．已知f (x )是定义在(－2，2)上的减函数，并且f (m －1)－f (1－2m )＞0，则实数m 的取值范围是 .14．已知函数F (x )＝f (x )＋g (x )，其中f (x )是x 的正比例函数，g (x )是x 的反比例函数，且F ⎝ ⎛⎭⎪⎫13＝16，F (1)＝8，则F (x )的解析式为 ．15．已知集合{1,2}A =-，{|1}B x ax ==，若B A ⊆，则由实数a 的所有可能的取值组成的集合为 .三、解答题（每小题10分，共50分）16．已知集合A ＝{x |－4≤x ≤－2}，集合B ＝{x |x ＋3≥0}．求：(1)A ∩B ；(2)A ∪B ；(3)∁R (A ∩B )．17. 已知函数f (x )＝⎪⎩⎪⎨⎧+x x x 222)2()21()1(≥<<--≤x x x (1)求f {f [f (3)]}的值；(2)求f (a )＝3，求a 的值；(3)画出函数的图像．18．已知集合A ＝{x |1<x <3}，集合B ＝{x |2m <x <1－m }．(1)当m ＝－1时，求A ∪B ；(2)若A ∪B ＝B ，求实数m 的取值范围；(3)若A ∩B ＝∅，求实数m 的取值范围．19．已知函数f (x )＝1a －1x (a >0，x >0)．(1)求证：f (x )在(0，＋∞)上是增加的；(2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．20．某蔬菜基地种植西红柿，由历年市场行情得知，从2月1日起的300天内，西红柿市场售价与上市时间的关系用左图的一条折线表示；西红柿的种植成本与上市时间的关系用右图的抛物线段表示.（Ⅰ）写出左图表示的市场售价与时间的函数关系P=f (t )；写出右图表示的种植成本与时间的函数关系式Q=g (t )；（Ⅱ）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大.（注：市场售价和种植成本的单位：元/100kg ，时间单位：天）2019—2020学年度第一学期高一年级第1次月考（数学）试题答案一、 选择题（本大题共10小题，每小题5分，共50分，在每小题的四个选项中，只有一个选项是符合题目要求的）1.C2. C 3． B 4．D 5．B 6. C 7. A 8．C 9．B. 10．D二、 填空题（每小题4分，共20分，）11．【答案】 [1，＋∞) 12. 【答案】[)()1,00,-⋃+∞13．【答案】(－32,21) 14．【答案】 F (x )＝3x ＋5x15．【答案】11,0,2⎧⎫-⎨⎬⎩⎭三、解答题（每小题10分，共50分）16．解：由已知得B ＝{x |x ≥－3}，(1)A ∩B ＝{x |－3≤x ≤－2}．(2)A ∪B ＝{x |x ≥－4}．(3)∁R (A ∩B )＝{x |x ＜－3或x ＞－2}．17. [解析] (1)∵－1<3<2，∴f (3)＝(3)2＝3.又 3≥2，∴f [f (3)]＝f (3)＝2×3＝6.又6≥2，∴f {f [f (3)]}＝f (6)＝2×6＝12.(2)当a ≤－1时，f (a )＝a ＋2.若f (a )＝3，则a ＋2＝3，∴a ＝1(舍去)．当－1<a <2时，f (a )＝a 2.若f (a )＝3，则a 2＝3，∴a ＝3，或a ＝－3(舍去)．当a ≥2时，f (a )＝2a .若f (a )＝3，则2a ＝3，∴a ＝32(舍去)．综上可知，a ＝ 3.(3)函数f (x )的图像如图所示，18．【解】 (1)当m ＝－1时，B ＝{x |－2<x <2}，则A ∪B ＝{x |－2<x <3}．(2)由A ∪B ＝B 即A ⊆B 知：⎩⎪⎨⎪⎧ 1－m >2m ，2m ≤1，1－m ≥3，得m ≤－2，即实数m 的取值范围为{m |m ≤－2}．(3)由A ∩B ＝∅得：①若2m ≥1－m ，即m ≥13时，B ＝∅，符合题意；②若2m <1－m 即m <13时，需⎩⎨⎧ m <13，1－m ≤1或⎩⎨⎧ m <13，2m ≥3，得0≤m <13或∅，即0≤m <13，综上知m ≥0，即实数m 的取值范围为{m |m ≥0}． 19．[解析] (1)设x 1，x 2是(0，＋∞)上的任意两个实数，且x 1<x 2.则f (x 1)－f (x 2)＝(1a －1x 1)－(1a －1x 2)＝1x 2－1x 1＝x 1－x 2x 1x 2.∵0<x 1<x 2，∴x 1－x 2<0，x 1x 2>0.∴x 1－x 2x 1x 2<0.∴f (x 1)<f (x 2)．∴函数f (x )在(0，＋∞)上是增加的．(2)∵f (x )在[12，2]上的值域是[12，2]，又∵f (x )在[12，2]上是增加的，∴⎩⎪⎨⎪⎧ f (12)＝12f (2)＝2，即⎩⎨⎧ 1a －2＝121a －12＝2.∴a ＝25.20．解（Ⅰ）,100)150()(;300200,30022000,300)(2+-=⎩⎨⎧≤<-≤≤-=t a t g t t t t t f 设将（50，150）代入得 ;3000,100)150(2001)(2≤≤+-=t t t g （Ⅱ）设时刻t 的纯收益为),()()(t g t f t h -= ①当,100)50(20012175212001)(,200022+--=++-=≤≤t t t t h t 时 ∴当t=50时;100)]([max =t h②当200,100)350(200121025272001)(,30022+--=-+-=≤<t t t t h t 时 ∴当t=300时取最大值87.5<100；故第50天时上市最好.。

（新课标）2018-2019学年度苏教版高中数学必修一高一（上）9月月考数学试卷一、填空题：（本大题共14个小题，每小题5分，共70分，把答案填写在题中横线上）1．下列所给关系正确的个数是．①π∈R；②∉Q；③0∈N*；④|﹣4|∉N*．2．设集合U={1，2，3，4，5，6}，M={1，2，4}，则∁U M= ．3．设集合A={x|﹣1＜x＜2}，集合B={x|1＜x＜3}，则A∪B= ．4．已知f（x）=，则f[f（0）]= ．5．函数f（x）=+的定义域为．6．函数，使函数值为5的x的值是．7．设A={（x，y）|y=﹣4x+6}，B={（x，y）|y=5x﹣3}，则A∩B= ．8．若函数f（x）在实数集R上是增函数，且f（x）＞f（1﹣x），则x的取值范围是．9．满足条件{1，2}⊆M⊆{1，2，3，4，5}的集合M的个数是．10．已知一个函数的解析式为y=x2，它的值域为{1，4}，这样的函数有个．11．已知集合A={x|1≤x＜5}，C={x|﹣a＜x≤a+3}．若C∩A=C，则a的取值范围是．12．已知全集U=R，函数y=+的定义域为集合A，函数y=的定义域为集合B．则集合（∁U A）∩（∁U B）= ．13．已知函数f（x），g（x）分别由下表给出：则满足f（g（x））=g（f（x））的x值为．x 1 2 3 4f（x） 1 3 1 3x 1 2 3 4g（x） 3 2 3 214．函数f（x）=2x2﹣mx+3，当x∈[2，+∞）时是增函数，当x∈（﹣∞，2]时是减函数，则f（1）= ．二、解答题：（本大题共6小题，共90分，解答应写出必要的文字说明、证明过程或演算步骤）15．集合A={﹣2}，B={x|ax+1=0，a∈R}，若A∩B=B，求a的值．16．求下列函数的值域（1）y=﹣，x∈[﹣3，0）∪（0，1]；（2）y=x2+4x+1，x∈[﹣3，0]．17．已知集合M是由三个元素﹣2，3x2+3x﹣4，x2+x﹣4组成，若2∈M，求x．18．已知f（x）是一次函数，且f[f（x）]=4x﹣1，求f（x）及f（2）．19．求证：函数f（x）=﹣﹣1在区间（0，+∞）上是单调增函数．20．函数f（x）是定义在（0，+∞）上的增函数，对任意的x，y∈（0，+∞），都有f（x+y）=f（x）+f（y）﹣1，且f（4）=5．（1）求f（2）的值；（2）解不等式f（m﹣2）≤3．参考答案与试题解析一、填空题：（本大题共14个小题，每小题5分，共70分，把答案填写在题中横线上）1．下列所给关系正确的个数是 2 ．①π∈R；②∉Q；③0∈N*；④|﹣4|∉N*．【考点】元素与集合关系的判断．【分析】根据元素与集合的关系进行判断．【解答】解：对于①π∈R：R是一切实数集，π是一个元素，所以π∈R是正确的，故A对．②∉Q：无理数，Q是有理数集，所以∉Q是正确的，故B对．③0∈N*：N*是大于0的正整数集，所以0∉N*，故C不对．④|﹣4|∉N*：N*是大于0的正整数集，|﹣4|=4∈N*，故D不对．综上所述：①②正确．故答案为：2．2．设集合U={1，2，3，4，5，6}，M={1，2，4}，则∁U M= {3，5，6} ．【考点】补集及其运算．【分析】题目是用列举法给出了两个数集，直接利用补集运算进行求解．【解答】解：因为集合U={1，2，3，4，5，6}，M={1，2，4}，则∁U M={3，5，6}．故答案为：{3，5，6}．3．设集合A={x|﹣1＜x＜2}，集合B={x|1＜x＜3}，则A∪B= {x|﹣1＜x＜3} ．【考点】并集及其运算．【分析】利用交集性质直接求解．【解答】解：∵集合A={x|﹣1＜x＜2}，集合B={x|1＜x＜3}，∴A∪B={x|﹣1＜x＜3}．故答案为：{x|﹣1＜x＜3}．4．已知f（x）=，则f[f（0）]= ﹣5 ．【考点】函数的值．【分析】根据定义域的范围代值计算即可．【解答】解：由题意，f（x）=，当x=0时，则f（0）=﹣1，那么f[f（0）]=f（﹣1），当x=﹣1时，f（﹣1）=﹣5．即f[f（0）]=f（﹣1）=﹣5故答案为﹣55．函数f（x）=+的定义域为[﹣1，2）U（2，+∞）．【考点】函数的定义域及其求法．【分析】根据负数不能开偶次方根和分母不能为零来求解，两者求解的结果取交集．【解答】解：根据题意：解得：x≥﹣1且x≠2∴定义域是：[﹣1，2）∪（2，+∞）故答案为：[﹣1，2）∪（2，+∞）6．函数，使函数值为5的x的值是﹣2 ．【考点】分段函数的解析式求法及其图象的作法；函数的值．【分析】根据分段函数的分段标准进行分类讨论，分别建立方程，求出满足条件的x即可．【解答】解：①当x≤0时，x2+1=5解得x=﹣2②当x＞0时，﹣2x=5解得x=﹣（舍去）综上所述，x=﹣2，故答案为﹣27．设A={（x，y）|y=﹣4x+6}，B={（x，y）|y=5x﹣3}，则A∩B= {（1，2）} ．【考点】交集及其运算．【分析】直接联立方程组，求出方程组是解，就是A与B的交集．【解答】解：由题意可知A={（x，y）|y=﹣4x+6}，B={（x，y）|y=5x﹣3}，所以解得，所以A∩B={（1，2）}．故答案为：{（1，2）}．8．若函数f（x）在实数集R上是增函数，且f（x）＞f（1﹣x），则x的取值范围是（，+∞）．【考点】函数单调性的性质．【分析】直接利用函数在R上是增函数，f（x）＞f（1﹣x）转化为x＞1﹣x求解即可．【解答】解：由题意：函数f（x）在实数集R上是增函数，由f（x）＞f（1﹣x），可得：x＞1﹣x，解得：x故答案为（，+∞）．9．满足条件{1，2}⊆M⊆{1，2，3，4，5}的集合M的个数是8 ．【考点】集合的包含关系判断及应用．【分析】根据已知中M满足条件{1，2}⊆M⊆{1，2，3，4，5}，列举出所有满足条件的集合M，可得答案．【解答】解：若M满足条件{1，2}⊆M⊆{1，2，3，4，5}，则M可能为：{1，2}，{1，2，3}，{1，2，4}，{1，2，5}，{1，2，3，4}，{1，2，3，5}，{1，2，4，5}，{1，2，3，4，5}共8个，故答案为：810．已知一个函数的解析式为y=x2，它的值域为{1，4}，这样的函数有9 个．【考点】函数的概念及其构成要素．【分析】由题意知，函数的定义域中，1和﹣1至少有一个，2和﹣2中至少有一个．【解答】解：∵一个函数的解析式为y=x2，它的值域为{1，4}，∴函数的定义域可以为{1，2}，{﹣1，2}，{1，﹣2}，{﹣1，﹣2}，{1，﹣1，2}，{﹣1，1，﹣2}，{1，2，﹣2}，{﹣1，2，﹣2}，{1，﹣1，﹣2，2}，共9种可能，故这样的函数共9个，故答案为9．11．已知集合A={x|1≤x＜5}，C={x|﹣a＜x≤a+3}．若C∩A=C，则a的取值范围是a≤﹣1 ．【考点】交集及其运算．【分析】由C∩A=C，得C⊆A，然后分C是空集和不是空集分类求解实数a的取值范围．【解答】解：由C∩A=C，得C⊆A，∵A={x|1≤x＜5}，C={x|﹣a＜x≤a+3}．当﹣a≥a+3，即a时，C=∅，满足C⊆A；当C≠∅时，有，解得：﹣＜a≤﹣1．综上，a的取值范围是a≤﹣1．故答案为：a≤﹣1．12．已知全集U=R，函数y=+的定义域为集合A，函数y=的定义域为集合B．则集合（∁U A）∩（∁U B）= {x|x＜﹣2} ．【考点】函数的定义域及其求法．【分析】分别求出集合A，B，再求补集，即可得到交集．【解答】解：A={x|}={x|x≥2}，U A={x|x＜2}．B={x|}={x|x≥﹣2且x≠3}，U B={x|x＜﹣2或x=3}，则（∁U A）∩（∁U B）={x|x＜﹣2}．故答案为：{x|x＜﹣2}．13．已知函数f（x），g（x）分别由下表给出：则满足f（g（x））=g（f（x））的x值为2，4 ．x 1 2 3 4f（x） 1 3 1 3x 1 2 3 4g（x） 3 2 3 2【考点】函数的值．【分析】结合表格，先求出内涵式的函数值，再求出外函数的函数值；分别将x=1，2，3，4代入f[g（x）]，g[f（x）]，判断出满足f[g（x）]=g[f（x）]的x．【解答】解：x=1时，f（g（1））=f（3）=1；g（f（1））=g（1）=3，不满足f（g（x））=g（f（x））；x=2时，f（g（2））=f（2）=3；g（f（2））=g（3）=3，满足f（g（x））=g（f（x））；x=3时，f（g（3））=f（1）=1；g（f（3））=g（1）=3，不满足f（g（x））=g（f（x））；x=4时，f（g（4））=f（2）=3；g（f（4））=g（3）=3，满足f（g（x））=g（f（x））；故答案为：2，414．函数f（x）=2x2﹣mx+3，当x∈[2，+∞）时是增函数，当x∈（﹣∞，2]时是减函数，则f（1）= ﹣3 ．【考点】二次函数的性质．【分析】利用当x∈[2，+∞）时是增函数，当x∈（﹣∞，2]时是减函数，得到2是函数的对称轴，然后求出m，直接代入求f（1）即可．【解答】解：函数f（x）=2x2﹣mx+3的对称轴为．∵当x∈[2，+∞）时是增函数，当x∈（﹣∞，2]时是减函数，∴x=2是函数f（x）=2x2﹣mx+3的对称轴，即，解得m=8．∴f（x）=2x2﹣8x+3，即f（1）=2﹣8+3=﹣3．故答案为：﹣3．二、解答题：（本大题共6小题，共90分，解答应写出必要的文字说明、证明过程或演算步骤）15．集合A={﹣2}，B={x|ax+1=0，a∈R}，若A∩B=B，求a的值．【考点】子集与交集、并集运算的转换．【分析】由A∩B=B即得，B⊆A，所以B的可能情况为：B=∅，或B={﹣2}，所以得到a=0，或．【解答】解：∵A∩B=B；∴B⊆A；∴B=Ø或B={﹣2}；当B=Ø时，方程ax+1=0无解，此时a=0；当B={﹣2}时，﹣2a+1=0，∴；∴a=0，或．16．求下列函数的值域（1）y=﹣，x∈[﹣3，0）∪（0，1]；（2）y=x2+4x+1，x∈[﹣3，0]．【考点】函数的值域．【分析】（1）可看出函数在[﹣3，0），（0，1]上都是增函数，从而根据单调性求出该函数的值域；（2）只需配方便可求出该函数的最大、最小值，从而得出该函数的值域．【解答】解：（1）在[﹣3，0），（0，1]上都是增函数；∴﹣3≤x＜0时，，0＜x≤1时，y≤﹣4；∴该函数值域为；（2）y=x2+4x+1=（x+2）2﹣3；∴x=0时，y取最大值1，x=﹣2时，y取最小值﹣3；∴该函数的值域为[﹣3，1]．17．已知集合M是由三个元素﹣2，3x2+3x﹣4，x2+x﹣4组成，若2∈M，求x．【考点】元素与集合关系的判断．【分析】集合M由3个元素组成，﹣2是其中一个，若2也是M中元素，需讨论3x2+3x﹣4=2和x2+x﹣4=2两种情况，根据集合的互异性，正确选取合适的答案即可．【解答】解：∵2∈M，当3x2+3x﹣4=2时，即x2+x﹣2=0，则x=﹣2或x=1．经检验，x=﹣2，x=1均不合题意，违反了集合的互异性．当x2+x﹣4=2时，即x2+x﹣6=0，则x=﹣3或2．经检验，x=﹣3或x=2均合题意．故答案为：x=﹣3或x=2．18．已知f（x）是一次函数，且f[f（x）]=4x﹣1，求f（x）及f（2）．【考点】函数解析式的求解及常用方法．【分析】设f（x）=ax+b，a≠0，代入已知式子，比较系数可得a、b的方程组，解之可得解析式及f（2）．【解答】解：由题意设f（x）=ax+b，a≠0∵f[f（x）]=f（ax+b）=a（ax+b）+b=a2x+ab+b又f[f（x）]=4x﹣1，∴a2x+ab+b=4x﹣1比较系数可得解得或．∴f （x ）=2x ﹣，或f （x ）=﹣2x+1，f （2）=4﹣=，或f （2）=﹣4+1=﹣3．19．求证：函数f （x ）=﹣﹣1在区间（0，+∞）上是单调增函数．【考点】函数单调性的判断与证明．【分析】首先，设两个自变量，然后，比较它们函数值的大小，最后，得到结论．【解答】解：任设x 1，x 2∈（0，+∞），x 1＜x 2，∴f （x 1）﹣f （x 2）==，∵x 1＜x 2，∴x 1﹣x 2＜0，∴f （x 1）﹣f （x 2）＜0，∴在区间（0，+∞）上是单调增函数．20．函数f （x ）是定义在（0，+∞）上的增函数，对任意的x ，y ∈（0，+∞），都有f （x+y ）=f （x ）+f （y ）﹣1，且f （4）=5．（1）求f （2）的值；（2）解不等式f （m ﹣2）≤3．【考点】抽象函数及其应用；函数单调性的性质．【分析】（1）令x=y=2，通过f（4）=5以及f（x+y）=f（x）+f（y）﹣1即可求f（2）的值；（2）利用（1）的结果，通过函数的单调性的性质，直接求解不等式f（m﹣2）≤3．【解答】解：（1）对任意的x，y∈（0，+∞），都有f（x+y）=f（x）+f（y）﹣1，且f（4）=5，令x=y=2，则f（4）=f（2+2）=2f（2）﹣1=5，解得f（2）=3．（2）由f（m﹣2）≤3，f（2）=3，得f（m﹣2）≤f（2）．∵f（x）是（0，+∞）上的增函数，m﹣2≤2且m﹣2＞0；⇒m≤4且m＞2∴2＜m≤4．不等式的解集为：{m|2＜m≤4}．2017年1月10日。

2019-2020学年高一数学上学期第一次月考试题(78)一．选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.）1. 已知全集{}0,1,2,3,4,5U =，{}2,4A =，{}0,1,2B =，则如图阴影部分表示的集合为（ ）A. {}0,2B. {}0,1,3C.{}0,1,4D. {}0,2,421在实数范围内有意义，则x 满足的条件是（ ）A ．12x ≥B ．12x ≤C ．12x =D ．12x ≠ 3．在同一直角坐标系中，函数y kx k =+与(0)k y k x-=≠的图象大致为（ ） A ． B ． C ． D ．4.下列四组函数中，表示相等函数的一组是（ ）A.2y =与y x = B.y =||y x =C.y =y x =D.x y x= 与0y x = 5.若{}251,2,4m m ∈++，则实数m 的取值集合为（ ）A. {}3B. {}1,3C.{}1,1-D. {}1,1,3-6．已知a 、b 、c 是△ABC 的三条边长，化简|a+b ﹣c|﹣|c ﹣a ﹣b|的结果为（ ）A ．2a+2b ﹣2cB ．2a+2bC ．2cD ．0 7. 《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过3500元的部分不必纳税，超过3500元的部分为全月应纳税所得额。

此项税款按下表分段累计计算：( )A.4800元B.6800元C.7850元D.15000元8. 已知()f x 和()g x 的定义域合值域均是{}1,2,3,4，其定义如下表：）A. {}1,2B. {}3,4C.{}1,3,4D. {}2,3,49．如图，直线y=k 和双曲线相交于点P ，过点P 作PA 0垂直于x 轴，垂足为A 0，x 轴上的点A 0，A 1，A 2，…A n 的横坐标是连续整数，过点A 1，A 2，…A n ：分别作x 轴的垂线，与双曲线（k ＞0）及直线y=k 分别交于点B 1，B 2，…B n 和点C 1，C 2，…C n ，则的值为（ ）A ．B ．C ．D ．10.在集合{}|1500M x N x =∈≤≤中既不被5整除，也不被11整除的元素有（ ）个A. 345B. 346C.355D. 36411．如图，将矩形ABCD 绕点A 旋转至矩形AB′C′D′位置，此时AC的中点恰好与D 点重合，AB′交CD 于点E ．若AB=6，则△AEC 的面积为（ ）A ．12B ．4C ．8D ．6 12. 已知函数()|25|,f x x =-若031a b ≤<+且(3)(3)f a f b =+，则232T a b =+的取值范围为（ ） A.[1,)+∞ B. [1,4] C. 7(,4]4 D. [3,)-+∞二．填空题（本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上）13.满足{}1,2A A ⋂=的集合A 的个数是____________14．已知实数a ，b 同时满足a 2+b 2﹣11=0，a 2﹣5b ﹣5=0，则b= ．15． 如右图，矩形ABCD 中，对角线AC 、BD 交于点O ，点E 是BC 上一点，且AB=BE ，∠1=15°，则∠2= ．16.若函数1,[0,1)()42,[1,2]x x f x x x +∈⎧=⎨-∈⎩，若[()][0,1]f f a ∈,则a 的取值范围是____________ 三．解答题（本大题共6小题，17题10分，其余各题12分，共70分．解答应写出文 字说明，证明过程或演算步骤．）17．先化简，再求值：，其中x 满足x 2+7x=0．18.已知集合|A x R y ⎧=∈=⎨⎩，{}|13B x R a x a =∈+≤≤ （1）若非空集合B 满足：R A C B R ⋃=，求实数a 的取值范围；（2）若A B φ⋂=，求实数a 的取值范围。

陕西省咸阳市2019-2020学年高一上学期数学第一次月考试卷（II）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2020·鹤壁模拟) 集合，，，则（）A .B .C .D .2. （2分）已知集合，则集合A的真子集个数为（）A . 31B . 32C . 3D . 43. （2分）定义在R上的函数f（x）对任意两个不相等实数a，b，总有＞0成立，则必有（）A . f（x）在R上是增函数B . f（x）在R上是减函数C . 函数f（x）是先增加后减少D . 函数f（x）是先减少后增加4. （2分）下列各组中两个函数是同一函数的是（）A . f（x）=，g（x）=B . f（x）=x , g（x）=C . f（x）=1, g（x）=D . f（x）=，g（x）=x﹣25. （2分）函数的定义域为（）A .B .C .D .6. （2分）设函数f（x）=，则f（f（﹣10））等于（）A .B . 10C . -D . -107. （2分） (2019高一上·张家港月考) 定义在R上的偶函数满足，且当时，，则的值为（）A . －1B . 0C . 1D . 28. （2分） (2019高一上·青冈期中) 函数的单调递增区间为（）A .B .C .D .9. （2分）已知是偶函数，当时，；若当时，恒成立，则的最小值为（）A . 1B .C .D .10. （2分）设集合A={x||x-2|＜1} ，，若，则的取值范围是（）A .B .C .D .11. （2分） (2019高一上·吴忠期中) 已知函数的值域为，则它的定义域为（）.A .B .C .D .12. （2分）(2017·舒城模拟) 函数的图象不可能是（）A .B .C .D .二、填空题 (共4题；共5分)13. （1分） (2019高一上·宿州期中) 若幂函数的图象经过点，则该函数的解析式为________14. （2分） (2019高三上·镇海期中) 已知点A（1，0），B（0，2），点在线段AB上，则直线AB的斜率为________；的最大值为________．15. （1分）已知函数是定义在R上的偶函数，则实数的值等于________．16. （1分） (2019高一上·新乡月考) 已知偶函数在区间上单调递增，则满足的x的取值范围是________．三、解答题 (共6题；共60分)17. （10分） (2019高一上·周口期中) 设集合，集合 .（1）当时，求；（2）若，求实数的取值范围.18. （10分） (2019高一下·汕头期末) 某生产厂家生产一种产品的固定成本为4万元，并且每生产1百台产品需增加投入0.8万元.已知销售收入（万元）满足（其中是该产品的月产量，单位：百台），假定生产的产品都能卖掉，请完成下列问题：（1）将利润表示为月产量x的函数；（2）当月产量为何值时，公司所获利润最大？最大利润为多少万元？19. （15分）已知f（x）=x2+2ax+2，x∈[﹣5，5]（1）当a=﹣1时，求f（x）的最值；（2）求f（x）的最小值；（3）当f（x）在区间[﹣5，5]上为单调函数，求实数a的取值范围．20. （10分） (2019高一上·厦门期中) 已知二次函数对一切实数，都有成立，且，， .（1）求的解析式；（2）记函数在上的最大值为，最小值为，若，当时，求的最大值.21. （5分） (2016高二下·东莞期中) 某宾馆有50个房间供游客居住，当每个房间定价为180元时，房间会全部住满；当每个房间的定价增加10元时，就会有一个房间空闲．如果游客入住房间，宾馆每间每天将花费20元的各种费用．当房间定价为多少的时候，宾馆获得的利润最大？22. （10分） (2016高一上·绵阳期末) 已知函数f（x）= ，x∈[2，6]．（1）证明f（x）是减函数；（2）若函数g（x）=f（x）+sinα的最大值为0，求α的值．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分)17-1、17-2、18-1、18-2、19-1、19-2、19-3、20-1、20-2、21-1、22-1、22-2、。