地球重力场的表达方式

第六章 地球重力场模型随着空间技术的进步和发展，现在不但有可能根据卫星轨道根数的变化精确地确定地球动力形状因子2J ，而且有可能结合卫星测高仪、卫星追踪卫星技术、卫星重力梯度仪等空间技术的测量结果以及地面重力测量结果计算出地球大地位球函数展开的高阶项系数。

以一组数值球函数展开系数表示的地球大地位称为地球重力场模型，地球重力场模型一方面支持卫星轨道的精确计算，另一方面可以给出地面上的长波重力异常场，为研究地球内部结构及其动力学过程提供重要的地面约束条件。

6.1 大地位的球函数展开现将第二章已经讨论过的大地位球函数展开中的有关公式汇总如下。

用r 表示地球外部空间任一点P 的径矢，则根据（2.2.18）式，地球在P 点的大地位球函数展开表示为其中kM 为地球的地心引力常数，a 为地球的赤道半径，θ、λ分别为P 点的地心余纬和经度，(cos )mn P θ为cos θ的n 阶m 次伴随勒让德多项式，(cos )cos mn P m θλ、(cos )sin mn P m θλ为归一化的n 阶m 次球面函数，根据（2.2-1.3）式、（2.2-1.6）式和（2.2-1.8）式，()n P x 、()n P x 、()mn P x 、()mn P x 分别为m n c 、m n s 和mn c 、mn s 分别为大地位球函数展开系数和规一化的大地位球函数展开系数，根据（2.2.20）式，有根据（2.3.4）式、（2.3.5）式，大地位二阶球函数展开系数等于其中A 、B 、C 分别为地球绕1Ox 、2Ox 和其旋转轴3Ox 轴的转动惯量，12I 、23I 、13I 分别为地球绕相应轴的惯性积，大地位球函数展开有时写成下面的形式nm J 、nm K 与大地位球函数展开系数m n c 、m n s 之间的关系为2J 称为地球的动力形状因子。

当3n 时，()n P x 、()mn P x 的表达式如表6.1.1所示。

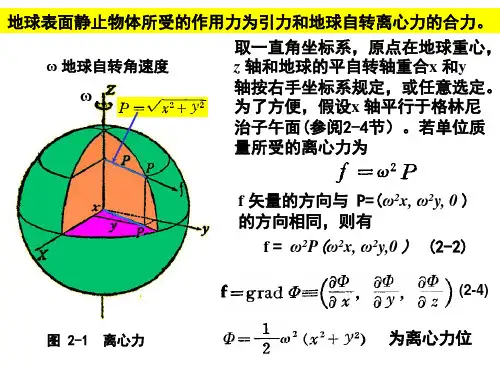
《应用重力学》第二讲地球重力场一、重力(Gravity)重力 = 地球引力惯性离心力微弱,可忽略=吸引力FF GM E R 3惯性离心力Cm RC = m ⎤ 2r重力GG=F+C地球重力场：在地球内部及其附近存在重力作用的空间。

④重力场强度:单位质量的物体在重力场中所受的重力 ( =G/m )④重力加速度g=G/m④重力加速度在数值上(包括方向)等于单位质量所受的重力，也就是等于重力场强度。

重力加速度重力重力场强度④重力勘探所提的重力都是指重力加速度或重力场强度。

重力(重力加速度)单位④在CGS单位制(克、厘米、秒)：“cm/s2 ”，“伽”或“Gal”1 cm/s2 = 1 Gal④在SI单位制(千克、米、秒)：“m/s2”，“g.u.”1 m/s2 = 106 g.u.1 Gal = 1 cm/s21 g.u. = 10-6m/s21 Gal = ? g.u.1 Gal (伽) = 1 cm/s2 = 10-2 m/s2 = 104 g.u.1 mGal (毫伽) = 10-5 m/s2 = 10 g.u.1 uGal (微伽) = 10-8 m/s2 = 10-2 g.u.重力的变化④包括随不同测点位置的空间变化以及同一测点的重力随时间的变化。

④空间上:地球形状、地形：引起约 6万 g.u. 的变化；地球自转：重力有 3.4万 g.u. 的变化;地下物质密度分布不均匀：能达到几千 g.u.变化人类的历史活动遗迹和建筑物等北赤南极道极在地球表面上，全球重力平均值约为9.8m/s2，赤道重力平均值为9.780m/s2，两极平均值为9.832 m/s2，从赤道到两极重力变化大约为0.05m/s2。

④时间上：潮汐变化：太阳、月亮等天体引力引起的重力的周期性变化，其大小可达 3 g.u.非潮汐变化：地球形状的变化和地下物质运动等引起的非周期性变化，其变化大小一般不超过 1 g.u.④海水每天有两次涨落运动，其中早晨出现的潮涨称为潮，晚上出现的潮落称为汐，总称潮汐。

正常椭球:一个形状和质量分布规则,接近于实际地球的旋转椭球。

它产生的重力场称为正常重力场。

正常重力场的等位面称为正常水准面。

因为正常椭球面是一个正常水准面，所以正常椭球又称水准椭球。

正常(地球)椭球是一个假想的球体。

是一个理想化的椭球体。

正常重力位U：近似的地球重力位。

是一个函数简单、不涉及地球形状和密度便可直接得到的地球重力位近似值的辅助重力位。

扰动位T：地球实际重力位W与正常重力位U之差。

T＝W－U根据扰动位T可求出大地水准面与正常水准面之差，便可最终解决地球重力位和形状的问题。

1、水准面: 重力等位面。

具有几何性质与物理性质。

1）、无数个；2）、复杂形状，不规则闭合，与铅垂线正交的曲面；3）、水准面彼此不平行，不相交；4）、每个水准面对应唯一的位能W＝常数，物体在水准面上移动重力不做功。

2、大地水准面：与平均海水面重合，不受潮汐、风浪及大气压影响，并延伸到大陆下面处处与铅垂线垂直的水准面。

1）、一个特定的重力等位面，唯一。

2）、其几何性质和物理性都很不规则，尚未能具体确定。

因而只能用一个平均海水面代替它。

3、似大地水准面：与大地水准面很接近的一个曲面，是由地面点沿铅垂线向下量取正常高所得的点形成的连续曲面。

1）、不是水准面2）、与水准面很接近，在海洋上与大地水准面完全重合，在大陆上几乎重合，在山区只有2～4m的差异。

4、正常椭球（水准椭球、等位椭球）：正常椭球：大地水准面的规则形状。

实际上，质量与地球质量相同，自转速度与地球自转速度相同的规则物体都可正常椭球。

目前都采用水准椭球作为正常椭球，又称等位椭球。

5、总地球椭球：与大地体最为密切的正常椭球。

1）、中心与地球质心重合，短轴与地球短轴重合；起始子午面与起始天文子午面重合；质量与地球的质量相同；2）、4个基本参数a e，fM，J2，ω；3）、与大地体最密合，要满足全球范围内与大地水准面的差距N的平方和最小。

6、参考椭球：大小与定位定向最接近于本国或本地区的地球椭球。

重力测量知识点总结高中第一部分：引言重力测量是地球科学研究中的重要组成部分，也是一门涉及物理、地质学、地理学等多学科交叉的学科。

重力测量主要是通过测定地球不同地点的重力加速度来了解地球内部结构、研究地质构造、地壳运动以及探测矿产资源等。

本文将从基本概念、重力测量方法、重力异常解释等方面进行详细介绍与总结。

第二部分：基本概念1. 重力重力是地球对物体吸引的力，是地球引力场的表现。

重力的作用使得物体朝向地球表面运动，它是地球上一切自然现象的基础。

在测量重力时，通常使用重力加速度（g）来表示重力大小，单位为m/s²。

2. 重力异常地球不是一个理想的等密度椭球体，其密度分布和形状都存在一定的不规则性，导致地球的引力场并非处处均匀。

这种非均匀性所引起的重力场偏离理想状态的现象称为重力异常。

重力异常可以是重力加速度值的偏差，也可以是地面上观测到的重力矢量与理想状态下的重力矢量之间的差异。

3. 重力异常的形成机制地球重力场的不均匀性主要受到地球内部密度分布不均匀、地壳结构的差异、地球自转引起的离心力和科里奥利力等因素的影响。

这些因素导致地球的引力场在空间和时间上存在一定的变化，从而形成了各种不同类型的重力异常。

第三部分：重力测量方法1. 重力测量仪器目前常用的重力测量仪器包括弹簧测重仪、绝对重力仪、相对重力仪等。

这些仪器可以测量地面上某一点的重力加速度，并能够在不同测点之间进行重力差测量，从而得到地球不同地点的重力场数据。

2. 重力测量方法重力测量方法包括绝对重力测量方法和相对重力测量方法。

绝对重力测量是指直接测定地面上某一点的绝对重力加速度数值，其精度较高，但测量速度较慢。

相对重力测量是指通过比较不同地点的重力加速度差值，来获得重力异常的分布情况。

相对重力测量速度较快，适合大范围的重力场调查。

3. 重力异常的解释通过对重力测量数据的分析和处理，可以得到地球的重力异常分布图，进而推断出地下构造、地质构造，甚至是矿产资源等信息。

重力场（earth's gravity field）受地球重力作用的空间范围。

研究地球的重力场，在大地测量学中可用以推求平均地球椭球的形状，建立国家大地网和国家水准网；在空间科学中用以确定空间飞行器受地球引力场作用的轨道改正；在固体地球物理学中用以研究地球内部构造及矿产资源分布。

由于地球内部质量分布的不规则性，致使地球重力场不是一个按简单规律变化的力场。

但从总的方面看，地球非常接近于一个旋转椭球，因此可将实际地球规则化，称为正常地球，同它相应的重力场称为正常重力场。

地球重力场的非规则部分称为异常重力场。

地球重力场中任一点的重力位与正常位之差值称为扰动位。

扰动位是由于地球的质量分布和形状与平均地球椭球有所不同而引起的。

与扰动位相应的有重力异常和扰动重力。

根据全球重力测量和卫星大地测量的结果，可以确定地球的总质量和地球的平均密度；配合天文测量结果，可以求出地球绕其自转轴的转动惯量；根据地面上大范围甚至全球范围的重力测量结果，可以研究地核-地幔边界的起伏，地幔地壳边界的起伏，地幔中的热对流，地壳均衡的状态等。

相对标高标高分相对标高和绝对标高。

相对标高表示建筑物各部分的高度。

相对标高是把室内首层地面高度定为相对标高的零点，用于建筑物施工图的标高标注。

在建筑施工图的总平面图说明上，一般都含有“本工程一层地面为工程相对标高±0.000米，绝对标高为36.55米”。

这里的一层地坪±0.000是相对于工程项目内的假定高度，但它比黄海平均海平面高36.55米。

当我们再施工到二层地面时，图纸上给出的二层地面建筑高度为+4.5米，那么我们说，二层地面比一层地面±0.000高出4.5米。

绝对标高绝对标高，我国是把黄海平均海平面定为绝对标高的零点，其他各地标高以此为基准。

任何一地点相对于黄海的平均海平面的高差，我们就称它为绝对标高。

这个标准在中国境内只在一个。

地球重力场地球重力场：在地球内部及其附近存在重力作用的空间。

重力场强度:单位质量的物体在重力场中所受的重力( =G/m )重力加速度g=G/m重力加速度在数值上(包括方向)等于单位质量所受的重力，也就是等于重力场强度。

重力加速度重力重力场强度重力勘探所提的重力都是指重力加速度或重力场强度。

重力(重力加速度)单位在CGS单位制(克、厘米、秒)：“cm/s2”，“伽”或“Gal”1 cm/s2 = 1 Gal在SI单位制(千克、米、秒)：“m/s2”，“g.u.”1 m/s2 = 106 g.u.重力的变化包括随不同测点位置的空间变化以及同一测点的重力随时间的变化。

空间上:9地球形状、地形：引起约6万g.u. 的变化；9地球自转：重力有3.4万g.u. 的变化;9地下物质密度分布不均匀：能达到几千g.u.变化9人类的历史活动遗迹和建筑物等时间上：9潮汐变化：太阳、月亮等天体引力引起的重力的周期性变化，其大小可达 3 g.u.9非潮汐变化：地球形状的变化和地下物质运动等引起的非周期性变化，其变化大小一般不超过 1 g.u.海水每天有两次涨落运动，其中早晨出现的潮涨称为潮，晚上出现的潮落称为汐，总称潮汐。

地球上海潮涨落主要是由月球还是太阳引起的？月球和太阳对地球的引力不但可以引起地球表面流体的潮汐（如海潮、大气潮），还能引起地球固体部分的周期性形变（固体潮）。

太阳的质量虽比月球的质量大得多，但月球同地球的距离比太阳同地球的距离近，月球的引潮力比太阳的引潮力大。

在日、月引力作用下，地球固体表面也会像海水一样产生周期性的涨落，这就是地球的潮汐现象，称为地球固体潮。

固体潮随时间和空间的变化，除了和地球、太阳、月亮三者之间相对位置的变化有关外，还和地球内部物质的物理性质有关。

因而，利用固体潮资料可以研究地壳内部物质的物理性质和各种物质的分布规律。

它在空间上的变化主要反映地壳和上地幔区域结构的变化。

它在时间上的变化可能与某些灾难性的地震有直接和间接的联系。

地球重力场公式范文地球重力场是指地球周围的重力场，其数学表达式是地球所产生的引力场强度。

根据牛顿引力定律，地球对物体的引力与物体质量和地球质量之间的乘积成正比，与物体与地球之间的距离的平方成反比。

因此，地球的重力场公式可以表示为：F=G*(m1*m2)/r^2其中，F是物体所受地球引力的大小，G是引力常数，m1和m2分别是地球和物体的质量，r是物体与地球的距离。

在实际应用中，考虑到地球是一个球体，地球的质量分布也不均匀，地球的重力场公式可以进一步进行修正，引入球面坐标系和各阶球谐函数等概念。

比较常用的修正公式是斯托克斯（Stokes）函数方法，即以球谐函数为基础的重力场展开方法。

斯托克斯函数方法将地球的重力场展开成无数个球谐函数的加和，得到如下公式：V=GM/r*[1-∑(Cn/r^n+Sn/r^(n+1))]其中，V是地球上其中一点的重力势能，G是引力常数，M是地球的质量，r是地球表面的地心距离，Cn和Sn是重力谐振项系数，n是重力梯度项阶数。

每个阶数的球谐函数代表了地球重力场的一个特定分布模式，从低阶到高阶，分别表示了地球重力场的整体性质和局部性质。

在实际测量中，通常只考虑前几个阶数的球谐函数。

例如，常见的重力场模型EGM96就采用了到360度的球谐函数展开，共有12,960个球谐函数。

除了斯托克斯函数方法外，还有直接测量和建模方法可以用于确定地球的重力场。

直接测量方法通过测量物体在地球表面上所受的重力加速度或重力位移来获得地球的重力场。

而建模方法则通过结合地球物理观测数据和数学建模算法来估计地球的重力场模型。

总结起来，地球的重力场可以通过牛顿引力定律和斯托克斯函数方法进行描述，这些数学模型和测量方法可以用于研究和解释地球引力的性质和分布。

第四章 地球的正常重力场重力测量结果表明,地球在其表面上的重力分布是有规律的；总的说来，它由赤道向两极逐渐增加，由赤道上的978Gal 逐渐增加到两极的983Gal 。

在大地测量中,参数合适的旋转椭球是地面点坐标的参考架，当参考椭球选定后,大地水准面相对参考椭球面的起伏不超过110m ，起伏只占参考椭球赤道半径的2×10—6.因而自然想到，用质量等于地球总质量、以地球自转角速度绕其极半径旋转的旋转椭球来模拟真实地球，用这种地球模型（正常场地球模型），在其表面上和外部空间产生的重力场称为地球的正常重力场.当正常场地球模型在地球内部定位后，地球的重力场可以分解为两部分,一部分是正常场地球模型在该点产生的重力场，第二部分为真实地球与正常场地球模型的密度分布不同在该点产生的重力场；前者称为地球在该点产生的正常重力场，后者称为地球在该点产生的重力异常场。

重力测量结果表明，当正常场地球模型选择合适后,大地水准面上的重力异常场不超过150 mGal ，约占地球正常重力场的1×10—4~2×10—4。

地球的重力异常场虽只占地球重力场的万分之一二，但它却包含了有关地球内部结构和大地水准面形状的重要信息，因而研究地球重力异常场空间分布规律以及它们与地球内部结构和大地水准面形状之间的关系已成为重力测量的重要目的之一。

根据第三章的结果,本章给出正常场地球模型在旋转椭球面上产生的重力、正常重力位二次导数张量以及它在其外部空间产生的大地位球函数展开系数.4。

1 旋转椭球的几何参数引入笛卡尔直角坐标系123Ox x x ,坐标原点O 置于旋转椭球的中心，3Ox 沿其极半径，12Ox x 在其赤道平面内，则旋转椭球面的方程为其子午椭圆的方程为其中a 、c 分别为旋转椭球的赤道半径和极半径，它们是决定旋转椭球形状的两个几何参数.考虑到参考椭球的赤道半径a 和极半径c 相差很小，其扁率 约为3×10—3量级，因而参考椭球的子午椭圆与圆非常接近，为了讨论问题方便，对子午椭圆常引入下面几个几何参数：子午椭圆的扁率α、第一偏心率e、第二偏心率'e有下述关系ϕ为A点的地心纬度,A点子午椭圆的法线与如图4.1.1所示,OA与Ox轴之间的角度Ox轴之间的角度B称为A点的大地纬度,因为子午椭圆与圆非常接近,A点的地心纬度和大地纬度相差很小,其差约为子午椭圆扁率的量级。

地球重力场的分类
地球的重力场可以根据不同的分类方式进行划分。

以下是两种常见的分类方式：
1. 空间分布方式：
a. 均匀重力场：也称为等势重力场，指在一个区域内重力场的引力大小和方向是均匀分布的。

在这种重力场中，重力的大小和方向在各个位置都是相等的。

b. 非均匀重力场：指在一个区域内重力场的引力大小和方向不均匀分布的情况。

在这种重力场中，不同位置的重力大小和方向可能存在差异。

2. 强度分布方式：
a. 重力加速度强度不变重力场：指在一个区域内，重力加速度的大小在不同位置上保持不变。

这种重力场在理论上比较理想，但在实际地球上并不完全存在。

b. 重力加速度强度变化重力场：指在一个区域内，重力加速度的大小在不同位置上有一定的变化。

这种重力场在实际地球上比较常见，由于地球表面不规则、存在地下大块状物质等因素，导致地球重力场的强度存在一定的不规则性。

需要注意的是，地球的重力场具有天然的复杂性，因为它受到地球内部物质分布、地球形状、海洋和大气的运动等多种因素的影响。

因此，地球的重力场往往是一个综合性的、复杂的场。