当前位置：文档之家 › 22圆内接多边形的性质与判定定理[1]

22圆内接多边形的性质与判定定理[1]

  • 格式：ppt
  • 大小：421.00 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

圆内接正多边形课件

圆内接正多边形课件

1. 用量角器等分圆：
知2－讲
由于同圆中相等的圆心角所对的弧相等，因此作相等的圆心角可
以等分圆周，从而得到正多边形．采用“先用量角器画一个
360 n
的圆心角，然后在圆上依次截取这个圆心角所对弧的等弧”，这
种方法简便，误差小，且可以画任意正多边形．
2. 用尺规等分圆：用尺规作图的方法等分圆周，然后依次连接圆
③各角相等的圆内接多边形是正多边形；
④正多边形既是轴对称图形又是中心对称图形；
⑤正n边形的中心角αn＝
360，且与每一个外角相等． n
其中正确命题有( )
A．2个 B．3个 C．4个 D．5个
知1－练
2 (202X·南京)已知正六边形的边长为2，则它的内切圆 的半径为( )
A．1
B. 3
C．2
D．2 3
3 一个圆的内接正四边形和外切正四边形的面积的比是 ()
A．1∶ 2 B．1∶2 C．2∶3 D．2∶π
知1－练
4 (2015·青岛)如图，正六边形ABCDEF内接于⊙O， 若直线PA与⊙O相切于点A，则∠PAB等于( )
A．30° B．35° C．45° D．60°
知1－练
5 (202X·泸州)以半径为1的圆的内接正三角形、正方
各边相等 各角相等
⇒正多边形．(2)证明一个多边形是正多边形的方法：①
利用定义，证出各边相等，各角相等；②利用圆内接多
边形，证明各边所对的弧相等，即把圆n等分，依次连
接各等分点，所得多边形即为正多边形．
知1－练
1 给出下列五个命题：
①各多边形都有内切圆和外接圆，且这两个圆是同心圆；
②各边相等的圆外切多边形是正多边形；
知识点 2 圆内接正多边形的画法

《圆内接正多边形》圆

《圆内接正多边形》圆

圆内接正多边形的面积与周长的关系
面积与周长的关系
分析圆内接正多边形的面 积与周长的关系，如面积 与周长的比值、面积与周 长的变化规律等。
面积与半径的关系
分析圆内接正多边形的面 积与半径的关系，如面积 与半径的函数关系、面积 与半径的变化规律等。
周长与半径的关系
分析圆内接正多边形的周 长与半径的关系，如周长 与半径的函数关系、周长 与半径的变化规律等。
对称性在构造复杂图形中的应用
02
在构造复杂图形时，可以利用圆内接正多边形的对称性，快速
确定图形的形状和位置。
对称性在解决几何问题中的应用
03
在解决几何问题时，可以利用圆内接正多边形的对称性，寻找
解题思路和简化计算过程。
05
圆内接正多边形的作图方法
利用尺规作图法作圆内接正多边形
定义
尺规作图法是指使用直尺和圆规等基本作图工具进行作图 的方法。
所有顶点都在给定圆上。
外接圆的半径R与边心距r的关系为R = r + d/2 。
圆内接正多边形的分类
01
02
03
等边圆内接多边形
每个内角都相等的圆内接 正多边形。
等腰圆内接多边形
每条边的长度都相等的圆 内接正多边形。
正方形
特殊的等边等腰圆内接正 四边形，具有特殊的性质 和用途。
02
圆内接正多边形的面积与周长
步骤
首先使用直尺确定圆心和半径，然后使用圆规在圆上截取 等长的弧线，依次连接各弧线的端点即可得到圆内接正多 边形。
特点
尺规作图法是一种基本的作图方法，具有简单、直观的特 点，但只能作出有限的几种圆内接正多边形，如正三角形 、正方形、正六边形等。
利用几何变换法过平移、旋转、对称等几何变换手段进行作图的方法

人教A版选修4-1配套练习第二讲2.2圆内接四边形的性质与判定定理 Word版含解析

人教A版选修4-1配套练习第二讲2.2圆内接四边形的性质与判定定理 Word版含解析

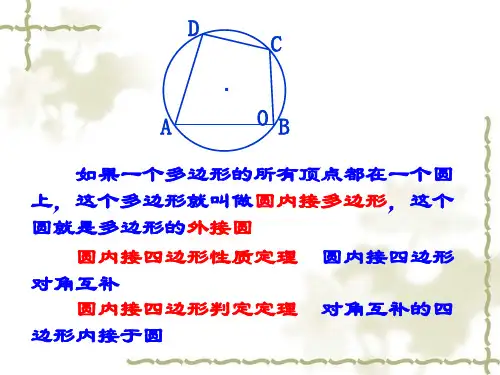
第二讲直线与圆的位置关系圆内接四边形的性质与判定定理级基础巩固一、选择题．圆内接平行四边形一定是( )．菱形．正方形．矩形．等腰梯形解析：由于圆内接四边形对角互补，平行四边形的对角相等，所以圆内接平行四边形的各角均为直角，故为矩形．答案：．已知，是⊙的两条直径，则四边形一定是( )．菱形．矩形．等腰梯形．正方形解析：，均为⊙的直径，故四边形的四个角均为直角，且对角线＝，所以四边形为矩形．答案：．四边形内接于圆，∠∶∠∶∠＝∶∶，则∠等于( )．°．°．°．°解析：由圆内接四边形的性质定理，∠＋∠＝°.又由∠∶∠＝∶，设∠＝，∠＝，则＝°，即＝°，所以∠＝＝°.故∠＝°－∠＝°.答案：.如图所示，四边形是⊙的内接四边形，为的延长线上一点，∠＝°，则∠等于( )．°．°．°．°解析：因为四边形是圆内接四边形，且∠＝°，由圆内接四边形性质知∠＝∠＝°，又由圆周角定理知∠＝∠＝°.答案：．如图所示，若是⊙的直径，是⊙的弦，∠＝°，则∠的度数为( )．°．°．°．°解析：如图所示，连接，则△是直角三角形，∠＝°，则∠＝°－∠＝°，根据同弧所对的圆周角相等，∠＝∠＝°.答案：二、填空题.如图所示，四边形是圆的内接四边形，延长与相交于点.若＝，。

2.2圆内接多边形的性质与判定定理

2.2圆内接多边形的性质与判定定理

(1)能否使图形中的一些线段和直线成为圆中的弦、半 径、直径等； (2)能否使图形中的角成为圆中的圆周角、圆心角等． 总之，利用四点共圆，便于集中条件应用圆的有关性质， 从而使问题得以解决．
典例剖析
【例 1】
如图所示，在圆内接四边形 ABCD 中，AC 平分 BD，且 AC
⊥BD，∠BAD＝72° ，求四边形其余的各角．
2．圆内接四边形判定定理的推论的证明
已知：如图，四边形 ABCD，延长 AB 到 E， ∠EBC＝∠CDA.求证：A，B，C，D 四点共圆． 证明：∵∠EBC＝∠CDA，且∠EBC＋∠ABC＝180° ， ∴∠CDA＋∠ABC＝180° . 由圆内接四边形的判定定理知， A，B，C，D 四点共圆．
第二讲 直线与圆的位置关系
二
圆内接多边形的性质与判定定理
学习目标 1.了解圆内接多边形、多边形的外接圆的概念． 2．理解圆内接四边形的两个性质定理、判定定理及推 论． 3．灵活运用圆内接四边形的性质和判定定理解决相关的 几何问题.
课 前 预 习 1.圆内接多边形 定义：如果多边形的所有顶点都在一个圆上，那么这个多
一点．∵A，B，C，D 四点共圆， ∴∠CDF＝∠ABC.
又AB＝AC，∴∠ABC＝∠ACB. 又∵∠ADB＝∠ACB， ∴∠ADB＝∠CDF. 又∠EDF＝∠ADB，∴∠EDF＝∠CDF. 即AD的延长线平分∠CDE.
(2)设O为外接圆圆心，连接AO交BC于H， 则△ABH≌△ACH，AH⊥BC. 连接OC，则∠OAC＝∠OCA＝15° . ∵∠BAC＝30° ，∴∠ACB＝75° .∴∠OCH＝60° . 3 设圆半径为r，则r＋ 2 r＝2＋ 3，解得r＝2. ∴外接圆的面积为4π.
外接圆 ． 圆内接多边形 ， 这个圆叫做多边形的__________ 边形叫做____________

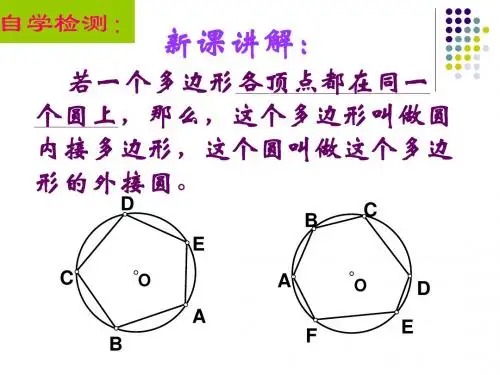
圆的内接多边形

圆的内接多边形

（C）∠A∶∠B∶∠C∶∠D ＝ 3∶2∶1∶4
（D）∠A∶∠B∶∠C∶∠D ＝ 4∶3∶2∶1
基础练习： 5 如图⊙O1与⊙O2都经过A、B两点，经 过点A的直线CD与⊙O1 交于点C，与 ⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E，与⊙O2 交于点F。
求证：CE∥DF
C E
O1
D A
B C
E
基础练习：
1、如图，四边形ABCD为⊙O 的内接四边形，已知∠BOD＝ 100°，求∠BAD及∠BCD的度 A 数。
O
B
D C
基础练习：
2求证：圆内接平行四边形是矩形。 已知：如图，四边形ABCD是 圆的内接四边形并且ABCD是 平行四边形。 B 求证：四边形ABCD A 是矩形。 O
D
A D E
A
80
B C
B
100
O C
D
基础练习：
(4)梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则 75° ∠C=_____ A
D
O B C
等腰 圆的内接梯形一定是＿＿＿＿＿梯形。
基础练习：
4若ABCD为圆内接四边形，则下列哪 个选项可能成立（ B ）
（A）∠A∶∠B∶∠C∶∠D ＝ 1∶2∶3∶4 （B）∠A∶∠B∶∠C∶∠D ＝ 2∶1∶3∶4
C
基础练习：
3.填空
180° (1)四边形ABCD内接于⊙O，则∠A+∠C=__ ， 180° ∠B+∠ADC=_____;若∠B=800， 80° 100° 则∠ADC=______ ∠CDE=______ (2)四边形ABCD内接于⊙O，∠AOC=1000 130° 50° 则∠B=______∠D=______ 45° (3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____,

圆内接四边形的性质与判定定理

圆内接四边形的性质与判定定理
A
•
B
E
•
H
O
O
C F G
D
D
•
C
E
O
•
H
O
A
B
F
G
D ·O O A
C
E H
·O O B
F
G
定理1 定理 圆内接四边形的对角互补
D
C
α
A
•
β
B
D
1
C
•
O
2
A
B
E
定理2 定理 圆内接四边形的外角等于 它的内角的对角
定理1 定理 圆内接四边形的对角互补 思考：定理1的逆命题成立吗？ 思考 即“若四边形的对角互补，则 该四边形为圆内接四边形 （四 点共圆）” 一个四边形内接于圆也称这 个四边形的顶点四点共圆
已知：四边形ABCD中，∠B + ∠D = 180 ，
o
求证：A、B、C、D四点共圆 分 ： 共 的 点 定 个 。 过 析 不 线 三 确 一 圆 经
A、 、 三 作⊙O， 需 明 O经 B C 点 只 证 ⊙ 过 D， 题 得 了 点 命 就 证 。 点D与⊙O的位置关系有几种呢？
(3)点 D 在圆上
推论：如果四边形的一个外角 等于它的内角的对角，那么这 个四边形的四个顶点共圆
例1、如图， O1与 ⊙ O 2 都经过 A 、 B 两点， ⊙ 经过点 A 的直线 CD 与 ⊙ O1交于点 C ，与 ⊙ O 2 交于点 D ，经过点 B 的直线 EF 与 ⊙ O1交于点 E ，与 ⊙ O 2 交于点 F ， 求证： CE // DF
圆内接四边形的性质 与判定定理
D ·O O A
C
B
如果一个多边形的所有顶点都 在一个圆上，这个多边形就叫做圆 在一个圆上，这个多边形就叫做圆 内接多边形， 内接多边形，这个圆就是多边形的 外接圆

圆内接正多边形

圆内接正多边形

圆内接正多边形什么是圆内接正多边形？圆内接正多边形，指的是一个正多边形可以恰好放在一个圆内，且正多边形的每个顶点都在圆周上。

圆内接正多边形也被称为圆内正多边形或圆多边形。

一个圆内接正多边形的特点是，它的每条边相等且每个角都是相等的。

这使得圆内接正多边形在数学、科学、工程和建筑等领域中有广泛的应用。

怎样构造圆内接正多边形？构造圆内接正多边形有多种方法。

以下介绍两种常见的方法：1. 中心构造法中心构造法是一种基于圆的方法。

它的步骤如下：1.以圆心为中心，画一个圆。

2.从圆心出发，以圆的半径为边长画出一个正四边形。

3.用圆上的点作为四边形的顶点，连接四个顶点和圆心，得到一个正八边形。

4.以同样的方式在正八边形的每个顶点上构造正四边形，得到一个正十六边形。

5.重复上述步骤，每一次都在前一个正多边形的顶点上构造正四边形，直到构造出一个足够接近圆内接正多边形的正多边形。

2. 分割法分割法是另一种构造圆内接正多边形的方法。

它的步骤如下：1.在圆上任取一点，作为第一个多边形的一个顶点。

2.以两个相邻点和圆心为中心，画出一个小扇形，将圆划分成若干个小扇形。

3.每个小扇形内部的角度等于圆心角（360度）的一部分，可以计算出每个小扇形的角度。

4.根据所要构造的正多边形的边数，将圆分割成相应的小扇形。

5.将每个小扇形的两个端点连线，得到一个近似圆内接正多边形。

可以根据实际需要逐渐增加分割的扇形数，使得构造出的正多边形更加接近于圆内接正多边形。

圆内接正多边形的性质除了每条边长度相等、每个角度相等外，圆内接正多边形还有其他几个重要的性质：1.圆内接正多边形的内角和等于360度。

2.圆内接正多边形的对角线相等，且交于圆心。

3.圆内接正多边形的外接圆的半径等于正多边形的边长的一半。

此外，圆内接正多边形的周长和面积可以很容易地计算出来，便于在实际问题中应用。

圆内接正多边形的应用圆内接正多边形在数学和其他领域中有广泛的应用，如：1.圆内接正多边形可以用来构建复杂的图形和形状，如著名的黄金分割比例、立体的正十二面体等。

圆内接四边形的性质和判定定理

圆内接四边形的性质和判定定理
圆内接四边形 的
性质和判定定理
D C
·
A
OB
如果一个多边形的所有顶点都在一个圆 上，这个多边形就叫做圆内接多边形，这个 圆就是多边形的外接圆
圆内接四边形性质定理 圆内接四边形 对角互补
圆内接四边形判定定理 对角互补的四 边形内接于圆
如果 n(n N*,n 4) 个点在同一个圆
上，也称这 n 个点共圆
M A
O1·
C
N
B
·O 2D
例2、如图，D为△ABC的边BC上一点， ⊙O1经过点B、D，交AB于另一点E，⊙O2 经 过点C、D，交AC于另一点F，⊙O1与⊙O2 交 于点G，求证：（1）∠BAC+∠EGF＝180°
（2）∠EAG＝∠EFG A
F E
G
O1·
·O2
B
D
C
例3、如图，以锐角三角形ABC的三边为 边向外作三个等边三角形ABD、BCE、CAG，求 证：△ABD、△BCE、△CAG的外接圆⊙O1 、 ⊙O2、⊙O3交于一点
一个四边形内接于圆也称这个四边形的
顶点四点共圆
D
C
D
C
·
A
OB
A
B
定理 若两点在一条线段同侧且对该线 段张角相等，则此两点与线段两个端点共圆
特别的，对定线段张角为直角的点共圆
例1、如图，⊙O1与⊙O2交于点M、N，直 线AB过M与⊙O1与⊙O2 分别交于点A、B，直 线CD过N与⊙O1与⊙O2 分别交于点C、D，求 证：AC//BD
D
A
G
O1 ·F
·O3
ቤተ መጻሕፍቲ ባይዱ
B
C
·O2
E

初中数学人教版九年级上册《圆内接多边形》课件

初中数学人教版九年级上册《圆内接多边形》课件
=2 2，则AE2 +BE2的值为( C
)
∵四边形BECF是⊙O的内接四边形，
∴∠AEC=∠BFC，∴△ACF=2 2，∠EFC=45°，∴EF2=16，
则AE2+BE2=BF2+BE2=EF2=16.
圆内接四边形的角的“三种关系”：
1.对角互补，若四边形ABCD为⊙O的内接四边形，则∠A＋∠C＝
人教版 九年级数学上
24.1.4
圆内接多边形
1.圆周角定义
1.顶点在圆上，
2.两边都与圆相交的角.（二者必须同时具备）.
2.圆周角定理
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该圆弧所对的
圆心角的一半；相等的圆周角所对的弧相等.
1.掌握圆内接四边形及其对角的性质.
2.掌握圆内接四边形外角的性质.
∴∠ADC+∠AEC=180°，
∴∠ADC=180°-∠AEC=100°.
如图，在△ABC中，∠ACB =90° ，过B，C两点的⊙O交AC于点D，交AB
于点E，连接EO并延长交⊙O于点F，连接BF，CF.若∠EDC= 135°，CF
=2 2，则AE2 +BE2的值为(
A.8
)
B.12
C.16
解：∵四边形BCDE内接于⊙O，且∠EDC=135°，
∴∠EFC=∠ABC=180°-∠EDC=45°，
∵∠ACB=90°，∴△ABC是等腰直角三角形，
∴AC=BC，
又∵EF是⊙O的直径，
∴∠EBF=∠ECF=∠ACB=90°，∴∠BCF=∠ACE，
D.20
如图，在△ABC中，∠ACB =90° ，过B，C两点的⊙O交AC于点D，交AB
于点E，连接EO并延长交⊙O于点F，连接BF，CF.若∠EDC= 135°，CF

圆内接四边形的性质与判定定理 课件

圆内接四边形的性质与判定定理 课件

2.如图，A,B,C,D四 点在同一个圆上，AD的延长线与BC的延 长线交于E点，且EC=ED． (1)证明：CD∥AB； (2)延长CD到F，延长DC到G，使得EF=EG， 证明：A,B,G,F四点共圆．
【解析】1.∵过点B，C，D作⊙O,则BC是直径， 又∵CE⊥AB,∴∠BEC=90°,∴点E也在⊙O上，故点B，C，D， E四点共圆. 答案：在 2.(1)因为EC=ED，所以∠EDC=∠ECD. 因为A，B，C，D四点在同一圆上， 所以∠EDC=∠EBA， 故∠ECD=∠EBA，所以CD∥AB.
(2)由(1)知，AE=BE，因为EF=EG， 故∠EFD=∠EGC, 从而∠FED=∠GEC. 连接AF，BG,则△EFA≌△EGB， 故∠FAE=∠GBE. 又CD∥AB，∠EAB=∠EBA， 所以∠FAB=∠GBA. 所以∠AFG+∠GBA=180°. 故A,B,G,F四点共圆.
【想一想】解答题2的关键点及思路是什么？ 提示：(1)当已知条件中出现圆内接四边形时，常用到圆内接 四边形的性质定理来获得角相等或互补，从而为证明三角形相 似或两直线平行等问题创造了条件. (2)当判定四点共圆时，要时刻掌握前面讲的四点共圆的判定 方法，灵活选择适当的方法判定.
圆内接四边形的综合应用 圆内接四边形的综合应用 此类问题综合性较强,考查知识点较为丰富,往往涉及圆内接四 边形的判定与性质的证明和应用,最终得到结论.
【典例训练】 1．如图，在△ABC中，∠A=60°，∠ACB=70°，CF是△ABC的 边AB上的高，FP⊥BC于点P，FQ⊥AC于点Q，则∠CQP的大小为 _____.
1.任意平行四边形的四个顶点在同一个圆上吗？ 提示：平行四边形的四个顶点不一定在同一个圆上，因为它的 对角相等，但不一定互补.当互补时，共圆. 2.在我们学过的特殊四边形中，有哪些四边形的四个顶点共圆？ 提示：有矩形、正方形、等腰梯形，因为它们的四个内角中相 对的两个内角互补.

《圆内接正多边形》PPT课件 (公开课)2022年北师大版 (3)

《圆内接正多边形》PPT课件 (公开课)2022年北师大版 (3)

温故育新：
运用幂的运算性质计算下列各题：
(1)(a5)5
(2)(a2b)3 (3) (2a)2(3a2)3 (4)(y)2yn1
实例引入：
七年级三班举办新年才艺展示，小明的 作品是用同样大小的纸精心制作的两幅 剪贴画，如下图所示，第一幅画的画面 大小与纸的大小相同，第二幅画的画面 在纸的上、下方各留有 1 x m 的空白。
正n边形的一个内角的度数是多
少？中心角呢？正多边形的中心角
与外角的大小有什么关系？
180 n-2
内角
n
360 n
中心角 外角
360 n
例：如图3－36，在圆内接正六边形ABCDEF中，半径OC=4， OG⊥BC ，垂足为点G，求正六边形的中心角、边长和 边心距。
解：连接 OC、OD ∵六边形ABCDEF为正六边形
∴ ∠COD= 360= 60° ∴ △COD为等边6 三角形 ∴ CD=OC=4 在Rt△COG中，OC=4，CG=2 ∴ OG= ∴正六边2形3ABCDE的中心角为60°， 边长为4，边心距为 。
23
用尺规作一个已知圆的内接正六边形
作法如下： （1）以圆周上任意一点为圆心，
以圆的半径为半径作弧，与圆 周交于一点； （2）以得到的交点为圆心，以圆 的半径为半径作弧与圆周交于 另一点，依次下去，在圆周上 等到六个点； （3）依次连接这六个点，就得到 了这个圆的内接正六边形。
（4）单项式乘以单项式，结果仍为单项式。
完成课本15页：随堂练习
延伸拓展：
一家住房的结构如图
y
2y
示，房子的主人打算把 卧室以外的部分全都铺
卫生间
卧室
上地砖，至少需要多少
x
厨房

22圆内接多边形的性质与判定定理[1]

22圆内接多边形的性质与判定定理[1]

3．圆内接四边形的判定定理及推论
定理：如果一个四边形的_对__角__互__补___，那么这个四边形的
四个顶点共圆．
内角的对角
推论：如果四边形的一个外角等于它的__________，那么
这个四边形的四个顶点共圆.
思考探究 1 任意平行四边形的四个顶点在同一个圆上 吗？
提示 平行四边形的四个顶点不一定在同一个圆上， 因为它的对角相等，但不一定互补．当互补时，共圆．
思考探究 2 在我们学过的特殊四边形中，有哪些四边形 的四个顶点共圆？
提示 有矩形、正方形、等腰梯形，因为它们的四个内角中 相对的两个内角互补.
【证明】 由A，B，D三点可以确定一个圆，设该圆为⊙O.
(1)如果点 C 在⊙O 的外部(如图①)，连接 BC，与圆相交于 点 E.∵∠1＝∠AEB，∠1＝∠2，∴∠2＝∠AEB.
而∠AEB>∠2，矛盾，故点 C 不可能在圆外． (2)如果点C在⊙O的内部(如图②)． 延长BC与圆相交于点E，连接AE， 则∠1＝∠AEB，而∠1＝∠2， ∴∠2＝∠AEB，与∠2>∠AEB矛盾． ∴点C不可能在圆内． 由(1)、(2)知，点C只能在圆上． ∴A，B，C，D四点共圆． 规律技巧 本例的证明应用了分类讨论的思想和反证法．
第二讲 直线与圆的位置关系
二 圆内接多边形的性质与判定定理
课前预习
1.圆内接多边形
定义：如果多边形的所有顶点都在一个圆上，那么这个多
边形叫做_圆__内__接___多__边__形 ， 这个圆叫做多边形的_外___接__圆____．
2．圆内接四边形的性质定理
定理 1：圆的内接四边形的_对__角___互__补__． 定理 2：圆内接四边形的外角等于它的ቤተ መጻሕፍቲ ባይዱ角的__对__角______．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二讲 直线与圆的位置关系
二 圆内接多边形的性质与判定定理
课前预习
1.圆内接多边形
定义：如果多边形的所有顶点都在一个圆上，那么这个多
边形叫做_圆__内__接___多__边__形 ， 这个圆叫做多边形的_外___接__圆____．
2．圆内接四边形的性质定理
定理 1：圆的内接四边形的_对__角___互__补__． 定理 2：圆内接四边形的外角等于它的内角的__对__角______．
而∠AEB>∠2，矛盾，故点 C 不可能在圆外． (2)如果点C在⊙O的内部(如图②)． 延长BC与圆相交于点E，连接AE， 则∠1＝∠AEB，而∠1＝∠2， ∴∠2＝∠AEB，与∠2>∠AEB矛盾． ∴点C不可能在圆内． 由(1)、(2)知，点C只能在圆上． ∴A，B，C，D四点共圆． 规律技巧 本例的证明应用了分类讨论的思想和反证法．
思考探究 2 在我们学过的特殊四边形中，有哪些四边形 的四个顶点共圆？
提示 有矩形、正方形、等腰梯形，因为它们的四个内角中 相对的两个内角互补.
【证明】 由A，B，D三点可以确定一个圆，设该圆为⊙O.
(1)如果点 C 在⊙O 的外部(如图①)，连接 BC，与圆相交于 点 E.∵∠1＝∠AEB，∠1＝∠2，∴∠2＝∠AEB.
3．圆内接四边形的判定定理及推论
定理：如果一个四边形的_对__角__互__补__如果四边形的一个外角等于它的__________，那么
这个四边形的四个顶点共圆.
思考探究 1 任意平行四边形的四个顶点在同一个圆上 吗？
提示 平行四边形的四个顶点不一定在同一个圆上， 因为它的对角相等，但不一定互补．当互补时，共圆．