圆的认识单元知识结构图

《圆的认识》单元知识点1、圆的认识(1) 直径是圆中所有线段中最长的一条。

(2) 半径和直径的关系：同一个圆里，直径是半径的两倍，半径 是直径的一半。

(3) 在同一个圆里，有无数条半径，所有半径的长度都相等。

(4) 在同一个圆里，有无数条直径，所有直径的长度都相等。

(5) 画圆时，圆规针尖固定的一点是圆心，圆规两脚之间距离是 半径。

圆心确定圆的位置，半径确定圆的大小、知识结构图广 圆各部分名称(圆心、直径、半径) 圆的认识 < 圆的画法、对称轴 圆的周长圆的认识r推导过程(渗透转化思想)圆的面积2 . . 2圆面积=n r X r= n r 。

即：S=n r 与圆相关的计算二、核心知识点半圆的周长、面积计算圆的周长=圆周率x 直径=圆周率x 半 径 X 2 (C =n d 或 C = 2 n r ) 组合图形求面积(6) 圆是轴对称图形，有无数条对称轴，对称轴就是直径所在的直线(7) 正方形里最大的圆：圆心是对角线交点，半径是正方形边长的一半。

(8) 长方形里最大的圆：圆心是对角线交点，半径是长方形宽的一半。

2、圆的周长(1) 圆周率：任何一个圆的周长除以它直径的商都是一个固定的数，我们把它叫做圆周率，用字母n表示。

n是一个无限不循环小数，n~ 3.14。

(2) 圆的周长二圆周率X直径二圆周率x半径X 2 (C=n d或C= 2(3) 半圆的周长二圆周长的一半+直径(C半圆二n d宁2+ d, C半圆二n r + 2r (4)常用数据(略，自己背诵)(5)同一个圆里，圆的周长是直径的n倍，圆的周长是半径的2 n倍。

3、圆的面积(1) 圆面积公式的推导过程把圆分成若干等份，剪开后，拼成了一个近似的长方形。

长方形的面积与圆的面积相等；长方形的长相当于圆周长的一半，宽相当于圆的半径。

因为：长方形面积二长X宽，所以：圆面积二n r X r= n r2。

即：S=n r2。

要求圆的面积只要知道圆的半径或者知道圆的半径的平方。

本单元教材主要内容有：认识圆、圆的周长和圆的面积等。

圆的认识包括圆的基本特征（认识圆心、半径和直径、半径和直径的长度间的关系）、掌握用圆规画圆的方法（加深对圆的认识）、圆是轴对称图形，有无数条对称轴。

圆的周长和面积计算公式的教学，加强了启发性和探索性，注意让学生动手操作，使学生在实践活动中通过交流、思考来探究圆的周长和面积计算方法，逐步导出和掌握计算公式。

对于圆的周长，让学生通过用线绕一绕，把圆放在直尺上滚一滚等方法来测量，然后再通过填表，运用不完全归纳法来探寻周长与直径的比值的规律，从而引出圆周率的概念。

对于圆的面积教学，则采用转化的方法，把圆的面积转化为熟悉的直线图形的面积来计算。

四、教学目标：1．知识与技能目标：认识圆，掌握圆的基本特征，理解直径与半径的相互关系，会用圆规画圆。

理解圆周率的意义，掌握圆周率的近似值，理解和掌握圆的周长与面积的计算公式，并能正确地计算圆的周长与面积。

2．数学思考目标：知道圆是轴对称图形，有无数条对称轴，知道圆心决定圆的位置，半径决定圆的大小，了解直径和对称轴的关系。

知道周长与面积的计算公式的推理过程，掌握归纳法与转化的方法。

3．解决问题能力：能够发现生活中与圆有关的简单数学问题并解决，分析问题、解决问题、解释过程的能力有所提高。

4．情感与态度目标：能够积极与他人合作解决数学活动中的难题，体会圆的知识与生活的密切联系，会用数学的语言描述周长和面积的计算公式的推理过程，感受数学思考过程的条理性和数学结论的确定性。

学习能力得到进一步提高。

五、重点难点及突破：本单元的教学大约需要8课时。

其中重难点是理解圆的特征、画圆、圆的周长与面积的计算。

对于圆的基本特征，让学生通过折、画、量等方式来寻找规律。

引导学生探究：在同一个圆里有多少条半径和直径？半径和直径的长度有什么关系？教学用圆规画圆时，应让学生明确：一是圆的位置和大小分别是由圆心和半径判定的，所以画圆时应先确定圆心，然后按照指定的长度为半径来画圆；二是圆的大小取决于半径的长短，与圆心的位置无关。

北师大版六年级上第一单元圆知识结构图
圆的认识（一）意义：圆是由一条曲线围成的封闭图形。

特征：1 圆上任意一点到圆心的距离都相等。

2 在同一个圆中，所有的半径（r）都相等，
所有的直径（d）也都相等，并且
d=2r,r=1/2d.
圆的认识（二） 1 圆是轴对称图形。

2找圆与其他图形的组合图形的对称轴。

欣赏与设计体会圆在图案设计中的应用，会用圆规设计简单
的图案。

圆的周长意义：围成圆的曲线一周的长是周长。

直径大的
圆，其周长就大。

圆的周长的计算方法：1 用滚动、绕线等方法测
量圆的周长。

2 圆的周长公式：C=2πr
或C=πd。

圆的面积意义：圆所占平面的大小叫作圆的面积。

方法：1 已知r 求S ，公式S=πr2.
)2.
2 已知d求s，公式S=π(d
2
3 已知C求S，公式S=π(C÷π÷2)2.
在此处键入公式。

圆圆的初步认识圆在同一平面内到定点的距离等于定长的点的集合叫做圆.这个定点叫做圆的圆心。

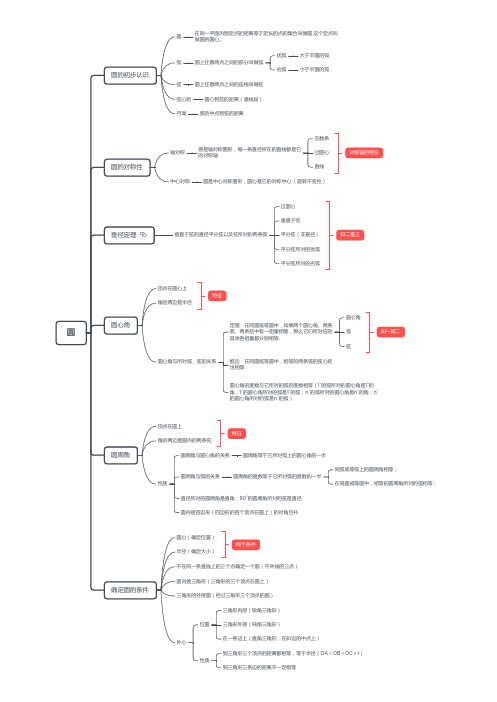
弧圆上任意两点之间的部分叫做弧优弧大于半圆的弧劣弧小于半圆的弧弦圆上任意两点之间的连线叫做弦弦心距圆心到弦的距离（垂线段）弓高弧的中点到弦的距离圆的对称性轴对称原是轴对称图形，每一条直径所在的直线都是它的对称轴无数条过圆心直线对称轴的特征中心对称圆是中心对称图形，圆心是它的对称中心.（旋转不变性）圆周角顶点在圆上角的两边是圆内的两条弦性质圆周角与圆心角的关系圆周角等于它所对弧上的圆心角的一半圆周角与弧的关系圆周角的度数等于它所对弧的度数的一半同弧或等弧上的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等；直径所对的圆周角是直角；90°的圆周角所对的弦是直径.圆内接四边形（四边形的四个顶点在圆上）的对角互补特征圆心角顶点在圆心上角的两边是半径圆心角与所对弧、弦的关系定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等.圆心角弧弦知一推二推论：在同圆或等圆中，相等的两条弧的弦心距也相等.圆心角的度数与它所对的弧的度数相等（1°的弧所对的圆心角是1°的角，1°的圆心角所对的弧是1°的弧；n°的弧所对的圆心角是n°的角，n°的圆心角所对的弧是n°的弧）特征垂径定理 垂直于弦的直径平分弦以及弦所对的两条弧过圆心垂直于弦平分弦（非直径）平分弦所对的优弧平分弦所对的劣弧知二推三确定圆的条件圆心（确定位置）半径（确定大小）两个条件不在同一条直线上的三个点确定一个圆（不共线的三点）圆内接三角形（三角形的三个顶点在圆上）三角形的外接圆（经过三角形三个顶点的圆）外心位置性质三角形内部（锐角三角形）三角形外部（钝角三角形）在一条边上（直角三角形，在斜边的中点上）到三角形三个顶点的距离都相等，等于半径（OA＝OB＝OC＝r）到三角形三条边的距离不一定相等。

圆的认识及知识结构图在六年级上册《圆》这一单元中，通过对曲线图形——圆的特征和有关知识的探索与学习，进一步掌握曲线图形的基本特征，促进学生空间观念的进一步发展。

为解决和圆有关的实际问题打下基础。

下面，我将从以下几个方面来谈我对这一单元教材的认识和我的主要教学策略：一、通过对课标的认识和把握：在本学段，即第二学段（4—6年级）的要求是：1．通过观察、操作，认识圆，掌握圆的特征，会用圆规画圆；2．知道圆是轴对称图形，进一步认识轴对称图形，能运用平移、轴对称和旋转设计简单的图案。

3．探索并掌握圆的周长和面积公式，能够正确计算圆的周长和面积。

4．经历从实际生活中发现问题、提出问题、解决问题的过程，体会圆的知识在生活中的广泛应用，初步形成综合运用数学知识解决问题的能力。

二、圆是一种曲线图形，它同直线图形有不同的特点。

所以“圆”的教学是学生系统认识曲线图形特征的开始。

本元《圆》，要认识圆的基本特征，会画圆，会计算圆的周长和面积并会灵活应用这些知识解决实际问题。

教材通过对圆的研究，组织学生通过动手操作：运用圆规画圆，使学生体会圆心确定了圆的位置，半径决定了圆的大小，使学生初步认识研究曲线图形的基本方法，同时，也渗透了曲线图形与直线图形的内在联系。

在这一单元里，教材还利用学生已有的对轴对称图形的初步认识探讨圆的轴对称特点，使学生进一步关于轴对称图形的知识系统化。

三、知识结构：本单元教材主要内容有：认识圆、圆的周长和圆的面积等。

圆的认识包括圆的基本特征（认识圆心、半径和直径、半径和直径的长度间的关系）、掌握用圆规画圆的方法，认识圆是轴对称图形，知道有无数条对称轴。

圆的周长和面积计算公式的教学，注意让学生动手操作，使学生在实践活动中通过交流、思考来探究圆的周长和面积计算方法，逐步导出和掌握计算公式，在教学的过程中要加强学生的启发性和探索性，对于圆的周长教学，让学生通过用线绕一绕，把圆放在直尺上滚一滚等方法来测量，然后再通过填表，来探寻周长与直径的比值的规律，从而引出圆周率的概念。

本单元教材主要内容有：理解圆、圆的周长和圆的面积等。

圆的理解包括圆的基本特征（理解圆心、半径和直径、半径和直径的长度间的关系）、掌握用圆规画圆的方法（加深对圆的理解）、圆是轴对称图形，有无数条对称轴。

圆的周长和面积计算公式的教学，增强了启发性和探索性，注意让学生动手操作，使学生在实践活动中通过交流、思考来探究圆的周长和面积计算方法，逐步导出和掌握计算公式。

对于圆的周长，让学生通过用线绕一绕，把圆放在直尺上滚一滚等方法来测量，然后再通过填表，使用不完全归纳法来探寻周长与直径的比值的规律，从而引出圆周率的概念。

对于圆的面积教学，则采用转化的方法，把圆的面积转化为熟悉的直线图形的面积来计算。

四、教学目标：1．知识与技能目标：理解圆，掌握圆的基本特征，理解直径与半径的相互关系，会用圆规画圆。

理解圆周率的意义，掌握圆周率的近似值，理解和掌握圆的周长与面积的计算公式，并能准确地计算圆的周长与面积。

2．数学思考目标：知道圆是轴对称图形，有无数条对称轴，知道圆心决定圆的位置，半径决定圆的大小，了解直径和对称轴的关系。

知道周长与面积的计算公式的推理过程，掌握归纳法与转化的方法。

3．解决问题水平：能够发现生活中与圆相关的简单数学问题并解决，分析问题、解决问题、解释过程的水平有所提升。

4．情感与态度目标：能够积极与他人合作解决数学活动中的难题，体会圆的知识与生活的密切联系，会用数学的语言描述周长和面积的计算公式的推理过程，感受数学思考过程的条理性和数学结论的确定性。

学习水平得到进一步提升。

五、重点难点及突破：本单元的教学大约需要8课时。

其中重难点是理解圆的特征、画圆、圆的周长与面积的计算。

对于圆的基本特征，让学生通过折、画、量等方式来寻找规律。

引导学生探究：在同一个圆里有多少条半径和直径？半径和直径的长度有什么关系？教学用圆规画圆时，应让学生明确：一是圆的位置和大小分别是由圆心和半径判定的，所以画圆时应先确定圆心，然后按照指定的长度为半径来画圆；二是圆的大小取决于半径的长短，与圆心的位置无关。

第二十四章《圆》小结一、本章知识结构框图二、本章知识点概括（一）圆的有关概念1、圆（两种定义）、圆心、半径；2、圆的确定条件：①圆心确定圆的位置，半径确定圆的大小；②不在同一直线上的三个点确定一个圆。

3、弦、直径；4、圆弧（弧）、半圆、优弧、劣弧；5、等圆、等弧，同心圆；6、圆心角、圆周角；7、圆内接多边形、多边形的外接圆；8、割线、切线、切点、切线长；9、反证法：假设命题的结论不成立，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立。

（二）圆的基本性质1、圆的对称性①圆是轴对称图形，任何一条直径所在的直线都是它的对称轴。

*②圆是中心对称图形，圆心是对称中心。

2、圆的弦、弧、直径的关系①垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

②平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

* [引申] 一条直线若具有：Ⅰ、经过圆心；Ⅱ、垂直于弦；Ⅲ、平分弦；Ⅳ、平分弦所对的劣弧；Ⅴ、平分弦所对的优弧，这五个性质中的任何两条，必具有其余三条性质，即“知二推三”。

（注意：具有Ⅰ和Ⅲ时，应除去弦为直径的情况）3、弧、弦、圆心角的关系①在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等。

③在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等。

归纳：在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等。

4、圆周角的性质①定理：在同圆或等圆中，同弧或等弧所对圆周角相等，都等于这条弧所对的圆心角的一半。

②在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等。

③推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

（三）与圆有关的位置关系1、点与圆的位置关系设⊙O的半径为r，OP=d则：点P在圆内d<r；点P在圆上d=r；点P在圆外d>r.2、直线与圆的位置关系设⊙O的半径为r，圆心O到l的距离为d则：直线l与⊙O相交d<r直线和圆有两个公共点；直线l与⊙O相切d=r直线和圆只有一个公共点；直线l与⊙O相离d>r直线和圆没有公共点。