条件平差原理

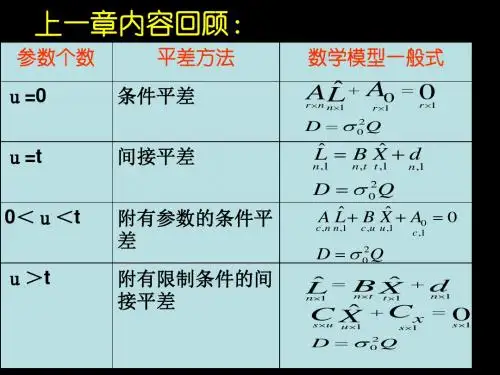
§9.1 条件平差原理
在条件观测平差中，以n 个观测值的平差值1
ˆ⨯n L 作为未知数，列出v 个未知数的条件式，
在min =PV V T 情况下，用条件极值的方法求出一组v 值，进而求出平差值。

9.1.1基础方程和它的解
设某平差问题，有n 个带有相互独立的正态随机误差的观测值 ，其相应的权阵
为 ， 它是对角阵，改正数为 ，平差值为 。

当有r 个多余观测时，则平差值 应
满足r 个平差值条件方程为：
⎪⎪
⎭
⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0
ˆˆˆ221122112211οο
οr L r L r L r b L b L b L b a L a L a L a n n n n n n （9-1） 式中i a 、i b 、…i r （i =1、2、…n ）——为条件方程的系数；
0a 、0b 、…0r ——为条件方程的常项数
以i
i i v L L +=ˆ（i =1、2、…n ）代入(9-1)得条件方程
（9-2）
式中a w 、b w 、……r w 为条件方程的闭合差，或称为条件方程的不符值，即
（9-3） 令
⎪⎪
⎪
⎪⎪
⎭
⎫
⎝⎛=⨯n n n n r r r r b b b a a a A
21
2121
⎪⎪
⎭
⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪
⎭⎪
⎪⎬
⎫
=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛
=⨯n n L L L L 211
⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛
=⨯n n L L L L ˆˆˆˆ2
11
1⨯n L n
n P ⨯1
⨯n V 1
ˆ⨯n L 1
ˆ⨯n L
则(9-1)及（9-2）上两式的矩阵表达式为
0ˆ0
=+A L
A （9-4） 0=+W AV （9-5）
上改正数条件方程式中V 的解不是唯一的解，根据最小二乘原理，在V 的无穷多组解中，取PV V T = 最小的一组解是唯一的，V 的这一组解，可用拉格朗日乘数法解出。

为此，设 ，K 称为联系数向量，它的唯数与条件方程个数相等，按拉格朗日乘数法解条件极值问题时，要组成新的函数：
)(2W AV K PV V T T +-=Φ 将Φ对V 求一阶导数，并令其为零得：
A K P V T T =
K A PV T =
K A V V T 1-= （9-6）
上式称为改正数方程，其纯量形式为
)(1
r i b i a i i i k r k b k a p v +++= （i =1、2、…n ） （9-7）
代 K A P V T 1-=入0=+W AV 得
01=+-W K A AP T
0=+W NK （9-8）
上式称为联系数法方程，简称法方程。

式中N 法方程系数距阵，为
⎥⎥⎥⎥⎥⎥⎥
⎥
⎥⎦
⎤⎢⎢⎢
⎢⎢⎢⎢
⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦
⎤⎢⎣⎡⎥⎦
⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥
⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤
⎢⎣⎡⎥⎦⎤⎢⎣⎡=P rr P br P ar P br P bb P ab P ar P ab p aa N
（9-9） 因N A AP A P A A AP N T T T T T T T ====---111)()( 故，N 是r 阶的对称方阵。

⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯r b a r w w w W 1⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n v v v V 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯οοοr b a A o r 1
r n T
n n n r r
r A P A N ⨯⨯-⨯⨯=1()r b a r
T k k k K =⨯1A
K P V V T T 22-=∂Φ∂⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n n p p p P 00000021
法方程的纯量形式为
⎪⎪⎪
⎪
⎪
⎭
⎪⎪
⎪
⎪
⎪⎬⎫=+⎥⎦⎤⎢⎣⎡+⋅⋅⋅+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+⎥⎦
⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+⎥⎦⎤
⎢⎣⎡++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡000r r b a b r b a a r b a w k p rr k p br k p ar w k p br k p bb k p ab w k p ar k p ab k p aa （9-10） 从法方程解出联系数K 后，将K 值代入改正数方程，求出改正数V 值，再求平差值
V L L +=ˆ，这样就完成了按条件平差求平差值的工作。

9.1.2 精度评定
当各被观测量的平差值求出后，下一步就是对观测精度及平差值或平差值函数的精度进行评定，下面来讨论这个问题。

1.单位权中误差
条件平差中单位权中误差
t
n PV
V T -±=0ˆσ
（9-11）
或 （9-12）
从中误差计算公式可知，为了计算0ˆσ
，关键是计算PV V T ()Pvv 。

下面将讨论PV V T ()Pvv 的计算方法。

（1）、由i V 直接计算
[]2222211n n v P v P v P Pvv +++= （9-13）
（2）、由联系数K 及常数项W 计算 因 0=+W AV
K A P V T 1-= 故()K A PP V K A P P V PV V T T T T T 11--==
K A V T T =
()K W K AV T T
-== （9-14） （3）、直接在高斯——杜力特表格中解算
将（9-4）的矩阵方程写为纯量形式则有
r r b b a a T k W k W k W PV V ++++=- 0
令 0=w W
[]
r
Pvv ±=0ˆσ
r r b b k W k W ++
]()[]()()[]1111-⋅⎥
⎦
⎤⎢⎣⎡-⋅-⋅--⋅r W r p
rr r W W r
r b
[])()(0w w r W w ⨯+=⋅= （9-15）
（2）平差值函数的权倒数
设有平差值函数为()
n
L L L f ˆ,,ˆ,ˆ21 =ϕ （9-16）
它的权函数式为：
n
n L d f L d f L d f ˆˆˆ2211+++= （9-17）
令()n T f f f f ,,21= ()
T n
L d L d L d L d ˆ,ˆ,ˆˆ21 = 则
L
d f d T ˆ=ϕ （9-18）
（9-19）
这就是高斯约化表中 的计算公式，其规律与[]r W w ⋅计算规律完全相同。

n
n L d L L d L L d L d ˆ)ˆ(ˆ)ˆ(ˆ)ˆ(2211∂∂++∂∂+∂∂=ϕϕϕϕ ⎥⎦
⎤⎢⎣
⎡⋅=r P ff ()()()⎥⎦⎤⎢⎣⎡-⋅⎥⎦
⎤⎢⎣⎡-⋅⎥⎦⎤
⎢⎣⎡-⋅--⎥⎦⎤⎢⎣⎡⋅⎥⎦
⎤⎢⎣⎡⋅⎥⎦⎤
⎢⎣⎡⋅-⎥⎦⎤⎢⎣⎡⎥
⎦⎤⎢⎣⎡⎥⎦⎤
⎢⎣⎡-
⎥⎦⎤⎢⎣⎡=1111111r P rf r P rr r P rf P bf P bb P bf P af P aa P af P ff P ϕϕ
P 1。