反比例函数及其图像画法
- 格式:docx
- 大小:98.80 KB
- 文档页数:6



反比例函数图像反比例函数,也称为倒数函数,是一种特殊的函数形式。
它的定义为:当一个变量的取值不断增加时,另一个变量的取值不断减小,两个变量之间存在着一个倒数的关系。
反比例函数可以表示为y = k/x,其中,k是一个常数,x和y分别表示两个变量的取值。
在这个函数中,x是自变量,y是因变量。
反比例函数的图像通常为一个由第一象限的正半轴上的一条直线和原点构成的曲线。
具体来说,当x取较大的正值时,y取较小的正值;当x取较小的正值时,y取较大的正值;当x取0时,y的值趋近于无穷大;当x取负值时,y的值亦为负值,但绝对值较小。
为了更好地理解反比例函数的图像,我们可以绘制一组函数值对应的点,然后将这些点连接起来,从而形成函数的图像。
下面我们将通过几个例子来说明。
例子1:考虑函数y = 2/x,在自变量x取不同的值时,查找相应的因变量y的值:当x取1时,y = 2/1 = 2;当x取2时,y = 2/2 = 1;当x取3时,y = 2/3 ≈ 0.67;当x取4时,y = 2/4 = 0.5;当x取5时,y = 2/5 ≈ 0.4;当x取10时,y = 2/10 = 0.2。
通过将这些点连接起来,我们可以得到反比例函数y = 2/x的图像。
图像呈现出一条从第一象限的正半轴开始的曲线,曲线与x轴以y轴为渐近线。
x 越大,y越小;x越小,y越大。
当x等于0时,函数的图像无定义。
例子2:再考虑函数y = 3/x,在自变量x取不同的值时,查找相应的因变量y的值:当x取1时,y = 3/1 = 3;当x取2时,y = 3/2 ≈ 1.5;当x取3时,y = 3/3 = 1;当x取4时,y = 3/4 ≈ 0.75;当x取5时,y = 3/5 ≈ 0.6;当x取10时,y = 3/10 = 0.3。
同样地,通过连接这些点,我们可以得到反比例函数y = 3/x的图像。
图像也呈现出一条从第一象限的正半轴开始的曲线,曲线与x轴以y轴为渐近线。

反比例函数图像反比例函数图像描述的是一种数学关系,其中一个变量的值与另一个变量的值成反比。
在数学上,反比例函数通常用公式y = k/x 来表示,其中 k 是一个常数,x 和 y 分别表示两个变量的值。
在本文中,我们将讨论反比例函数图像的性质、特点以及如何绘制。
一、反比例函数图像的性质反比例函数图像具有以下几个显著特点:1. 渐近线:反比例函数图像在 x 轴和 y 轴上分别有一个渐近线。
当x 趋近于正无穷时,y 趋近于零;当 y 趋近于正无穷时,x 趋近于零。
2. 对称性:反比例函数图像关于第一象限和第三象限的原点对称。
即,若 (x, y) 是函数图像上的一点,则 (-x, -y) 也是图像上的一点。
3. 单调性:反比例函数图像在第一象限和第三象限上是单调递减的,而在第二象限和第四象限上是单调递增的。
二、绘制反比例函数图像的步骤下面我们将介绍如何绘制反比例函数图像的步骤:1. 确定定义域和值域:反比例函数的定义域为除去 x=0 的所有实数,值域为除去 y=0 的所有实数。
2. 找出特殊点:根据反比例函数的公式,当x=0 时,y 的值不存在。
因此,我们需要找出除了这个点以外的其他特殊点。
例如,当x=1 时,y=k;当 x=2 时,y=k/2;当 x=3 时,y=k/3;以此类推。
3. 绘制渐近线:根据反比例函数的性质,我们可以绘制出与 x 轴和y 轴平行的渐近线。
在第一象限和第三象限中,当 x 趋近于正无穷时,y 趋近于零;在第二象限和第四象限中,当 y 趋近于正无穷时,x 趋近于零。
4. 绘制多个点:根据找出的特殊点,以及定义域和值域的限制,绘制出函数图像上的多个点。
5. 绘制曲线:根据连接这些点的趋势,可在图像上绘制出平滑的曲线。
注意,曲线应该遵循反比例关系,并与渐近线保持一定的距离。
三、实例演示下面通过一个实例来演示如何绘制反比例函数图像。
假设有一个反比例函数 y = 4/x,我们将按照上述步骤进行绘制。

怎样利用几何画板画反比例函数
反比例函数的图像是双曲线,它是用平滑的曲线把一些特殊的点连接起来的,这是反比例函数的图像教学中的难点。
几何画板软件是一个用于几何动态研究的绘图工具,可以动态的展示图像的变化过程。
下面将讲解利用几何画板画反比例函数的方法。
(几何画板中文官网)
画确定的反比例函数
1.选择“绘图”—“定义坐标系”命令,建立坐标系。
2.在绘图区鼠标右键选择新建函数,打开新建函数对话框,输入函数如1/x,点击“确定”按钮,这样在绘图区域就会出现函数表达式。
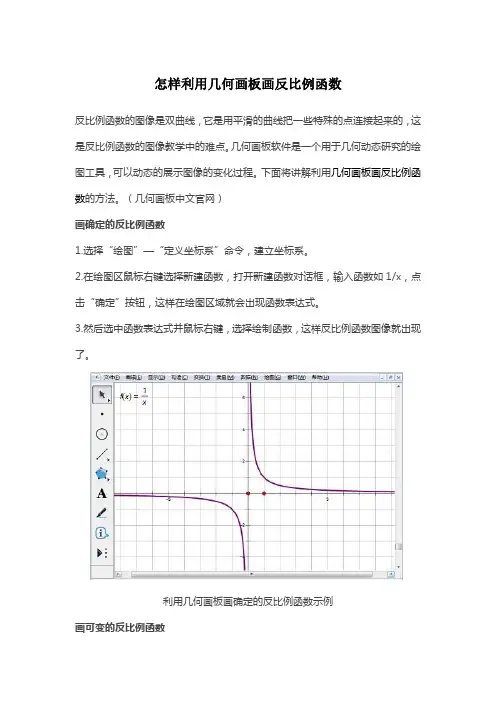
3.然后选中函数表达式并鼠标右键,选择绘制函数,这样反比例函数图像就出现了。
利用几何画板画确定的反比例函数示例
画可变的反比例函数
1.在x轴上建立一个点P,然后度量点P的横坐标。
2.在绘图区鼠标右键选择新建函数,打开新建函数对话框,以其横坐标为可变参数,选定横坐标,输入函数X P/x,点击“确定”按钮,得到函数表达式。
3.然后选中函数表达式并鼠标右键,选择绘制函数,绘制函数图像。
当拖动点P 移动时,函数也会随之变化。
利用几何画板画可变的反比例函数示例
提示:如果对系统自带的占满整个绘图区的坐标系不是很满意的,可以在自定义工具下调用蚂蚁坐标系或者飞狐坐标系。
另绘制反比例函数的方法还有利用描点法画图像,比较复杂,以后的教程中会讲解。
以上内容介绍了利用几何画板画反比例函数的方法,方法比较简单。
对于新用户来说,刚接触几何画板,这是比较好的一个几何画板入门教程。

在几何画板中,怎么画出反比例函数图象的一部分?画反比例图象可以事先设置函数的定义域,然后再绘制出函数的图象;但在制卷和编制课件的实际操作中往往是先绘制出软件所默认函数的图象,然后才根据页面的空间情况进行取舍,下面根据我在实际操作中所得介绍两种情况供各位参考,但愿能起到抛砖引玉的作用:问题1:怎样画反比例函数的函数图象一个分支的的一部分?方法一:绘制反比例函数图象(如:2y x=)→ 选定反比例函数图象(任意点选一个分支即可) → 右键 → 属性 → 绘图 → 范围输入数值(如下图输入的是..0606x 30≤≤) →确定即可.特别说明:在图象有箭头的情况下,鼠标置于图象的箭头端,此时会呈现一个“×”状,鼠标左键按住后还可以根据需要随意将图象拉长和缩短,最后在属性里把“显示箭头和端点”前面的“√”去掉,“隐去”箭头和端点.方法二:绘制反比例函数图象(如:2yx=)→ 用点工具在反比例函数图象标出两个点(如下面左图的B C 、点) → 分别选定点 → 右键 → 横坐标(如图的..B C x 064x 339==,) →按照方法一操作 … 范围输入数值(如下图输入的是..064x 339≤≤)→ 确定把点和标签隐藏(见下面右图).也可以根据需要仿照方法一的特别说明进行拉伸.问题2:怎样“同时”画反比例函数图象各自的两个分支的部分图象,并且要使两个部分要关于原点成中心对称?按照问题1的方法先画好一个分支的部分(本例仍按问题1的方法来操作函数2yx=在第一象限的分支的部分) → 再画出一个同样的的反比例函数图象(如图在同一坐标系内再画一个同样的函数图象2yx=) → 右击刚画好的图象 → 在属性里改动自变量的取值范围(根据反比例函数图象两个分支的中心对称性可知B C 、的关于原点O 为中心对称的点为''B C 、,即..BC x 064x 339==,的关于原点的对称点坐标应为''..B C x 064x 339=-=-,,所以其相应的自变量的取值范围由..064x 339≤≤改写为..064x 339-≤≤- → 确定即可 →根据试卷和课件需要设置好线条的粗细、颜色等(见下面的右图).郑宗平 2015/5/25• • • • • • • • • • • • ••••••【唯美句子】走累的时候,我就到升国旗哪里的一角台阶坐下,双手抚膝,再闭眼,让心灵受到阳光的洗涤。
1、正比例函数
定义:
形如y=kx(k为常数,且k≠0),我们就说y是x的正比例函数。
正比例函数是特殊的一次函数【一次函数的一般形式为y=kx+b(b不为0,k为常数)】。
图象作法:
a.列表(待定系数)
b.描点
c.连线
正比例函数的图象是一条直线,一定经过坐标的原点;
当k>0时,图象经过一、三象限,y随x的增大而增大;
当k<0时,图象经过二、四象限,y随x的增大而减小。
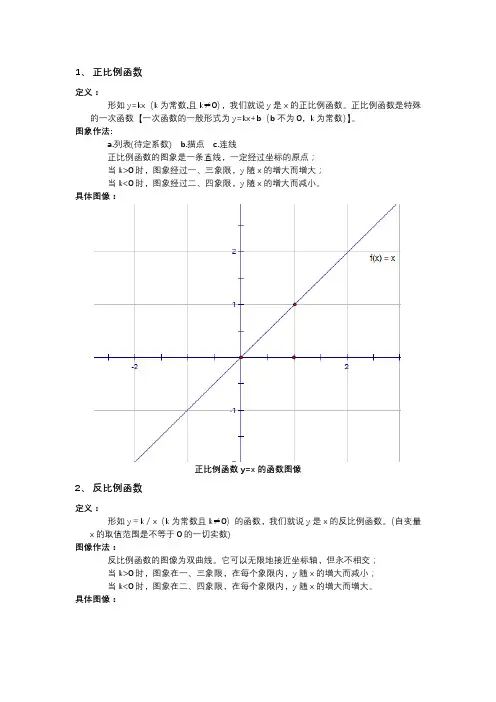
具体图像:
正比例函数y=x的函数图像
2、反比例函数
定义:
形如y=k/x(k为常数且k≠0)的函数,我们就说y是x的反比例函数。
(自变量x的取值范围是不等于0的一切实数)
图像作法:
反比例函数的图像为双曲线。
它可以无限地接近坐标轴,但永不相交;
当k>0时,图象在一、三象限,在每个象限内,y随x的增大而减小;
当k<0时,图象在二、四象限,在每个象限内,y随x的增大而增大。
具体图像:
反比例函数y=1/x的函数图像。



一、反比例函数图象的画法步骤①列表:自变量的取值应以原点为中心,在原点的两侧取三对(或三对以上)互为相反数的值,填写 y值时,只需计算一侧的函数值,另一侧的函数值是与之对应的相反数;②描点:描出一侧的点后,另一侧可根据中心对称去描点;③连线:按照从左到右的顺序连接各点并延伸,连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线,注意双曲钱的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不与坐标轴相交。
二、反比例函数的图像及性质反比例函数的图象:1.反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x≠0,函数y≠0,所以,它的图像与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
2.反比例函数的图像属于以原点为对称中心的中心对称的双曲线,反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(y≠0)。
不同象限分比例函数图像:常见画法:反比例函数图象的画法:(1)列表:(2)描点:在平面直角坐标系中标出点。
(3)连线:用平滑的曲线连接点。
当双曲线在一三象限,K>0,在每个象限内,Y随X的增大而减小。
当双曲线在二四象限,K<0,在每个象限内,Y随X的增大而增大。
常见画法当两个数相等时那么曲线呈弯月型。
k的意义及应用:过反比例函数(k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积。
过反比例函数过一点,作垂线,三角形的面积为。
研究函数问题要透视函数的本质特征。
反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x 轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。
从而有k的绝对值。
反比例函数及其图像画法1.教学目标知识与技能1.反比例函数的图象和性质.2.能根据所给的条件,确定反比例函数.3.画反比例函数的图像过程与方法1.在具体问题中探索数量关系,理解反比例函数的概念,2.能画出反比例函数的图象,掌握反比例函数的主要性质.3.提高观察、分析、归纳的能力,感悟数形结合的数学思想方法.情感、态度与价值观1.勇于探索,敢于探究2.培养合作交流精神,数学在生活中的重要性.2.学情分析本届九年级学生基础高低参差不齐,有的基础较牢,成绩较好。
当然也有个别学生没有养成良好的学习习惯、行为习惯。
这样要因材施教,使他们在自原有的基础上不断发展进步。
从考试情况来看:优等生占8%,学习发展生占55%。
总体情况分析:学生两极分化十分严重,优等生比例偏小,学习发展生所占比例太大,其中发展生大多数对学习热情不高,不求上进。
而其中的优等生大多对学习热情高,但对问题的分析能力、计算能力、、概括能力存在严重的不足,尤其是所涉及的知识拓展和知识的综合能力方面不够好,学生反应能力弱。
根据以上情况分析:产生严重两极分化的主要原因是学生在学生基础太差,学习习惯差,许多学生不会进行知识的梳理,同时学生面临毕业和升学的双重压力等,致使许多学生产生了厌学心理。
为了彻底解决了以上问题,应据实际情况,创新课堂教学模式,推行“自主互动”教学法,真正让学生成为课堂的主人,体验到“我上学,我快乐;我学习,我提高”。
首先从培养学生的兴趣入手,分类指导,加大平日课堂的要求及其它的有力措施,平日认真备课、批改作业,做好优生优培和学习困难生转化工作。
数学基本概念的教学对于学生学好数学是很重要的。
在复习中,既要注意概念的科学性,又要注意概念形成的阶段性。
由于概念是逐步发展的,因此要特别注意遵循循序渐进,由浅入深的原则。
对于某些概念不能一次就透彻地揭示其涵义,也不应把一些初步的概念绝对化。
在教学中要尽可能做到通俗易懂,通过对分析、比较、抽象、概括,使学生形成概念,并注意引导学生在学习,生活和劳动中应用学过的概念,以便不断加深对概念的理解和提高运用数学知识的能力。
学习测评
A 卷:夯实基础卷
(测试时间:60分钟 测试满分:100分)
一、判断题(本大题共3小题,每小题4分,共12分):
1. 当x 与y 的乘积是一个定值时,y 就是x 的反比例函数,x 也是y 的反比例函数( )
2. 当y 与x +1成反比例时,y 就是x 的反比例函数. ( )
3. 一个函数不是正比例函数,就是反比例函数. ( )
二、选择题(本大题共4小题,每小题4分,共16分):
4. 下列函数中,y 是x 的反比例函数的是:() A.x y 5﹣= B.5
x ﹣=y C.1﹣kx y = D.12﹣x y = 5. 如果函数 是反比例函数,则m 的值为: ( ) A. B. C. D. 6. 若函数 是反比例函数,则m 的值为: ( ) A. ±3 B. ﹣3 C. 3 D. 0
7. 某化工厂现有400t 煤,这些煤能烧的天数y 与平均每天的耗煤量x 之间的函数关系式是: ( )
A. B. B. D. 三、填空题(本大题共4小题,每小题4分,共16分):
8. 已知三角形的面积是5,则三角形的高h 与底边长
的函数关系是 ;此时h 是
的 . 9. 贵广铁路全程长达857 km ,最高时速可达250㎞/h .某动车从起点贵阳市出发至终点广州市所需的时间t (h )与行驶的平均速度v (km/h )之间的函数关系式为.(不考虑自变量的取值范围)
10. 超级分类:
325﹣m x
y =2
=m 0=m 1﹣=m 1=m 102
)3(﹣﹣m x m y =a )0≠(400x x y =)0(400>x x
y =)0≥(400x x y =)0(400<x x
y =a
其中一次函数有 ;二次函数有 ;反比例函数有: .
11. 已知参加施工的人数y 与完成工程的时间t 成反比例关系.当施工人数为5人时,需要8天才能完成这项工程.为加快工程进度,现要求4天完成这项工程,则应派 人去施工才能完成任务.
四、解答题(本大题共2小题,共25分.答题应写出文字说明、演算过程步骤):
13.(15分)你吃过拉面吗?有人能把拉面拉得细如发丝,同时还能丝丝分明.实际上,拉面师傅在制作拉面时渗透着数学知识.当制作拉面的面团体积一定时,面条的总长度与拉面的粗细程度成反比例函数.面条的总长度与粗细程度的关系如图所示:
(1)写出y 与S 的函数关系.
(2)当面条的总长度为128 m 时,面条的粗细是多少?
(3)当面条的粗细为0.016 cm ²时,面条的总长度是多少?
1-2x y x 2y x 31y 1-x 3y x 3y x 1y 3x 2y =======;⑦;⑥;⑤;④;③;②①.m k x
k y 1m )5,1(10.12的值,的图像上,求)均在反比例函数,(和点分)已知点( B A
B 卷:能力提升卷
一、经典中考题(4分):
. .
二、知识交叉题(12分):
三、课标新题型(15分):
如图所示,某农户有一段25米长的旧围墙(如图AB 所示).现打算利用该围墙的一部分或者全部为一边建设一块面积为100 m 2的矩形鸡舍(图中矩形CDEF ,CD <EF ),已知整修旧围墙的价格为1.75元/米,而新建篱笆的价格为4.5元/米,设所利用的旧围墙CF 的长度为x 米,修建好鸡舍所需的费用为y 元.
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围;
(2)若利用旧围墙12 m ,则计划修建费用应为多少?
=
=m x 4m y 1-m 4-m 2是反比例函数,则)﹣(若.y 1x 9y 4x 0y 1x x y 1x y y y y 2121的值时,求当时,;当时,成正比例,且当与成正比例,与,其中已知函数-=====++=
1. √
2. ×
3. ×
4. A 解析:B 选项为正比例函数;C 选项若k=0则不是反比例函数;D 为一次函数.故选A.
5. D 解析: 根据题意,得2m-3=1,解得m=2. 故选D.
6. B 解析:根据题意,得1102
﹣﹣=m ,且0 ≠3﹣m ,解得3﹣=m .故选B. 7. B 8. 答案 ;反比例函数. 9. 答案
10. 答案 ①③④;⑥;②⑤⑦
11. 答案 10 解析:
12. 解析 解:∵点A 在反比例函数x k y =的图像上,∴1
5k =,解得k=5;…5分 ∴反比例函数的解析式为x y 5=;………………………………6分 又∵点B 也在反比例函数的图像上,∴ ,即m=5.……10分 13. 解析 解:(1)根据题意设该函数解析式为: …………1分
函数图像经过点P (4,32),代入上式,得
…………………………………4分 解方程,得
………………………………5分
答:y 与s 之间的函数表达式为
…………………………7分 (2)当y=128时,面条的粗细 ;解得:1=s .……10分
答:当面条的长度为128 m 时,面条的粗细为1mm 2.……11分
(3) ∵ 0.016cm 2=1.6mm 2,∴面条粗细6.1=s ;
代入解析式得:806
.1128==y .………………………………14分 答:当粗细为0.016mm 2时,面条的长度为80 m.…………15分
a h 10=v t 857=.t 40y t 84t y ∴t y =×==;即总工程量成反比例关系,与∵.10440y 4t ∴4===,则天完成这项工程,现要求15=m )0(≠=k s k y .4
32k =.128=k )0,0(128>>s y s y =s 128128=
一、经典中考题:
答案:0 解析:根据题意得⎩⎨⎧=≠114042﹣﹣﹣
﹣m m m ;解得0=m . 二、知识交叉题:
解析:本题函数y 是由y 1和y 2两个函数组成,应运用待定系数法求解,先
根据题意分别设出y 1、y 2与x 的函数关系式,再代入数值计算,通过解方程求出
比例系数.本题应注意y 1与x 和y 2与x 的函数关系中的比例系数并不一样,所以
不能都设为k ,应用不同的字母表示.
解:由题可得:
…………………………………2分 ……………………………………3分
…………………………………………………6分 …………………………………………………8分 ……………………………………………………9分 ……………………………………12分
三、课标新题型:
解析:可先利用面积把长与宽表示出来,求出y 与x 之间的关系.再利用x=12求出y 的值.
解:(1)
………………………………1分 …………………………………………4分 ………9分 (2) ………14分 ………………………………15分
41411214)1(24294501294;01)1(;0);0()1(2121212121222111=--+-⨯=-=-+=∴⎩⎨⎧-==⎪⎪⎩⎪⎪⎨⎧=+=+====++=∴+=≠=≠+=)(时,当解得则有时,时,当∵)(y x x x y k k k k k k y x y x x k x k y y y y k x k y k x k y ).25≤10(90025.6)200(5.475.1∴,100∴,,100x x x x x x y x CD x CF S CDEF <∵矩形+=++====.150150129001225.690025.612∴).25≤10(90025.6)1(元即计划修建费用应为,时,当<知由=+×=+==+=x x y x x x x y。