青海省西宁市17学年高一数学下学期第二次月考试题

西宁市第二十一中学2017-2018学年第二学期4月份月考高一数学试卷考试时间：120分钟 试卷满分：150分 命题人：高二数学备课组一、选择题（共12小题，每题5分，共60分） 1、设全集为,集合,则( )A. B.C. D. 2、若数列满足,,则( ) A.7 B.13 C.40 D.121 3.若为实数,且,则下列命题正确的是( )A. B. C . D.4、在△ABC 中，如果sin :sin :sin 2:3:4A B C =，那么最大角的余弦值等于（ ）2A.3 2B.-3 1C.-3 1D.-45、已知32x >，则函数y ＝2x+324-x 的最小值是( ) A. 7 B. 3 C. 9 D. 56、.在△ABC 中，A B B A 22sin tan sin tan ⋅=⋅，那么△ABC 一定是（ ） A ．锐角三角形 B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形7、等差数列}{n a 中，1815153120,a a a ++==则s （ ） A ．240B ．220C ．360D ．-3608、已知,,,则的最小值是( )A. B . C. D.9、设,x y 满足约束条件12x y y x y +≤⎧⎪≤⎨⎪≥-⎩,则3z x y =+的最小值为（ ）A ．5 B. 3 C.7 D.-8 10、不等式对于恒成立,那么的取值范围是( ) A.B.C.D.11、等差数列{}n a 的前n 项和为n S ，若01≠a ，44a S =，则=58S S （ ） A 1 B 2 C 3 D 4 12、如图,在中,是边上的点,且,则的值为( )A. B. C. D.二、 选择题（共4小题，每题5分，共20分）13、等差数列{}n a 的前m 项的和是30，前2m 项的和是100，则它的前3m 项的和是 . 14、已知数列的前项和为,则数列的通项公式为 . 15、在中,,这个三角形的面积为,则外接圆的直径是16、已知△ABC 的三边分别是a 、b 、c ，且面积4222c b a S -+=，则角C=____________三、解答题（共6题，17题10分，其余每题12分）17、若不等式的解集是.1.求的值;2.求不等式的解集.18、在锐角ABC ∆中，边a 、b 是方程220x -+=的两根，A 、B 满足2s i n (A B +0=，解答下列问题：1）求C 的度数； （2）求边c 的长度； （3）求ABC ∆的面积.19、已知等差数列;1,16a 5107n ==+a a a ｝中，｛ （1）求143a a +的值及该数列的通项公式；（2）已知数列已知32b n n +=a ，求证数列}{b n 是等差数列 （3）并求出数列}{b n 的前n 项和20、.已知A 、B 、C 为ABC ∆的三内角，且其对边分别为a 、b 、c ，若21sin sin cos cos =-C B C B ． （Ⅰ）求A ；（Ⅱ）若4,32=+=c b a ，求ABC ∆的面积．21、已知等差数列的前项和为且1.求数列的通项公式2.当为何值时,取最小值,最小值是多少22、某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ，公园由长方形的休闲区A 1B 1C 1D 1 和环公园人行道组成.已知休闲区A 1B 1C 1D 1的面积为4000平方米，人行道的宽分别为4米和10米.（1）若设休闲区的长米，求公园ABCD所占面积S关于的函数的解析式；（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？西宁市第二十一中学2017-2018学年第二学期4月份月考高一数学答案一.选择填空17.答案：1.依题意,可知方程的两个实数根为和,由韦达定理得:,解得:.2..18..19.略20.答案：1.2.解析：1.∵,,∴,∴,又,∴,∵的面积,∴,由,解得2.由,得得,∴或.①当时,则,由(1)知,,又∴.∴;②当时,则,代入,得,,∴.综上可得的面积为.21. .答案：1.由已知条件得2.当或时,最小22答案：⑴⑵要使公园所占面积最小，休闲区A1B1C1D1的长为100米、宽为40米.解析：（1）利用休闲区A1B1C1D1的面积为4000平方米，表示出，进而可得公园ABCD所占面积S关于x的函数S（x）的解析式；（2）利用基本不等式确定公园所占最小面积，即可得到结论．⑴由，知⑵当且仅当时取等号∴要使公园所占面积最小，休闲区A1B1C1D1的长为100米、宽为40米考点：基本不等式在最值问题中的应用；根据实际问题选择函数类型．点评：本小题是使用了基本不等式求最值，要注意其使用条件：一正二定三相等。

西宁市第四高级中学第二学期第二次月考试卷高 二 数 学第I 卷（选择题）一、选择题（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.若复数3i()12i a z a +=∈+R 实部与虚部相等，则a 的值等于（ ） Ａ．-1Ｂ．3Ｃ．-9Ｄ．92.已知函数()y f x =在定义域[4,6]-内可导，其图象如图，记()y f x =的导函数为'()y f x =，则不等式'()0f x ≥的解集为（ ）A ．411[,1][,6]33- B.7[3,0][,5]3-C ．[4,3][0,1][5,6]- D. 411[4,][1,]33--3.若曲线()sin f x x x =⋅在x=2π处的切线与直线ax+2y+1=0互相垂直，则实数a 等于（ ）A ．2B ．1C -2D ．-14.设⎪⎩⎪⎨⎧∈-∈=]2,1[2]1,0[)(2x x x x x f ，则⎰2)(dx x f 的值为（ ）A ．43 B ．54 C ．65 D ．67 5.用反证法证明命题：“若a 、b 、c 是三连续的整数，那么a 、b 、c 中至少有一个是偶数”时，下列假设正确的是（ ） A ．假设a 、b 、c 中至多有一个偶数 B ． 假设a 、b 、c 中至多有两个偶数C ．假设a 、b 、c 都是偶数D ． 假设a 、b 、c 都不是偶数6. .用0，1，2，3，4，5这六个数字组成没有重复数字的三位数,其中偶数共有（ ）A ．40个B ．42个C ．48个D ．52个7．若1()n x x+展开式的二项式系数之和为64，则展开式的常数项为（ ）A ．10B ．20C ．30D ．1208. 由曲线()xf x e =与直线1,1y x ==所围成的图形面积是（ ）A ．eB ．1e -C ．2e -D ．1e + 9．从1,2，3,4，5中不放回地依次取2个数，事件A ＝“第1次取到的是奇数”，B ＝“第2次取到的是奇数”，则P （B ｜A ）＝（ ）A 、15B 、310C 、25D 、1210.小王通过英语听力测试的概率是13，他连续测试3次，那么其中恰有1次获得通过的概率是（ ）A ．49B ．29C ．427D ．22711.如果随机变量),1(~2σξ-N ，且4.0)13(=-≤≤-ξP ，则)1(≥ξP 等于（ ） A ．4.0 B ．3.0 C ．2.0 D ．1.0 12．.设()f x 、()g x 分别是定义在R 上的奇函数和偶函数,当0x <时,()()()()0f x g x f x g x ''+>.且(3)0g =.则不等式()()0f x g x <的解集是 （ ） A ．（－3,0)∪(3,+∞) B ．(－3,0)∪(0, 3) C ．(－∞ ,- 3)∪(3,+∞) D ．(－∞,－ 3)∪(0, 3)第II 卷（非选择题）二、填空题（本大题共4小题，每小题5分，共20分.将答案填在答题卷相应位置上.）13..设随机变量ξ的概率分布列为(),1,2,3,,62k cP k k ξ===，其中c 为常数，则()2P ξ≤ 的值为________ .14．已知55104)1()1()1)(2(++⋅⋅⋅+++=-+x a x a a x x ，则=++531a a a ______.15.已知(,),3,(21)9B n p E D ξξξ=+=，则p 的值是 16. 已知xxe x f =)(，记'''1211()(),()(),,()()n n f x f x f x f x f x f x +===()n N *∈,则=)(x f n (用x 表示).三、解答题（本大题共6小题，满分70分.解答须写出文字说明、证明过程和演算步骤.）17．（本题满分10分）已知复数2(1)2(5)3i i z i++-=+．（1）求z ；（2）若()z z a b i +=+，求实数,a b 的值．18.（本小题12分）一个口袋内有4个不同的红球,6个不同的白球. (1)从中任取4个球,红球个数不少于白球个数的取法有多少种?(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7的取法19．（本题满分12分）用数学归纳法证明：)(3)2)(1()1(433221*N n n n n n n ∈++=+⨯+⋅⋅⋅+⨯+⨯+⨯20．（本小题12分）已知函数()32f x x ax bx c =-+++图像上的点))1(,1(f P 处的切线方程为31y x =-+，函数3)()(2+-=ax x f x g 是奇函数． （1）求函数)(x f 的表达式； （2）求函数)(x f 的极值.21.（本小题12分）甲、乙两人同时参加一次面试，已知在备选的10道试题中，甲能答对其中的6道，乙能答对其中的8道，规定每次考试都从备选题中随机抽出3道题进行测试，至少答对2道题才算通过。

西宁市16—17学年第二学期第二次月考试卷高一数学一、选择题：（本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 若a<b<c，则下列结论中正确的是( )A. a|c|<b|c|B. ab<acC. a－c<b－cD.【答案】C【解析】选项A中c＝0时不成立；选项B中a≤0时不成立；选项D中取a＝－2，b＝－1，c ＝1验证，不成立，故选C.2. 等比数列x，3x＋3，6x＋6，…的第四项等于( )A. －24B. 0C. 12D. 24【答案】A【解析】由x，3x+3，6x+6成等比数列得选A.考点：该题主要考查等比数列的概念和通项公式，考查计算能力.3. 当x>1时，不等式x＋≥a恒成立，则实数a的取值范围是( )A. (－∞，2]B.【答案】D考点：基本不等式.4. 等差数列{a n}满足，则其前10项之和为( )A. －9B. －15C. 15D. ±15【答案】D【解析】由已知(a4＋a7)2＝9，所以a4＋a7＝±3，从而a1＋a10＝±3.所以S10＝×10＝±15.故选D.5. 已知△ABC中，三内角A、B、C成等差数列，边a、b、c依次成等比数列，则△ABC是( )A. 直角三角形B. 等边三角形C. 锐角三角形D. 钝角三角形【答案】B【解析】∵△ABC中，三内角的度数成等差数列，∴，又，∴°.又边依次成等比数列，∴，在△ABC中,由余弦定理得：，∴，∴，∴，∴，又，∴为等边三角形。

故选B.6. 设变量x，y满足约束条件，则Z=x+2y的最大值为( )A. 1B. 2C. 6D. 7【答案】A【解析】作出一组平行线的，这一组平行线与平面区域有公共点时，且直线在y轴的截距最大，则最大.由图可知，当经过直线和的交点B(3,2)时，最大.最大值为=7.故选D.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意前面的系数为负时，截距越大，值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.7. 已知数列{a n}满足(n＋2)a n＋1＝(n＋1)a n，且a2＝，则a n等于( )A. B. C. D.【答案】A【解析】因为(n＋2)·a n＋1＝(n＋1)a n，所以，又当n＝1时，3a2＝2a1，所以a1＝a2＝.所以.故选A.8. 已知，则f(x)>－1的解集为( )A. (－∞，－1)∪(0，＋∞)B. (－∞，－1)∪(0，1)∪(1，＋∞)C. (－1，0)∪(1，＋∞)D. (－1，0)∪(0，1)【答案】B【解析】依题意，若，则x>0且x≠1；若>－1，则x<－1，综上所述．故选B.9. 在平面直角坐标系中，已知第一象限的点（a,b）在直线2x+3y-1=0上，则的最小值为（）A. 24B. 2 5C. 26D. 27【答案】A【解析】∵第一象限的点在直线上，∴，且，即，∴.当且仅当，即时，的最小值为，故选B.点睛：在用基本不等式求最值时，应具备三个条件：一正二定三相等.①一正：关系式中，各项均为正数；②二定：关系式中，含变量的各项的和或积必须有一个为定值；③三相等：含变量的各项均相等，取得最值.10. 执行如图所示的程序框图，如果输出S=132，则判断框中应填（）A. i≥10？B. i≥11？C. i≥12？D. i≤11？【答案】C【解析】程序执行过程中的数据变化如下：，，，，不成立，输出.故选：B.11. 已知等比数列{a n}满足=,,则=( )A. 2B. 1C.D.【答案】B【解析】试题分析：设等比数列{a n}的公比为q，则由已知得：，即：，解得：，因此，故选C．考点：等比数列．12. 设是等差数列{a n}的前项和，若，则（）A. B. C. D.【答案】D【解析】试题分析：由等差数列的性质可得，，，仍成等差数列，∵，∴，∴，∴，，∴两式相加可得，∴，∴，故选A.考点：等差数列的前项和.二、填空题：（本大题共4小题，每小题5分，共20分）13. 在△ABC中，∠C＝90°，M是BC的中点．若sin∠BAM＝，则sin∠BAC＝________．【答案】【解析】因为，所以.如图，在△ABM中，利用正弦定理，得，所以.在Rt△ACM中，有．由题意知BM＝CM，所以．化简，得.所以，解.再结合，∠BAC为锐角可解得＝.14. 在等差数列{a n}中，若a3＋a4＋a5＋a6＋a7＝25，则a2＋a8＝________．【答案】10【解析】试题分析：据等差数列的性质可知，项数之和相等的两项之和相等，化简已知的等式即可求出a5的值，然后把所求的式子也利用等差数列的性质化简后，将a5的值代入即可求出值．解：由a3+a4+a5+a6+a7=（a3+a7）+（a4+a6）+a5=5a5=450，得到a5=90，则a2+a8=2a5=180．故答案为：180．考点：等差数列的性质．15. 用秦九韶算法求多项式f(x)=6+5+4+3+2+x当x=2时的值时，＝________．【答案】【解析】. 当x=2时的值时,点评：利用秦九韶算法求多项式的值首先要将多项式改写为每个括号内为关于x的一次式的形式，由内层括号到外层括号依次为.16. 不等式（a-2）+2(a-2) x-4<0对一切x R恒成立，则实数的取值范围是________．【答案】3【解析】试题分析：当时恒成立，当时，利用二次函数图象知，所以答案应填：．考点：含参二次不等式恒成立．【思路点晴】本题主要考查是含参数二次不等式的恒成立问题，属于中档题．解题时一定注意对的分类讨论，不能忘记的情况，同时，要结合二次函数图象及方程根的情况，应该开口向下，判别式小于零，列出满足的条件求解．三、解答题：（本大题共6小题，共70分）17. 设△ABC的内角A，B，C的对边分别为a，b，c，a＝b tan A，且B为钝角．(1)证明：B－A＝；(2)求sin A＋sin C的取值范围．【答案】（1）见解析；（2）.【解析】试题分析：(Ⅰ)运用正弦定理将化简变形,再解三角方程即可获解；(Ⅱ)将角用表示,换元法求函数的值域即可.试题解析：(Ⅰ)由及正弦定理，得，∴，即，又为钝角，因此，故，即；(Ⅱ)由（1）知，，∴，于是，∵，∴，因此，由此可知的取值范围是．考点：正弦定理、三角变换，二次函数的有关知识和公式的应用.18. 公差不为零的等差数列{a n}中，a3＝7，且a2，a4，a9成等比数列．(1)求数列{a n}的通项公式；(2)设b n＝2a n，求数列{b n}的前n项和S n．【答案】（1）a n＝3n－2；（2）.【解析】试题分析：（1）设数列的公差为d，根据a3=7，又a2，a4，a9成等比数列，可得（7+d）2=（7-d）（7+6d），从而可得d=3，进而可求数列{a n}的通项公式；（2）先确定数列{b n}是等比数列，进而可求数列{b n}的前n项和S n．试题解析：(1)由数列{a n}为公差不为零的等差数列，设其公差为d，且d≠0.因为a2，a4，a9成等比数列，所以a＝a2·a9，即(a1＋3d)2＝(a1＋d)(a1＋8d)，整理得d2＝3a1d.因为d≠0，所以d＝3a1.①因为a3＝7，所以a1＋2d＝7.②由①②解得a1＝1，d＝3，所以a n＝1＋(n－1)×3＝3n－2.故数列{a n}的通项公式是a n＝3n－2.(2)由(1)知b n＝23n－2，因为＝＝8，所以{b n}是等比数列，且公比为8，首项b1＝2，所以S n＝＝.19. 已知函数f(x)＝x2－2x－8，g(x)＝2x2－4x－16．(1)求不等式g(x)<0的解集；(2)若对一切x>2，均有f(x)≥(m＋2)x－m－15成立，求实数m的取值范围．【答案】（1）{x|－2<x<4}；（2）(－∞，2].【解析】试题分析：（1）通过分解因式法进行求解；（2）作差，分离常数，将问题转化为求最值问题，再利用基本不等式求最值．试题解析：（1）g（x)＝2x2－4x－16＜0，∴（2x＋4)（x－4)＜0，∴－2＜x＜4，∴不等式g（x)＜0的解集为{x|－2＜x＜4}．（2）∵f（x)＝x2－2x－8.当x＞2时，f（x)≥（m＋2)x－m－15恒成立，∴x2－2x－8≥（m＋2)x－m－15，即x2－4x＋7≥m（x－1)．∴对一切x＞2，均有不等式成立．而＝（x－1)＋－2≥2－2＝2（当且仅当x＝3时等号成立)，∴实数m的取值范围是（－∞，2]．考点：1.一元二次不等式的解法；2.基本不等式．【方法点睛】本题考查一元二次不等式的解法、基本不等式的应用以及含参数的不等式恒成立问题，属于中档题；在处理含参数的不等式恒成立问题时，往往利用“分离参数法”将参数进行分离，使不等式恒成立问题转化为求函数的最值问题，如本题中将“对于恒成立”转化为“对于恒成立”，即求的最小值.20. 设数列{a n}的前n项和为S n＝2n2，{b n}为等比数列，且a1＝b1，b2(a2－a1)＝b1．(1)求数列{a n}和{b n}的通项公式；(2)设c n＝，求数列{c n}的前n项和T n．【答案】（1）a n＝4n－2，；（2）T n＝.【解析】略21. 在锐角△ABC中，三个内角A，B，C所对的边分别为a，b，c，且ac sin C＝(a2＋c2－b2)·sin B．(1)若C＝，求A的大小；(2)若a≠b，求的取值范围．【答案】（1）；（2）.【解析】试题分析：（1）将已知等式变形，整理得, 可得，由此可得C=2B或C+2B=π，最后结合三角形内角和定理和∠C, 即可算出∠A的大小．（2）根据三角形为非等腰三角形，结合（1）中化简的结果可得C=2B，利用△ABC是锐角三角形，得到B的范围，又即可得范围.试题解析：(1)因为ac sin C＝(a2＋c2－b2)sin B，所以＝＝2＝2cos B，所以sin C＝sin 2B，所以C＝2B或C＋2B＝π.若C＝2B，C＝，则A＝ (舍去)．若C＋2B＝π，C＝，则A＝.故A＝.(2)若三角形为非等腰三角形，则C＝2B且A＝π－B－C＝π－3B，又因为三角形为锐角三角形，因为0＜2B＜，0＜π－3B＜，故＜B＜.而＝＝2cos B，所以∈(，)．22. 某工厂建造一间地面面积为12的背面靠墙的矩形小房，房屋正面的造价为1200元- 11 - ，房屋侧面的造价为800元，屋顶的造价为5800元．若墙高为3，且不计房屋背面的费用，则建造此小房的最低总造价是多少元？【答案】当|AB |＝3 m ，|BC |＝4 m 时，能使整个框架用材料最少.【解析】试题分析：试题解析：设总造价为Z 元,则有. ∴. 当时，即时，Z 有最小值34600，此时答：长4m ,宽3m .最低总造价为34600元点睛：在用基本不等式求最值时，应具备三个条件：一正二定三相等.①一正：关系式中，各项均为正数；②二定：关系式中，含变量的各项的和或积必须有一个为定值；③三相等：含变量的各项均相等，取得最值.。

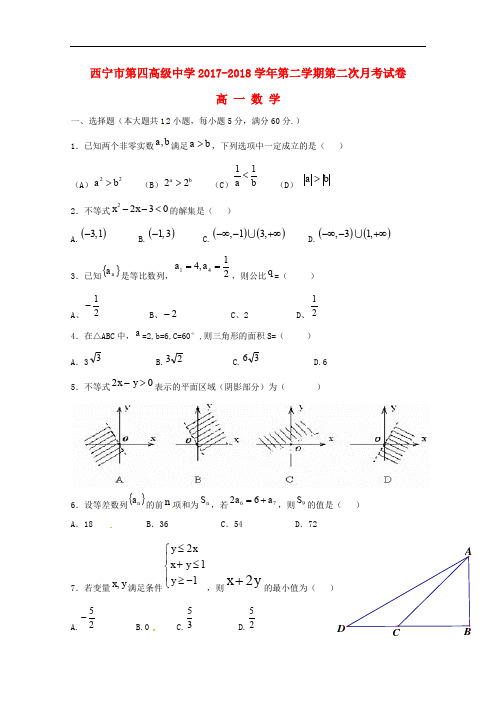
西宁市第四高级中学2017-2018学年第二学期第二次月考试卷高 一 数 学一、选择题（本大题共12小题，每小题5分，满分60分.）1．已知两个非零实数,a b 满足a b >，下列选项中一定成立的是（ ）（A ）22a b > （B ）22a b> （C ）11a b < （D ） a b > 2．不等式2230x x --<的解集是（ ）A.()3,1- B.()1,3- C.()(),13,-∞-+∞ D.()(),31,-∞-+∞3．已知{}n a 是等比数列，21,441==a a ，则公比q =（ ）A 、21-B 、2-C 、2D 、214．在△ABC 中，a =2,b=6,C=60°,则三角形的面积S=（ ） A ．33 B.23 C.36 D.6 5．不等式02>-yx 表示的平面区域（阴影部分）为（ ）6．设等差数列{}n a 的前n 项和为n S ，若7662a a +=，则9S 的值是（ ）A ．18B ．36C ．54D ．727．若变量,x y 满足条件211y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则2x y +的最小值为（ ）A.52-B.0C.53D.528．如图，塔AB 底部为点B ，若,C D 两点相距为100m 并且与点B 在同一水平线上，现从,C D 两点测得塔顶A 的仰角分别为45o和30o，则塔AB 的高约为（精确到0.1m，1.73≈，1.41≈）m.（ ）A. 36.5B. 115.6C. 120.5D. 136.5 9．在ABC ∆中,内角A 、B 、C 所对的边分别是a 、b 、c ,若222222c a b ab =++,则ABC ∆是（ ）A ．等边三角形B ．锐角三角形C ．直角三角形D ．钝角三角形10．函数()x x y 383-=（380≤≤x ）的最大值是（ ）A 、 0B 、34C 、4D 、1611．当5n =时，执行如图所示的程序框图，输出的S 值为 A.2 B.4 C.7 D.1112．已知数列{}n a 中，()243,111≥∈+==*-n N n a a a n n 且，则数列{}n a 通项公式na 为 （ ） A ．13n - B ．138n +- C ．32n - D ．3n二、填空题（本大题共4小题，每小题5分，共20分.将答案填在答题卷相应位置上.）13．不等式212≥++x x 的解集是__________. .14．设等差数列{}n a 满足115=a ,312-=a ,{}n a 的前n 项和n S 的最大值为M,则lg M =__________．15．若(1,)x ∈+∞，则21y x x =+-的最小值是__________. ．16．已知数列{}n a 的首项11a =，且满足11(2)n n n n a a a a n ---=≥，则__________.三、解答题（本大题共6小题，满分70分.解答须写出文字说明、证明过程和演算步骤.）17. （本小题满分10分）已知关于x 的不等式).(042R k kx x ∈>+-（1）当5=k 时，解该不等式；（2）若不等式对一切实数x 恒成立，求k 的取值范围.18．（本小题满分12分）在C ∆AB 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足cos C sin 0c -A =．（1）求角C 的大小；（2）已知4b =，C ∆AB 的面积为c 的值．19．（本小题满分12分）已知等比数列{}n a 的公比1q >，1a ，2a 是方程2320x x -+=的两根．（1）求数列{}n a 的通项公式；（2）求数列{}2n n a ⋅的前n 项和n S ．20．（本小题满分12分）在ABC ∆中，已知π11sin()214A +=,1cos(π)2B -=-. （1）求sin A 与B 的值；（2）若角A ，B ，C 的对边分别为a ，b ，c ，且5a =，求b ，c 的值.21．（本小题满分12分）已知在等比数列}{n a 中，11=a ，且2a 是1a 和13-a的等差中项. （1）求数列}{n a 的通项公式； （2）若数列}{n b 满足)(12*N n a n b n n ∈+-=，求}{n b 的前n 项和nS .22．（本小题满分12分） 我国发射的天宫一号飞行器需要建造隔热层。

{正文}2017-2018学年度青海西宁市第二十一中学第二学期高一3月月考数学试题一、选择题（共10小题，每题5分，共50分）1．已知集合M={x|0≤x<2}，N={x|x 2-2x-3<0}，则M ∩N=（ ）A ．{x|0≤x<1}B ．{x|0≤x<2}C ．{x|0≤x ≤1}D ．{x|0≤x ≤2}2．设a ，b 是非零实数，若a ＜b ，则下列不等式成立的是（ ）A ．a 2＜b 2B ．a 3＜b 3C ．a 1＜b1D ．a 1＞b1 3．在△ABC 中，∠A ＝45°，∠B ＝60°，a ＝2，则b 等于（ ）A ．6B ．2C ．3D ．264．下列命题中正确的是（ ）A ．若a>b ，则ac 2>bc 2B ．若a>b ，c<d ，则dbc a > C ．若a>b ，c>d ，则a-c>b-d D ．若ab>0，a>b ，则ba 11< 5．关于x 的一元二次不等式ax 2+bx+1>0的解集为{x|-1<x<31}，则ab 的值为（ ）A ．-6B ．-5C ．6D ．56．在锐角△ABC 中，角A ，B 对应的边分别为a ，b 。

若b B a =sin 2，则角A=（ ）A ．60°B ．30°或150°C ．60°或120°D ．30°7．在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≥≥+-≤-+00202y y x y x 表示的平面区域的面积是（ ）A ．42B ．4C ．22D ．28．若x ，y 满足约束条件⎪⎩⎪⎨⎧≤-+≤-≤+-0220201y x y x y x ，则z=x+y 的最大值是（ ）A ．-3B ．0.5C ．1D ．1.59．设,,5,33x y x y x y ∈+=+R 且则的最小值是（ ）A．B．C．D ．1010．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若A a B c C b sin cos cos =+，则△ABC 的形状为（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定二、填空题（共4小题，每题5分，共20分）11．在△ABC 中，a ∶b ∶c ＝1∶2∶3，则sinA ∶sinB ∶sinC=12．已知点A （3,1）和点B （-4,6）在直线023=+-a y x 的两侧，则a 的取值范围是 。

西宁市2017-2018学年度第二学期末调研测试卷高一数学第Ⅰ卷（共60分）一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把你认为正确的选项序号填入相应题号的表格内） 1. 设a ，b ，c R ∈，且a b >，则下列选项中一定成立的是（ ） A ． ac bc > B ．11a b< C ． 22a b > D ．33a b > 2. 如图为一串白黑相间排列的珠子，按这种规律往下排起来，那么第36颗珠子应是什么颜色（ ）A ．白色B ．黑色C ．白色可能性大D ．黑色可能性大3. 奥林匹克会旗中央有5个互相套连的圆环，颜色自左至右，上方依次为蓝、黑、红，下方依次为黄、绿，象征着五大洲.在手工课上，老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作，每人分得1个，则事件“甲分得红色”与“乙分得红色”是（ ）A ．对立事件B ．不可能事件C ． 互斥但不对立事件D ．不是互斥事件4. 在ABC ∆中，60A ∠=︒，a =b =ABC ∆解的情况（ ）A ． 无解B ．有唯一解 C. 有两解 D ．不能确定 5. 一组数据的茎叶图如图所示，则数据落在区间[]22,30内的概率为A ．0.2B ． 0.4 C. 0.5 D ．0.6 6. 设()()13M a a =+-，()22N a a =-，则（ ）A ．M N >B ．M N ≥ C. M N < D ．M N ≤ 7. 已知x ，22x +，33x +是一个等比数列的前三项，则x 的值为（ ） A ．-4或-1 B ． -4 C. -1 D ．4或18. 某班有49位同学玩“数字接龙”游戏，具体规则按如图所示的程序框图执行(其中a 为座位号)，并以输出的值作为下一轮输入的值.若第一次输入的值为8，则第三次输出的值为（ ）A ． 8B ．15 C. 20 D ．369. 用系统抽样法从160名学生中抽取容量为20的样本，将160名学生从1-160编号.按编号顺序平均分成20组(1～8号，9～16号，…，153～160号)，若第15组中抽出的号码为118，则第一组中按此抽签方法确定的号码是（ ） A ． 7 B ． 6 C. 5 D ．410. 具有线性相关关系的变量x ，y 满足的一组数据如表所示，若y 与x 的回归直线方程为3ˆ32yx =-，则m 的值为（ ） A ． 4 B ．92C. 5 D ．6 11. 若不等式组,50,02,y a x y x ≥⎧⎪-+≥⎨⎪≤≤⎩表示的平面区域是一个三角形，则实数a 的取值范围为（ ）A ．5a <B ． 7a ≥ C. 57a ≤< D ．5a <或7a ≥ 12. 公比不为1的等比数列{}n a 的前n 项和为n S ，且12a -，212a -，3a 成等差数列，若11a =，则4S =（ ）A ． -5B ． 0 C. 5 D ．7二、填空题（本大题共4小题，每小题5分，共20分，将答案填写在题中的横线上） 13. 二次函数2()y ax bx c x R =++∈的部分对应值如下表：则不等式20ax bx c ++<的解集是 ．14. 右图是一个边长为4的正方形二维码，为了测算图中黑色部分的面积，在正方形区域内随机投掷400个点，其中落入黑色部分的有225个点，据此可估计黑色部分的面积为 ．15. 若数列{}n a 的前n 项和为22n S n =，则34a a +的值为 ．16. 已知2x >，求()122f x x x =+-的最小值 ． 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 渔政船在东海某海域巡航，已知该船正以/时的速度向正北方向航行，该船在A点处时发现在北偏东30︒方向的海面上有一个小岛，继续航行20分钟到达B 点，此时发现该小岛在北偏东60︒方向上，若该船向正北方向继续航行，船与小岛的最小距离为多少海里？ 18. 在“六一”联欢会上设有一个抽奖游戏.抽奖箱中共有12张纸条，分一等奖、二等奖、三等奖、无奖四种.从中任取一张，不中奖的概率为12，中二等奖或三等奖的概率是512. （Ⅰ）求任取一张，中一等奖的概率； （Ⅱ）若中一等奖或二等奖的概率是14，求任取一张，中三等奖的概率. 19. 已知等差数列{}n a 的前n 项和为n S ，且37a =，5726a a +=. （Ⅰ）求n a 及n S ；（Ⅱ）令()nn S b n N n+=∈，求证：数列{}n b 为等差数列 20. 某中学从高三男生中随机抽取n 名学生的身高，将数据整理，得到的频率分布表如下所示，（Ⅰ）求出频率分布表中①和②位置上相应的数据，并完成下列频率分布直方图；（Ⅱ）为了能对学生的体能做进一步了解，该校决定在第3，4，5组中用分层抽样抽取6名学生进行不同项目的体能测试，若在这6名学生中随机抽取2名学生进行引体向上测试，则第4组中至少有一名学生被抽中的概率.21. 在锐角ABC ∆中，a ，b ，c 是角A ，B ，C 2sin c A =. （Ⅰ）求角C 的度数；（Ⅱ）若c =ABC ∆的面积为2，求a b +. 22. 设函数()23f x x x =-（Ⅰ）若不等式()f x m ≥对任意[]0,1x ∈恒成立，求实数m 的取值范围； （Ⅱ）在（Ⅰ）的条件下，当m 取最大值时，设0x >，0y >且240x y m ++=，求11x y+的最小值.西宁市2017-2018学年度第二学期末调研测试卷高一数学参考答案及评分意见一、选择题1-5: DACBD 6-10: CBABA 11、12：CA 二、填空题13. ()2,3- 14. 9 15. 24 16.4+ 三、解答题17. 解：根据题意画出相应的图形，如图所示，过C 作CD AD ⊥，由题意得：2060AB =⨯= (海里) ∵30A ∠=︒，60CBD ∠=︒ ∴30BCA ∠=︒，则ABC ∆为等腰三角形，所以BC =在BCD ∆中，∵60CBD ∠=︒，CD AD ⊥，BC =∴152CD =则该船向北继续航行，船与小岛的最小距离为7.5海里.18. 解：设任取一张，抽得一等奖、二等奖、三等奖、不中奖的事件分别为A ，B ，C ，D ，它们是互斥事件. 由条件可得1()2P D =，5()()()12P B C P B P C +=+=， （Ⅰ）由对立事件的概率公式知()()()()51111112212P A P B C D P B C P D =-++=-+-=--=， 所以任取一张，中一等奖的概率为112； （Ⅱ）∵1()4P A B +=，而()()()P A B P A P B +=+ ∴111()4126P B =-=， 又()()()512P B C P B P C +=+=，∴1()4P C = 所以任取一张，中三等奖的概率为14.19. 解:（Ⅰ）设等差数列的首项为1a ，公差为d ，由题意有1127.21026,a d a d +=⎧⎨+=⎩解得13a =，2d =，则()()1132121n a a n d n n =+-=+-=+，()()()1321222n n n n n a a S n n ++⎡⎤+⎣⎦===+（Ⅱ）因为(2)2n n S n n b n n n+===+， 又()1321n n b b n n +-=+-+=， 所以，数列{}n b 为等差数列.20. 解:（Ⅰ）由题可知，第1组：50.050n=，得100n =第2组的频数为0.35010035⨯=人， 第3组的频数为300.300100=. 即①处的数据为35，②处的数据为0.300.（Ⅱ）因为第3，4，5组共有60名学生，所以利用分层抽样，在60名学生中抽取6名学生，每组分别为：第3组：306360⨯=人； 第4组：206260⨯=人；第5组：106160⨯=人.所以第3，4，5组分别抽取3人，2人，1人.设第3组的3位同学为1A ，2A ，3A ，第4组的2位同学为1B ，2B ，第5组的1位同学为C ， 则从6位同学中抽两位同学的可能有12A A ，13A A ，11A B ，12A B ，1A C ，23A A ，21A B ，22A B ，2A C ，31A B ，32A B ，3A C ，12B B ，1B C ，2B C 共15种；其中第4组的两位同学至少有一位同学被选中的有：11A B ，12A B ，21A B ，22A B ，31A B ，32A B ，12B B ，1B C ，2B C 共9种可能.所以第4组的两位同学至少有一位同学被选中的概率93155P ==.21. 解:2sin c A =2sin sin A C A =， 因为ABC ∆为锐角三角形，所以sin C =，故3C π=.（Ⅱ）因为1sin 2ABC S ab C ∆== 所以6ab =，又c =3C π=，由余弦定理2222cos c a b ab C =+-，得227a b ab =+-，所以()()227318a b ab a b =+-=+- 所以()225a b += 则5a b +=.22. 解:（Ⅰ）因为函数2()3f x x x =-的对称轴为32x =，且开口向上， 所以2()3f x x x =-在[]0,1x ∈上单调递减，所以()min ()1132f x f ==-=-， ∴2m ≤-.（Ⅱ）根据题意，由（Ⅰ）可得2m =-， 即2420x y +-=， 所以21x y +=. 所以21x y +=. ∵0x >，0y >则1111()(2)x y x y x y+=++ 2(3)y xx y=++3≥+3=+当且仅当2y xx y=，即1x =，12y =-时，等号成立.所以11x y+的最小值为3+.。

西宁市2016-2017学年度第二学期末调研测试卷高一数学一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若a b >，则下面一定成立的是( ) A ．ac bc >B ．1a b >C ．11a b <D ．22a c bc 32.把红、蓝、白3张纸牌随机地分发给甲、乙、丙三个人，每人分得1张，事件“甲分得红牌”与事件“乙分得红牌”是( )A ．对立事件B ．不可能事件C ．互斥但不对立事件D ．以上都不对3.不等式10x y +->表示的区域在直线10x y +-=的( ) A ．右上方B ．右下方C ．左上方D ．左下方4.已知在等比数列{}n a 中，11a =，59a =，则3a =( ) A ．3±B ．3C.5±D ．5 5.下列叙述错误的是( )A ．若事件A 发生的概率为()P A ，则()01P A ＃B ．互斥事件不一定是对立事件，但是对立事件一定是互斥事件C.两个对立事件的概率之和为1 D ．对于任意两个事件A 和B ，都有()()()P A B P A P B =+6.两灯塔,A B 与海洋观察站C 的距离都为a ，灯塔A 在C 的北偏东30°，B 在C 的南偏东60°，则,A B 两灯塔之间距离为() A ．2a B ．3a C.2a D ．a7.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位：件)，若这两组数据的中位数相等，且平均值也相等，则x 和y 的值分别为( )A ．3，5B ．5，5 C.3，7 D ．5，7。

青海省西宁市2017-2018学年高一数学12月月考试题（考试时间：120分钟 试卷满分：150分）一、选择题（共12小题，每题5分，共60分） 1、下列命题正确的是（ ）A 、第二象限角必是钝角B 、终边相同的角一定相等C 、相等的角终边必相同D 、不相等的角终边必不相同 2、sin330︒等于 （ ） A．2-B ．12-C ．12D．23.下列函数中，即是单调函数又是奇函数的是 （ ）A ．x y 3log =B ．xy 3= C ．21x y = D ．3x y =4．函数()14log -=x y a ，）且10(≠>a a 图象必过的定点是 ( )A ．）（1,41B ．）（0,1C ．）（1,0D ．）（0,21 5．函数()1f x x x=--的图象（）． A. 关于原点对称 B. 关于直线y x =对称C. 关于x 轴对称 D. 关于y 轴对称6．若函数x x x f 2-)12(2=+，则)3(f 等于( )A.3B.2C.1D.0 7、为了得到函数R x x y ∈+=),32cos(π的图象，只需把函数x y 2cos =的图象（ ）A 、向左平行移动3π个单位长度 B 、向右平行移动3π个单位长度 C 、向左平行移动6π个单位长度 D 、向右平行移动6π个单位长度8.设函数()⎪⎩⎪⎨⎧>+≤+=1,21,12x ax x x x f x ，若()()a f f 41=，则实数a 等于（ ）A ．21 B ．34C. 2 D ．4 9.设51log ,2,512512==⎪⎭⎫⎝⎛=c b a ，则（ ）A ．b a c <<B ．a b c <<C ．b c a <<D ．c b a <<10.方程31()|log |3x x =的解的个数是 （ ）A ．3B ．2C ．1D ．0 11．同一坐标系下，函数y=x+a 与函数y=a x的图象可能是（）A B C D12.函数)(x f y =在[]2,0上单调递增，且函数)2(+x f 是偶函数，则下列结论成立的是（ ） A ．()⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛<27251f f f B ．()⎪⎭⎫ ⎝⎛<<⎪⎭⎫ ⎝⎛27125f f fC. ()12527f f f <⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛ D ．()⎪⎭⎫ ⎝⎛<<⎪⎭⎫ ⎝⎛25127f f f 二、填空题（共4小题，每题5分，共20分）13.计算=+-32)27(2lg 4lg 32lg ． 14． f (x )＝x 2－2x (x ∈[2,4])的最小值为. 15．函数的定义域是16．已知偶函数在单调递减，，若，则的取值范围是__________．三、解答题（共6题，其中第17题10分，18-22题每题12分，满分70分）17（本小题满分10分）① 已知31cos =α，02π<<-α，求)cos()πcos(cos )2πcos(αααα--+的值．② 已知21tan =α，求ααααcos sin cos 3sin +-的值．18．(本小题满分12分)19.（本小题满分12分）已知幂函数12)22()(+++-=m x m m x f 为偶函数．（1）求)(x f 的解析式；（2）若函数1)1(2)(+--=x a x f y 在区间（2，3）上为单调函数，求实数a 的取值范围．20（本小题满分12分）已知)(x f 是定义在R 上的奇函数，且当0>x 时，34)(2+-=x x x f .（1）求)]1([-f f 的值； （2）求函数)(x f 的解析式.21（本小题满分12分）函数)2()sin()(πϕϕω<++=b x A x f 的图象如图所示，（1）求该函数的表达式（2）求)(x f 取得最大值时x 的值的集合。

2017-18学年第一学期第二次月考试卷高 一 数 学一、选择题（本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1．已知集合M ＝{x|x<3}，N ＝{x|2log 1x >}，则M ∩N 等于( )A ．∅B ．{x|0<x<3}C ．{x|1<x<3}D ．{x|2<x<3}2．17cos 4π⎛⎫- ⎪⎝⎭的值是（ ）A ．12 B． D3、 当时，幂函数为增函数，则实数的值为 ( )A.B.C.或D.4．设f(x)＝3x＋3x －8，用二分法求方程3x＋3x －8＝0在x∈(1,2)内近似解的过程中，计算得到f(1)<0，f(1.5)>0，f(1.25)<0，则方程的根落在区间( )A ．(1,1.25)B ．(1.25,1.5)C ．(1.5,2)D ．不能确定5．函数1lg 4)(--=x x x f 的定义域是( ) A ．),4[+∞ B ．),10(+∞ C ． ),10()10,4(+∞⋃ D ．),10()10,4[+∞⋃ 6.函数f(x)＝3log 82x x -+的零点一定位于区间()A.(5，6)B.(3，4)C.(2，3)D.(1，2)7．设12log 3a =，0.21()3b =，132c =，则A.cb a << B.a bc << C.c a b << D.b a c <<8.已知函数f(x)＝a x ＋log a x(a>0且a ≠1)在[1，2]上的最大值与最小值之和为log a 2＋6，则a 的值为( )A.12B.14 C.2D.49．函数是（ ）A ．周期为π的奇函数B ． 周期为π的偶函数C ．周期为2π的奇函数D ． 周期为2π的偶函数10( )A ．(,3)-∞-B ．(,3]-∞-C ．(,1)-∞-D ．(3,1)--11．若函数a 23(2)()log (2)x x f x x x -+≤⎧=⎨>⎩在R 上是减函数，则实数a 的取值范围为( )A.21≤a ＜1 B.0＜a ≤21C. a ＞1D.1＜a ≤2 12.．若函数f(x)为偶函数，且在[)0+∞，上是增函数，又f(－3)=0，则不等式 (x －2) f(x)<0的解集为（ ）A. (－2，3)B. (－3，－2)∪(3，＋∞)C. (－3，3)D. (－∞，－3)∪(2，3)第II 卷二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卷相应位置上） 13．已知扇形的圆心角为，弧长为，则该扇形的面积为 _________14.函数()()log 2301a y x a a =-+>≠且恒过定点为 _________15．已知sin α＋2cos α＝0，则2sin αcos α－cos 2α的值是________ 16．若函数f(x)＝|2x －2|－b 有两个零点，则实数b 的取值范围是____三、解答题（本大题共6小题，满分70分。

2017-18学年第一学期第二次月考试卷高 一 数 学一、选择题（本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1．已知集合M ＝{x|x<3}，N ＝{x|2log 1x >}，则M ∩N 等于( )A ．∅B ．{x|0<x<3}C ．{x|1<x<3}D ．{x|2<x<3}2．17cos 4π⎛⎫- ⎪⎝⎭的值是（ ）A ．12 B．2- D．23、 当时，幂函数为增函数，则实数的值为 ( )A.B.C.或D.4．设f(x)＝3x ＋3x －8，用二分法求方程3x ＋3x －8＝0在x∈(1,2)内近似解的过程中，计算得到f(1)<0，f(1.5)>0，f(1.25)<0，则方程的根落在区间( )A ．(1,1.25)B ．(1.25,1.5)C ．(1.5,2)D ．不能确定5．函数1lg 4)(--=x x x f 的定义域是( ) A ．),4[+∞ B ．),10(+∞ C ． ),10()10,4(+∞⋃ D ．),10()10,4[+∞⋃ 6.函数f(x)＝3log 82x x -+的零点一定位于区间()A.(5，6)B.(3，4)C.(2，3)D.(1，2)7．设12log 3a =，0.21()3b =，132c =，则A.cb a << B.a bc << C.c a b << D.b a c <<8.已知函数f(x)＝a x ＋log a x(a>0且a ≠1)在[1，2]上的最大值与最小值之和为log a 2＋6，则a 的值为( )A.12B.14 C.2D.49．函数是（ ）A ．周期为π的奇函数B ． 周期为π的偶函数C ．周期为2π的奇函数D ． 周期为2π的偶函数10( )A ．(,3)-∞-B ．(,3]-∞-C ．(,1)-∞-D ．(3,1)--11．若函数a 23(2)()log (2)x x f x x x -+≤⎧=⎨>⎩在R 上是减函数，则实数a 的取值范围为( )A.21≤a ＜1 B.0＜a ≤21C. a ＞1D.1＜a ≤2 12.．若函数f(x)为偶函数，且在[)0+∞，上是增函数，又f(－3)=0，则不等式 (x －2) f(x)<0的解集为（ ）A. (－2，3)B. (－3，－2)∪(3，＋∞)C. (－3，3)D. (－∞，－3)∪(2，3)第II 卷二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卷相应位置上） 13．已知扇形的圆心角为，弧长为，则该扇形的面积为 _________14.函数()()log 2301a y x a a =-+>≠且恒过定点为 _________15．已知sin α＋2cos α＝0，则2sin αcos α－cos 2α的值是________ 16．若函数f(x)＝|2x －2|－b 有两个零点，则实数b 的取值范围是____三、解答题（本大题共6小题，满分70分。