弹性力学---第2章边界条件(6-7)
- 格式:ppt
- 大小:1.44 MB
- 文档页数:24

弹性力学课后答案第二章习题的提示与答案2-1 是2-2 是2-3 按习题2-1分析。
2-4 按习题2-2分析。
2-5 在的条件中,将出现2、3阶微量。
当略去3阶微量后,得出的切应力互等定理完全相同。
2-6 同上题。
在平面问题中,考虑到3阶微量的精度时,所得出的平衡微分方程都相同。
其区别只是在3阶微量(即更高阶微量)上,可以略去不计。
2-7 应用的基本假定是:平衡微分方程和几何方程─连续性和小变形,物理方程─理想弹性体。
2-8 在大边界上,应分别列出两个精确的边界条件;在小边界(即次要边界)上,按照圣维南原理可列出3个积分的近似边界条件来代替。
2-9 在小边界OA边上,对于图2-15(a)、(b)问题的三个积分边界条件相同,因此,这两个问题为静力等效。
2-10 参见本章小结。
2-11 参见本章小结。
2-12 参见本章小结。
2-13 注意按应力求解时,在单连体中应力分量必须满足(1)平衡微分方程,(2)相容方程,(3)应力边界条件(假设 )。
2-14 见教科书。
2-15 2-16 见教科书。
见教科书。
2-17 取它们均满足平衡微分方程,相容方程及x=0和的应力边界条件,因此,它们是该问题的正确解答。
2-18 见教科书。
2-19 提示:求出任一点的位移分量和,及转动量,再令 ,便可得出。
第三章习题的提示与答案3-1 本题属于逆解法,已经给出了应力函数,可按逆解法步骤求解:(1)校核相容条件是否满足,(2)求应力,(3)推求出每一边上的面力从而得出这个应力函数所能解决的问题。
3-2 用逆解法求解。
由于本题中 l>>h, x=0,l 属于次要边界(小边界),可将小边界上的面力化为主矢量和主矩表示。
3-3 见3-1例题。
3-4 本题也属于逆解法的问题。
首先校核是否满足相容方程。
再由求出应力后,并求对应的面力。
本题的应力解答如习题3-10所示。
应力对应的面力是:主要边界:所以在边界上无剪切面力作用。



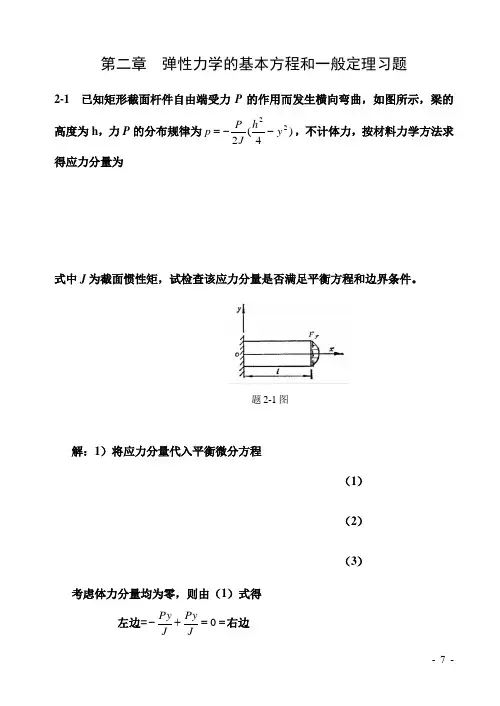
- 7 -第二章 弹性力学的基本方程和一般定理习题2-1 已知矩形截面杆件自由端受力P 的作用而发生横向弯曲,如图所示,梁的高度为h ,力P 的分布规律为)4(222y h J P p --=,不计体力,按材料力学方法求得应力分量为式中J 为截面惯性矩,试检查该应力分量是否满足平衡方程和边界条件。
解:1)将应力分量代入平衡微分方程 (1) (2)(3)考虑体力分量均为零,则由(1)式得左边===+-0JPy J Py 右边 题2-1图- 8 - 将应力分量代入平衡微分微分方程的(2)、(3),显然平衡微分方程满足。
2)应力边界条件 n m l T zx yx x x ττσ++= (4) n m l T zy y xy y τστ++= (5)n m l T z yz xz z σττ++=(6)这里必须注意:应力边界条件必须满足所有的边界,而不是仅仅求出待定常数。
下面考虑上边界 i )上边界0,1,0===n m l ,0,0,0===z y x T T T将上式代入(4)、(5)、(6)式,得0)(2==hy yx τ 0)(2==h y y σ 0)(2==h y yz τ上式就是简化后的边界条件。
必须强调的是:在考察边界条件时,需将已知的边界坐标值代入表达式。
将应力分量代入上面三式,显然三式成立。
ii )下边界0,1,0=-==n m l ,0,0,0===z y x T T T将上式代入(4)、(5)、(6)式,得0)(2=-=hy yx τ 0)(2=-=h y y σ 0)(2=-=h y yz τ将应力分量代入上面三式,显然三式成立。
- 9 -iii )右边界0,0,1===n m l ,,0=x T )4(222y h J P T y --=0,=z T 应注意:所有的面力都是与坐标正向一致为正。
将上式代入(4)、(5)、(6)式,得0)(==l x x σ)4(2)(22y h J P lx xy --==τ0)(==l x xz τ同样,在检验边界条件时,应该将l x =的值代入,显然三式成立。






1 / 1第一章 绪论 弹性力学基本假设: 1、连续性假设指组成物体的介质充满了物体所占的空间,物体中不存在任何间隙。
2、均匀性假设物体内的每一点都具有相同的力学性质3、各向同性假设。
指物体内一点的各个方向上的力学性质相同。
4、完全弹性假设指物体在载荷作用下发生变形,当这些荷载拆除以后物体能完全恢复到原来的形状和大小,而没有任何残余变形。
5、小变形假设假定物体内各点在载荷作用下所产生的位移远小于物体原来的尺寸,因而应变分量和转角都远小于1。
6、无初应力假设假定物体的初始状态为自然状态,即载荷作用以前物体内没有应力。
第二章 弹性力学的基本方程 平衡微分方程:000yx x zxx xy y zy y yz xz zz F x y z F xyzF x y zτσττστττσ∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂边界条件:()()()x xy xz s x xy y yz s y xz yz z s z l m n T l m n T l m n T στττστττσ++=++=++=斜面应力公式(Cauchy 公式):x x xy zx y xy y zy z xz yz z T l m n T l m n T l m nστττστττσ=++=++=++ 斜截面上的全应力:T υ斜截面上的正应力:x y z T l T m T n υσ=++斜截面上的总剪应力:222T υυυτσ=-几何方程:;;;x yz y xy z xy u w vx y z v u w y z x w v u z x yεγεγεγ∂∂∂==+∂∂∂∂∂∂==+∂∂∂∂∂∂==+∂∂∂物理方程:()()()2(1)1;2(1)1;2(1)1;x x y z xy xy y y x z yzyz z z y x zx zxv v E E v v E E v v E E εσσσγτεσσσγτεσσσγτ⎡⎤⎣⎦⎡⎤⎣⎦⎡⎤⎣⎦+=-+=+=-+=+=-+=体积应变:x y z θεεε=++x =()y z σσσΘ++12Evθ-=Θ 第三章 平面问题的直角坐标解法 平衡方程:00yxx x xy yy F x yF x yτστσ∂∂++=∂∂∂∂++=∂∂ 几何方程:;;x y xy u v u v x y y xεεγ∂∂∂∂===+∂∂∂∂ 边界条件:;x yx x xy y yl m T l m T σττσ+=+=位移边界条件:;xx y yu u u u ==平面应变:22222y xyx xy y xετε∂∂∂+=∂∂∂平面应力:222220;0;0z z zxy x yεεε∂∂∂===∂∂∂ 平面问题应力解:22222x x y y xy F xy F y x x yϕσϕσϕτ∂=-∂∂=-∂∂=-∂∂相容方程:444422420y x x y ϕϕϕ∂∂∂++=∂∂∂∂ 第四章 平面问题的极坐标解法 平衡微分方程:10210r r r r r r F r r r F r r rθθθθθθτσσσθτστθ∂-∂+++=∂∂∂∂+++=∂∂几何方程:1;1r r r r r u u u r r r u u u r r rθθθθθεεθγθ∂∂==+∂∂∂∂=+-∂∂物理方程:()()r 11;2(1)r r r rv v E E v Eθθθθθεσσεσσγτ=-=-+=相容方程:22222211()0r r r r ϕθ∂∂∂++=∂∂∂ 第五章 应力张量=0x xy xzyx y yz zx zy z σστττσστττσσ---。
第二章应力状态分析一、内容介绍弹性力学的研究对象为三维弹性体,因此分析从微分单元体入手,本章的任务就是从静力学观点出发,讨论一点的应力状态,建立平衡微分方程和面力边界条件。
应力状态是本章讨论的首要问题。
由于应力矢量与内力和作用截面方位均有关。
因此,一点各个截面的应力是不同的。
确定一点不同截面的应力变化规律称为应力状态分析。
首先是确定应力状态的描述方法,这包括应力矢量定义,及其分解为主应力、切应力和应力分量;其次是任意截面的应力分量的确定—转轴公式;最后是一点的特殊应力确定,主应力和主平面、最大切应力和应力圆等。
应力状态分析表明应力分量为二阶对称张量。
本课程分析中使用张量符号描述物理量和基本方程,如果你没有学习过张量概念,请进入附录一,或者查阅参考资料。
本章的另一个任务是讨论弹性体内一点-微分单元体的平衡。
弹性体内部单元体的平衡条件为平衡微分方程和切应力互等定理;边界单元体的平衡条件为面力边界条件。
二、重点1、应力状态的定义:应力矢量;正应力与切应力;应力分量;2、平衡微分方程与切应力互等定理;3、面力边界条件;4、应力分量的转轴公式;5、应力状态特征方程和应力不变量;知识点:体力;面力;应力矢量;正应力与切应力;应力分量;应力矢量与应力分量;平衡微分方程;面力边界条件;主平面与主应力;主应力性质;截面正应力与切应力;三向应力圆;八面体单元;偏应力张量不变量;切应力互等定理;应力分量转轴公式;平面问题的转轴公式;应力状态特征方程;应力不变量;最大切应力;球应力张量和偏应力张量§2.1 体力和面力学习思路:本节介绍弹性力学的基本概念——体力和面力,体力F b和面力F s的概念均不难理解。
应该注意的问题是,在弹性力学中,虽然体力和面力都是矢量,但是它们均为作用于一点的力,而且体力是指单位体积的力;面力为单位面积的作用力。
体力矢量用F b表示,其沿三个坐标轴的分量用F b i(i=1,2,3)或者F b x、F b y和F b z表示,称为体力分量。