20181115小学奥数练习卷(知识点:正、反比例)含答案解析
- 格式:docx
- 大小:234.56 KB
- 文档页数:24
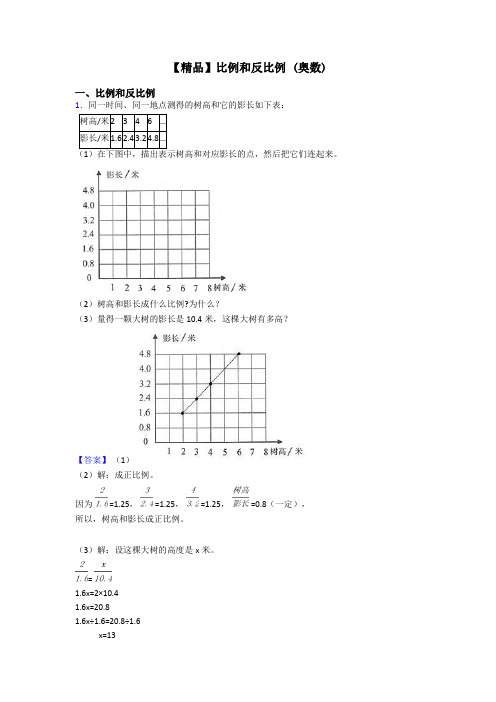
【精品】比例和反比例 (奥数)一、比例和反比例1.同一时间、同一地点测得的树高和它的影长如下表:树高/米2346…影长/米1.62.43.24.8…(2)树高和影长成什么比例?为什么?(3)量得一颗大树的影长是10.4米,这棵大树有多高?【答案】(1)(2)解:成正比例。
因为 =1.25, =1.25, =1.25, =0.8(一定),所以,树高和影长成正比例。
(3)解:设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答:这棵大树的高度是13米。
【解析】【分析】(1)观察统计图可知,横轴表示树高,竖轴表示影长,据此先描点,再连线,据此作图;(2)分别用树高:影长,求出比值,当比值一定时,成正比例,据此判断;(3)根据题意可知,设这棵大树的高度是x米,用树高:影长=树高:影长,据此列正比例解答.2.一辆货车从甲地去相距315千米的乙地送货。
已知前3时行了135千米,如果用同样的速度行完剩下的路程,还要行几时?(用比例解)【答案】解:设还要行x时。
=x =4答:还要行4时。
【解析】【分析】因为速度相同即一定,故路程与时间成正比例,所以,前3小时行的路程:3=剩下的路程:需要的时间,设所需时间为x小时,则可以用这个等量关系列出比例式。
3.某工程队要铺设一条公路,前20天已铺设了2.8千米,照这样计算,剩下的4.2千米,还要多少天才能铺完?(用比例解)【答案】解:设还要x天才能铺完。
2.8∶20=4.2∶xx=30答:还要30天才能铺完。
【解析】【分析】照这样计算的意思就是每天铺的长度不变,铺的长度与天数成正比例,先设出未知数,根据每天铺的长度不变列出比例解答即可。
4.表中x和y是两个成比例的量,观察表格并填完整。
X36181210y51020X361812109y510151820空位中x和y的值。
5.小兰看一本故事书,每天看10页,12天看完,若每天看15页,几天可以看完?【答案】解:设x天可以看完。

小学反比例试题及答案一、说明本文将针对小学反比例试题及答案进行论述,为了使内容清晰易懂,将分为两个部分,第一部分是反比例的基本概念及性质,第二部分是一些常见的小学反比例试题及详细答案解析。
二、反比例的基本概念及性质1. 反比例的定义反比例是指两个量之间的关系,当一个量增大时,另一个量会相应地减小;反之,当一个量减小时,另一个量会相应地增大。
这两个量的乘积是一个常数。
2. 反比例的表示方式反比例可以用以下方式表示:- 两个量的乘积等于一个常数:xy = k(其中x和y为两个变量,k为常数);- 一个量与另一个量的倒数成正比:y = k/x。
3. 反比例的性质- 当x = 0时,y不存在,即在反比例关系中不存在0值;- 当x > 0时,y < 0,即当一个变量增大时,另一个变量必然减小;- 当x < 0时,y > 0,即当一个变量减小时,另一个变量必然增大;- 反比例的图像是一条倾斜的曲线,它在第一象限和第三象限中。
三、小学反比例试题及答案解析以下是一些常见的小学反比例试题及详细答案解析。
题目一:甲工人需要10天完成一项工作,如果增加工人数量到2人,那么需要多少天才能完成这项工作?答案解析:假设2人需要x天完成工作。
由反比例的关系可以得到:10 × 1 = x × 2得到方程10 = 2x,解方程得到x = 5。
因此,2人需要5天完成这项工作。
题目二:某种水果每个包装中有8个,现在有24个包装,需要多少个人能够把这些包装装车?答案解析:假设需要x个人能够把包装装车。
由反比例的关系可以得到:8 × 24 = x × 1得到方程192 = x,解方程得到x = 192。
因此,需要192个人才能将这些包装装车完毕。
题目三:一辆汽车以每小时60千米的速度行驶,到达目的地需要5小时。
如果以80千米每小时的速度行驶,需要多长时间才能到达相同的目的地?答案解析:假设需要x小时才能到达相同的目的地。

小升初数学正比例和反比例专题讲解及训练(含试题与答案)主要内容正比例和反比例学习目标1、使学生结合实际情境认识成正比例和反比例的量,能根据正、反比例的意义判断两种相关联的量是否成正比例或反比例。
2、使学生初步认识正比例的图像是一条直线,能利用给出的具有正比例关系的数据在方格纸上画出相应的直线,能根据具有正比例关系的一个量的数值看图估计另一个量的数值。
3、使学生在认识成正比例、反比例的量的过程中,初步体会数量之间相依互变的关系,感受有效表示数量关系及其变化规律的不同数学模型,进一步提升思维水平。
4、使学生进一步体会数学与日常生活的密切联系,增强探索数学知识和规律的意识,养成积极主动地参与学习活动的习惯,提高学好数学的信心。
考点分析1、两种相关联的量,一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的比的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值,正比例关系可以用这样的式子来表示:xy= K (一定)。
2、用“描点法”可以得到正比例的图像,正比例的图像是一条直线。
对照图像,能根据一种量的值,估计另一种量相对应的值。
3、两种相关联的量,一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。
如果用字母x和y分别表示两种相关联的量,用k表示它们的积,反比例关系可以用这样的式子来表示:xy = K (一定)。
4、两个变量的比值一定,这两个变量成正比例;两个变量的积一定,这两个变量成反比例;没有上述两种关系,这两个变量不成比例。
典型例题例1、(正比例的意义)一列火车行驶的时间和路程如下表。
这两种量有什么关系?分析与解:(1)从上表可以看出,表中有时间和路程两种量。
(2)从左往右看,时间扩大,路程也扩大;从右往左看,时间缩小,路程也缩小。

正反比例应用题及答案正反比例应用题及答案正反比例,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例应用题是反比例的意义和解比例等知识的综合运用。
【数量关系】判断正比例或反比例关系是解这类应用题的关键。
许多典型应用题都可以转化为正反比例问题去解决,而且比较简捷。
【解题思路和方法】解决这类问题的重要方法是:把分率(倍数)转化为比,应用比和比例的性质去解应用题。
正反比例问题与前面讲过的倍比问题基本类似。
例1 修一条公路,已修的是未修的1/3,再修300米后,已修的变成未修的.1/2,求这条公路总长是多少米?解由条件知,公路总长不变。
原已修长度∶总长度=1∶(1+3)=1∶4=3∶12现已修长度∶总长度=1∶(1+2)=1∶3=4∶12比较以上两式可知,把总长度当作12份,则300米相当于(4-3)份,从而知公路总长为300÷(4-3)×12=3600(米)答:这条公路总长3600米。
例2 张晗做4道应用题用了28分钟,照这样计算,91分钟可以做几道应用题?解做题效率一定,做题数量与做题时间成正比例关系设91分钟可以做X应用题则有28∶4=91∶X28X=91×4 X=91×4÷28 X=13答:91分钟可以做13道应用题。
例3 孙亮看《十万个为什么》这本书,每天看24页,15天看完,如果每天看36页,几天就可以看完?解书的页数一定,每天看的页数与需要的天数成反比例关系设X天可以看完,就有24∶36=X∶1536X=24×15 X=10答:10天就可以看完。
例4 一个大矩形被分成六个小矩形,其中四个小矩形的面积如图所示,求大矩形的面积。
解由面积÷宽=长可知,当长一定时,面积与宽成正比,所以每一上下两个小矩形面积之比就等于它们的宽的正比。
又因为第一行三个小矩形的宽相等,第二行三个小矩形的宽也相等。

比例尺和正反比例【知识要点】1.正反比例判断:(商正积反,其它不成比例)两个相关联的量之间的比值(商) 一定,这两个量成正比例;两个相关联的量之间的乘积一定,这两个量成反比例。
2.正反比例应用题3.比例尺=图上距离:实际距离。
【热身训练】( 1) 13× a = 15× b ,那么 a:b =( ) : ( ),( 2)÷=943( )=( ):8=()12 ( 3) a:b = 2:3,b:c = 3:5,则 a:b:c =( ) : ( )∶( )。
( 4)比例尺=( )( ),图上距离=( 实际距离乘以比例尺 ),实际距离=( );如果图上距离一定,实际距离和比例尺成( )比例;如果实际距离一定,图上距离和比例尺成( )比例。
( 5)路程一定,已走的路程和未走的路程( )比例。
( 6)三角形的高一定,它的面积与底( )比例。
( 7) 4x = 7y , x 和 y ( )比例。
( 8)铺地总面积一定,每块方砖的边长与所需的块数( )比例。
(9) 速度一定,路程和时间( ) 比例。
(10) 总价一定,每件商品的价格和所买的数量( ) 比例。
【例题】例 1 一台抽水机 5 小时抽水 40 立方米,照这样计算, 9 小时抽水多少立方米?例 2 某车队运送一批救灾物品,原计划每小时行 60 千米, 6.5 小时到达灾区,实际每小时行了 78 千米,照这样计算,行完全程需要多少小时?例 3 一对互相咬合的齿轮,主动轮有 100 个齿,每分钟转 90 转,要使从动轮每分钟转 300 转,从动轮应有多少个齿?例 4 下午 2: 00 时,小明测得一棵树的影长 1.5 米,同时测得小华的影长 0.5 米。
已知小华的身高为 150 厘米。
( 1)这棵树有多高?( 2)下午 4: 00 时,测得小华的影长为 0.8 米,同时这棵树的影长是多少?练习:一、填空 1.51=3:( )=( ):25=( )%=( )(填小数) 2.比例尺为 1:5000000 的地图,表示实际距离是图上距离的( )倍,也就是图上距离是实际距离的( ),即图上 1 厘米表示实际距离( )千米。

正反比例应用题及答案正反比例应用题及答案正反比例,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
反比例应用题是反比例的意义和解比例等知识的综合运用。
【数量关系】判断正比例或反比例关系是解这类应用题的关键。
许多典型应用题都可以转化为正反比例问题去解决,而且比较简捷。
【解题思路和方法】解决这类问题的重要方法是:把分率(倍数)转化为比,应用比和比例的性质去解应用题。
正反比例问题与前面讲过的倍比问题基本类似。
例1 修一条公路,已修的是未修的1/3,再修300米后,已修的变成未修的.1/2,求这条公路总长是多少米?解由条件知,公路总长不变。
原已修长度∶总长度=1∶(1+3)=1∶4=3∶12现已修长度∶总长度=1∶(1+2)=1∶3=4∶12比较以上两式可知,把总长度当作12份,则300米相当于(4-3)份,从而知公路总长为300÷(4-3)×12=3600(米)答:这条公路总长3600米。
例2 张晗做4道应用题用了28分钟,照这样计算,91分钟可以做几道应用题?解做题效率一定,做题数量与做题时间成正比例关系设91分钟可以做X应用题则有28∶4=91∶X28X=91×4 X=91×4÷28 X=13答:91分钟可以做13道应用题。
例3 孙亮看《十万个为什么》这本书,每天看24页,15天看完,如果每天看36页,几天就可以看完?解书的页数一定,每天看的页数与需要的天数成反比例关系设X天可以看完,就有24∶36=X∶1536X=24×15 X=10答:10天就可以看完。
例4 一个大矩形被分成六个小矩形,其中四个小矩形的面积如图所示,求大矩形的面积。
解由面积÷宽=长可知,当长一定时,面积与宽成正比,所以每一上下两个小矩形面积之比就等于它们的宽的正比。
又因为第一行三个小矩形的宽相等,第二行三个小矩形的宽也相等。
正比例和反比例练习题及答案一、对号入座。
1、35:=20÷16==%=2、因为X=2Y,所以X:Y=:,X和Y成比例。
3、一个长方形的长比宽多20%,这个长方形的长和宽的最简整数比是。
4、向阳小学三年级与四年级人数比是3:4,三年级人数比四年级少% 四年级比三年级多%5、甲乙两个正方形的边长比是2:3,甲乙两个正方形的周长比是,甲乙两个正方形的面积比是。
6、一个比例由两个比值是2的比组成,又知比例的外项分别是1.2和5,这个比例是。
7、已知被减数与差的比是5:3,减数是100,被减数是。
8、在一幅地图上量得甲乙两地距离6厘米,乙丙两地距离8厘米;已知甲乙两地间的实际距离是 120千米,乙丙两地间的实际距离是千米;这幅地图的比例尺是。
9、从2:8、1.6:和:这三个比中,选两个比组成的比例是。
10、一块铜锌合金重180克,铜与锌的比是2:3,锌重克。
如果再熔入30克锌,这时铜与锌的比是。
二、明辨是非。
1、一项工程,甲队40天可以完成,乙队50天可以完成。
甲乙两队的工作效率比是4:5。
2、圆柱体与圆锥体的体积比是3:1,则圆柱体与圆锥体一定等底等高。
3、甲数与乙数的比是3:4,甲数就是乙数的。
4、比的前项和后项同时乘以同一个数,比值不变。
5、总价一定,单价和数量成反比例。
6、实际距离一定,图上距离与比例尺成正比例。
7、正方体体积一定,底面积和高成反比例。
8、订阅《今日泰兴》的总钱数和份数成正比例。
三、选择题。
1、把一个直径4毫米的手表零件,画在图纸上直径是8厘米,这幅图纸的比例尺是。
A、1:B、2:1C、1:20D、20:12、已知=1.2、=1.2,所以X和Y比较。
A、X大B、YC、一样大3、如果A×2=B÷3,那么A:B=。
A、2:B、3:C、1:D:14、一个三角形的三个内角的度数比是2:3:4,这个三角形是。
A、锐角三角形B、直角三角形C、钝角三角形5、体积和高都相等的圆柱体和圆锥体,它们底面积的比是。
苏教版小学数学六年级下册《正、反比例的练习》同步练习及参考答案【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【答案】解:每天步行上学的速度和时间是两种相关联的量,它们与家到学校的距离有下面的关系:速度×时间=家到学校的距离(一定);已知家到学校的距离一定,也就是每天步行上学的速度和时间的乘积一定,所以走路的速度与所用的时间反比例;故答案为:反.【总结】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
二、选择题1.C=πd中,如果c一定,π和d()A.成正比例B.成反比例C.不成比例【答案】:B2.从南京到南通,汽车车轮的直径与转数()A.成正比例B.成反比例C.不成比例【答案】:B3.钟面上分针转动的圈数与天数()A.成正比例B.成反比例C.不成比例【答案】:A三、解答题2.根据表格填空:(1)表中两种相关联的量是()。
(2)当时间扩大时,行驶的路程也随着();当时间缩小时,行驶的路程也随着()。
(3)在变化过程中,()始终没有发生变化。
(4)汽车行驶的时间和路程成()关系。
(5)当汽车行驶8时,路程是()千米,汽车要到600千米的地方,需要()时。
【答案】解:(1)表中两种相关联的量是汽车行驶的时间和汽车行驶的路程。
(2)当时间扩大时,行驶的路程也随着扩大;当时间缩小时,行驶的路程也随着缩小.(3)在变化过程中,速度始终没有发生变化。
(4)汽车行驶的时间和路程成正比例关系。
(5)当汽车行驶8时时,路程是:240÷3×8=640千米,汽车要到600千米的地方,需要:600÷(240÷3)=7.5时。
故答案为:汽车行驶的时间和汽车行驶的路程,扩大,缩小,速度,正比例,640,7.5。
六年级下册数学试题-第四单元《正反比例》(含解析)北师大版《正反比例》是六年级下册数学试题的第四单元,本单元主要涉及正比例、反比例等概念和解题方法。
通过学习本单元的内容,同学们将能够掌握解决正反比例问题的基本方法,提高数学解题能力。
本文将以简洁明了的方式,逐步介绍本单元试题及其解析。
一、正比例正比例是指两个量之间的变化关系是成正比的。
当一个量的值增加(或减少)的同时,另一个量的值也按照一定比例增加(或减少)。
1. 试题一已知两个正比例关系的量分别是x和y,当x=4时,y=8;当x=6时,y=12。
当x=10时,y等于多少?解析:我们可以根据已知的两个点(4,8)和(6,12)计算出这两个点所代表的斜率:斜率 = (y2 - y1) / (x2 - x1)= (12 - 8) / (6 - 4)= 4 / 2= 2由此可知,斜率为2。
根据比例关系,我们可以得到以下等式:y = kx代入已知的点(4,8),得到:8 = 4kk = 2再代入x=10,解出y:y = 2 * 10y = 20所以,当x=10时,y等于20。
2. 试题二已知量A和量B成正比,当A=3时,B=7;当A=9时,B=21。
则当A=6时,B等于多少?解析:同样地,我们可以通过已知的两个点(3,7)和(9,21)计算斜率:斜率 = (21 - 7) / (9 - 3)= 14 / 6= 7 / 3由此可知,斜率为7/3。
根据比例关系,我们可以得到以下等式:B = (7/3)A代入已知的A=6,解出B:B = (7/3) * 6B = 14所以,当A=6时,B等于14。
二、反比例反比例是指两个量之间的变化关系是成反比的。
当一个量的值增加(或减少)的同时,另一个量的值按照其倒数的比例减少(或增加)。
3. 试题三已知两个反比例关系的量分别是x和y,当x=2时,y=6;当x=5时,y=2。
当x=7时,y等于多少?解析:我们可以根据已知的两个点(2,6)和(5,2)计算出这两个点所代表的斜率:斜率 = (2 - 6) / (5 - 2)= -4 / 3由此可知,斜率为-4/3。
正比例和反比例习题精选一、判断.1.一个因数不变,积与另一个因数成正比例.()2.长方形的长一定,宽和面积成正比例.()3.大米的总量一定,吃掉的和剩下的成反比例.()4.圆的半径和周长成正比例.()5.分数的分子一定,分数值和分母成反比例.()6.铺地面积一定,方砖的边长和所需块数成反比例.()7.铺地面积一定,方砖面积和所需块数成反比例.()8.除数一定,被除数和商成正比例.()二、选择.1.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量.()A.成正比例B.成反比例C.不成比例2.和一定,加数和另一个加数.()A.成正比例B.成反比例C.不成比例3.在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成正比例关系是(),成反比例关系是().A.汽车每次运货吨数一定,运货次数和运货总吨数.B.汽车运货次数一定,每次运货的吨数和运货总吨数.C.汽车运货总吨数一定,每次运货的吨数和运货的次数.三、填空.1.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成正比例的量,它们的关系叫做(),关系式是().2.两种()的量,一种量变化,另一种量(),如果这两种量中()的两个数的()一定,这两种量就叫做成反比例的量,它们的关系叫做(),关系式是().3.一房间铺地面积和用砖数如下表,根据要求填空.铺地面积(平方米)1 2 3 4 5用砖块数25 50 75 100 125(1)表中()和()是相关联的量,()随着()的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(),比值是();第五组这两种量相对应的两个数的比是(),比值是().(3)上面所求出的比值所表示的的意义是(),铺地面积和砖的块数的()是一定的,所以铺地面积和砖的块数().4.练习本总价和练习本本数的比值是().当()一定时,()和()成()比例.二、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.2.被除数一定,商和除数.3.小明的年龄和他的体重.4.天数一定,生产零件的总个数和每天生产零件的个数.三、思考.、、三种量的关系是:×=1.如果一定,那么和成()比例;2.如果一定,那么和成()比例;3.如果一定,那么和成()比例.参考答案一、判断.(√)(√)(×)(√)(√)(×)(√)(√)二、选择.1.(B )2.(C )3.(C ).1.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(比值)一定,这两种量就叫做成正比例的量,它们的关系叫做(正比例关系),关系式是((一定)).2.两种(相关联)的量,一种量变化,另一种量(随着变化),如果这两种量中(相对应)的两个数的(积)一定,这两种量就叫做成反比例的量,它们的关系叫做(反比例关系),关系式是((一定)).(1)表中(铺地面积)和(用砖块数)是相关联的量,(用砖块数)随着(铺地面积)的变化而变化.(2)表中第三组这两种量相对应的两个数的比是(75∶3),比值是(25);第五组这两种量相对应的两个数的比是(125∶5),比值是(25).(3)上面所求出的比值所表示的的意义是(每平方米用砖块数),铺地面积和砖的块数的(比值)是一定的,所以铺地面积和砖的块数(正比例).4.练习本总价和练习本本数的比值是(练习本单价).当(练习本单价)一定时,(练习本总价)和(练习本本数)成(正)比例.二、判断下面每题中的两种量是不是成比例,成什么比例,并说明理由.1.平行四边形的高一定,它的底和面积.理由:因为,高一定,就是平行四边形面积与底的比值一定.所以,平行四边形的面积与底成正比例.2.被除数一定,商和除数.理由:因为被除数一定,就是商和除数的乘积一定,所以,商和除数成反比例.3.小明的年龄和他的体重.理由:小明的年龄和他的体重虽然也是一对相关联的量,但是这两个量的变化并没有什么规律,找不出哪个是不变量,所以,小明的年龄和他的体重不成比例.4.天数一定,生产零件的总个数和每天生产零件的个数.理由:因为,天数一定,就是生产零件的总个数和每天生产零件的个数的比值一定,所以,生产零件的总个数和每天生产零件的个数成正比例.三、思考.、、三种量的关系是:×=1.如果一定,那么和成(正)比例;2.如果一定,那么和成(正)比例;3.如果一定,那么和成(反)比例.。
小学奥数练习卷(知识点:正、反比例)第Ⅰ卷(选择题)一.选择题(共1小题)1.用方砖铺地,当铺地面积一定时,方砖的边长和所需方砖块数的关系是()A.正比例关系B.反比例关系C.不成比例关系D.不能确定第Ⅱ卷(非选择题)二.填空题(共12小题)2.如图,将1个大长方形分成了9个小长方形,其中位于角上的3个小长方形的面积分别为9,15和12,由第4个角上的小长方形的面积等于.3.如图,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形是.4.有两条绳子,它们的长度相等,但粗细不同.如果从两条绳子的一端点燃,细绳子40分钟燃尽,粗绳子120分钟燃尽,一次两条同时点燃,经过一段时间后,又同时把它们熄灭,这时量得细绳子还有10厘米没有燃尽,粗绳子还有30厘米没燃尽.这两条绳子原来的长度是厘米.5.如图,一个矩形被分成八个小矩形,其中有五个小矩形的面积如图数字所示,那么这个大矩形面积是.6.亨亨用100张贴纸把他的桌面贴满.莎莎的一张贴纸面积只有亨亨的一张贴纸面积的一半,而她的桌面面积则为亨亨的桌面面积的2倍.那么莎莎最少要用她的贴纸张才能把她的桌面贴满.7.如图所示,一块长方形地被两条直线分成四个小长方形,其中三个的面积分别是20平方米、25平方米、40平方米,问:另一个小长方形的面积(阴影部分)是平方米.8.某平行四边形花圃里种植四种不同颜色的鲜花,现需将该花圃划分成四块平行四边形小花圃(如图),已知其中三块花圃的面积分别是10平方米,24平方米,36平方米,则第四块小花圃的面积是平方米.9.小兰的身高是1.5米,她的影长是2.4米,如果同一时间,同一地点,测得一棵树的影长时,因树靠近一段围墙,影长不全落在地上,有一部分落在墙上,她测得落在地面上的影长是3.2米,留在墙上的影高是0.5米,这棵树的高度是米.10.一块长方形地用两条直线分成四块长方形地,其中三块长方形面积分别是12,18,30平方米,第四块面积是平方米.11.有一只刻度均匀但不准确的温度计,将它放在100摄氏度的沸水中,示数为99摄氏度;将它放在0摄氏度的冰水中,示为数为4摄氏度,则将它放在25摄氏度的教室中,示数为.12.的分子分母减去同一数之后为,则减去的数是.13.小明利用暑假到一家自行车厂勤工俭学,讲好了干7个星期,老板给他一辆自行车外加200元作报酬,后因他只做了4个星期,老板给了他一辆自行车外加20元钱的报酬,则一辆自行车的价值是元.三.解答题(共14小题)14.如图,半径分别是15厘米、10厘米、5厘米的圆形齿轮A、B、C为某传动机械的一部分,A匀速转动后带动B匀速转动,而后带动C匀速转动,请问:(1)当A匀速顺时针转动,C是顺时针转动还是逆时针转动?(2)当A转动一圈时,C转动了几圈?15.在下午时分,小强在泥地上量度得某大厦的影子的长度是10米.小强实时把一根长35厘米的木棍的七份之一插入泥中,使木棍垂直竖立在大厦前面的地上,小强量度得木棍的影子的长度是5厘米.小强利用这些数据准确计算得大厦的高度是d米,求d的值.16.小华登山,从山脚到途中A点的速度是千米/时,从A点到山顶的速度是2千米/时.他到达山顶后立即按原路下山,下山速度是4千米/时,下山比上山少用了小时.已知途中B点到山顶的路程比A点到山顶的路程少500米,且小华从A点开始上山至下山到达B点恰好用了1小时.问:从山脚到山顶的路程是多少千米?17.一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩.问另一个长方形的面积是多少亩?18.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.(1)大齿轮和小齿轮在同一时间内转动时,哪个齿轮转得更快?哪个齿轮转的圈数最多?(2)转过的总齿数一定时,每个齿轮的齿数和转过的圈数是什么关系?(3)大齿轮40个齿,小齿轮24个齿,如果大齿轮每分钟转90圈,小齿轮每分钟转多少圈?19.要加工600个零件,师傅先做了2个小时,徒弟接着做了9个小时,正好完成任务.已知师傅1小时加工零件个数正好等于徒弟3小时加工的零件个数,求师傅和徒弟每小时各加工零件多少个?20.植物园里菊花与月季花的盆数之比是3:4,兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.如果月季比兰花多50多盆,那么菊花比郁金香少多少盆?21.已知猫跑5步的路程与狗跑3步的路程相同,猫跑7步的路程与兔跑5步的路程相同.而猫跑3步的时间与狗跑5步的时间相同,猫跑5步的时间与兔跑7步的时间相同,求猫、狗和兔的速度之比.22.从一块铜板上剪下半径4分米和半径2分米的两个圆形的铜片.半径4分米的铜片重600克,半径2分米的铜片重多少克?23.甲、乙、丙三个齿轮的齿数分别为28个、20个、35个.它们互相咬合,当甲转动5圈时,乙、丙两齿轮各转多少圈?24.将一个大长方形如图分割为16个小长方形.图上已标出部分小长方形的面积.那么,阴影小长方形的面积是多少?25.甲庙宇供奉一尊高为l公尺的菩萨,信众们为菩萨上金身(用黄金涂在菩萨像的全部表面),共用了黄金3公斤.乙庙宇不甘示弱,也拟为其供奉的一尊高为l0公尺,外形完全相似的菩萨上金身.若涂在菩萨身上黄金的厚度全部都相同,请问乙庙宇需用黄金多少公斤?26.如图,长方形ABCD,ABEF,AGHF的长与宽的比相同,且,长方形BEHG的周长是22,求长方形ECDF的面积.27.一堆糖果,分给大、小幼儿班,每人可得6块;只分给大班,每人可得10块.若只分给小班,则每人可得几块?参考答案与试题解析一.选择题(共1小题)1.用方砖铺地,当铺地面积一定时,方砖的边长和所需方砖块数的关系是()A.正比例关系B.反比例关系C.不成比例关系D.不能确定【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.【解答】解:方砖面积×方砖块数=铺地的总面积(一定),可以看出,每块方砖的面积与方砖块数成反比例关系,而每块方砖的面积等于边长的平方,也就是说,铺地的方砖的面积一定时方砖的块数只是与方砖边长的平方成比例关系,与边长不成比例关系.故选:C.【点评】此题重点考查正比例和反比例的意义.二.填空题(共12小题)2.如图,将1个大长方形分成了9个小长方形,其中位于角上的3个小长方形的面积分别为9,15和12,由第4个角上的小长方形的面积等于20.【分析】设D的面积为x,因为A和B,C和D的长一定,所以A和B,C和D 的面积之比相等,于是有9:12=15:x,解比例即可.【解答】解:如图,设D的面积为x,9:12=15:x9x=12×15x=x=20答:第4个角上的小长方形的面积等于20.故答案为:20.【点评】此题解答的关键在于根据“A和B,C和D的长一定”,推出A和B,C和D的面积之比也相等.3.如图,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形是EFGH.【分析】如图所示,小正方形的面积之和为30时,两正方形的面积差最小,则大正方形的面积越大,据此即可求解.【解答】解:小正方形的面积之和为30时,两正方形的面积差最小,则大正方形的面积越大,即EFGH的面积较大;故答案为:EFGH.【点评】采用极端思想,求得大正方形的面积较大,是解答本题的关键.4.有两条绳子,它们的长度相等,但粗细不同.如果从两条绳子的一端点燃,细绳子40分钟燃尽,粗绳子120分钟燃尽,一次两条同时点燃,经过一段时间后,又同时把它们熄灭,这时量得细绳子还有10厘米没有燃尽,粗绳子还有30厘米没燃尽.这两条绳子原来的长度是40厘米.【分析】因为粗,细两条绳子的长度相等,细绳子40分钟可以燃尽,而粗绳子120分钟才燃尽,所以在时间相同的情况下细绳子燃尽3份,粗绳子燃尽1份,则2份为30﹣10=20(厘米),每份为10厘米,绳子原长为30+10=40(厘米).【解答】解:120:40=3:1,(30﹣10)÷(3﹣1)×4,=20÷2×4,=10×4,=40(厘米);答:这两条绳子原来的长度是40厘米.故答案为:40.【点评】此题较抽象,应认真分析,根据题意进行推导,得出:在时间相同的情况下细绳子燃尽3份,粗绳子燃尽1份,依此为突破口,进行解答.5.如图,一个矩形被分成八个小矩形,其中有五个小矩形的面积如图数字所示,那么这个大矩形面积是198.【分析】由长方形的面积=长×宽,可知等宽的两个长方形面积的比等于长的比,根据这个等量关系列出算式求解.【解答】解:根据长方形的性质,第一块面积为:20×(36÷16)=45第七块面积为:16×(30÷20)=24;第四块面积为:30×(12÷24)=15;大长方形的面积为:45+20+30+15+36+16+24+12=198;如图故答案为:198.【点评】此题主要是找到等宽的两个长方形,根据面积的比等于长的比进行求解.6.亨亨用100张贴纸把他的桌面贴满.莎莎的一张贴纸面积只有亨亨的一张贴纸面积的一半,而她的桌面面积则为亨亨的桌面面积的2倍.那么莎莎最少要用她的贴纸400张才能把她的桌面贴满.【分析】根据题意,把亨亨的每张贴纸的面积看作单位“1”,则莎莎的一张贴纸面积为“”,亨亨的桌面面积为1×100=100,因为她的桌面面积则为亨亨的桌面面积的2倍,那么莎莎的桌面面积为200,因此莎莎最少要用贴纸200÷,解决问题.【解答】解:1×100×2÷=200×2=400(张)答:莎莎最少要用她的贴纸400张才能把她的桌面贴满.故答案为:400.【点评】此题解答的关键在于把亨亨的每张贴纸的面积看作单位“1”,表示出莎莎的一张贴纸面积,根据亨亨的桌面面积,求得莎莎的桌面面积,进而解决问题.7.如图所示,一块长方形地被两条直线分成四个小长方形,其中三个的面积分别是20平方米、25平方米、40平方米,问:另一个小长方形的面积(阴影部分)是50平方米.【分析】由长方形的面积=长×宽,可知等宽的两个长方形面积的比等于长的比,根据这个等量关系列出比例求解即可.【解答】解:根据长方形的性质,得20和25所在的长方形的长的比是4:5.设要求的第四块的面积是x平方厘米,则40:x=4:5,x=50;所以阴影部分的面积是50平方米.故答案为:50.【点评】此题主要是找到等宽的两个长方形,根据面积的比等于长的比进行求解.8.某平行四边形花圃里种植四种不同颜色的鲜花,现需将该花圃划分成四块平行四边形小花圃(如图),已知其中三块花圃的面积分别是10平方米,24平方米,36平方米,则第四块小花圃的面积是15平方米.【分析】平行四边形的面积=底×高,若高一定,则平行四边形的面积与底的比值一定,即平行四边形的面积和底成正比例关系,据此即可列比例求解.【解答】解:设第四小块花圃的面积是x平方米,则10:x=24:36,24x=36×10,x=,x=15,答:第四小块花圃的面积是15平方米.故答案为:15.【点评】解答此题的关键是弄清楚哪两种量成何比例,于是即可列比例求解.9.小兰的身高是1.5米,她的影长是2.4米,如果同一时间,同一地点,测得一棵树的影长时,因树靠近一段围墙,影长不全落在地上,有一部分落在墙上,她测得落在地面上的影长是3.2米,留在墙上的影高是0.5米,这棵树的高度是 2.5米.【分析】根据题意知道,同一时间,同一地点测得物体的高度与影子的长度的比值一定,即物体的高度与影子的长度成正比例,由此设出这棵树在地面上的影子对应的树的实际高度,列出比例求出地面上的影子对应的树的高度,再加上墙上的影子的长度就是这棵树的高度.【解答】解:设这棵树在地面上的影子对应的实际高度为x米,1.5:2.4=x:3.2,2.4x=1.5×3.2,x=,x=2,2+0.5=2.5(米),答:这棵数的高度是2.5米.故答案为:2.5.【点评】注意此题中树的影子分为两部分,一部分在地面,一部分在墙上,计算树的实际高度时,算出地面上的影子对应的实际高度再加上墙上的影子的长度就是树的实际高度.10.一块长方形地用两条直线分成四块长方形地,其中三块长方形面积分别是12,18,30平方米,第四块面积是45平方米.【分析】设最小的长方形的长为a,则宽为,则可以用a分别出面积为18和30平方米的边长,从而据此求出第四块的面积.【解答】解:设最小的长方形的长为a,则宽为,则第四块地的面积:×(18÷),×a,=45(平方米);答:第四块面积是45平方米.故答案为:45.【点评】解答此题的关键是:用已知面积的长方形的边长表示出第四块地的边长,从而求出其面积.11.有一只刻度均匀但不准确的温度计,将它放在100摄氏度的沸水中,示数为99摄氏度;将它放在0摄氏度的冰水中,示为数为4摄氏度,则将它放在25摄氏度的教室中,示数为27.75摄氏度.【分析】将温度计放在100摄氏度的沸水中,示数为99摄氏度;将它放在0摄氏度的冰水中,示为数为4摄氏度,则说明温度计的每个刻度所表示的温度是(99﹣4)÷100,把它放在25摄氏度的教室中,示数则为4+25×[(99﹣4)÷100],(4为起始温度所以加上),然后计算即可.【解答】解:4+25×[(99﹣4)÷100],=4+25×0.95,=27.75(摄氏度).故答案为:27.75摄氏度.【点评】刻度均匀但不准确,则找出100度在它的显示是多少个刻度,算出他的一个刻度是正确的多少度,然后在进行计算.12.的分子分母减去同一数之后为,则减去的数是19.【分析】设减去的数为x,则根据题意得出,=,再根据比例的性质(即内项之积等于外项之积),解比例即可得出答案.【解答】解:设减去的数为x,=,(71﹣x)×3=(97﹣x)×2,213﹣3x=194﹣2x,x=19,答:减去的数是19.故答案为:19.【点评】解答此题的关键是,根据题意设出未知数,再根据数量关系,列出比例式,解比例即可.13.小明利用暑假到一家自行车厂勤工俭学,讲好了干7个星期,老板给他一辆自行车外加200元作报酬,后因他只做了4个星期,老板给了他一辆自行车外加20元钱的报酬,则一辆自行车的价值是220元.【分析】因为他的日工资是不变的,据此可列方程求解.【解答】解:设自行车的价值是x元,,49x+980=28x+5600,21x=4620,x=220,答:一辆自行车的价值是220元.【点评】此题关键是利用日工资是不变,即可用方程求解.三.解答题(共14小题)14.如图,半径分别是15厘米、10厘米、5厘米的圆形齿轮A、B、C为某传动机械的一部分,A匀速转动后带动B匀速转动,而后带动C匀速转动,请问:(1)当A匀速顺时针转动,C是顺时针转动还是逆时针转动?(2)当A转动一圈时,C转动了几圈?【分析】(1)互助啮合的两个齿轮转动方向是相反的,B与A转动的方向相反,C又与B转动的方向相反,即C与A转动的方向一致.(2)互助啮合的两个齿轮其半径(或直径或周长)与转速成反比,由A、B、C 的直径即可确定当A转动一圈时,C转动了几圈.【解答】解:(1)如图,答:当A匀速顺时针转动,C是顺时针转动.(2)A:B:C=15:10:5=3:2:1答:当A转动一圈时,C转动了3圈.【点评】互助啮合的两个齿轮或交叉皮带链接的两个轮,转动方向都相反,平行皮带链接的两个轮转动方向相同,不论哪种情况,轮半径(或直径或周长)与转速成反比.15.在下午时分,小强在泥地上量度得某大厦的影子的长度是10米.小强实时把一根长35厘米的木棍的七份之一插入泥中,使木棍垂直竖立在大厦前面的地上,小强量度得木棍的影子的长度是5厘米.小强利用这些数据准确计算得大厦的高度是d米,求d的值.【分析】同一时刻、同一地方每米物体的影长一定的,则物体的影长和物体实际长度成正比例,列比例解答即可.【解答】解:35厘米=0.35米,0.35×=0.05(米),由题意可得:10:d=0.05:(0.35﹣0.05)0.05d=10×0.3d=60.答:d为60米.【点评】此题首先判定两种量成正比例,然后列出比例式进行解答即可.16.小华登山,从山脚到途中A点的速度是千米/时,从A点到山顶的速度是2千米/时.他到达山顶后立即按原路下山,下山速度是4千米/时,下山比上山少用了小时.已知途中B点到山顶的路程比A点到山顶的路程少500米,且小华从A点开始上山至下山到达B点恰好用了1小时.问:从山脚到山顶的路程是多少千米?【分析】如图:可以看到AB相距0.5千米,“小华从A点开始上山至下山到达B 点恰好用了1小时”我们不妨让小华下山也走到A点,这样一共走了1+0.5÷4=小时,因为从A点上山与从山顶到A点路程相同,根据反比例的意义,上山与下山的速度比是2:4=1:2,因此上山与下山的时间比是2:1,把按2:1分配,上山用了小时,可得出从A点上山路是2×=1.5千米;可算出A点上山顶与山顶到A点所用的时间差为:1.5÷2=小时,1.5÷4=小时,﹣=小时,因此﹣=小时的时间差是在行山脚与A点这段路程中产生的.这段路程中上、下山的速度比是:4=2:3,则时间比为3:2,而时间差为小时,可见3份与2份差1份是小时,因此上山的3份时间是小时,×=4千米,也可求得结果为5.5千米.【解答】解:如图:500米=0.5千米,1+0.5÷4=小时,上山与下山的速度比是2:4=1:2,因此上山与下山的时间比是2:1,2+1=3,1×=(小时),1×=(小时),得出从A点上山路是2×=1.5千米;1.5÷2﹣1.5÷4=小时,下山的速度比是:4=2:3,则时间比为3:2,(﹣)÷(3﹣2)×3×2+1.5,=1.5×+1.5,=5.5(千米);答:从山脚到山顶的路程是5.5千米.【点评】此题属于较复杂的行程问题,解答此题应认真分析、进行分段解答:先求出山脚到A的路程,然后求出A到山顶的路程,然后相加即可.17.一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩.问另一个长方形的面积是多少亩?【分析】由长方形的面积=长×宽,可知等宽的两个长方形面积的比等于长的比,根据这个等量关系列出比例求解即可.【解答】解:根据长方形的性质,得25和20所在的长方形的长的比是5:4,设要求的第三块的面积是x亩,则x:30=5:4,解得:x=37.5;答:另一个长方形的面积是37.5亩.【点评】此题主要是找到等宽的两个长方形,根据面积的比等于长的比进行求解.18.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.(1)大齿轮和小齿轮在同一时间内转动时,哪个齿轮转得更快?哪个齿轮转的圈数最多?(2)转过的总齿数一定时,每个齿轮的齿数和转过的圈数是什么关系?(3)大齿轮40个齿,小齿轮24个齿,如果大齿轮每分钟转90圈,小齿轮每分钟转多少圈?【分析】(1)根据在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的;(2)根据每个齿轮的齿数和转过的圈数成反比即可求解;(3)可设小齿轮每分钟转x圈,根据等量关系:在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,列出方程求解即可.【解答】解:(1)大齿轮和小齿轮在同一时间内转动时,两个齿轮转得一样快,小齿轮转的圈数最多;(2)转过的总齿数一定时,每个齿轮的齿数和转过的圈数是反比关系;(3)设小齿轮每分钟转x圈,依题意有24x=40×90解得x=150答:小齿轮每分钟转150圈.【点评】考查了正、反比例的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.19.要加工600个零件,师傅先做了2个小时,徒弟接着做了9个小时,正好完成任务.已知师傅1小时加工零件个数正好等于徒弟3小时加工的零件个数,求师傅和徒弟每小时各加工零件多少个?【分析】根据题意可知:师傅和徒弟每小时加工零件个数的比是3:1,设徒弟做了9个小时,相当于师傅做了x个小时,然后列出比例,求出相当于师傅做的时间,进而求出师傅独做所需的时间,用600除以师傅独做所需的时间,即可求出师傅每小时加工零件的个数,然后用师傅每小时加工零件的个数除以3,可以求出徒弟每小时加工零件的个数.【解答】解:设徒弟做了9个小时,相当于师傅做了x个小时,则:9:x=3:1x=3师傅每小时加工:600÷(3+2)=120(个)徒弟每小时加工:120÷3=40(个)答:师傅每小时加工120个,徒弟每小时加工零件40个.【点评】此题比较简单,根据师傅和徒弟每小时加工零件个数的比是3:1,设出未知数,列出方程,求出徒弟做了9个小时,相当于师傅做的时间,是解答此题的关键.20.植物园里菊花与月季花的盆数之比是3:4,兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.如果月季比兰花多50多盆,那么菊花比郁金香少多少盆?【分析】兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.我们设郁金香有x盆,则兰花有x盆,菊花有x盆.又菊花与月季花的盆数之比是3:4,所以月季有×(x)盆.根据月季比兰花多50多盆,列出方程50<×(x)﹣x<60,解出x,然后再求出菊花的盆数,用郁金香的盆数减去菊花的盆数即可.【解答】解:设郁金香有x盆,月季比兰花多m盆.且50<m<60根据题意得:×(x)﹣x=mx﹣x=mx=mx=因为x代表花的盆数,不能是分数,30不能被7整除.所以m应是7的倍数,有50<m<60,所以m=56.x===240(盆)x﹣x=240﹣×240=240﹣192=48(盆)答:菊花比郁金香少48盆.【点评】本题含有多个未知数,要设其中的一个,然后用含x的代数式,表示出另外几个,根据题目中的等量关系列出方程解答.21.已知猫跑5步的路程与狗跑3步的路程相同,猫跑7步的路程与兔跑5步的路程相同.而猫跑3步的时间与狗跑5步的时间相同,猫跑5步的时间与兔跑7步的时间相同,求猫、狗和兔的速度之比.【分析】设猫每一步跑x米,5步就是5x米,7步就是7x米那么,狗3步跑5x 米,每一步跑米;兔5步跑7x米,每一步跑米.设猫跑一步的时间为t秒,3步就是3t秒,5步就是5t秒那么,狗跑5步时间是3t秒,每一步的时间是秒;兔跑7步的时间是5t秒,每一步的时间是秒.由此表示出猫、狗、兔的速度,再作比化简即可.【解答】解:设猫每一步跑x米,5步就是5x米,7步就是7x米那么,狗3步跑5x米,每一步跑米;兔5步跑7x米,每一步跑米.设猫跑一步的时间为t秒,3步就是3t秒,5步就是5t秒那么,狗跑5步时间是3t秒,每一步的时间是秒;兔跑7步的时间是5t秒,每一步的时间是秒.猫的速度为,狗的速度为÷=×=,兔的速度为=猫:狗:兔=::=225:625:441答:猫、狗和兔的速度之比是225:625:441.【点评】本题设出数据表示出三者的速度,再作比,化简即可求解.22.从一块铜板上剪下半径4分米和半径2分米的两个圆形的铜片.半径4分米的铜片重600克,半径2分米的铜片重多少克?【分析】因为是同一物体,所以体积的比即重量的比,因为是从一块铜板上剪下,即高度一样,所以面积的比即重量的比,由此列出比例式,解答即可.【解答】解:设半径2分米的铜片重x克,则:600:x=(3.14×42):(3.14×22)600:x=4:1x=150答:半径2分米的铜片重150克.【点评】此题考查了正、反比例,明确面积的比即重量的比,是解答此题的关键.23.甲、乙、丙三个齿轮的齿数分别为28个、20个、35个.它们互相咬合,当甲转动5圈时,乙、丙两齿轮各转多少圈?【分析】因为齿数×圈数=转过的总齿数(一定),所以齿数与圈数成反比例,得出甲乙齿轮所转圈数比为20:28,甲丙齿轮所转圈数比为35:28,再依条件即可求出乙齿轮转的圈数和丙齿轮转的圈数.【解答】解:甲乙齿轮所转圈数比为20:28=5:7,乙:5÷5×7=7(圈);甲丙齿轮所转圈数比为35:28=5:4,丙:5÷5×4=4(圈);答:乙齿轮转7圈,丙齿轮转4圈.【点评】解答此题的关键是理解互相咬合的两个齿轮转过的总齿数一定,齿数与圈数成反比例,由此进一步解决问题.24.将一个大长方形如图分割为16个小长方形.图上已标出部分小长方形的面积.那么,阴影小长方形的面积是多少?。