小学数学五年级下册第二单元《长方体的表面积》课时练习

长方体和正方体的总棱长、表面积和体积公式专练长方体和正方体都有：12条棱、6个面、8个顶点长方体的总棱长= （长+宽+高）× 4 （单位：长度单位）正方体的总棱长= 棱长× 12 （单位：长度单位）长方体的表面积=（长×宽 + 长×高 + 宽×高）×2（单位：平方单位）长方体的体积= 长×宽×高字母表示：V = abh（单位：立方单位）正方体的表面积=（棱长×棱长）×6（单位：平方单位）正方体的体积= 棱长×棱长×棱长字母表示：V= a3（单位：立方单位）长方体（或正方体）的体积= 底面积×高字母表示：V=sh（单位：平方单位）无盖的盒子的表面积=长×宽 +（长×高 + 宽×高）×2（只算一个底面）面积单位的换算：1平方厘米＝100平方毫米; 1平方分米=100平方厘米;1平方米＝100平方分米; 1公倾＝10000平方米；1平方公里＝100公顷体积单位：1立方米=1000立方分米； 1立方分米=1000立方厘米容积单位：1升=1000毫升； 1升=1立方米； 1毫升=1立方厘米1立方分米=1升； 1立方厘米=1毫升； 1立方米=1000升；应用题类型：（1）教室粉刷墙面，求总面积，应用以上公式计算。

（要除去一个底面）（2）测量不规则物体的体积用排水法：水面上升的高度×容器底面积 = 物体的体积（3）表面积的变化要会分析：长方体或正方体被锯开后，一次会增加两个面；反之，两个相同，体或长方体拼在一起，一次会减少两个面。

1、把一个长方体的小木块截成两段，就成了两个完全相等的正方体，于是这两个正方体的棱长之和比原来那个长方体的棱长之和增加40厘米，原来那个长方体的面积是多少平方厘米？解：截成各正方体的棱长为：40÷8=5（厘米）原长方体的长为：5×2=10（厘米）原长方体的表面积为：10×5×4+5×5×2=250（平方厘米）2、把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体截成两个长方体，使这两个长方体表面积之和最大，这时表面积之和是多少平方厘米？解：（7×6＋7×5＋6×5）×2＋7×6×2=（42+35+30）×2＋7×6×2=107×2＋84=298（平方厘米）3、在棱长为10厘米的正方体玻璃缸内装满水，然后将这些水倒入长20厘米、宽10厘米的长方体玻璃缸内，这个玻璃缸内水深多少厘米？（玻璃厚度忽略不计）解：10×10×10=1000（立方厘米）1000÷20÷10=5（厘米）4、将一个表面涂有红色的长方体分割成若干个体积为1立方厘米的小正方体，其中一点红色都没有的小正方体只有5块。

五年级下册数学一课一练长方体的表面积4∣北师大版2021秋3. 长方体的外表积1.填空。

〔1〕长方体或正方体6个面的〔〕叫做它的外表积。

〔2〕正方体是由〔〕个完全相反的〔〕围成的平面图形，正方体有〔〕条棱，它们的长度都〔〕，正方体有〔〕个顶点。

〔3〕一个长2分米、宽3分米、高是的1分米的长方体，它的占空中积最小是〔〕平方分米，最大是〔〕平方分米。

〔4〕由于正方体是长、宽、高都〔〕的长方体，所以正方体是〔〕的长方体。

2.选择。

〔把正确答案的序号填在括号里〕〔1〕一个长方体无盖鱼缸的长是30厘米，宽20厘米，高25厘米，这个鱼缸的用料是〔〕。

A. 21平方厘米B.31平方分米C.31平方厘米〔2〕用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的外表积是〔〕。

A.添加了B.增加了C.没有变〔3〕长方体的大小由〔〕决议。

A、长B、宽C、高D、长、宽、高〔4〕一个正方体的棱长之和为24分米，它的外表积是〔〕。

A.6平方分米B.24平方分米C.48平方分米3.求下面各图的外表积。

(单位：分米)4.将一个横截面是正方形的长方体平均截成2段，每段长3厘米，外表积添加了32平方厘米，这个长方体原来的外表积是多少？5.一个底面是正方形的长方体，一切棱长的和是60厘米，它的高是7厘米，这个长方体的外表积是多少平方厘米？6.一间教室长8米、宽7米，高3米，如今要用涂料粉刷它的四壁和顶棚。

假设扣除门、窗和黑板30平方米，求要粉刷的面积有多大？假设每平方米用涂料0.2千克，一共需求多少千克涂料？【参考答案与解析】1.〔1〕总面积；〔2〕6 正方体 12 相等 8 ；〔3〕2 6 〔解析：占空中积值得是底面积〕；〔4〕相等特殊；2.〔1〕B；〔2〕B；〔3〕A；〔4〕B；3. 136平方厘米 150平方厘米。

4. 128平方厘米。

5. 144平方厘米。

6. 146平方米 29.2千克。

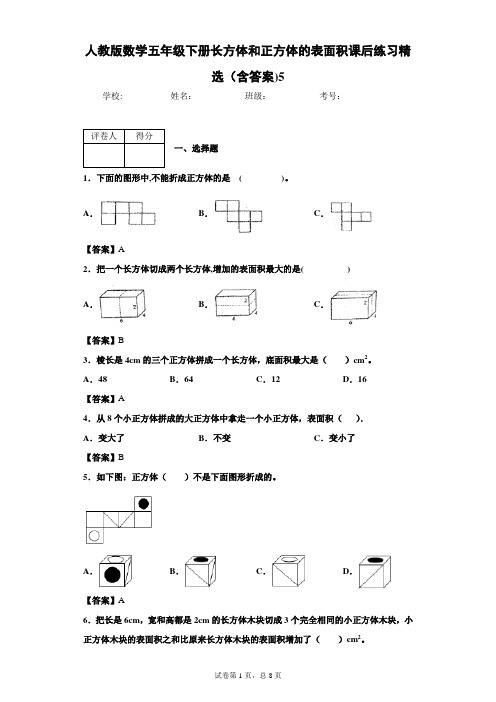
人教版数学五年级下册长方体和正方体的表面积课后练习精选（含答案)5学校:___________姓名：___________班级：___________考号：___________一、选择题1．下面的图形中,不能折成正方体的是( )。

A．B．C．【答案】A2．把一个长方体切成两个长方体,增加的表面积最大的是( )A．B．C．【答案】B3．棱长是4cm的三个正方体拼成一个长方体，底面积最大是（）cm2。

A．48 B．64 C．12 D．16【答案】A4．从8个小正方体拼成的大正方体中拿走一个小正方体，表面积（）．A．变大了B．不变C．变小了【答案】B5．如下图：正方体（）不是下面图形折成的。

A．B．C．D．【答案】A6．把长是6cm，宽和高都是2cm的长方体木块切成3个完全相同的小正方体木块，小正方体木块的表面积之和比原来长方体木块的表面积增加了（）cm2。

A．4 B．8 C．12 D．16【答案】D7．计算下列物体的表面积：(1)（2）【答案】(1)286平方厘米；（3）864平方厘米8．一个棱长2厘米的正方体切成两个长方体，表面积增加了（）平方厘米。

A．4 B．6 C．8【答案】C9．将一个长宽高分别为21厘米、15厘米和9厘米的长方体“切成”完全相同的三个小长方体后，表面积的和比原来长方体的表面积最多增加( )平方厘米。

A．1260 B．540 C．2400 D．639【答案】A10．在一个棱长为1分米的正方体的8个角上，各锯下一个棱长为1厘米的正方体，现在它的表面积和原来比（）A．不变B．减少C．增加D．无法确定【答案】A11．下列图形中，（）不能折成一个正方体。

A．B．C．【答案】C12．一小瓶啤酒是250ml，要装满一桶2升的啤酒桶，需要这样的小瓶（）瓶．A．4 B．8 C．16【答案】B13．一个正方体展开有6个面。

图①给出了其中5个面，最后一个面应该在图②的（）位置。

A．AB．BC．CD．D【答案】D14．把3个棱长为1cm的小正方体搭成如下图的组合体，表面积比原来3个小正方体的表面积之和减少了（）cm2。

《长方体的表面积（2）》同步练习2基础碰碰车知识点1长方体表面积的含义及计算方法1．填一填。

(1)长方体( )个面的( )，叫做它的表面积。

(2)长方体的相对的面的面积( )。

(3)一个长方体的长、宽、高分别是8厘米、7厘米、6厘米，它的所有棱长的和是( )厘米，它的表面积是( )厘米2。

(4)一个长方体的长、宽、高分别扩大到原来的2倍，表面积扩大到原来的( )倍。

(5)一个长方体，其中三个面的面积分别是10厘米2.8厘米2和6厘米2，这个长方形的表面积是( )厘米2。

(6)一个长方体长3厘米，宽3厘米，高4厘米，这个长方体有2个面是( )形，长方体的表面积是( )厘米2。

(7)一个长方体的棱长总和是80厘米，长10厘米，宽是7厘米，高是( )厘米。

知识点2正方体表面积的计算方法2．(1)求正方体的表面积就是求正方体( )个面的面积之和。

(2)一个正方体的棱长是9厘米，它的每个面的面积是( )厘米2，这个正方形的表面积是( )厘米2。

(3)一个正方体的表面积是96分米2，它的棱长是( )分米。

(4)把一个棱长为6厘米的正方体分成两个大小相同，形状相同的长方体，每个长方体的表面积是( )厘米2。

3．计算下面图形的表面积。

（单位：厘米）升级跷跷板4．判一判。

(1)正方体棱长扩大3倍，它的表面积就扩大6倍。

( )(2)长方体上没有正方形的面。

( )(3)棱长是6厘米的正方体，表面积是36厘米2。

( )5．解决问题。

(1)一个正方体的棱长是6厘米，它所有的棱长的和是多少厘米？它的表面积是多少？(2)做一个长50厘米、宽25厘米、高40厘米的玻璃鱼缸，至少要用多大面积的玻璃？(3)如图，这是一个长方体油箱。

(4)一个小食堂长10米，宽8米，高5米，要粉刷四壁和顶棚。

扣除门窗面积18.4米2，平均每平方米用石灰0.2千克，一共用石灰多少千克？智慧摩天轮6．有一个棱长是6厘米的正方体，如果把这个正方体切分成棱长是2厘米的小正方体，那么这些小正方体的表面积之和是多少？7．一个长方体的棱长和是72厘米，它的长是9厘米，宽6厘米，它的表面积是多少平方厘米？答案与点拨1．(1)6面积之和(2)相等(3)84 292 (4)4 (5)48(6)正方66 (7)32. (1)6 (2)81 486 (3)4 (4)1443．(5×4＋5×4＋5×5)×2=130(厘米2)5×5×6=150(厘米2)4．(1)× (2)× (3)×5．(1)6×12=72（厘米） 6×6×6=216（厘米2）(2)50×25＋(50×40＋25×40)×2=7250(厘米2)(3)(5×4＋5×4＋4×4)×2=112(分米2)(4)(10×5×2＋5×8×2＋10×8－18.4)×0.2=48. 32（千克）6．(6÷2)×(6÷2)×(6÷2)=27（个）2×2×6 =24（厘米2） 24×27=648(厘米2)7．(72－9×4－6×4)÷4=3（厘米）(9×6＋9×3＋6×3)×2=198（厘米2）。

长方体、正方体练习题班级姓名一、填空：1、长方体或者正方体（）叫做它的表面积。

2、一个正方体的棱长是10厘米，它的表面积是（）平方厘米。

3、一个长方体长4分米，宽3分米，高2分米，它的表面积是（）平方分米。

4、正方体的棱长之和是60分米，它的表面积是（）平方分米。

5、用两个长5厘米，宽3厘米，高2厘米的长方体拼成一个表面积尽可能小的正方体，这个拼成的长方体的表面积是（）平方厘米。

6、一个正方体的底面积是25平方分米，它的表面积是（）平方分米，它的体积是（）立方分米。

7、一个长方体，长是5厘米，宽3厘米，高1厘米，这个长方体的棱长总和是，表面积是，体积是。

8、一个正方体的棱长总和是24分米，它的表面积是，体积是。

9、3个棱长是1厘米的正方体小方块排成一行，形成的长方体的表面积是，体积是。

10、用同样的小正方体拼成一个大正方体，至少用个这样的小正方体。

11、一个正方体的表面积是36平方厘米，把它放在桌子上占的面积是（）平方厘米。

12、一个长方体长5厘米，宽5厘米，高4厘米，这个长方体有2个面是（）形，有（）个面的面积相等，长方体的表面积是（）。

13、把一根长80厘米、宽5厘米、高5厘米的长方体木材，锯成长度都是40厘米的两段，表面积比原来增加了。

14、把两个同样大小的长方体拼成一个正方体，这个正方体的棱长是10厘米，原来长方体的表面积平方厘米，体积是立方厘米。

15、用3个棱长4分米的正方体粘合成一个长方体，长方体的表面积比3个正方体的表面积少( )平方分米。

16、焊接一个长7cm、宽2cm、高1cm的长方体框架，至少要用（）cm的铁丝。

二、判断：1、物体所占空间的大小叫做物体的体积。

（）2、正方体的棱长扩大2倍，它的体积就扩大8倍。

（）3、容积和体积的计算方法相同，但意义不同。

（）4、正方体的棱长是6厘米，它的表面积和体积相等。

（）5、相邻的面积单位之间的进率是100。

（）6、表面积相等的物体，它们的体积也一定相等。

《长方体和正方体的表面积》练习一．选择题。

1、一只无盖的正方体鱼缸，棱长是4分米，做这只鱼缸至少要用玻璃（）平方分米。

A．80 B.90 C.96 D.642．两个棱长1厘米的正方体木块，拼成一个长方体，这个长方体表面积是（）平方厘米。

A．12 B.10 C．83．一个长方体长5厘米，宽5厘米，高4厘米，这个长方体的表面积是（）平方厘米。

A．110 B．120 C．1304．正方体的棱长扩大3倍，它的表面积就扩大（）倍。

A．3 B．6 C.9 D.12二．填空题。

1．长方体或正方体6个面的总面积叫做它的（）。

2．一个长方体的长是8厘米，宽6厘米，高3厘米，它的表面积是( )平方分米。

3.一个正方体的棱长是5分米，它的表面积是( )平方分米。

4.一个长5分米、宽4分米、高3分米的长方体，它占地面积最大是( )，表面积是( )。

三．判断题。

1.求一个无盖的长方体鱼缸的表面积，就是求这个长方体前后左右和底面这5个面的面积。

（）2.正方体的表面积=棱长×棱长×4。

（）3.一个正方体的表面积是48平方分米，把它放在桌子上占的面积是8平方分米。

（）4.把一个正方体锯成2个相同的长方体，它的表面积增加了6平方厘米，原来正方体的表面积是36平方厘米。

（）四．解答题。

1、一个长方体的长是12厘米，宽8厘米，高是6厘米，它的表面积是多少平方厘米？2、一个无盖的长方体鱼缸，底面是边长5分米的正方形，高4分米，做这样的一个鱼缸至少要用多少平方分米的玻璃？3、做20个棱长为30厘米的小正方体纸箱，至少需要多少平方米硬纸？4.一个卫生间长2.4米，宽1.8米，高3米。

如果在四壁贴上花墙砖，贴墙砖的高为2米，地面镶上地砖，不贴瓷砖的面积为多少平方米？参考答案一．选择题。

1.答案：A解析：一只无盖的正方体鱼缸，棱长是4分米，求做这只鱼缸至少要用玻璃多少平方分米，也就是求这个正方体5个面的面积。

列式为4×4×5=80平方分米，选择A2.答案：B解析：两个棱长1厘米的正方体木块，拼成一个长方体，求这个长方体表面积是多少平方厘米。

第二单元《长方体二》第一课时长方体的认识一、填空。

1、长方体有（）个面，（）条棱，（）个顶点。

2、正方体有（）个面，（）条棱，（）个顶点。

3、长方体的棱长总和公式是（）。

4、正方体的棱长总和公式是（）。

5、长方体的（）个面（）（填一定或不一定）是长方形，可能有（）个面是正方形。

6、至少用（）个小正方体才能拼成一个大正方体。

7、正方体是（）的长方体。

8、长方体的棱长之和是96cm，长是9cm，宽是8cm，高是（）。

9、一个长方体放在桌面上最多只能看到（）个面。

10、一个正方体的棱长总和是36厘米，它的一条棱长是（）厘米，一个面的面积是（）厘米。

二、判断。

1. 正方体的6个面的面积一定都相等。

（）2. 正方体也叫做立方体。

（）3. 一个长方体（不含正方体）最多有4个面的面积相等。

（）4. 如果一个长方体的12条棱的长度都相等，这个长方体一定是正方体。

（）5. 正方体的六个面都是正方形，长方体的六个面都是长方形。

（）三、填一填。

三、解决问题。

1、棱长为8cm的正方体，棱长总和是多少厘米？2、右图是一个长方体灯笼框架，制作一个这样的框架，至少需要多少厘米长的木条（单位：厘米）。

3、已知一个正方体的棱长总和是84cm，它的一个面的面积是多少？4、用金属条制作长方体柜台的框架，做这个柜台用了20米长的金属条，柜台长3米，宽0.8米，高是多少？5、制作一个长30cm、宽20cm、高20cm的长方体框架，至少需要多少厘米长的木条？第二课时展开与折叠一、选一选。

1、在下面的图形中，（）是正方体的表面展开图。

2、下面的图形经过折叠不能围成一个长方体的是（）。

3、如图所示的立方体，如果把它展开，可以是下列图形中的（）。

二、连一连。

二、按要求做一做。

1、一个长方体的展开图如下，标出上、下、前、后、左、右六个面。

2、下列哪些图形沿虚线剪开能折叠成正方形。

（）（）（）（）（）（）第三课时长方体的表面积一、填一填。

1、正方体是由（）个完全相同的（）围成的立体图形，正方体有（）条棱，它们的长度都（），正方体有（）个顶点。

3.2.1 长方体和正方体的表面积1. 填一填。

(1)一个长方体，它的长是2米，宽和高都是0.6米。

它的表面积是()平方米。

(2)一个正方体的棱长是0.4米，这个正方体的表面积是()平方米。

(3)一个正方体的棱长和是36分米，这个正方体的表面积是()平方分米。

(4)一个长方体的长是8厘米，宽是4厘米，高是2厘米。

这个长方体六个面中最大的一个面的面积是()平方厘米，最小的一个面的面积是()平方厘米。

这个长方体的表面积是()平方厘米。

2.一个正方体的棱长的总和是36 cm，它的表面积是多少平方厘米？3. 一个长方体木箱，长1.2米、宽0.8米、高0.6米，做这个木箱至少要用多少平方米的木板？如果这个木箱无盖呢？4. 把一个棱长是5分米的正方体木箱的表面涂上油漆，一共需油漆多少克？(每平方分米用漆5克。

)5. 要制作12节长方体铁皮烟囱，每节长2米、宽4分米、高3分米，要用多少平方米的铁皮？6. 一块”舒肤佳”牌香皂长8厘米、宽5厘米、高4厘米，商场进行促销活动，把3块同样的香皂装在一起销售。

请你设计一下，怎样才能最节省包装纸？并且算一算至少需要多少平方厘米包装纸。

答案1. (1)5.52(2)0.96(3)54(4)3281122.( 36÷12)²×6=54（平方厘米）3. (1.2×0.8＋1.2×0.6＋0.8×0.6)×2＝4.32(平方米)无盖：4.32－1.2×0.8＝3.36(平方米)4. 5²×6×5＝750(克)5. 4分米＝0.4米3分米＝0.3米(0.4×2＋0.3×2)×2×12＝33.6(平方米)6. (8×5＋8×4＋5×4)×2×3－8×5×4＝392(cm²)1。