与《垂径定理及其推论的应用》有关的中考题集锦(2006年)

垂径定理的应用专题试题精选附答案一．选择题（共9小题）1．（2015•潍坊）将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水部分的面积是（）A．（π﹣4）cm2 B．（π﹣8）cm2 C．（π﹣4）cm2D．（π﹣2）cm22．（2015•滕州市校级四模）当宽为3cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm）那么该圆的半径为（）A．8cm B．9cm C．cm D．10cm3．（2015•鄂城区模拟）在截面为半圆形的水槽内装有一些水，如图．水面宽AB为6分米，如果再注入一些水后，水面AB上升1分米，水面宽变为8分米，则该水槽截面直径为（）A．5分米B．6分米C．8分米D．10分米4．（2015•杭州模拟）某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧（如图所示），他量了下两砖之间的距离刚好是80cm，聪明的你，请你算出大石头的半径是（）A．40cm B．30cm C．20cm D．50cm5．（2014•无锡校级模拟）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器厚度，则球的半径为（）A．5cm B．6cm C．7cm D．8cm6．（2015•江夏区模拟）在某岛A的正东方向有台风，且台风中心B距离小岛A km，台风中心正以30km/h的速度向西北方向移动，距离中心50公里以内圆形区域（包括边界）都受影响，则小岛A受到台风影响的时间为（）A．不受影响 B．1小时C．2小时D．3小时7．（2015•浙江模拟）如图，有一圆弧形门拱，拱高AB=1m，跨度CD=4m，那么这个门拱的半径为（）A．2m B．2.5m C．3m D．5m8．（2014•南宁）在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm9．（2014•滦县一模）已知如图，圆柱OO1的底面半径为13cm，高为10cm，一平面平行于圆柱OO1的轴OO1，且与轴OO1的距离为5cm，截圆柱得矩形ABB1A1，则截面ABB1A1的面积是（）A．240cm2B．240πcm2C．260cm2D．260πcm2二．填空题（共15小题）10．（2015•衢州）一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽CD等于m．11．（2015•黔南州）如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A、B，并使AB与车轮内圆相切于点D，半径为OC⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径是．12．（2015•六盘水）赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图，若桥跨度AB约为40米，主拱高CD约10米，则桥弧AB所在圆的半径R= 米．13．（2015•东营）如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB 为0.8m，则排水管内水的深度为m．14．（2015•杭州模拟）为了节省空间，时尚装修的设计师设计出一款餐桌，餐桌的两边翻开后会成圆形桌面（如图1）．餐桌两边AB和CD平行且相等（如图2），小华用皮带尺量出AC=1.6米，AB=0.8米，那么桌面翻成圆桌后，桌子面积会增加平方米．（结果保留π）15．（2014•茂名）如图，小丽荡秋千，秋千链子的长OA为2.5米，秋千向两边摆动的角度相同，摆动的水平距离AB为3米，则秋千摆至最高位置时与最低价位置时的高度之差（即CD）为米．16．（2015•夏津县一模）一副量角器与一块含30°锐角的三角板如图所示放置，三角板的直角顶点C落在量角器的直径MN上，顶点A，B恰好都落在量角器的圆弧上，且AB∥MN．若AB=8cm，则量角器的直径MN= cm．17．（2015•黄岛区校级模拟）一破损光盘如图所示，测得所剩圆弧两端点间的距离AB长为8厘米，弧的中点到弧所对弦的距离为2厘米，则这个光盘的半径是厘米．18．（2015•孝义市一模）如图，某公园的一角有一块草坪（阴影部分），实线部分是沿草坪外围的一条小路，小路由两条相等的线段AC、BD和圆弧CD组成，其中AC、BD分别与圆弧CD相切于点C、D．经过测量，线段CD与半径OD都为60米，则这条小路的长度为米．19．（2015•江岸区校级模拟）为了测量某小球的直径，技术人员将小球放到透明烧杯上，如图是过球心O作为截面图，已知烧杯的高度是13cm，测得l=8cm，h=11cm，则小球的直径为cm．20．（2014•台州）如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为cm．21．（2014•杭州模拟）某居民区一处圆形下水管道破裂，修理人员准备更换一段与原管道同样粗细的新管道．如图，水面宽度原有60cm，发现时水面宽度只有cm，同时水位也下降65cm，则修理人员应准备的半径为cm的管道．22．（2014•绍兴）把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为．23．（2006•黑龙江）如图，一条公路的转弯处是一段圆弧（图中的AB），点O是这段弧的圆心，AB=120m，C是AB上一点，OC⊥AB，垂足为D，CD=20m，则这段弯路的半径为m．24．（2005•锦州）如图是一个俱乐部的徽章．徽章的图案是一个金色的圆圈，中间是一个矩形，矩形中间又有一个蓝色的菱形，徽章的直径为2cm，则徽章内的菱形的边长为cm．三．解答题（共6小题）25．（2015•麻城市校级模拟）图1是某希望小学放心食堂售饭窗口外遮雨棚的示意图（尺寸如图所示），遮雨棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是遮雨棚顶部截面的示意图，所在圆的圆心为O．遮雨棚顶部是用一种帆布覆盖的，求覆盖遮雨棚顶的帆布的面积（不考虑接缝等因素，计算结果保留π）．26．（2015•余姚市校级模拟）如图是大型输气管的截面图（圆形），某次数学实践活动中，数学课题学习小组为了计算大型输气管的直径，在圆形弧上取了A，B两点并连接AB，在劣弧AB上取中点C连接CB，经测量米，∠ABC=36.87°，请根据这些数据计算出大型输气管的直径（精确到0.1米）．（sin36.87°≈0.60，cos36.87°≈0.80，tan36.87°≈0.75）27．（2015•从化市一模）某公园管理人员在巡视公园时，发现有一条圆柱形的输水管道破裂，通知维修人员到场检测，维修员画出水平放置的破裂管道有水部分的截面图（如图）．（1）请你帮忙补全这个输水管道的圆形截面（不写作法，但应保留作图痕迹）；（2）维修员量得这个输水管道有水部分的水面宽AB=cm，水面最深地方的高度为6cm，请你求出这个圆形截面的半径r及破裂管道有水部分的截面图的面积S．28．（2015•普陀区一模）如图，某新建公园有一个圆形人工湖，湖中心O处有一座喷泉，小明为测量湖的半径，在湖边选择A、B两个点，在A处测得∠OAB=45°，在AB延长线上的C处测得∠OCA=30°，已知BC=50米，求人工湖的半径．（结果保留根号）29．（2015春•敦煌市校级期中）如图，公路MN和公路PQ在点P处交会，且∠QPN=30°．点A处有一所中学，AP=160m，一辆拖拉机从P沿公路MN前行，假设拖拉机行驶时周围100m 以内会受到噪声影响，那么该所中学是否会受到噪声影响，请说明理由，若受影响已知拖拉机的速度为18km/h，那么学校受影响的时间为多长？30．（2015秋•滨湖区期中）如图，一条公路的转弯处是一段圆弧AB．（1）作出AB所在圆的圆心O；（用直尺和圆规作图，保留作图痕迹，不写作法）（2）若弧AB的中点C到弦AB的距离为20m，AB=80m，求AB所在圆径．垂径定理的应用专题试题精选附答案参考答案一．选择题（共9小题）1．A；2．C；3．D；4．D；5．A；6．C；7．B；8．A；9．A；二．填空题（共15小题）10．1.6；11．50cm；12．25；13．0.8；14．；15．0.5；16．4；17．5； 18．120+2π；19．10；20．50；21．50；22．5； 23．100；24．1；三．解答题（共6小题）25．；26．；27．；28．；29．；30．；。

专题24.3 垂径定理【十大题型】【人教版】【题型1 利用垂径定理求线段长度】 (1)【题型2 利用垂径定理求角度】 (5)【题型3 利用垂径定理求最值】 (9)【题型4 利用垂径定理求取值范围】 (13)【题型5 利用垂径定理求整点】 (18)【题型6 利用垂径定理求面积】 (22)【题型7 垂径定理在格点中的运用】 (26)【题型9 垂径定理与分类讨论中的综合运用】 (33)【题型10 垂径定理的应用】 (37)【题型1 利用垂径定理求线段长度】【例1】（2022•雨花区校级开学）如图，⊙O的半径OD⊥弦AB交AB于点C，连接AO并延长交⊙O于13点E，连接EC．若AB＝8，EC＝2，则CD的长为（ ）A．1B．3C．2D．4【分析】由垂径定理得出AC＝BC＝4，连接BE，由∠CBE＝90°及CE长度求出BE＝6，在Rt△ABE中求出AE＝10，从而得出半径OA＝OD＝5，再在Rt△AOC中求出OC，从而得出答案．【解答】解：∵OD⊥AB，AB＝8，∴AC＝BC＝4，如图，连接BE，∵AE是⊙O的直径，∴∠ABE＝90°，13∵CE＝2，=CE2−BC2=(213)2−42=∴BE6，=AB2+BE2=82+62=则AE10，∴AO＝OD＝5，=AO2−AC2=52−42=在Rt△AOC中，OC3，则CD＝OD﹣OC＝2，故选：C．【变式1-1】（2022•宁津县二模）如图，已知圆O的半径为10，AB⊥CD，垂足为P，且AB＝CD＝16，则OP的长为（ ）6282A．6B．C．8D．【分析】根据题意作出合适的辅助线，然后根据垂径定理、勾股定理即可求得OP的长，本题得以解决．【解答】解：作OE⊥AB交AB与点E，作OF⊥CD交CD于点F，如右图所示，则AE＝BE，CF＝DF，∠OFP＝∠OEP＝90°，又∵圆O 的半径为10，AB ⊥CD ，垂足为P ，且AB ＝CD ＝16，∴∠FPE ＝90°，OB ＝10，BE ＝8，∴四边形OEPF 是矩形，OE ＝6，同理可得，OF ＝6，∴EP ＝6，∴OP ，=62+62=62故选：B ．【变式1-2】（2022•建华区二模）如图，⊙O 的直径AB 与弦CD 相交于点E ，若AE ＝5，EB ＝1，∠AEC ＝30°，则CD 的长为（ ）A ．5B ．2C ．4D ．3222+3+1【分析】因为∠AED ＝30°，可过点O 作OF ⊥CD 于F ，构成直角三角形，先求得⊙O 的半径为3，进而求得OE ＝3﹣1＝2，根据30°角所对的直角边等于斜边的一半，得出OFOE ＝1，再根据勾股定=12理求得DF 的长，然后由垂径定理求出CD 的长．【解答】解：过点O 作OF ⊥CD 于F ，连接DO ，∵AE ＝5，BE ＝1，∴AB ＝6，∴⊙O 的半径为3，∴OE ＝3﹣1＝2．∵∠AEC ＝30°，∴OF ＝1，2∴CF＝2，2∴CD＝2CF＝4，故选：C．【变式1-3】（2022春•徐汇区校级期中）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA3交弦AB于点E，且CE＝CB，若BE＝2AE，CD＝5，那么⊙O的半径为　2　．【分析】先证明△AFO和△BCE是等边三角形，设DE＝x，根据CD＝5列方程，求出x得到=3AD，从而得解．【解答】解：如图，记DC与⊙O交于点F，连接AF、OF、OB，过点C作CT⊥AB于点T，连接OE，OT．∵D为半径OA的中点，CD⊥OA，∴FD垂直平分AO，∴FA＝FO，又∵OA＝OF，∴△AOF是等边三角形，∴∠OAF＝∠AOF＝∠AFO＝60°，∵CE＝CB，CT⊥EB，∴ET＝TB，∵BE＝2AE，∴AE＝ET＝BT，∵AD＝OD，∴DE∥OT，∴∠AOT＝∠ADE＝90°，∴OE＝AE＝ET，∵OA＝OB，∴∠OAE＝∠OBT，∵AO＝BO，AE＝BT，∴△AOE≌△BOT（SAS），∴OE＝OT，∴OE＝OT＝ET，∴∠ETO＝60°，∴∠OAB＝∠OBA＝30°，∠AED＝∠CEB＝60°，∴△CEB是等边三角形，∴CE＝CB＝BE，设DE＝x，∴AE＝2x，BE＝CE＝4x，∴CD＝5x＝5，∴x＝1，=3∴AD，3∴AO＝2．3故答案为：2．【题型2 利用垂径定理求角度】【例2】（2022•泰安模拟）如图，⊙O的半径OA，OB，且OA⊥OB，连接AB．现在⊙O上找一点C，使OA2+AB2＝BC2，则∠OAC的度数为（ ）A ．15°或75°B ．20°或70°C ．20°D ．30°【分析】设圆的半径是r ，作直径BD ，作BC 关于直径BD 的对称线段BE ，连接EC ，BE ，ED ，AC ，再由直角三角形的性质即可解答．【解答】解：如图，设圆的半径是r ，则AO ＝r ，BO ＝r ，作直径BD ，作BC ⊙O 的弦BC ，使∠DBC ＝30°，作BC 关于直径BD 的对称线段BE ，连接EC ，BE ，ED ，AC ，直角△BED 中，可以得∠EBD ＝30°，∵线段BE 与线段BC 关于直线BD 对称，∴BC ＝BE ，∴BD 垂直平分线段CE ，∴，DE =CD ∴∠CBD ＝30°而∠BCA ∠AOB ＝45°．=12在△ABC 中，∠OAC ＝180°﹣∠ABO ﹣∠CBD ﹣∠ACB ﹣∠BAO ＝15°．同理，当E 为C 时，∠OAC ＝75°．故∠OAC 的度数为15°或75°．故选：A ．【变式2-1】（2022秋•天心区期中）如图，已知⊙O 半径OA ＝4，点B 为圆上的一点，点C 为劣弧上AB的一动点，CD ⊥OA ，CE ⊥OB ，连接DE ，要使DE 取得最大值，则∠AOB 等于（ ）A ．60°B ．90°C ．120°D ．135°【分析】如图，延长CD 交⊙O 于P ，延长CE 交⊙O 于T ，连接PT ．根据垂径定理以及三角形的中位线定理，可得DE PT ，当PT 是直径时，DE 的长最大，再证明∠AOB ＝90°，即可解决问题．=12【解答】解：如图，延长CD 交⊙O 于P ，延长CE 交⊙O 于T ，连接PT ．∵OA ⊥PC ，OB ⊥CT ，∴CD ＝DP ，CE ＝TE ，∴DE PT ，=12∴当PT 是直径时，DE 的长最大，连接OC ，∵OP ＝OC ＝OT ，OD ⊥PC ，OE ⊥CT ，∴∠COD ＝∠POA ，∠COB ＝∠BOT ，∴∠AOB ＝∠COA +∠COB∠POT ＝90°，=12故选：B ．【变式2-2】（2022秋•青田县期末）如图，在⊙O 中，半径OC 过弦AB 的中点E ，OC ＝2，OE ．=2（1）求弦AB 的长；（2）求∠CAB 的度数．【分析】（1）连接OB ，先由垂径定理得OC ⊥AB ，AE ＝BE ，OB ＝OC ＝2，再由勾股定理求出BE ，即可求解；=2（2）先证△BOE 是等腰直角三角形，得∠BOC ＝45°，再由圆周角定理即可求解．【解答】解：（1）连接OB ，如图所示：∵半径OC 过弦AB 的中点E ，∴OC ⊥AB ，AE ＝BE ，OB ＝OC ＝2，∴BE ，=OB 2−OE 2=22−(2)2=2∴AB ＝2BE ＝2；2（2）由（1）得：BE ＝OE ，OC ⊥AB ，∴△BOE 是等腰直角三角形，∴∠BOC ＝45°，∴∠CAB ∠BOC ＝22.5°．=12【变式2-3】（2022秋•开州区期末）如图，在⊙O 中，弦BC 与半径OA 垂直于点D ，连接AB 、AC ．点E 为AC 的中点，连接DE ．（1）若AB ＝6，求DE 的长；（2）若∠BAC ＝100°，求∠CDE 的度数．【分析】（1）根据垂径定理得到，则AC ＝AB ＝6，然后根据直角三角形斜边上的中线性质得AB =AC 到DE 的长；（2）利用等腰三角形的性质和三角形的内角和计算出∠C ＝40°，然后利用ED ＝EC 得到∠CDE ＝∠C ＝40°．【解答】解：（1）∵BC ⊥OA ，∴，∠ADC ＝90°，AB =AC ∴AC ＝AB ＝6，∵点E 为AC 的中点，∴DE AC ＝3；=12（2）∵AB ＝AC ，∴∠B ＝∠C ，∵∠BAC ＝100°，∴∠C （180°﹣100°）＝40°，=12∵点E 为AC 的中点，∴ED ＝EC ，∴∠CDE ＝∠C ＝40°．【题型3 利用垂径定理求最值】【例3】（2022•威海模拟）⊙O 中，点C 为弦AB 上一点，AB ＝1，CD ⊥OC 交⊙O 于点D ，则线段CD 的最大值是（ ）A ．B ．1C ．D ．21232【分析】因为CD ⊥OC 交⊙O 于点D ，连接OD ，△OCD 是直角三角形，则CD ，因为半=OD 2−OC 2径OD 是定值，当OC 取得最小值时线段CD 取得最大值．【解答】解：连接OD ，∵CD ⊥OC 交⊙O 于点D ，∴△OCD 是直角三角形，根据勾股定理得CD ，=OD 2−OC 2∵半径OD 是定值，∴当OC ⊥AB 时，线段OC 最小，此时D 与B 重合，CD ，=OB 2−OC 2∵OC ⊥AB ，∴AC ＝BC AB ，=12=12∴CD BC ．=OB 2−OC 2==12故选：A ．【变式3-1】（2022•河北模拟）如图所示，在⊙O 中，AB 为弦，OC ⊥AB 交AB 于点D ．且OD ＝DC ．P为⊙O 上任意一点，连接PA ，PB ，若⊙O 的半径为1，则 S △PAB 的最大值为（ ）A ．1B ．C ．D ．233334332【分析】连接OA ，如图，利用垂径定理得到AD ＝BD ，，再根据OD ＝DC 可得到ODOA AC =BC =12，所以AD ，由勾股定理，则AB ．△PAB 底AB 不变，当高越大时面积越大，即P 点到=12=32=3AB 距离最大时，△APB 的面积最大．则当点P 为AB 所在优弧的中点时，此时PD ＝PO +OD ＝1，△APB 的面积最大，然后根据三角形的面积公式计算即可．+12=32【解答】解：连接OA ，如图，∵OC ⊥AB ，∴AD ＝BD ，∵OD ＝DC ，∴OD OA ，=12=12∴AD ，AB ＝2AD ．=OA 2−OD 2=32=3当点P 为AB 所对的优弧的中点时，△APB 的面积最大，此时PD ＝PO +OD ＝1．+12=32∴△APB 的面积的最大值为．=12AB ⋅PD =12×3×32=334故选：C ．【变式3-2】（2022秋•龙凤区校级期末）如图，矩形ABCD 中，AB ＝20，AD ＝15，P ，Q 分别是AB ，AD 边上的动点，PQ ＝16，以PQ 为直径的⊙O 与BD 交于点M ，N ，则MN 的最大值为 8　．3【分析】过A 点作AH ⊥BD 于H ，连接OM ，如图，先利用勾股定理计算出BD ＝25，则利用面积法可计算出AH ＝36，再证明点O 在AH 上时，OH 最短，此时HM 有最大值，最大值为4，然后根据垂3径定理可判断MN 的最大值．【解答】解：过A 点作AH ⊥BD 于H ，连接OM ，如图：∵四边形ABCD 是矩形，∴∠BAD ＝90°，在Rt △ABD 中，BD 25，=AB 2+AD 2=202+152=∵AH ×BDAD ×AB ，12×=12×∴AH 12，=20×1525=∵⊙O 的直径为16，∴⊙O 的半径为8，∴点O 在AH 上时，OH 最短，∵HM ，=OM 2−OH 2∴此时HM 有最大值，OH ＝AH ﹣OA ＝4，则最大值为4，82−42=3∵OH ⊥MN ，∴MN ＝2MH ，∴MN 的最大值为2×48．3=3故答案为：8．3【变式3-3】（2022秋•延平区校级期末）在Rt △ABC 中，∠C ＝90°，BC ＝3，AC ＝4，D 、E 分别是AC 、BC 上的一点，且DE ＝3，若以DE 为直径的圆与斜边AB 相交于M 、N ，则MN 的最大值为（ ）A ．B ．C ．D ．9106585125【分析】由题意可知，C 、O 、G 三点在一条直线上OG 最小，MN 最大，再由勾股定理求得AB ，然后由三角形面积求得CF ，最后由垂径定理和勾股定理即可求得MN 的最大值．【解答】解：过O 作OG ⊥AB 于G ，连接OC 、OM ，∵DE ＝3，∠ACB ＝90°，OD ＝OE ，∴OC DE ，=12=32只有C 、O 、G 三点在一条直线上OG 最小，∵OM ，=32∴只有OG 最小，GM 才能最大，从而MN 有最大值，过C 作CF ⊥AB 于F ，∴G 和F 重合时，MN 有最大值，∵∠ACB ＝90°，BC ＝3，AC ＝4，∴AB 5，=BC 2+AC 2=32+42=∵AC •BC AB •CF ，12=12∴CF ，=AC ×BC AB =4×35=125∴OG ＝CF ﹣OC，=125−32=910∴MG ，=OM 2−OG 2=(32)2−(910)2=65∴MN ＝2MG，=125故选：D ．【题型4 利用垂径定理求取值范围】【例4】（2022•包河区校级二模）如图，在⊙O 中，直径AB ＝10，CD ⊥AB 于点E ，CD ＝8．点F 是弧BC 上动点，且与点B 、C 不重合，P 是直径AB 上的动点，设m ＝PC +PF ，则m 的取值范围是（ ）A ．8＜m ≤4B ．4m ≤10C ．8＜m ≤10D ．6＜m ＜1055＜【分析】连接PD ，DF ，OC ，BD ，利用垂径定理可得AB 是CD 的垂直平分线，则PC ＝PD ；利用三角形的任意两边之和大于第三边，可得不等式PD +PF ≥DF （当D ，P ，F 在一条直线上时取等号），结合图形即可得出结论．【解答】解：连接PD ，DF ，OC ，BD ，如图，∵CD ⊥AB ，BA 为⊙O 的直径，∴CE ＝EDCD ＝4，=12∵OC AB ＝5，=12∴OE 3，=OC 2−CE 2=∴BE ＝OE +OB ＝8．∴BD 4．=BE 2+DE 2=5∵P 是直径AB 上的动点，CD ⊥AB ，∴AB 是CD 的垂直平分线，∴PC ＝PD ．∵m ＝PC +PF ，∴m ＝PD +PF ，由图形可知：PD +PF ≥DF （当D ，P ，F 在一条直线上时取等号），∵点F 是弧BC 上动点，且与点B 、C 不重合，∴DC ＜DF ≤直径，∴8＜m ≤10．故选：C ．【变式4-1】（2022•佛山）如图，⊙O 的直径为10cm ，弦AB ＝8cm ，P 是弦AB 上的一个动点，求OP 的长度范围．【分析】过点O 作OE ⊥AB 于点E ，连接OB ，由垂径定理可知AE ＝BEAB ，再根据勾股定理求出=12OE 的长，由此可得出结论．【解答】解：过点O 作OE ⊥AB 于点E ，连接OB ，∵AB ＝8cm ，∴AE ＝BE AB 8＝4cm ，=12=12×∵⊙O 的直径为10cm ，∴OB 10＝5cm ，=12×∴OE 3cm ，=OB 2−BE 2=52−42=∵垂线段最短，半径最长，∴3cm ≤OP ≤5cm ．【变式4-2】（2022秋•盐都区校级月考）如图，点P 是⊙O 内一定点．（1）过点P 作弦AB ，使点P 是AB 的中点（不写作法，保留作图痕迹）；（2）若⊙O 的半径为13，OP ＝5，①求过点P 的弦的长度m 范围；②过点P 的弦中，长度为整数的弦有 4　条．【分析】（1）连接OP并延长，过点P作AB⊥OP即可；（2）①过点P的所有弦中，直径最长为26，与OP垂直的弦最短，由垂径定理和勾股定理求出AB＝24，即可得出答案；②过P点最长的弦为直径26，最短的弦24，长度为25的弦有2条，即可得出结论．【解答】解：（1）如图1，连接OP并延长，过点P作AB⊥OP，则弦AB即为所求；（2）①过点P的所有弦中，直径最长为26，与OP垂直的弦最短，连接OA，如图2所示：∵OP⊥AB，=OA2−OP2=132−52=∴AP＝BP12，∴AB＝2AP＝24，∴过点P的弦的长度m范围为24≤m≤26；②∵过P点最长的弦为直径26，最短的弦24，∴长度为25的弦有两条，∴过点P的弦中，长度为整数的弦共有4条，故答案为：4．【变式4-3】（2022秋•天河区校级期中）已知⊙O的半径为5，点O到弦AB的距离OH＝3，点P是圆上一动点，设过点P且与AB平行的直线为l，记直线AB到直线l的距离为d．（1）求AB的长；（2）如果点P只有两个时，求d的取值范围；（3）如果点P有且只有三个时，求连接这三个点所得到的三角形的面积．【分析】（1）连接OA，根据勾股定理求出AH，根据垂径定理得出即可；（2）求出HC和HD的值，结合图形得出即可；（3）先找出符合条件时的位置，求出三角形的高和底边，根据三角形的面积公式求出即可．【解答】解：（1）连接OA，如图1，∵点O到弦AB的距离OH＝3，∴AB⊥OC，∴∠OHA＝90°，AB＝2AH，在Rt△AHO中，OA＝5，OH＝3，由勾股定理得：AH＝4，∴AB＝2AH＝8；（2）延长CO 交⊙O 于D ，如图2，∵CH ＝5﹣3＝2，HD ＝5+3＝8，∴点P 只有两个时d 的取值范围是2＜d ＜8；（3）如图3，∵CH ＝5﹣3＝2，HD ＝5+3＝8，∴点P 有且只有三个时，d ＝2，如图，P 在C 、E 、F 处，连接OE ，∵OC ⊥AB ，AB ∥EF ，∴OC ⊥EF ，∴EF ＝2EM ，∵OE ＝5，OM ＝5﹣2﹣2＝1，CM ＝2+2＝4，∴由勾股定理得：EM 2；=52−12=6∴EF ＝2EM ＝4，6∴S △CEF EF ×CM 44＝8=12×=12×6×6即点P 有且只有三个时，连接这三个点所得到的三角形的面积是8．6【题型5 利用垂径定理求整点】【例5】（2022•山海关区一模）已知⊙O 的直径CD ＝10，CD 与⊙O 的弦AB 垂直，垂足为M ，且AM ＝4.8，则直径CD 上的点（包含端点）与A 点的距离为整数的点有（ ）A ．1个B ．3个C ．6个D ．7个【分析】利用勾股定理得出线段AD 和AC 的长，根据垂线段的性质结合图形判断即可．【解答】解：∵CD 是直径，∴OC ＝OD CD 10＝5，=12=12×∵AB ⊥CD ，∴∠AMC ＝∠AMD ＝90°，∵AM ＝4.8，∴OM 1.4，=52−4．82=∴CM ＝5+1.4＝6.4，MD ＝5﹣1.4＝3.6，∴AC 8，AD 6，=4．82+6．42==4．82+3．62=∵AM ＝4.8，∴A 点到线段MD 的最小距离为4.8，最大距离为6，则A 点到线段MD 的整数距离有5，6，A 点到线段MC 的最小距离为4.8，最大距离为8，则A 点到线段MC 的整数距离有5，6，7，8，直径CD 上的点（包含端点）与A 点的距离为整数的点有6个，故选：C ．【变式5-1】（2022秋•新昌县期末）如图，AB 是⊙O 的弦，OC ⊥AB 于点C ，连接OB ，点P 是半径OB 上任意一点，连接AP ，若OB ＝5，OC ＝3，则AP 的长不可能是（ ）A ．6B ．7C ．8D ．9【分析】首先利用勾股定理得出AC 的长，求出AB 长，再利用三角形边之间的关系进而得出AO≤AP≤AB，即可得出答案．【解答】解：连接OA，∵OC⊥AB于点C，OB＝5，OC＝3，=52−32=∴BC4，∴AB＝2×4＝8，∵AO≤AP≤AB，∴5≤AP≤8，∴AP的长度不可能是：9（答案不唯一）．故选：D．【变式5-2】（2022•桥西区校级模拟）如图，AB是⊙C的弦，直径MN⊥AB于点O，MN＝10，AB＝8，如图以O为原点建立坐标系．我们把横纵坐标都是整数的点叫做整数点，则线段OC长是　3　，⊙C 上的整数点有　12　个．【分析】过C作直径UL∥x轴，连接AC，根据垂径定理求出AO＝BO＝4，根据勾股定理求出OC，再得出答案即可．【解答】解：过C作直径UL∥x轴，连接CA ，则AC 10＝5，=12×∵MN 过圆心C ，MN ⊥AB ，AB ＝8，∴AO ＝BO ＝4，∠AOC ＝90°，由勾股定理得：CO 3，=AC 2−OC 2=52−42=∴ON ＝5﹣3＝2，OM ＝5+3＝8，即A （﹣4，0），B （4，0），M （0，8），N （0，﹣2），同理还有弦QR ＝AB ＝8，弦WE ＝TS ＝6，且WE 、TS 、QR 都平行于x 轴，Q （﹣4，6），R （4，6），W （﹣3，7），E （3，7），T （﹣3，﹣1），S （3，﹣1），U （﹣5，3），L （5，3），即共12个点，故答案为：3；12．【变式5-3】（2022秋•肇东市期末）已知⊙O 的半径为5，点O 到弦AB 的距离为3，则⊙O 上到弦AB 所在直线的距离为2的点有（ ）A ．4个B ．3个C ．2个D ．1个【分析】过O 点作OC ⊥AB ，交⊙O 于P ，由OC ＝3，OA ＝5，得到PC ＝2，即点P 到直线AB 的距离为2；在直线的另一边，圆上的点到直线的最远距离为8，而圆为对称图形，则还有两个点M ，N 到直线AB 的距离为3．【解答】解：过O 点作OC ⊥AB ，交⊙O 于P ，如图，∴OC ＝3，而OA ＝5，∴PC ＝2，即点P 到直线AB 的距离为2；在直线的另一边，圆上的点到直线的最远距离为8，而圆为对称图形，∴在直线AB 的这边，还有两个点M ，N 到直线AB 的距离为2．故选：B ．【题型6 利用垂径定理求面积】【例6】（2022•武汉模拟）如图，在半径为1的⊙O 中有三条弦，它们所对的圆心角分别为60°，90°，120°，那么以这三条弦长为边长的三角形的面积是（ ）A ．B ．1C ．D ．23222【分析】连接OA 、OB 、OC 、OD 、OE 、OF ，则△AOB 、△COD 分别为等边三角形，等腰直角三角形，进而可得到AB 、CD 长；再过点O 作OH ⊥EF 于点H ，根据垂径定理可得EF ＝2EH ，∠EOH ＝∠FOH ＝60°，根据锐角三角形函数可求出FH ，进而可得EF ；再根据AB 2+CD 2＝EF 2可判断以AB 、CD 、EF 为边的三角形为直角三角形，即可求出其面积．【解答】解：如图，连接OA 、OB 、OC 、OD 、OE 、OF ，则∠AOB ＝60°，∠COD ＝90°，∠EOF ＝120°，在Rt △COD 中，CD ．=12+12=2∵OA ＝OB ，∴△AOB 是等边三角形，∴AB ＝OA ＝1，过点O 作OH ⊥EF 于点H ，则EF ＝2EH ，∠EOH ＝∠FOH ＝60°，∴FH ＝1．×32=32∴EF ＝2FH ．=3∵，即AB 2+CD 2＝EF 2，12+(2)2=(3)2∴以AB 、CD 、EF 为边的三角形为直角三角形，∴其面积为：．12×2×1=22故选：D ．【变式6-1】（2022秋•黄州区校级月考）如图，矩形MNGH 的四个顶点都在⊙O 上，顺次连接矩形各边的中点，得到菱形ABCD ，若BD ＝12，DF ＝4，则菱形ABCD 的面积为　96　．【分析】先连接OH ，根据BD ＝12得出OD 长，那么可得到圆的半径为OD +DF ，利用三角形全等可得菱形边长等于圆的半径，再根据勾股定理求出OA 的长，由S 菱形ABCD ＝4S △AOD 即可得出结论．【解答】解：如图：连接OH ，∵BD ＝12，DF ＝4∴⊙O 的半径r ＝OD +DFBD +DF 12+4＝10，=12=12×∴OH ＝10在Rt △HOD 与Rt △ADO 中，OD ＝OD ，AO ＝HD ，∠AOD ＝∠HDO ＝90°∴△AOD ≌△GDO ，∴OH ＝AD ＝10，在Rt △AOD 中，∵AD ＝10，OD ＝6，∴OA 8，=AD 2−OD 2=102−62=∴S 菱形ABCD ＝4S △AOD ＝46×8＝96．×12×故答案为：96．【变式6-2】（2022秋•西城区校级期中）如图，AB 为⊙O 直径，过点O 作OD ⊥BC 于点E ，交⊙O 于点D ，CD ∥AB ．（1）求证：E 为OD 的中点；（2）若CB ＝6，求四边形CAOD的面积．【分析】（1）根据全等三角形的判定和性质以及垂径定理证明即可；（2）根据平行四边形的判定和勾股定理解答即可．【解答】证明：（1）在⊙O 中，OD ⊥BC 于E ，∴CE ＝BE ，∵CD ∥AB ，∴∠DCE ＝∠B ，在△DCE 与△OBE 中，{∠DCE =∠B CE =BE∠CED =∠BEO ∴△DCE ≌△OBE （ASA ），∴DE＝OE，∴E是OD的中点；（2）连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵OD⊥BC，∴∠CED＝90°＝∠ACB，∴AC∥OD，∵CD∥AB，∴四边形CAOD是平行四边形，∵E是OD的中点，CE⊥OD，∴OC＝CD，∵OC＝OD，∴OC＝OD＝CD，∴△OCD是等边三角形，∴∠D＝60°，∴∠DCE＝90°﹣∠D＝30°，∴在Rt△CDE中，CD＝2DE，∵BC＝6，∴CE＝BE＝3，∵CE2+DE2＝CD2＝4DE2，=33∴DE，CD＝2，3∴OD＝CD＝2，3∴四边形CAOD的面积＝OD•CE＝6．【变式6-3】（2022•新洲区模拟）如图，点A，C，D均在⊙O上，点B在⊙O内，且AB⊥BC于点B，BC⊥CD于点C，若AB＝4，BC＝8，CD＝2，则⊙O的面积为（ ）A ．B ．C ．D ．125π4275π4125π9275π9【分析】利用垂径定理和勾股定理建立方程求出ON ，再求出半径后，根据圆面积的计算方法进行计算即可．【解答】解：如图，连接OA 、OC ，过点O 作OM ⊥CD 于M ，MO 的延长线于AB 延长线交于N ，则四边形BCMN 是矩形，∵OM ⊥CD ，CD 是弦，∴CM ＝DM CD ＝1＝BN ，=12∴AN ＝AB +BN ＝4+1＝5，设ON ＝x ，则OM ＝8﹣x ，在Rt △AON 、Rt △COM 中，由勾股定理得，OA 2＝AN 2+ON 2，OC 2＝OM 2+CM 2，∵OA ＝OC ，∴AN 2+ON 2＝OM 2+CM 2，即52+x 2＝（8﹣x ）2+12，解得x，=52即ON ，=52∴OA 2＝52+（）2，52=1254∴S ⊙O ＝π×OA2π，=1254故选：A ．【题型7 垂径定理在格点中的运用】【例7】（2022秋•襄都区校级期末）如图所示，一圆弧过方格的格点AB，试在方格中建立平面直角坐标系，使点A的坐标为（0，4），则该圆弧所在圆的圆心坐标是（ ）A．（﹣1，2）B．（1，﹣1）C．（﹣1，1）D．（2，1）【分析】连接AC，作出AB、AC的垂直平分线，其交点即为圆心．【解答】解：如图所示，连接AC，作出AB、AC的垂直平分线，其交点即为圆心．∵点A的坐标为（0，4），∴该圆弧所在圆的圆心坐标是（﹣1，1）．故选：C．【变式7-1】（2022春•海门市期中）如图所示，⊙P过B、C两点，写出⊙P上的格点坐标．【分析】根据同圆的半径相等可得点P的坐标．【解答】解：由图形可知：⊙P上的格点坐标为（4，2）．【变式7-2】（2022•商城县三模）如图所示的网格中，每个小正方形的边长均为1，点A、B、C均在小正方形的顶点上，点C 同时也在上，若点P 是的一个动点，则△ABP 面积的最大值是 88　AB BC 5−．【分析】作AB 的垂直平分线交AB 于D ，交于E ，圆心为0，则点O 在DE 上，连接AB AE 、BE ，CF ⊥OE 于F ，如图，设⊙O 的半径为r ，OD ＝x ，利用勾股定理得到r 2＝x 2+42①，r 2＝（x +2）2+22②，则利用②﹣①可求出得x ＝2，所以r ＝2，DE ＝22，然后根据55−三角形面积公式，点P 点与点E 重合时，△ABP 面积的最大值．【解答】解：作AB 的垂直平分线交AB 于D ，交于E ，圆心为0，则点O 在DE 上，连接AB AE 、BE ，CF ⊥OE 于F ，如图，设⊙O 的半径为r ，OD ＝x ，在Rt △BOD 中，r 2＝x 2+42①，在Rt △OCF 中，r 2＝（x +2）2+22②，②﹣①得4+4x +4﹣16＝0，解得x ＝2，∴OD ＝2，∴r 2，=22+42=5∴DE ＝OE ﹣OD ＝22，5−∵点P 是的一个动点，BC ∴点P 点与点E 重合时，△ABP 面积的最大值，最大值为8×（22）＝88．12×5−5−故答案为：88．5−【变式7-3】（2017秋•靖江市校级月考）如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）：（1）利用网格作出该圆弧所在圆的圆心D点的位置，并写出D点的坐标为　（2，1）　；13（2）连接AD、CD，则⊙D的半径为 ，∠ADC的度数为　90°　．【分析】（1）利用网格特点，作AB和BC的垂直平分线，然后根据垂径的推论可判定它们的交点为D点，从而得到D点坐标；（2）先利用勾股定理计算出DA、DC、AC，然后利用勾股定理的逆定理证明∠ADC的度数为90°．【解答】解：（1）如图，点D为所作，D点坐标为（2，1）；=22+32=13=22+32=13=12+52=26（2）AD，CD，AC，∵DA2+DC2＝AC2，∴△ADC为直角三角形，∠ADC＝90°，13即⊙D的半径为，∠ADC的度数为90°．13故答案为（2，1）；，90°．【题型8 垂径定理在坐标系中的运用】【例8】（2022•博山区一模）如图，在平面直角坐标系中，半径为5的⊙E与y轴交于点A（0，﹣2），B（0，4），与x轴交于C，D，则点D的坐标为（ ）(4−26，0)(−4+26，0)(−4+26，0)(4−26，0)A．B．C．D．【分析】过O点作EH⊥AB于H，EF⊥CD于F，连接ED，如图，根据垂径定理得到CF＝DF，AH＝BH＝3，所以OH＝1，再利用勾股定理计算出EH＝4，则EF＝1，OF＝4，接着利用勾股定理计算出FD，然后计算出OD，从而得到D点坐标．【解答】解：过O点作EH⊥AB于H，EF⊥CD于F，连接ED，如图，则CF＝DF，AH＝BH∵A（0，﹣2），B（0，4），∴AB＝6，∴BH＝3，∴OH＝1，=EB2−BH2=52−32=在Rt△BHE中，EH4，∵四边形EHOF为矩形，∴EF＝OH＝1，OF＝EH＝4，=DE2−EF2=52−12=6在Rt△OEF中，FD2，6−∴OD＝FD﹣OF＝24，6−∴D（24，0）．故选：B．【变式8-1】（2022秋•西林县期末）如图，⊙P 与y 轴交于点M （0，﹣4），N （0，﹣10），圆心P 的横坐标为﹣4．则⊙P 的半径为（ ）A ．3B ．4C ．5D ．6【分析】过点P 作PD ⊥MN ，连接PM ，由垂径定理得DM ＝3，在Rt △PMD 中，由勾股定理可求得PM 为5即可．【解答】解：过点P 作PD ⊥MN ，连接PM ，如图所示：∵⊙P 与y 轴交于M （0，﹣4），N （0，﹣10）两点，∴OM ＝4，ON ＝10，∴MN ＝6，∵PD ⊥MN ，∴DM ＝DNMN ＝3，=12∴OD ＝7，∵点P 的横坐标为﹣4，即PD ＝4，∴PM 5，=PD 2+DM 2=42+32=即⊙P 的半径为5，故选：C ．【变式8-2】（2022•印江县三模）如图，直线l 为y ＝x ，过点A 1（1，0）作A 1B 1⊥x 轴，与直线l 交于点B 1，以原点O 为圆心，OB 1长为半径画圆弧交x 轴于点A 2；再作A 2B 2⊥x 轴，交直线l 于点B 2，以原点O 为圆心，OB 2长为半径画圆弧交x 轴于点A 3；…，按此作法进行下去，则点A 2022的坐标为 （（）2021，0）　．2=2=2【分析】利用直线y＝x平分第一、三象限，则B1（1，1），由于OA2＝OB1OA1，OA3＝OB2 =222OA2＝（）2，依此变化规律得到OA2022＝（）2021，从而得到点A2022的坐标．【解答】解：∵A1（1，0）作A1B1⊥x轴，与直线y＝x交于点B1，∴OA1＝1，B1（1，1），∵以原点O为圆心，OB1长为半径画圆弧交x轴于点A2，=2=2∴OA2＝OB1OA1，∵以原点O为圆心，OB2长为半径画圆弧交x轴于点A3，=2=2×2=2∴OA3＝OB2OA2（）2，2同理可得OA4＝（）3，•••2∴OA2022＝（）2021，2∴点A2022的坐标为（（）2021，0）．2故答案为：（（）2021，0）．【变式8-3】（2015•宜春模拟）如图，半径为5的⊙P与y轴交于点M（0，﹣4），N（0，﹣10），函数y＝﹣2x+m图象过点P，则m＝　﹣15　．【分析】过P点作PE⊥ON交y轴于点E，连接PM，由点M（0，﹣4），N（0，﹣10）得MN＝6，所以ME＝NE＝3，得E（0，﹣7），由勾股定理得PE＝4，故P（﹣4，﹣7），代入y＝﹣2x+m得m．【解答】解：过P点作PE⊥ON交y轴于点E，连接PM，∵点M（0，﹣4），N（0，﹣10），∴MN＝6，∴ME＝NE＝3，∴E（0，﹣7），∵PM＝5，=52−32=∴PE4，∵点P在第三象限，∴P（﹣4，﹣7），代入y＝﹣2x+m得，m＝﹣15，故答案为：﹣15．【题型9 垂径定理与分类讨论中的综合运用】【例9】（2022秋•化德县校级期末）⊙O的半径为10cm，弦AB∥CD，且AB＝12cm，CD＝16cm，则AB 和CD的距离为（ ）A．2cm B．14cm C．2cm或14cm D．10cm或20cm【分析】分两种情况考虑：当圆心位于AB与CD之间时，连接OA，OC，如图1所示，过O作EF⊥AB，由AB∥CD，得到EF⊥CD，利用垂径定理得到E、F分别为AB、CD的中点，分别求出OE 与OF，由OE+OF即可得到EF的长；当圆心在AB与CD一侧时，连接OA，OC，如图2所示，过O 作EF⊥AB，由AB∥CD，得到EF⊥CD，同理求出OE与OF，由OE﹣OF即可求出EF的长．【解答】解：当圆心位于AB与CD之间时，连接OA，OC，如图1所示，过O作EF⊥AB，由AB∥CD，得到EF⊥CD，∴E、F分别为AB、CD的中点，∴AE＝6cm，CF＝8cm，在Rt△AOE中，OA＝10cm，AE＝6cm，根据勾股定理得：OE＝8cm，在Rt△COF中，OC＝10cm，CF＝8cm，根据勾股定理得到OF＝6cm，此时AB和CD的距离EF＝8+6＝14cm；当圆心在AB与CD一侧时，连接OA，OC，如图2所示，过O作EF⊥AB，由AB∥CD，得到EF⊥CD，同理求出OE＝8cm，OF＝6cm，此时AB和CD的距离EF＝8﹣6＝2cm，综上，AB和CD的距离为2cm或14cm．故选：C．【变式9-1】（2022•包河区二模）已知圆O的半径为5，弦AB＝8，D为弦AB上一点，且AD＝1，过点D作CD⊥AB，交圆O于C，则CD长为（ ）A．1B．7C．8或1D．7或1【分析】连接OB，OC1，过O作OE⊥CD，OF⊥AB，则四边形EDFO是矩形，根据矩形的性质得到=52−42=OE＝DF，OF＝DE，根据勾股定理得到BF3，得到OE＝DF＝3，由勾股定理得到C1E=52−32=4，于是得到结论．【解答】解：如图，连接OB，OC1，过O作OE⊥CD，OF⊥AB，则四边形EDFO是矩形，∴OE＝DF，OF＝DE，∵圆O的半径为5，弦AB＝8，∴AF＝BF＝4，=52−42=∴BF3，∵AD＝1，∴DF＝3，∴OE ＝DF ＝3，∴C 1E 4，=52−32=∴C 2E ＝4，∴C 1D ＝7，C 2D ＝1，∴CD 长为7或1，故选：D ．【变式9-2】（2022秋•方正县期末）如图，⊙O 的弦AB 与半径OC 垂直，点D 为垂足，OD ＝DC ，AB ＝2，点E 在⊙O 上，∠EOA ＝30°，则△EOC 的面积为　1或2　．3【分析】设⊙O 的半径为x （x ＞0），则OD ＝DC x ，根据垂径定理可知AD ，在Rt △ADO 中=12=3利用勾股定理即可求出x 值，再分点E 在外和点E 在上两种情况考虑△EOC 的面积，当点E 在AC AC 外时，通过角的计算可得出∠COE ＝90°，利用三角形的面积公式即可求出S △EOC 的值；当点E 在AC 上时，过点E 作EF ⊥OC 于点F ，通过角的计算可得出∠COE ＝30°，由此可得出EF 的长度，利用AC 三角形的面积公式即可求出S △EOC 的值．综上即可得出结论．【解答】解：依照题意画出图形，连接OA ．设⊙O 的半径为x （x ＞0），则OD ＝DCx ．=12∵OC ⊥AB 于点D ，∴∠ADO ＝90°，AD ＝DB AB ．=12=3在Rt △ADO 中，AO ＝x ，OD x ，AD ，=12=3∴∠OAD ＝30°，∠AOD ＝60°，AD x ，=AO 2−OD 2=32=3解得：x ＝2．当点E 在外时，∠COE ＝∠AOD +∠EOA ＝90°，AC ∴S △EOC EO •OC ＝2；=12当点E 在上时，过点E 作EF ⊥OC 于点F ，AC ∵∠COE ＝∠AOD ﹣∠EOA ＝30°，∴EF OE ＝1，=12∴S △EOC OC •EF ＝1．=12综上可知：△EOC 的面积为1或2．故答案为：1或2．【变式9-3】（2022秋•淮南月考）如图，已知⊙O 的半径为2．弦AB 的长度为2，点C 是⊙O 上一动点，若△ABC 为等腰三角形，则BC 2的长为 8或12或4　．±43【分析】当△ABC 为等腰三角形时，分两种情况：①如图1，AC ＝BC ，在AB 的两侧各有一个符合条件的点C ，根据勾股定理可得结论；②如图2，当AB ＝AC 时，连接OC 3，AO ，AO 交BC 3于E ，则BE ＝C 3E ，根据直角三角形30度的性质和勾股定理，垂径定理可得结论．【解答】解：当△ABC 为等腰三角形时，分以下两种情况：①如图1，以AB 为底边时，AC ＝BC ，连接C 1C 2，AO ，则C 1C 2过圆心O ，∴C 1C 2⊥AB ，∴AD AB ＝1，=12∵OA ＝2，∴OD ，=22−12=3∴C 1D ＝2，C 2D ＝2，+3−3∴BC 128+4，BC 228﹣4；=(2+3)2+12=3=(2−3)2+12=3②如图2，以AB 为腰时，AB ＝AC 3＝BC 4＝2，连接OC 3，AO ，AO 交BC 3于E ，则BE ＝C 3E ，BC 42＝4，∵OC 3＝AO ＝AC 3＝2，∴△AC 3O 是等边三角形，∴∠EOC 3＝60°，∴∠OC 3E ＝30°，∴C 3E ，=3∴BC 3＝2，3∴BC 32＝（2）2＝12，3综上，BC 2＝8或12或4．±43故答案为：8或12或4．±43【题型10 垂径定理的应用】【例10】（2022秋•武昌区校级期末）某地有一座圆弧形拱桥，它的跨度（弧所对的弦的长）24m ，拱高（弧的中点到弦的距离）4米，则求拱桥的半径为（ ）A ．16mB ．20mC ．24mD ．28m【分析】设圆弧形拱桥的圆心为O ，跨度为AB ，拱高为CD ，连接OA 、OD ，设拱桥的半径为R 米，由垂径定理得AD AB ＝12（米），再由勾股定理得出方程，解方程即可．=12【解答】解：设圆弧形拱桥的圆心为O ，跨度为AB ，拱高为CD ，连接OA 、OD ，如图：设拱桥的半径为R 米，由题意得：OD ⊥AB ，CD ＝4米，AB ＝24米，则AD ＝BD AB ＝12（米），OD ＝（R ﹣4）米，=12在Rt △AOD 中，由勾股定理得：R 2＝122+（R ﹣4）2，解得：R ＝20，即桥拱的半径R 为20m ，故选：B ．【变式10-1】（2022•望城区模拟）《九章算术》是我国古代著名数学经典，其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺．如图，已知弦AB＝1尺，弓形高CD＝1寸，（注：1尺＝10寸）问这块圆柱形木材的直径是（ ）A．13寸B．6.5寸C．26寸D．20寸【分析】设⊙O的半径为r寸．在Rt△ADO中，AD＝5，OD＝r﹣1，OA＝r，则有r2＝52+（r﹣1）2，解方程即可；【解答】解：设⊙O的半径为r寸．在Rt△ADO中，AD＝5，OD＝r﹣1，OA＝r，则有r2＝52+（r﹣1）2，解得r＝13，∴⊙O的直径为26寸，故选：C．【变式10-2】（2022秋•西城区校级期中）京西某游乐园的摩天轮采用了国内首创的横梁结构，风格更加简约．如图，摩天轮直径88米，最高点A距离地面100米，匀速运行一圈的时间是18分钟．由于受到周边建筑物的影响，乘客与地面的距离超过34米时，可视为最佳观赏位置，在运行的一圈里最佳观赏时长为　12　分钟．【分析】先求摩天轮转动的角速度为＝20°/分，再求出OC ＝OD ﹣CD ＝22（米），则OCOB ，得=12∠OBC ＝30°，然后求出最佳观赏位置的圆心角为240°，即可求解．【解答】解：如图所示：摩天轮转动的角速度为：360°÷18分＝20°/分，由题意得：AD ⊥BC ，AD ＝88米，AM ＝100米，CM ＝BN ＝34米，则OB ＝OD ＝44（米），DM ＝AM ﹣AD ＝12（米），∴CD ＝CM ﹣DM ＝34﹣12＝22（米），∴OC ＝OD ﹣CD ＝22（米），∴OC OB ，=12∵∠OCB ＝90°，∴∠OBC ＝30°，∴∠BOC ＝90°﹣30°＝60°，∴∠AOB ＝180°﹣∠BOC ＝120°，∴最佳观赏位置的圆心角为2×120°＝240°，∴在运行的一圈里最佳观赏时长为：240°÷20°/分＝12（分钟），故答案为：12．【变式10-3】（2022•浙江）如图，公园内有一个半径为20米的圆形草坪，A ，B 是圆上的点，O 为圆心，∠AOB ＝120°，从A 到B 只有路，一部分市民为走“捷径”，踩坏了花草，走出了一条小路ABAB ．通过计算可知，这些市民其实仅仅少走了 15　步（假设1步为0.5米，结果保留整数）．（参考数据： 1.732，π取3.142）3≈【分析】作OC ⊥AB 于C ，如图，根据垂径定理得到AC ＝BC ，再利用等腰三角形的性质和三角形内角和计算出∠A ＝30°，则OC ＝10，AC ＝10，所以AB ≈69（步），然后利用弧长公式计算出的长，3AB 最后求它们的差即可．【解答】解：作OC ⊥AB 于C ，如图，则AC ＝BC ，∵OA ＝OB ，∴∠A ＝∠B （180°﹣∠AOB ）（180°﹣120°）＝30°，=12=12在Rt △AOC 中，OC OA ＝10，AC OC ＝10，=12=33∴AB ＝2AC ＝2069（步）；3≈而的长84（步），AB =120⋅π⋅20180≈的长与AB 的长多15步．AB 所以这些市民其实仅仅少走了 15步．故答案为15．。

垂径定理一.选择题★1．如图1，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，那么弦AB的长是（）A．4 B．6 C．7 D．8答案：D★★2．如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的一个动点，则线段OM 长的最小值为（）A．2 B．3 C．4 D．5答案：B★★3．过⊙O内一点M的最长弦为10 cm，最短弦长为8cm，则OM的长为（）A．9cm B．6cm C．3cm D．cm41答案：C★★4．如图，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA、OB在O 点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（）A．12个单位 B．10个单位 C．1个单位 D．15个单位答案：B★★5．如图，O⊙的直径AB垂直弦CD于P，且P是半径OB的中点，6cmCD ，则直径AB的长是（）A． B． C． D．答案：D★★6．下列命题中，正确的是（）A．平分一条直径的弦必垂直于这条直径B．平分一条弧的直线垂直于这条弧所对的弦C．弦的垂线必经过这条弦所在圆的圆心D．在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心答案：D★★★7．如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为( )A．5米 B．8米 C．7米 D．53米答案：B★★★8．⊙O的半径为5cm，弦AB//CD，且AB=8cm,CD=6cm,则AB与CD之间的距离为( )A． 1 cm B． 7cm C． 3 cm或4 cm D． 1cm 或7cm答案：D★★★9．已知等腰△ABC的三个顶点都在半径为5的⊙O上，如果底边BC的长为8，那么BC边上的高为( )A．2 B．8 C．2或8 D．3答案：C二.填空题★1．已知AB是⊙O的弦，AB＝8cm，OC⊥AB与C，OC=3cm，则⊙O的半径为 cm 答案：5 cm★2．在直径为10cm的圆中，弦AB的长为8cm，则它的弦心距为 cm答案：3 cm★3．在半径为10的圆中有一条长为16的弦，那么这条弦的弦心距等于答案：6★★4．已知AB是⊙O的弦，AB＝8cm，OC⊥AB与C，OC=3cm，则⊙O的半径为 cm 答案：5 cm★★5．如图，⊙O的直径AB垂直于弦CD，垂足为E，若∠COD＝120°，OE＝3厘米，则CD＝厘米图 4答案：★★6．半径为6cm的圆中，垂直平分半径OA的弦长为 cm.答案：★★7．过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm，则OM的长等于cm★★8．已知AB是⊙O的直径，弦CD⊥AB，E为垂足，CD=8，OE=1，则AB=____________ 答案：★★9．如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD ＝l，则弦AB的长是答案：6★★10．某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，半径OA＝10m，则中间柱CD的高度为 m答案：4★★11．如图，在直角坐标系中，以点P为圆心的圆弧与轴交于A、B两点，已知P(4，2)和A(2，0)，则点B的坐标是答案：(6，0)★★12．如图，AB 是⊙O 的直径，OD ⊥AC 于点D ，BC=6cm ，则OD= cm答案：3★★13．如图，矩形ABCD 与圆心在AB 上的圆O 交于点G 、B 、F 、E ，GB=10，EF=8，那么AD=答案：3★★14．如图，⊙O 的半径是5cm ，P 是⊙O 外一点,PO=8cm ，∠P=30º,则AB= cmPBAO答案：6★★★15．⊙O 的半径为13 cm ，弦AB ∥CD ，AB ＝24cm ，CD ＝10cm ，那么AB 和CD 的距离是 Cm 答案：7cm 或17cm★★★16．已知AB 是圆O 的弦，半径OC 垂直AB ，交AB 于D ，若AB=8，CD=2，则圆的半径为 答案：5★★★17．一个圆弧形门拱的拱高为1米，跨度为4米，那么这个门拱的半径为米 答案：52★★★18．在直径为10厘米的圆中,两条分别为6厘米和8厘米的平行弦之间的距离是厘米 答案：7或1★★★19．如图，是一个隧道的截面，如果路面AB 宽为8米，净高CD 为8米，那么这个 隧道所在圆的半径OA 是___________米答案：5★★★20．如图，AB 为半圆直径，O 为圆心，C 为半圆上一点，E 是弧AC 的中点，OE 交弦AC 于点D 。

专题2.2 垂径定理及其推论【十大题型】【苏科版】【题型1 由垂径定理及其推论判断正误】 (1)【题型2 根据垂径定理与勾股定理综合求值】 (2)【题型3 根据垂径定理与全等三角形综合求值】 (3)【题型4 在坐标系中利用垂径定理求值或坐标】 (5)【题型5 利用垂径定理求平行弦问题】 (6)【题型6 利用垂径定理求同心圆问题】 (7)【题型7 垂径定理的实际应用】 (8)【题型8 垂径定理在格点中的运用】 (9)【题型9 利用垂径定理求整点】 (11)【题型10 利用垂径定理求最值或取值范围】 (12)【知识点1垂径定理及其推论】（1）垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．（2）垂径定理的推论推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧．推论3：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．【题型1由垂径定理及其推论判断正误】【例1】（2023春·九年级单元测试）如图，CD是⊙O的直径，弦AB⊥CD于点E，连接BC、BD，下列结论中不一定正确的是（）A．AE=BE B．AD=BD C．OE=DE D．AC=BC【变式1-1】（2023春·北京海淀·九年级人大附中校考阶段练习）在学习了《圆》这一章节之后,甲、乙两位同学分别整理了一个命题:甲:相等的弦所对的圆心角相等;乙:平分弦的直径垂直于这条弦.下面对这两个命题的判断,正确的是A．甲对乙错B．甲错乙对C．甲乙都对D．甲乙都错【变式1-2】（2023春·全国·九年级专题练习）下列命题正确的是（）A．垂直于弦的直径平分弦所对的两条弧B．弦的垂直平分线经过圆心C．平分弦的直径垂直于弦D．平分弦所对的两条弧的直线垂直于弦【变式1-3】（2023·福建三明·泰安模拟）如图，AB是⊙O的直径，弦CD⊥AB于点E，则下列结论正确的是（ ）A．DE=BE B．BC=BDC．△BOC是等边三角形D．四边形ODBC是菱形【题型2根据垂径定理与勾股定理综合求值】【例2】（2023·贵州遵义·统考三模）在半径为r的圆中，弦BC垂直平分OA，若BC=6，则r的值是（）A B．C．D【变式2-1】（2023春·浙江·九年级统考阶段练习）如图，已知⊙O的半径为5，弦AB=8，点E在AB上运动，连结OE，过点E作EF⊥OE交⊙O于点F，当EF最大时，OE+EF的值为．【变式2-2】（2023·湖北孝感·校联考一模）如图，△ABC内接于⊙O，OC⊥OB，OD⊥AB于D交AC于E 点，已知⊙O的半径为1，则AE2+CE2的值为（）A．1B．2C．3D．4【变式2-3】（2023春·江苏泰州·九年级校考阶段练习）如图，在⊙O中，AB是直径，P为AB上一点，过点P作弦MN，∠NPB=45°．（1）若AP=2，BP=6，求MN的长；（2）若MP=3，NP=5，求AB的长；（3）当P在AB上运动时（∠NPB=45°不变）请求出其范围．【题型3根据垂径定理与全等三角形综合求值】【例3】（2023春·江苏·九年级专题练习）如图，⊙O的弦AB垂直于CD，点E为垂足，连接OE．若AE＝1，AB=CD=6，则OE的值是（ ）A．B．C．D．【变式3-1】（2023春·全国·九年级专题练习）如图，AB为圆O直径，F点在圆上，E点为AF中点，连接EO，作CO⊥EO交圆O于点C，作CD⊥AB于点D，已知直径为10，OE＝4，求OD的长度．【变式3-2】（2023·上海·统考中考真题）已知：在圆O内，弦AD与弦BC交于点G,AD=CB,M,N分别是CB和AD 的中点，联结MN,OG．（1）求证：OG⊥MN；（2）联结AC,AM,CN，当CN//OG时，求证：四边形ACNM为矩形．【变式3-3】（2023春·江西赣州·九年级统考期末）按要求作图(1)如图1，已知AB是⊙O的直径，四边形ACDE为平行四边形，请你用无刻度的直尺作出∠AOD的角平分线OP；(2)如图2，已知AB是⊙O的直径，点C是BD的中点，AB∥CD，请你用无刻度的直尺在射线DC上找一点P，使四边形ABPD是平行四边形．【题型4在坐标系中利用垂径定理求值或坐标】【例4】（2023春·九年级单元测试）如图，在平面直角坐标系中，⊙P的圆心坐标是(3,a)(a>3)，半径为3，函数y=x的图像被⊙P截得的弦AB的长为a的值是（ ）A．4B．3+C．D．3+【变式4-1】（2023·全国·九年级专题练习）如图，在平面直角坐标系中，点A的坐标是(10,0)，点B的坐标是(8,0)，点C，D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，求点C的坐标．【变式4-2】（2023·江苏南京·九年级专题练习）如图，在平面直角坐标系中，一个圆与两坐标轴分别交于A、B、C、D四点．已知A（6，0），B（﹣2，0），C（0，3），则点D的坐标为．【变式4-3】（2023春·湖北鄂州·九年级校联考期末）如图，在平面直角坐标系中，⊙O经过点(0,10)，直线y=kx+2k−4与⊙O交于B、C两点，则弦BC的最小值是（）A．B．C．D．以上都不对【题型5利用垂径定理求平行弦问题】【例5】（2023·全国·九年级专题练习）在半径为10的⊙O中，弦AB=12，弦CD=16，且AB∥CD，则AB 与CD之间的距离是．【变式5-1】（2023春·浙江杭州·九年级校考阶段练习）如图，矩形ABCD与圆心在AB上的☉O交于点G，B，F，E，GB =5，EF =4，那么AD = ．【变式5-2】（2023春·九年级课时练习）如图，AB，CD是半径为15的⊙O的两条弦，AB＝24，CD＝18，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上任意一点，则PA＋PC的最小值为．【变式5-3】（2023·全国·九年级专题练习）如图，A，B，C，D在⊙O上，AB//CD经过圆心O的线段EF⊥AB 于点F，与CD交于点E，已知⊙O半径为5．（1）若AB=6，CD=8，求EF的长；（2）若CD=EF=BF，求弦AB的长；【题型6利用垂径定理求同心圆问题】【例6】（2023春·湖北孝感·九年级校联考阶段练习）如图，两个圆都是以O为圆心．（1）求证：AC=BD；（2）若AB=10，BD=2，小圆的半径为5，求大圆的半径R的值．【变式6-1】（2023春·浙江台州·九年级统考期末）如图，一人口的弧形台阶，从上往下看是一组同心圆被一条直线所截得的一组圆弧．已知每个台阶宽度为32cm（即相邻两弧半径相差32cm），测得AB=200cm，AC=BD=40cm，则弧AB所在的圆的半径为cm【变式6-2】（2023春·九年级课时练习）将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水面AB的宽度是（ ）cm.A．6B．C．D．【变式6-3】（2023·浙江杭州·九年级）如图，两个同心圆的半径分别为2和4，矩形ABCD的边AB和CD分别是两圆的弦，则矩形ABCD面积的最大值是．【题型7垂径定理的实际应用】【例7】（2023·浙江温州·校联考二模）如图，是某隧道的入口，它的截面如图所示，是由APB和直角∠ACB 围成，且点C也在APB所在的圆上，已知AC=4m，隧道的最高点P离路面BC的距离DP=7m，则该道路的路面宽BC=m；在APB上，离地面相同高度的两点E，F装有两排照明灯，若E是AP的中点，则这两排照明灯离地面的高度是m．【变式7-1】（2023春·浙江嘉兴·九年级平湖市林埭中学校联考期中）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．(1)请你用直尺和圆规补全这个输水管道的圆形截面（保留作图痕迹）；(2)若这个输水管道有水部分的水面宽AB=8cm，水面最深地方的高度为2cm，求这个圆形截面的半径．【变式7-2】（2023春·河北邢台·九年级校联考期末）“筒车”是一种以水流作动力，取水灌田的工具．如图，“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆，已知圆心O始终在水面上方．且当圆被水面截得的弦AB 为6米时，水面下盛水筒的最大深度为1米（即水面下方部分圆上一点距离水面的最大距离）．(1)求该圆的半径；(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时，则水面下盛水筒的最大深度为多少米？【变式7-3】（2023·湖南·统考中考真题）问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图①）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都按逆时针做匀速圆周运动，每旋转一周用时120秒．问题设置：把筒车抽象为一个半径为r的⊙O．如图②，OM始终垂直于水平面，设筒车半径为2米．当t=0时，某盛水筒恰好位于水面A处，此时∠AOM=30°，经过95秒后该盛水筒运动到点B处．（参考数据，≈1.414 1.732）问题解决：(1)求该盛水筒从A处逆时针旋转到B处时，∠BOM的度数；(2)求该盛水筒旋转至B处时，它到水面的距离．（结果精确到0.1米）【题型8垂径定理在格点中的运用】【例8】（2023春·湖北武汉·九年级校联考期末）如图是由小正方形组成的7×6网格，每个小正方形的顶点叫做格点．仅用无刻度的直尺在给定网格中完成画图．(1)在图（1）中，A，B，C三点是格点，画经过这三点的圆的圆心O，并在该圆上画点D，使AD=BC；(2)在图（2）中，A，E，F三点是格点，⊙I经过点A．先过点F画AE的平行线交⊙I于M，N两点，再画弦MN的中点G．【变式8-1】（2023春·辽宁盘锦·九年级校考阶段练习）如图，平面直角坐标系中有一段弧经过格点（正方形网格交点）A、B、C，其中B(2,3)，则圆弧所在圆的圆心坐标为．【变式8-2】（2023春·河南驻马店·九年级统考期末）小英家的圆形镜子被打碎了，她拿了如图（网格中的每个小正方形边长为1）的一块碎片到玻璃店，配制成形状、大小与原来一致的镜面，则这个镜面的半径是．【变式8-3】（2023·北京·九年级专题练习）如图，在每个小正方形的边长为1cm的网格中，画出了一个过格点A，B的圆，通过测量、计算，求得该圆的周长是cm．（结果保留一位小数）【题型9利用垂径定理求整点】【例9】（2023春·九年级课时练习）如图，AB是⊙C的弦，直径MN⊥AB于点O，MN=10，AB=8，如图以O为原点建立坐标系．我们把横纵坐标都是整数的点叫做整数点，则线段OC长是，⊙C上的整数点有个．【变式9-1】（2023春·全国·九年级统考期中）⊙O的直径为10，弦AB=6，P是弦AB上一动点，满足线段OP的长为整数的点P有处不同的位置．【变式9-2】（2023春·九年级单元测试）如图，在平面直角坐标系中，A(0,4),B(4,4),C(6,2)．注：把在平面直角坐标系中横纵坐标均为整数的点称为格点(latticepo int)．（1）若经过A、B、C三点的圆弧所在的圆心为M，则点M的坐标为；（2）若画出该圆弧所在的圆，则在整个平面坐标系网格中该圆共经过格点．【变式9-3】（2023·湖南邵阳·校联考一模）⊙O的直径为10，弦AB=8，点P为AB上一动点，若OP的值为整数，则满足条件的P点有个．【题型10利用垂径定理求最值或取值范围】【例10】（2023春·湖北武汉·九年级校考阶段练习）如图，矩形ABCD的顶点A，C在半径为5的⊙O上，D(2,1)，当点A在⊙O上运动时，点C也随之运动，则矩形ABCD的对角线AC的最小值为（）．A．B．C．10+D．【变式10-1】（2023·广东佛山·统考二模）如图，⊙O的半径为5cm，弦AB=8cm，P是弦AB上的一个动点，则OP的长度范围是（）A．8≤OP≤10B．5≤OP≤8C．4≤OP≤5D．3≤OP≤5【变式10-2】（2023春·浙江金华·九年级统考期中）如图，⊙O的半径OF⊥弦AB于点E，C是⊙O上一点，EF=2，AB=12，CE的长的最大值为．【变式10-3】（2023春·全国·九年级专题练习）如图，以G(0,1)为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙G上一动点，CF⊥AE于F，则弦AB的长度为；当点E在⊙G 的运动过程中，线段FG的长度的最小值为．。

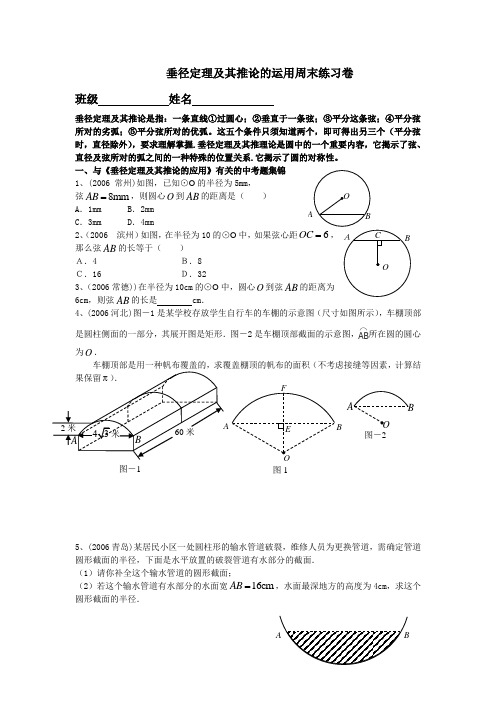
垂径定理及其推论的运用周末练习卷班级 姓名垂径定理及其推论是指：一条直线①过圆心；②垂直于一条弦；③平分这条弦；④平分弦所对的劣弧；⑤平分弦所对的优弧。

这五个条件只须知道两个，即可得出另三个（平分弦时，直径除外），要求理解掌握.垂径定理及其推理论是圆中的一个重要内容，它揭示了弦、直径及弦所对的弧之间的一种特殊的位置关系.它揭示了圆的对称性。

一、与《垂径定理及其推论的应用》有关的中考题集锦 1、(2006 常州)如图，已知⊙O 的半径为5mm ，弦8mm AB =，则圆心O 到AB 的距离是（ ）A ．1mmB ．2mmC ．3mmD ．4mm2、（2006 滨州）如图，在半径为10的⊙O 中，如果弦心距6OC =，那么弦AB 的长等于（ ）Ａ．4 Ｂ．8Ｃ．16 Ｄ．32 3、（2006常德))在半径为10cm 的⊙O 中，圆心O 到弦AB 的距离为6cm ，则弦AB 的长是 cm ．4、(2006河北)图－1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图－2是车棚顶部截面的示意图，⌒AB所在圆的圆心为O ．车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结5、(2006青岛)某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下面是水平放置的破裂管道有水部分的截面． （1）请你补全这个输水管道的圆形截面；（2）若这个输水管道有水部分的水面宽16cm AB=圆形截面的半径．图－1 图－2图16、(2006上海)本市新建的滴水湖是圆形人工湖．为测量该湖的半径，小杰和小丽沿湖边选取A ，B ，C 三根木柱，使得A ，B 之间的距离与A ，C 之间的距离相等，并测得BC 长为240米，A 到BC 的距离为5米，如图所示．请你帮他们求出滴水湖的半径．7、(2006烟台)如图，用一块直径为a 的圆桌布平铺在对角线长为a 的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x 为（ ）Ａ．)1aＢ．12aＣ．24a -Ｄ．(2a - 8、(2006 湛江)如图，⊙O 的半径为5，弦AB 的长为8，点M 在线段AB（包括端点A B ，）上移动，则OM 的取值范围是（ ）Ａ．35OM ≤≤ Ｂ．35OM <≤Ｃ．45OM ≤≤ Ｄ．45OM <≤9、(2006 镇江)如图，已知⊙O 的半径为5mm ，弦8mm AB =，则圆心O 到AB 的距离是（ ）A ．1mmB ．2mmC ．3mmD ．4mm10、（2006 菏泽）如图，底面半径为5dm 的圆柱形油桶横放在水平地面上，向桶内加油后，量得长方形油面的宽度为8dm ，则油的深度（指油的最深处即油面到水平地面的距离）为（ ）Ａ．2dm Ｂ．3dm Ｃ．2dm 或3dm Ｄ．2dm 或8dm 11、（2006 衡阳）如图，水平放置的一个油管的截面半径为13cm ，其中有油部分油面宽AB 为24cm ，则截面上有油部分油面高CD （单位：cm ）为 . 12、（2006 新疆）如图，⊙O 的半径长为12cm ，弦16cm AB =． （1）求圆心到弦AB 的距离．（2）考生注意：本小题为超量给分题，超量分2分 如果弦AB 的两端点在圆周上滑动（AB 弦长不变），那么弦AB 的中点形成什么样的图形？13、（2006 沈阳）如图，已知在⊙O 中，直径10MN =，正方形ABCD 的四个顶点分别在半径OM ，OP 以及⊙O 上，并且45POM =∠，则AB 的长为 ．14、（2006 湘潭）如图，在半径为2的⊙O 中，弦AB的长为_______AOB =∠15、（2006 兰州A ）在⊙O 中，弦CD 与直径AB 相交于点P ，夹角为30，且分直径为1:5两部分，6AB =厘米，则弦CD 的长为（ ）厘米．Ａ．Ｂ．Ｃ．Ｄ．16、（2006 辽宁十一市）如图，已知⊙O 的半径是10，弦AB 长为16．现要从弦AB 和劣弧 AB 组成的弓形上画出一个面积最大的圆，所画出的圆的半径为 ． 17、（2006 浙江湖州）如图，在⊙O 中，AB 是弦，OC AB ⊥，垂足为C ，若16AB =，6OC =，则⊙O 的半径OA 等于（ ）Ａ．16 Ｂ．12 Ｃ．10 Ｄ．818、（2006 漳州）如图，已知⊙O 中，MN 是直径，AB 是弦，垂足为C ，由这些条件可推出结论 （不添加辅助线，论）．19、（2006龙岩三县）如图，已知⊙O 的半径为5，弦8AB P =，是弦AB 上一点，且2PB =，则_____OP =．二、小结（1）在计算中的运用例1．如图，半径为2的圆内有两条互相垂直的弦AB 和CD ，它们的交点E 到圆心O 的距离等于1，则22CD AB +＝（ ） A ．28 B ．26 C ．18 D ．35∙1 图MNEO DCBA例2．如图，⊙O 的直径AB 和弦CD 相交于E ，若AE ＝2cm ，BE ＝6cm ，∠CEA ＝300，求：（1）CD 的长；（2）C 点到AB 的距离与D 点到AB 的距离之比．（2）在证明中的应用例3．不过圆心的直线l 交⊙O 于C 、D 两点，AB 是⊙O 的直径，AE ⊥l 于E ，BF ⊥l 于F ． （1）如图，在下面三个圆中分别补画出满足上述条件的具有不同位置关系的图形； （2）请你观察（1）中所画的图形，写出一个各图都具有的两条线段相等的结论（不再标注其它字母，找结论的过程中所连辅助线不能出现在结论中，不写推理过程）； （3）请你选择（1）中的一个图形，证明（2）所得出的结论．∙①∙②∙③（3）在实际问题中的运用例4．如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？∙ 2 图 E O D C B A。

（垂径定理）一、选择题1. 已知下列命题：①平分弦的直径必平分这条弦所对的弧②同圆中两条弦所夹的弧相等，则这两条弦平行③平分弧的直线必经过圆心④等腰三角形顶角平分线所在直线必过其外接圆圆心，其中错误命题的个数是()A. 1个B. 2个C. 3个D. 4个2. 已知⊙O的直径AB=12cm，P为OB中点，过P作弦CD与AB相交成30°角，则弦CD 的长为( )A. B. C. D.3. 已知AB为⊙O的直径，弦CD⊥AB，垂足为E，则下列结论错误的是( )A. CE=DEB.C. ∠BAC=∠BADD. AC>BD4. 已知：如图1，AB是⊙O的直径，弦EF⊥AB于点D，如果EF=8，AD=2，则⊙O的半径是( )A. 5B.C. 4D.5. 已知点P是半径为5的⊙O内一定点，且OP=4，则过点P的所有弦中，弦长可能取的整数值为()A. 5，4，3B. 10，9，8，7，6，5，4，3C. 10，9，8，7，6D. 12，11，10，9，8，7，66. 如图2，EF是⊙O的直径，AB是弦，EF=10cm，AB=8cm，则E、F两点到直线AB的距离之和为( )A. 3cmB. 4cmC. 8cmD. 6cm7. 如图3，⊙O的直径为25，点P是弦AB的中点，弦CD过P点，且AB=20，CD=24，则cos∠APC的值为()A. B. C. D.8. 在⊙O中，弦AB的长为8cm，圆心到弦AB的距离为3cm，则⊙O的半径为___。

9. 如图4，同心圆中，大圆的弦AB交小圆于C、D，已知AB=4，CD=2，O到AB的距离等于1，则两个同心圆的半径之比为_____(大圆半径比小圆半径)10. ⊙O的弦AB与直径CD垂直，CD=1，则的长度为____。

11. (2004甘肃)如图5，有一圆弧形门拱的拱高AB为1米，跨度CD为4米，则这个门拱的半径为____米。

12. ⊙O的直径为10，弦AB=6，P是AB上一动点，则OP的取值范围是____。

垂径定理的应用专题试题精选附答案一．选择题（共9小题）1．（2015•潍坊）将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水部分的面积是（）A．（π﹣4）cm2B．（π﹣8）cm2C．（π﹣4）cm2D．（π﹣2）cm22．（2015•滕州市校级四模）当宽为3cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm）那么该圆的半径为（）A．8cm B．9cm C．cm D．10cm3．（2015•鄂城区模拟）在截面为半圆形的水槽内装有一些水，如图．水面宽AB为6分米，如果再注入一些水后，水面AB上升1分米，水面宽变为8分米，则该水槽截面直径为（）A．5分米B．6分米C．8分米D．10分米4．（2015•杭州模拟）某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧（如图所示），他量了下两砖之间的距离刚好是80cm，聪明的你，请你算出大石头的半径是（）A．40cm B．30cm C．20cm D．50cm5．（2014•无锡校级模拟）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器厚度，则球的半径为（）A．5cm B．6cm C．7cm D．8cm6．（2015•江夏区模拟）在某岛A的正东方向有台风，且台风中心B距离小岛A km，台风中心正以30km/h的速度向西北方向移动，距离中心50公里以内圆形区域（包括边界）都受影响，则小岛A受到台风影响的时间为（）A．不受影响 B．1小时C．2小时D．3小时7．（2015•浙江模拟）如图，有一圆弧形门拱，拱高AB=1m，跨度CD=4m，那么这个门拱的半径为（）A．2m B．2.5m C．3m D．5m8．（2014•南宁）在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm9．（2014•滦县一模）已知如图，圆柱OO1的底面半径为13cm，高为10cm，一平面平行于圆柱OO1的轴OO1，且与轴OO1的距离为5cm，截圆柱得矩形ABB1A1，则截面ABB1A1的面积是（）A．240cm2B．240πcm2C．260cm2D．260πcm2二．填空题（共15小题）10．（2015•衢州）一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽CD等于m．11．（2015•黔南州）如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A、B，并使AB与车轮内圆相切于点D，半径为OC⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径是．12．（2015•六盘水）赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图，若桥跨度AB约为40米，主拱高CD约10米，则桥弧AB所在圆的半径R=米．13．（2015•东营）如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB 为0.8m，则排水管内水的深度为m．14．（2015•杭州模拟）为了节省空间，时尚装修的设计师设计出一款餐桌，餐桌的两边翻开后会成圆形桌面（如图1）．餐桌两边AB和CD平行且相等（如图2），小华用皮带尺量出AC=1.6米，AB=0.8米，那么桌面翻成圆桌后，桌子面积会增加平方米．（结果保留π）15．（2014•茂名）如图，小丽荡秋千，秋千链子的长OA为2.5米，秋千向两边摆动的角度相同，摆动的水平距离AB为3米，则秋千摆至最高位置时与最低价位置时的高度之差（即CD）为米．16．（2015•夏津县一模）一副量角器与一块含30°锐角的三角板如图所示放置，三角板的直角顶点C落在量角器的直径MN上，顶点A，B恰好都落在量角器的圆弧上，且AB∥MN．若AB=8cm，则量角器的直径MN=cm．17．（2015•黄岛区校级模拟）一破损光盘如图所示，测得所剩圆弧两端点间的距离AB长为8厘米，弧的中点到弧所对弦的距离为2厘米，则这个光盘的半径是厘米．18．（2015•孝义市一模）如图，某公园的一角有一块草坪（阴影部分），实线部分是沿草坪外围的一条小路，小路由两条相等的线段AC、BD和圆弧CD组成，其中AC、BD分别与圆弧CD相切于点C、D．经过测量，线段CD与半径OD都为60米，则这条小路的长度为米．19．（2015•江岸区校级模拟）为了测量某小球的直径，技术人员将小球放到透明烧杯上，如图是过球心O作为截面图，已知烧杯的高度是13cm，测得l=8cm，h=11cm，则小球的直径为cm．20．（2014•台州）如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为cm．21．（2014•杭州模拟）某居民区一处圆形下水管道破裂，修理人员准备更换一段与原管道同样粗细的新管道．如图，水面宽度原有60cm，发现时水面宽度只有cm，同时水位也下降65cm，则修理人员应准备的半径为cm的管道．22．（2014•绍兴）把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为．23．（2006•黑龙江）如图，一条公路的转弯处是一段圆弧（图中的AB），点O是这段弧的圆心，AB=120m，C是AB上一点，OC⊥AB，垂足为D，CD=20m，则这段弯路的半径为m．24．（2005•锦州）如图是一个俱乐部的徽章．徽章的图案是一个金色的圆圈，中间是一个矩形，矩形中间又有一个蓝色的菱形，徽章的直径为2cm，则徽章内的菱形的边长为cm．三．解答题（共6小题）25．（2015•麻城市校级模拟）图1是某希望小学放心食堂售饭窗口外遮雨棚的示意图（尺寸如图所示），遮雨棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是遮雨棚顶部截面的示意图，所在圆的圆心为O．遮雨棚顶部是用一种帆布覆盖的，求覆盖遮雨棚顶的帆布的面积（不考虑接缝等因素，计算结果保留π）．26．（2015•余姚市校级模拟）如图是大型输气管的截面图（圆形），某次数学实践活动中，数学课题学习小组为了计算大型输气管的直径，在圆形弧上取了A，B两点并连接AB，在劣弧AB上取中点C连接CB，经测量米，∠ABC=36.87°，请根据这些数据计算出大型输气管的直径（精确到0.1米）．（sin36.87°≈0.60，cos36.87°≈0.80，tan36.87°≈0.75）27．（2015•从化市一模）某公园管理人员在巡视公园时，发现有一条圆柱形的输水管道破裂，通知维修人员到场检测，维修员画出水平放置的破裂管道有水部分的截面图（如图）．（1）请你帮忙补全这个输水管道的圆形截面（不写作法，但应保留作图痕迹）；（2）维修员量得这个输水管道有水部分的水面宽AB=cm，水面最深地方的高度为6cm，请你求出这个圆形截面的半径r及破裂管道有水部分的截面图的面积S．28．（2015•普陀区一模）如图，某新建公园有一个圆形人工湖，湖中心O处有一座喷泉，小明为测量湖的半径，在湖边选择A、B两个点，在A处测得∠OAB=45°，在AB延长线上的C处测得∠OCA=30°，已知BC=50米，求人工湖的半径．（结果保留根号）29．（2015春•敦煌市校级期中）如图，公路MN和公路PQ在点P处交会，且∠QPN=30°．点A处有一所中学，AP=160m，一辆拖拉机从P沿公路MN前行，假设拖拉机行驶时周围100m 以内会受到噪声影响，那么该所中学是否会受到噪声影响，请说明理由，若受影响已知拖拉机的速度为18km/h，那么学校受影响的时间为多长？30．（2015秋•滨湖区期中）如图，一条公路的转弯处是一段圆弧AB．（1）作出AB所在圆的圆心O；（用直尺和圆规作图，保留作图痕迹，不写作法）（2）若弧AB的中点C到弦AB的距离为20m，AB=80m，求AB所在圆径．垂径定理的应用专题试题精选附答案参考答案一．选择题（共9小题）1．A；2．C；3．D；4．D；5．A；6．C；7．B；8．A；9．A；二．填空题（共15小题）10．1.6；11．50cm；12．25；13．0.8；14．；15．0.5；16．4；17．5；18．120+2π；19．10；20．50；21．50；22．5；23．100；24．1；三．解答题（共6小题）25．；26．；27．；28．；29．；30．；。

垂径定理的应用知识考点:垂径定理及其推论是指:一条直线①过圆心;②垂直于一条弦;③平分这条弦(平分弦时，直径除外);④平分弦所对的劣弧;⑤平分弦所对的优弧。

“知二推三”数学符号：①CD过O点；②ABCD⊥；③BMAM=;④AC BC=;⑤AD BD=;一、作弦心距+用勾股定理思考1：如图，O的弦AB长为m，圆心O到AB的弦心距为d，O的半径为r，试探究r,m,d 之间的数量关系．①单勾股例1如图，在ABCBACBC=，以点C为圆心，CB为半径∠=︒，2∠=︒，20∆中，已知130ACB的圆交AB于点D，则BD的长为．（限时训练第3题）例1 变式1 例2 【变式练习1】如图，AB为O的直径，弦CD ABEB=，则O的CD=，1⊥于点E，已知6半径为．（课堂完成）②双勾股例2 如图，已知半径为2的O 有两条互相垂直的弦AB 和CD ，其交点E 到圆心O 的距离为1，则22AB CD += ．（限时训练第6题）【变式练习2】（2018长沙26题改编）如图，A ，B ，C ，D 是半径为1的O 上按逆时针方向排列的四个动点，AC BD ⊥，当2267AC BD +时，求OE 的取值范围；（课堂完成）二、弧中点→连半径，得垂径思考2： 如图，AB 是O 的弦，C 是AB 的中点，你能得到那些结论?例2 如图，AB 为O 直径，D 为BC 弧的中点，DE AC ⊥于E ， （1）求证：DE 为O 的切线；（2）已知：2CE =，4DE =，求O 的半径．（限时训练第7题）【变式练习3】如图，CD为O的直径，弦AB CD=，⊥，垂足为E，AB BFAB=，则弦AF的长度为．（课堂完成）1CE=，6【变式练习4】如图，已知AB是O的直径，O与Rt ACD∆的两直角边分别交于点E、F，点F是弧BE的中点，90∠=︒，连接AF．C（1）求证：直线DF是O的切线．（2）若1BD=，2∠的值．（课堂完成）OB=，求tan AFC【拓展提升】如图，在平面直角坐标系xoy 中，点E 在x 轴的正半轴上，E 交x 轴于A 、B 两点，交y 轴于C 、D 两点，且G 为BC 弧的中点，若点A 的坐标为(2,0)-，4AE =（1）求点C 的坐标； （2）求CAG ∠的度数；（3）若F 点的坐标为(10,0)，问直线FG 与E 的位置关系，并说明理由．限时训练1．如图，一条公路的转弯处是一段圆弧()AB ，点O 是这段弧所在圆的圆心，40AB m =，点C 是AB 的中点，点D 是AB 的中点，且10CD m =，则这段弯路所在圆的半径为( ) A ．25mB ．24mC ．30mD ．60m2．如图，O 的半径为4，ABC ∆是O 的内接三角形，连接OB 、OC ．若BAC ∠与BOC ∠互补，则弦BC 的长为( ) A ．33B ．43C ．53D ．63第1题 第2题 第3题3．如图，在ABC ∆中，已知130ACB ∠=︒，20BAC ∠=︒，2BC =，以点C 为圆心，CB 为半径的圆交AB 于点D ，则BD 的长为 ．4．如图，AB 是O 的弦，C 、D 分别是弦AB 和弧AB 的中点，OC AB ⊥于C ，若25AB cm =，1CD cm =，则O 的半径长为 cm ．第4题 第5题 第6题5．如图，一下水管道横截面为圆形，直径为100cm ，下雨前水面宽为60cm ，一场大雨过后，水面宽为80cm ，则水位上升 cm ．6．如图，已知半径为2的O 有两条互相垂直的弦AB 和CD ，其交点E 到圆心O 的距离为1，则22AB CD += ．7．如图，AB 为O 直径，D 为BC 弧的中点，DE AC ⊥于E ， （1）求证：DE 为O 的切线；（2）已知：2CE =，4DE =，求O 的半径．（此部分课堂完成）【变式练习1】 如图，AB 为O 的直径，弦CD AB ⊥于点E ，已知6CD =，1EB =，则O 的半径为 ．【变式练习2】（2018长沙26题改编）如图，A ，B ，C ，D 是半径为1的O 上按逆时针方向排列的四个动点，AC BD ⊥，当2267AC BD +时，求OE 的取值范围；【变式练习3】如图，CD 为O 的直径，弦AB CD ⊥，垂足为E ，AB BF =，1CE =，6AB =，则弦AF 的长度为 ．（课堂完成）【变式练习4】如图，已知AB 是O 的直径，O 与Rt ACD ∆的两直角边分别交于点E 、F ，点F 是弧BE 的中点，90C ∠=︒，连接AF ． （1）求证：直线DF 是O 的切线．（2）若1BD =，2OB =，求tan AFC ∠的值．（课堂完成）可做出周考的剩题1．如图，AB 是O 的直径，4AB =，点M 是OA 的中点，过点M 的直线与O 交于C 、D 两点．若45CMA ∠=︒，则弦CD 的长为 ．2．已知O 的直径10CD cm =，AB 是O 的弦，AB CD ⊥，垂足为M ，且8AB cm =，则AC 的长为( ) A ．25cmB ．45cmC ．25cm 或45cmD ．23cm 或43cm3．如图，点C 为AB 弧的中点，点D 为O 上一点，30D ∠=︒，4BC cm =，求O 的半径长．。

垂径定理练习题及答案垂径定理练习题及答案垂径定理是几何学中的一个重要定理，它解决了关于圆的切线和半径之间的关系问题。

在学习和应用垂径定理时，我们需要通过大量的练习题来巩固理论知识，并提高解题能力。

下面将给出一些垂径定理的练习题，并附上详细的解答，希望能对大家的学习有所帮助。

练习题一：在一个圆中，直径为10厘米，且过圆心的直径AC与切线BD相交于点E。

若AC=8厘米，求BE的长度。

解答：根据垂径定理，切线BD与半径AC垂直，所以∠BAC=90°。

由此可知，三角形BAC是一个直角三角形。

根据勾股定理可得：BA²+AC²=BC²代入已知条件，得：BA²+8²=10²化简得：BA²+64=100移项得：BA²=36开方得：BA=6由于∠BAC=90°，所以BE也是直径，即BE=10厘米。

练习题二：在一个圆中，直径为16厘米，切线AB与半径CD相交于点E。

若AE=3厘米，求BE的长度。

解答：同样地，根据垂径定理，切线AB与半径CD垂直，所以∠CAD=90°。

由此可知，三角形CAD是一个直角三角形。

根据勾股定理可得：CA²+AD²=CD²代入已知条件，得：CA²+16²=CD²化简得：CA²+256=CD²移项得：CA²=CD²-256开方得：CA=√(CD²-256)根据垂径定理，AE是半径CD的垂直平分线，所以AE=DE。

又已知AE=3厘米，所以DE=3厘米。

由于∠CAD=90°，所以BE也是直径，即BE=16厘米。

练习题三：在一个圆中，直径为12厘米，切线AB与半径CD相交于点E。

若AE=5厘米，求BE的长度。

解答：同样地，根据垂径定理，切线AB与半径CD垂直，所以∠CAD=90°。

垂径定理及其推论的应用 我们所学的几何知识可以理解为对“构图”的研究：根据．．给定的（或构造的）．．．．．．．．．几何图．．．形提出相关．．．．．的概念．．．和．问题．．（或者根据问题构造图形），并加以研究．．．．．．．．．．．．．．．．．．. 例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）.请你用上面的思想和方法对下面关于圆的问题进行研究：(1) 如图1，在圆O 所在平面上，放置一条．．直线m （m 和圆O 分别交于点A 、B ），根据这个图形可以提出的概念或问题有哪些（直接写出两个即可）？(2) 如图2，在圆O 所在平面上，请你放置与圆O 都相交且不同时经过圆心．．．．．．．的两条．．直线m 和n （m 与圆O 分别交于点A 、B ，n 与圆O 分别交于点C 、D ）.请你根据所构造的图形提出一个结论，并证明之.(3) 如图3，其中AB 是圆O 的直径，AC 是弦，D 是的中点，弦DE ⊥AB 于点F . 请找出点C 和点E 重合的条件，并说明理由.答案：解：(1) 弦（图中线段AB）、弧（图中的ACB 弧）、弓形、求弓形的面积（因为是封闭图形）等.（写对一个给1分，写对两个给2分）(2) 情形1 如图21，AB 为弦，CD 为垂直于弦AB 的直径. …………………………3分 结论：（垂径定理的结论之一）. …………………………………………………………………………4分 证明：略（对照课本的证明过程给分）. ……………………………………………………………7分 情形2 如图22，AB 为弦，CD 为弦，且AB 与CD 在圆内相交于点P .结论：PD PC PB PA ⋅=⋅. 证明：略. 情形3 （图略）AB 为弦，CD 为弦，且m 与n 在圆外相交于点P .结论：PD PC PB PA ⋅=⋅.证明：略. 情形4 如图23，AB 为弦，CD 为弦，且AB ∥CD . 结论： = .图1 图2A 图3 m 图21AD BC证明：略.（上面四种情形中做一个即可，图1分，结论1分，证明3分；其它正确的情形参照给分；若提出的是错误的结论，则需证明结论是错误的）(3) 若点C 和点E 重合，则由圆的对称性，知点C 和点D 关于直径AB 对称. …………………………………………8分 设x BAC =∠，则x BAD =∠，x ABC -︒=∠90.…………………………………………9分 又D 是的中点，所以ABC ACD CAD CAD ∠-︒=+∠=∠1802，即)90(18022x x -︒-︒=⋅.………………………………………………………………………………10分 解得︒=∠=30BAC x .………………………………………………………………………………………11分 （若求得AC AB 23=或FB AF ⋅=3等也可，评分可参照上面的标准；也可以先直觉猜测点B 、C 是圆的十二等分点，然后说明）ABC A图3 图22 图23m。