高中物理竞赛角动量守恒定律

• 角动量守恒定律是物理学的基本定律之一。 • 适用于宏观、微观、高速、低速范围。 • 可导出行星运动的开普勒第二定律。
v2r2 v1r1 mv2r2 mv1r1 12
质点的角动量守恒定律
若Mo r F 0， 则L r p 常矢量
• 外力的矢量和为零，但所有外力对参考点力矩的矢 量和未必为0（如：一对力偶），则质点系的角动量 就不守恒； • 所有外力都通过固定点时，即使系统所受合外力不 为0，但对该点每个外力的力矩为零，则系统的角动 量守恒。 • 应用角动量守恒定律时要注意参考点位置的选取。
25
质点系动能定理 A外 + A内 Ek
功能原理 A外 + A内非保 E
动量定理 I p
角动量定理
t2 M dt L t1
机械能守恒定律
质点系动量守恒定律
角动量守恒定律
A外 + A内非保 0, E 0 F外 0 ， p 常矢量 若Mo 0，L 常矢量
能量守恒定律
22
守恒定律
（1）守恒定律是关于变化过程的规律。 不究过程细节而能对系统的状态下结论， 这是各个守恒定律的特点和优点。
曲线运动
直线运动：
O
并非质点作周期性曲线运动才有角动量！
5
例题
地球绕太阳的运动可以近似地看作匀速圆周运动， 求：地球对太阳中心的角动量。
解：
L mrv 2.71040(kg m2 / s)
6
例题 2-20
F
k
e2 r2
h
2
解：
L mvr n h
2
F
k
e2 r2
man
m v2 r
n2h2
第二章 运动的守恒量和守恒定律

例2 A、B两圆盘绕各自的中心轴转动，角速度分别为
：A=50rad.s-1, B=200rad.s-1。已知A 圆盘半径
RA=0.2m, 质量mA=2kg, B 圆盘的半径RB=0.1m,
质量mB=4kg. 试求两圆盘对心衔接后的角速度 .
解：以两圆盘为系统，尽管在衔接过 程中有重力、轴对圆盘支持力及轴向
u=50m/s远大于飞船的速率v(= r) ，所以此 角动量近似地等于dm ru。在整个喷气过程
中喷出废气的总的角动量Lg应为
Lg＝ 0 mdm rumru
定轴转动刚体的角动量守恒定律
当宇宙飞船停止旋转时，其角动量为零。系统这时 的总角动量L1就是全部排出的废气的总角动量，即 为
L1Lg＝mru
刚体角动量和角动量守恒定律
1. 定轴转动刚体的角动量定理
刚体定轴转动定理：
Mz
d J
dt
由几个物体组成的系统，如果它们对同一给定
轴的角动量分别为 、J11 、…J2，2
则该系统对该轴的角动量为：
Lz Jii
i1,2,
i
对于该系统还有 M Zdd LtZd dt i Jii
定轴转动刚体的角动量定理
在外力矩作用下，从 t0 t ，
E1 2JA2 A1 2JBB 21 2JAJB2
1.3 2140J
定轴转动刚体的角动量守恒定律
例题4-13 恒星晚期在一定条件下，会发生超新星 爆发，这时星体中有大量物质喷入星际空间，同时 星的内核却向内坍缩，成为体积很小的中子星。中 子星是一种异常致密的星体，一汤匙中子星物体就 有几亿吨质量！设某恒星绕自转轴每45天转一周， 它 的 内 核 半 径 R0 约 为 2107m ， 坍 缩 成 半 径 R 仅 为 6103m的中子星。试求中子星的角速度。坍缩前后 的星体内核均看作是匀质圆球。

15
质点5-系2 角角动动量量守恒守定恒律
由
外
若
则
或
恒矢量
当质点系所受的合外力矩为零时，其角动量守恒。
16
两人质量相等
既忽略 滑轮质量
终点线
一 人 用 力 上 爬
又忽略 轮绳摩擦
终点线
一 人 握 绳 不 动
可能出现的情况是:
1(1) 两人同时到达； (2) 用力上爬者先到； (3) 握绳不动者先到； (4) 以上结果都不对。
解 因作用于物体的合外力矩为零，
故物体角动量守恒，得
O
vB
mv Ad mv Bl
lB
∴
vB

mvAd ml

4(m / s)
物体角动量： LB mv Bl
LB 1kg m2 / s
d
m vA
A
31
例7 我国第一颗东方红人造卫星的椭圆轨道长半轴为a = 7.79 ×
106 m，短半轴为 b = 7.72×106 m，周期 T = 114 min，近地点和远 地点距地心分别为 r1 = 6.82×106 m和 r2 = 8.76×106 m。（1）证明 单位时间内卫星对地心位矢扫过的面积为常量；（2）求卫星经 近地点和远地点时的速度V1 和V2 。
[ C] 【例3 】 一质点作匀速率圆周运动时,它的 （A）动量不变，对圆心的角动量也不变。 （B）动量不变，对圆心的角动量不断改变。 （C）动量不断改变，对圆心的角动量不变。 （D）动量不断改变，对圆心的角动量也不断改变。
[C]
19
1）角动量。 2）角动量守恒定律。 33）有心力与角动量守恒定律。
称为
若质点所受的合外力的方向始终通过参考点，其角动量守恒。如行星 绕太阳运动，以及微观粒子中与此类似的运动模型，服从角动量守恒定律。

F
F
力心
30 有心力：运动质点所受的力总是通过一个固定点。
特征：r // F ,
L 恒矢量 !
质点对力心的 角动量永远守恒！
40 质点对某点的角动量守恒，对另一点不一定守恒。
50 角动量守恒，不见得动量守恒。
比较 动量定理
dP
F
t2
dt
Fdt ΔP
t1
F 0 P 0
角动量定理
dL
M
t2
——质点角动量守恒定律
M
0FF过 O0点，： 中 心 力 （ 如 行 星 受中
L
·m
v （中心F 力）r
•
O
心恒 L
星的万有 r (mv )
引力） 常矢量
（1） mv r sin=const.，
（2）轨道在同一平面内。
讨论
r
F 0
r
10 M r F 0 r // F
20 是普遍规律，宏观、微观都适用。
方法二：
大小：M rF sin
方向：与 r F 相同
M
0
rP F
★ 分散力（力分散在一区域内） M r F
元力矩 dM r dF
总力矩 M dM rdF sin
例唱机的转盘绕着通过盘心的固定竖直轴转动， 唱片放上去后将受转盘的摩擦力作用而随转盘转 动。设唱片可以看成是半径为R的均匀圆盘，质
质点的角动量和角动量守 恒定律
§2-7 质点的角动量和角动量守恒定律 一、角动量（动量矩）
由于动量 不能描述转动问题。
引入质点对参考点O的角动量（angular momentum）：
L r p r (mv)
大小： L rmv sin

39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 反顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚韧勤 勉。
46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
高中物理竞赛复赛能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。

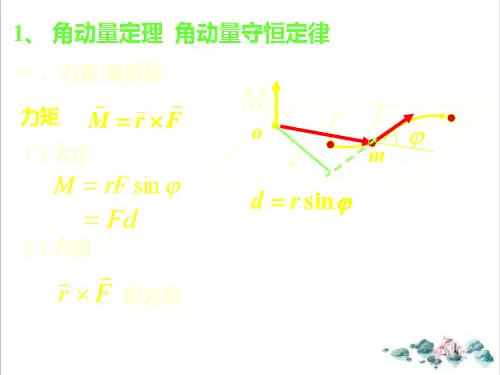
高中物理竞赛辅导讲义第6篇 角动量【知识梳理】 1．力矩（1）力对轴的力矩 力矩=力×力臂（2）力对参考点的力矩 M r F =⨯从参考点指向力的作用点的矢量r 与作用力F 的矢积。

大小 sin M Fr α=；方向 由右手螺旋定则确定。

2．角动量为了描述质点相对某一参考点的运动，可仿照力矩的定义引入动量矩的概念。

从给定的参考点指向质点的矢量和质点动量的矢积称为质点对于参考点的的动量矩。

L r p =⨯，大小 sin L pr θ=，方向 由右手螺旋定则确定。

动量矩又称角动量。

角动量是矢量，方向由右手螺旋定则确定。

3．冲量矩仿照力对时间的积累效应叫冲量，引入冲量矩的概念。

力对时间的积累效应Mt叫做冲量矩。

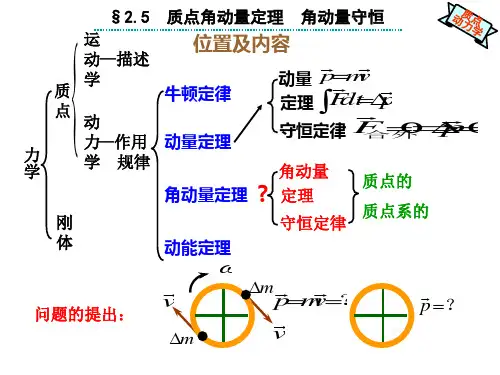
4．质点角动量定理质点对任参考点的角动量的增量等于外力的冲量矩。

21M t L L ⋅∆=- 。

质点对参考点的角动量的时间变化率等于外力对该点的力矩。

L M t∆=∆。

5．角动量守恒定律当质点所受外力对固定参考点（简称定点）的力矩为零时，质点对该点的角动量守恒。

6．转动惯量 在经典力学中，转动惯量（又称质量惯性矩，简称惯距）通常以I 或J 表示，SI 单位为kg·m 2。

对于一个质点，I =mr 2，其中m 是其质量，r 是质点和转轴的垂直距离。

转动惯量在转动中的角色相当于平动中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

7．描述平动与描述转动的相关物理量对照平动转动质量m转动惯量I=∑Δm i r i2速度v=Δx/Δt角速度ω=Δθ/Δt = v/r加速度a=Δv/Δt角加速度β=Δω/Δt = aτ/r动量p=m v角动量（动量矩）L=Iω = Σm i r i2力F力矩M = Fr sinθ牛顿第二定律F=ma刚体定轴转动定律M=Iβ冲量Ft冲量矩Mt动量定理Ft=Δp角动量定理Mt=ΔL动量守恒条件F=0 角动量守恒条件M=0平动动能m v2/2 转动动能Iω2/2【例题选讲】1．如图所示，质量为m的小球自由落下，某时刻具有速度v，此时小球与图中的A、B、C三点恰好位于某长方形四个顶点，且小球与A、C点的距离分别为l1、l2。

由此可得，每个质点相对于质心的动量分别为
m1 m 2 m1v1 p1 u u m1 m 2 p 2 m 2 v 2 u
两质点的 约化质量
⑵ 利用质心表达式，每个质点相对于质心的位矢分别为
m2 r1 r2 m2 r12 r1 r1 rc m1 m2 m1 m2 m1 r2 r1 m1r12 r2 r2 rc m1 m2 m1 m2
2 3

3 2
B
mg
由（1）和（2）可得
LdL m gR cos d
2 g sin
8

L
0
LdL m 2 gR 3 cosd L mR 0 L 2 g sin R 2 mR
第六章 角动量守恒
例题6.2 摆长为l 的锥摆作匀速圆周运动，摆线与铅 垂线成 角，求摆球速率. z
解：如图，在圆锥摆的运动过程 中，摆球相对支点 O的角动量为 .L是一个可以绕z轴 L r mv 旋转的矢量.将其分解两个分量 Lz , L ,其大小分别为

O

Lz
L
L
Lz mvl sin L mvl cos
显然，Lz 不变，而 L 随时间改变.如图,有
7
第六章 角动量守恒
例6.1 一小球沿竖直的光滑圆轨道由静止开始下滑. 求小球在B点时对环心的角动量和角速度.
解:力矩分析
M mgR cos
dL M dt
O
用角动量定理：
R
t =0 A
N
又
dL mgR cos dt （1） 2 2 d （2） L mR mR

角动量守恒定律的公式
1. 角动量守恒定律公式。

- 对于质点，角动量L = r× p（其中r是质点相对于某参考点的位矢，p = mv 是质点的动量，×表示矢量叉乘）。

- 在合外力矩M = 0时，角动量守恒，即L_1 = L_2。

- 对于定轴转动的刚体，角动量L = Iω（其中I是刚体对轴的转动惯量，ω是刚体的角速度）。

当合外力矩M = 0时，I_1ω_1=I_2ω_2。

2. 相关知识点（人教版教材相关内容补充）
- 转动惯量。

- 对于离散质点系，I=∑_im_ir_i^2，其中m_i是第i个质点的质量，r_i是该质点到转轴的垂直距离。

- 对于质量连续分布的刚体，I = ∫ r^2dm。

不同形状的刚体转动惯量有不同的计算公式，例如，对于质量为m、半径为R的均匀圆盘绕通过圆心且垂直于盘面的轴转动，其转动惯量I=(1)/(2)mR^2；对于质量为m、长为l的细棒绕通过中心且垂直于棒的轴转动，I=(1)/(12)ml^2。

- 角动量定理。

- 对于质点，M=(dL)/(dt)（M是合外力矩），这表明质点所受合外力矩等于它的角动量对时间的变化率。

- 对于刚体定轴转动，M = Iα（α是角加速度），结合L = Iω也可推导出
M=(dL)/(dt)。

的速率向东奔跑, 他感到风从北方吹来,当他奔跑的速率加倍时, 则感到风从东北方向吹来, 求风的速度。
或 牛顿力学规律在伽利略变换下形式不变
A,B,C三个质点相互间有相对运动
M dL F dp
dt
dt
对质点系而言：（以两个质点为例）
设有质点m1 、 m2
分别受外力 F1 F2
外力矩 M1 M2
作用在质点系的角冲量等于系 统角动量的增量。
三、角动量守恒定律
若 则：
M合
dL
外
力
矩 0
0L
恒矢量
dt
M dL dt
角动量守恒定律：若对某一参考点, 系统(质点)所 受合外力矩恒为零时，则此质点系(质点)对该参考 点的角动量将保持不变。
注意：角动量守恒定律是宇宙中普遍成立的定律，无 论在宏观上还是微观领域中都成立。
已知：
v sd = 10 正东
vcs
v fd = 10 v cs = 20
正西 北偏西30o
•
vfd vsd
vcd vcs v sd
vcd 10 3 km / h 方向正北
vcs vcd
v fd v fc vcd
300
v fc v fd vcd
人地 cos 450
2人
地
4.23(m
s
1
)
质点动力学(二) 人 地 人 地
450 450
风 人
风 地
二、力学的相对性原理
aAC aAB aBC
aBC 0, 同一质点的加速度在两个相互间作匀速 aAC aAB 直线运动的参照系中是相同的。
在牛顿力学中,力与参考系无关，质量与运动无关 F F

由N个质点组成的质点系
mi
ri
Fi
fi
vi
Pi · ·i · ·
Fi
·fi j· ·fj i
· j
由N个质点组成的质点系
ri
(Fi
fi )
ri
Fi
ri
fi
d Ji dt
(i 1,2,N)
i
ri Fi
i
ri fi
i
d Ji
dt
d J1 d J 2 d J N dJ
dt dt
M
x
M y
M
z
dJ x
dt dJ y
dt dJ z
dt
作用在质点上力矩在某 方向的分量等于对同一 参考 点角动量在该方向上的 分量的时间变化率
t t0
M x dt
Jx
J x0
t
t0 t
M y dt
Jy
J y0
t0 M z dt
Jz
J z0
作用在质点上冲量矩在某方向上的分量等于对 同一参考点角动量在该方向上分量的增量
v0
m
ko
m
v0
解、以初始时刻两球连线中点o为定点来 考察体系的角动量
初始时
a
a
J mv0 2 mv0 2 mv0a
体系水平方向不受外力,竖直方向外力的合 力为零,体系角动量守恒.当弹簧达到最大 伸长时,小球无径向速度,体系的角动量为
v0
m
ko
m
v0
J ' mv b mv b mvb 22
设猴一边的绳相对地下落的速度为| u | u
则猴对地的速度为 (v'u) j
r1 m(v'u) j r2 mu j 0

只是在解决转动问题时，用角动量定理较简便
§2.5 角动量定理、守恒定律—例
例 日：点处已到知日：心地距球离在为近日r2 点。处求到：日在心远距日离点为处r1的，速速度度为v2
v1
，在远
。
解：①分析：地球在太阳有心力作用下绕日运动，角动量守恒
②应用定律：
L1 L2
r 1 m v 1 r 2 m v 2
大小：MrFsin
M
o
r
F
Fd（力乘力臂）
d
m
方向： 右螺旋
单位：SI：N·m
2.说明
有心力：受力始终指向（或离开）某个中心 如：
质点受有心力作用时，力对力心的力矩=0 oF
太阳
v2
地球
MFd 0 v1
§2.5 质点角动量定理 角动量守恒（一角动量 二力矩）
2.5.3 质点的角动量定理 想法：动量随时间的变化率
当M合外0时 dLd t0 L恒矢量
即：当质点系对某点的合外力矩为零时，则质点系对该点 的角动量保持不变
§2.5 角动量定理 角动量守恒定律
说明：1.各量守恒的条件： 动量守恒 质点角动量守恒 质点系角动量守恒
F合外0 M合0 M合外0
2.对问题的求解方法： 可牛顿定律、可动量定理、可角动量定理、 可动能定理、…
v
LALB rA m v0rB m v
O l B
大小 rlA 0m m0 0vs vli9 m ns0 virnBmsvin v0l0 , k
两个未知量？
mA
rA
rB
只保守力做功→机械能守恒
1 2m0 2v1 2m2v 1 2k(ll0)2
可解
例：（P55：例2-13）已知：初始A(m1)、B(m2)同高，之后A 由

“角动量及角动量守恒定律的应用角动量（angular momentum) 在物理学中是与物体到原点的位移和动量相关的物理量。

概念：转动物体的转动惯量(rotational inertia) 和角速度(angular velocity) 的乘积叫做它的角动量。

L = IωI 是转动惯量，ω（欧米伽）是角速度。

角动量在经典力学中表示为到原点的位移和动量的叉乘，通常写做L 。

角动量是矢量。

L= r×p其中，r表示质点到旋转中心（轴心）的距离（可以理解为半径），L表示角动量。

p 表示动量。

角动量的方向：角动量是r（参考点到质点的距离矢量）叉乘动量，是两个矢量的叉乘，在右手坐标系里遵循右手螺旋法，即右手四指指向r的方向，转过一个小于180度的平面角后四指指向动量的方向，则大拇指所指的方向就是角动量的方向。

在不受外力矩作用时，体系的角动量是守恒的。

角动量在量子力学中与角度是一对共轭物理量。

角动量是一种特殊的动量，它的大小取决于转动的速率和转动物体的质量分布。

角动量守恒定律（conservation of angular momentum,law of）物理学的普遍定律之一。

反映质点和质点系围绕一点或一轴运动的普遍规律。

反映不受外力作用或所受诸外力对某定点（或定轴）的合力矩始终等于零的质点和质点系围绕该点（或轴）运动的普遍规律。

例如一个在有心力场中运动的质点，始终受到一个通过力心的有心力作用，因有心力对力心的力矩为零，所以根据角动量定理，该质点对力心的角动量守恒。

因此，质点轨迹是平面曲线，且质点对力心的矢径在相等的时间内扫过相等的面积。

如果把太阳看成力心，行星看成质点，则上述结论就是开普勒行星运动三定律之一。

一个不受外力或外界场作用的质点系，其质点之间相互作用的内力服从牛顿第三定律，因而质点系的内力对任一点的主矩为零，从而导出质点系的角动量守恒。

如质点系受到的外力系对某一固定轴之矩的代数和为零，则质点系对该轴的角动量守恒。

球滑到点 B （任意角度 θ ）时对环心 O 的角动量和角速
度。
解
小球受力
FN、
P
作用,
FN对O点的力矩为零，
重力矩垂直板面向里
M rF
M mgRcos
由质点的角动量定理
mgRcos dL
dt
dL mgRcos dt
ቤተ መጻሕፍቲ ባይዱ
10/19
dL mgRcos dt
考虑到 d dt, L mRv mR 2
L mr 2 J
L
r
p
r
mv
L
o
p
m r
※ 质点的角动量定理
M
dL
dt
作用于质点的合外力对参考点 O 的力矩，等于质点 对该点 O 的角动量随时间的变化率。
dp
F，
dL
？
dt
dt
质点角动量定理的推导，由
L
r
p
M
dL
dt
dL
d
(r
p)
r
dp
dr
p
dt dt
Miin 0 ，
Miex
d dt
(
miri 2 )
d( J )
dt
M
d( J )
dL
dt
dt
Mdt dL
Mdt
dL
d
( J )
t2 t1
Mdt
J2
J1
转动物体所受合外力矩的冲量矩等于在这段时间内转 动物体角动量的增量——定轴转动刚体的角动量定理。
※ 非刚体定轴转动的角动量定理
t2 t1
Mdt
J 22
J11
14/19
L2

dA内 F1 dr1 F2 dr2 F2 dr1 F2 dr2 F2 (dr2 dr1) F2 d(r2 r1) 0
dr1
F1
rm1 1
O
F2
dr2
m2 r2
内力的功不影响刚体的转动动能。
刚体绕定轴转动动能定理只适用于刚体的定轴转动。
4
刚体的重力势能
以xOy 平面为重力势能零参考面
t2
t1
Mdt
J2
J1
非刚体定轴转动的角动量定理
t2
t1
Mdt
J 22
J11
当转轴给定时，作用在物体上的冲量
矩等于角动量的增量．——定轴转动的角
动量定理
11
3 刚体定轴转动的角动量守恒定律
若 M 0，则 L J =常量
如果物体所受的合外力矩等于零， 或者不受外力矩的作用，物体的角动量 保持不变．——角动量守恒定律
5
刚体的力学系统的机械能
当 A外 + A非保内 = 0 时，有
E Ek Ep 恒量
（系统的机械能守恒定律）
对含有刚体的力学系统，若在运动过程中，只
有保守内力作功，而外力和非保守内力都不作
功，或作功的总和始终为零，则该系统的机械
能守恒。
6
力学系统的机械能应包括
质点的动能、重力势能，弹性势能； 平动刚体的平动动能、重力势能； 定轴转动刚体的转动动能、重力势能，即
12
讨论
➢ 守恒条件 M 0
若 J 不变，不变； 若 J 变， 也变，但 L J 不变.
➢ 内力矩不改变系统的角动量.
➢ 在冲击等问题中M in M exL 常量
➢ 角动量守恒定律是自然界的一个基本定律.

-- 行星单位时间内扫过的面积相等。
设：在合外力矩M的作用下， 推广到n个质点的质点系：
a c 角动量守恒定律：当系统所受外力矩矢量和为零时，质点系的角动量保持不变。
解：设行星绕太阳运 彗星接近太阳时势能转换成动能，而远离太阳时，动能转换成势能。
因为行星是在有心力的作用下运动的，故角动量守恒（L不变），行星的质量是常数.
动,在时间 内，从a
因t很小 ab ab s s vt 因为行星是在有心力的作用下运动的，故角动量守恒（L不变），行星的质量是常数.
例 用角动量守恒定律导出开普勒第二定律
作直线bc垂直于oa，
动,在时间 内，从a
h vt sin -- 行星单位时间内扫过的面积相等。
彗星接近太阳时势能转换成动能，而远离太阳时，动能转换成势能。
v 为 。(行星质量为m)
作直线bc垂直于oa，
作直线bc垂直于oa， h ab sin 这就是为什么彗星运转周期为几十年，而经过太阳时只有很短的几周时间。
注意：角动量守恒定律是宇宙中普遍成立的定律，无论在宏观上还是微观领域中都成立。 动,在时间 内，从a
角动量定理（积分形式）
注意：角动量守恒定律是宇宙中普遍成立的定律，无论在宏观上还是微观领域中都成立。
A 1 rvt sin
2
1 mrv sin t
2m
1 L t 2m
r
a
c
h
O
A s b
L
A 1 L t 2 m
因为行星是在有心力的作用下运动的，故角动
量守恒（L不变），行星的质量是常数.
所以 A / t 恒量（证毕）
例：彗星绕太阳作椭圆轨道运动，太阳位于椭圆轨 道的一个焦点上，问系统的角动量是否守恒？近日 点与远日点的速度谁大？

角动量及角动量守恒定律-k大量天文观测表明TmV sin& =常量定义：运动质点m对O点的角动量为L = Fx p = Hx mv 大小：Z = rmvsvnO 方向：〒x（加〒）出L=rXmV则77L=-^-<Fx»l v) = TT-X/MV + rx 生鄂^得# = r x r质点加対参考点o的d r堑千位置矿矽乖所坯的齐角动量的angular momentum吋间变化率莎"矢量尸乂来合外力炉/ -> 二二—F ................. ^-■■■■•.. ... ..... —-亠一亠g ^ ■■■I ■川工= 一二_一】大小M—FYsmG =Fd即力北Af = F X F方向垂直于天亓所决定的平面，出右螺旋法则定指向。

得质点m対给定参考点o的角动量的时I'川变化率=7 x F -M 所受的介外力矩称为质点的角动量龙理的微分形式如果各分力与。

点共面,力矩只含止、反两种方向。

可设顺时针为止向，用代数法求合力矩9质点的角动量守恒定律根据质点的角动量定理^=M ( M=r x F)若M=r x F =0则帶=0即L =常矢量当质点加所受的合外力对某参考点0的力雪历为零时，质点对该点的角动量的时间变化率豁为零，即质点对该点的角动量L守恒。

称为质点的角动量守恒定律若质点所受的合外力的方向始终通过参考点，其角动量守恒，如行星绕太阳运动，以及微观粒子中与此类似的运动模型，服从角动量守恒定律。

质点系的角动量dZ _^T7质点受:外力的时间变化率^dT~i Mi外矩的矢量和 称为 质’点:条旳角动量定瑾微分形式由菲=干莎外=図 j 匸。

"=!z odL =K-Ko 若 M = O 贝！J ZT = Lo 或 L =恒矢量当质点系所受的合外力矩为零时，苴角动量守恒。

.of angular :of partical systei 0 “点白勺箱勻云力质点系的角动量V 2Z =孚 L*=S Af XW/Vzi各质点对给定参考点的角动量的矢量和•丙恵济旳加动垦走翼 将 三=号乙=孚耳厉对时间求导#=?#=? ［^=耳［vi^miVi +A ； x/w/fl/J+ A} x 用■=耳［右x Fi 内 +右x 尺外］得=另M i 内+三M ，外=E M i 外=s dr X7M/P/ + 不X 哥-（加了厉）］ 某给定 O参考点尺rj dW1r 2m2二见内 用内F L 外内力矩在求矢 量和时成对相消惯性系中某给定参考点/Mi我国第i颗人造卫星沿椭圆轨道运动，地球的中心O为该椭圆的一个焦点•已知地球半径R=6378 kin,卫星与地］fli的最近距离Zi=439km, 与地Ifli的最远距离/2=2384 km・若卫星在近地点A\的速度s=8.1 km-s,则卫星在远地点Ai 的速度s= _____________________ .1.如木题图，一质最为m的质点白由降落，在某时刻具有速度v。