分数除法一1

数学六年级上册第三单元分数除法怎么判断单位1
1．第三单元分数除法判断单位“1”的方法和第二单元乘法中的方法一样，抓住关键词：谁的几分之，谁就是单位“1”；“多几分之几时”
抓住“多”的部分是谁的几分之几，谁是就是单位“1”；或“少几分之几”时，抓住“少”的部分是“谁的”几分之几，谁就是单位“1”。

不妨试试，有问题再问。

2、总的来说：题中“的”前面，“是”后面都是单位一，还有一种就是：例如“男生比女生少3分之1”这句话可以理解为“男生少的人数是女生的3分之1”，可得出单位一是女生人数，技巧就是“比”后面是单位一。

最重要的是理解！
3、份数量“的”前面的量就是单位“1”。

比如苹果是梨的1/2.梨就是单位“1”
4、单位“1”在分数中是指1个整体，它可以是一个物体，也可以是一些物体。

往往是把所平均分的对象看做单位“1”，如一个苹果的三分之一，就是把一个苹果看做单位“1”，如果是一堆苹果的三分之一，就是把一堆苹果看做单位“1”。

分数除法一教学反思6篇分数除法一教学反思篇14月22日上午，是我校五年级的家长开放日，我上了一节《分数与除法》的公开课。

课后有幸得到了我的导师——广西师大熊宜勤教授的点评，由于当时时间比较紧，我们要赶到拱极小学去听黄智云老师的课，匆忙之中熊教授给我提出了两点宝贵意见：1.在重难点的突破上花的时间还不够.2.练习的设计量过多,没有很好的为本节课服务。

听了她的建议以后，我陷入了深深的反思之中。

是啊，都十几年的教龄了，怎么还会犯这样的错误呢？备课时，我只考虑到家长们要来听课，脑子里想得更多的是怎样才能把课上活？煞费苦心的创设了一个猪八戒分饼的情境，虽然这样能把整节课的教学内容串联在一起，整体感比较强，学生也很喜欢，但是却没有把例2中的重难点抓住。

我的本意原是想把课堂交给学生，引导学生进行具体操作，让学生在具体操作中得出3除以4的商，以明确每人分得的不满1块，可用分数来表示，让学生明白一块饼的就等于3块饼的。

可是在教学时，由于没有及时引导学生突出单位“1”，再加上没有使用展台操作，学生的理解就是没有那么到位。

接着，我在教学例2后，引导学生观察黑板上的几个算式，总结归纳出分数与除法的关系也只用了1分多钟的时间，很多学生印象还不够深刻就进入了练习环节，以至于后面的练习出现了卡壳现象。

回想自己的这一节课，真的是有太多不足的地方。

带着熊教授给我提出的问题，第二天，我聆听了苏文俊老师上的这节课。

课一开始，她就复习了上节课中我们学习的分数的意义和分数单位等内容，接着创设了分饼情境，（1）把6块饼平均分给2个同学，每人分得多少块？（2）把1块饼平均分给2个同学，每人分得多少块？（3）把1块饼平均分给3个同学，每人分得多少块？6÷21÷21÷3从数据上看，看得出都是苏老师精心设计的。

从商是整数到商可以用小数也可以用分数表示，到除不尽需要用分数表示的思路，充分地让学生体会到解决问题的策略。

在复习了把一个数平均分，用除法计算的同时，突出了知识间的联系。

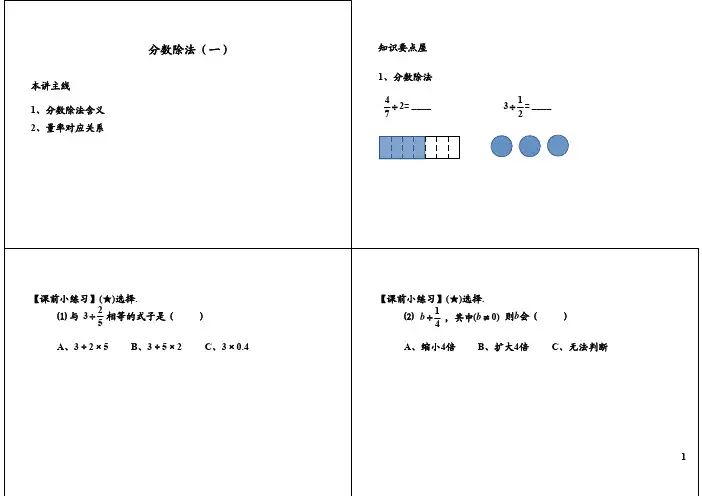
三、分数除法
1、分数除法
第一课时 分数除法1
课题：分数除法1
教学目标：
1、让学生理解分数除法的运算意义。

2、掌握分数除以整数的计算方法。

3、培养学生的计算能力和分析能力。

教学过程：
一、活动一：
1、出示例1
每盒水果糖重100克，3盒有多重？
（1） 读题，理解题意
（2） 列式：100×3=300
（3） 把乘法算式改成两道除法算式
300÷3=100 300÷100=3
（4）用千克做单位怎样列式？
101×3=10
3 （5）用同样的方法改写成除法算式
2、小结：分数除法的意义
二、活动二：
1、出示例2 把一张纸的5
4平均分成2份，每份是这张纸的几分之几？自己试着折一折，算一算 （1） 把54平均分成2份，就是把4个51平均分成2份，每份就是2个51，就是5
2 （2） 把54平均分成3份，每份就是54的31，也就是54×3
1 （3） 根据上面的折纸实验和算式，你发现什么规律？
2、小结：（略）
三、巩固练习：
1、第28页的“做一做”
2、练习八的第2题
四、作业
练习八的第1、3题。

一分数除法1.分数除法（1）分数除法的意义和分数除以整数知识点一：分数除法的意义整数除法的意义：已知两个因数的积与其中一个因数，求另一个因数的运算。

已知两个因数的积与其中一个因数，求另一个因数，用（除法）计算。

的意义是：已知两个因数的积是，其中一个因数是3，求另一个因数是多少。

分数除法的意义与整数除法的意义相同，都是已知两个因数的积与其中一个因数，求另一个因数的运算。

或者说把平均分成三份，取其中的一份。

知识点二：分数除以整数的计算方法把一个数平均分成整数份，求其中的几份就是求这个数的几分之几是多少。

分数除以整数（0除外）的计算方法：（1）用分子和整数相除的商做分子，分母不变。

（2）分数除以整数，等于分数乘这个整数的倒数。

练习：1、填空（1）根据和分数除法意义可得：（），（）。

（2）把m长的绳子平均剪成4段，每段是m的（）。

（3）打字员打一份文件，打了20分钟后还剩，平均每分钟打这份文件的（）。

2.列式计算。

（1）一个数的6倍是，这个数是多少？（2）的是多少？3.一根绳子长22米，看图列式计算（2）一个数除以分数知识点一：一个数除以分数的计算方法一个数除以分数，等于这个数乘分数的倒数。

知识点二：分数除法的统一计算法则甲数除以乙数（0除外），等于甲数乘乙数的倒数。

知识点三：商与被除数的大小关系一个数（0除外）除以小于1的数，商大于被除数，除以1，商等于被除数，除以大于1的数，商小于被除数。

0除以任何数商都为0.练习：1.算一算2.填空。

（1）的是（），它和÷（）得数相同。

（2）分数除法可以转化为（）进行计算，计算过程中，转变成乘（）的倒数。

3.判断。

（1）两个真分数相除，商大于被除数。

（）（2）一个数除以假分数，商一定小于被除数。

（）2．解决问题知识点一：已知一个数的几分之几是多少，求这个数的应用题解法列方程解题的关键：找出题中数量间的等量关系。

用算术法解除法应用题的关键：找准已知数量对应的单位“1”的几分之几。