当前位置：文档之家 › 自动控制理论第版夏德钤 翁贻方第二章控制系统的数学模型

自动控制理论第版夏德钤 翁贻方第二章控制系统的数学模型

  • 格式：ppt
  • 大小：2.46 MB
  • 文档页数：76

下载文档原格式

  / 76

合集下载

自动控制理论第2版(夏德钤著)课后习题答案下载

自动控制理论第2版(夏德钤著)课后习题答案下载

自动控制理论第2版（夏德钤著）课后习题答案下载夏德钤的《自动控制理论第2版》比拟全面和详细地介绍了经典控制理论的根本内容。

以下是为大家的自动控制理论第2版（夏德钤著），希望能对你有帮助!目前普通高等院校“自动控制理论(原理)”教学学时大致有三种，48学时、64学时和80学时。

自动控制理论(原理)涉及专业比拟多，教学内容以经典控制理论为主，控制对象依据专业而不同。

本书主要适用专业为：电气工程及其自动化，机械设计及其自动化，电子信息工程。

局部内容(例如控制对象方面的例题)稍加修改，也可以适应其他如建筑环境与能源应用工程专业等。

本教材是与上述的教学学时和专业相配套的教学参考书(80学时及以上的还需要略微补充一点内容)，同时也可作为学生自学教材。

在编写《自动控制理论》的过程中，我们重视根底理论知识，参加拉普拉斯变换内容，从第3章开始，参加MATLAB仿真的内容。

通过细化根轨迹和频率特性绘图过程，使学生更好地掌握图形绘制，掌握自动控制系统的分析和设计方法。

在注重应用的前提下，精选教学内容和配套习题，在文字表达方面力求清晰、准确，教材内容适度。

本教材的所有编者长期工作在教学第一线，也有很强的自动控制和电气控制的实践经历，我们力求将这些经历融入本教材中。

本书第1章由赵浩老师编写，第2章和第6章由朱宁老师编写，第3章由童佳老师编写，第4章由丁立军编写，第5章由高慧敏老师编写，第7章由林立老师编写。

陈叠峰和任美华两位同学编写了局部的MATLAB章节。

由于编者水平有限、编写时间紧迫，教材中难免有缺点和错误，恳请读者批评指正，以使我们有更大的进步。

[1] 编者xx年8月第1章自动控制的根本知识1.1自动控制的开展历史和根本概念1.2自动控制的根本控制方式1.3自动控制系统的分类1.4自动控制系统的性能指标习题1第2章控制系统的数学模型2.1数学模型的根本概念2.2控制系统数学模型——微分方程2.3拉普拉斯变换与反变换2.4传递函数2.5控制系统的动态构造图、信号流图与梅逊公式习题2第3章线性系统的时域分析法3.1系统分析的根本假设条件和分析指标3.2一阶系统的时域分析3.3二阶系统的时域分析3.4高阶系统的时域响应3.5线性定常系统的稳定性3.6线性系统的稳态误差计算3.7用MATLAB辅助分析控制系统时域性能习题3第4章控制系统的根轨迹法4.1根轨迹的根本概念4.2绘制根轨迹的规那么和方法4.3广义根轨迹4.4控制系统根轨迹的性能分析4.5用MATLAB绘制根轨迹习题4第5章控制系统的频域分析法5.1频率特性的根本概念5.2对数频率特性及其绘制5.3幅相频率特性及其绘制5.4稳定判据5.5稳定裕度5.6系统的开、闭环频率特性与阶跃响应的关系5.7MATLAB在频率法中的应用习题5第6章控制系统的校正6.1控制系统校正的根本概念6.2根本控制规律和常用校正装置6.3频率校正方法6.4反应校正6.5复合控制方法6.6Simulink在控制系统仿真中的应用习题6第7章离散控制系统7.1离散控制系统根本概念7.2信号的采样与复现7.3离散控制系统的数学模型7.4离散系统分析7.5应用MATLAB进展离散系统分析习题7参考文献1.2.3.。

浙江大学自动控制理论课第二章控制系统的数学模型

浙江大学自动控制理论课第二章控制系统的数学模型

t
L1
G
s
1 T
1t
eT
由式2 31 得
uc(t)
g (t
0
)ur ( )d
1 0T
1 (t )
e T d
1t
1e T
2、ur t t
uc
t
t
1
1 t
e T d
1
1t
eT
0T
T
t
1t
e d t T Te T
0
3、ur t sin t
ur
t
t
1
1
eT
即i C duc dt
消去中间变量 i，则有:
LC
d 2uc dt 2
RC
duc dt
uc
ur
2020/5/11 图2-1 Ｒ-L-C电路
课件
3
自动控制理论
例2-2. 试写出图2-2电路的微分方程
解 由基尔霍夫定律列出下列方程组
1
C1
(i1 i2 )dt Байду номын сангаас1R1 ur
1
1
C2 i2dt i2 R2 C1 (i1 i2 )dt
图2-6 直流他励发电机电路图
2020/5/11
课件
8
自动控制理论
由电机学原理得：
L
diB dt
iB R
U1
（2-5）
EG C1 C1LiB C2iB （2-6）
把式（2-6）代入（2-5），则得
τG
dEG dt
EG
K2U1
（2-7）
式中
G
L R
;
K2
C1L R
2020/5/11

自动控制理论第四版夏德钤翁贻方版

自动控制理论第四版夏德钤翁贻方版
第一章 自动控制的一般概念
1-1 自动控制的基本原理与方式
1、自动控制技术及应用 （1）什么是自动控制
无人直接参与 利用外加设备或装置（控制器） 使机器、设 备或生产过程（被控对象）的某个工作状态或参数（被控量） 自动按预定的规律运行
外作用
控制器
被控对象
被控量
（2）自动控制技术的应用
工业、农业、导航、核动力 理和其它许多社会生活领域
（3）智能控制理论 （发展方向） 以控制论、信息论、仿生学为基础
3、反馈控制理论 （1）自动控制系统
被控对象、控制器按一定的方式连接所组成的系统
最基本的连接方式是反馈方式，按该方式连接的系统 称为反馈控制系统
（2）反馈控制原理 控制器对被控对象施加的控制作用取自被控
量的反馈信息，用来不断修正被控量与输入量之间的 偏差，从而对被控对象进行控制。
输入
输出
（电扇调档）
按扰动控制：利用可测量的扰动量，产生一种补偿作用，
（顺馈控制） 以减少或抵消扰动对输出量的影响。
（3） 复合控制方式 按偏差控制与按扰动控制相结合
1-2 自动控制系统举例
飞机示意图
给定电位器
反馈电位器
给 θ0 定
装 置
飞机方块图 扰动
放 大
舵 机
器
反馈电 位器
垂直 陀螺仪
飞 θc 机
f (t) A Sin(t )
第二章 控制系统的数学模型
1、线性连续控制系统 用线性微分方程描述 P11 定常、时变
a0
d nc(t) dt n

a1
d n1c(t) dt n1

an1
dc(t) dt

an c(t )

自动控制原理 教学课件 作者 潘丰 02 控制系统数学模型1

自动控制原理 教学课件 作者 潘丰 02 控制系统数学模型1

RC
duo dt
uo
ur
G(s)
LCs2
1 RCs
1
由复阻抗可直接写出：
G(s) uc 1/ Cs
1
ui R Ls 1/ Cs LCs2 RCs 1
由常用的六种典型环节组成的系统传表达式函如下：
江南大学物联网工程学院——自动控制原理
比例环节
滞后环节
一阶微分环 节（m个）
m
G(s) C(s) R(s) s
建模（微分方程）步骤：
第一步：明确系统输入、输出量，列写各组成环节输出与 输入的数学表达式。
根据系统遵循的物理定律——如牛顿定律、基尔霍 夫电流和电压定律、能量守恒定律等。
第二步：联立各环节的数学表达式，消去中间变量，得到描 述 系统输出、输入关系的微分方程。
第三步：标准化。
左“出”=右“入”，且各微分项均按降幂排列。见P19 公式（2-8）所示。
dn dt n
c(t )
a1
d n1 dt n1
c(t )
an1
d dt
c(t )
an c(t )
b0
dm dt m
r(t)
b1
d m1 dt m1
r(t)
bm 1
d dt
r(t)
bm r(t )
(n m)
式中：c(t)是系统输出量，r(t)是系统输入量； 各系数均是常数。
设r(t)和c(t)及其各阶系数在t=0是的值均为零，即零初始条 件，则对上式中各项分别求拉氏变换，可得到：
G(s)
C(s) R(s)
b0 sm b1 sm1 bm1 s bm sn a1 sn1 an1 s an
(n m)

《自动控制原理》 胡寿松 习题答案(附带例题课件)

《自动控制原理》 胡寿松 习题答案(附带例题课件)
《自动控制原理》电子教案
自动控制原理
电子教案
《自动控制原理》电子教案
《自动控制原理》课程教学大纲
课程编号： 课程名称：自动控制原理 英文名称：Automatic Control Theory 课程类型:：专业基础必修课 总 学 时：64 学 学 时：64 分：4 讲课学时：56 上机学时：8
适用对象：电气工程及其自动化专业（电力系统及自动化、电力系统继电保护、电网监控技术、供 用电技术专业方向） 先修课程： 高等数学、大学物理、积分变换、电路、数字电子技术、模拟电子技术
大纲制订人：杨志超 大纲审定人：李先允 制订日期：2005 年 6 月
7
《自动控制原理》电子教案
自动控制原理授课计划（64 学时）
2．利用 MATLAB 程序绘制控制系统阶跃响应曲线、计算性能指标，讨论开环放大倍数对闭环系统响 应速度、稳定性和稳态误差的影响 。 （验证性实验） 2 学时
3． 利用 MATLAB 程序绘制控制系统的 Nyquist 曲线、 Bode 图， 计算控制系统的幅值裕度和相位裕度。 （验证性实验） 4．利用 MATLAB 软件设计控制系统（设计性实验） 2 学时 2 学时
六、实验报告要求
每次上机实验必须提交实验报告。实验报告由实验原理、实验内容、仿真程序、实验数据记录及分析 处理等内容组成。
七、考核方式与成绩评定标准
实验成绩：预习 10%、上机操作 50%、报告 40%
八、教材及主要参考资料
教 材： 《自动控制理论实验指导书》 ，王芳、杨志超编写，2007 年 参考书：《自动控制原理》，国防工业出版社，王划一主编，2001 年 《基于 MATLAB 的系统分析与设计》-控制系统，楼顺天、于卫编著，西安电子科技大学出 版社，1999 年 《MATLAB 控制系统设计与仿真》，赵文峰编著，西安电子科技大学出版社，2002 年

自动控制理论 翁思义第二章 自动控制系统的数学模型

自动控制理论 翁思义第二章 自动控制系统的数学模型

式中：
k
R2 R1 R2
,T
R1C
四、惯性环节
时域方程：Ty ' (t) y(t) kx(t), t 0
传递函数：G(s)
Y (s) X (s)
k Ts 1
当输入为单位阶跃函数时,有Ty ' (t) y(t) k，可解得：
y(t
)
k
(1
e
t T
)，式中：k为放大系数，T为时间常数。
当k=1时，输入为单位阶跃函数时,时域响应曲线和零极点分布
G(s) U c (s) Tc s U r (s) Tc s 1
式中 Tc RC
微分环节实例
[实例]
x(t)
R1
C
R2 y(t)
X (s) Z1 ( s)
Y (s) Z2 (s)
, Z2
R2, Z1
R2
R1 1 R1Cs
G(s) Y (s) R2 (1 R1Cs) k(Ts 1) X (s) R1 R2 R1R2Cs kTs 1
例2：求解微分方程
y 4y 5y 0, y(0) y(0) 1
微分方程两边同时取拉氏变换（初始条件不为零）
s2F (s) sf (0) f (0) 4sF (s) 4 f (0) 5F (s) 0
s5
s5
s23
F (s) s2 4s 5 (s 2)2 1 (s 2)2 1
K*
a sn c sn1 c s c
0
n1
1
0
(s zi )
i 1
n
(s p )
j
Pj 为传递函数的极点
b.传递函数的时间常数表示形式
j 1
m
G(s) bm an

自动控制理论-第二章

自动控制理论-第二章

2-1 控制系统的时域数学模型
1、控制系统微分方程的建立 （1）举例 例1：电路无源网络 试列写以 u (t ) 为输入量，以 u (t )为 输出量的网络微分方程
i
o
解：设回路电流为 i(t ) ，由基尔霍夫 定律可写出回路方程为
di ( t ) 1 + i ( t ) dt + Ri ( t ) = u i ( t ) dt C ∫ 1 u o (t ) = i ( t ) dt C ∫ L
f 2 (t )
c(t ) = c1 (t )
作用时， c(t ) = c2 (t ) 叠加性：当 f (t ) 、 f (t ) 同时作用时，c(t ) = c1 (t ) + c2 (t ) 均匀性：当 f (t ) = A ⋅ f1 (t ) 时， c(t ) = A ⋅ c1 (t ) 线性系统的叠加原理表明：两个外作用同时加于系统所产生的 总输出，为各个外作用单独作用时分别产生的输出之和。
[
]
1 1 1 F ( s ) + n f ( −1) (0) + L + f ( − n ) (0) n s s s
式中
f
( −1)
f ( −1) (0)、f ( −2) (0) L f ( − n ) (0)
(−n)
为
f (t )
的各重积分在 t = 0 时的值。如果
(0) = f ( −2 ) (0) = L = f
(0) = 0 ，则有
L ∫ L ∫ f (t )(dt ) n =
[
]
1 F (s) sn
（4）初值定理 若函数 f (t ) 及其一阶导数都是可拉氏变换的，则
f (0 + ) = lim f (t ) = lim sF ( s)

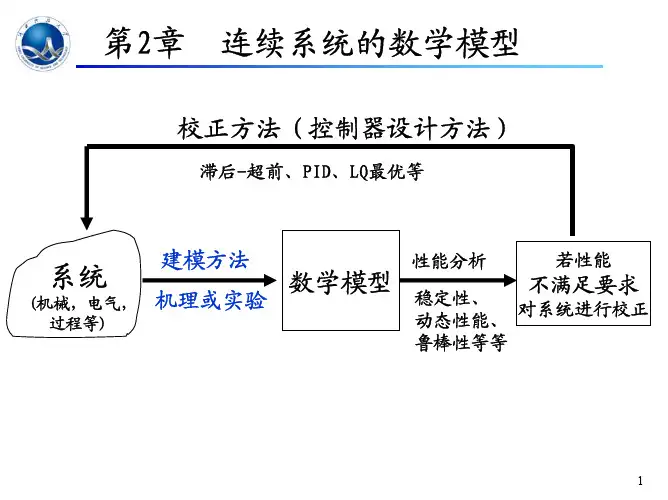
自动控制原理(王万良)第二章

自动控制原理(王万良)第二章

+ bm−1s m−1 + + an−1s n−1 +
+ b1s + b0 + a1s + a0
Y (s) = G(s)U (s) y(t) = L−1{Y (s)} = L−1{G(s)U (s)}
U(s) 系统G(s) Y(s)
系统微分方程与传递 函数可以直接转换!
17
关注传递函数和微分方程的对应关系
预备知识——拉普拉斯变换 典型信号的拉氏变换
10
11
拉普拉斯变换的性质（基本定理）
12
有理分式的分解（1）：极点为相异实数的情况
13
有理分式的分解（2）：出现极点为相同实数的情况
14
例：
15
有理分式的分解（3）：出现极点为相异复数数的情况
16
2.3.1 传递函数与脉冲响应函数的定义
定义：在零初始条件下，线性定常系统（环节）输出的拉氏变换与 输入的拉氏变换之比，称为该系统（环节）的传递函数。
∴ m d 2 x(t) + f dx(t) + Kx(t) = F (t)
dt 2
dt
上例RLC网络
LC
d 2uo dt 2
+
RC
duo dt
+ uo
=
ui
思考与理解:传递函数只是 对系统的数学描述，并不 反映系统的物理构成。
8
例2.4 (P18)
C
R2
。ur R1
－
R1 ＋
。 。uc
9
2.3 传递函数
5
例2.1
一阶RC网络系统
i = C duc dt
u1 = iR

自动控制理论 夏德钤 上 课后答案【khdaw_lxywyl】

自动控制理论 夏德钤 上 课后答案【khdaw_lxywyl】

1 2 n n 1 2
e
n t
1 2 2 sin 1 n t arctg n
加了 z 1 的零点之后，超调量 M p 和超调时间 t p 都小于没有零点的情况。
3-13
系统中存在比例-积分环节
K 1 1 s 1 ，当误差信号 et 0 时，由于积分作用，该环节的输出保持不变，故系 s
U 2 s R 1 1 R U 1 s R Cs 1 4
(c)
U 2 s R R 1 1 Cs 1 U 1 s R 4
m
图 A-2-2
题 2-11 系统信号流程图
2-12
(a)
C s 1 abcdef agdef abcdi adgi Rs 1 cdh
3-11
s
15s , ( n 0.4rad / s, 1.25) ，过阻尼系统，无超调。
（1）当 a = 0 时， 0.354, n 2 2 。 （2） n 不变，要求 0.7 ，求得 a = 0.25
1 2 n 2 , t 0 ct e sin 1 n t arctg 2 1 1 n 比 较 上 述 两 种 情 况 ， 可 见 有 z 1 零 点 时 ， 单 位 脉 冲 响 应 的 振 幅 较 无 零 点 时 小 ， 而 且 产 生 相 移 ， 相 移 角 为 1 2 n n n
案
网
e s lim C 0 lim s 0 s 0
co
首先求系统的给定误差传递函数
m
s (0.1s 1) 0 0.1s 2 s 500 d 500(0.2s 1) 1 C1 lim e s lim 2 2 s 0 s 0 ds (0.1s s 500) 500 e s lim C 0 lim s 0 s 0 C 2 lim s 0 rs (t ) sin 5t s (t ) 5 cos 5t r rs (t ) 25 sin 5t

自动控制原理 第2章数学模型

自动控制原理 第2章数学模型

y y0 K ( x x0 ) 或写为 y Kx
即：线性化方程
式中，
y0

f ( x0 )，K

df dx
，y
x x0
y
y0，x
x x0
严格地说，经过线性化后的所得的系统微分方程式，只 是近似地表征系统的运动情况。
实践证明，对于绝大多数的控制系统，经过线性化后所 得的系统数学模型，能以较高的精度反映系统的实际运动过 程，所以线性化方法是很有实际意义的。
绝对的线性元件和线性系统不存在
非线性微分方程的线性化
实际物理元件或系统都是非线性的，构成系统的元件 都具有不同程度的非线性。
建立的动态方程就是非线性微分方程，对其求解有诸 多困难，因此，对非线性问题做线性化处理确有必要。
线性化:在满足一定条件的前提下，用近似的线性系统代 替非线性方程。
线性化的基本条件:非线性特性必须是非本质的，系统各 变量对于工作点仅有微小的偏离。
第二章 控制系统的数学模型
本章内容
2.1 控制系统的时域数学模型 2.2 控制系统的复数域数学模型 2.3 控制系统的结构图/方框图 2.4 梅森公式与信号流图
系统的数学模型
数学模型
描述系统输入、输出变量以及内部各变量之间关系的 数学表达式。
分析和设计任何一个控制系统，首要任务是建立系统 的数学模型。
b0s m a0s n
b1s m 1 a1s n 1
... bm 1s ... an 1s
bm an
N(s)=0 系统的特征方程，特征根 特征方程决定着系统的动态特性。 N(s)中s的最高阶次等于系统的阶次。
系统传递函数的极点就是系统的特征根。 零点和极点的数值完全取决于系统的结构参数。

自动控制原理各章知识精选全文完整版

自动控制原理各章知识精选全文完整版
⑴ 偏差、误差的概念
(s), (t) E(s), e(t) cdesired (t) c(t)
E(s) 1 (s)
H
G (s)
1
H
H
⑵ e(t) ets (t) ess (t)
暂态 稳态
单位负反馈系统开环传函
r(t)
1 2
t2
时稳态误差
Ts 1 E(s) Ts 1 s3
e(t)
T
2. 运动方程式
确定输入量、输出量 列写各元件运动方程 消除中间变量 化为标准形式
RL
u1
C u2
Fi
K
m
f
y
L
C
u1
u2
R
R1
u1
C
R2 u2
LC
d 2u2 dt 2
RC
du2 dt
u2
u1
m
d2y dt 2
f
dy dt
Ky
Fi
LC
d 2u2 dt 2
RC
du2 dt
u2
RC
du1 dt
tg1 1 2 cos1
p e 1 2 100 %
d. c(t) c() c() t ts
2%或5%
4 ts n
2%
3 ts n
5%
d. N : 振荡次数
N ts Td
Td
2 d
d n 1 2
tr , t p 评价响应速度
p , N 评价阻尼程度
ts
以分析，并将分析结果应用于工程系统的综合和自然界 系统的改善。 自动控制
毋需人直接参与，而是被控制量自动的按预定规律变 化的控制过程。
4. 开环控制、闭环控制、反馈控制原理

自动控制原理电子版

自动控制原理电子版

第二章 自动控制系统的数学模型研究一个自动控制系统，除了对系统进行定性分析外，还必须进行定量分析，进而探讨改善系统稳态和动态性能的具体方法。

控制系统的运动方程式（也叫数学模型）是根据系统的动态特性，即通过决定系统特征的物理学定律，如机械﹑电气﹑热力﹑液压﹑气动等方面的基本定律而写成的。

它代表系统在运动过程中各变量之间的相互关系 ，既定性又定量地描述了整个系统的动态过程。

因此，要分析和研究一个控制系统的动态特性，就必须列写该系统的运动方程式，即数学模型。

第一节 系统动态微分方程模型常用的列写系统或环节的动态微分方程式的方法有两种﹕一种是机理分析法，即根据各环节所遵循的物理规律（如力学﹑电磁学﹑运动学﹑热学等）来编写。

另一种方法是实验辩识法，即根据实验数据进行整理编写。

在实际工作中，这两种方法是相辅相成的，由于机理分析法是基本的常用方法，本节着重讨论这种方法。

下面通过简单示例介绍机理分析法的一般步骤。

图2-1 RLC 网络[例2-1] 列写图2-1所示RLC 网络的微分方程。

解 1． 明确输入、输出量网络的输入量为电压)(t u r ，输出量为电压)(t u c 。

2．列出原始微分方程式。

根据电路理论得 )()(1)()(t Ri dt t i Cdt t di Lt u r ⎰++= （2-1） 而 ⎰=dt t i C t u c )(1)( （2-2） 式中)(t i 为网络电流，是除输入、输出量之外的中间变量。

3．消去中间变量将式（2-2）两边求导，得)(1)(t i C dt t du c = 或 dtt du C t i c )()(= （2-3） 代入式（2-1）整理为 )()()()(22t u t u dt t du RC dtt u d LC r c c c =++ （2-4） 显然，这是一个二阶线性微分方程，也就是2-1所示RLC 无源网络的数学模型。

[例2-2] 试列写图2-2所示电枢控制直流电动机的微分方程，要求取电枢电压)(t u a（V ）为输入量，电动机转速)(t m ω)(s rad 为输出量。

《自动控制理论_第2版（夏德钤）》习题答案详解

《自动控制理论_第2版（夏德钤）》习题答案详解

《⾃动控制理论_第2版（夏德钤）》习题答案详解《⾃动控制理论第2版（夏德钤）》习题答案详解第⼆章2-1 试求图2-T-1所⽰RC ⽹络的传递函数。

(a)11111111+=+?=Cs R R CsR Cs R z ，22R z =，则传递函数为： 2121221212)()(R R Cs R R R Cs R R z z z s U s U i o +++=+= (b) 设流过1C 、2C 的电流分别为1I 、2I ，根据电路图列出电压⽅程：=++=)(1)()]()([)(1)(2221111s I s C s U s I s I R s I sC s U o i 并且有)()1()(122211s I sC R s I s C += 联⽴三式可消去)(1s I 与)(2s I ，则传递函数为：1)(1111)()(222111221212211112++++=+ ++=s C R C R C R s C C R R R s C R s C s C R sC s U s U i o 2-2 假设图2-T-2的运算放⼤器均为理想放⼤器，试写出以i u 为输⼊，o u 为输出的传递函数。

(a)由运算放⼤器虚短、虚断特性可知：dtduC dt du C R u i i 0+-=，0u u u i c -=，对上式进⾏拉⽒变换得到)()()RCs s U s U i 1)()(0+= (b)由运放虚短、虚断特性有：022=-+--R u R u u dt du Cc c i c ，0210=+R u R u c ，联⽴两式消去c u 得到02220101=++?u R u R dt du R CR i 对该式进⾏拉⽒变换得0)(2)(2)(20101=++s U R s U R s sU R CR i 故此传递函数为)4(4)()(10+-=RCs R R s U s U i (c)02/2/110=+-+R uR u u dt du Cc c c ，且21R u R u c i -=，联⽴两式可消去c u 得到0222101=++?Ru R u dt du R CR i i 对该式进⾏拉⽒变换得到0)(2)(2)(2011=++?s U Rs U R s sU R CR i i 故此传递函数为RCs R R s U s U i 4)4()()(110+-= 2-3 试求图2-T-3中以电枢电压a u 为输⼊量，以电动机的转⾓θ为输出量的微分⽅程式和传递函数。

自动控制理论第2版夏德钤 翁贻方第二章控制系统的数学模型

自动控制理论第2版夏德钤 翁贻方第二章控制系统的数学模型

例2-1:图2-1为RC四端无源网络。试列写以U1(t)
为输入量，U2(t)为输出量的网络微分方程。
解：设回路电流i1、i2，根据克希霍夫定律，列
写方程组如下
R1
R2
U1 R1i1Uc1
(1)
1
Uc1
C1
(i1 i2)dt
(2)
Uc1R2i2Uc2
(3)
Uc2

1 C2
i2dt
n=1/T——无阻尼自然振荡频率。共轭复数极点为：
5．微分环节
式中
——比例系数,是随工作点A（x0，y0)不 同而不同的常数
具有两个以上输入量的非线性系统线性化处理方法与前述 方法相似。
求线性化微分方程的步骤 ① 按物理和化学定律，列出系统的原始方程式，确定平衡点处
各变量的数值。 ② 找出原始方程式中间变量与其它因素的关系，若为非线性函
数，在原平衡点邻域内，各阶导数存在并且是唯一的，则可 进行线性化处理。 ③ 将非线性特性展开为泰勒级数，忽略偏差量的高次项，留下 一次项，求出它的系数值。 ④ 消去中间变量，在原始方程式中，将各变量用平衡点的值用 偏差量来表示。
• 同一系统对不同的输入，可求得不同的传递函数，但其特征 多项式唯一。
• 在给定输入和初始条件下，解微分方程可以得到系统的输出 响应，包括两部分 系统响应=零输入响应+零状态响应 零输入响应——在输入为零时，系统对零初始状态的响应； 零状态响应——在零初始条件下，系统对输入的响应。
传递函数的几点性质
于是电动机可作为测速发电机使用。
•
第二节线性系统的输入—输出传递函数描述
一、传递函数 １．定义：线性定常系统的传递函数，定义为零
初始条件下，系统输出量的拉氏变换与输入量 的拉氏变换之比。零初使条件是指当t≤0时,系统 r(t)、c(t)以及它们的各阶导数均为零。 线性系统微分方程的一般形式为

自动控制原理(数学模型)精选全文完整版

自动控制原理(数学模型)精选全文完整版

t 0
s
证明：由微分定理 df (t) estdt s F (s) f (0)
0 dt
lim df (t) estdt lim s F (s) f (0)
s 0 dt
s
左 df (t) limestdt 0 0 dt s
lim
s
s F(s)
f (0 )
0
f
二、非线性系统微分方程的线性化
例5 已知某装置的输入输出特性如下，求小扰动线性化方程。
y( x ) E0 cos[x(t )]
解. 在工作点(x0, y0)处展开泰勒级数
y( x)
y(x0)
y( x0 )( x
x0 )
1 2!
y( x0 )( x
x0 )2
取一次近似，且令
y(x) y(x) y(x0) E 0 sin x0 ( x x0 )
1
s(s a)( s b)
f
lim
s0
s
ss
1
as
b
1 ab
例12
Fs
s2
ω ω2
f sinωt t
lim s
s0
s2
ω ω2
0
3 用拉氏变换方法解微分方程
系统微分方程
y(t) a1 y(t) a2 y(t) 1(t)
y(0) y(0) 0
L变换
(s2
a1s
a2 )Y (s)
0
1 1
1 1 2 j
2j
s
j
s
j
2j
s2
2
s2
2
2 拉氏变换的几个重要定理
（1）线性性质 La f1(t) b f2(t) a F1(s) b F2(s)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
时输出量的拉氏变换式C(s),对其求拉氏反变换可得到系统的 响应 c(t)，称为系统的零状态响应。 • 系统响应的特性由传递函数决定，而和系统的输入无关。传 递函数则由系统的结构与参数决定。 • 传递函数的分母多项式即为微分方程的特征多项式，为1+开 环传递函数。
• 同一系统对不同的输入，可求得不同的传递函数，但其特征 多项式唯一。
第二章 控制系统的数学模型
本章知识点： •线性系统的输入－输出传递函数描述 •建立机电系统数学模型的机理分析法 •传递函数的定义与物理意义 •典型环节的数学模型 •框图及化简方法 •信号流程图与梅逊公式应用 •非线性数学模型的小范围线性化
第一节 线性系统的输入/输出时间函数描述
物理模型——任何元件或系统实际上都是很复杂的， 难以对它作出精确、全面的描述，必须进行简化 或理想化。简化后的元件或系统称为该元件或系 统的物理模型。简化是有条件的，要根据问题的 性质和求解的精确要求来确定出合理的物理模型。
-
图2 - 6
电枢控制直流电动机原理图
动机轴上的总负载转矩。激
磁磁通为常值。
机理分析法建立系统数学模型举例 解：列写电枢电路平衡方程
Ua(t)Ladidat(t)Raia(t)Ea ①
＋ if
-
La Ra
＋ ia
Ua
Ea SM
m
负 载
J mf m
-
图2-6 电枢控制直流电动机原理图
Ea——电枢反电势，其表达式为 Ea=Ceωm（t） ② Ce——反电势系数（v/rad/s）
• 实验辩识法 对系统施加某种测试信号 （如阶跃、脉冲、正弦等），记录基本 输出响应（时间响应、频率响应），估 算系统的传递函数。
机理分析法建立系统数学模型举例
R1
R2
由(4)、(5)得
i2
C2
dUc2 dt
C2
dU2 dt
U1
C1
C2
U2
由(2)导出 i1C 1dU dtc1i2C 1dU dtc1C 2dd U tU2 图2-1
•
第二节线性系统的输入—输出传递函数描述
一、传递函数 １．定义：线性定常系统的传递函数，定义为零
初始条件下，系统输出量的拉氏变换与输入量 的拉氏变换之比。零初使条件是指当t≤0时,系统 r(t)、c(t)以及它们的各阶导数均为零。 线性系统微分方程的一般形式为
ddnct(nt)a1ddnt1nc(1t)......an1dcd(tt)anc(t)
dnr(t) dn1r(t)
dr(t)
b0 dtn b1 dtn1 ......a1 dt a1r(t)
当初始条件均为0时,对上式两边求拉氏变换，得
系统的传递函数
C R ((S S))b 0 ssn m a b 11 ssn m 1 1
b m 1sb m an 1san
传递函数G(S)是复变函数，是S的有理函数。且有
这就是RC四端网络的数学模型，为二阶线性 常微分方程。
机理分析法建立系统数学模型举例
＋
例2-2 图2-6 所示为电枢控 制直流电动机的微分方程，
if
-
La
Ra
要求取电枢电压Ua(t)（v）为 ＋
输入量，电动机转速
ia
m
ωm（t）（rad/s）为输出量， Ua
Ea S M
负 载 J mf m
列写微分方程。图中Ra(Ω)、 La(H)分别是电枢电路的电阻 和电感，Mc(N·M)是折合到电
n=1/T——无阻尼自然振荡频率。共轭复数极点为：
5．微分环节
微分是积分的逆运算,按传递函数的不同,微分环节可 分为三种：理想微分环节、一阶微分环节（也称为比例 加微分环节）和二阶微分环节。相应的微分方程为 ：
相应的传递函数为：
6．延迟环节
延迟环节又称为纯滞后环节、时滞环节。其输 出信号比输入信号迟后一定的时间。就是说，延
（3）典型环节的概念只适用于能够用线性定 常数学模型描述的系统。
传递函数可表示成零、极点表示：
系统传递函数有时还具有零值极点，设传递函数
中有个零值极点,并考虑到零极点都有实数和共轭复
数的情况,则传递函数的后两种表示的一般形式为：
可见，系统传递函数是由一些常见基本因子,如式上中的
(js+1)、1/(Tis+1)等组成。即系统传递函数表示为上式时，系统
传递函数是这些常见基本因子的乘积。这些常见基本因子代表 的环节称为典型环节。任何复杂的系统都可以用若干典型环节 构成。具有相同基本因子传递函数的元件，可以是不同的物理 元件，但都具有相同的运动规律。
从传递函数的表示式中可以看到，传递函数的 基本因子对应的典型环节有比例环节、积分环节、 微分环节、惯性环节、振荡环节和延迟环节等。
l．比例环节
比例环节又称为放大环节，其输出量与输入量之间的关 系为固定的比例关系，即它的输出量能够无失真、无延迟地 按一定的比例关系复现输入量。时域中的代数方程为
c(t)=Kr(t) t 0 式中K为比例系数或传递系数，有时也称为放大系数
由③、④求出ia(t)，代入①，同时②亦代入①，得
LaJmd2 dm t(t)(LafmRaJm)ddm t(t)(RafmCmCe)m(t) ⑤
CmUa(t)LadM dct(t)RaMc(t)
在工程应用中，由于电枢电路电感La较小， 通常忽略不计，故⑤可简化为
T 其m d 中d m t(t)m (t)K 1 U a(t) K 2 M c(t) ⑥
m≤n。
极点——传递函数分母s多项式
的根，也即线性微分方程特征方程的特征值。 零点——传递函数分子s多项式
N ( s ) b 0 s m b 1 s m 1 b m 1 s b m
的根。
• 传函是由微分方程在初始条件为零时进行拉氏变换得到的。 • 如果已知系统的传递函数和输入信号,则可求得初始条件为零
R1
R2
U1
C1
C2
U2
图2-1 RC组成的四端网络
R 1 R 2 C 1 C 2d d 2 U t2 2 (R 1 C 1 R 1 C 2 R 2 C 2 )d d U t2 U 2 U 1
U 2 (s)
1
U 1 (s) R 1 R 2 C 1 C 2 s2 (R 1 C 1 R 1 C 2 R 2 C 2 )s 1
数学模型——物理模型的数学描述。是指描述系统 输入、输出以及内部各变量之间动态关系的数学 表达式。
数学建模——从实际系统中抽象出系统数学模型的 过程。
建立物理系统数学模型的方法
• 机理分析法 对系统各部分的运动机理进 行分析，按 照它们遵循的物理规律、化 学规律列出各物理量之间的数学表达式, 建立起系统的数学模型。
L-变换 C(S)=KR(S)
所以比例环节的传递函数为 ：
完全理想的比例环节是不存在的。对某些系统 当做比例环节是一种理想化的方法。
2．惯性环节
惯性环节又称为非周期环节，其输入量和输出量之间的 关系可用下列微分方程来描述：
L-变换 TSC(S)+C(S)=KR(S)
1
传递函数 G(S)= C(s)/ R(s) =
RC组成的四端网络
将i1、i2代入(1)、(3)，则得
U 1R 1i1R 2i2U c2
R 1 (C 1d U d tc1 C 2d d U t2)R 2 C 2d d U t2 U 2
机理分析法建立系统数学模型举例
R 1 [C 1d d t(R 2 i2 U 2 ) C 2d d U t2 ] R 2 C 2d d U t2 U 2 R 1 C 1 R 2 C 2 d d 2 U t2 2 R 1 C 1 d d U t2 R 1 C 2 d d U t2 R 2 C 2 d d U t2 U 2 R 1 R 2 C 1 C 2d d 2 U t2 2 (R 1 C 1 R 1 C 2 R 2 C 2 )d d U t2 U 2 U 1
• 系统传递函数是系统单位脉冲响应g(t)的 拉氏变换L[g(t)]。
例2－3 求例2－1系统的传递函数。 已知其输入－输出微分方程
R 1 R 2 C 1 C 2d d 2 U t2 2 (R 1 C 1 R 1 C 2 R 2 C 2 )d d U t2 U 2 U 1
设初始状态为零， 对方程两边求拉氏 变换，得
此即为RC四端网络的传递函数。
第三节 非线性数学模型的小范围线性化
严格讲，任何实际系统都存在不同程 度的非线性。对于非本质非线性数学模 型，可采用小范围线性化方法。
设一非线性数学 模型如图所示。
设函数y=f（x）在（x0，y0） 点附近连续可微(此即为非线性 系统数学模型线性化的条件）, 则附近可展将开函成数泰f（勒x级）数在（x0，y0）
• 在给定输入和初始条件下，解微分方程可以得到系统的输出 响应，包括两部分 系统响应=零输入响应+零状态响应 零输入响应——在输入为零时，系统对零初始状态的响应； 零状态响应——在零初始条件下，系统对输入的响应。
传递函数的几点性质
• 传递函数G(s)是复变量s的有理真分式函数， m≤n，且所有系数均为实数。
C（t）=Kt
上式说明，只要有一个恒定的输入量作用于积分环节， 其输出量就与时间成比例地无限增加。
4．振荡环节 振荡环节的微分方程
是：
相应的传递函数为：
式中 T——时间常数；
——阻尼系数（阻尼比），且0＜ ＜1。 振荡环节的传递函数具有
一对共轭复数极点,在复平面S上的位置见图2-8所示,传递函数可改写为：
Tm
Ra
RaJm fm CmCe
K1
Ra
Cm fm CmCe
电动机机电Cem时(t)U 间a(t) 常数（s）
K2