自控原理—第2章 (1)
- 格式:pdf
- 大小:6.72 MB
- 文档页数:84

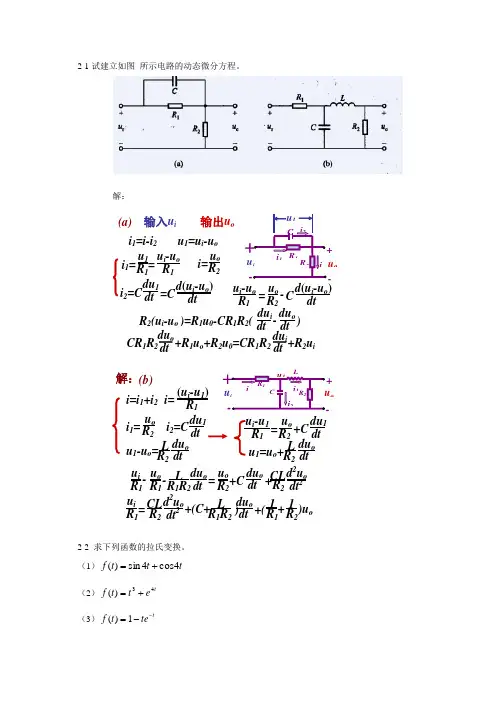
2-1试建立如图 所示电路的动态微分方程。
解:输入u i 输出u ou 1=u i -u oi 2=C du 1 dt )- R 2(u i -u o )=R 1u 0-CR 1R 2( du i dt dt du oC + - u i o R 1R 2 i 1 i i 2u 1i 1=i-i 2 u o i= R 2u 1 i 1= R 1 = u i -u o R 1 dt d (u i -u o ) =C C d (u i -u o ) dtu o - R 2 = u i -u o R 1 CR 1R 2 du o dt du idt +R 1u o +R 2u 0=CR 1R 2 +R 2u i(a)i=i 1+i 2 i 2=C du 1 dtu o i 1= R 2 u 1-u o = L R 2 du o dt R1i= (u i -u 1) (b)C+-iu o R 1R 2i 1 ii 2Lu 1 = R 1 u i -u 1 u o +C R 2 du 1 dtu 1=u o + L R 2 du o dtdu o dt R 1R 2 L du o dt + CL R 2 d 2u o dt 2 = - - u i R 1 u o R 1 u o R 2 +C )u o R 1R 2 L du o dt ) CL R 2 d 2u o dt 2 = + +( u i R 1 1 R 11 R 2+(C+ 解:2-2 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+= (2)te t tf 43)(+= (3)t te t f --=1)((4)te t tf 22)1()(-= 解:(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s s+42+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t 解:L [t 3+e 4t ]= 3!s 41s-4+ 6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:解:2-3求下列函数的拉氏反变换。


自控原理第二章习题答案自控原理第二章习题答案自控原理是一门研究控制系统的学科,它关注的是如何设计和优化控制系统,以实现系统的稳定性和性能。
在学习自控原理的过程中,习题是一个非常重要的组成部分,通过解答习题可以帮助我们更好地理解和掌握自控原理的知识。
在本文中,我将为大家提供自控原理第二章习题的答案,希望对大家的学习有所帮助。
1. 什么是反馈控制系统?它有哪些特点?答:反馈控制系统是一种通过测量输出信号,并将其与期望输出信号进行比较,然后根据比较结果对系统进行调整的控制系统。
它的特点包括:- 反馈环节:反馈控制系统中包含了一个反馈环节,通过测量输出信号,将其反馈给系统进行调整,以实现期望的输出。
- 自动调节:反馈控制系统能够根据反馈信号自动地对系统进行调节,无需人工干预。
- 稳定性:反馈控制系统能够提高系统的稳定性,使系统能够快速地恢复到期望状态。
- 抗干扰性能:反馈控制系统能够减小外部干扰对系统的影响,提高系统的抗干扰能力。
2. 什么是比例控制器?它的传递函数是怎样的?答:比例控制器是一种最简单的控制器,它根据误差的大小与比例增益之间的关系来调节系统的输出。
比例控制器的传递函数可以表示为:Gc(s) = Kp其中,Gc(s)为比例控制器的传递函数,Kp为比例增益。
3. 什么是积分控制器?它的传递函数是怎样的?答:积分控制器是一种根据误差的累积值来调节系统的输出的控制器。
积分控制器的传递函数可以表示为:Gc(s) = Ki/s其中,Gc(s)为积分控制器的传递函数,Ki为积分增益,s为复变量。
4. 什么是微分控制器?它的传递函数是怎样的?答:微分控制器是一种根据误差的变化率来调节系统的输出的控制器。
微分控制器的传递函数可以表示为:Gc(s) = Kd*s其中,Gc(s)为微分控制器的传递函数,Kd为微分增益,s为复变量。
5. 什么是比例积分控制器?它的传递函数是怎样的?答:比例积分控制器是一种同时具有比例和积分控制功能的控制器。

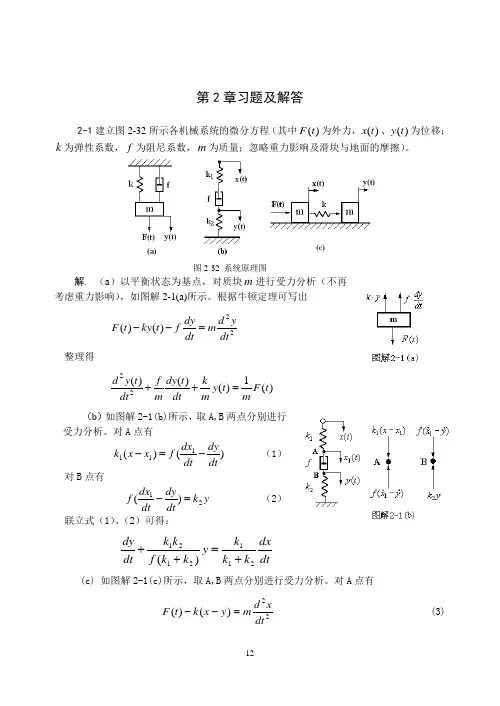


第二章 习题解析2-4 当系统处于零初始条件下时,给系统输入单位阶跃响应信号,其输出响应为2()1t t y t e e --=-+试求该系统的传递函数。
参考解答:2111421()()21(2)(1)s s Y s R s s s s s s s s++=-+==++++ 22()42()()32Y s s s G s R s s s ++==++2-5 某可控硅整流器的输出电压d 2cos U KU αΦ=式中,K 为常数;2U Φ为整流变压器副边相电压有效值;α为可控硅的控制角。
设α在0α附近作微小变化,试将d U 与α的关系式线性化。
参考解答:将非线性微分方程d 2cos U KU αΦ=进行线性化,即在平衡点α0 附近将其展为泰勒级数取一次近似,线性化后用变量增量的线性方程ΔU d = C Δα 代替原来的非线性方程,式中常数2020sin sin dd dU C KU U KU d ααααααΦΦ===-→∆=-∆略去增加量符号“Δ”,上式可简写为20sin d U KU ααΦ=- 2-6 试求图2-70所示电路的传递函数()/()y r U s U s 。
参考解答:图 a)可作出该无源电路的动态结构图(图a-1)亦可作成图(图a-2)所示由结构图等效变换可求得传递函数212()11()()11c r U s R Cs bTs U s R R Cs Ts ++==+++式中21212(),1R T R R C b R R =+=<+ ,该网络称为滞后网络。
图 b)由图(b )网络可作出其动态结构图(b-1),简化为(b-2)即可得传递函数:112221122112212()(1)(1)()()1y r U s R C s R C s U s R C R C s R C R C R C s ++=++++该网络称为滞后-超前网络(滞后-超前电路)。
2-7 试求图2-71所示有源电路的传递函数y r ()/()U s U s 。

第二章 自动控制系统的数学模型研究一个自动控制系统,除了对系统进行定性分析外,还必须进行定量分析,进而探讨改善系统稳态和动态性能的具体方法。
控制系统的运动方程式(也叫数学模型)是根据系统的动态特性,即通过决定系统特征的物理学定律,如机械﹑电气﹑热力﹑液压﹑气动等方面的基本定律而写成的。
它代表系统在运动过程中各变量之间的相互关系 ,既定性又定量地描述了整个系统的动态过程。
因此,要分析和研究一个控制系统的动态特性,就必须列写该系统的运动方程式,即数学模型。
第一节 系统动态微分方程模型常用的列写系统或环节的动态微分方程式的方法有两种﹕一种是机理分析法,即根据各环节所遵循的物理规律(如力学﹑电磁学﹑运动学﹑热学等)来编写。
另一种方法是实验辩识法,即根据实验数据进行整理编写。
在实际工作中,这两种方法是相辅相成的,由于机理分析法是基本的常用方法,本节着重讨论这种方法。
下面通过简单示例介绍机理分析法的一般步骤。
图2-1 RLC 网络[例2-1] 列写图2-1所示RLC 网络的微分方程。
解 1. 明确输入、输出量网络的输入量为电压)(t u r ,输出量为电压)(t u c 。
2.列出原始微分方程式。
根据电路理论得 )()(1)()(t Ri dt t i Cdt t di Lt u r ⎰++= (2-1) 而 ⎰=dt t i C t u c )(1)( (2-2) 式中)(t i 为网络电流,是除输入、输出量之外的中间变量。
3.消去中间变量将式(2-2)两边求导,得)(1)(t i C dt t du c = 或 dtt du C t i c )()(= (2-3) 代入式(2-1)整理为 )()()()(22t u t u dt t du RC dtt u d LC r c c c =++ (2-4) 显然,这是一个二阶线性微分方程,也就是2-1所示RLC 无源网络的数学模型。
[例2-2] 试列写图2-2所示电枢控制直流电动机的微分方程,要求取电枢电压)(t u a(V )为输入量,电动机转速)(t m ω)(s rad 为输出量。
习 题 22-1 试证明图2-77(a )所示电气网络与图2 77(b )所示的机械系统具有相同的微分方程。
图2-77习题2—1图证明:首先看题2-1图中(a )()()()s U s U s U C R R -=()()()()s U Cs R s CsU s U R s I R R R R ⎪⎭⎫⎝⎛+=+=11 ()()s I s C R s U C ⎪⎪⎭⎫⎝⎛+=221()()()[]s U s U s C R s C R s U C R C -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=112211 ()()s U s C R s C R s U s C R s C R R C ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+1122112211111 ()()()()()()s U R s C R s C s C R s U R s C R s C s C R R C11122211122211111+⨯+=⎥⎦⎤⎢⎣⎡++⨯+2—2试分别写出图2-78中各有源网络的微分方程。
图2-78 习题2-2图解: (a )()()()t u R t u R dt t du Co r r 211-=+ (b )()()()⎥⎦⎤⎢⎣⎡+-=t u R dt t du C t u R r o 2o 111(c)()()()⎥⎦⎤⎢⎣⎡+-=t u dt t du C R t u R r c c 211 2—3某弹簧的力一位移特性曲线如图2—79所示。
在仅存在小扰动的情况下,当工作点分别为x 0=-1.2,0,2.5时,试求弹簧在工作点附近的弹性系数。
解:由题中强调“仅存在小扰动"可知,这是一道非线性曲线线性化处理的问题。
于是有,在x 0=—1.2,0,2。
5这三个点处对弹簧特性曲线做切线,切线的导数或斜率分别为:1)()()35.5625.2805.175.040402.1==----=-=x dx df2)20020400=--==x dx df 3)65.2155.0320355.2==--==x dx df2- 4图2—80是一个转速控制系统,其中电压u 为输入量,负载转速ω为输出量。
第二章控制系统的数学模型数学模型时域模型频域模型方框图和信号流图第二章控制系统的数学模型控制系统的时域数学模型2-1 1 控制系统的时域数学模型控制系统的复数域数学模型2 控制系统的复数域数学模型2-2控制系统的结构图和信号流图3 控制系统的结构图和信号流图2-3.21 控制系统的时域数学模型控制系统的时域数学模型1.1. 1. 线性元件的微分方程线性元件的微分方程2.2.2. 控制系统微分方程的建立控制系统微分方程的建立3. 3. 线性系统的特性3.线性系统的特性4. 4. 线性定常微分方程的求解线性定常微分方程的求解5. 5. 非线性微分方程的线性化非线性微分方程的线性化6.6.6. 运动的模态运动的模态.21 控制系统的时域数学模型控制系统的时域数学模型列写系统运动方程的步骤•确定系统的输入量和输出量.•根据系统所遵循的基本定律,依次列写出各元件的运动方程.•消中间变量,得到只含输入、输出量的标准形式.如图例2.1RLC 电路,试列写以u u c (t)为输出量的网络微分方程。
i(t))()()()(t u t Ri t u t di L r c =++解:u r (t)dt =dt t i t u c )(1)(∫c)()()(22t u dt t du RC dtt u d LC c c c =++例2.2图为机械位移系统。
试列写质量m 在外力F作用下位移(t)的运动方程在外力F作用下位移y(t)的运动方程。
dt t dy f t F )()(1=解:阻尼器的阻尼力:)()(2t ky t F =弹簧弹性力:)()()()(2122t F t F t F dtt y d m −−=)()()()(22t F t ky t dy f t y d m =++整理得:dt dt• 全面了解系统的工作原理、结构组成和支配系统运动的规律,确定系统的输入量和输出量;•一般从系统的输入端开始,根据各元件或环节所遵循的物理规律,一次列些它们的微分方程•将各环节或元件的微分方程联立起来并消去中间变量,求取一个仅含有系统输入量和输出量的微分方程;•将方程化成标准型。
一般情况下微分方程的阶次和系统中独立储能元件的个数相等。
•线性——叠加性、齐次性2d )()()(2f t c t c dt d t c dt =++•方法——经典法和拉氏变换法t r t r +=¾经典法,系统齐次方程的解系统齐次方程的解,,只与系统特性有)(t r 系统的全响应为:)()(h 关,也称系统的自由响应或固有响应h ,特解,由系统的激励决定由系统的激励决定,的强制响应或受迫响应.)(t r p¾拉氏变换法•考虑初始条件考虑初始条件,,对微分方程中的每一项进行拉氏变换行拉氏变换,,微分方程变换为s •求出输出量拉氏变换函数的表达式求出输出量拉氏变换函数的表达式;•对输出量拉氏变换函数求逆变换出量的时域表达式, 即为微分方程的解2d d 微分方程初始条件, 输入¾例2-6)(2u dt t u dt o o +1.0)0(,1.0)0(=′=o o u u4. 4. 线性定常微分方程的求解4.线性定常微分方程的求解微分方程求解方法¾拉氏变换法常用变换公式)0()()(−−=⎥⎤⎢⎡f s sF t df L ⎦⎣dt ()0()()(222−′−−=⎤⎡f f s s F s t f d L ⎥⎦⎢⎣dt 部分分式法求拉氏逆变换.lim lim 0sF t ==:)()(0f f s t ∞→→++初值lim )(lim )(0sF t f f s t →∞→==∞终值:•严格地说,实际控制系统的某些元件含有一定的非线性特性,而非线性微分方程的求解非常困难。
如果某些非线性特性在一定的工作范围内,可以用线性系统模型近似,称为非线性模型的线性化•非线性微分方程能进行线性化的一个基本假设是变量偏离其预期工作点的偏差甚小,这种线性化通常称为小偏差线性化小偏差线性化:用台劳级数展开,略去二阶以上导数项。
一附近变化、假设:x , y 在平衡点(x 0,y 0)附近变化,即x =x 0+△x , y =y 0+△y二xdx x df y Δ⋅=Δ)(二、近似处理x x =0+Δ⋅+=Δ+=00)()(x x df x f y y y 三、数学方法L+Δ⋅=222)()(10x dx x f d dxx x =!20x x )x (df y ⋅略去高阶无穷小项x dx )x (f y y 0x x 00Δ+=Δ+==¾将一个自变量的函数y =f (x 点处(x 0, y 0)展开展开,,进行线性化进行线性化..y 设函数y =f (x )在(x 0, y 0)点连续可微点连续可微,泰勒级数展开泰勒级数展开,,1+−+==''00'0(!2))(()()(f x x x f x f x f y 当增量(x -x 0)较小时较小时,,略去其高次幂项略去其高次幂项, )(()()(0'00x f x f x f y y =−=−x x x −=Δ0y y y −=Δ令′线性化方程: , (,0x f K x K y =Δ=Δ¾将两个自变量的函数y =f (x 工作点处(x 10, x 20)展开展开,,进行线性化进行线性化.设函数在(x 10, x 20)点连续可微点连续可微,,同样在该点附近用泰勒级数展开泰勒级数展开,,当增量较小时当增量较小时,,略去其高次幂项略去其高次幂项, −),(2010x x f y y −=Δ令1011x x x =Δ线性化方程:22x x =Δ1x f x f y Δ⎟⎟⎞⎜⎜⎛∂+Δ⎟⎟⎞⎜⎜⎛∂=Δ,2,120102010x x x x x x ⎠⎝∂⎠⎝∂–确定系统的输入和输出–建立原始方程组(t);q (t)q dt dh(t)C 21−=–非线性模型线性化)(t h 22220020()()()()()[()()]()q t h t dq t q t q t h t h t q t α==+−=011h h dh t t h t h t t =−=−⇒Δ=–系统微分方程的求取Rq dh(t)122002()()[()()]()q q q R R (t)h(t)dtRC =+微分方程的齐次解为:n t i k k λ∑−1k j i i h e tc t r ∑+==+=1)(把函数称为该微分方程所描述运动的模态, 也叫振型. 每一种模态代表t t t n e e e λλλ,,,21L 一种类型的运动形态.例如, 特征根是共轭复根时, 其函数模态为和. t e t ωσsin t e t ωσcos2-2 2 控制系统的复数域数学模型控制系统的复数域数学模型1. 1. 传递函数的定义和性质传递函数的定义和性质2.2.2. 传递函数的零点和极点传递函数的零点和极点3.3.3. 传递函数的极点和零点对输出的影响传递函数的极点和零点对输出的影响4. 4. 典型元部件的传递函数4.典型元部件的传递函数5. 5. 典型环节及其传递函数典型环节及其传递函数.¾定义系统零状态响应的拉氏变换与激励的拉氏变换之比换之比,,用G (s )表示表示..信号系统中称线性定常系统微分方程)()(11110dt d a t c dtd a t c dt d a n n n n n +++−−−L )()(11110b t r dt d b t r dt d b m m m m m +++=−−−L )()(1110s b s b s b s C s G n n m m +++==−−L )(10a s a a s R +++L•传递函数表征了系统对输入信号的传递能力,是系统的固有特性,与输入信号类型及大小无关。
固有特性与输入信号类型及大小无关•传递函数只适用于线性连续定常系统。
•传递函数仅描述系统的单输入/单输出特性。
不同的物理系统可以有相同的传递函数。
同一系统中,不同物理量之间对应的传递函数也不相同。
•传递函数与微分方程的相通性。
•初始条件为零时,系统单位脉冲响应的拉氏变换为系统的传递函数。
为系统的传递函数•实际系统中有n≥m,n称为系统的阶数,系数为实数。
¾定义m ms b s b s C G +==10)()(s s b −n n s a s a s R s +10)()()(((1010s p s a z −==G (s )的分母多项式之根构成系统的极点,分子多项式之根构成系统的零点,即p j 是极点,z i 是零点.*K 数把极点和零点画在s 平面上,即为系统的零点分布图,简称极零图。
其中用“X ”表示极点,用“O ⎧j ω零点⎪⎨σ⎪⎩极点⎪⎨⎧⎪⎩方法一:依据系统微分方程求确定输入方法:依据系统微分方程求确定输入传递函数方法二:依据原始方程组代入消元求传递函数方法三:点网络系统可利用复阻抗直接求取传递函数方法四依据系统的输入输出信号求传递函数:–确定系统的输入和输出–建立原始方程组(t);q (t)q dtdh(t)C 21−=–非线性模型线性化)(t h 22220020()()()()()[()()]()q t h t dq t q t q t h t h t q t α==+−=011h h dh t t h t h t t =−=−⇒Δ=–系统微分方程的求取Rq dh(t)122002()()[()()]()q q q R R (t)h(t)dtRC=+rq 1h 2h 1R 2R 0q ⎪⎧−⎪⎧=−0r 110r (s)Q (s)Q (t)h c (t)q (t)q &⎪⎪⎪⎪⎨−=⇒⎪⎪⎪⎪⎨=−−=c 010*******(s)Q (s)Q (s)H (s)Q (t)h c qc(t)(t)q R (t)h (t)h (t)q &⎪⎪⎪⎩=⎪⎪⎪⎩=22c 22c R (s)H (s)Q R (t)h (t)q )s C R C R C (R s C C R R 1(s)Q (s)Q G(s)12221122121r c ++++==R (s)H G(s)22==LR 2R Cu u ++u +1rc__1_121)//R 1(R U +21212r c R cs 1R csLs )//R cs 1(R cs(s)U (s)G(s)=+⋅++==()(s)U G(s)2=12121R L)s C R (R )LCs R (R ++++(s)U 1应用复阻抗概念和分压定理使电网络传递函数的求取过程大大简化!!系单阶输初始条件的输系统单位阶跃输入及零初始条件下的输出响应为:求传递函数。