解决旋转问题的思路方法.docx

平面几何旋转解题技巧平面几何旋转解题技巧：让图形“转”起来的奇妙魔法嘿，大家好呀！今天咱来唠唠平面几何里超有意思的旋转解题技巧，这简直就是让那些图形“活”起来的奇妙魔法啊！你想想，那些个图形一个个呆呆地在那，好像没啥头绪，可一旦让它们“转一转”，嚯，那可就大不一样啦，就像给它们注入了灵魂一样。

记得我刚开始接触旋转解题技巧的时候，那叫一个懵啊，看着题目里的图形，我就想：“这咋转啊？转到哪去啊？”就像一只无头苍蝇到处乱撞。

但是，随着慢慢琢磨和不断练习，嘿，我还真就摸到点门道了。

比如说有一次，碰到一个看似超级复杂的三角形问题，线条交错得我眼睛都花了。

我正挠头的时候，突然灵机一动，心想：“要不把这个三角形转一下试试？”嘿，你还别说，一转，那些之前乱七八糟的线条瞬间就变得清晰明了起来，关系一下子就理顺了，答案也就呼之欲出啦！还有一次，遇到一个图形，怎么看都觉得缺少点什么关键信息。

我左思右想，突然一拍脑袋：“哎呀，我怎么忘了旋转这一招啊！”于是我大胆地把图形进行了旋转，哇塞，就像打开了一个隐藏的宝藏，那些隐藏的条件和关系一下子都冒出来啦，这解题不就轻而易举了嘛。

我觉得呀，旋转解题技巧就像是一把神奇的钥匙，能打开平面几何那神秘的大门。

不过呢，要想用得好这把钥匙，还得胆大心细。

不能怕把图形转坏喽，大胆地去尝试，万一转对了呢，那可就是“柳暗花明又一村”啦！当然啦，也得细心观察，仔细琢磨，找到旋转的最佳角度和方法。

有时候我都觉得自己就像个小魔法师，拿着旋转这个魔法棒，在平面几何的世界里尽情挥舞，把那些难题一个个都给解决掉。

那感觉，真是爽歪歪啊！总之呢，平面几何旋转解题技巧真的是超级实用又有趣。

大家要是还没试过，赶紧去试试看吧，相信你们一定会被这个奇妙的魔法所折服，也一定会在解题的过程中感受到那无穷的乐趣和成就感。

让我们一起在平面几何的世界里，用旋转技巧尽情地玩耍吧！哈哈！。

初中几何旋转解题思路
初中几何旋转解题思路一般分为以下几步：
1. 确定旋转中心和旋转角度：题目中一般会明确给出旋转中心和旋转角度，如果没有明确给出，需要根据题目条件自行判断。

通常情况下，旋转中心是图形的某个顶点、中心或边上的某个点，旋转角度是90度、180度或360度等。

2. 画出旋转后的图形：根据旋转中心和旋转角度，将原来的图形进行旋转，画出旋转后的图形。

3. 利用对称性质求解：利用旋转后的图形和原来的图形之间的对称性质，求出题目所要求的内容。

比如可以利用旋转后的图形与原图形完全重合的特点，求出各个角度、边长等。

4. 常用的解题方法：根据题目的要求，常用的解题方法有：利用对称性质、利用垂直、平行关系、利用相似三角形、利用等角关系等。

需要注意的是，在解决几何旋转问题时，需要结合实际情况选择合适的方法，同时要注意图形的对称性质和角度、边长等量的计算。

此外，多做一些练习题可以提高解题的技巧和效率。

1/ 1。

中考数学热点专题复习图形的旋转建南民中张中建♦识记巩固1、旋转：在平面内，把一个图形绕,按旋转的图形运动，叫做旋转.2、图形旋转的三个要素：（1）; （2）; （3）.3、旋转的特征：（1）图形的和都没有发生变化；（2）相等，相等；（3）对应点到旋转中心的距离;（4）图形中的每一点都绕着旋转中心旋转同样大小的,对应点与旋转中心连线的夹角是.4、旋转对称图形识别：观察图形是否存在一点，围绕这一点旋转一定角度后能否与图形5、经过两次对称轴相交的轴对称变换，相当于一次.6、在成中心对称的两个图形中，连结对称点的线段都经过对称中心，并且被对称中心平分. 反过来，如果两个图形的对应点连成的线段都经过某一点，并且被该点,那么这两个图形一定关于这一点成中心对称.♦识记巩固参考答案：1、某一点—定方向〜定角度2、（1）旋转中心（2）旋转方向（3）旋转角度3、（1）形状大小（2）对应线段对应角（3）相等（4）角度对应角4、重合5、旋转6、平分♦给你提个醒图形在旋转变换过程中会发生许多变化，但是同样也有许多关系并不会随着图形的变化而变化，这就是旋转变换中的不变关系，是解决旋转变换问题的关键之一。

我们要善于归纳以不变应万变的方法和从特殊到一般的数学思想。

♦典例解析例题1：如图1,已知矩形ABED,点。

是边DE的中点，且AB = 2AD.（1）判断△ABC的形状，并说明理由；（2）保持图1中ABC固定不变，绕点C旋转DE所在的直线到图2中（当垂线段AD. 3E在直线初V的同侧），试探究线段A。

、BE, DE长度之间有什么关系？并给予证明；（3）保持图2中固定不变，继续绕点C旋转DE所在的直线肱N到图3中的位置（当垂线段A。

、3E在直线初V的异侧）.试探究线段A。

、BE、DE长度之间有什么关系？并给予证明.图3例题1图例题2： RtAAB C与RtAFED是两块全等的含30°、60°角的三角板，按如图(一)所示拼在一起，C8与DE重合.(1)求证：四边形A8FC为平行四边形；(2)取BC中点。

初中数学旋转问题解题技巧
1. 嘿，你知道吗？遇到旋转问题别慌张！比如像钟表指针的转动，那就是旋转呀！咱就拿这个例子说，看到旋转角，那就是关键线索啊，可别小瞧它！
2. 同学们，旋转问题里找对应边对应角很重要哦！就好像拼图似的，得把它们都对上才行。

比如说一个三角形旋转后，那对应的边和角不就得赶紧找到呀！
3. 哎呀呀，旋转图形里的中心对称点可得看准了！你想想看，就像游乐场的摩天轮中心一样重要呢！比如给定一个图形绕着某个点旋转，那这个点不就是核心嘛！
4. 嘿，注意旋转方向呀！顺时针还是逆时针可不能搞错啊，这就好比走路，方向错了可就到不了目的地啦。

就像那个风车旋转，得清楚是怎么转的呀！
5. 别忘了利用旋转前后图形全等这个特性哦！这多有用呀！好比原来的你和现在的你，本质上还是同一个人呀！比如知道了一个图形旋转前的情况，那旋转后的很多性质就可以利用全等知道啦！
6. 哇塞，在做旋转问题时可以动手画一画呀！亲手画的过程就像给自己搭房子，一砖一瓦都清楚。

像一个四边形旋转，动手画画不就更直观了嘛！
7. 你们有没有发现呀，有些旋转问题和生活中的现象超像的！就像风扇的转动一样。

比如说判断图形经过旋转后的样子，是不是和风扇转了一圈很类似呀！
8. 哈哈，遇到复杂的旋转问题别头疼，一步步来呀！就像爬山，一步一步总能到山顶。

比如那个多次旋转的问题，不要怕，慢慢分析总会搞清楚的！
9. 反正呀，初中数学的旋转问题没那么难，只要用心去琢磨，就像研究自己喜欢的东西一样，总能找到方法解决的！
我的观点结论：只要掌握好方法和技巧，初中数学旋转问题就能轻松搞定！。

高中数学旋转解题技巧在高中数学中，旋转是一个常见的解题技巧，它可以帮助我们简化问题，找到更直观的解题方法。

本文将介绍几种常见的旋转解题技巧，并通过具体的题目进行说明，帮助读者更好地掌握这些技巧。

一、旋转解题的基本原理旋转解题是将原问题通过旋转变换转化为一个更简单的问题，从而利用几何性质进行求解。

在旋转解题中，我们通常会用到以下几个基本原理：1. 旋转不改变长度和角度：旋转只改变了原图形的位置和方向，但不改变图形的长度和角度关系。

因此，在旋转解题中，我们可以利用旋转后的图形与原图形的对应关系来求解问题。

2. 旋转对称性：旋转对称性是指图形在某个旋转变换下保持不变。

利用旋转对称性，我们可以将原问题转化为一个与之等价的旋转对称问题，从而简化求解过程。

3. 旋转变换的性质：旋转变换具有保角性和保持直线平行性的性质。

利用这些性质，我们可以推导出旋转后的图形与原图形的一些几何关系，进而解决问题。

二、旋转解题的实际应用下面我们通过几个具体的题目来说明旋转解题的应用方法和技巧。

题目一：已知一个平面图形，将其逆时针旋转90度，再将旋转后的图形绕原点顺时针旋转60度，得到的图形与原图形重合。

求原图形的类型。

解析：根据题目描述，我们可以得知旋转后的图形与原图形重合，说明它们是同一个图形。

根据旋转变换的性质，逆时针旋转90度相当于顺时针旋转270度，再绕原点顺时针旋转60度相当于逆时针旋转300度。

因此，旋转后的图形相当于逆时针旋转270度再逆时针旋转300度，即逆时针旋转570度。

根据旋转对称性，逆时针旋转570度等于顺时针旋转360度加上逆时针旋转210度。

所以，原图形的类型是正五边形。

题目二：已知一个圆的半径为r，以圆心为中心，将圆逆时针旋转60度，得到的图形与原图形重合。

求r的值。

解析：根据题目描述，旋转后的图形与原图形重合，说明它们是同一个图形。

根据旋转变换的性质，逆时针旋转60度相当于顺时针旋转300度。

因此，旋转后的图形相当于逆时针旋转300度。

初中几何旋转解题技巧引言几何学作为数学的一个重要分支，是初中数学教育中不可或缺的一部分。

而在几何学中，旋转是一种常见的变换方式。

通过旋转，我们可以改变图形的位置、形状和方向，从而解决与旋转相关的问题。

本文将介绍初中几何中常见的旋转解题技巧。

什么是旋转在几何学中，旋转是指将一个图形绕着某个点或某条线进行转动，使得图形保持形状不变但位置发生改变的操作。

我们可以通过角度来描述旋转的程度，常用单位为度（°）或弧度（rad）。

旋转解题技巧1. 确定旋转中心在解决旋转问题时，首先需要确定一个旋转中心。

这个中心可以是图形内部的一个点，也可以是图形外部的一个点。

根据问题给出的条件来选择合适的旋转中心。

2. 确定旋转方向确定了旋转中心后，接下来需要确定旋转方向。

根据问题描述和图形特点来判断顺时针还是逆时针方向进行旋转。

3. 确定旋转角度旋转角度是解决旋转问题的关键。

根据问题给出的条件，确定旋转角度。

常见的旋转角度有90°、180°和360°等。

4. 应用旋转公式在确定了旋转中心、旋转方向和旋转角度后，我们可以根据几何学中的旋转公式来解题。

以下是常见的几个旋转公式：•绕原点逆时针旋转θ°：对于坐标(x, y)，其逆时针旋转θ°后的新坐标为(x cosθ - y sinθ, x sinθ + y cosθ)。

•绕原点顺时针旋转θ°：对于坐标(x, y)，其顺时针旋转θ°后的新坐标为(x cosθ + y sinθ, -x sinθ + y cosθ)。

•绕任意点逆时针旋转θ°：先将图形平移使得旋转中心位于原点，然后按照绕原点逆时针旋转的方式计算新坐标，最后再将图形平移回原来位置。

5. 注意坐标变换在应用上述旋转公式进行计算时，需要注意坐标变换。

通常情况下，我们使用直角坐标系进行计算，在计算过程中需要将问题中给出的坐标转换为直角坐标系下的坐标，最后再将计算得到的坐标转换回原来的坐标系。

旋转变换解题的高效技巧与策略在解决数学或几何问题时，旋转变换是一种常用且有效的技巧。

通过旋转图形或坐标系，我们可以简化问题，找到更加高效的解决方案。

本文将介绍使用旋转变换解题的一些技巧与策略，并通过一些实例来加深理解。

首先，让我们来了解旋转变换的基本原理。

旋转变换是将图形或坐标系绕某个中心点旋转一定角度的操作。

它可以改变图形的朝向、位置和形状，使问题更易于理解和解决。

一、利用旋转变换简化图形问题当我们面对一个复杂的图形问题时，可以尝试通过旋转变换将其简化。

以下是一个实例：问题：一个正方形ABCD，边长为2，要证明两条对角线相等。

解决方案：我们可以通过旋转变换将问题简化。

将正方形绕其中心点O逆时针旋转90度，得到正方形A'B'C'D'。

由于旋转不改变长度和角度，故正方形A'B'C'D'的边长也为2，且AB'与AD'相交于点E。

接下来，我们可以通过证明三角形ABE与三角形ADE全等来得到结论。

因为旋转变换不改变形状，所以两个相等的角旋转后仍然相等。

因此，我们可以得出结论：正方形ABCD的两条对角线相等。

通过利用旋转变换简化问题，我们可以更清晰地理解并解决问题。

二、利用旋转变换求解几何问题旋转变换还可以用于解决一些几何问题。

以下是一个实例：问题：一个等边三角形ABC，要证明角度BAC的大小。

解决方案：我们可以通过旋转变换求解。

将等边三角形ABC绕顶点A逆时针旋转60度，得到等边三角形ABA'。

由于旋转不改变角度大小，我们可以得知角BAA'的大小为60度。

又因为等边三角形ABA'的三条边长度相等，所以角BAA'、角BAC和角CAC'也相等。

通过旋转变换，我们可以得出结论：角BAC的大小为60度。

三、旋转变换在坐标系中的应用除了图形问题和几何问题，旋转变换还可以在坐标系中得到应用。

以下是一个实例：问题：平面上有一条线段AB，坐标分别为A(2, 4)和B(6, 8)，要求将线段绕原点顺时针旋转45度后的坐标。

旋转综合题解题方法归纳
嘿，同学们！今天咱就来好好唠唠这旋转综合题的解题方法。

咱先说说这旋转是啥玩意儿呀，就好比一个东西在那滴溜溜地转呀转，一转就转出好多新情况新问题来啦！那面对这些个转来转去的题，咱可不能发懵呀！
首先呢，咱得把题目里的条件都看仔细咯，一个小细节都别放过。

这就好比你找宝藏，得把每个角落都瞅清楚了，不然宝贝就溜走啦！
然后呢，咱得在脑子里构建出那个旋转的画面，想象一下那个图形是
怎么转的，转到哪里去了。

比如说有个三角形在那转，那它的边呀角呀肯定都跟着变啦。

这时
候咱就得抓住那些不变的量，这可是解题的关键哟！就像在混乱中找
到那根定海神针一样。

还有啊，多画画图，别嫌麻烦！画着画着你可能就突然灵光一闪，
找到解题的突破口啦。

有时候一个巧妙的图能让你一下子看清问题的
本质呢。

再就是利用好那些定理呀公式呀，什么全等啦相似啦，这些都是咱
的得力武器呀！就像孙悟空的金箍棒，一挥就能把难题打得落花流水。

咱举个例子哈，有个图形转呀转，转到你都快不认识它了。

这时候你就得静下心来，看看能不能找到和之前学过的哪个图形有点像，然后把那些定理啥的往上套一套。

哎呀，说不定答案就出来啦！
同学们，别害怕这些旋转综合题，它们就是纸老虎！只要咱掌握了方法，多练练，就一定能把它们拿下。

就像武松打虎一样，勇敢地冲上去，把难题给解决掉！相信自己，咱肯定行！加油吧！咱在解题的道路上一路向前冲，什么难题都挡不住咱前进的脚步！。

中考旋转问题解题技巧
1. 哎呀呀，你知道吗，中考旋转问题里有个超重要的技巧就是找关键点呀！就像拼图一样，找到了关键点就能把整个图形拼凑起来啦！比如在这个图形里，找到那个关键的顶点，然后围绕它进行分析，疑惑是不是一下就解开啦？
2. 嘿，告诉你哦，旋转问题中要特别注意图形的对称性！这就好比是一把钥匙，能打开解题的大门呀！像这个图形，一旦发现了它的对称性，哇塞，解题思路不就一下子出来了嘛！
3. 哇哦，可别小看了观察已知条件这个步骤呀！它就像指明灯一样重要呢！比如这里给了这些条件，那我们就得像侦探一样，仔细分析，从中找到线索呀，你说是不是很有趣呢？
4. 哟呵，在解决旋转问题时，我们要大胆去尝试想象图形运动的过程呀！这就好像让图形在我们脑海里跳舞一样！像碰到这种情况，想象一下图形旋转之后的样子，好多问题就迎刃而解啦！
5. 哈哈，千万别忘了利用相似三角形这个好帮手呀！它可是解决旋转问题的得力干将！就好比是给我们配备了一件强大的武器！比如在这个例子里，通过相似三角形，一下子就能突破难关啦！
6. 哎呀呀，最后一点也很关键哦，那就是要多练习！只有不断练习，才能在考场上应对自如呀！就像运动员训练一样，练得多了自然就厉害啦！比如多做一些这样的题目，到时候就不会手忙脚乱啦！
我的观点结论就是：中考旋转问题并不可怕，只要掌握了这些技巧，多练习，遇到问题冷静分析，就一定能取得好成绩！。

旋转练习题技巧旋转练习题是数学中常见的类型之一，涉及到图形的旋转、对称性和对应关系。

通过掌握旋转练习题的解题技巧，可以提高数学解题的效率和准确性。

本文将介绍一些旋转练习题的技巧，帮助读者更好地理解和解决这类问题。

1. 理解旋转概念在解决旋转练习题之前，首先要理解旋转的概念。

旋转是指将一个图形绕某一固定点旋转一定角度后得到的新图形。

旋转通常涉及到角度的度数、旋转方向（顺时针或逆时针）以及旋转中心等要素。

了解这些概念对于解题至关重要。

2. 利用旋转对称性旋转练习题常常利用图形的旋转对称性来解答。

在解题过程中，应该观察图形是否具有旋转对称性。

如果有，可以通过寻找一些旋转对称的特征来简化问题。

例如，正方形在旋转90度、180度和270度之后仍然是自身，这种旋转对称性可以用来解决涉及到正方形的旋转练习题。

3. 观察图形的关系解决旋转练习题时，要观察图形之间的关系。

通过观察可以发现一些规律，从而简化问题。

例如，有些图形在旋转一定角度后与原图形相似，而有些则发生了形状的改变。

通过观察这些关系，可以找到解决问题的突破口。

4. 使用旋转变换公式旋转练习题可以通过旋转变换公式来解决。

旋转变换公式是描述图形绕旋转中心旋转一定角度后的坐标变换规律。

根据具体的题目要求，可以利用旋转变换公式计算出旋转后的坐标，并进而解决问题。

5. 注意图形的旋转方向在解决旋转练习题时，要注意图形的旋转方向。

旋转方向通常分为顺时针和逆时针两种，根据题目要求选择合适的旋转方向进行计算。

如果选择的旋转方向与题目要求不符，答案会有所偏差。

6. 利用旋转图形的对称性图形的旋转常常涉及到对称性。

利用图形的对称性可以简化问题。

例如，对于一个旋转图形，在旋转某一角度后，图形上的某些点的位置可能会通过旋转回到原来的位置。

这种情况下，可以通过利用图形的对称性来确定旋转后的位置。

总结：旋转练习题技巧是解决这类数学问题的关键。

通过理解旋转概念、利用旋转对称性、观察图形关系、使用旋转变换公式、注意旋转方向和利用图形的对称性，可以更好地解决旋转练习题，提高数学解题能力。

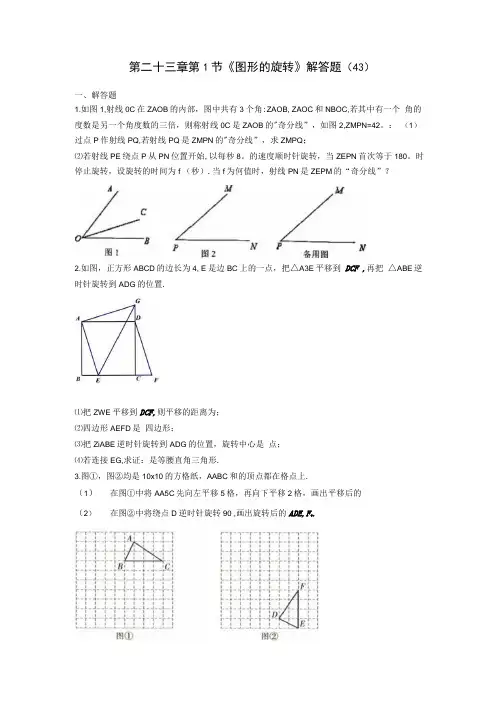
第二十三章第1节《图形的旋转》解答题（43）一、解答题1.如图1,射线0C在ZAOB的内部，图中共有3个角:ZAOB, ZAOC和NBOC,若其中有一个角的度数是另一个角度数的三倍，则称射线0C是ZAOB的"奇分线”，如图2,ZMPN=42。

：（1）过点P作射线PQ,若射线PQ是ZMPN的"奇分线”，求ZMPQ；⑵若射线PE绕点P从PN位置开始,以每秒8。

的速度顺时针旋转，当ZEPN首次等于180。

时停止旋转，设旋转的时间为f （秒）.当f为何值时，射线PN是ZEPM的“奇分线”？2.如图，正方形ABCD的边长为4, E是边BC上的一点，把△A3E平移到DCF ,再把△ABE逆时针旋转到ADG的位置.⑴把ZWE平移到DCF,则平移的距离为；⑵四边形AEFD是四边形；⑶把ZiABE逆时针旋转到ADG的位置，旋转中心是点；⑷若连接EG,求证：是等腰直角三角形.3.图①，图②均是10x10的方格纸，AABC和的顶点都在格点上.（1）在图①中将AA5C先向左平移5格，再向下平移2格，画出平移后的（2）在图②中将绕点D逆时针旋转90 ,画出旋转后的ADE,F t.1 1 ,,4.如图，直线；y = -----------x + 2父y轴于点A,交x轴于点C,抛物线y = —x +bx + c2 4（1）直接写出点A,点B,点C的坐标及抛物线的解析式；（2）在直线AC上方的抛物线上有一点M,求四边形面积的最大值及此时点M 的坐标；（3）将线段绕x轴上的动点P（m,O）顺时针旋转90。

得到线段00',若线段00'与抛物线只有一个公共点，请结合函数图象，求m的取值范围.5.在RtA/lBC中，ZABC=90。

，/ACB=30。

，将△ABC绕点C顺时针旋转一定的角度a得到点A、B的对应点分别是。

、E.7. （1）（问题发现）如图1, AABC和ZVIDE都是等腰直角三角形，ZBAC^ZDAE^90°,延长朗到点F,使得AF^AC,连接DF、BE,贝。

旋转问题的解题技巧
1. 哎呀呀，遇到旋转问题不要慌！你看那电风扇转得多快呀，就像我们解题的思路一样要迅速找到关键。

比如一个图形绕着一个点旋转，那就要紧紧抓住旋转中心这个关键呀！是不是一下子就清楚啦？
2. 嘿，你知道吗，旋转问题有个绝招来啦！想象一下时钟的指针转动，这就跟我们要解的旋转问题很像呀。

像那种给出旋转前后的图形，我们就得观察它们之间的变化规律呀，这招超好用的呀！
3. 哇哦，解决旋转问题还得学会找特点呢！就像每个玩具都有它独特的地方一样。

比如知道了旋转的角度和方向，解题不就容易多了嘛！你说是不是呀？
4. 哈哈，面对旋转问题就得大胆去尝试呀！好比划船，不尝试怎么知道能不能到对岸呢。

试试不同的方法，也许答案就冒出来啦，就像突然找到宝藏一样惊喜呀！
5. 诶呀，旋转问题里可藏着不少秘密呢！就像一个神秘的盒子等你去打开。

像是两个图形通过旋转重合，那我们就找找它们重合的关键点嘛，这样不就柳暗花明啦？
6. 哟呵，要善于利用对称性来解决旋转问题呀！好比照镜子，对称的两边是不是很好找呀。

碰到有对称关系的旋转，那答案准能快速找到啦！
7. 哇，旋转问题可不能死脑筋呀！要像脑筋急转弯一样灵活。

例如给定一个复杂的图形旋转，我们别害怕，一点点分析，总会找到解题思路的啦！
8. 嘿呀，总之记住这些解题技巧，旋转问题就难不倒你啦！不管遇到什么难题，都可以像勇士一样去战斗，把答案给攻克下来呀！
我的观点结论就是：掌握了这些技巧，再难的旋转问题都能迎刃而解！。

10解题技巧专题巧用旋转进行计算在解题过程中，有时我们可以巧用旋转来进行计算，以简化问题、加快解题速度。

下面将介绍几种巧用旋转进行计算的技巧。

1.点的旋转：对于一个点(x,y)，我们可以将其逆时针旋转θ度得到新的点(x',y')，计算方法如下：x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这种技巧可以用来求解两点之间的距离、判断点的位置关系等问题。

2.向量的旋转：对于一个向量(x,y)，我们同样可以将其逆时针旋转θ度得到新的向量(x',y')，计算方法与点的旋转类似。

x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这种技巧可以用来求解向量的和、点积、叉积等问题。

3. 复数的旋转：对于一个复数a + bi，我们可以将其旋转θ度得到新的复数c + di，计算方法同样类似。

c = (a + bi) * cosθd = (a + bi) * sinθ这种技巧可以用来求解复数的乘法、除法等问题。

4.矩阵的旋转：对于一个二维矩阵，我们可以将其逆时针旋转θ度得到新的矩阵，计算方法如下：对于一个点(x,y)在原矩阵中的位置(i,j)，新矩阵中该点的位置为：i' = j * sinθ + i * cosθj' = j * cosθ - i * sinθ这种技巧可以用来求解矩阵的转置、乘法、快速幂等问题。

在实际应用中，我们可以根据具体问题选择合适的旋转方法。

例如，在计算几何中，通过旋转可以使问题简化为求解两点之间的距离或者判断一些点是否在条直线上，从而简化问题的求解过程。

在矩阵运算中，可以通过旋转将矩阵进行转置或者快速幂运算，提高运算效率。

巧用旋转进行计算可以节省时间、简化问题，但在应用时也需要注意旋转角度的选择和计算的正确性。

在实际解题过程中，可以通过举例或者推导来验证旋转计算的正确性，避免出现错误的结果。

旋转数学题解题方法技巧旋转数学题解题方法技巧一、旋转数学题的概念旋转数学是一类涉及空间几何图形的解题方法，旋转数学指的是利用图形来进行运算，在几何中，空间几何图形可以提供重要的知识，从而有助于解决数学问题，其中包括一些比较复杂的问题，比如多面体的旋转等。

二、旋转数学题的解题方法技巧1、明确旋转数学题的形式要根据旋转数学题的具体形式来确定解题思路，一般分为三类：（1）旋转图形的形状（比如圆形、正方形等），（2）旋转图形的大小，（3）旋转图形的角度。

2、确定解题步骤旋转数学题的问题可以分为几个部分：（1）确定图形定义的方向；（2）计算旋转的角度；（3）构造旋转图形的方法；（4）通过旋转图形计算相关的变量。

3、构造图形因为解答题目需要利用空间几何图形，而空间几何图形的构造也非常重要。

首先，需要仔细观察题目，根据题目中提供的图形信息，明确图形的各个点和线段的关系；其次，根据题目中给出的角度，用测量角度的工具来确定图形的具体方位。

4、确定旋转角度求解旋转数学题的时候，需要确定旋转角度，这一步非常重要，而且需要花费一定的时间。

如果知道图形的始末点，那么可以用直角三角形的关系式求出旋转角度，如果不知道图形的始末点，可以运用角平分线求出旋转角度。

5、计算变量解答旋转数学题的时候，除了确定旋转方向和角度外，还需要计算出与旋转相关的变量，例如图形的面积、夹角等等。

如果题目中出现复杂的几何图形，可以使用它们的公式来计算出任何一个变量。

6、解答问题有了图形的关系、旋转角度及其他变量的信息，就可以解答旋转数学题了，根据所要求的条件，将计算得到的变量结合起来，就可以解出题目要求的结果了。

解决简单的平移和旋转问题平移和旋转是几何学中常见的操作，它们在许多领域中都有广泛的应用，包括计算机图形学、物理学、机器人学等等。

本文将介绍如何解决简单的平移和旋转问题，并提供相应的示例。

一、平移问题的解决方法平移是指物体在平面内沿着指定的方向移动一段距离。

在平移问题中，我们需要知道物体的起始位置和平移的距离，然后通过相应的计算得到物体的最终位置。

解决平移问题的一种常见方法是使用坐标系。

我们可以将物体的起始位置和平移的距离都用坐标表示，然后通过坐标的加法运算得到物体的最终位置。

具体步骤如下：1. 定义坐标系：选择一个合适的原点和坐标轴方向，并标记出单位长度。

2. 表示物体的起始位置和平移的距离：用坐标表示物体的起始位置，并用一个向量表示平移的距离。

3. 进行坐标的加法运算：将物体的起始位置和平移的距离进行相加，得到物体的最终位置。

例如，假设物体的起始位置为(2, 3)，平移的距离为(4, -1)，我们可以按照上述步骤进行计算：起始位置 + 平移的距离 = (2, 3) + (4, -1) = (6, 2)因此，物体的最终位置为(6, 2)。

二、旋转问题的解决方法旋转是指物体围绕一个中心点旋转一定角度。

在旋转问题中，我们需要知道物体的起始位置、旋转的角度以及旋转中心点的位置，然后通过相应的计算得到物体的最终位置。

解决旋转问题的一种常见方法是使用旋转矩阵。

旋转矩阵是一个二维矩阵，可以通过一定的计算将物体的坐标点旋转到相应的位置。

具体步骤如下：1. 定义旋转矩阵：根据旋转的角度，构造一个旋转矩阵。

旋转矩阵的构造方法有多种，可以通过数学公式或者绕坐标轴旋转的方式进行计算。

2. 表示物体的起始位置和旋转中心点：用坐标表示物体的起始位置，并用一个点表示旋转中心点的位置。

3. 进行坐标的旋转计算：将物体的起始位置和旋转中心点进行坐标变换，得到物体相对于旋转中心点的新位置。

4. 进行坐标的平移计算：将物体相对于旋转中心点的新位置再进行坐标变换，得到物体相对于原始坐标系的最终位置。

旋转和投影的解题思路教案引言：解题是我们在学习过程中经常会遇到的任务，而在解题的过程中，旋转和投影是两个常见的问题。

本文将为大家介绍一些解决旋转和投影问题的思路和方法。

1. 旋转解题思路1.1 了解问题要求首先，在解决旋转问题之前，我们需要明确问题的要求。

具体而言，我们需要知道物体旋转的轴线、旋转的角度以及旋转的方向。

1.2 确定旋转的坐标系在进行旋转操作时，我们需要确定一个坐标系来描述旋转后物体的位置。

通常情况下，我们可以选择以旋转轴线为轴来确定一个坐标系。

1.3 应用旋转公式根据旋转的角度，我们可以利用旋转公式来计算旋转后的坐标。

对于二维平面上的旋转，我们可以使用以下公式：新的x坐标 = 原x坐标 * cos(旋转角度) - 原y坐标 * sin(旋转角度)新的y坐标 = 原x坐标 * sin(旋转角度) + 原y坐标 * cos(旋转角度)对于三维空间的旋转，我们可以使用类似的公式来计算旋转后的坐标。

2. 投影解题思路2.1 确定投影平面在解决投影问题之前，我们需要确定一个投影平面。

投影平面通常以二维平面为基准，可以是水平平面、垂直平面或者其他倾斜的平面。

2.2 确定投影方向确定了投影平面后，我们需要确定投影的方向。

投影方向可以是垂直于投影平面的方向，也可以是倾斜的方向。

2.3 计算投影坐标根据物体在三维空间中的坐标和投影平面的位置，我们可以利用类似三角函数的方法来计算物体在投影平面上的坐标。

3. 结合旋转和投影的解题思路在一些问题中，我们不仅需要考虑物体的旋转，还需要考虑投影。

在这种情况下，我们可以将旋转和投影的解题思路结合起来，以求解复杂的问题。

3.1 确定旋转和投影的次序在结合旋转和投影的解题过程中，我们需要先确定旋转的次序，然后再进行投影。

这是因为旋转的结果直接影响投影的位置和形状。

3.2 依次应用旋转和投影公式根据旋转和投影的要求，我们可以按照旋转次序依次应用旋转公式，然后再根据投影的要求应用投影公式，以求解旋转和投影结合的问题。

如何有效解决初中数学中的形旋转与平移问题题目：如何有效解决初中数学中的形旋转与平移问题形旋转与平移是初中数学中的重要内容之一，它们既是数学常识的延伸，也是培养学生思维能力和创造力的重要途径。

然而，由于形旋转与平移问题本身的复杂性和抽象性，许多初中生在解决这类问题时感到困惑。

本文将探讨如何有效解决初中数学中的形旋转与平移问题，包括提供一些解题方法和技巧。

一、形旋转问题的解决方法形旋转是指通过旋转一个物体使其围绕某个轴或点发生旋转，从而改变物体的位置或形状。

解决形旋转问题的方法主要包括以下几点：1. 确定旋转中心和旋转角度：在解决形旋转问题时，首先需要确定旋转中心和旋转角度。

旋转中心是旋转操作的中心点，旋转角度表示物体相对于旋转中心旋转的角度。

确定这两个要素可以帮助学生更好地理解形旋转问题。

2. 利用几何性质：几何性质是解决形旋转问题的重要工具。

学生可以根据不同的几何性质来分析和解决旋转问题。

例如，对于一个正方形绕某个点旋转90度，可以利用正方形的对称性质来确定旋转后的形状和位置。

3. 运用角度概念和三角函数：形旋转问题涉及到角度的概念，因此学生需要掌握相关的角度知识，并能够灵活地运用三角函数来解决问题。

例如，在解决一个关于旋转角度的问题时，学生可以利用正弦或余弦函数来计算旋转后的位置坐标。

二、平移问题的解决方法平移是指通过沿着某个方向将一个物体从一个位置移动到另一个位置，而保持其形状和大小不变。

解决平移问题的方法主要包括以下几点：1. 明确平移的方向和距离：在解决平移问题时，学生需要明确平移的方向和距离。

平移的方向可以是水平方向、垂直方向或者其他任意方向，距离表示物体从一个位置到另一个位置的位移长度。

确定这两个要素可以帮助学生更好地理解平移问题。

2. 利用平移的性质：平移具有保持形状和大小不变的性质，学生可以利用这一性质来解决平移问题。

例如，对于一个正方形平移到另一个位置，可以直接保持其边长不变，只需将每个顶点按照平移方向和距离进行相应的平移。