精选东华理工大学物理练习试卷答案角动量守恒资料

第5章角动量角动量守恒定律一、本章总结1.请总结角动量、角动量守恒定律一章的知识点。

2.请画出本章的知识脉络框图。

二、填空题1. 如图所示，圆盘绕着与盘面垂直且过圆心O 的轴旋转，轴固定且光滑，转动角速度为ω。

这时，一对力偶沿着盘面作用在圆盘上（每个力大小为F ），圆盘的角速度ω 。

（填增大、减小或不能确定）2. 一个立方体放在粗糙的水平地面上，其质量分布均匀，为50 kg ，边长为1m 。

现用一水平拉力F 作用于立方体的定边中点。

如果地面摩擦力足够大，立方体不会滑动，那么要使该立方体翻转90︒，拉力F 至少为 。

3.一长为L 、质量为M 的均匀细棒，放在水平面上。

通过棒的端点O 有一垂直于水平面的光滑固定转轴，如图所示。

一质量为m 、速率为v 的子弹在水平面内垂直射向细棒，随后以速率v 21穿出，这时细棒的角速度 。

4. 刚体角动量守恒的充分而必要的条件是 。

5. 气候变暖造成地球两极的冰山融化，海平面因此上升。

这种情况将使地球的转动惯量 ，自转角速度 ，角动量 ，自转动能 。

（填变大、变小或不变）三、推导题6.试推导质量为m ，半径为R 的实心球体的转动惯量？（答：252mR ）四、计算和证明题7.如图所示，一个质量均匀分布的梯子靠墙放置，和地面成θ角，下端A 处连接一个弹性系数为k 的弹簧。

已知梯子的长度为l ，重量为W ，靠墙竖直放置时弹簧处于自然伸长，所有接触面均光滑。

如果梯子处于平衡状态，求地面、墙面对梯子的作用力，以及W 、k 、l 和θ满足的关系。

（答：W ；kl cos θ；OF Fω O v 21v 俯视图θsin 2kl W =）8. 半径为r = 1.5 m 的飞轮，初角速度ω0= 10 rad ⋅s -1，角加速度α= -5 rad ⋅s -2。

试问经过多长时间飞轮的角位移再次回到初始位置？此时飞轮边缘上的线速度为多少？（答：4s ；-15m ⋅s -1）9.质量分别为m 和2m 的两物体(都可视为质点)，用一长为l 的刚性细杆（质量为M ）相连，系统绕通过杆且与杆垂直的竖直固定轴O 转动。

《大学物理I 》作业 No.03 角动量 角动量守恒定律 （A 卷）班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题[ ]1、一质点沿直线做匀速率运动时，(A) 其动量一定守恒，角动量一定为零。

(B) 其动量一定守恒，角动量不一定为零。

(C) 其动量不一定守恒，角动量一定为零。

(D) 其动量不一定守恒，角动量不一定为零。

答案：B答案解析：质点作匀速直线运动，很显然运动过程中其速度不变，动量不变，即动量守恒；根据角动量的定义v m r L⨯=，质点的角动量因参考点（轴）而异。

本题中，只要参考点（轴）位于质点运动轨迹上，质点对其的角动量即为零，其余位置均不会为零。

故(B)是正确答案。

[ ]2. 两个均质圆盘A 和B 密度分别为A ρ和B ρ，若A ρ>B ρ，两圆盘质量与厚度相同，如两盘对通过盘心且垂直于盘面的轴的转动惯量各为A J 和B J ，则 (A) A J >B J(B) B J >A J(C) A J ＝B J(D) A J 、B J 哪个大，不能确定答案：B答案解析：设A 、B 联盘厚度为d ，半径分别为A R 和B R ，由题意，二者质量相等，即B B A A d R d R ρπρπ22=因为B A ρρ>，所以22B A R R <，由转动惯量221mR J =，则B A J J <。

[ ]3．对于绕定轴转动的刚体，如果它的角速度很大，则 (A) 作用在刚体上的力一定很大 (B) 作用在刚体上的外力矩一定很大(C) 作用在刚体上的力和力矩都很大 (D) 难以判断外力和力矩的大小答案：D 答案解析：由刚体质心运动定律和刚体定轴转动定律知：物体所受的合外力和合外力矩只影响物体运动的加速度和角加速度，因此无法通过刚体运动的角速度来判断外力矩的大小，正如无法通过速度来判断物体所受外力的大小一样。

第5章 角动量 角动量守恒定律自测题答案一、选择题 1、（D ） 2、（D ） 3、（D ） 4、（C ） 5、（B ） 6、（C ） 7、（D ） 8、（D ） 9、（A ）10、（B ） 11、（B ） 12、(C) 13、(D) 14、（A ） 15、（C ） 16．（C ） 17、（A ） 18、（B ） 19、（B ） 20、（C ） 二、填空题1、ML 2T -1 ；2、s m kg /2⋅ ；3、不一定；4、不一定；5、动量；6、角动量；7、恒定；8、为零；9、mrv ； 10、角动量； 11、2； 12、m v d ； 13、不为零； 14、10； 15、6 。

三、计算题1.有一质量为0.5g 的质点位于平面上P(3，4)点处，其速度为j i v43+=，并受到了一力j F5.1=的作用。

求其对坐标原点的角动量和作用在其上的力矩。

解：质点对坐标原点的位矢为 j i r43+= （2分） 则其对坐标原点的角动量为)43()43(105.03j i j i v m r L+⨯+⨯⨯=⨯=- （4分） 0= （1分） 作用在该质点上的力矩为j j i F r M5.1)43(⨯+=⨯= （4分） k5.4= （1分）2.一质量为1.0kg 的质点，受到一力j t i t F)43()12(-+-=的作用，其中t 以s 为单位，F以N 为单位。

开始时质点静止于坐标原点，求t =2s 时质点对原点的角动量。

解：质点的加速度为j t i t a)43()12(-+-=（1分）由dtv d a =，得 （2分）jt t i t t dtj t i t dta v t)423()(])43()12[(22-+-=-+-==⎰⎰ （2分）由dtr d v =，得 （2分）j t t i t t dt j t t i t t dtv r t)221()2131(])423()[(2323022-+-=-+-==⎰⎰ （2分）当t =2s 时，ji r432-=，j iv 22-=ji F23+= （2分）此时质点对原点的角动量为k j i j i v m r L326)22()432(=-⨯-=⨯=（1分）3.一质量为1.0kg 的质点，沿kj t i t r3)1()12(32+++-=曲线运动，其中t 的单位为s ，r的单位为m ，求在t =1.0s 时质点对原点的角动量和作用在其上的力矩。

2012年东华理工大学《大学物理》竞赛培训试题一、选择题（每题3分，共30分）1、在由两个质点组成的系统中，若质点之间只有万有引力作用，且此系统所受的外力的矢量和为零。

则此系统（）A 动量和机械能守恒，但角动量是否守恒不能确定B动量守恒，但角动量和机械能是否守恒不能确定C动量和角动量守恒，但机械能是否守恒不能确定D机械能和角动量守恒。

但动量是否守恒不能确定。

2、一端固定在天花板上的长细线下，悬吊一装满水的瓶子（瓶的重量不可忽略），瓶底有一小孔，在摆动过程中，瓶内的水不断向外漏，如忽略空气阻力，则从开始漏水到水漏完为止的整个过程中，此摆的摆频率（）A越来越大 B越来越小 C先变大后变小 D先变小后变大 E 保持不变3、在静电场中，如果通过闭合曲面（高斯面）S的电通量为零，则下面说法中正确的是（）A 高斯面上的电场一定处处为零 B高斯面内一定没有电荷C高斯面内的净电荷一定为零 D高斯面上一定没有电场线穿出4、平行板电容器两极板间相互作用力F与两极板间电压U的关系是（）A B C D5、一平行板电容器充电后仍与电源连接，若用绝缘手柄将电容器两极板距离拉大，则极板上电量Q、电场强度大小E和电场能量W将发生如下变化（）A．Q增大、E增大、W增大 B .Q减小、E减小、W减小C．Q减小、E减小、W增大 D .Q增大、E增大、W减小二、填空题（每题4分共40分）1. 灯距地面高度为h1，一个人身高为h2，在灯下以匀速率v沿水平直线行走，如图所示．他的头顶在地上的影子M点沿地面移动的速度为v M= ．2. 一根质量为m、长为l的均匀细杆，可在水平桌面上绕通过其一端的竖直固定轴转动．已知细杆与桌面的滑动摩擦系数为ν，则杆转动时受的摩擦力矩的大小为________________．3. 右图为一理想气体几种状态变化过程的p－V图，其中MT为等温线，MQ为绝热线，在AM、BM、CM三种准静态过程中：(1) 温度降低的是__________过程；(2) 气体放热的是__________过程．4. 图中曲线表示一种轴对称性静电场的场强大小E的分布，r表示离对称轴的距离，这是由______________________产生的电场．5. 如图，均匀磁场中放一均匀带正电荷的圆环，其线电荷密度为μ，圆环可绕通过环心O与环面垂直的转轴旋转．当圆环以角速度ω 转动时，圆环受到的磁力矩为_________________，其方向__________________________．6. 磁换能器常用来检测微小的振动．如图，在振动杆的一端固接一个N匝的矩形线圈，线圈的一部分在匀强磁场中，设杆的微小振动规律为x=A cos ωt,线圈随杆振动时，线圈中的感应电动势为_______________________．7. 一平行板空气电容器的两极板都是半径为R的圆形导体片，在充电时，板间电场强度的变化率为d E/d t．若略去边缘效应，则两板间的位移电流为________________________．8. 一平面简谐波沿x轴负方向传播．已知x= -1 m处质点的振动方程为，若波速为u，则此波的表达式为________________________________________________．9. 如图所示的杨氏双缝干涉装置，若用单色自然光照射狭缝S，在屏幕上能看到干涉条纹．若在双缝S1和S2的一侧分别加一同质同厚的偏振片P1、P2，则当P1与P2的偏振化方向相互______________时，在屏幕上仍能看到很清晰的干涉条纹．三、计算题1、如图是长为质量为的均质细杆处于水平静止状态。

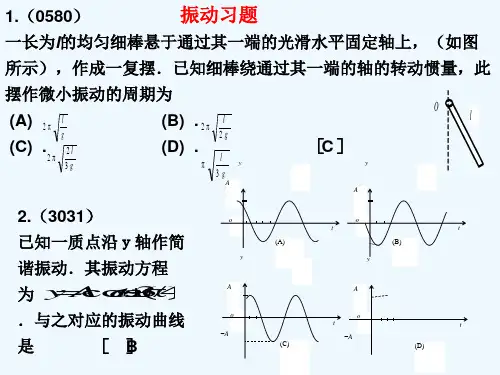
第三章 动量与角动量一、选择题[ A ] 1．（基础训练2）一质量为m 0的斜面原来静止于水平光滑平面上，将一质量为m 的木块轻轻放于斜面上，如图3-11．如果此后木块能静止于斜面上，则斜面将(A) 保持静止． (B) 向右加速运动．(C) 向右匀速运动． (D) 向左加速运动．提示：假设斜面以V 向右运动。

由水平方向动量守恒得0(cos )0m V m V v θ+-= ，而0v =，得0V =［C ］2.（基础训练3）如图3-12所示，圆锥摆的摆球质量为m ，速率为v ，圆半径为R ，当摆球在轨道上运动半周时，摆球所受重力冲量的大小为(A) 2m v ． (B) 22)/()2(v v R mg m π+(C) v /Rmg π．(D) 0．提示：2T mg I G ⨯= ， vRT π2=[ B ]3. （自测提高2）质量为20 g 的子弹，以400 m/s 的速率沿图3-15入一原来静止的质量为980 g 的摆球中，摆线长度不可伸缩．子弹射入后开始与摆球一起运动的速率为 (A) 2 m/s ． (B) 4 m/s ． (C) 7 m/s ． (D) 8 m/s ．提示：对摆线顶部所在点角动量守恒。

2sin 30()mv l M m lV ︒=+;其中m 为子弹质量，M 为摆球质量，l 为 摆线长度。

［D ］4．（自测提高4）用一根细线吊一重物，重物质量为5 kg ，重物下面再系一根同样的细线，细线只能经受70 N 的拉力.现在突然向下拉一下下面的线.设力最大值为50 N ，则(A)下面的线先断． (B)上面的线先断． (C)两根线一起断． (D)两根线都不断．提示：下面的细线能承受的拉力大于所施加的最大力，所以下面的细线不断。

对重物用动量定理：0'''=--⎰⎰⎰++dt T mgdt dt T t t t t t 下上't 为下拉力作用时间，由于't t >>，因此，上面的细线也不断。

第5章角动量角动量守恒定律一、本章总结1.请总结角动量、角动量守恒定律一章的知识点。

2.请画出本章的知识脉络框图。

二、填空题1. 如图所示，圆盘绕着与盘面垂直且过圆心O 的轴旋转，轴固定且光滑，转动角速度为ω。

这时，一对力偶沿着盘面作用在圆盘上（每个力大小为F ），圆盘的角速度ω 。

（填增大、减小或不能确定）2. 一个立方体放在粗糙的水平地面上，其质量分布均匀，为50 kg ，边长为1m 。

现用一水平拉力F 作用于立方体的定边中点。

如果地面摩擦力足够大，立方体不会滑动，那么要使该立方体翻转90︒，拉力F 至少为 。

3.一长为L 、质量为M 的均匀细棒，放在水平面上。

通过棒的端点O 有一垂直于水平面的光滑固定转轴，如图所示。

一质量为m 、速率为v 的子弹在水平面内垂直射向细棒，随后以速率v 21穿出，这时细棒的角速度 。

4. 刚体角动量守恒的充分而必要的条件是 。

5. 气候变暖造成地球两极的冰山融化，海平面因此上升。

这种情况将使地球的转动惯量 ，自转角速度 ，角动量 ，自转动能 。

（填变大、变小或不变）三、推导题6.试推导质量为m ，半径为R 的实心球体的转动惯量？（答：252mR ）四、计算和证明题7.如图所示，一个质量均匀分布的梯子靠墙放置，和地面成θ角，下端A 处连接一个弹性系数为k 的弹簧。

已知梯子的长度为l ，重量为W ，靠墙竖直放置时弹簧处于自然伸长，所有接触面均光滑。

如果梯子处于平衡状态，求地面、墙面对梯子的作用力，以及W 、k 、l 和θ满足的关系。

（答：W ；kl cos θ；OF Fω O v 21v 俯视图θsin 2kl W =）8. 半径为r = 1.5 m 的飞轮，初角速度ω0= 10 rad ⋅s -1，角加速度α= -5 rad ⋅s -2。

试问经过多长时间飞轮的角位移再次回到初始位置？此时飞轮边缘上的线速度为多少？（答：4s ；-15m ⋅s -1）9.质量分别为m 和2m 的两物体(都可视为质点)，用一长为l 的刚性细杆（质量为M ）相连，系统绕通过杆且与杆垂直的竖直固定轴O 转动。

第二章 守恒定律1、 质量为m 的小球系于绳的一端，绳长为l ，上端A 固定，（如图示）。

今有水平变力F 作用在该小球上时，使小球极其缓慢地移动，即在所有位置上均处于近似力平衡状态，直到绳子与竖直方向成θ角，（1）试用变力作功方法计算F 力的功。

（2）重力作功多大？解：根据力的平衡可得： ⎩⎨⎧θ=θ=cos T mg sin T Fθ=∴tan mg F（1）⎰θθ⎰⋅θ=θ=⎰⋅=cos d tan mg cos Fds s d F A F l⎰θ-=θθ=θ0)cos 1(mg d sin mg l l（2）⎰⎰θ--=θθ-=π+θ=⎰⋅=θ0P )cos 1(mg d )sin (mg )2cos(mgds s d g m A l l2、地球质量M 、半径R ，一质量m 的质点处于距地心 r=3R 处，求质点地球系统在此相对位置时的引力势能，（1）取无穷远处为零势能参考位置； （2）取地球表面为零势能参考位置。

解：（1）取()0E p =∞ 则⎰⎰-==-=⋅=∞∞∞R 3R 3R32P R3G Mmr1G Mmdr r Mm G s d F E 保 (2) 取()0R E p = 则⎰⎰==-=⋅=R R 3R R 3RR32p R3G Mm2r1G Mmdr r Mm G s d F E 保 A θ T Fmg 图2-1图2-23、如图所示，一绳索跨过无摩擦的滑轮，系在质量为1Kg 的物体上。

起初物体静止在无摩擦的水平面上，若用5N 的恒力作用在绳索另一端，使物体向右作加速运动，当系在物体上的绳索从与水平面成300角变为370角时，力对物体所作的功为多大？（已知滑轮与水平面之间的距离d=1m ）。

解：⎰θ=⎰⋅=dx cos F x d F A()J 69.1dx xd Fx 2x 1x 22=⎰+-=4、一质量为m 的小球系在线的一端，线的另一端固定在墙上的钉子上，线长为ι0 ，先将小球拉至水平位置A 处，然后放手，试求小球摆至B 点处的速度、加速度以及绳子张力大小？解：2B 0mv 21sin mg =θlθ=sin g 2v 0l θ=θ==sin g 2)sin g 2(v a 02002n l l l θ==θcos g a ma cos mg t tθ=θ+θ==θ-sin mg 3sin mg 2sin mg T vmsin mg T 02l1m 300 370 F x x OO l 0 AθTB图2-45、一根均匀链条的质量为m ，总长为ι，一部分放在光滑的桌面上，另一部分从桌面边缘下垂，下垂的长度为a ，开始时链条静止，求链条刚好全部离开桌面时的速率。