大学物理-下-计算题参考答案

大学物理考卷（下学期）一、选择题（每题4分，共40分）A. 速度B. 力C. 位移D. 加速度2. 在国际单位制中，下列哪个单位属于电学基本单位？A. 安培B. 伏特C. 欧姆D. 瓦特A. 物体不受力时，运动状态不会改变B. 物体受平衡力时，运动状态会改变C. 物体受非平衡力时，运动状态不变D. 物体运动时，必定受到力的作用A. 功B. 动能C. 势能D. 路程A. 速度大小B. 速度方向C. 动能D. 动量6. 下列哪个现象属于光的衍射？A. 彩虹B. 海市蜃楼C. 水中倒影D. 光照射在单缝上产生的条纹A. 恢复力与位移成正比B. 恢复力与位移成反比C. 恢复力与位移的平方成正比D. 恢复力与位移的平方成反比8. 一个电路元件的电压u与电流i的关系为u=2i+3，该元件是：A. 电阻B. 电容C. 电感D. 非线性元件A. 电磁波在真空中传播速度小于光速B. 电磁波在介质中传播速度大于光速C. 电磁波在真空中传播速度等于光速D. 电磁波在介质中传播速度等于光速10. 一个理想变压器的初级线圈匝数为1000匝，次级线圈匝数为200匝，若初级线圈电压为220V，则次级线圈电压为：A. 110VB. 220VC. 440VD. 880V二、填空题（每题4分，共40分）1. 在自由落体运动中，物体的加速度为______。

2. 一个物体做匀速圆周运动，其线速度的大小不变，但方向______。

3. 惠更斯原理是研究______现象的重要原理。

4. 一个电阻的电压为10V，电流为2A，则该电阻的功率为______。

5. 根据电磁感应定律，当磁通量发生变化时，会在导体中产生______。

6. 在交流电路中，电阻、电感和电容元件的阻抗分别为______、______和______。

7. 一个单摆在位移为0时速度最大，此时摆球所受回复力为______。

8. 光的折射率与光的传播速度成______比。

9. 一个电子在电场中受到的电势能变化量为______。

第11章光的量子效应及光子理论一、 选择题1. 金属的光电效应的红限依赖于: 【 C 】(A)入射光的频率； (B)入射光的强度；(C)金属的逸出功； (D)入射光的频率和金属的逸出功。

2. 已知某单色光照射到一金属表面产生了光电效应，若此金属的逸出电势是U 0（使电子从金属逸出需做功eU 0），则此单色光的波长λ必须满足： 【 A 】hceU )D (;hceU )C (;eU hc )B (;eU hc)A (0≥≤≥≤λλλλ 3. 关于光电效应有下列说法：(1) 任何波长的可见光照射到任何金属表面都能产生光电效应；(2) 对同一金属如有光电子产生，则入射光的频率不同，光电子的初动能不同； (3) 对同一金属由于入射光的波长不同，单位时间内产生的光电子的数目不同； (4) 对同一金属，若入射光频率不变而强度增加一倍，则饱和光电流也增加一倍。

其中正确的是： 【 D 】(A) (1)，(2)，(3)； (B) (2)，(3)，(4)； (C) (2)，(3)； (D)(2)，(4)二、填空题1. 当波长为300 nm 光照射在某金属表面时，光电子的能量范围从0到.J 100.419-⨯在作上述光电效应实验时遏止电压为V 5.2U a =；此金属的红限频率Hz 104140⨯=ν。

2. 频率为100MHz 的一个光子的能量是J 1063.626-⨯，动量的大小是s N 1021.234⋅⨯-。

3. 如果入射光的波长从400nm 变到300nm ，则从表面发射的光电子的遏止电势增大（增大、减小）V 03.1U =∆。

4. 某一波长的X 光经物质散射后，其散射光中包含波长大于X 光和波长等于X 光的两种成分，其中大于X 光波长的散射成分称为康普顿散射。

三、计算题1. 已知钾的红限波长为558 nm ，求它的逸出功。

如果用波长为400 nm 的入射光照射，试求光电子的最大动能和遏止电压。

由光电方程2m mv 21A h +=ν，逸出功0h A ν=，0chA λ=，eV 23.2A =用波长为400nm 的入射光照射，光电子的最大动能：A h mv 212m -=ν A chE km -=λ，将nm 400=λ和eV 23.2A =代入得到：eV 88.0E km =遏止电压：a 2m eU mv 21=，2m a mv e21U =，V 88.0U a = 2. 从铝中移出一个电子需要4.2 eV 的能量，今有波长为200 nm 的光投射至铝表面。

《大学物理》（下）期末统考试题（A 卷）说明 1考试答案必须写在答题纸上，否则无效。

请把答题纸撕下。

一、 选择题（30分，每题3分）1．一质点作简谐振动，振动方程x=Acos(ωt+φ)，当时间t=T/4(T 为周期)时，质点的速度为：(A) -Aωsinφ； (B) Aωsinφ； (C) -Aωcosφ； (D) Aωcosφ参考解：v =dx/dt = -Aωsin (ωt+φ),cos )sin(424/ϕωϕωπA A v T T T t -=+⋅-== ∴选(C)2．一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的(A) 7/6 (B) 9/16 (C) 11/16 （D ）13/16 (E) 15/16 参考解：,1615)(2212421221221221=-=kA k kA kA mv A ∴选（E ）3.一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：(A) 它的动能转换成势能．(B) 它的势能转换成动能．(C) 它从相邻的一段质元获得能量其能量逐渐增大．(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小．参考解：这里的条件是“平面简谐波在弹性媒质中传播”。

由于弹性媒质的质元在平衡位置时的形变最大，所以势能动能最大，这时动能也最大；由于弹性媒质的质元在最大位移处时形变最小，所以势能也最小，这时动能也最小。

质元的机械能由最大变到最小的过程中，同时也把该机械能传给相邻的一段质元。

∴选（D ）4．如图所示，折射率为n 2、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3，已知n 1＜n 2＜n 3．若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束①与②的光程差是(A) 2n 2 e ． (B) 2n 2 e －λ / 2 .(C) 2n 2 e －λ． (D) 2n 2 e －λ / (2n 2)． 参考解：半波损失现象发生在波由波疏媒质到波密媒质的界面的反射现象中。

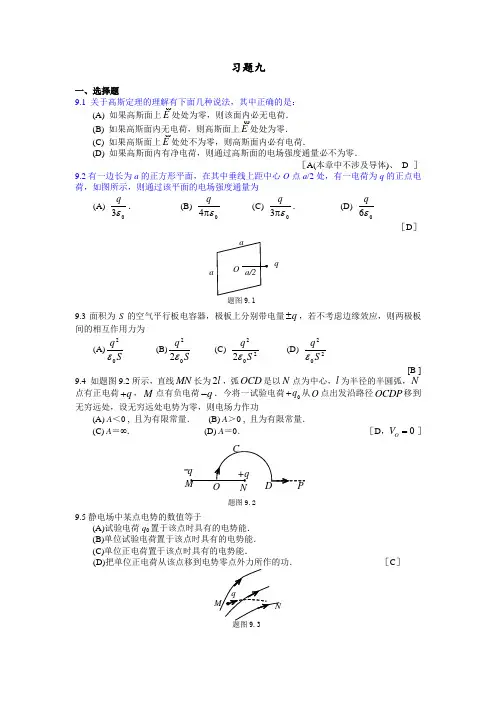
习题九一、选择题9.1 关于高斯定理的理解有下面几种说法，其中正确的是：(A) 如果高斯面上E处处为零，则该面内必无电荷．(B) 如果高斯面内无电荷，则高斯面上E处处为零．(C) 如果高斯面上E处处不为零，则高斯面内必有电荷．(D) 如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零．［A(本章中不涉及导体)、 D ］ 9.2有一边长为a 的正方形平面，在其中垂线上距中心O 点a /2处，有一电荷为q 的正点电荷，如图所示，则通过该平面的电场强度通量为(A)03 q ． (B) 04 q (C) 03 q ． (D) 06 q ［D ］q题图9.19.3面积为S 的空气平行板电容器，极板上分别带电量q ，若不考虑边缘效应，则两极板间的相互作用力为(A)S q 02(B)S q 022 (C) 2022S q (D) 202Sq [B ]9.4 如题图9.2所示，直线MN 长为2l ，弧OCD 是以N 点为中心，l 为半径的半圆弧，N 点有正电荷q ，M 点有负电荷q ．今将一试验电荷0q 从O 点出发沿路径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功(A) A ＜0 , 且为有限常量． (B) A ＞0 , 且为有限常量．(C) A ＝∞． (D) A ＝0． ［D ，0O V ］-题图9.29.5静电场中某点电势的数值等于 (A)试验电荷q 0置于该点时具有的电势能．(B)单位试验电荷置于该点时具有的电势能． (C)单位正电荷置于该点时具有的电势能．(D)［C ］9.6已知某电场的电场线分布情况如题图9.3所示．现观察到一负电荷从M 点移到N 点．有人根据这个图作出下列几点结论，其中哪点是正确的？(A) 电场强度M N E E ． (B) 电势M N U U ．(C) 电势能M N W W ． (D) 电场力的功A ＞0．［C ］ 二、计算题9.7 电荷为q 和2q 的两个点电荷分别置于1x m 和1x m 处．一试验电荷置于x 轴上何处，它受到的合力等于零？ x2q q 0解：设试验电荷0q 置于x 处所受合力为零，根据电力叠加原理可得022220000(2)(2)ˆˆ0041414141q q q q q q i i x x x x 即：22221(2)0121011x x x x22212210x x x x2610(322)x x x m 。

8．在圆柱形空间内有一磁感应强度为 的均匀磁场，如图所示， 的大小以速率dB/d t变化。有一长度为l0的金属棒先后放在磁场的两个不同位置1(a b)和2( )，则金属棒在这两个位置时棒内的磁感应电动势的大小关系为[B]
(A) (B) .
(C) (D)
解:
二． 填空题：
1．一段导线被弯成圆心在O点、半径为R的三段圆弧 、 、 ，它们构成了一个闭合回路， 位于XOY平面内， 和 分别位于另两个坐标面中（如图）。均匀磁场 沿X轴正方向穿过圆弧 与坐标轴所围成的平面。设磁感应强度随时间的变化率为K(K>0)，则闭合回路a b c a中
5．如图所示的一细螺绕环，它由表面绝缘的导线在铁环上密绕而成，每厘米绕10匝。当导线中的电流I为2.0A时，测得铁环内的磁感应强度的大小B为1.0T，则可求得铁环的相对磁导率 为（真空磁导率 ）：[B]
(A) (B)
(C) (D)63.3
解：n=10匝/cm=1000匝/m
二．填空题：
1．铜的相对磁导率 ，其磁化率 ，它是抗磁性磁介质。 ∴
方向:
或：
(2)取顺时针方向为回路L的正方向.
, 的方向与L的正方向一致;
, 的方向与L的正方向相反.
4．如图所示，有一根长直导线，载有直流电流I，近旁有一个两条对边与它平行并与它共面的矩形线圈，以匀速度 沿垂直于导线的方向离开导线．设t=0时，线圈位于图示位置，求：
(1) 在任意时刻t通过矩形线圈的磁通量．
4．关于稳恒磁场的磁场强度 的下列几种说法哪个是正确的？[C]
(A) 仅与传导电流有关。(还与磁化电流有关)
(B)若闭合曲线内没有包围传导电流，则曲线上各点的 必为零。（闭合曲线外有传导电流）
(C)若闭合曲线上各点 均为零，则该曲线所包围传导电流的代数和为零。

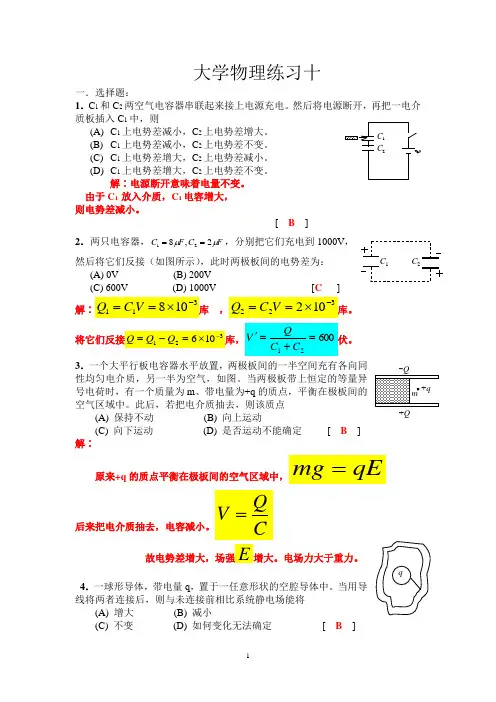
大学物理习题册计算题及答案三 计算题1. 一质量m = 0.25 kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点。

弹簧的劲度系数k = 25N ·m -1。

(1） 求振动的周期T 和角频率.(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v 0及初相. （3) 写出振动的数值表达式。

解：（1) 1s 10/-==m k ω 63.0/2=π=ωT s（2） A = 15 cm ，在 t = 0时，x 0 = 7。

5 cm,v 0 〈 0 由 2020)/(ωv +=x A得 3.1220-=--=x A ωv m/s π=-=-31)/(tg 001x ωφv 或 4/3∵ x 0 > 0 , ∴ π=31φ（3) )3110cos(10152π+⨯=-t x (SI ）振动方程为)310cos(1015)cos(2πϕω+⨯=+=-t t A x （SI ）﹡2. 在一平板上放一质量为m =2 kg 的物体，平板在竖直方向作简谐振动，其振动周期为T = 21s ，振幅A = 4 cm ，求 （1） 物体对平板的压力的表达式.(2) 平板以多大的振幅振动时，物体才能离开平板。

解：选平板位于正最大位移处时开始计时，平板的振动方程为 t A x π4cos = （SI)t A x ππ4cos 162-=（SI ） （1） 对物体有 x m N mg=- ① t A mg x m mg N ππ4cos 162+=-= （SI) ② 物对板的压力为 t A mg N F ππ4cos 162--=-= (SI ）t ππ4cos 28.16.192--= ③(2) 物体脱离平板时必须N = 0，由②式得 04cos 162=+t A mg ππ (SI ）A qt 2164cos π-=π 若能脱离必须 14cos ≤t π （SI ）即 221021.6)16/(-⨯=≥πg A m三 计算题﹡1。

大学物理 下 复习题 部分计算题 参考答案 答案来自网络 仅供参考1四条平行的载流无限长直导线，垂直通过一边长为a 的正方形顶点，每条导线中的电流都是I ，方向如图，求正方形中心的磁感应强度。

⎪⎭⎫⎝⎛a I πμ02解0222Iaμπ=2.如图所示的长空心柱形导体半径分别为1R 和2R ，导体内载有电流I ，设电流均匀分布在导体的横截面上。

求 （1）导体内部各点的磁感应强度。

（2）导体内壁和外壁上各点的磁感应强度。

解：导体横截面的电流密度为2221()IR R δπ=-在P 点作半径为r 的圆周，作为安培环路。

由0B dl I μ∙=∑⎰得 222201012221()2()I r R B r r R R Rμπμδπ-=-=-即 22012221()2()I r R B r R R μπ-=- 对于导体内壁，1r R =，所以 0B = 对于导体外壁，2r R =，所以 022IB R μπ=3. 如图， 一根无限长直导线，通有电流I ， 中部一段弯成圆弧形，求图中O 点磁感应强度的大小。

解：根据磁场叠加原理，O 点的磁感应强度是)A (-∞、)ABC (和)C (∞三段共同产生的。

)A (-∞段在O 点磁感应强度大小：)cos (cos x4IB 2101θθπμ-=将6021πθθ==，，a 213cosa x ==π代入 得到：)231(a 2IB 01-=πμ，方向垂直于纸面向里； )C (∞段在O 点磁感应强度大小：)cos (cos x4IB 2102θθπμ-=将πθππθ=-=216，，a 213cos a x ==π带入得到：)231(a 2I B 02-=πμ，方向垂直向里；)ABC (段在O 点磁感应强度大小：⎰=203a Idl 4B πμ，)a 32(a I 4B 203ππμ=，a6IB 03μ=，方向垂直于纸面向里。

O 点磁感应强度的大小：321B B B B ++=，)231(a I a6IB 00-+=πμμ, 方向垂直于纸面向里。

第十章 气体动理论一、选择题参考答案1． B ；2． A ；3． B ；4． B ；5． B ；6． A ；7． C ；8． B ；9． C ；10． C ；11． A ；12． C ； 13． C ；14． D ；15． D ；16． C ；17． B ；18． C ；19． B ；20． C ；21． B ；22． B ；23． D ；24． D ；25． C ；26． A ；27． B ；28． B ；29． A ；30． D二、填空题参考答案1、（1）气体分子的大小与气体分子的距离比较，可以忽略不计；）气体分子的大小与气体分子的距离比较，可以忽略不计； （2）除了分子碰撞的瞬间外，分子之间的相互作用力可以忽略；）除了分子碰撞的瞬间外，分子之间的相互作用力可以忽略； （3）分子之间以及分子与器壁之间的碰撞是完全弹性碰撞。

）分子之间以及分子与器壁之间的碰撞是完全弹性碰撞。

2、体积、温度和压强，分子的运动速度（或分子运动速度、分子的动量、分子的动能）3、一个点；一条曲线；一条封闭曲线。

、一个点；一条曲线；一条封闭曲线。

4、s /m kg 101.2-23×´；s ×´229m /1031；a 5P 104´5、1；46、kT 23；kT 25；mol/25M MRT7、12.5J ；20.8J ；24.9J 。

8、1:1；2:1；10:3。

9、241092.3´10、1:1:1 11、（1）ò¥100d )(v v f ；（2）ò¥100d )(v v Nf12、（1）ò¥d )(v v v Nf ；（2）òò¥¥v v f(v)dv v v v /d )(0f ；（3）ò¥0d )(vv v f13、氩；氦、氩；氦14、1000m/s ； 10002´m/s15、2000m/s ；500m/s16、保持不变、保持不变17、495m/s 18、219、12M M20、17s 1042.5-´；cm 1065-´三、计算题参考答案1．解：．解：据力学平衡条件，当水银滴刚好处在管的中央维持平衡，表明左、右两边氢气的体积相等，压强也相等。

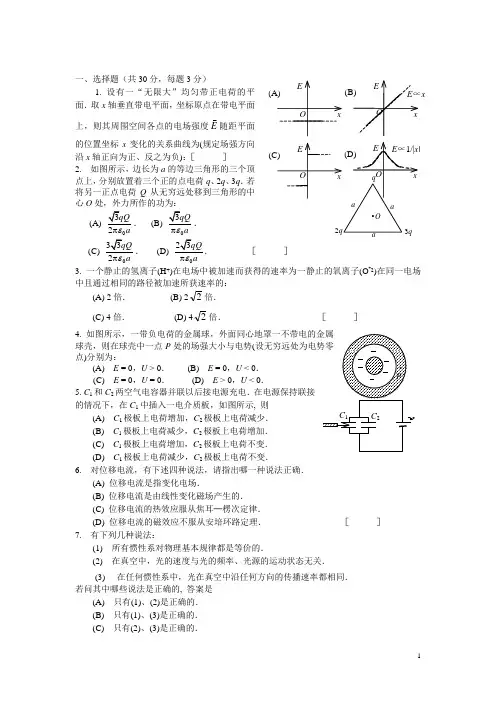
一、选择题（共30分，每题3分）1. 设有一“无限大”均匀带正电荷的平面．取x 轴垂直带电平面，坐标原点在带电平面上，则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负)：［ ］2. 如图所示，边长为a 的等边三角形的三个顶点上，分别放置着三个正的点电荷q 、2q 、3q ．若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为：(A) 0． (B) 0．(C)0． (D) 0 ［ ］3. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的：(A) 2倍． (B) 22倍．(C) 4倍． (D) 42倍． ［ ］ 4. 球壳，则在球壳中一点P 处的场强大小与电势(点)分别为：(A) E = 0，U > 0． (B) E = 0，U < 0．(C) E = 0，U = 0． (D) E > 0，U < 0． 5. C 1和C 2两空气电容器并联以后接电源充电．在电源保持联接的情况下，在C 1中插入一电介质板，如图所示, 则 (A) C 1极板上电荷增加，C 2极板上电荷减少． (B) C 1极板上电荷减少，C 2极板上电荷增加． (C) C 1极板上电荷增加，C 2极板上电荷不变． (D) C 1极板上电荷减少，C 2极板上电荷不变． 6. 对位移电流，有下述四种说法，请指出哪一种说法正确． (A) 位移电流是指变化电场．(B) 位移电流是由线性变化磁场产生的． (C) 位移电流的热效应服从焦耳─楞次定律．(D) 位移电流的磁效应不服从安培环路定理． ［ ］ 7. 有下列几种说法： (1) 所有惯性系对物理基本规律都是等价的． (2) 在真空中，光的速度与光的频率、光源的运动状态无关．(3) 在任何惯性系中，光在真空中沿任何方向的传播速率都相同．若问其中哪些说法是正确的, 答案是 (A) 只有(1)、(2)是正确的． (B) 只有(1)、(3)是正确的． (C) 只有(2)、(3)是正确的．x(D) 三种说法都是正确的． ［ ］8. 在康普顿散射中，如果设反冲电子的速度为光速的60％，则因散射使电子获得的能量是其静止能量的(A) 2倍． (B) 1.5倍．(C) 0.5倍． (D) 0.25倍． ［ ］ 9. 已知粒子处于宽度为a 的一维无限深势阱中运动的波函数为 ax n a x n π=sin 2)(ψ ， n = 1, 2, 3, … 则当n = 1时，在 x 1 = a /4 →x 2 = 3a /4 区间找到粒子的概率为(A) 0.091． (B) 0.182． (C) 1． . (D) 0.818． ［ ］10. 氢原子中处于3d 量子态的电子，描述其量子态的四个量子数(n ，l ，m l ，m s )可能取的值为(A) (3，0，1，21-)． (B) (1，1，1，21-)． (C) (2，1，2，21)． (D) (3，2，0，21)． ［ ］二、填空题（共30分）11.（本题3分）一个带电荷q 、半径为R 的金属球壳，壳内是真空，壳外是介电常量为ε 的无限大各向同性均匀电介质，则此球壳的电势U =________________． 12. （本题3分）有一实心同轴电缆，其尺寸如图所示，它的内外两导体中的电流均为I ，且在横截面上均匀分布，但二者电流的流向正相反，则在r < R 1处磁感强度大小为________________．13.（本题3分）磁场中某点处的磁感强度为)SI (20.040.0j i B-=，一电子以速度j i66100.11050.0⨯+⨯=v (SI)通过该点，则作用于该电子上的磁场力F 为__________________．(基本电荷e =1.6×10-19C) 14.（本题6分，每空3分）四根辐条的金属轮子在均匀磁场B 中转动，转轴与B 平行，轮子和辐条都是导体，辐条长为R ，轮子转速为n ，则轮子中心O 与轮边缘b 之间的感应电动势为______________，电势最高点是在______________处． 15. （本题3分） 有一根无限长直导线绝缘地紧贴在矩形线圈的中心轴OO ′上，则直导线与矩形线圈间的互感系数为_________________．16.（本题3分）真空中两只长直螺线管1和2，长度相等，单层密绕匝数相同，直径之比d 1 / d 2 =1/4．当它们通以相同电流时，两螺线管贮存的磁能之比为W 1 / W 2=___________．17. （本题3分）静止时边长为 50 cm 的立方体，当它沿着与它的一个棱边平行的方向相对于地面以匀速度 2.4×108 m ·s -1运动时，在地面上测得它的体积是____________．18. （本题3分）以波长为λ= 0.207 μm 的紫外光照射金属钯表面产生光电效应，已知钯的红限频率 ν 0=1.21×1015赫兹，则其遏止电压|U a | =_______________________V ．(普朗克常量h =6.63×10-34 J ·s ，基本电荷e =1.60×10-19 C) 19. （本题3分）如果电子被限制在边界x 与x +∆x 之间，∆x =0.5 Å，则电子动量x 分量的不确定量近似地为________________kg ·m ／s ． (取∆x ·∆p ≥h ，普朗克常量h =6.63×10-34 J ·s) 三、计算题（共40分） 20. （本题10分）电荷以相同的面密度σ 分布在半径为r 1＝10 cm 和r 2＝20 cm 的两个同心球面上．设无限远处电势为零，球心处的电势为U 0＝300 V ． (1) 求电荷面密度σ．(2) 若要使球心处的电势也为零，外球面上电荷面密度应为多少，与原来的电荷相差多少？［电容率ε0＝8.85×10-12 C 2 /(N ·m 2)］ 21. （本题10分）已知载流圆线圈中心处的磁感强度为B 0，此圆线圈的磁矩与一边长为a 通过电流为I 的正方形线圈的磁矩之比为2∶1，求载流圆线圈的半径． 22．（本题10分） 如图所示，一磁感应强度为B 的均匀磁场充满在半径为R 的圆柱形体内，有一长为l 的金属棒放在磁场中，如果B 正在以速率dB/dt 增加，试求棒两端的电动势的大小，并确定其方向。

大学物理下复习题（附答案）第一章填空题自然界中只存在正负两种电荷，同种电荷相互排斥，异种电荷相互吸引。

（）对自然界中只存在正负两种电荷，同种电荷相互吸引，异种电荷相互排斥。

（）错电荷电量是量子化的。

（）对物体所带电量可以连续地取任意值。

（）错物体所带电量只能是电子电量的整数倍。

（）对库仑定律只适用于真空中的点电荷。

（）对电场线稀疏处的电场强度小。

（）对电场线稀疏处的电场强度大。

（）错静电场是有源场。

（）对静电场是无源场。

（）错静电场力是保守力。

（）对静电场力是非保守力。

（）错静电场是保守力场。

（）对静电场是非保守力场。

（）错电势是矢量。

（）错电势是标量。

（）对等势面上的电势一定相等。

（）对沿着电场线的方向电势降落。

（）对沿着电场线的方向电势升高。

（）错电场中某点场强方向就是将点电荷放在该点处所受电场力的方向。

（）错电场中某点场强方向就是将正点电荷放在该点处所受电场力的方向。

（）对电场中某点场强方向就是将负点电荷放在该点处所受电场力的方向。

（）错电荷在电场中某点受到电场力很大，该点场强E一定很大。

（）错电荷在电场中某点受到电场力很大，该点场强E不一定很大。

（）对在以点电荷为中心，r为半径的球面上，场强E处处相等。

（）错在以点电荷为中心，r为半径的球面上，场强E大小处处相等。

（）对如果在高斯面上的E处处为零，肯定此高斯面内一定没有净电荷。

（）对根据场强与电势梯度的关系可知，在电势不变的空间电场强度为零。

（）对如果高斯面内没有净电荷，肯定高斯面上的E处处为零。

（）错正电荷由A移到B时，外力克服电场力做正功，则B点电势高。

对导体达到静电平衡时，导体内部的场强处处为零。

（）对第一章填空题已一个电子所带的电量的绝对值e= C。

1.602*10-19或1.6*10-19真空中介电常数值为=0ε C 2.N -1.m -2。

8.85*10-12 真空中有一无限长带电直棒，电荷线密度为λ，其附近一点P 与棒的距离为a ，则P 点电场强度E 的大小为 。

单元一 简谐振动一、 计算题17. 作简谐运动的小球，速度最大值为3m v =cm/s ，振幅2A =cm ，若从速度为正的最大值的某时刻开始计算时间。

（1）求振动的周期；（2）求加速度的最大值；（3）写出振动表达式。

解：（1）振动表达式为 cos()x A t ωϕ=+振幅0.02A m =，0.03/m v A m s ω==，得 0.031.5/0.02m v rad s A ω=== 周期 22 4.191.5T s ππω=== （2）加速度的最大值 2221.50.020.045/m a A m s ω==⨯= （3）速度表达式 sin()cos()2v A t A t πωωϕωωϕ=-+=++由旋转矢量图知，02πϕ+=， 得初相 2πϕ=-振动表达式 0.02cos(1.5)2x t π=-（SI ）18. 已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒。

求此简谐振动的振动方程。

解：设振动方程为 )cos(φω+=t A x 由曲线可知： A = 10 cm当t = 0，φcos 1050=-=x ，0sin 100<-=φωv解上面两式，可得 初相 32π=φ由图可知质点由位移为 x 0 = -5 cm 和v 0 < 0的状态到x = 0和 v > 0的状态所需时间t = 2 s ，代入振动方程得 )322cos(100π+=ω 则有 2/33/22π=π+ω， ∴ 125π=ω 故所求振动方程为 )32125cos(1.0ππ+=t x (SI) 19. 定滑轮半径为R ，转动惯量为J ，轻绳绕过滑轮，一端与固定的轻弹簧连接，弹簧的倔强系数为K ；另一端挂一质量为m 的物体，如图。

现将m 从平衡位置向下拉一微小距离后放手，试证物体作简谐振动，并求其振动周期。

(设绳与滑轮间无滑动，轴的摩擦及空气阻力忽略不计)。

x (cm) t -5 10 O -102 (18)题解：以物体的平衡位置为原点建立如图所示的坐标。

大学物理下册习题及答案热力学（一）一、选择题：1、如图所示，当汽缸中的活塞迅速向外移动从而使汽缸膨胀时，气体所经历的过程（A）是平衡过程，它能用P—V图上的一条曲线表示.（B）不是平衡过程，但它能用P—V图上的一条曲线表示.（C）不是平衡过程，它不能用P—V图上的一条曲线表示.（D）是平衡过程，但它不能用P—V图上的一条曲线表示. [ ]2、在下列各种说法中，哪些是正确的？ [ ]（1）热平衡就是无摩擦的、平衡力作用的过程.（2）热平衡过程一定是可逆过程.（3）热平衡过程是无限多个连续变化的平衡态的连接.（4）热平衡过程在P—V图上可用一连续曲线表示.（A）（1）、（2）（B）（3）、（4）（C）（2）、（3）、（4）（D）（1）、（2）、（3）、（4）3、设有下列过程： [ ]（1）用活塞缓慢的压缩绝热容器中的理想气体.（设活塞与器壁无摩擦）（2）用缓慢地旋转的叶片使绝热容器中的水温上升.（3）冰溶解为水.（4）一个不受空气阻力及其它摩擦力作用的单摆的摆动.其中是逆过程的为（A）（1）、（2）、（4）（B）（1）、（2）、（3）（C）（1）、（3）、（4）（D）（1）、（4）4、关于可逆过程和不可逆过程的判断： [ ]（1）可逆热力学过程一定是准静态过程.（2）准静态过程一定是可逆过程.（3）不可逆过程就是不能向相反方向进行的过程.（4）凡有摩擦的过程，一定是不可逆过程.以上四种判断，其中正确的是（A）（1）、（2）、（3）（B）（1）、（2）、（4）（C）（2）、（4）（D）（1）、（4）5、在下列说法中，哪些是正确的？ [ ]（1）可逆过程一定是平衡过程.（2）平衡过程一定是可逆的.（3）不可逆过程一定是非平衡过程.（4）非平衡过程一定是不可逆的.（A）（1）、（4）（B）（2）、（3）（C）（1）、（2）、（3）、（4）（D）（1）、（3）6、置于容器内的气体，如果气体内各处压强相等，或气体内各处温度相同，则这两种情况下气体的状态[ ]（A）一定都是平衡态.（B）不一定都是平衡态.（C）前者一定是平衡态，后者一定不是平衡态.（D）后者一定是平衡态，前者一定不是平衡态.7、气体在状态变化过程中，可以保持体积不变或保持压强不变，这两种过程 [ ]（A）一定都是平衡过程.（B）不一定是平衡过程.（C）前者是平衡态，后者不是平衡态.（D）后者是平衡态，前者不是平衡态.8、一定量的理想气体，开始时处于压强，体积，温度分别为P1、V1、T1，的平衡态，后来变到压强、体积、温度分别为P2、V2、T2的终态.若已知V2 > V1, 且T2 = T1 , 则以下各种说法正确的是: [ ]（A）不论经历的是什么过程，气体对外净做的功一定为正值.（B）不论经历的是什么过程，气体从外界净吸的热一定为正值.（C）若气体从始态变到终态经历的是等温过程，则气体吸收的热量最少.（D）如果不给定气体所经历的是什么过程，则气体在过程中对外净做功和外界净吸热的正负皆无法判断.二、填空题：1、在热力学中，“作功”和“传递热量”有着本质的区别，“作功”是通过__________来完成的; “传递热量”是通过___________来完成的.2、设在某一过程P中，系统由状态A变为状态B，如果______________________________________________________，则过程P为可逆过程；如果______________________________________________________则过程P为不可逆过程.3、同一种理想气体的定压摩尔热容C p大于定容摩尔热容C v，其原因是_____________________________________________________________________.4、将热量Q传给一定量的理想气体，（1）若气体的体积不变，则热量转化为________________________________.（2）若气体的温度不变，则热量转化为________________________________.（3）若气体的压强不变，则热量转化为________________________________.5、常温常压下，一定量的某种理想气体（可视为刚性分子自由度为i），在等压过程中吸热为Q，对外作功为A，内能增加为ΔE，则A / Q = ____________. ΔE / Q = _____________.6、3 mol的理想气体开始时处在压强P1 = 6 at m、温度T1 = 500K的平衡态.经过一个等温过程，压强变为P2 = 3 atm.该气体在等温过程中吸收的热量为Q = _____________J.(摩尔气体常量R = 8.31 J•mol-1•K-1)7、2 mol单原子分子理想气体，经一等容过程后，温度从200K上升到500K，若该过程为准静态过程，气体吸收的热量为_________；若为不平衡过程，气体吸收的热量为___________.8、卡诺制冷机，其低温热源温度为T2 = 300 K，高温热源温度为T1 = 450 K，每一循环从低温热源吸收Q2 = 400 J.已知该制冷机的制冷系数为1212TTTAQw-==（式中A为外界对系统作的功），则每一循环中外界必须作功A = _________.三、计算题：1、有1 mol刚性多原子分子的理想气体，原来的压强为1.0 atm ，温度为27˚C，若经过一绝热过程，使其压强增加到16 atm .试求：（1）气体内能的增量；（2）在该过程中气体所作的功；（3）终态时，气体的分子数密度.（1 atm = 1.013×105 Pa，玻耳滋曼常数k = 1.38×10-23J•K-1摩尔气体常量R=8.31J•mol-1•K-1）2、如图所示，a b c d a为1 mol单原子分子理想气体的循环过程，求：（1）气体循环一次，在吸热过程中从外界共吸收的热量；（2）气体循环一次对外做的净功；（3）证明Ta Tc = T b T d.3、一气缸内盛有一定量的单原子理想气体.若绝热压缩使其容积减半，问气体分子的平均速率为原来的几倍？热力学（二）1、理想气体向真空作绝热膨胀. [ ]（A）膨胀后，温度不变，压强减小.（B）膨胀后，温度降低，压强减小.（C）膨胀后，温度升高，压强减小.（D）膨胀后，温度不变，压强不变.2、氦、氮、水蒸气（均视为理想气体），它们的摩尔数相同，初始状态相同，若使他们在体积不变情况下吸收相等的热量，则 [ ]（A）它们的温度升高相同，压强增加相同.（B）它们的温度升高相同，压强增加不相同.（C）它们的温度升高不相同，压强增加不相同.（D）它们的温度升高不相同，压强增加相同.3、一个绝热容器，用质量可忽略的绝热板分成体积相等的两部分.两边分别装入质量相等、温度相同的H2和O2.开始时绝热板P固定.然后释放之，板P将发生移动（绝热板与容器壁之间不漏气且摩擦可以忽略不计），在达到新的平衡位置后，若比较两边温度的高低，则结果是：[ ]（A）H2比O2温度高.（B）O2比H2温度高.（C）两边温度相等且等于原来的温度.（D）两边温度相等但比原来的温度降低了.4、如图所示，一绝热密闭的容器，用隔板分成相等的两部分，左边盛有一定量的理想气体，压强为Po，右边为真空.今将隔板抽去，气体自由膨胀，当气体达到平衡时，气体的压强是[ ]（A）Po （B）Po/2 （C）2 r / Po （D）Po/2 r （ r = Cp / Cv ）5、1 mol理想气体从P-V图上初态a分别经历如图所示的（1）或（2）过程到达末态b.已知Ta < Tb，则这两过程中气体吸收的热量Q1和Q2的关系是 [ ]（A）Q1 > Q2 > 0 （B）Q2 > Q1 > 0 （C）Q2 < Q1 < 0（D）Q1 < Q2 < 0 （E）Q1 = Q2 > 06、有两个相同的容器，容积固定不变，一个盛有氦气，另一个盛有氢气（看成刚性分子理想气体），它们的温度和压强都相等，现将5 J的热量传给氢气，使氢气温度升高，如果使氦气也升高同样的温度，则应向氦气传递的热量是 [ ]（A）6 J （B）5 J（C）3 J （D）2 J7、一定量的理想气体经历acb过程时吸热200 J.则经历acbda过程时，吸热为（A）–1200 J （B）–1000 J（C）–700 J （D）1000 J [ ]8、对于室温下的双原子分子理想气体，在等压膨胀的情况下，系统对外所作的功与从外界吸收的热量之比A / Q等于 [ ]（A）1 / 3 （B）1 / 4（C）2 / 5 （D）2 / 79、如果卡诺热机的循环曲线所包围的面积从图中的a b c d a增大为a b’c’d a，那么循环ab cda与a b’c’da所作的净功和热机效率变化情况是： [ ]（A）净功增大，效率提高. （B）净功增大，效率降低.（C）净功和效率都不变. （D）净功增大，效率不变.一、填空题：1、如图所示，已知图中画不同斜线的两部分分别为S1和S2，那么（1）如果气体的膨胀过程为a—1—b，则气体对外做功A= ;（2）如果气体进行a—2—b—1—a的循环过程,则它对外做功A =2、已知1 mol的某种理想气体（可视为刚性分子），在等压过程中温度上升1 K，内能增加了20.78 J，则气体对外做功为__________,气体吸收热量为__________.3、刚性双原子分子的理想气体在等压下膨胀所作的功为A，则传递给气体的热量为___ ____________.4、热力学第二定律的克劳修斯叙述是：_________________________________________；开尔文叙述是____________________________________________.5、从统计的意义来解释：不可逆过程实质上是一个________________________________________的转变过程.一切实际过程都向着____________________________________________的方向进行.6、由绝热材料包围的容器被隔板隔为两半，左边是理想气体，右边是真空.如果把隔板撤去，气体将进行自由膨胀过程，达到平衡后气体的温度_________（升高、降低或不变），气体的熵___________（增加、减小或不变）.二、计算题：1、一定量的单原子分子理想气体，从A态出发经等压过程膨胀到B态，又经绝热过程膨胀到C态，如图所示.试求这全过程中气体对外所作的功，内能的增量以及吸收的热量.2、如果一定量的理想气体，其体积和压强依照V = a / 的规律变化，其中a为已知常数.试求：（1）气体从体积V1膨胀到V2所作的功；（2）体积为V1时的温度T1与体积为V2时的温度T2之比.3、一卡诺热机（可逆的），当高温热源的温度为127°C、低温热源温度为27°C时，其每次循环对外作净功8000 J.今维持低温热源的温度不变，提高高温热源温度，使其每次循环对外作净功10000 J.若两个卡诺循环都工作在相同的两条绝缘线之间，试求：（1）第二个循环热机的效率；（2）第二个循环的高温热源的温度.4、一定量的刚性双原子分子的理想气体，处于压强P1= 10 atm、温度T1 = 500K的平衡态，后经历一绝热过程达到压强P2 = 5 atm、温度为T2的平衡态.求T2.热力学(三)一、选择题1、设高温热源的热力学温度是低温热源的热力学温度的n倍，则理想气体在一次卡诺循环中，传给低温热源的热量是从高温热源吸取的热量的(A) n倍 (B) n–1倍(C) 倍 (D) 倍 [ ]2、一定量理想气体经历的循环过程用V-T曲线表示如题2图，在此循环过程中，气体从外界吸热的过程是(A) A→B (B) B→C(C) C→A (D) B→C和C→A [ ]3、所列题3图分别表示某人设想的理想气体的四个循环过程，请选出其中一个在物理上可能实现的循环过程的图的标号. [ ]V P （A）P （B）绝热绝热C B 等温等容等容O V O 等温 VP 等压（C）P （D）A 等温绝热绝热绝热绝热O T O V O V题图题3图4、理想气体卡诺循环过程的两条绝热线下的面积大小(图中阴影部分)，分割为S1和S2，则二者的大小关系是(A) S1 > S2 (B) S1 = S2(C) S1 < S2 (D) 无法确定 [ ]PS2 S1V.对此说法，有如下几种评论，哪种是正确的？(A) 不违反热力学第一定律，但违反热力学第二定律.(B) 不违反热力学第二定律，但违反热力学第一定律.(C) 不违反热力学第一定律，也不违反热力学第二定律.(D) 违反热力学第一定律，也违反热力学第二定律. [ ]6、一绝热容器被隔板分成两半，一半是真空，另一半是理想气体，若把隔板抽出，气体将进行自由膨胀，达到平衡后(A) 温度不变，熵增加. (B) 温度升高，熵增加.(C) 温度降低，熵增加. (D) 温度不变，熵不变. [ ]7、一定量的理想气体向真空作绝热自由膨胀，体积由V1增至V2，在此过程中气体的(A) 内能不变，熵增加. (B) 内能不变，熵减少.(C) 内能不变，熵不变. (D) 内能增加，熵增加. [ ]8、给定理想气体，从标准状态 (P0，V0，T0)开始作绝热膨胀，体积增大到3倍，膨胀后温度T、压强P与标准状态时T0、P0之关系为 (γ为比热比) [ ](A) T = ( ) r T0 ; P = ( ) r-1 P0. (B) T = ( ) r-1 T0 ; P = ( ) r P0.(C) T = ( ) -r T0 ; P = ( ) r-1 P0. (D) T = ( ) r-1 T0 ; P = ( ) -r P0.一、填空题：1、在P-V图上(1) 系统的某一平衡态用来表示；(2) 系统的某一平衡过程用来表示；(3) 系统的某一平衡循环过程用来表示.2、P-V图上的一点，代表；P-V图上任意一条曲线，表示；3、一定量的理想气体，从P-V图上状态A出发，分别经历等压、等温、绝热三种过程，由体积V1膨胀到体积V2，试画出这三种过程的P—V图曲线，在上述三种过程中：（1）气体对外作功最大的是过程；(2) 气体吸热最多的是过程；V2( 均视为刚性分子的理想气体)，它们的质量比为m1：m2E1：E2 = ，如果它们分别在等压过程中吸收了相同的热量，则它们对外作功之比为A1：A2 = .(各量下角标1表示氢气，2表示氦气)5、质量为2.5 g的氢气和氦气的混合气体，盛于某密闭的气缸里 ( 氢气和氦气均视为刚性分子的理想气体)，若保持气缸的体积不变，测得此混合气体的温度每升高1K，需要吸收的热量等于2.25 R ( R为摩尔气体常量).由此可知，该混合气体中有氢气 g，氦气 g；若保持气缸内的压强不变，要使该混合气体的温度升高1K，则该气体吸收的热量为 . (氢气的M mol = 2×10 -3 kg，氦气的M mol = 4×10 -3 kg)6、一定量理想气体，从A状态 (2P1，V1) 经历如图所示的直线过程变到B状态 (P1，2V1)，则AB过程中系统作功A = ；内能改变△E = .第6题图第7题图7、如图所示，理想气体从状态A出发经ABCDA循环过程，回到初态A点，则循环过程中气体净吸的热量Q = .8、有一卡诺热机，用29kg空气为工作物质，工作在27℃的高温热源与–73℃的低温热源之间，此热机的效率η= .若在等温膨胀的过程中气缸体积增大2.718倍，则此热机每一循环所作的功为 .(空气的摩尔质量为29×10-3kg·mol-1)二、计算题：1、一定量的某种理想气体，开始时处于压强、体积、温度分别为P0 = 1.2×106 P0，V0 = 8.31×10-3m3，T0 = 300K的初态，后经过一等容过程，温度升高到T1 = 450 K，再经过一等温过程，压强降到P = P0的末态.已知该理想气体的等压摩尔热容与等容摩尔热容之比C P/C V=5/3，求：(1)该理想气体的等压摩尔热容C P和等容量摩尔热容C V.(2)气体从始态变到末态的全过程中从外界吸收的热量.2、某理想气体在P-V图上等温线与绝热线相交于A点，如图，已知A点的压强P1=2×105P0，体积V1 = 0.5×10-3 m3，而且A点处等温线斜率与绝热线斜率之比为0.714，现使气体从A点绝热膨胀至B点，其体积V2 = 1×10-3 m3，求(1) B 点处的压强；(2) 在此过程中气体对外作的功.3、1 mol单原子分子的理想气体，经历如图所示的可逆循环，联结AC两点的曲线III的方程为P = P0 V2 / V20，A点的温度为T0.(1)试以T0，R表示I、II、III过程中气体吸收的热量.(2)求此循环的效率.(提示：循环效率的定义式η= 1– Q2 / Q1, Q1循环中气体吸收的热量，Q2为循环中气体放出的热量).气体动理论 (一)一、选择题：1、一个容器内贮有1摩尔氢气和1摩尔氦气，若两种气体各自对器壁产生的压强分别为P1和P2，则两者的大小关系是：(A) P1 > P2 (B) P1 < P2(C) P1 = P2 (D) 不确定的. [ ]2、若理想气体的体积为V，压强为P，温度为T，一个分子的质量为m，k为玻耳兹曼常量，R为摩尔气体常量，则该理想气体的分子数为：(A) PV / m . (B) PV/(KT).(C) PV / (RT). (D) PV/(mT). [ ]3、有一截面均匀的封闭圆筒，中间被一光滑的活塞分隔成两边，如果其中的一边装有0.1kg某一温度的氢气，为了使活塞停留在圆筒的正中央，则另一边应装入同一温度的氧气质量为：[ ](A) 1 / 16 kg (B) 0.8 kg(C) 1.6 kg (D) 3.2 kg4、在一密闭容器中，储有A、B、C三种理想气体，处于平衡状态，A种气体的分子数密度为n1，它产生的压强为P1，B种气体的分子数密度为2 n1，C种气体的分子数密度为3 n1，则混合气体的压强P为(A) 3 P1 (B) 4 P1(C) 5 P1 (D) 6 P1 [ ]5、一定量某理想气体按PV2 = 恒量的规律膨胀，则膨胀后理想气体温度(A) 将升高 (B) 将降低(C) 不变 (D)升高还是降低，不能确定 [ ]6、如图所示，两个大小不同的容器用均匀的细管相连，管中有一水银滴作活塞，大容器装有氧气，小容器装有氢气，当温度相同时，水银滴静止于细管中央，试问此时这两种气体的密度哪个大？(A)氧气的密度大. (B)氢气的密度大.(C)密度一样大. (D)无法判断. [ ]一、填空题：1、对一定质量的理想气体进行等温压缩，若初始时每立方米体积内气体分子数为1.96×1024，当压强升高到初值的两倍时，每立方米体积内气体分子数应为 .2、在推导理想气体压强公式中，体现统计意义的两条假设是：(1) ；(2) .3、某理想气体在温度为27℃和压强为1.0×10-2 atm情况下，密度为11.3 g / m3，则这气体的摩尔质量M= .(摩尔气体常量R = 8.31 J·mol-1·K-1)mol4、在定压下加热一定量的理想气体，若使其温度升高1K时，它的体积增加了0.005倍，则气体原来的温度是 .5、下面给出理想气体状态方程的几种微分形式，指出它们各表示什么过程.(1) p d V = (M / M mol) R d T表示过程.(2) V d p = (M / M mol) R d T表示过程.(3) p d V + V d p = 0 表示过程.6、氢分子的质量3.3×10 –24 g，如果每秒有1023个氢分子沿着与容器器壁的法线成45°角的方向以105cm·s-1的速率撞击在2.0 cm 2 面积上(碰撞是完全弹性的)，则此氢气的压强为 .7、一气体分子的质量可以根据该气体的定容比热容来计算，氩气的定容比热容Cv = 0.314 kJ·kg-1·K-1，则氩原子的质量m = .(1 k c a l = 4.18×103 J)8、分子物理是研究的学科，它应用的基本方法是方法.9、解释下列分子运动论与热力学名词：(1) 状态参量：；(2) 微观量：；(3) 宏观量：；二、计算题：1、黄绿光的波长是5000 Å (1 Å =10-10m)，理想气体在标准状态下，以黄绿光的波长为边长的立方体内有多少个分子？（玻耳兹曼常量k = 1.38×10 -23J·K-1）2、两个相同的容器装有氢气，以一细玻璃管相连通，管中用一滴水银作活塞，如图所示，当左边容器的温度为0℃，而右边容器的温度为20℃时，水银滴刚好在管的中央，试问，当左边容器温度由0℃增到5℃，而右边容器温度由20℃增到30℃时，水银滴是否会移动？如何移动？3、假设地球大气层由同种分子构成，且充满整个空间，并设各处温度T相等.试根据玻璃尔兹曼分布律计算大气层分子的平均重力势能εp.(已知积分公式 X n e -ax d x = n ！/ a n+1)热力学（一） (答案)一、 1．C 2．B 3．D 4．D 5．A 6．B 7．B 8．D二、 1．物体作宏观位移，分子之间的相互作用.2．能使系统进行逆向变化，回复状态，而且周围一切都回复原状.系统不能回复到初；态；或者系统回复到初态时，周围并不能回复原状.3．在等压升温过程中，气体要膨胀而作功，所以要比气体等体升温过程多吸收一部分热量.4．（1）气体的内能，（2）气体对外所做的功，（3）气体的内能和对外所做的功5．2/i+2,i/i+2 6．8.64×103 7．7.48×103 J ,7.48×103 J8．200J热力学（二）答案一、1．A 2.C 3.B 4.B 5.A 6.C 7.B 8.D 9.D二、1．S1+S2，-S1 2. 8.31J, 29.09J 3.7A/24、不可能把热量从低温物体自动传到高温物体而不引起外界变化不可能制造出这样循环工作的热机,它只从单一热源吸热来作功,而不放出热量给其他物体,或者说不使外界发生任何变化.5. 从概率较小的状态到概率较大的状态，状态概率增大（或熵增大）6．不变； 增加热力学（三）答案一、1、C 2、A 3、B 4、B 5、C 6、A 7、A 8、D二、1、一个点，一条曲线，一条封闭线 2、（参看1题）3、等压，等压 4、1：2，5：3，5：7 5、1.5，1，3.25R 6、23P 1V 1，0 7、1.62×104J 8、33.3%，831×105J气体动理论（一）答案一、1.C 2. B 3.C 4.D 5.B 6.A二、1、3.92×1024 2、（1）沿空间各方向运动的分子数相等；（2）v x 2=v y 2=v z 23、27．9g/mol4、200K5、等压，等容，等温6、2．33×103 Pa7、6.59×10-26 kg8、物体热现象和热运动规律、统计9、（1）描述物体运动状态的物理量；（2）表征个别分子状况的物理量，如分子大小、质量、速度等；（3）表征大量分子集体特征的物理量，如P 、V 、T 、C 等.气体动理论(二) 答案。

《大学物理》下册试卷及答案纯碱感动破旧一些不在此列厅局级一些在地一工作2022年-2022年《大学物理》（下）考试试卷一、选择题（单选题，每小题3分，共30分）：1、两根无限长平行直导线载有大小相等方向相反的电流I，I以dI/dt的变化率增长，一矩形线圈位于导线平面内（如图所示），则。

(A),矩形线圈中无感应电流；(B),矩形线圈中的感应电流为顺时针方向；(C),矩形线圈中的感应电流为逆时针方向；(D),矩形线圈中的感应电流的方向不确定；2,如图所示的系统作简谐运动，则其振动周期为。

(A),T 2 mmsin ；(B), T 2 ；kkmcos；kmsin；kcos(C), T 2(D), T 23，在示波器的水平和垂直输入端分别加上余弦交变电压，屏上出现如图所示的闭合曲线，已知水平方向振动的频率为600Hz，则垂直方向的振动频率为。

(A),200Hz；(B), 400Hz；(C), 900Hz；(D), 1800Hz；4，振幅、频率、传播速度都相同的两列相干波在同一直线上沿相反方向传播时叠加可形成驻波，对于一根长为100cm的两端固定的弦线，要形成驻波，下面哪种波长不能在其中形成驻波？。

(A),λ=50cm；(B), λ=100cm；(C), λ=200cm；(D), λ=400cm；5，关于机械波在弹性媒质中传播时波的能量的说法，不对的是。

(A),在波动传播媒质中的任一体积元，其动能、势能、总机械能的变化是同相位的；(B), 在波动传播媒质中的任一体积元，它都在不断地接收和释放能量，即不断地传播能量。

所以波的传播过程实际上是能量的传播过程；(C), 在波动传播媒质中的任一体积元，其动能和势能的总和时时刻刻保持不变，即其总的机械能守恒；(D), 在波动传播媒质中的任一体积元，任一时刻的动能和势能之和与其振动振纯碱感动破旧一些不在此列厅局级一些在地一工作幅的平方成正比；6，以下关于杨氏双缝干涉实验的说法，错误的有。

单元一 简谐振动一、 选择、填空题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ 【 C 】(A) 物体处在运动正方向的端点时，速度和加速度都达到最大值；(B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为π34，则t=0时，质点的位置在： 【 D 】(A) 过A 21x =处，向负方向运动； (B) 过A 21x =处，向正方向运动； (C) 过A 21x -=处，向负方向运动；(D) 过A 21x -=处，向正方向运动。

3. 将单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止释放任其振动，从放手开始计时，若用余弦函数表示运动方程，则该单摆的初相为： 【 B 】(A) θ； (B) 0； (C)π/2； (D) -θ4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为： 【 B 】(A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： 【 C 】(A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动； (D) 两种情况都不能作简谐振动。

6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： 【 C 】)4(填空选择)5(填空选择A2332,3)D (;A 22,43or ,4)C (;A 23,65,6)B (;A 21,32or ,3)A (±±±±±±±±±±±±，ππππππππ7. 如果外力按简谐振动的规律变化，但不等于振子的固有频率。

习题一一、选择题1．如图所示，半径为R 的圆环开有一小空隙而形成一圆弧，弧长为L ，电荷Q -均匀分布其上。

空隙长为()L L R ∆∆<<，则圆弧中心O 点的电场强度和电势分别为 [ ] （Ａ）200,44Q L Qi R L Rπεπε-∆-； （Ｂ）2200,84Q L Qi R L Rπεπε-∆-； （Ｃ）200,44Q L Qi R L Rπεπε∆； （Ｄ）200,44Q L Q Li R L RLπεπε-∆-∆。

答案：A解：闭合圆环中心场强为0，则圆弧产生的场强与空隙在圆心处产生的场强之和为0。

由于空隙 ∆l 非常小，可视为点电荷，设它与圆弧电荷密度相同，则所带电荷为/Q L L -∆，产生的场强为204Q L i R L πε∆，所以圆弧产生的场强为204OQ LE i R Lπε-∆=；又根据电势叠加原理可得04O Q U Rπε-= .2．有两个电荷都是＋q 的点电荷，相距为2a 。

今以左边的点电荷所在处为球心，以a 为半径作一球形高斯面。

在球面上取两块相等的小面积S 1和S 2，其位置如图所示。

设通过S 1和S 2的电场强度通量分别为1Φ和2Φ，通过整个球面的电场强度通量为S Φ，则［ ］ （A ）120, /S q εΦ>ΦΦ=； （B ）120, 2/S q εΦ<ΦΦ=；（C ）120, /S q εΦ=ΦΦ=； （D ）120, /S q εΦ<ΦΦ=。

答案：D解：由高斯定理知0Φ=S q 。

由于面积S 1和S 2相等且很小，场强可视为均匀。

根据场强叠加原理，120,0E E =<，所以12Φ0,Φ0=>。

3．半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为 [ ]答案：B2∝2∝rRr R解：由高斯定理知均匀带电球体的场强分布为()302041 ()4qrr R R E q r R r πεπε⎧<⎪⎪=⎨⎪>⎪⎩，所以选（B ）。

静电场(一)一. 选择题:1.解:在不考虑边缘效应的情况下，极板间的电场等同于电荷均匀分布，密度为o = ±q/S的两面积无限大平行薄板之间的电场一-匀强电场，一板在另一板处之电场强度为£ = o/(2s0)，方向垂直于板面.所以，极板间的相互作用力F =q・E = q2 /(2件)。

故选(B)。

2.解：设置八个边长为a的立方体构成一个大立方体，使A(即Q)位于大立方体的中心.所以通过大立方体每一侧面的电场强度通量均为q/(6&o),而侧面abed是大立方体侧面的1/4,所以通过侧面abed的电场强度通量等于q/(24%).选(C)。

3.解:寸亘•丞=jpdV/£°适用于任何静电场.选(A)。

4.解：选(B)。

5.解:据高斯定理知：通过整个球面的电场强度通=q/&. ■内电荷通过昂、&的电通量相等且大于零; 外电荷对品的通量为负，对&的通量为正. 所以0>1 <0>2 •故(D)对。

二. 填空题：1.解：无限大带电平面产生的电场E= —2&oA L 八(5 2(5 3(5A 区：E A= ------------------ = ------2s0 2s02g0CL L b 2b bB 区：E R = ------------ = ------2s0 2s 02s0C区"c=三+至=至2s n 2s n 2s n2.解：据题意知，P点处场强方向若垂直于OP,则入在P点场强的OP分量与Q在P点的场强E QP一定大小相等、方向相反.即Jcp = ------------- c os——= ----------- =也冲= -------- , O — aA .2%。

3 4%。

4%。

之3. 解：无限长带电圆柱体可以看成由许多半径为r 的均匀带电无限长圆筒叠加而成，因此 其场强分布是柱对称的，场强方向沿圆柱半径方向，距轴线等距各点的场强大学相等。

汉A一、单项选择题(本大题共5小题，每题只有一个正确答案，答对一题得3分,共15分）1、强度为的自然光，经两平行放置的偏振片，透射光强变为，若不考虑偏振片的反射和吸收，这两块偏振片偏振化方向的夹角为【】A。

30º；B。

45º；C.60º；D。

90º.2、下列描述中正确的是【】A。

感生电场和静电场一样，属于无旋场；B。

感生电场和静电场的一个共同点，就是对场中的电荷具有作用力;C.感生电场中可类似于静电场一样引入电势;D。

感生电场和静电场一样,是能脱离电荷而单独存在.3、一半径为R的金属圆环，载有电流，则在其所围绕的平面内各点的磁感应强度的关系为【】A。

方向相同，数值相等; B。

方向不同，但数值相等；C.方向相同，但数值不等；D.方向不同,数值也不相等。

4、麦克斯韦为建立统一的电磁场理论而提出的两个基本假设是【】A。

感生电场和涡旋磁场; B。

位移电流和位移电流密度；C。

位移电流和涡旋磁场; D.位移电流和感生电场.5、当波长为λ的单色光垂直照射空气中一薄膜（n〉1)的表面时，从入射光方向观察到反射光被加强，此膜的最薄厚度为【】A。

; B。

;C. ；D。

;二、填空题（本大题共15小空，每空2分,共30 分.）6、设杨氏双缝缝距为1mm，双缝与光源的间距为20cm，双缝与光屏的距离为1m.当波长为0。

6μm的光正入射时,屏上相邻暗条纹的中心间距为.7、一螺线管的自感系数为0。

01亨，通过它的电流为4安，则它储藏的磁场能量为焦耳。

8、一质点的振动方程为(SI制），则它的周期是，频率是，最大速度是。

9、半径为R的圆柱形空间分布均匀磁场,如图，磁感应强度随时间以恒定速率变化，设为已知，则感生电场在r〈R区域为，在r〉R区域为.10、一个电子射入的均匀磁场中，当电子速度为时，则电子所受的磁力=。

11、自然光入射到两种媒质的分界面上，当入射角等于布儒斯特角i B时，反射光线与Id折射光线之间的夹角等于.12、铝的逸出功为4。