喀什地区 高一数学12月份月考卷子-秦俊凯

-第一学期高邮中学 高一数学十二月考试卷4一．填空题：（本大题共14小题，每小题5分，共70分）1．若{1,2,3,4},{1,2},{2,3}U M N ===，则)(N M C U = ． 2．cos 20()3π-的值是 ． 3．函数()3cos 24f x x π⎛⎫=+⎪⎝⎭的最小正周期为 ．4．函数()lg(1)f x x =++的定义域是 ．5．在ABC ∆中，点D 是BC 的中点，已知(3,2)AB =-，(5,1)AC =--，则AD 的坐标为 ．6．三个数5.06，65.0，6log 5.0的大小按从小到大顺序为 ． 7．若函数 1 (0)()(2) (0)x x f x f x x +≥⎧=⎨+<⎩，则(2)f -=__________ ．8．设a <0,角α的终边经过点P (-3a ,4a ),那么sin α+2cos α的值等于: ． 9．函数3sin(2)6y x π=-+的单调递减区间为_____________．10．要得到函数()sin 23f x x π⎛⎫=-⎪⎝⎭的图象，只需将()sin 2f x x =的图象向右平移()02ρρπ<<个单位，则ρ= ．11．12,e e 是两个不共线的向量，已知122AB e ke =+，123CB e e =+122CD e e =-,且D B A ，，三点共线，则实数k = .12．已知)(x f 是定义域为R 的奇函数)(x f ，若当(0,)∈+∞x 时，()lg =f x x ，则满足()0>f x 的x 的取值范围是 .13．已知1cos(75),180903αα+=-<<-其中,则sin(105)cos(375)αα-+-的值为 ．14．关于向量有下列命题：(1)若,;a b a c b c ⋅=⋅=则 (2)若0,00a b a b ⋅===则或;(3),,,()()1,2,0..a b c b c a a c b c a b a b a b ⋅-⋅==-=⋅=若为非零向量则与垂直.(4)若则其中正确命题的个数是 二．解答题：（本大题共6小题，共90分） 15．（本小题满分14分）已知向量(1,2),(2,3)a b =-=． (1) 若(3)//()a b a kb -+，求k 的值； (2) 若()a ma b ⊥-，求m 的值；16．(本题满分14分)已知弹簧下方挂的小球做上下振动时，小球离开平衡位置的距离S 与t 的函数关系为sin(),(0,0,,0)2S A t A t πωϕωϕ=+>><≥，下图是其图象的一部分，试根据图象回答下列问题： （1）求小球振动时的振幅和周期； （2）求S 与t 的函数解析式．已知向量m n m),1,(sin ),1,32(cos αα=--=与n 为共线向量，且]0,2[πα-∈ （Ⅰ）求ααcos sin +的值 （Ⅱ）求ααααcos sin cos sin -的值18．（本题满分16分）某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时可全部租出；当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.（1）当每辆车的月租金为3600元时，能租出多少辆车？（2）当每辆车的月租金定为多少元时，租赁公司的月效益最大？最大效益是多少？已知OAB ∆的顶点坐标为(0,0)O ,(2,9)A ,(6,3)B -,点P 的横坐标为14，且OP PB λ=.点Q 是边AB 上一点,且0OQ AP ⋅=.(Ⅰ)求实数λ的值与点P 的坐标； (Ⅱ)求点Q 的坐标；(Ⅲ)若R 为线段OQ 上的一个动点,试求()RO RA RB ⋅+的最小值.本小题满分16分)已知函数3()lg()3xf x x-=+，其中 (3,3)x ∈- （1）判别函数()f x 的奇偶性；（2）判断并证明函数()f x 在(3,3)-上单调性；（3）是否存在这样的负实数k ，使22(cos )(cos )0f k f k θθ-+-≥对一切R θ∈恒成立，若存在，试求出k 取值的集合；若不存在，说明理由。

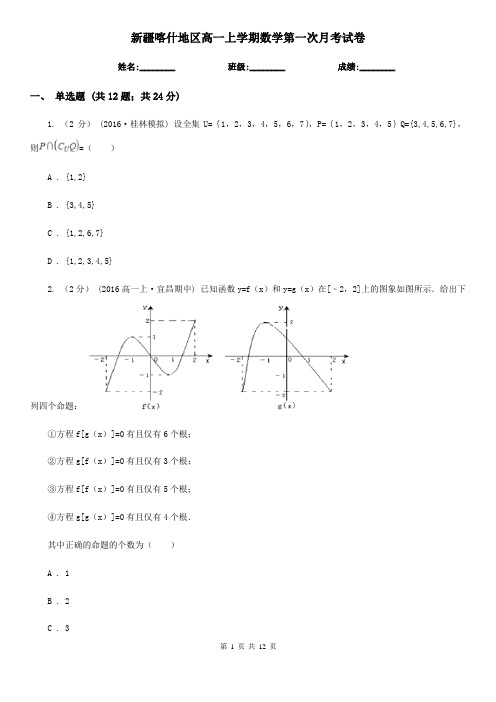
新疆喀什地区高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2016·桂林模拟) 设全集U=｛1，2，3，4，5，6，7｝，P=｛1，2，3，4，5｝Q={3,4,5,6,7}，则=（）A . {1,2}B . {3,4,5}C . {1,2,6,7}D . {1,2,3,4,5}2. （2分） (2016高一上·宜昌期中) 已知函数y=f（x）和y=g（x）在[﹣2，2]上的图象如图所示．给出下列四个命题：①方程f[g（x）]=0有且仅有6个根；②方程g[f（x）]=0有且仅有3个根；③方程f[f（x）]=0有且仅有5个根；④方程g[g（x）]=0有且仅有4个根．其中正确的命题的个数为（）A . 1B . 2C . 3D . 43. （2分）如图，U为全集，M，N是集合U的子集，则阴影部分所表示的集合是（）A . M∩NB . ∁U（M∩N）C . （∁UM）∩ND . （∁UN）∩M4. （2分）已知函数，则（）A . 0B . 2C . －2D . 45. （2分） (2019高一上·四川期中) 若对于定义域内的任意实数都有，则（）A .B .C .D .6. （2分）在以下四组函数中，表示同一个函数的是（）A . f（x）=x+1，B . f（x）=1，C . y=|x|，D . ，g（x）=x+17. （2分） (2017高一上·丰台期中) 函数y=f（x）是定义域为R的奇函数，当x≥0时，f（x）=x2﹣2x，函数f（x）与函数y=1的交点个数为（）A . 0B . 1C . 2D . 38. （2分）已知是（-， +）上的增函数，那么a的取值范围是（）A . (1，+)B . (-,3)C . [， 3)D . (1,3)9. （2分）函数y= 的值域是（）A . （﹣∞，﹣1）B . （0，+∞）C . [1，+∞）D . （ 0，1]10. （2分） (2016高一上·蓟县期中) 设函数f（x）= ，则f（）的值为（）A .B . ﹣C .D . 1811. （2分）(2018·石嘴山模拟) 函数的图象为（）A .B .C .D .12. （2分） (2016高一下·湖北期中) 已知函数y=f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，若不等式f（a）≥f（x）对任意x∈[1，2]恒成立，则实数a的取值范围是（）A . （﹣∞，1]B . [﹣1，1]C . （﹣∞，2]D . [﹣2，2]二、填空题 (共4题；共4分)13. （1分） (2018高一上·黑龙江期中) 函数的定义域为________．14. （1分） (2016高一上·南京期中) 已知a，b为常数，若f（x）=x2+4x+3，f（ax+b）=x2+10x+24，则5a﹣b=________．15. （1分） (2016高一上·定州期中) 设f（x）是奇函数，且在（0，+∞）内是减函数，又f（﹣2）=0，则（x﹣3）•f（x）＜0的解集是________16. （1分） (2019高二上·邵阳期中) 若不等式的解集为R，实数的取值范围是________.三、解答题 (共6题；共60分)17. （10分） (2019高一上·平遥月考)（1）（2）18. （10分）已知函数f（x）=（Ⅰ）画出f（x）的图象；（Ⅱ）写出f（x）的单调递增区间．19. （10分）已知a，b是实数，函数f（x）=x|x﹣a|+b．（1）当a=2时，求函数f（x）的单调区间；（2）当a＞0时，求函数f（x）在区间[1，2]上的最大值；（3）若存在a∈[﹣3，0]，使得函数f（x）在[﹣4，5]上恒有三个零点，求b的取值范围．20. （10分） (2019高二下·常州期中) 已知函数 , .（1）若，求的单调区间；（2）求函数在上的最值；（3）当时，若函数恰有两个不同的零点，求的取值范围.21. （10分）定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数f（x）=1+a•（）x+（）x ，（1）当a=1时，求函数f（x）在（﹣∞，0）上的值域，并判断函数f（x）在（﹣∞，0）上是否为有界函数，请说明理由；（2）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．22. （10分） (2017高一上·肇庆期末) 已知函数，且该函数的图象过点（1，5）．（Ⅰ）求f（x）的解析式，并判断f（x）的奇偶性；（Ⅱ）判断f（x）在区间（0，2）上的单调性，并用函数单调性的定义证明你的结论．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分)17-1、17-2、18-1、19-1、20-1、20-2、20-3、21-1、22-1、。

双牌二中(èr zh ōn ɡ)2021-2021学年上学期高一数学12月月考试卷2021年12月时间是：120分钟 总分：150分一、选择题〔每一小题5分，一共50分〕 1、集合，那么M 与N 的关系是( )A 、B 、C 、D 、2、“〞是“的( )A 、必要不充分条件B 、充分不必要条件C 、充分必要条件D 、既不充分也不必要条件 3、函数的定义域是( )A 、B 、C 、D 、4、假设成等比数列，那么的值是( )A 、B 、C 、3D 、5、 假设函数的图象关于轴对称，那么在区间上( )A 、是增函数B 、是减函数C 、有增有减D 、不能确定增减 6、，那么用表示为( )A 、B 、C 、D 、7、在等差数列中，，那么数列}{n a 的通项公式为( ) A.、B 、C 、D 、8、函数(h ánsh ù) 的反函数是( )A 、y =B 、y =C 、y =D 、y =9、数列}{n a 、，那么数列的前10项和为( )A 、31B 、C 、D 、10、，假设，那么a 的取值范围为( )A 、B 、C 、D 、二、填空题〔每一小题4分，一共20分〕。

11、数列}{n a 中，那么数列}{n a 的通项为___ _________。

12、函数的值域为___________。

13、等差数列}{n a 中，，且，是数列}{n a 的前项和，假设n S 取得最大值，那么n =__________。

14、假设m 是m+n 与n 的等差中项，n 是m 与mn 的等比中项，那么。

15、函数；给出以下命题：①)(x f 有最小值；②当时，)(x f 的值域为R ；③当时，)(x f 在上有反函数；④假设(ji ǎsh è))(x f 在),2[∞+上是增函数，那么实数a的取值范围为。

其中正确的序号为____________。

三、解答题〔写出必要的解题步骤和证明过程，一共计80分〕 16、〔满分是12分〕正项等比数列}{n a 满足：，，，求数列}{n b 的前10项和。

新疆2020年高一上学期数学12月月考试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）（）A .B .C .D .2. （2分） (2018高一上·北京期中) 已知集合，则（）A .B .C .D .3. （2分） (2020高二下·赣县月考) 设函数是奇函数（）的导函数，，当时，，则使得成立的的取值范围是（）A .B .C .D .4. （2分）已知x，y为正实数，则（）A . 2lgx+lgy=2lgx+2lgyB . 2lg（x+y）=2lgx•2lgyC . 2lgx•lgy=2lgx+2lgyD . 2lg（xy）=2lgx•2lgy5. （2分） (2019高一上·成都月考) 若，则的值为（）A .B .C . 0D . 16. （2分） (2016高一下·驻马店期末) 一扇形的中心角为2，对应的弧长为4，则此扇形的面积为（）A . 1B . 2C . 4D . 87. （2分） (2019高一上·涟水月考) 点是角的终边与单位圆的交点，则的值为（）A .B .C .D .8. （2分） (2017高一上·长春期中) 若f（x）是偶函数，且当x∈[0，+∞）时，f（x）=x﹣1，则f（x﹣1）＜0的解集是（）A . （﹣1，0）B . （﹣∞，0）∪（1，2）C . （1，2）D . （0，2）9. （2分） (2017高二上·汕头月考) 为了得到函数的图像，只需把函数的图像（）A . 向左平移个长度单位B . 向右平移个长度单位C . 向左平移个长度单位D . 向右平移个长度单位10. （2分） (2016高一下·黄陵开学考) 已知f（x）=ax5+bx﹣ +2，f （2）=4，则 f（﹣2）=（）A . 0B . 1C . 2D . 311. （2分） (2018高三上·沈阳期末) 已知函数若方程恰有两个不同的解，则实数a的取值范围是（）A .B .C .D .12. （2分）如图,函数y=f(x)的图像是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x 的解集为（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2019高一上·江苏月考) 已知幂函数的图象经过点，则的值为________.14. （1分） (2019高三上·吉林月考) 设函数，则的值等于________．15. （1分）化简：（1+）sin2θ=________16. （1分）设x∈R，对于使f（x）≤M恒成立的所有常数M中，我们把M的最小值叫做f（x）的上确界．例如f（x）=﹣x2+2x，x∈R的上确界是1．若a，b∈R+ ，且a+b=1，则﹣的上确界为________三、解答题 (共4题；共40分)17. （10分） (2017高一上·乌鲁木齐期中) 设全集，集合或．求（1）；（2）记，且，求的取值范围.18. （10分）函数f(x)＝1.1x ， g(x)＝ln x＋1，h(x)＝x 的图象如图所示，试分别指出各曲线对应的函数，并比较三个函数的增长差异(以1，a ， b ， c ， d ， e为分界点)．19. （10分） (2017高一上·武汉期末) 已知 =（sinx，cosx）， =（sinx，k）， =（﹣2cosx，sinx ﹣k）．（1）当x∈[0， ]时，求| + |的取值范围；（2）若g（x）=（ + ）• ，求当k为何值时，g（x）的最小值为﹣．20. （10分） (2020高三上·长春月考) 已知函数（1）若函数的值域为，求实数的值；（2）若对任意的成立，求实数的取值范围。

新疆2021版高一上学期数学12月月考试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2019高三上·砀山月考) 设全集，集合，，则（）A .B .C .D .2. （2分） (2019高一上·河东期末)A .B .C .D .3. （2分）已知函数的定义域是,则实数的取值范围是（）A .B .C .D .4. （2分） (2019高一上·西安月考) 设，则函数的零点所在的区间为（）A . （0,1）B .C .D .5. （2分）(2017·孝义模拟) 已知函数f（x）= ，则f（﹣4）=（）A .B .C .D .6. （2分） (2016高一下·商水期中) 已知角θ的顶点与原点重合，始边与x轴正半轴重合，终边在直线y=2x 上，则的值为（）A .B .C .D .7. （2分） (2019高二上·会宁期中) 若，则的最小值为（）A .B .C .D .8. （2分） (2019高三上·景德镇月考) 已知，，则（）A .B .C .D .9. （2分）设f（x）是定义在R上的奇函数，且在区间（0，+∞）上是单调递增，若，△ABC的内角满足f（cosA）＜0，则A的取值范围是（）A . （，）B . （，π）C . （0，）∪（，π）D . （，）∪（，π）10. （2分） (2020高一上·焦作期中) 对于函数，下列判断错误的是（）A . 是偶函数B . 在上单调递减，在上单调递增C . 有两个零点D . 的值域为，二、填空题 (共7题；共7分)11. （1分）(2017·镇海模拟) 定义域为{x|x∈N* ，1≤x≤12}的函数f（x）满足|f（x+1）﹣f（x）|=1（x=1，2，…11），且f（1），f（4），f（12）成等比数列，若f（1）=1，f（12）=4，则满足条件的不同函数的个数为________．12. （1分） (2020高三上·重庆月考) 已知，，则 ________．13. （1分） (2016高一上·绍兴期中) 设函数g（x）=x2﹣2（x∈R），则f（x）的值域是________．14. （1分） (2020高一下·海淀期中) 已知，，则 ________.15. （1分） (2016高一上·商州期中) 函数y=ax+1+1（a＞0且a≠1）的图象必经过定点________16. （1分） (2019高一上·江苏月考) 给出下列四个命题:①函数是奇函数;②若角C是的一个内角，且，则是钝角三角形;③已知是第四象限角，则 ;④已知函数（）在区间单调递增，则 .其中正确命题的序号是________.17. （1分）扇形的周长是20，当扇形的圆心角为________弧度时扇形的面积最大．三、解答题 (共5题；共60分)18. （10分）已知函数f（x）=﹣4x+2x+1+15（Ⅰ）求函数f（x）的零点；（Ⅱ）若函数的定义域为[﹣1，0]，求函数f（x）的值域．19. （10分）已知α为第三象限角，且f（α）= ．（1）化简f（α）；（2）若α=﹣π，求f（α）的值．（3）若f（α）= ，求cos（π+α）的值．20. （10分） (2019高一上·成都月考) 已知是关于的方程（）的两个根．（1）求的值；（2）求的值．21. （15分） (2020高二下·武汉期中) 某湿地公园内有一条河，现打算建一座桥将河两岸的路连接起来，剖面设计图纸如下：其中，点为x轴上关于原点对称的两点，曲线段BCD是桥的主体，C为桥顶，且曲线段BCD在图纸上的图形对应函数的解析式为，曲线段均为开口向上的抛物线段，且分别为两抛物线的顶点，设计时要求：保持两曲线在各衔接处（）的切线的斜率相等.（1）求曲线段在图纸上对应函数的解析式,并写出定义域；（2）车辆从A经B倒C爬坡，定义车辆上桥过程中某点P所需要的爬坡能力为：（该点P与桥顶间的水平距离）（设计图纸上该点处的切线的斜率），其中的单位：米.若该景区可提供三种类型的观光车:①游客踏乘；②蓄电池动力；③内燃机动力.它们的爬坡能力分别为0.8米,1.5米,2.0米,又已知图纸上一个单位长度表示实际长度1米,试问三种类型的观光车是否都可以顺利过桥?22. （15分） (2016高一上·银川期中) 已知函数f（x）=1﹣（a＞0且a≠1）是定义在R上的奇函数．（1）求a的值；（2）求f（x）的值域；（3）若关于x的方程|f（x）（2x+1）|=m有1个实根，求实数m的取值范围；（4）当x∈（0，1]时，t•f（x）≥2x﹣2恒成立，求实数t取值范围．参考答案一、单选题 (共10题；共20分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：二、填空题 (共7题；共7分)答案：11-1、考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：答案：17-1、考点：解析：三、解答题 (共5题；共60分)答案：18-1、考点：解析：答案：19-1、答案：19-2、答案：19-3、考点：解析：答案：20-1、答案：20-2、考点：解析：答案：21-1、答案：21-2、考点：解析：答案：22-1、答案：22-2、答案：22-3、答案：22-4、考点：解析：。

新疆喀什地区高一上学期数学12月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）已知集合A={x|﹣2＜x＜2}，B={x|x＜1}，则A∪B=（）A . （﹣∞，2）B . （﹣∞，1）C . （1，+∞）D . （2，+∞）2. （2分）若集合，，则=（）A .B .C . 或D . 或3. （2分）若，则（）A .B .C .D .4. （2分）判断下列各组中的两个函数是同一函数的为（）（1），；（2），；（3），；（4），；（5），。

A . （1），（2）B . （2），（3）C . （4）D . （3），（5）5. （2分） (2016高一上·桐乡期中) 函数y=x2﹣2tx+3在[1，+∞）上为增函数，则t的取值范围是（）A . t≤1B . t≥1C . t≤﹣1D . t≥﹣16. （2分）(2018·大庆模拟) 已知是定义在上的奇函数，当时， .若，则的大小关系为（）A .B .C .D .7. （2分） (2016高一上·临沂期中) 函数f（x）=|x﹣2|的图象为（）A .B .C .D .8. （2分） (2016高一上·清远期末) 己知函数（其中）的值域为（）A .B . [﹣1，2]C .D .9. （2分） (2019高一上·柳州月考) 已知函数，若实数是函数的零点，且，则的值为（）A . 恒为正值B . 等于0C . 恒为负值D . 不大于010. （2分） (2016高二下·无为期中) 函数f（x）=|lgx|﹣（）x的零点个数为（）A . 3B . 0C . 1D . 2二、填空题 (共7题；共8分)11. （2分） (2017高一上·肇庆期末) 计算： =________．12. （1分）有一扇形其弧长为6，半径为3，则该扇形面积为________该弧所对弦长为________．13. （1分） (2019高一下·嘉定月考) 点从出发，沿单位圆逆时针方向运动弧长到达点，则点的坐标为________.14. （1分） (2019高一上·嘉兴期中) 已知函数，当时，，则的取值范围是________．15. （1分）已知幂函数(m∈Z)为偶函数，且在(0，＋∞)上是增函数，则f(2)的值为________．16. （1分）(2017·昆明模拟) 已知函数则f（x）≤2的解集为________．17. （1分） (2016高一上·浦东期中) 若关于x的不等式＞0的解集为R，则k的范围为________三、解答题 (共4题；共35分)18. （5分）设集合A={x|x2﹣3x+2=0}，B={x|x2+2（a﹣1）x+（a2﹣5）=0}（1）若A∩B={2}，求实数a的值；（2）若A∪B=A，求实数a的取值范围19. （10分） (2019高一上·杭州期中) 已知实数a≠0，函数（1）若，求，的值；（2）若，求的值．20. （10分） (2019高一上·广东月考) 已知函数，如果存在给定的实数对（），使得恒成立，则称为“S-函数”.（1）判断函数是否是“S-函数”；（2）若是一个“S-函数”，求出所有满足条件的有序实数对；（3）若定义域为的函数是“S-函数”，且存在满足条件的有序实数对和，当时，的值域为，求当时函数的值域.21. （10分） (2019高一上·忻州月考) 已知函数在上有最大值1和最小值0，设 .（1）求m，n的值；（2）若不等式上有解，求实数的取值范围。

盐山中学2021-2021学年度第一学期高一数学12月份月考卷 评卷人 得分 一、单项选择〔每一小题4分，一共56分〕1、设，，那么〔 〕 A. B. C. D. 2、定义在R 上的偶函数f(x)在[0，＋∞)上是增函数，且f()＝0，那么不等式18f (log )0x >的解集是 ( )A. (0，)B. (2，＋∞)C. (0，)∪(2，＋∞)D. (，1)∪(2，＋∞)3、假设且,那么在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限4、α为锐角，且sinα＝45，那么cos(π＋α)＝( ) A. －35 B. 35 C. －45 D. 45 5、如图,2弧度的圆心角所对的弦长为2,这个圆心角所对应的扇形面积是( )A. B. C. D.6.()00-sin 25,cos 25αα设角终边上一点，则的一个可能值为（ ）A. 065B. -065C. 0115D. 0155 7.y sin(2)x θθπθ=+∈已知函数为偶函数，【0，】，则为（ ） A. 2π B. 3π C. 4π D. π8.a=cos2, b=cos3,c=cos4,以下四个选项正确的选项是〔 〕A.a>c>bB. b>c>aC. b>c>aD. c>a>b 9.4sin cos =3ααα+若是三角形的内角，且，则这个三角形是（ ）10. 223,x x +-已知函数f(x)=log 则函数y=f(x)的零点所在区间为（ ） A. (0,1) B. (1,2) C. (2,3) D. (3,4)11、以下各对角中，终边一样的角是〔 〕A. B. C. D.12、函数的图象大致为〔 〕A. B.C. D.13、函数()2110sin 10sin 2f x x x =---， ,2x m π⎡⎤∈-⎢⎥⎣⎦的值域为1,22⎡⎤-⎢⎥⎣⎦，那么实数m 的取值范围是〔 〕A. ,03π⎡⎤-⎢⎥⎣⎦B. ,06π⎡⎤-⎢⎥⎣⎦C. ,36ππ⎡⎤-⎢⎥⎣⎦D. ,63ππ⎡⎤-⎢⎥⎣⎦14. 0001cos(75),sin(15)cos -3βββ+=-+已知则（105）的值是（ ）A. 13B. 23C. 13 -D. 23- 评卷人得分 二、填空题〔每一小题4分一共24分〕1717cos()sin()44ππ---的值_________16、是定义在上奇函数，当时，，那么_________． 17、x 满足13-sinx 22≤≤，那么角x 的取值范围为_______________________. 18、函数的单调增区间是_______________________．19、|cos θ|≤|sin θ|，]02θπ⎡∈⎣，，那么θ的取值范围为__________．． 20.11cos 6m 136x m ππ⎛⎤=+⎥⎝⎦若方程在区间，上只有一个解，则实数的取值范围 __________________评卷人得分 三、解答题21、〔10分〕〔1〕假设5sin 13α=-，求tan α的值． 〔2〕tan 2x =，求4sin 2cos 3sin 5cos x x x x -+的值．22.〔12分〕()=sin(2)35-,66[0,]f x x ππππ+⎡⎤⎢⎥⎣⎦已知函数，（1）利用五点法作出函数在区间上的图像。

2015-2016学年度巴楚二中学校12月高一月考卷（数学）问卷考试时间：120分钟第I 卷（选择题一、选择题1．已知集合}0)3)(1(|{<--=x x xA ，}42|{<<=x xB ，则=B A （A ）}32|{<<x x （B ）}31|{<<x x（C ）}43|{<<x x （D ）}41|{<<x x2．若函数()y f x =的定义域是[0,2]，则函数)12(-=x f y 的定义域是（ ） A ．[0,1] B ．[0,2] C ．⎥⎦⎤⎢⎣⎡2321， D ．[]3,1-3．下列函数定义域是R 且在区间()0,1是递增函数的（ ） A ．|1|y x =+ B ．y =．1y x=D ．24y x =-+ 4．已知函数⎩⎨⎧≤>=0,20,log )(3x x x x f x，则91((f f =（ ）. A ．12 B ．14 C ．16 D．185．已知幂函数()yf x =的图像经过点)41,2(，则它的单调增区间为A ．),0(+∞B ．[)+∞,0 C ．)0,(-∞ D ．),(+∞-∞ 6．函数()2xf x e x =+-的零点所在的一个区间是（ ）（A ）()-2,-1 （B ）()-1,0 （C ）()0,1 （D ）()1,2 7． 将分针拨快10分钟，则分针转过的弧度数是（ ） A ．3π B ．3π- C ．6π D ．6π- 8．角α的终边过点(1,2)P -，则sin α等于（ ）A ．． 9．若sin =α-135，且α的第四象限角，则tan α=（ ） A ．12 B ．-12 C ．5 D ．-510．函数()lg(1)f x x =-+ ） A ．(1,3) B ． [1,3] C ．(1,3] D ． [1,3) 11．计算sin 77cos 47sin13cos 43-的值等于（ ）A ．12 B C (二班选作)为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象，只需把函数sin 2y x =的图象（ ）A ．向左平移3π个单位长度 B ．向右平移3π个单位长度C ．向左平移6π个单位长度D ．向右平移6π个单位长度12．sin 1212ππ-的值为（ ） A ．0 B ．2- C ．2 D ．2(二班选作)函数f （x ）＝2sin （ωx ＋φ）（ω>0，－<φ<）的部分图象如图所示，则这个函数的周期和初相分别是（ ） A ．2，－ B ．2，－ C ．，－D ．，－第II 卷（非选择题）二、填空题13．已知2(1)f x x -=，则 ()f x = ． 14．方程21124x -=的解x = ． 15．已知函数y ＝f(x)的图像是连续不间断的曲线，且有如下的对应值：则函数y ＝f(x)在区间[1,6]上的零点至少有________个． 16．（二班选作）将函数()2sin 2f x x =的图象上每一点向右平移6π个单位，得函数()y g x =的图象，则()g x = ．若3sin()25πα+=，则cos 2α= ． 三、解答题写出必要的文字说明或解题过程，否则不予给分 17．（本小题满分10分）角α的终边上有一点P （m ，5），且cos α=m13（m ≠0）,求sin α+cos α的值．18．（本题共12分）（1）计算323log 39)641(5932log 4log 55---+-（2）解方程：3)96(log 3=-x19．（12分）已知32121=+-a a ．求下列各式的值（1）1a a +（2）22a a -+20．（12分）求函数[)246(15)y x x x =-+∈，的值域。