64基和维数(二)
- 格式:ppt
- 大小:383.50 KB
- 文档页数:22


线性空间基和维数的求法方法一 根据线性空间基和维数的定义求空间的基和维数,即:在线性空间V 中,如果有n 个向量n αα,,1 满足:(1)n ααα,2,1 线性无关。
(2)V 中任一向量α总可以由n ααα,,21, 线性表示。
那么称V 为n 维(有限维)线性空间,n 为V 的维数,记为dim v n =,并称n ααα,,2,1 为线性空间V 的一组基。
如果在V 中可以找到任意多个线性无关的向量,那么就成V 为无限维的。
例1 设{}0V X AX ==,A 为数域P 上m n ⨯矩阵,X 为数域P 上n 维向量,求V 的维数和一组基。
解 设矩阵A 的秩为r ,则齐次线性方程组0AX =的任一基础解系都是V 的基,且V 的维数为n r -。
例2 数域P 上全体形如0a a b ⎛⎫⎪-⎝⎭的二阶方阵,对矩阵的加法及数与矩阵的乘法所组成的线性空间,求此空间的维数和一组基。
解 易证0100,1001⎛⎫⎛⎫⎪ ⎪-⎝⎭⎝⎭为线性空间0,a V a b p a b ⎧⎫⎛⎫=∈⎨⎬ ⎪-⎝⎭⎩⎭|的一组线性无关的向量组,且对V 中任一元素0a a b ⎛⎫ ⎪-⎝⎭有00100+1001a a b a b ⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 按定义0100,1001⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭为V 的一组基,V 的维数为2。
方法二 在已知线性空间的维数为n 时,任意n 个向量组成的线性无关向量组均作成线性空间的基。
例3 假定[]n R x 是一切次数小于n 的实系数多项式添上零多项式所形成的线性空间,证明:()()()211,1,1,,1n x x x ----构成[]n R x 的基。
证明 考察()()1121110n n k k x k x -⋅+-++-=由1n x-的系数为0得0n k =,并代入上式可得2n x -的系数10n k -=依此类推便有110n n k k k -====,故()()11,1,,1n x x ---线性无关又[]nR x 的维数为n ,于是()()11,1,,1n x x ---为[]nR x 的基。


基与维数的几种求法线性空间基和维数的求法方法一根据线性空间基和维数的定义求空间的基和维数,即:在线性空间v中,如果有n个向量α1,,αn满足用户:(1)α1,α2,αn线性无关。
(2)v中任一向量α总可以由α1,α2,,αn线性则表示。
那么称v为n维(有限维)线性空间,n为v的维数,记为dimv=n,并称α1,α2,,αn为线性空间v的一组基为。
如果在v中可以找到任意多个线性无关的向量,那么就成v为无限维的。
基准1设v=xax=0,a为数域p上m⨯n矩阵,x为数域p上n佩向量,谋v的维数和一组基为。
解设矩阵a的秩为r,则齐次线性方程组ax=0的任一基础解系都是v的基,且v的维数为n-r。
基准2数域p上全体形似对矩阵的乘法及数与矩阵的乘法所共同组成⎪的二阶方阵,-ab⎪⎪的线性空间,谋此空间的维数和一组基为。
⎪⎪0a⎪⎪⎪01⎪⎪00⎪为线性空间,v=|a,b∈p⎪⎪的一组线性毫无关系的向⎪⎪⎪⎪-10⎪⎪01⎪⎪⎪-ab⎪⎪⎪0a⎪⎪0a⎪⎪01⎪⎪00⎪量组,且对v中任一元素⎪=a⎪+b⎪⎪有ab1001-ab⎪⎪⎪⎪⎪⎪⎪⎪⎪01⎪⎪00⎪⎪,⎪为v的一组基为,v的维数为2。
⎪10⎪⎪01⎪方法二在已知线性空间的维数为n时,任意n个向量组成的线性无关向量组均作成线性空间的基。
基准3假设r[x]n就是一切次数大于n的实系数多项式迎上零多项式所构成的线性空间,证明:1,(x-1),(x-1),,(x-1)构成r[x]n的基。
证明实地考察k1⋅1+k2(x-1)++kn(x-1)的系数为0得kn=0,并代入上式可得xn-2的系数kn-1=0依此类推便存有kn=kn-1==k1=0,故1,(x-1),,(x-1)又r[x]的维数为n,于是1,(x-1),,(x-1)为r[x]的基。
方法三利用定理:数域p上两个非常有限佩线性空间同构的充份必要条件就是它们存有相同的维数。
例4设a=⎪,证明:由实数域上的矩阵a的全体实系数多项式f(a)共同组成的空间v=⎪f(a)|a=⎪⎪⎪0-1⎪⎪⎪⎪与复数域c作为实数域r上的线性空间10⎪⎪⎪v'={a+bi|a,b∈r}同构,并非谋它们的维数。
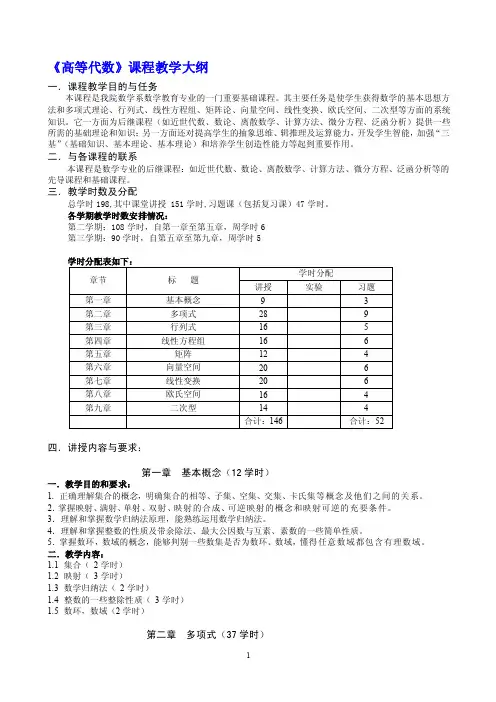
《高等代数》课程教学大纲一.课程教学目的与任务本课程是我院数学系数学教育专业的一门重要基础课程。
其主要任务是使学生获得数学的基本思想方法和多项式理论、行列式、线性方程组、矩阵论、向量空间、线性变换、欧氏空间、二次型等方面的系统知识。
它一方面为后继课程(如近世代数、数论、离散数学、计算方法、微分方程、泛函分析)提供一些所需的基础理论和知识;另一方面还对提高学生的抽象思维、辑推理及运算能力,开发学生智能,加强“三基”(基础知识、基本理论、基本理论)和培养学生创造性能力等起到重要作用。
二.与各课程的联系本课程是数学专业的后继课程:如近世代数、数论、离散数学、计算方法、微分方程、泛函分析等的先导课程和基础课程。
三.教学时数及分配总学时198,其中课堂讲授 151学时,习题课(包括复习课)47学时。
各学期教学时数安排情况:第二学期:108学时,自第一章至第五章,周学时6第三学期:90学时,自第五章至第九章,周学时5四.讲授内容与要求:第一章基本概念(12学时)一.教学目的和要求:1. 正确理解集合的概念,明确集合的相等、子集、空集、交集、卡氏集等概念及他们之间的关系。
2.掌握映射、满射、单射、双射、映射的合成、可逆映射的概念和映射可逆的充要条件。
3.理解和掌握数学归纳法原理,能熟练运用数学归纳法。
4.理解和掌握整数的性质及带余除法、最大公因数与互素、素数的一些简单性质。
5.掌握数环,数域的概念,能够判别一些数集是否为数环、数域,懂得任意数域都包含有理数域。
二.教学内容:1.1 集合(2学时)1.2 映射(3学时)1.3 数学归纳法(2学时)1.4 整数的一些整除性质(3学时)1.5 数环,数域(2学时)第二章多项式(37学时)一.教学目的和要求:1.掌握数域上一元多项式的概念、运算以及多项式的和与积的次数。
2.正确理解多项式的整除概念和性质。
理解和掌握带余除法。
3.掌握最大公因式的概念、性质、求法以及多项式互素的概念和性质4.理解不可约多项式的概念,掌握多项式唯一因式分解定理。

基和维数的关系
基和维数是线性代数中的两个重要概念,它们之间有着密切的关系。
在矩阵论中,基的数量决定了矩阵的列空间的维数,也就是列向量的线性独立的数量。
因此,如果一个矩阵的列向量数量为 n,但其列向量中有重复的向量,那么矩阵的列空间的维数就会小于 n。
这时,我们需要找到一组线性无关的向量作为基,从而得到列空间的基和维数。
另一方面,矩阵的行空间的维数也和其基的数量有关系。
矩阵的行空间是由其行向量张成的向量空间,而行向量的数量和它们的线性独立的数量相同。
因此,矩阵的行空间的维数取决于它的行向量的线性独立的数量,也就是它的基的数量。
除了列空间和行空间,矩阵还有一个重要的概念——零空间。
零空间是由矩阵的所有零空间向量张成的向量空间。
零空间向量是指矩阵乘以该向量得到的结果为零向量的向量。
矩阵的零空间的维数也和其基的数量有关系。
根据线性代数的基本定理,矩阵的列空间和零空间的维数之和等于矩阵的列数。
因此,如果知道了矩阵的列空间的维数,就可以求得它的零空间的维数。
总之,基和维数在线性代数中起着至关重要的作用。
它们的关系非常紧密,互相影响。
通过矩阵的基和维数,我们可以更好地理解矩阵的性质和特征。




基与维数的基本概念与应用线性代数是现代数学中非常重要的一部分,而作为线性代数的基本概念之一,基与维数在很多领域中都有着重要的应用和作用。
在本文中,我们将着眼于基与维数的基本概念和应用,希望能够给读者带来全面且深入的了解。
基的概念基是线性空间的一个基本概念。
在线性代数中,所谓线性空间就是一个向量空间的特殊情形,向量空间由向量组成,这些向量可以用数字来表示。
而基就是指这些向量的数量最少的子集,这个子集中的向量可以表示出这个向量空间中的其他所有向量。
具体来说,基的定义是:如果一个向量空间V中的向量集S有以下两个性质:1. 向量集S中的向量是线性无关的;2. 向量集S中的任意向量都可以用向量集S中的有限个向量线性组合表示(即,对于任意一个向量v∈V,都存在一组系数a1,a2,……,an使得v=a1s1+a2s2+……+ansn,其中si∈S,ai∈K,K是所在域)那么,S就是V的一个基。
基的一些性质包括:1. 基是线性无关的。
2. 基中的任意向量都不可由其他向量线性组合得到。
3. 维数相同的向量空间会有同样数量的基。
4. 所有向量空间都有基,包括零向量空间。
维数的概念维数是向量空间的另一个重要概念。
在数学中,向量空间的维数是指基中向量的数量的大小。
具体来说,如果一个向量空间V有一个n个线性无关向量的基,那么V就称为一个n维向量空间。
维数可以理解为空间中向量的独立自由度,向量空间的维数可以用来区分不同的向量空间,也用来确定矩阵的秩等重要性质。
基的应用基作为线性代数中的基本概念,应用十分广泛。
以下列举了一些基的应用:1. 矩阵乘法:矩阵乘法的前提是两个矩阵的行列数满足要求。
具体来说,矩阵A的列数必须等于矩阵B的行数。
而每一个矩阵可以看做是向量空间中向量的组合,因而矩阵的乘法实际上就是向量之间的线性组合,而基恰好是向量的组合表示。
2. 解方程组:在线性代数中,矩阵可以看做是线性方程组的系数,而矩阵的秩和向量空间的维数有密切关系。

以下是求基和维数的典型题目:1.设V是数域F上的线性空间,α1, α2, ..., αs是V中的一组向量,β是V中的一个向量。
证明:如果α1, α2, ..., αs线性无关,且α1, α2, ...,αs, β线性相关,那么β可以由α1, α2, ..., αs线性表示。
2.设A是n阶方阵,证明:R(A) + N(A) = n,其中R(A)表示A的秩,N(A)表示A的零空间的维数。
3.设V是数域F上的n维线性空间,α1, α2, ..., αn是V的一组基,A是V上的一个线性变换。
证明:如果A在基α1, α2, ..., αn下的矩阵是A,那么A的值域R(A)的维数等于A的秩r(A)。
4.设V是数域F上的n维线性空间,α1, α2, ..., αs是V中的一组线性无关的向量。
证明:存在V中的一组基β1, β2, ..., βn,使得α1, α2, ...,αs可以由β1, β2, ..., βs线性表示。
5.设V是数域F上的n维线性空间,证明:V中任意n个线性无关的向量都可以作为V的一组基。
6.设V和W是数域F上的两个有限维线性空间,T是从V到W的一个线性映射。
证明:如果T是单射,那么dim V ≤ dim W。
7.设V是数域F上的n维线性空间,W是V的一个子空间,α1, α2, ..., αm是W中的一组基。
证明:存在V中的一组基β1, β2, ..., βn,使得β1, β2, ..., βm是W中的一组基。
8.设V是数域F上的n维线性空间,证明:V中的任意一个向量都可以表示为V的一组基的线性组合,且这种表示方式是唯一的。
9.设V和W是数域F上的两个有限维线性空间,T是从V到W的一个线性映射。
证明:R(T) + N(T) = dim V,其中R(T)表示T的值域的维数,N(T)表示T的核的维数。
10.设A是一个n阶矩阵,证明:矩阵A的秩r(A)加上矩阵A的零空间的维数n - r(A)等于n。
《高等代数》课程教学总体安排一、课程名称:高等代数二、课程性质与类型:专业必修课,理论课三、课程总学时及学分:150学时,学分四、教学目的与要求:教学目的:高等代数是数学与应用数学专业必修基础课,也是一门重要主干课程,是中学代数的提高,也是近代数学的基础。
通过本课程的教学,使学生掌握高等代数的基本知识,基本方法,基本思路,适当地了解代数的一些历史,一些背景,以加深对中学数学的理解,获得独立分析和解决有关的理论和实际问题的能力,并为进一步学习其他后继课程:近世代数、微分方程、泛函分析等,以及将来从事教学,科研及其他实际工作打下基础。
教学基本要求:基本掌握全书的基本概念;能独立处理书后的绝大部分习题;通过本书抽象理论的学习,提高自学能力,数学思维,专业素质,以便阅读较深的文献。
五、教材及参考书目教材:张禾瑞,郝炳新著,高等代数,高等教育出版社,2007年6月第四版,ISBN:7-04-021465-9,主要参考书:[1] 北京大学数学系,高等代数,高等教育出版社,2003年7月第三版ISBN:7-04-011915-3[2] 李师正等编,高等代数解题方法与技巧,高等教育出版社,2004 年2月版ISBN:7-04-012942-6[3] 徐仲,陆全,张凯院,高等代数考研教案,西北工业大学出版社,2006年6月出版,ISBN:7-5612-2088-X六、考核方式及成绩计算方法期末进行闭卷考试,综合平时学习态度、课堂表现、平时作业确定学生学习成绩。
具体计算方法为:学科成绩=期末考试成绩×90%+平时成绩×10%七、课程教学日历第一章基本概念教学安排说明章节题目:§1.5数环数域学时分配:2学时。
教学时数为2学时本章教学目的与要求:掌握数环和数域概念,判别方法,理解有理数域的最小性。
其它:本章以自学为主,只讲授第五节课堂教学方案§1.5数环数域课程名称:§1.5数环数域授课时数:2学时授课类型:理论课教学方法与手段:讲授法教学目的与要求:掌握数环和数域概念,判别方法,理解有理数域的最小性。
线性空间的基与维数线性空间是线性代数中的重要概念,它在数学和应用领域中都有广泛的应用。
本文将探讨线性空间的基与维数,以及它们在线性代数中的意义和应用。
一、线性空间的概念与性质线性空间是指一个具备了加法运算和数乘运算的集合,且满足以下性质:1. 封闭性:对于任意向量组成的集合S,如果对于任意向量a,b∈S和任意标量c∈F(其中F表示该线性空间定义域内的域),都有a + b和c·a仍然属于S,则称S是该线性空间的一个子空间;2. 零向量:对于线性空间V,存在一个特殊的向量0,使得对于任意向量v∈V,有v + 0 = v;3. 加法逆元:对于线性空间V中的任意向量v,存在一个逆元向量−v,使得v + (−v) = 0;4. 结合律和分配律:对于线性空间V中的任意向量a,b和c,有(a + b) + c = a + (b + c)和c(a + b) = ca + cb。
二、线性空间的基在线性空间V中,如果存在一组向量{v1, v2, ..., vn},满足:1. 这组向量线性无关;2. 任意向量v∈V都可以由这组向量线性表示。
那么,这组向量{v1, v2, ..., vn}被称为线性空间V的一个基。
基是线性空间中最重要的概念之一,它可以用来表示线性空间中的任意向量。
三、线性空间的维数线性空间的维数是指该线性空间的基所包含的向量个数。
记线性空间V的维数为dim(V),则对于线性空间V的任意基,它所包含的向量个数都相同,即dim(V)是唯一确定的。
维数的概念在线性代数中具有重要的意义。
它可以用来衡量线性空间的大小以及其所能表示的向量的种类。
维数为1的线性空间只包含一个向量,而维数为n的线性空间可以表示任意n维向量。
四、线性空间的维数与基的关系线性空间的维数与其基是密切相关的。
根据线性代数的基本定理,任意线性空间中的所有基都包含相同数量的向量,即具有相同的维数。
设线性空间V的维数为n,则任意一个基包含n个线性无关的向量。
例1数域P 上全体形解易证I a.bep\P 1、 (J 0, AO+h 为V 的一组基,V线性空间基和维数的求法 (邓云斯、李秀珍、高华艳)方法一(定义法):根据线性空间基和维数的走义求空间的基和维数,即:在线性空间V 中,如 果有〃个向呈满足:⑴ms …,弘线性无关;(2)V 中任一向星a 总可以由 6,氏2,.久线性表示.那么称V 为n 维(有限维践性空间,"为V 的维数,记为dim v = n , 并称 qar :%为线性空间V 的一组基•如果在V 中可以找到任意多个线性无关的向呈,那么V 就成为无限维的.的二阶方阵,对矩阵的加法及数与矩阵的乘法所组成的线性空间r 求此空间的维数和一组基.方法二(维数确定基法):在已知线性空间的维数为〃时,任意〃个向呈组成的线性无关向呈组 均作成线性空间的基.例2假走/?[•{]”是一切次数小于〃的实系数多项式添上零多项式所形成的线性空间,证明: l,(x —l ),(x —1)2,…,(x —1)' I 构成/?[虬的基.证明何•1 +他(牙一1) +・・・+兌(尤一1)"“ =0 由疋"的系数为0得心=0 ,并代入上式可得疋J 的系数k n _{ = 0 依此类推便有k“=kz=・.・ = k\=0 , 故1,(—1),…,(―1厂线性无关组,且对V 中任一元素 0 b '0 1 、一 1 0按定义 r0>又川虬的维数为心于是1心一1),…心一1)2为乩吐的基方法三(利用同构求维数法):数域P上两个有限维线性空间同构的充分必要条件是它们有相同的维数.(0 _1\例3设人= ,证明:由实数域上的矩阵A的全体实系数多项式/(A)组成的空间11 °丿f fo -1YV=y(A)\A=(与复数域C作为实数域/?上的线性空间I I】。
/V = {a+bi\ a.b w R}同构,并求它们的维数.证明V中任一多项式可记为f(A)=aE+bA,(abwR),建立V到V的如下映射b:e =a A +Z?J—> /;(4) = «]£+/?[A wR)易证CT是/到V上既是单射又是满射即一一映射.再设弘=心+加,a^b. eR.K eR,则有■■■厶■b(y + a2) =+«2)4-(/?1+优"]=(® +a1)E+(b x 4-Z?2)A = <7(a1) + o-(6Z2)<T( toj) = b( ka、+ kbj) = ka{E+ka y A = kb(xj故cr是/到'/的同构映射,所以V到V同构另外,易证H的一个基为1 , / ,故dimV =2vV^V.•.dimV = 2方法四(求可逆矩阵确走基法):设冬,勺,匕与卩、、・•••、卩“是"维线性空间V中两组向星,已知0],02,・-,0”可由少心,…“线性表出:A =如匕+佝勺+- + %心Pl =叱|+eg+••• + %"5令人=«21 如…d\Cl nl Cl n2 …a nn 7如果^,色,…,%为V 的一组基,另吆当且仅当A 可逆时,卩\、卩J …、卩"也是u 的一组基. 例4已知1,圮疋,_?是卩[虬的一组基,证明1,1 +兀(1 +龙)2,(1+刃'也是“[虬的一组基・ 证明因为l = ll + 0x+0x 2+0-x 3l + x = 1-1 + 1-x+O-x 2+0-x 3(l + x)~ = 1-1 + 2-x+l-x 2+0x 3(1 + X)3= 1 • 1 + 3 • A + 3 • x 2+1 • X 311110 0 0 1所以1,1 + X, (1 + ,(1 +町"也为P [x]4的一组基.方法五(向呈等价求基法):如果空间y 中一向量组与V 中一组基等价,则此向量组一走为此 空间的一组基.例5设/?卜】2表示次数不超过2的一切实系数一元多项式添上零多项式所构成的线性空间 的一组基,证明x 2+ x,疋一圮% +1为这空间的一组基. 证明 k } (x 2+x)+k 2 (x 2一/)+他(兀+1) = 0 则 k l +k 2=0< « _ 他 + £3 = o&3=0解得他=鸟2=/=0于是V 2+ X, * - X, X + 1线性无关,它们皆可由%2, X, 1线性表示,因此A-2+ X, F - X, X+ 1与 x\x,\等价,从而R[X ]2中任意多项式皆可由x 2+x t x 2-x,x+\线性表示,故X2 + X,x2 -x,x + l 为[x],的基.方法六(求两个子空间交集的基确走维数法):对以一组向量a\、j、卩、、P"为列向呈做成的矩阵施行行初等变换和列初等变换,不改变矩阵卬,色,0,02间的线性关系•任何一个m x H(j B、矩阵A ,总可以通过行初等变换和列变换化为标准阶梯型矩阵:' ,其中表示邛介I。