切线长定理与三角形内切圆

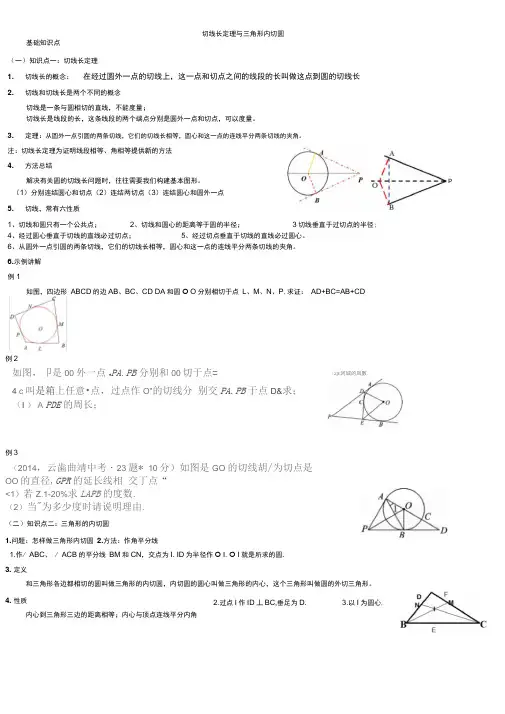
基础知识点（一）知识点一：切线长定理1.切线长的概念： 在经过圆外一点的切线上，这一点和切点之间的线段的长叫做这点到圆的切线长 2. 切线和切线长是两个不同的概念切线是一条与圆相切的直线，不能度量；切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。

3. 定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

注：切线长定理为证明线段相等、角相等提供新的方法4. 方法总结解决有关圆的切线长问题时，往往需要我们构建基本图形。

（1）分别连结圆心和切点（2）连结两切点（3）连结圆心和圆外一点5. 切线，常有六性质1、切线和圆只有一个公共点；2、切线和圆心的距离等于圆的半径； 3切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点； 5、经过切点垂直于切线的直线必过圆心。

6、从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

6.示例讲解例1如图，四边形 ABCD 的边AB 、BC 、CD DA 和圆O O 分别相切于点 L 、M 、N 、P ,求证： AD+BC=AB+CD 例2如图，卩是00外一点t PA.PB 分别和00切于点=4 c 叫是箱上任意•点，过点作O"的切线分 别交PA.PB 于点D&求；（I ） A PDE 的周长；例3（2014，云歯曲靖中考・23题* 10分）如图是GO 的切线胡/为切点是OO 的直径,GPR 的延长线相 交丁点“<1）若Z.1-20%求LAPB 的度数.（2）当"为多少度时请说明理由.（二）知识点二：三角形的内切圆1.问题：怎样做三角形内切圆2.方法：作角平分线1.作/ ABC 、 / ACB 的平分线 BM 和CN ，交点为I. ID 为半径作O I. O I 就是所求的圆.3. 定义和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。

切线长定理及三角形的内切圆一知识讲解〈基础）【学习目标】l.了解切线长定义：理解三角形的内切圆及内心的定义：2.掌握切线长定理：利用切线长定理解决相关的计算和证明．【要点梳理】要点一、切线长定理1.切线长：经过圆外一点能够作圆的两条切线，切线上这一点到切点间的线段长叫做这点到圆的切线长．要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称．切线是直线，而非线段．2.切线长定理z从圆外一点作圆的两条切线，两切线长相等，圆心与这一点的连线平分两条切线的夹角．要点诠释：切线长定理包含两个结论：线段相等和角相等．要点二、三角形的内切圆1.三角形的内切圆z与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫作圆的外切三角形．三角形的内心到三角形的三边距离相等．2.三角形的内心z三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心．三角形的内心是这个三角形的三条角平分线的交点．要点诠释z(1）任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形：(2）解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积户即S=;Pr (S 7'J 三角形的面积P为三角形的周长r为内切圆阳）(3）三角形的外心与内心的区别：名称｜确定方法｜图形｜性质外心（三角形｜三角形三边中垂线的外接圆的圆｜交点心）AB(1)OA=OB=OC: (2）外心不一定在三角形内部内心（三角形三角形三条角平分线内切圆的圆的交点心）【典型例题】类型一、切线长定理B c(1)到三角形三边距离相等：(2) O A、OB、oc分别平分L'.'.BAC、ζABC、丘ACB:(3）内心在三角形内部．。

1.(2叫湛江校级脚己知PA,PB :5t别切。

于A、B E为劣弧础上一点过E,#,1¥Ji;JJ�交PA于C、交PB于D.(1）若PA吨，求6PCD的周长．(2）若ζP=50°求ζDOC.p【答案与解析】解：(1）连接OE,..PA、PB与圆0相切，:.PA=PB=6,同理可得：AC=CE,BD=DE,6PCD的周长＝PC+PD+CD=PC+PD+CE+DE=PA+PB=12: (2）γPA PB与圆O相切，二ζOAP＝ζOBP=90。

【学习目标】1. 知识技能(1)理解圆的切线的有关性质并能灵活运用.(2)理解切线长及切线长定理.(3)体验并理解三角形内切圆的性质.2. 解决问题通过例题的教学, 培养学生解决实际问题的能力和应用数学的意识．3. 数学思考(1)通过动手操作、合作交流, 经历圆的切线的性质定理的产生过程.(2)体验切线长定理, 并能正确、灵活地运用.(3)通过作图操作, 经历三角形内切圆的产生过程．4. 情感态度通过动手操作, 反复尝试, 合作交流, 培养探索精神和合作意识．【学习重难点】1. 重点: (1)切线的性质定理、切线长定理.(2)三角形的内切圆.2. 难点：切线性质的灵活运用.课前延伸切线的判定方法:(1)和圆________公共点的直线是圆的切线.(2)和圆心距离等于________的直线是圆的切线.(3)经过________且________的直线是圆的切线.课内探究一、课内探究:1. 如图27－2－131, AB为⊙O的直径, C为⊙O上一点, AD和过点C的切线互相垂直,垂足为D.求证: AC平分∠DAB.2．如图27－2－132, △ABC的内切圆⊙O与BC, CA, AB分别相切于点D, E, F, 且AB ＝9 cm, BC＝14 cm, CA＝13 cm, 求AF、BD、CE的长．图27－2－131图27－2－132 图27－2－1333. 如图27－2－133所示, △ABC的内心为I, ∠A＝50°, O为△ABC的外心, 求∠BOC 和∠BIC的度数.二、课堂反馈训练1. 如图27－2－134, PA切⊙O于点A, 该圆的半径为3, PO＝5, 则PA的长等于________.2．如图27－2－135, ⊙O的半径为5, PA切⊙O于点A, ∠APO＝30°, 则切线长PA为________．(结果保留根号)图27－2－134图27－2－135 图27－2－1363．如图27－2－136所示, PA, PB, DE分别切⊙O于点A, B, C, 如果PA＝8 cm, 求△PDE的周长．。

切线长定理和三角形的内切圆切线长定理和三角形的内切圆，这俩玩意儿看上去有点高深莫测，但其实嘛，真没那么复杂，大家来轻松聊聊。

想象一下，你在一个阳光明媚的下午，跟朋友们一起聚会，话题从生活琐事聊到数学，大家哈哈大笑，结果你一不小心提到了这两样东西。

你朋友们肯定会瞪大眼睛，疑惑地问：“这是什么鬼？”别急，让我来给你解解惑。

切线长定理就像是数学界的小秘密。

啥意思呢？就是在一个圆外，如果你画一条切线，这条线跟圆的交点只有一个，那就有点意思了。

这条切线的长度与从圆心到切线的距离有关。

大家可能会想，听起来好像没啥用。

切线长定理就像生活中的一条真理，适用性非常广。

举个例子，如果你想用一根绳子围住一个圆，绳子长短跟你离这个圆的远近有直接关系。

这种简单的道理其实在很多地方都能找到，比如你在超市排队，越靠近收银台，越容易看到商品，哈哈，明白了吗？说到内切圆，它就像是三角形里的小秘密武器。

内切圆的意思就是一个圆，它刚好能碰到三角形的三条边。

听上去是不是很神奇？这就好比你想象一下，一个小朋友在玩捉迷藏，躲在一个房间的正，四周都有墙壁，但它总能找到一个最舒服的位置，这就是内切圆的感觉。

三角形的每一条边都可以算得上是“朋友”，而这个内切圆就像是它们的聚会地点。

更妙的是，内切圆的半径跟三角形的面积和周长有着密不可分的关系。

这就像是你在聚会中，跟朋友们聊得开心的同时，气氛越好，大家就越会聚在一起，形成一种共鸣。

再说切线长定理和内切圆的关系。

这俩玩意儿就像是一对黄金搭档。

在三角形里，如果我们在三角形的每一边画切线，切线的长度与内切圆的半径又有妙不可言的联系。

简而言之，切线的长度告诉你这个圆有多大，而内切圆又是三角形的灵魂。

大家可以想象，内切圆就像是三角形的情感核心，而切线则是把这情感包围起来的纽带。

它们互相依存，缺一不可。

我们可以通过简单的图形来理解这一切。

想象一下，一个大三角形，中间有一个小圆，圆正好包裹住三角形的每一条边。

你站在三角形的某个顶点，伸出手，发现能碰到内切圆的点。

切线长定理及三角形的内切圆—知识讲解（提高）责编：常春芳【学习目标】1.了解切线长定义；理解三角形的内切圆及内心的定义；2.掌握切线长定理；利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线长定理1．切线长：经过圆外一点能够作圆的两条切线，切线上这一点到切点间的线段长叫做这点到圆的切线长.要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段. 2．切线长定理：从圆外一点作圆的两条切线，两切线长相等，圆心与这一点的连线平分两条切线的夹角.要点诠释：切线长定理包含两个结论：线段相等和角相等.要点二、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫作圆的外切三角形.三角形的内心到三角形的三边距离相等.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心是这个三角形的三条角平分线的交点.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).名称确定方法图形性质外心(三角形外接圆的圆心) 三角形三边中垂线的交点(1)OA=OB=OC；(2)外心不一定在三角形内部内心(三角形内切圆的圆心) 三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB；(3)内心在三角形内部.【典型例题】类型一、切线长定理1.（2015•常德）已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为3，∠EAC=60°，求AD的长．【答案与解析】证明：（1）如图1，连接FO，∵F为BC的中点，AO=CO，∴OF∥AB，∵AC是⊙O的直径，∴CE⊥AE，∵OF∥AB，∴OF⊥CE，∴OF所在直线垂直平分CE，∴FC=FE，OE=OC，∴∠FEC=∠FCE，∠0EC=∠0CE，∵∠ACB=90°，即：∠0CE+∠FCE=90°，∴∠0EC+∠FEC=90°，即：∠FEO=90°，∴FE为⊙O的切线；（2）如图2，∵⊙O的半径为3，∴AO=CO=EO=3，∵∠EAC=60°，OA=OE，∴∠EOA=60°，∴∠COD=∠EOA=60°，∵在Rt△OCD中，∠COD=60°，OC=3，∴CD=，∵在Rt△ACD中，∠ACD=90°，CD=，AC=6，∴AD=．【总结升华】本题是一道综合性很强的习题，考查了切线的判定和性质，三角形的中位线的性质，勾股定理，线段垂直平分线的性质等，熟练掌握定理是解题的关键．举一反三：【变式】已知：如图，在梯形 ABCD中，AB∥DC，∠B=90°，AD=AB+DC，AD是⊙O的直径．求证：BC和⊙O相切．【答案】作OE⊥BC，垂足为E，∵ AB∥DC，∠B=90°，∴ OE∥AB∥DC，∵ OA=OD，∴ EB=EC，∴ BC是⊙O的切线．2.已知：如图，AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD，求证：DC是⊙O的切线．【答案与解析】解：连接OD．∵ OA=OD，、∴∠1=∠2．∵ AD∥OC，∴∠1=∠3，∠2=∠4．∴∠3=∠4．又∵ OB=OD，OC=OC，∴△OBC≌△ODC．∴∠OBC=∠ODC．∵BC是⊙O的切线，∴∠OBC=90°，∴∠ODC=90°，∴ DC是⊙O的切线．【总结升华】因为AB是直径，BC切⊙O于B，所以BC⊥AB．要证明DC是⊙O的切线，而DC和⊙O有公共点D，所以可连接OD，只要证明DC⊥OD．也就是只要证明∠ODC=∠OBC.而这两个角分别是△ODC和△OBC的内角，所以只要证△ODC≌△OBC．这是不难证明的．举一反三：【变式】已知：∠MAN=30°，O 为边AN 上一点，以O 为圆心、2为半径作⊙O ，交AN 于D 、E 两点，设AD=x ，⑴如图⑴当x 取何值时，⊙O 与AM 相切；⑵如图⑵当x 为何值时，⊙O 与AM 相交于B 、C 两点，且∠BOC=90°．【答案】解：（1）设AM 与⊙O 相切于点B ，连接OB ，则OB ⊥AB ；在Rt △AOB 中，∠A=30°， 则AO=2OB=4， ∴ AD=AO-OD ， 即AD=2．x=AD=2. （2）过O 点作OG⊥AM 于G∵OB=OC=2，∠BOC=90°，∴BC=22 ∵OG⊥BC，2，2，在Rt △OAG 中，∠A=30°∴OA=2OG=22，MNEDO图（1）．MANEDBCO图（2）∴x=AD=22－23.（2014•高港区二模）矩形ABCD中，AB=4，AD=3，以AB为直径在矩形内作半圆．DE切⊙O于点E（如图），则tan∠CDF的值为（）A．B．C．D．【答案】B；【解析】解：如图，设FC=x，AB的中点为O，连接DO、OE．∵AD、DE都是⊙O的切线，∴DA=DE=3．又∵EF、FB都是⊙O的切线，∴EF=FB=3﹣x．∴在Rt△DCF中，由勾股定理得，（6﹣x）2=x2+42，解得，x=，则tan∠CDF===．故选B．类型二、三角形的内切圆4.（2015•西青区二模）已知四边形ABCD中，AB∥CD，⊙O为内切圆，E为切点．（Ⅰ）如图1，求∠AOD的度数；（Ⅱ）如图1，若AO=8cm，DO=6cm，求AD、OE的长；（Ⅲ）如图2，若F是AD的中点，在（Ⅱ）中条件下，求FO的长．OCBA【答案与解析】解：（Ⅰ）∵⊙O 为四边形ABCD 的内切圆， ∴AD、AB 、CD 为⊙O 的切线， ∴OD 平分∠ADC，OA 平分∠BAD， 即∠O DA=∠ADC，∠OAD=∠BAC， ∵AB∥CD，∴∠ADC+∠BAC=180°， ∴∠ODA+∠OAD=90°， ∴∠AOD=90°；（Ⅱ）在Rt△AOD 中，∵AO=8cm，DO=6cm ， ∴AD==10（cm ），∵AD 切⊙O 于E ，∴OE⊥AD， ∴OE•AD=OD•OA， ∴OE==（cm ）；（Ⅲ）∵F 是AD 的中点， ∴FO=AD=×10=5（cm ）．【总结升华】本题考查了三角形的内切圆与内心，也考查了切线长定理． 举一反三：【变式】如图，△ABC 中，∠C=90°，BC=4，AC=3，⊙O 内切与△ABC ，则△ABC 去除⊙O 剩余阴影部分的面积为（ ）A.12-πB. 12-2πC. 14-4πD. 6-π【答案】D.。