切线长定理和内切圆

七.切线长定理及三角形地内切圆一、教案目标：1、理解切线长地定义及切线长定理，并能够利用切线长定理计算与证明2、理解三角形地内切圆和内心地概念，注意区分三角形地内心与外心二、教案内容1、切线长概念及定理:<1 )切线长地概念：经过圆外一点作圆地切线，这点和切点之间地线段地长，叫做这点到圆地切线长•提问：经过直线外一点可以做圆地几条切线？它们地切线长有什么关系？为什么？<2 线长定理：_________________________________________ . b5E2RGbCAP如图：P为O O外一点，PA、PB分别与O O相切，切点分别为A、B，贝U PA=PB，PO 平分/ APB举例练习：(1) 如上图，连接AB，(1>写出图中所有地垂直关系；(2>写出图中所有地全等三角形(3>如果PA=4cm,PD=2cm,求半径0A地长•<2 ) 如图，PA，PB分别为O 0地切线，切点分别为A、B，/P=60 ° ，PA =10 cm，那么AB 地长为•(3) 如图，PA，PB分别为O O地切线，AC为直径，切点分别为A、B，N P=70 ° ，则N C = .2、三角形地内切圆与三角形地内心<1)概念：与三角形各边都相切地圆叫做三角形地________________内切圆地圆心叫做三角形地__________ .地交点；<2 )三角形地内心是三角形地 ________________________________p1EanqFDPw它到三角形三边地_____________ 相等，是内切圆地__________ •提问：三角形地内心在三角形地 _____________ ，与三角形地形状______________举例练习:(1) 如图若/ A=40o,M分别为△ ABC地外心、内心、垂心时，求/ BMC地度数.(2＞如图,△ ABC中,E是内心，/ A地平分线和△ ABC地外接圆相交于点D,求证：DE=DB.练习1、如图，PA , PB分别为O O地切线，切点分别为A、B , PA =10 ,在劣弧AB上任取一点C ,过C作O O地切线，分别交PA, PB于D , E ,则厶PDE地周长是DXDiTa9E3d2.如图,PA 切O O于A , PB 切O O 于B , /APB =90° , OP =4, 地半径为_________ .3.如图，O O半径为1, P为O O外一点，切O O于点A, PA =1, AB是OO地弦，且AB = 42 , PB地长为______________ .4.如图，.APB =60 ° ,半径为2地O O切PB于P点，若将O O在PB上向右滚动，则当滚动到O O与PA也相切时，圆心O移动地水平距离是 _________ . RTCrpUDGiT5•如图，PA、PB分别与O O相切于A、B两点，C是O O上一点，且-ACB =55 ,则• P 等于<)A. 70B. 65C. 110D. 5511.如图,Rt △ ABC 中，/ C =90 ° , E 为AC 上一点，以CE 为直径地O O 切AB 于D 点，AD = 4, AE =2.求 BD 地长.A.梯形B.菱形C.矩形D.平行四边形7.如图,AB 、 AC 与O O 相切于点B 、C , . A 二50。

九年级上册数学《第二十四章 圆》 24.2点和圆、直线和圆的位置关系 24. 第3课时 切线长定理 & 三角形的内切圆◆1、切线长的定义：经过圆外一点作圆的切线，这点和切点之间的线段的长叫做切线长． 【注意】①切线是直线，不能度量．②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量． ◆2、切线长定理: 过圆外一点所画的圆的两条切线长相等. ∵ P A 、PB 分别切☉O 于 A 、B ， ∴ P A = PB ， ∠OP A = ∠OPB .切线长定理为证明线段相等、角相等提供了新的方法.◆1、三角形的内切圆：与三角形各边都相切的圆叫做这个三角形的内切圆. 【注意】一个圆可以有无数个外切三角形，但是一个三角形只有一个内切圆.◆2、三角形的内心:三角形内切圆的圆心叫做这个三角形的内心.这个三角形叫做这个圆的外切三角形. ◆3、三角形内心的性质：三角形的内心就是三角形三条角平分线的交点.三角形的内心到三角形的三边的距离相等.如图，☉I 是△ABC 的内切圆，点 I 是△ABC 的内心，△ABC 是☉I 的外切三角形. ◆4、三角形外心、内心的区别：名称 确定方法 图形 性质POAB外心：三角形外接圆的圆心三角形三边中垂线的交点1、外心到三顶点的距离相等；2、外心不一定在三角形的内部．内心：三角形内切圆的圆心三角形三条角平分线的交点1、内心到三边的距离相等；2、内心在三角形内部．【例题1】（2022秋•潮州期末）如图，P 为⊙O 外一点，P A 、PB 分别切⊙O 于点A 、B ，CD 切⊙O 于点E ，分别交P A 、PB 于点C 、D ，若P A ＝8，则△PCD 的周长为（ ） A ．8B ．12C ．16D ．20【变式11】（2023•怀化三模）如图，AB 、AC 、BD 是⊙O 的切线，切点分别是P 、C 、D ．若AB ＝10，AC ＝6，则BD 的长是（ ） A ．3B ．4C ．5D ．6【变式12】如图，⊙O 为△ABC 的内切圆，AC ＝10，AB ＝8，BC ＝9，点D ，E 分别为BC ，AC 上的点，且DE 为⊙O 的切线，则△CDE 的周长为（ ） A ．9B ．7C ．11D ．8【变式13】（2022秋•南沙区校级期末）如图，四边形ABCD 是⊙O 的外切四边形，且AB ＝8，CD ＝15，则四边形ABCD 的周长为 ．【变式14】（2022秋•红旗区校级期末）以正方形ABCD 的AB 边为直径作半圆O ，过点C 作直线切半圆于点F ，交AB 边于点E ，若△CDE 的周长为12，则直角梯形ABCE 周长为（ ） A ．12B ．13C ．14D ．15【变式15】如图，P A 、PB 是⊙O 的切线，切点分别是A 、B ，直线EF 也是⊙O 的切线，切点为Q ，交P A 、PB 于点E 、F ，已知P A ＝12cm ，∠P ＝40°OCBAO CBA①求△PEF的周长；②求∠EOF的度数．【变式16】如图，P A、PB、CD是⊙O的切线，点A、B、E为切点．（1）如果△PCD的周长为10，求P A的长；（2）如果∠P＝40°，①求∠COD；②连AE，BE，求∠AEB．【例题2】（2022秋•东城区期中）如图，已知⊙I是△ABC的内切圆，点I是内心，若∠A＝28°，则∠BIC等于（）A．99°B．102°C．104°D．152°【变式21】（2023•东安县模拟）如图，在△ABC中，∠A＝70°，点I是内心，则∠BIC的大小为（）A．130°B．140°C．105°D．125°【变式22】如图所示，已知⊙I是△ABC的内切圆，D、E、F是切点，∠C＝60°，∠DIF＝140°，则∠B为（）A．40°B．50°C．60°D．80°【变式23】如图，在△ABC中，∠B＝50°，⊙O是△ABC的内切圆，分别切AC，AB，BC于点D，E，̂上一点，则∠EPF的度数为（）F，P是DFA．50°B．55°C．60°D．65°【变式24】（2023•聊城）如图，点O是△ABC外接圆的圆心，点I是△ABC的内心，连接OB，IA．若∠CAI＝35°，则∠OBC的度数为（）A．15°B．17.5°C．20°D．25°【变式25】（2023•陇县一模）如图所示，△ABC内接于⊙O，点M为△ABC的内心，若∠C＝80°，则∠MAN的度数是（）A．50°B．55°C．60°D．80°【例题3】（2023•青海一模）如图，⊙O 与△ABC 的边AB 、AC 、BC 分别相切于点D 、E 、F ，如果AB＝4，AC ＝5，AD ＝1，那么BC 的长为 ．【变式31】（2022秋•同心县期末）如图，⊙O 是△ABC 的内切圆，点D ，E ，F 为切点，AD ＝4，AC ＝10，BC ＝14，则BD 长为 ．【变式32】如图，①ABC 中，①C ＝90°，AC ＝12，BC ＝5，①O 与①ABC 的三边相切于点D 、E 、F ，则AD 长为（ ） A ．8B ．10C ．12D ．14【变式33】如图，①O 分别切①ABC 的三条边AB 、BC 、CA 于点D 、E 、F 、若AB ＝5，AC ＝6，BC ＝7，求AD 、BE 、CF 的长．【变式34】已知△ABC 的内切圆半径r =√3，D 、E 、F 为切点，∠ABC ＝60°，BC ＝8，S △ABC =10√3，求AB 、AC 的长．【变式35】（2022秋•津南区期末）如图，△ABC 的内切圆⊙O 与BC 、CA 、AB 分别相切于点D 、E 、F ．（1）若∠ABC ＝50°，∠ACB ＝75°，求∠BOC 的度数； （2）若AB ＝13，BC ＝11，AC ＝10，求AF 的长．【例题4】（2023•天心区校级三模）如图，⊙O 是△ABC 的内切圆，若△ABC 的周长为18，面积为9，则⊙O 的半径是（ ） A ．1B ．√2D ．2【变式41】已知一个三角形的三边长分别为5、5、6，则其内切圆的半径为（ ）A ．3B ．5C ．32D ．52【变式42】（2023•邵阳县一模）如图所示，⊙O 是等边三角形ABC 的内切圆，若AB ＝4，则⊙O 的半径是（ ） A ．√32B ．1C ．2√33D ．2【变式43】（2022秋•齐河县期末）如图，⊙O 的直径AB 为10cm ，弦BC 为8cm ，∠ACB 的平分线交⊙O于点D ，△ADB 的内切圆半径是（ ） A ．12B ．5（√2−1）C ．5（√2+1）D ．5√22【变式44】如图，这条花边中有4个圆和4个正三角形，且这条花边的总长度AB 为4，则花边上正三角形的内切圆半径为（ ） A ．√33B ．23√3C ．1D ．√3【变式45】如图，圆O 是△ABC 的内切圆，其中AB ＝7，BC ＝5，AC ＝8，求其内切圆的半径．【例题5】（2023春•江岸区校级月考）如图，△ABC 是一块绿化带，将阴影部分修建为花圃，已知AB ＝13，AC ＝5，BC ＝12，阴影部分是△ABC 的内切圆，则花圃的面积为 ．【变式51】（2022秋•河西区校级期末）如图，⊙I 是直角△ABC 的内切圆，切点为D 、E 、F ，若AF ＝10，BE ＝3，则△ABC 的面积为 ．【变式52】等边三角形的边长为4，则它的内切圆面积等于（ ）A ．4πB ．43πC ．23πD ．163π【变式53】如图，在四边形ABCD 中，AB ＝CB ，AD ＝CD ．若∠ABD ＝∠ACD ＝30°，AD ＝1，则△ABC的内切圆面积 （结果保留π）．【变式54】如图，①O 内切于正方形ABCD ，O 为圆心，作①MON ＝90°，其两边分别交BC ，CD 于点N ，M ，若CM +CN ＝4，则①O 的面积为（ ） A ．πB ．2πC ．4ππ【例题6】（2023•越秀区校级二模）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，则△ABC的内切圆的半径r是（）A．2B．3C．4D．无法判断【变式61】（2023•沭阳县一模）直角三角形中，两直角边的长分别为3与4，则其内切圆半径为．【变式62】（2022秋•防城港期末）在《九章算术》卷九中记载了一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”其意思是：“如图，今有直角三角形勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆（内切圆）的直径是多少步？”根据题意，该内切圆的直径为步．【变式63】（2022秋•金华期末）如图，⊙O是△ABC的内切圆，切点分别为D，E，F，且∠A＝90°，BC=52，CA＝2，则⊙O的半径是．【变式64】（2022秋•黔西南州期中）如图，已知O是△ABC的内心，连接OA，OB，OC．若△ABC内切圆的半径为2，△ABC的周长为12，求△ABC的面积．【变式65】（2022秋•天河区校级期末）如图，已知⊙O为Rt△ABC的内切圆，切点分别为D，E，F，且∠C＝90°，AB＝13，BC＝12．（1）求BF的长；（2）求⊙O的半径r．【变式66】如图，在Rt△ABC中，∠C＝90°，⊙O是△ABC的内切圆，半径为r，切点为D、E、F，连接OD，OE，OF．（1）若BC＝6，AC＝8，则r＝；（2）若Rt△ABC的周长为L，面积为S，则S，L，r之间有什么数量关系，并说明理由．【例题7】如图是一块△ABC余料，已知AB＝20cm，BC＝7cm，AC＝15cm，现将余料裁剪成一个圆形材料，则该圆的最大面积是．【变式71】如图，在平面直角坐标系中，已知点A（3√2，0），点B在第一象限，且AB与直线l：y＝x2平行，AB长为4，若点P是直线l上的动点，则△P AB的内切圆面积的最大值为．【变式72】（2022秋•鼓楼区校级月考）在Rt△ABC中，∠ACB＝90°，BC＝6，AC＝8，直线l经过△ABC的内心O，过点C作CD⊥l，垂足为D，连接AD，则AD的最小值是．【变式73】已知一块等腰三角形钢板的底边长为60cm，腰长为50cm．（1）求能从这块钢板上截得的最大圆的半径．（2）用一个圆完全覆盖这块钢板，这个圆的最小半径是多少？（3）求这个等腰三角形的内心与外心的距离．【例题8】如图，点E是①ABC的内心，AE的延长线和①ABC的外接圆①O相交于点D，过D作直线DG①BC．（1）若①ACB＝80°，则①ADB＝；①AEB＝．（2）求证：DE＝CD；（3）求证：DG是①O的切线．【变式81】（2022秋•泗阳县期末）已知，如图，AB为⊙O的直径，△ABC内接于⊙O，BC＞AC，点P 是△ABC的内心，延长CP交⊙O于点D，连接BP．（1）求证：BD＝PD；（2）已知⊙O的半径是3√2，CD＝8，求BC的长．【变式82】（2023•庐阳区校级一模）如图，已知⊙O是Rt△ABC的外接圆，点D是Rt△ABC的内心，BD的延长线与⊙O相交于点E，过E作直线l∥AC．（1）求证：l是⊙O的切线；（2）连接CE，若AB＝3，AC＝4，求CE的长．【变式83】（2022秋•江夏区校级期末）如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆交于点D．（1）如图1，连接DB，求证：DB＝DE；（2）如图2，若∠BAC＝60°，求证：AB+AC=√3AD．【变式84】如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆⊙O相交于点D过D作直线DG ∥BC．（1）若∠ACB＝70°，则∠ADB＝；∠AEB＝．（2）求证：DE＝CD；（3）求证：DG是⊙O的切线．【变式85】如图，已知点D在⊙O的直径AB延长线上，点C为⊙O上，过D作ED⊥AD，与AC的延长线相交于E，CD为⊙O的切线，AB＝2，AE＝3．（1）求证：CD＝DE；（2）求BD的长；（3）若∠ACB的平分线与⊙O交于点F，P为△ABC的内心，求PF的长．。

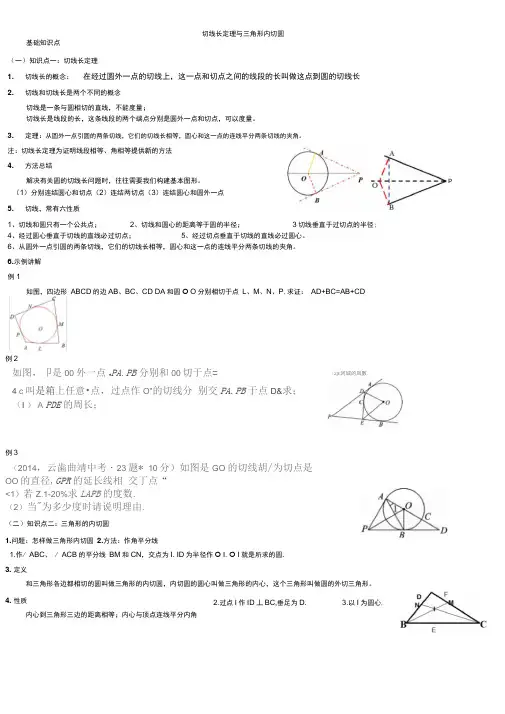
基础知识点（一）知识点一：切线长定理1.切线长的概念： 在经过圆外一点的切线上，这一点和切点之间的线段的长叫做这点到圆的切线长 2. 切线和切线长是两个不同的概念切线是一条与圆相切的直线，不能度量；切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。

3. 定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

注：切线长定理为证明线段相等、角相等提供新的方法4. 方法总结解决有关圆的切线长问题时，往往需要我们构建基本图形。

（1）分别连结圆心和切点（2）连结两切点（3）连结圆心和圆外一点5. 切线，常有六性质1、切线和圆只有一个公共点；2、切线和圆心的距离等于圆的半径； 3切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点； 5、经过切点垂直于切线的直线必过圆心。

6、从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

6.示例讲解例1如图，四边形 ABCD 的边AB 、BC 、CD DA 和圆O O 分别相切于点 L 、M 、N 、P ,求证： AD+BC=AB+CD 例2如图，卩是00外一点t PA.PB 分别和00切于点=4 c 叫是箱上任意•点，过点作O"的切线分 别交PA.PB 于点D&求；（I ） A PDE 的周长；例3（2014，云歯曲靖中考・23题* 10分）如图是GO 的切线胡/为切点是OO 的直径,GPR 的延长线相 交丁点“<1）若Z.1-20%求LAPB 的度数.（2）当"为多少度时请说明理由.（二）知识点二：三角形的内切圆1.问题：怎样做三角形内切圆2.方法：作角平分线1.作/ ABC 、 / ACB 的平分线 BM 和CN ，交点为I. ID 为半径作O I. O I 就是所求的圆.3. 定义和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。

切线长定理及三角形的内切圆一知识讲解〈基础）【学习目标】l.了解切线长定义：理解三角形的内切圆及内心的定义：2.掌握切线长定理：利用切线长定理解决相关的计算和证明．【要点梳理】要点一、切线长定理1.切线长：经过圆外一点能够作圆的两条切线，切线上这一点到切点间的线段长叫做这点到圆的切线长．要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称．切线是直线，而非线段．2.切线长定理z从圆外一点作圆的两条切线，两切线长相等，圆心与这一点的连线平分两条切线的夹角．要点诠释：切线长定理包含两个结论：线段相等和角相等．要点二、三角形的内切圆1.三角形的内切圆z与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫作圆的外切三角形．三角形的内心到三角形的三边距离相等．2.三角形的内心z三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心．三角形的内心是这个三角形的三条角平分线的交点．要点诠释z(1）任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形：(2）解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积户即S=;Pr (S 7'J 三角形的面积P为三角形的周长r为内切圆阳）(3）三角形的外心与内心的区别：名称｜确定方法｜图形｜性质外心（三角形｜三角形三边中垂线的外接圆的圆｜交点心）AB(1)OA=OB=OC: (2）外心不一定在三角形内部内心（三角形三角形三条角平分线内切圆的圆的交点心）【典型例题】类型一、切线长定理B c(1)到三角形三边距离相等：(2) O A、OB、oc分别平分L'.'.BAC、ζABC、丘ACB:(3）内心在三角形内部．。

1.(2叫湛江校级脚己知PA,PB :5t别切。

于A、B E为劣弧础上一点过E,#,1¥Ji;JJ�交PA于C、交PB于D.(1）若PA吨，求6PCD的周长．(2）若ζP=50°求ζDOC.p【答案与解析】解：(1）连接OE,..PA、PB与圆0相切，:.PA=PB=6,同理可得：AC=CE,BD=DE,6PCD的周长＝PC+PD+CD=PC+PD+CE+DE=PA+PB=12: (2）γPA PB与圆O相切，二ζOAP＝ζOBP=90。

切线长和切线长定理及圆与圆的位置关系一、切线长和切线长定理：⑴ 切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长．⑵ 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．二、三角形内切圆1． 定义：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．2． 多边形内切圆：和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形．3．直角三角形的内切圆半径与三边关系OF ED C BACBA CBAcbacba（1） （2）图（1）中，设a b c ，，分别为ABC ∆中A B C ∠∠∠，，的对边，面积为S则内切圆半径（1）s r p =，其中()12p a b c =++； 图（2）中，90C ∠=︒，则()12r a b c =+-、abr a b c=++重难点：切线的判定定理；切线的性质定理及其运用它们解决一些具体的题目．1.切线长定理及切线性质的应用例题1（2011·济宁）如图，AB 是⊙O 的直径，AM 和BN 的两条切线，DE 切⊙O 于点E ，交AM 与于点D ，交BN 于点C ，F 是CD 的中点，连接OF 。

（1） 求证：OD ∥BE;(2) 猜想：OF 与CD 有何数量关系？并说明理由。

解：（1）证明：连接OE∵AM 、DE 是⊙O 的切线，OA 、OE 是⊙O 的半径 ∴∠ADO=∠EDO,∠DAO=∠DEO=90°…………1分∴∠AOD=∠EOD=21∠AOE …………2分 ∵∠ABE=21∠AOE ∴∠AOD=∠ABE ∴OD ∥BE …………3分 (2) OF =21CD …………4分 理由：连接OC∵BE 、CE 是⊙O 的切线∴∠OCB=∠OCE …………5分 ∵AM ∥BN∴∠ADO+∠EDO+∠OCB+∠OCE=180° 由（1）得 ∠ADO=∠EDO∴2∠EDO+2∠OCE=180° 即∠EDO+∠OCE=90° …………6分 在Rt △DOC 中， ∵ F 是DC 的中点 ∴OF =21CD ……7分 三、圆与圆的位置关系重点：两个圆的五种位置关系中的等价条件及它们的运用． 难点：探索两个圆之间的五种关系的等价条件及应用它们解题． 易错点：1）圆与圆位置关系中相交时圆心距在两圆半径和与差之间， 2）没有公共点要考虑外离和内含的两种情况 3）有一个公共点要考虑内切与外切两种情况4）两圆相交求的公共弦多对的圆周角，求出圆心距一般都有两种情况圆与圆的位置关系的应用 例题2（2011•绍兴）如图，相距2cm 的两个点A 、B 在直线l 上．它们分别以2cm/s 和1cm/s的速度在l 上同时向右平移，当点A ，B 分别平移到点A 1，B 1的位置时，半径为1cm 的⊙A 1，与半径为BB 1的⊙B 相切．则点A 平移到点A 1，所用的时间为为多少秒?考点：圆与圆的位置关系。

切线长定理及三角形的内切圆—知识讲解（提高）责编：常春芳【学习目标】1.了解切线长定义；理解三角形的内切圆及内心的定义；2.掌握切线长定理；利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线长定理1．切线长：经过圆外一点能够作圆的两条切线，切线上这一点到切点间的线段长叫做这点到圆的切线长.要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段. 2．切线长定理：从圆外一点作圆的两条切线，两切线长相等，圆心与这一点的连线平分两条切线的夹角.要点诠释：切线长定理包含两个结论：线段相等和角相等.要点二、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫作圆的外切三角形.三角形的内心到三角形的三边距离相等.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心是这个三角形的三条角平分线的交点.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).名称确定方法图形性质外心(三角形外接圆的圆心) 三角形三边中垂线的交点(1)OA=OB=OC；(2)外心不一定在三角形内部内心(三角形内切圆的圆心) 三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB；(3)内心在三角形内部.【典型例题】类型一、切线长定理1.（2015•常德）已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为3，∠EAC=60°，求AD的长．【答案与解析】证明：（1）如图1，连接FO，∵F为BC的中点，AO=CO，∴OF∥AB，∵AC是⊙O的直径，∴CE⊥AE，∵OF∥AB，∴OF⊥CE，∴OF所在直线垂直平分CE，∴FC=FE，OE=OC，∴∠FEC=∠FCE，∠0EC=∠0CE，∵∠ACB=90°，即：∠0CE+∠FCE=90°，∴∠0EC+∠FEC=90°，即：∠FEO=90°，∴FE为⊙O的切线；（2）如图2，∵⊙O的半径为3，∴AO=CO=EO=3，∵∠EAC=60°，OA=OE，∴∠EOA=60°，∴∠COD=∠EOA=60°，∵在Rt△OCD中，∠COD=60°，OC=3，∴CD=，∵在Rt△ACD中，∠ACD=90°，CD=，AC=6，∴AD=．【总结升华】本题是一道综合性很强的习题，考查了切线的判定和性质，三角形的中位线的性质，勾股定理，线段垂直平分线的性质等，熟练掌握定理是解题的关键．举一反三：【变式】已知：如图，在梯形 ABCD中，AB∥DC，∠B=90°，AD=AB+DC，AD是⊙O的直径．求证：BC和⊙O相切．【答案】作OE⊥BC，垂足为E，∵ AB∥DC，∠B=90°，∴ OE∥AB∥DC，∵ OA=OD，∴ EB=EC，∴ BC是⊙O的切线．2.已知：如图，AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD，求证：DC是⊙O的切线．【答案与解析】解：连接OD．∵ OA=OD，、∴∠1=∠2．∵ AD∥OC，∴∠1=∠3，∠2=∠4．∴∠3=∠4．又∵ OB=OD，OC=OC，∴△OBC≌△ODC．∴∠OBC=∠ODC．∵BC是⊙O的切线，∴∠OBC=90°，∴∠ODC=90°，∴ DC是⊙O的切线．【总结升华】因为AB是直径，BC切⊙O于B，所以BC⊥AB．要证明DC是⊙O的切线，而DC和⊙O有公共点D，所以可连接OD，只要证明DC⊥OD．也就是只要证明∠ODC=∠OBC.而这两个角分别是△ODC和△OBC的内角，所以只要证△ODC≌△OBC．这是不难证明的．举一反三：【变式】已知：∠MAN=30°，O 为边AN 上一点，以O 为圆心、2为半径作⊙O ，交AN 于D 、E 两点，设AD=x ，⑴如图⑴当x 取何值时，⊙O 与AM 相切；⑵如图⑵当x 为何值时，⊙O 与AM 相交于B 、C 两点，且∠BOC=90°．【答案】解：（1）设AM 与⊙O 相切于点B ，连接OB ，则OB ⊥AB ；在Rt △AOB 中，∠A=30°， 则AO=2OB=4， ∴ AD=AO-OD ， 即AD=2．x=AD=2. （2）过O 点作OG⊥AM 于G∵OB=OC=2，∠BOC=90°，∴BC=22 ∵OG⊥BC，2，2，在Rt △OAG 中，∠A=30°∴OA=2OG=22，MNEDO图（1）．MANEDBCO图（2）∴x=AD=22－23.（2014•高港区二模）矩形ABCD中，AB=4，AD=3，以AB为直径在矩形内作半圆．DE切⊙O于点E（如图），则tan∠CDF的值为（）A．B．C．D．【答案】B；【解析】解：如图，设FC=x，AB的中点为O，连接DO、OE．∵AD、DE都是⊙O的切线，∴DA=DE=3．又∵EF、FB都是⊙O的切线，∴EF=FB=3﹣x．∴在Rt△DCF中，由勾股定理得，（6﹣x）2=x2+42，解得，x=，则tan∠CDF===．故选B．类型二、三角形的内切圆4.（2015•西青区二模）已知四边形ABCD中，AB∥CD，⊙O为内切圆，E为切点．（Ⅰ）如图1，求∠AOD的度数；（Ⅱ）如图1，若AO=8cm，DO=6cm，求AD、OE的长；（Ⅲ）如图2，若F是AD的中点，在（Ⅱ）中条件下，求FO的长．OCBA【答案与解析】解：（Ⅰ）∵⊙O 为四边形ABCD 的内切圆， ∴AD、AB 、CD 为⊙O 的切线， ∴OD 平分∠ADC，OA 平分∠BAD， 即∠O DA=∠ADC，∠OAD=∠BAC， ∵AB∥CD，∴∠ADC+∠BAC=180°， ∴∠ODA+∠OAD=90°， ∴∠AOD=90°；（Ⅱ）在Rt△AOD 中，∵AO=8cm，DO=6cm ， ∴AD==10（cm ），∵AD 切⊙O 于E ，∴OE⊥AD， ∴OE•AD=OD•OA， ∴OE==（cm ）；（Ⅲ）∵F 是AD 的中点， ∴FO=AD=×10=5（cm ）．【总结升华】本题考查了三角形的内切圆与内心，也考查了切线长定理． 举一反三：【变式】如图，△ABC 中，∠C=90°，BC=4，AC=3，⊙O 内切与△ABC ，则△ABC 去除⊙O 剩余阴影部分的面积为（ ）A.12-πB. 12-2πC. 14-4πD. 6-π【答案】D.。

切线长定理及内切圆》的说课．教材分析本节内容在前几节课基本掌握了圆的基础知识的前提下来进行的，尤其前一节学习了圆的切线的性质与判定后，由圆的对称性引出过圆外一点有两条切线，从而研究该种情况下渗透的数学原理，继而引入到三角形中探讨其内心的性质，对今后的学习有至关重要的作用.b5E2RGbCAP 二．教案目标复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理，然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念，最后应用它们解决一些实际问题．p1EanqFDPw＜一）知识与技能目标：1. 了解切线长的概念.2. 切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角. DXDiTa9E3d3. 三角形的内切圆及三角形内心的性质. ＜二）过程与方法目标：让学生亲自动手操作：过圆外一点做该圆的切线，体会切线长定理的由来，继而探究其中的内涵. 而后，再将其应用浓缩于角形中，探究内心的性质. RTCrpUDGiT＜三）情感目标：通过这一节课的学习，让学生真正体会到研究数学问题的乐趣和与其他同学共同探讨问题的合作精神.＜四）重难点及关键1 ．重点：切线长定理及其运用．2 ．?难点与关键：切线长定理的导出及其证明和运用切线长定理解决一些实际问题．三．说教法、学法＜一）教法：数学是一门培养人的思维，发展人的思维的重要学科，什么样的教法必带来相应的学法. 一节课不能是单一的教法，因此，在讲授本节课时，我将采用以下方法进行教案：5PCzVD7HxA ＜1）视觉图想法：播放电脑制作的动画，让学生在视听结合的环境中激发学习热情，加深体验，同时也为即将提出的问题做好铺垫. jLBHrnAILg＜2）情景教案法：创设问题情境，以学生感兴趣的，并容易回答的问题为开端，让学生在各自熟悉的场景中轻松、愉快的回答老师提出的问题后，带着成功的喜悦进入新课的学习. xHAQX74J0X ＜3）启发性教案法：启发性原则是永恒的. 在教师的启发下，让学生成为课堂的主体＜二）学法本节课采用小组合作的学习方式让学生遵循“操作——观察——猜想——验证——归纳——应用——总结”的主线进行学习LDAYtRyKfE四、教案流程：<一）复习引入1 .已知△ ABC作三个内角平分线，说说它具有什么性质？2 •点和圆有几种位置关系？你能说说在这一节中应掌握几个方面的知识？3 .直线和圆有什么位置关系？切线的判定定理和性质定理，它们如何？老师点评：<1）在黑板上作出△ ABC的三条角平分线，并口述其性质：？①三条角平分?内切圆的圆心是三角形三条角平分线线相交于一点；②交点到三条边的距离相等. Zzz6ZB2Ltk<2 ） < 口述）点和圆的位置关系有三种，点在圆内 FT d<r ;点在圆上 FT d=r ;点在圆外_J d>r ；不在同一直线上的三个点确定一个圆；反证法的思想.dvzfvkwMIl <3 ） <口述）直线和圆的位置关系同样有三种：直线 L 和O O 相交 d<r ;直线L 和O 相切二d=r ;直线L 和O O 相离_J d>r ;切线的判定定理：？经过半径的外端并且垂直于半 径的直线是圆的切线；切线的性质定理：圆的切线垂直于过切点的半径.rqyn14ZNXI <二）探索新知从上面的复习，我们可以知道，过O O 上任一点A 都可以作一条切线，？并且只有一条，根据下面提出的问题操作思考并解决这个问题.EmxvxOtOco 问题：在你手中的纸上画出O 0,并画出过 A 点的唯一切线 PA ?连结PO ?沿着直线 P0将纸对折，设圆上与点 A 重合的点为B,这时，0B 是O O 的一条半径吗？ PB 是O O 的切 线吗？利用图形的轴对称性，说明圆中的 PA 与PB, / APO 与/ BPO 有什么关系？ SixE2yXPq5学生分组讨论，老师抽取 3〜4位同学回答这个问题.老师点评：0B 与OA 重叠，0A 是半径，0B 也就是半径了 .又因为 0B 是半径，PB 为 0B?勺外端，又根据折叠后的角不变，所以 PB 是O 0的又一条切线，根据轴对称性质， ？我 们很容易得到 PA=PB / APO / BPO 6ewMyirQFL我们把PA 或PB 的长，即经过圆外一点作圆的切线，这点和切点之间的线段的长，？叫 做这点到圆的切线长.从上面的操作几何我们可以得到：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条 切线的夹角. 下面，我们给予逻辑证明.例1.如图，已知PA PB 是O 0的两条切线.求证：PA=PB / OPA=/ OPB 证明：••• PA PB 是O O 的两条切线.••• 0A1AP, OBL BP又 OA=OB OP=OP• Rt △ AOP^ Rt △ BOP• PA=PB / OPA / OPB因此，我们得到切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条 切线的夹角. 我们刚才已经复习，三角形的三条角平分线于一点， 并且这个点到三条边的距离相等.＜同刚才画的图）设交点为 I ，那么I 至U AB AC BC 的距离相等，如图所示，因此以点 I 为圆心，点I 到BC 的 距离ID 为半径作圆，则O I 与厶ABC 的三条边都相 切. kavU42VRUs与三角形各边都相切的圆叫做三角形的内切圆,的交点，叫做三角形的内心. y6v3ALoS89 例2.如图，已知O O 是厶ABC 的内切圆，切点为 D 、E 、F ,如果 AE=1, CD=2 BF=3,且厶 ABC 的面积为6.求内切圆的半径 r . M2ub6vSTnP分析：直接求内切圆的半径有困难，由于面积是已知的，？因此要转化为面积法来求.就需添加辅助线，如果连结AO BO CO就可把三角形ABC分为三块，？那么就可解决.OYujCfmUCw解：连结AO BO COTO 0是厶ABC的内切圆且D E、F是切点.••• AF=AE=1 BD=BF=3 CE=CD=2••• AB=4, BC=5 AC=3又S A ABC=6•••习<4+5+3) r=6• r=1答：所求的内切圆的半径为1.＜三）巩固练习教材P106 练习.＜四）应用拓展例3.如图，O O的直径AB=12cm AM BN是两条切线，DC切O O于E,交AM于D, ? 交BN 于C,设AD=x BC=y. eUts8ZQVRd＜1 ）求y与x的函数关系式，并说明是什么函数？＜2 ）若x、y是方程2t2-30t+m=0的两根，求x, y的值.＜3）求厶COD勺面积.分析：＜1）要求y与x的函数关系，就是求BC与AD的关系,根据切线长定理：DE=AD=x CE=CB=y即DC=x+y,又因为AB=12,所以只要作DF丄BC垂足为F,那么 X l +X 2=值.＜3 ）连结0E 便可求得. 解：＜1）过点D 作DF 丄BC,垂足为F ,则四边形 ABFD 为矩形.VO 0切 AM BN CD 于 A 、B E••• DE=AD CE=CB■/ AD=x, CB=y• CF=y-x , CD=x+y在 Rt △ DCF 中，D(C=D F 2+C F 22 2 2即<x+y ) =<x-y ) +12• xy=36• y= E 为反比例函数；＜2 ）由x 、y 是方程2t-30t+m=0的两根，可得:x+y=AB根据勾股定理，便可求得.＜2）v x , y 是 2t -30t+m=0 的两根，同理可得：xy=36 • x=3, y=12 或 x=12, y=3.<3 )连结 OE 贝U OEL CD• S A COD = 寸 CD ・OE=勺 *AD+BC ) X X 15X=45cm＜五）归纳小结 ＜学生归纳，老师点评）本节课应掌握：1•圆的切线长概念； 2.切线长定理； 3 .三角形的内切圆及内心的概念.＜六）、布置作业1 .教材P117 综合运用5、6、7、8.2•选用课时作业设计.X l X 2 = ，便可求得 x 、 y 的五：课堂反思：第三课时作业设计一、选择题.1 .如图1, PA PB分别切圆O于A、B两点，C为劣弧AB上一点，/ 〈APB=30 ，则/ACB=< ) .GMsIasNXkAA . 60 °B . 75°C.105° D . 120 °A. 60 ° B . 75° C . 105° D . 120°a叵□(1> (2>(3>(4>TIrRGchYzg2 .从圆外一点向半径为9的圆作切线，已知切线长为18, ?从这点到圆的最短距离为通过本节课的教案，力图让学生从探究中掌握切线长定理及在三角形中的应用，对内心的性质要对比外心类比记忆.sQsAEJkW5T< )•A . 9」B . 9<」-1 )C . 9<」-1 )D . 93 .圆外一点P, PA PB分别切O O于A、B, C为优弧AB上一点，若/ ACB=a则/APB=< ) 7EqZcWLZNXA . 180 ° -aB . 90 ° -aC . 90° +aD . 180 ° -2a二、填空题1. 如图2, PA PB分别切圆O于A、B,并与圆O的切线，分别相交于C、D, ?已知PA=7cm则厶PCD的周长等于__________ . lzq7IGfO2E2•如图3，边长为a的正三角形的内切圆半径是______________ .3.如图4，圆O内切Rt△ ABC切点分别是D E、F,则四边形OECF是_____________ .三、综合提高题1. 如图所示，EB EC是O O的两条切线，B、C是切点，A D是O O上两点，？如果/ E=46°,Z DCF=32，求/ A 的度数.zvpgeqJ1hkLEJ2. 如图所示，PA PB是O O的两条切线，A B为切点, 求证/ ABO=? / APB.3 .如图所示，已知在厶ABC中，/ B=90°, O是AB上一点，以0为圆心，0B釣半径的圆与AB交于点E,与AC切于点D. NrpoJac3v1<1 ）求证：DE// 0C<2 ）若AD=2, DC=3 且AD2=AE- AB,求因的值.答案：一、1. C 2 . C 3 . D二、1. 14cm 2 . | a 3 .正方形三、1.解：T EB EC是O 0的两条切线，••• EB=EC •••/ ECB玄EBC又/ E=46°，而/ E+Z EBC+Z ECB=180，/ ECB=67 ,又/ DCF+Z ECB+Z DCB=180 ,•Z BCD=180 -67 °-32 °=81 °,又Z A+Z BCD=180 ,•Z A=180° -81 °=99 °2. 证明：连结OR OA OP交AB于C,•/ B是切点，•••/ OBP=90 , Z OAP=90? , ?•Z BOP Z APO•/ OA=OB •••/ BOP玄AOC •Z OCB=90 ,vZ OBA Z OPB •••/ OBA= | Z APB3. <1）证明：连结OD则Z ODC=R Z , Z ODE Z OED由切线长定理得：CD=CB ?•Rt△ODC^ Rt △OBC •Z COB Z COD•••/ DOE+2/ OED=180 ,又/ DOE+2/ COB=180 , ?/-Z OED=/ COB 二DE// OC<2）由AD=2, DC=3得：BC=3 AB=4,又;AD2=AE - AB ••• AE=1,--BE=3 OB=i BE= i …=】申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

九年级数学切线长定理与三角形内切圆知识点讲解及练习【知识点精讲】（一）知识要点----切线长定理1.切线长：经过圆外一点的圆的切线上，这点和切点之间线段的长，叫做这点到圆的切线长。

如图，PA,PB即为P点到圆的切线长。

2.切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

（二）知识要点----三角形内切圆1.三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心。

练习1.已知：如图，AB 为⊙O 的直径，PA 、PC 是⊙O 的切线，A 、C 为切点，∠BAC =30． （1）求∠P 的大小；（2）若AB =6，求PA 的长．【总结】切线长定理包括线段相等和角相等两个结论，利用切线长定理可以证明线段相等、角相等、弧相等以及垂直关系等。

2.如图，已知AB 是⊙O 的直径，点P 在BA 的延长线上，PD 切⊙O 于点D ，过点B 作BE ⊥PD ，交PD 的延长线于点C ，连接AD 并延长，交BE 于点E ．（1）求证：AB=BE ；（2）连结OC ，如果PD=∠ABC=，求OC 的长．603.如图，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于D，过C 作CG∥AE交BA的延长线于点G．（1）求证：CG是⊙O的切线；4.如图，在平面直角坐标系xOy中，点A在第一象限，点B在x轴的正半轴上，∠OAB=90°．⊙P1是△OAB的内切圆，且P1的坐标为（3，1）．（1）OA的长为__________，OB的长为__________；（2）点C在OA的延长线上，CD∥AB交x轴于点D．将⊙P1沿水平方向向右平移2个单位得到⊙P2，将⊙P2沿水平方向向右平移2个单位得到⊙P3，按照同样的方法继续操作，依次得到⊙P4，…⊙Pn．若⊙P1，⊙P2，…⊙Pn均在△OCD的内部，且⊙Pn恰好与CD相切，则此时OD的长为__________．（用含n的式子表示）【总结】三角形内切圆的圆心是三角形三条角平分线的交点，它到三角形三条边的距离都相等。

切线长定理和三角形内切圆一、教学目标(一)知识与技能：1.了解切线长的概念，会作三角形的内切圆；2.理解切线长定理，了解三角形的内切圆和三角形的内心的概念，熟练掌握它的应用.(二)过程与方法：经历探究三角形的内切圆的过程，掌握切线长及其定理.(三)情感态度与价值观：经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力和初步演绎推理能力，能有条理地、清晰地阐述自己的观点.二、教学重点、难点重点：会作三角形的内切圆，了解三角形的内切圆和三角形的内心的概念，理解切线长定理，熟练掌握它的应用.难点：切线长定理的导出及其证明和运用切线长定理解决一些实际问题.三、教学过程知识预备如图，AB是⊙O的切线，切点为B，AO⊥BC，∠A=30°，则：(1)∠ABO=___°，∠BOE=___°；(2)BD=___，BE=___，∠BOE=∠____.画一画1.如何过⊙O外一点P画出⊙O的切线？2.这样的切线能画出几条？如图，过圆外一点P有两条直线PA，PB分别与⊙O相切.经过圆外一点的圆的切线上，这点和切点之间线段的长，叫做这点到圆的切线长.切线与切线长有什么区别与联系？切线和切线长是两个不同的概念：1.切线是一条与圆相切的直线；2.切线长是线段的长，这条线段的两个端点分别是圆外一点和切点.探究如图，PA，PB是⊙O的两条切线，切点分别为A，B.在半透明的纸上画出这个图形，沿着直线PO将图形对折，图中的PA与PB，∠APO与∠BPO有什么关系？如图，连接OA和OB.∵ PA和PB是⊙O的两条切线∴ OA⊥AP，OB⊥BP又 OA=OB，OP=OP∴ R t△AOP≌R t△BOP (HL)∴ PA=PB，∠APO=∠BPO由此得到切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.定理应用格式：∵ PA 、PB 分别切⊙O 于A 、B∴ PA=PB ，∠APO=∠BPO.切线长定理为证明线段相等、角相等提供新的方法思考如图是一块三角形的铁皮，如何在它上面截下一块圆形的用料，并且使截下来的圆与三角形的三条边都相切？如图，分别作出∠B 、∠C 的平分线BM 和CN ，设它们相交于点I ，那么点I 到AB ，BC ，CA 的距离都相等.以点I 为圆心，点I到BC 的距离ID 为半径作圆，则⊙I 与△ABC 的三条边都相切，圆I 就是所求作的圆.与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.例2如图，△ABC 的内切圆⊙O 与BC 、CA 、AB 分别相切于点D 、E 、F ，且AB=9，BC=14，CA=13.求AF 、BD 、CE 的长.解：设AF=x ，则AE=x ，CD=CE=AC-AE=13-x ，BD=BF=AB-AF=9-x由BD+CD=BC ，可得(13-x )+(9-x )=14解得 x =4因此 AF=4，BD=5，CE=9练习1.如图，△ABC 中，∠ABC=50°，∠ACB=75°，点O 是△ABC 内心.求∠BOC 的度数.解：∵ 点O 是△ABC 的内心∴ OB 、OC 分别平分∠ABC 、∠ACB∴ ∠OBC=∠ABC=×50°=25°∠OCB=∠ACB=×75°=37.5°∴ ∠BOC=180°-∠OBC-∠OCB=180°-25°-37.5°=117.5°2.△ABC 的内切圆半径为r ，△ABC 的周长为l ，求△ABC 的面积.解：如图，设△ABC 的内心为O ，连接OA ，OB ，OC ，则点O 到AB ，BC ，AC 的距离为r .∴ S △ABC =S △AOB +S △BOC +S △AOC=×AB×r +×BC×r +×AC×r =×(AB+BC+AC)×r =lr 课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？四、教学反思教学过程中，强调用切线长定理可解决有关求角度、周长的问题. 明确三角形内切圆的圆心是三角形三条角平分线的交点，到三边的距离相等.212121212121212121。