闭环频率特性的基本特点

5.3 控制系统的频率特性
在绘制各个典型环节频率特性的基础上， 可以绘制控制系统的频率特性。
5.3.1 控制系统开环频率特性的Nyquist图
一个控制系统的开环传递函数可以写成典型
环节的连乘积形式。
1
举例 一个开环传递函数为
K ( s 1) G( s) 2 2 s(T1s 1)(T2 s 2 T2 s 1)
27
2
对于非单位反馈系统， 在其开环频率特性幅值
G( j)H ( j) 很大的频段内， 闭环频率特性
1 ( j ) H ( j )
即近似等于反馈环节频率特性的倒数。
对于开环放大倍数 K 很大的闭环系统，在低频段
具有这个特点。
28
3
对于非单位反馈系统， 一般来说， 其开环
频率特性的高频段幅值很小。在这一频段内， 闭环
1
当 0 时，放大环节、惯性环节、振荡环节、
一阶微分环节、二阶微分环节的幅角均为 00 。
。 只有积分环节， 0 时，相角为 900 当
如果开环传递函数中含有 v 个积分环节，开环频率 特性的Nyquist图在 0 的起始处幅角为 v 900 。


6
2
当 0 时， 放大环节的幅值为 K ，
21
[例5-5] 控制系统的开环传递函数为
10( s 1) G( s) s(2.5s 1)(0.04s 2 0.24s 1)
绘制系统的渐近开环对数幅频特性和相频特性。
22
100 Magnitude (dB)
Asymptotic Bode Diagram
-20dB/dec
50
20
频率特性近似等于系统前向通道的频率特性。 一般来说，闭环系统在高频段内显示这一性质。 在工程实践中， 当开环幅频特性

(s)
1 s
H
2
(s)
=

2
(
s)
1 s
1(s) = H1(s)s = H2 (ns)ns = 2 (ns)
3. 频带宽度 b 与快速性的关系（一般情况）
r1(t) = 1(t)
h1 (t )
1(s)
r2 (t) = 1(t)
h2 (t)
2 (s)
h(t)
h2
h1
M ()
0.707M (0)
20log G 0
c
高频段
G( j) 1 ( j) = G( j) G( j)
1+ G(j)
闭环幅频特性近似等于开环幅频特性，因此，开环幅频特性的高频段近似反映 了系统对高频输入的抑制作用，高频段的分贝值越低，系统抵抗高频干扰的能力越强。
20log G
-20dB/dec
-40dB/dec
t→
s→0
当 M (0) = 1 时，稳态误差 ess = 0 当 M (0) 1 时，稳态误差 ess 0
M ()
2. 闭环幅频峰值 M m 与平稳性的关系
一阶系统 (s) = 1
M () = 1
Ts +1
(T)2 +1
幅频特性曲线无峰值，阶跃响应无超调，平稳性好。
二阶系统
(s)
越低，系统抵抗高频干扰的能力越强。
本章小结 • 频率特性的定义、物理意义和图示方法； • 典型环节的频率特性； • 系统的开环频率特性（开环幅相特性曲线和对数频率特性曲线）； • 频率稳定判据（Nyquist稳定判据和对数频率稳定判据）； • 稳定裕度的概念及计算方法； • 闭环频率特性与系统阶跃响应的关系； • 开环频率特性与系统阶跃响应的关系。

( ) j (
)
M ()e j ()
闭环系统的幅频特性与相频特性为 M () ( j)
() ( j) 闭环系统对数幅频特性为 20lg M () 20lg ( j)
闭环幅频特性如下图示，其主要的频域指标有：
M ()
Mr
M (0) 1 0.707
0
r
b
▪ 闭环幅频特性的零频值M(0)
零频率振幅值M(0)即ω为零时闭环幅频特性值。它反应了 系统的稳态精度，M(0)越接近于1，系统的精度越高。M(0)≠1 时，则表示系统有稳态误差。
▪ 二阶系统
闭环系统为二阶闭环系统的闭环频率特性为
(
j )
C( R(
j ) j )
(1
2 n2
1 )
j2 n
M ( )e j ( )
闭环幅频特性、相频特性为
M ()
1
(1
2 n2
)2
(2
n
)2
2
(
)
arctg
1
n 2
n2
0 0.707 时，产生谐振
令
dM
d
0
得谐振频率r
n
1 2 2
第七节 闭环频率特性
闭环系统的时域性能，可以根据闭环频率特性来估算。 对一、二阶系统，时域指标与闭环频域指标有着确定的关系， 对于高阶系统，二者则有近似的对应关系。
一、闭环频率特性主要性能指标
闭环和开环频率特性之间的关系为：
R(s)
-
G(s)
C(s)
( j) G( j) 1 G( j)
1
A()e j A()e
▪ 高频段
高频段指开环幅相特性曲线在中频段以后的区段 10c 这部分特性是由开环传递函数小时间常数环节决定的。

② 对典型欠阻尼二阶系统而言，性能指标与系统的特征参数有关。欠 阻尼二阶系统的特征参数是阻尼系数z 和无阻尼震荡频率w。
tp 2 wd wn 1z

d%e

z
1z 2
100%
4 zw ，当Δ 2时 n ts 3 ，当Δ 5时 zw n
③ 对临界阻尼和过阻尼二阶系统而言，性能指标只有ts 。
1 c( ) lim c(t ) lim s ( s ) lim (w ) M (0) t s 0 s w 0
系统的稳态误差为 当n =0时
essr 1 M (0)
essr 1 M (0) 1 1+ K
K M ( 0) 1 1+ K
K越大稳态误差越小，M(0)越接近于1
② 频率响应的高频区(远高于幅值穿越频率的区域)，表征了闭环系统输 出响应的起始部分；
③ 频率响应的中频区(靠近幅值穿越频率的区域)，表征了闭环系统的稳
定性和瞬态性能。 闭环频率特性的Mp、wp和wb 开环频率特性的wc、g、wg和Kg(Lg)
都是中频特性
（四）典型二阶系统的频域指标与瞬态性能指标的关系
2 w n 典型二阶系统开环传递函数为： Gk ( s) s( s + 2zw n ) 2 wn 开环频率特性为： Gk ( jw ) ( jw )( jw + 2zw n )
。即g 180°+ wc)，wc满足Awc)1
(2)闭环频率特性性能指标 设单位反馈系统的开环传递函数和开环频率特性为 m
G ( s)
K s
(1 + s)
i i 1 n j 1 j
(1 + T s)

180 G ( j c ) c 180 90 tg 2 n -1 c 90 - tg 2 n -1 2 n tg c tg -1 2 4 2 1 2 2
1
90 - tg -1 tg 1
1

有了γ 与ξ 之一一对应的关系，近似 ξ =0.01γ ，且ξ ～δ ﹪有一一对应的关系。
在已知M（ω ），α （ω ）前提下， 可得到|GB（jω ）|，∠GB（jω ）。
§5—7 系统频域分析
一、频域指标：
1、零频值：M（0）或A（0） 频率为0时，闭环频率特性的幅频值，零频值 M（0）与系统型别的关系。
k 1 v 0 M (0) lim G ( j ) 1 k 1 v0
1 M r 1.8 p 0.16 0.4(M r 1) 多阶：估算公式： k ts c k 2 1.5( M r -1) 2.5( M r -1) 1 M r 1.8
且
Mr 1 sin
（35°≤γ ≤90°）
三、由闭环幅频特性曲线估算时域指标
d 2 1 g ( ) 2(1 2 )( 2 2 ) 2(2 )2 0 dt n n n n
2 2 n (1 2 2 ) 2 2 g ( ) 4 (1 ) 2 n 2
2 2 g ( ) (1 2 ) (2 ) n n
ω M α
ω1
ω2
ωr Mr
2、尼柯尔斯图（以φ 为横坐标，L(ω )为纵坐标）
将等M圆和等N圆转换成对数幅值和相角坐标图上， 形成尼柯尔斯图。 P187图 5—59
绘入对数幅—相图，对应有：
ω M(db) α （ω ） ω1 ω2 ……

110 2 10 2 10 A( ) G ( j ) ( 2 ) ( ) 11 2 112 2 112 2 10 10 ( ) arctg arctg arctg 110 110 11
7
由已知r(t)=sin(t+30°)，得 w=1
5.1 频率特性的概念
一、定义：
线性系统对正弦输入信号的稳态响应称频率响应。
二、特点：
设系统的闭环传递函数
b0 s m b1s m1 ... bm G( s) ............(n m) n n 1 a0 s a1s ... an
输入r(t)=Arsinwt，则 ：
w
A(w)
G(jw)
n G(j ) 2 2 (j ) 2n (j ) n
A( ) G ( j ) 1
P(w)
P
n 2
(n 2 ) 2 (2 n ) 2
2
2 2 2 [1 ( ) ] (2 ) n n
10
2 n ( ) G ( j ) arctg 2 n 2
C1 C2 Cn d d* C(s) ... s s1 s s2 s sn s jw s jw
求拉氏反变换得：
C (t ) C1e C2e ... Cn e de
s1t s2t sn t
jt
d e
* jt
（si 为系统的闭环特征根。）
穿越频率wc： w=1时，L(w)=0，因此wc=1
27
L(w) 20 – 20db/dec 0 w
积分环节
0 90
0.1
1

8由开环频率特性分析闭环系统在频率特性分析中，我们可以通过开环频率特性来分析闭环系统的性质和性能。

闭环系统是由开环系统和反馈环路组成的，因此我们首先要了解开环系统的频率特性。

开环系统的频率特性主要有两种表示方法：Bode图和Nyquist图。

其中，Bode图将系统的增益和相位的频率响应以对数坐标的形式展示出来，Nyquist图则将系统的频率响应以复数形式表示。

Bode图是一种常用的分析频率特性的方法。

通过绘制系统的增益曲线和相位曲线，我们可以直观地了解系统在不同频率下的表现。

Bode图的横坐标是以对数形式表示的频率，在高频率时值较大，在低频率时值较小。

纵坐标分别表示增益和相位。

Nyquist图是由实部和虚部构成的复平面中的一个图形。

Nyquist图的横坐标是对应于扫频的频率，在频率趋近无穷大时，图形会逼近一个点。

纵坐标表示对应频率下的增益和相位。

通过分析开环系统的频率特性，我们可以得到以下信息：1. 增益裕度：增益裕度是指系统增益与稳定边界之间的差距。

稳定边界是系统增益曲线与-180°相位曲线交点的位置。

增益裕度越大，系统越稳定。

我们可以通过Bode图或Nyquist图来确定系统的增益裕度。

2. 相位裕度：相位裕度是指系统的相位曲线与-180°相位线之间的差距。

相位裕度越大，系统越稳定。

我们可以通过Bode图或Nyquist图来确定系统的相位裕度。

3. 截止频率：截止频率是指系统增益曲线与零增益线交点的频率。

截止频率决定了系统的带宽，即系统能够承载的最高频率。

通过Bode图可以直观地确定系统的截止频率。

4.相位裕度和增益裕度的关系：相位裕度和增益裕度之间存在一定的关系。

当增益裕度增加时，相位裕度通常会减小。

因此，在频率特性分析中，我们需要权衡增益裕度和相位裕度，以实现系统的稳定性和性能。

在闭环系统中，反馈环路能够通过将部分输出信号重新输入到系统中来调节系统的性能，因此闭环系统的频率特性与开环系统有所不同。

1. 开环频率特性与闭环频率特性关系(单位负反馈)
在闭环频率特性的低频段，由于这时开环幅值远大于1，故单位反馈系统
的闭环频率特性M(jω)≈1。
在高频段，由于开环频率特性的幅值很小，故反馈控制系统的闭环频率特 性与前向通道的频率特性几乎重合。
对非单位反馈系统，M(j)与G(j)的关系为:在低频段由于 A(ω)=|G(jω)H(jω)|>>1，故非单位反馈系统的闭环频率特性 近似等于反馈通道频率特性的倒数。
“频带宽、峰值小，过渡过程性能好”
闭环频率特性中频段的形状对系统暂态特性的影响很大，
通常用带宽频率、谐振峰值和谐振频率来加以刻画。
二阶系统的谐振频率及谐振频率
r n 1 2
2
M
r

1 2 1
2
0
2 2
0 . 707
截止频率及带宽 零频幅值M(0) 表示频率接近于零时，系统输出的幅值与输入幅值之比 。 在频率接近于零时，M(0)=1，则输出幅值能完全准确地反映输入 幅值。零频幅值M(0)越接近于1，系统稳态误差就将越小。 M(jω)| ω=0=M(0)
G (j ) 1 G (j ) H (j ) 1 H (j ) 1 G (j ) H (j ) 1 H (j ) 1 G K (j ) G K (j ) G (j ) H (j )
M (j )
闭环频率特性曲线绘制的方法 o 等M圆和等N圆 o 尼柯尔斯曲线 • 如何利用闭环频率特性分析动态响应：
二阶系统的闭环频域指标
谐振峰值
Mr
：
Mr 1 2 1
2
谐振峰值
(0 0.707)

带宽指标取决于下列因素：
1、对输入信号的再现能力。
大的带宽相应于快的响应速度。
2、对高频噪声必要的滤波特性。
为了使系统能够精确地跟踪任意输入信号，系统必须具 有大的带宽。但是，从噪声的观点来看，带宽不应当太大。 因此，对带宽的要求是矛盾的，好的设计通常需要折衷考虑。 具有大带宽的系统需要高性能的元件，因此，元件的成本通 常随着带宽的增加而增大。
10:03
11
M ()
G( j) 1 G( j)

A()
1
[1 A2 () 2A() cos ()]2

[
1
1
－cos ()]2＋sin2 ()
A()
一般情况，在 M () 的极大值附近， () 变化较小，且使 M () 为 极值的谐振频率 r 常位于c 附近。
10:03
8
（2）开环频域指标和时域指标的关系
对于典型的二阶系统：
R(s)
需确定 和 c 与 的关系。
wn2
_ s(s 2wn )
C(s)
G( j)

2 n


2 n
(900 arctan )
j( j 2 n ) 2 4 2 2
2 n
sin
(35o 90o )
上述公式一般偏于保守，即实际性能比估计结果要好。
控制系统在进行初步设计时，使用经验公式，可以保证系统达
到性能指标的要求且留有一定的余地。
10:03
10
典型二阶系统估算时域指标方法：
（1）确定相角裕度 （2）根据 查P22,图5-42对应的 （3）由 计算得到 % ，ts
cos (r ) cos (c ) cos

主要内容系统闭环频率特性通过频率特性曲线分析稳态性能指标频域动态性能指标频率域特性指标与时域瞬态指标的关系2)()(1)()()(1s H s G s H s G s H +⋅=4环幅频特性。

闭环幅频特性曲线闭环对数幅频曲线二、由闭环频率特性分析系统的时域响应频率特性分析法比时域性能分析简便，且有成熟的图解法可供使用，但频率特性分析是一种概略性的间接方法，在要求系统性能指标直接而具体时，还需从时域响应面进行讨论。

在已知闭环系统稳定的条件下，可根据系统的闭环幅频特性曲线，对系统的动态过程进行定性分析与定量估算。

51、通常的闭环频域有以下几个指标：V零频幅值：ω=0时闭环幅频特性的数值(反映系统静差（误差）)V谐振频率ωr：闭环系统频率特性出现谐振峰值时的频率值V谐振峰值M r：系统闭环频率特性幅值的最大值，反映系统的平稳性，并非所有闭环频率特性的中频段有谐振峰值，若出现了谐振峰值，表明系统的阻尼比较小615M r、σ与ζ的关系曲线当相角裕量γ为30o ~60o 时，对应二阶系统的阻尼比ζ为0.3~0.6在ζ≤0.707时，二阶系统的相角裕量γ与阻尼比ζ之间的关系近似为：ζ=0.01γV谐振频率ωr表征系统瞬态响应的速度。

ωr值越大,响应时间越快。

对于弱阻尼系统(ζ较小),谐振频率ωr与阶跃响应的阻尼振荡频率ωd接近。

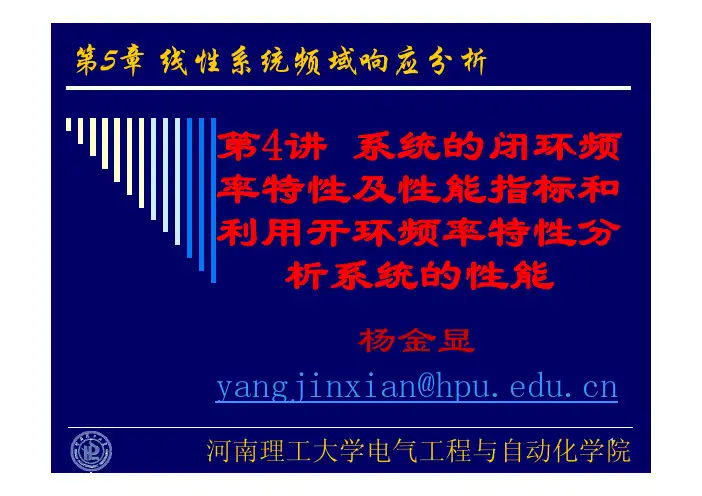
V截止频率（带宽频率）ωb当系统闭环幅频特性的幅值M(ω)降到零频率幅值的0.707(或零分贝值以下3dB)时，对应的频率ωb称为截止频率。

0～ωb的频率范围称为带宽它反映系统的快速性和低通滤波特性。

V剪切率ωc幅值=1时的频率ωc，称为剪切率，它既反映系统的相角裕度(相角裕度大,剪切率应较平缓),又表征系统从噪声中辨别信号的能力(剪切率平缓,带宽ωb大,对高频噪声的抑制不利)。

17应注意，剪切频率ωc处斜率平缓(如以-20dB/dec过0dB线)时，系统相角裕量大；而斜率陡峭时，说明具有负相角的环节集图5 剪切率中叠加于此，带来大的负相角,如图5所示，则易造成系统不稳定。

因此，已知系统的开环频率特性，就可以求出系统的闭 环频率特性，也就可以绘制出系统的闭环频率特性。 由于求出的闭环频率特性分子分母通常不是因式分解的 形式，故其频率特性图一般不如开环频率特性图容易画。 但是随着计算机的应用日益普及，其冗长的计算工作量 可以很容易地由计算机完成。另一方面，已知开环幅频 特性，可以定性的估计系统闭环频率特性。
4.5.1 由开环频率特性估计闭环频率特性
4.5.2 系统频域指标
开环频域指标

ωc——开环截止频率（幅值穿越频率），开环
对数幅频特性曲线与零频特性曲线 与-180度线交点处的频率。 γ——相位裕量 Kg——幅值裕量

4.5.2 系统频域指标
求带宽越宽；高频滤波的要求，为滤掉高频噪声，带宽又不能太宽。
4.5.2 系统频域指标

Mr——谐振峰值，闭环频率特性幅值的极大值。标志系统的相对 稳定性。
Mr
1
2
2 1 越小，系统的阻尼越大，越易稳定下来。一般取Mr ≤1.4。
，Mr值越大，系统的阻尼闭越小，越易振荡。 Mr值

闭环频域指标

ωb——闭环截止频率，闭环对数幅值L(ω)下降到-3dB时的角频率。
闭环系统将高于截止频率的信号分量滤掉，而允许低于截止频率的信
号分量通过。

ωBW——带宽，指闭环系统的对数幅值不低于-3dB时所对应的频 率范围(0≤ ωBW≤ ωb)。
带宽表征了系统响应的快速性。 对带宽的要求取决于两方面的因素：响应速度的要求，响应越快，要
4.5.1 由开环频率特性估计闭环频率特性
设系统为单位反馈，则
X o j G j X i j 1 G j

第五章 频域分析法目的：①直观，对高频干扰的抑制能力。

对快(高频)、慢(低频)信号的跟踪能力。

②便于系统的分析与设计。

③易于用实验法定传函。

§5.1 频率特性一. 定义)()()()(1n p s p s s s G +⋅⋅⋅+=θ在系统输入端加一个正弦信号：t R t r m ωsin )(⋅=))(()(22ωωωωωj s j s R s R s R m m -+⋅=+⋅=↔ 系统输出：))(()()()()(1ωωωθj s j s R p s p s s s Y m n-+⋅⋅+⋅⋅⋅+=t j t j e A e A t y t y ωω⋅+⋅+=↔-瞬态响应)()(1若系统稳定，即)(s G 的极点全位于s 左半平面，则 0)(l i m 1=∞→t y t稳态响应为：tj tj ss eA eA t y ωω⋅+⋅=-)(而)(21)()(22ωωωωωj G R jj s s R s G A m j s m -⋅-=+⋅+⋅⋅=-=)(21)()(22ωωωωωj G R jj s s R s G A m j s m ⋅=-⋅+⋅⋅== ∴t j m tj m ss e j G R je j G R j t y ωωωω⋅⋅+⋅-⋅-=-)(21)(21)( =])()([21t j t j m e j G e j G R jωωωω-⋅--⋅⋅ 又)(s G 为s 的有理函数，故)()(*ωωj G j G -=，即φωωj e j G j G )()(= φωωj e j G j G -=-)()(∴][)(21)()()(φωφωω+-+--⋅=t j t j mss e e j G R jt y =)sin()(φωω+⋅⋅t j G R m =)sin(φω+⋅t Y m可见：对稳定的线性定常系统，加入一个正弦信号，其稳态响应也是一个同频率的正弦信号。

其幅值是输入正弦信号幅值的)(ωj G 倍，其相移为)(ωφj G ∠=。

·145·第5章 线性系统的频域分析法重点与难点一、基本概念 1. 频率特性的定义设某稳定的线性定常系统，在正弦信号作用下，系统输出的稳态分量为同频率的正弦函数，其振幅与输入正弦信号的振幅之比)(ωA 称为幅频特性，其相位与输入正弦信号的相位之差)(ωϕ称为相频特性。

系统频率特性与传递函数之间有着以下重要关系：ωωj s s G j G ==|)()(2. 频率特性的几何表示用曲线来表示系统的频率特性，常使用以下几种方法：（1）幅相频率特性曲线：又称奈奎斯特（Nyquist ）曲线或极坐标图。

它是以ω为参变量，以复平面上的矢量表示)(ωj G 的一种方法。

（2）对数频率特性曲线：又称伯德（Bode ）图。

这种方法用两条曲线分别表示幅频特性和相频特性。

横坐标为ω，按常用对数lg ω分度。

对数相频特性的纵坐标表示)(ωϕ，单位为“°”（度）。

而对数幅频特性的纵坐标为)(lg 20)(ωωA L =，单位为dB 。

（3）对数幅相频率特性曲线：又称尼柯尔斯曲线。

该方法以ω为参变量，)(ωϕ为横坐标，)(ωL 为纵坐标。

3. 典型环节的频率特性及最小相位系统 （1）惯性环节：惯性环节的传递函数为11)(+=Ts s G 其频率特性 11)()(+===j T s G j G j s ωωω·146·对数幅频特性 2211lg20)(ωωT L +=(5.1)其渐近线为⎩⎨⎧≥-<=1 )lg(2010)(ωωωωT T T L a (5.2) 在ωT =1处，渐近线与实际幅频特性曲线相差最大，为3dB 。

对数相频特性)(arctg )(ωωϕT -= (5.3)其渐近线为⎪⎩⎪⎨⎧≥︒-<≤+<=10 90101.0 )lg(1.0 0)(ωωωωωϕT T T b a T a (5.4)当ωT =0.1时，有b a b a -=+=1.0lg 0 (5.5)当ωT =10时，有b a b a +=+=︒-10lg 90 (5.6)由式（5.5）、式（5.6）得︒=︒-=45 45b a因此：⎪⎩⎪⎨⎧≥︒-<≤︒-<=10 90101.0 )10lg(451.0 0)(ωωωωωϕT T T T a (5.7)（2）振荡环节：振荡环节的传递函数为10 121)(22<<++=ξξTs S T s G·147·其频率特性)1(21|)()(22ωωξωωT j Ts s G j G j s -+=== 对数幅频特性2222224)1(lg 20)(ωξωωT T L +--= (5.8)其渐近线为⎩⎨⎧≥-<=1)lg(4010)(ωωωωT T T L a (5.9) 当707.0<ξ时，在221ξω-=T 处渐近线与实际幅频特性曲线相差最大，为2121lg20ξξ-。

频率，就可确定闭环频率特性在这个频率时的幅值。
三、等相角轨迹（等N圆）
2020年4月13日
F( jw ) P jQ
1 P jQ
tg1 Q tg1 Q
P
1 P
设
tg=N N
tg(tg1 Q P
tg1 Q ) 1 P
Q P2 P Q2
整理可得
(P 1)2 (Q 1 )2 1 ( 1 )2
(w) F( jw) G( jw) 1 G( jw)
R(s) 1
H (s)
C(s) G(s)H (s)
-
对于非单位反馈系统，闭环系统的频率特性F(jw)
F( jw )
G( jw )
1
G( jw)H ( jw) 1
GK
( jw
2
)
1 G( jw )H ( jw ) H ( jw ) 1 G( jw )H ( jw ) H ( jw ) 1 GK ( jw )
震荡频率wn。
tp
wn
1z 2
wd
z
d % e 1z 2 100%
ts
4
zw3 n
，当Δ ，当Δ
2时 5时
zwn
③ 对临界阻尼和过阻尼二阶系统而言，性能指标只有ts 。
⒊ 对高阶系统，如果有主导极点存在，也可利用上述公 式进行计算。
16
（二） 频域性能指标
⑴开环频率特性性能指标
① 幅值稳定裕度 Kg(Lg) 系统开环相频特性为－180°时，系统开环频率特性幅值的
的频率 wb 称为带宽频率。频率范围 w [0, wb ] 称为
系统带宽。
（三） 频率特性的重要性质
⒈ 频率尺度与时间尺度的反比关系
若有两个系统的频率特性F1(jw)和F2(jw)有如下关系

闭环控制频率随着科技的不断进步，闭环控制系统在许多领域中得到了广泛应用。

闭环控制系统通过不断采集反馈信号，并与参考信号进行比较，调节控制器的输出信号，以实现系统的稳定控制。

频率是一个重要的控制参数，它表示控制系统响应的快慢程度。

本文将以闭环控制频率为主题，探讨闭环控制频率的意义、影响因素以及如何优化闭环控制频率。

闭环控制频率对系统的稳定性和响应速度有着重要影响。

频率高的闭环控制系统能够更快地响应参考信号的变化，实现更精确的控制目标。

而频率低的闭环控制系统反应迟缓，可能导致系统无法及时调整，造成系统不稳定。

闭环控制频率受多种因素的影响。

首先是控制器的响应速度。

控制器的响应速度越快，闭环控制系统的频率就越高。

因此，在设计闭环控制系统时，需要选择合适的控制器，以确保系统具有足够的频率响应。

其次是反馈信号的采样速率。

采样速率指的是控制系统对反馈信号进行采样的频率。

如果采样速率过低，闭环控制系统可能无法准确地捕捉到反馈信号的变化，从而影响系统的频率响应。

因此，在设计闭环控制系统时，需要合理选择采样速率，以确保系统具有足够的频率响应。

信号传输的延迟也会影响闭环控制系统的频率响应。

信号传输的延迟指的是信号从被采集到被处理再到被输出的时间。

如果信号传输的延迟过大，闭环控制系统可能无法及时响应参考信号的变化，从而影响系统的频率响应。

因此，在设计闭环控制系统时，需要减小信号传输的延迟，以提高系统的频率响应。

为了优化闭环控制频率，可以采取一些措施。

首先是选择合适的控制器。

不同的控制器具有不同的频率响应特性，需要根据具体的应用需求选择合适的控制器。

其次是合理调整采样速率。

采样速率过低会影响系统的频率响应，而采样速率过高则会增加系统的计算负担。

因此，需要在满足系统需求的前提下，选择合理的采样速率。

最后是优化信号传输的延迟。

通过优化信号传输的路径和算法，可以减小信号传输的延迟，提高系统的频率响应。

闭环控制频率是一个重要的控制参数，它影响着闭环控制系统的稳定性和响应速度。