闭环、开环频率特性与阶跃响应的关系
- 格式:pdf
- 大小:408.17 KB
- 文档页数:17


控制工程基础一、 填空题(每空1分,15题共20分)1. 控制系统由 控制对象和控制器 两部分组成。
2. 建立系统数学模型的方法有 分析法 和 实验法 两种。
3. 按其数学模型是否满足 叠加性 ,控制系统可分为线性系统和非线性系统。
4.随动系统是指 在外界作用下,系统的输出能相应于输入在广阔范围内按任意规律变化的系统5. 经典控制理论采用的数学模型主要 传递函数 以为基础;现代控制理论采用的数学模型主要以为 状态空间方程 基础。
6. 工程上常用的线性化方法是 将非线性函数在平衡点附近展开成Taylor 级数,然后去掉高次项以得到线性函数 。
7. 广义误差平方积分性能指标特点 既不允许大的动态误差e(t)长期存在,又不允许大的误差变化率长期存在 。
8. 校正元件按在系统中的连接方式可分为串联校正、 反馈校正 和 顺馈校正 等。
9. 系统频率特性指标中的谐振频率是指 幅频特性A(ω)出现最大值Amax 时的频率 。
10.系统传递函数与其单位脉冲响应函数的关系是 拉氏反变换 。
11.系统稳定的充要条件是 闭环系统特征根具有负实部 。
12.某线性定常系统的单位斜坡响应为t e t t y 2)(-+=,0≥t 。
其单位阶跃响应为 t e 221=- 。
13.在工程控制实践中,为使系统有满意的稳定性储备,一般其幅值裕度应满足 大于6dB 或大于2 。
14.最小相位系统是指 传递函数所有零点和极点均在复平面s 的左半平面内 。
15.已知系统开环传递函数为)1(9)(+=s s s G K ,则系统的固有频率、阻尼比以及单位斜坡输入所引起的稳态误差分别为 3 、 61 、 1 。
二、单项选择题(每题2分,10题共20分)1.下面关于微分环节的控制作用描述中正确的是: ( D )(A)使相位滞后 (B)减小系统的阻尼 (C)抗高频干扰 (D)使相位超前2.稳态误差除了与系统的型别、传递函数有关外,还与下述哪一项有关? ( D )(A) 阶次 (B) 振荡频率 (C) 阻尼比 (D) 输入信号类型3.二阶振荡系统幅值衰减的快慢取决于: ( C )(A) d ω (B)n ξω (C) 特征根实部绝对值 (D) 特征根虚部的分布情况4.系统输出的拉氏变换完全取决于: ( B )(A)系统的传递函数的极点位置 (B)系统的初始状态、输入及其传递函数(C)系统的传递函数 (D)系统的固有特性5.相位滞后校正环节相当于: ( A )(A )低通滤波器 (B )高通滤波器 (C )带通滤波器 (D ) 带阻滤波器6.下图为一阶系统单位脉冲响应曲线,则下列说明正确的是: ( B )(A) 系统的输出为0,2)(2≥=-t e t t ω (B) 系统的输出为0,)(≥=-t e t t ω(C) 系统传递函数为)12(1)(+=s s G (D) 系统单位脉冲响应调整时间为2s7. PI 控制类似于: ( C )(A) 增益调整 (B) 相位超前校正 (C) 相位滞后校正 (D) 相位滞后-超前校正8.某单位反馈系统的闭环传递函数为)2(1)(+=s s G ,则输入t t r 2sin 2)(=时稳态输出的幅值为: ( D )(A )2 (B )2/2 (C )2 (D )19.已知下列系统的开环传递函数为)1)(1)(1)(1()1)(1()(432165++++++=s T s T s T s T s s T s T K s G (所有参数均大于0),则下图中所给幅相曲线中正确的是: ( A )10.用Nyquist 稳定判据判断上面第9小题所给开环系统所对应的闭环系统的稳定性,所得结论正确的是: ( D )(A)0=P ,1=Z ;不稳定 (B)0=P ,2=Z ;不稳定(C)0=P ,1=Z ;稳定 (D) 0=P ,0=Z ;稳定三、简答题(2题共10分)1、简述系统开环对数频率特性曲线中三频段分析法及其适用范围。

1、反馈:输出信号被测量环节引回到输入端参与控制的作用。
2、开环控制系统与闭环控制系统的根本区别:有无反馈。
3、线性及非线性系统的定义及根本区别:当系统的数学模型能用线性微分方程描述时,该系统的称为线性系统。
非线性系统:一个系统,如果其输出不与其输入成正比,则它是非线性的。
根本区别:线性系统遵从叠加原理,而非线性系统不然。
4、传递函数的定义及特点:零初始条件下,系统输出量的拉斯变换与输入量的拉斯变换的比值。
用G〔s〕表示。
特点:1〕、传递函数是否有量纲取决于输入与输出的性质,同性质无量纲。
2〕、传递函数分母中S的阶数必n不小于分子中的S的阶数m,既n=>m ,因为系统具有惯性。
3〕、假设输入已给定,则系统的输出完全取决于其传递函数。
4〕、物理量性质不同的系统,环节和元件可以具有相同类型的传递函数。
5〕、传递函数的分母与分子分别反映系统本身与外界无关的固有特性和系统同外界的关系。
5、开环函数的定义:前向通道传递函数G〔s〕与反馈回路传递函数H(s)之积。
6、时间响应的定义和组成:系统在激励信号作用下,输出随时间的变化关系。
按振动来源分为:零状态响应和零输入响应。
按振动性质:自由响应和强迫响应。
7、瞬态性能指标以及反映系统什么特性:性能指标:上升时间tr、峰值时间tp、最大超调量Mp、调整时间ts、振荡次数N。
这些性能指标主要反映系统对输入的响应的快速性。
8、稳态误差的定义及计算公式:系统进入稳态后的误差。
稳态误差反映稳态响应偏离系统希望值的程度。
衡量控制精度的程度。
稳态误差不仅取决于系统自身结构参数,而且与输入信号有关。
系统误差:输入信号与反馈信号之差。
9、减少输入引起稳态误差的措施:增大干扰作用点之前的回路的放大倍数K1,以及增加这一段回路中积分环节的数目。
10、频率响应的概念:线性定常系统对谐波输入的稳态响应称为频率响应。
11、频率特性的组成:幅频特性和相频特性。
12、稳定性的概念:系统在扰动作用下,输出偏离原平衡状态,待扰动消除后,系统能回到原平衡状态〔无静差系统〕或到达新的平衡状态〔有静差系统〕。

4.6 频率特性与系统的动态性能4.6 频率特性与系统的动态性能控制系统的频率特性与系统的动态性能之间有密切的关系。
分析控制系统的动态特性,可以利用开环频率特性,也可以利用闭环频率特性。
二阶系统的频率特性与动态性能的时域指标之间又确定的关系,而高阶系统则不存在确定的函数关系。
4.6.1 开环频率特性与系统的动态响应若把系统的开环对数频率特性划分为低频段,中频段和高频段,这三部分对控制系统动态过程的影响是不同的。
开环频率特性的低频段主要影响阶跃响应动态过程的最后阶段,而开环频率特性的高频段主要影响阶跃响应动态过程的起始阶段。
对动态性能影响最重要的是中频段。
所以,常用开环频率的低频段估计系统的稳态性能,而用中频段估计系统的动态响应。
开环频率特性的低频段通常指第一个转折频率前的频段。
这一频段的对数幅频特性质取决于系统的积分环节和放大系数。
图4.29是开环频率特性低频段的几种情况。
图4.29 开环频率特性的低频段图 4.29(a)所示的系统低频段是平行于横轴的直线。
这说明系统中不含积分环节,是零型系统。
这种系统的单位阶跃响应是有误差的,而且可以根据对数幅频特性确定放大系数K,从而计算出系统的稳态误差。
图4.29(b)所示的系统,由于低频段的斜率为-20dB/十倍频程,可以断定系统含有一个积分环节,是Ⅰ型环节。
系统的放大系数可在处求得。
稳态误差可按Ⅰ型系统计算。
图4.29(c)所示的系统是Ⅱ型系统,系统的放大系数可按求取或在对数幅频特性曲线-40dB/十倍频程与轴的交点处求取,此时有。
系统的稳态误差按Ⅱ型系统的稳态误差计算。
开环频率特性曲线的中频段是截止频率附近的频段,截止频率就是使的频率。
即幅值曲线穿越零分贝线的频率。
这一频段,对数幅频特性的形状直接影响到系统的稳定裕量。
从而对系统动态响应过程的主要性能指标产生影响。
用开环频率特性中频段评价控制系统的动态性能,常用到的就是截止频率(穿越频率)和相位裕量。



.1.线性系统和非线性系统的根本区别在于线性系统满足迭加原理,非线性系统不满足迭加原理。
2.令线性定常系统传递函数的分母多项式为零,则可得到系统的特征方程3. 时域分析法研究自动控制系统时最常用的典型输入信号是阶跃函数4.设控制系统的开环传递函数为G(s)=)2s )(1s (s 10++,该系统为I 型系统5.二阶振荡环节的相频特性)(ωθ,当∞→ω时,其相位移)(∞θ为-180° 6. 根据输入量变化的规律分类,控制系统可分为 恒值控制系统、随动控制系统和程序控制系统7.采用负反馈连接时,如前向通道的传递函数为G(s),反馈通道的传递函数为H(s),则其等效传递函数为 )s (H )s (G 1)s (G +8. 一阶系统G(s)=1+Ts K 的时间常数T 越大,则系统的输出响应达到稳态值的时间(越长) 9.拉氏变换将时间函数变换成复变函数 10.线性定常系统的传递函数,是在零初始条件下系统输出信号的拉氏变换与输入信号的拉氏变换之比 11.若某系统的传递函数为G(s)=1Ts K +,则其频率特性的实部R(ω)是 22T1K ω+12. 微分环节的频率特性相位移θ(ω)= 90° 13. 积分环节的频率特性相位移θ(ω)= -90° 14.传递函数反映了系统的动态性能,它与系统的结构参数有关15. 系统特征方程式的所有根均在根平面的左半部分是系统稳定的充分必要条件 16. 有一线性系统,其输入分别为u 1(t)和u 2(t)时,输出分别为y 1(t)和y 2(t)。
当输入为a 1u 1(t)+a 2u 2(t)时(a 1,a 2为常数),输出应为a 1y 1(t)+a 2y 2(t)17. I 型系统开环对数幅频渐近特性的低频段斜率为-20(dB/dec)18. 设系统的传递函数为G(s)=255252++s s ,则系统的阻尼比为2119.正弦函数sin t ω的拉氏变换是 22s ω+ω20.二阶系统当0<ζ<1时,如果增加ζ,则输出响应的最大超调量%σ将 减小21.主导极点的特点是距离虚轴很近 22.余弦函数cos tω的拉氏变换是22s sω+23.设积分环节的传递函数为G(s)=s1,则其频率特性幅值M(ω)=ω124. 比例环节的频率特性相位移θ(ω)= 0° 25. 奈奎斯特稳定性判据是利用系统的.开环幅相频率特性来判据闭环系统稳定性的一个判别准则。

1.凡是输入输出关系符合_______和齐次性的系统称之为线性系统。
2.叠加原理是线性系统的基本性质之一,对于非线性系统,叠加原理_____成立。
3.线性系统与非线性系统的本质区别是是否满足_______。
4.输入输出模型是对系统的外部描述,_______是这种描述的是最基本的形式,传递函数、框图、信号流图均是由它导出。
5.根轨迹法与频域法都是建立在_______基础上的,需用要根据其画出相应的图,进而进行分析。
6.控制理论有四个重要概念:动态、模型、互联和______,这四个概念是系统分析和设计的关键。
7.计算机网络IP协议采用开环控制,TCP协议则采用______控制。
8.自动控制系统主要由对象、检测单元、执行单元和________等四个基本部分构成。
9.控制理论把系统满足物理约束条件下的负载扰动抑制、测量噪声衰减、指令跟踪、系统结构及参数变化的不确定性问题,归结为求解反馈系统的稳定性、快速性、准确性和_______。
10.反馈是处理不确定性的工具,采用反馈控制,要使系统达到稳定性、_______、准确性、鲁棒性的要求。
11.________是处理不确定性的工具,采用反馈控制,要使系统达到稳定性、快速性、准确性、鲁棒性的要求。
12.灵敏度函数不但可以描述系统对于过程参数变化的鲁棒性,同时也刻画了闭环系统对于______的抑制性能。
13.灵敏度函数不但可以描述系统对于过程_______的鲁棒性,同时也刻画了闭环系统对于扰动的抑制性能。
)14.对于物理系统,由于系统的因果性,传递函数分母的阶次n总是_________分子的阶次m。
15.传递函数2(3)ss++的极点是________。
16.传递函数23(2)(3)ss++的零点是________。
17.传递函数5(3)ss s++的有限零点是________。
18.传递函数23ss++的有限极点是________。
19.线性系统渐近稳定的充要条件是其特征方程的所有根均位于_______。
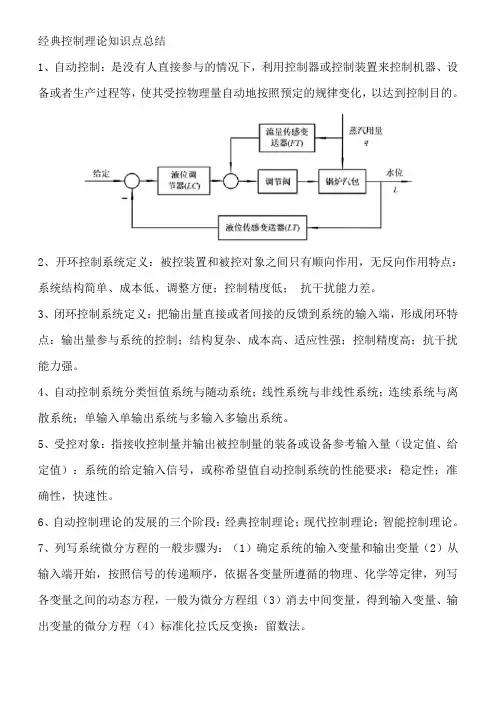
经典控制理论知识点总结1、自动控制:是没有人直接参与的情况下,利用控制器或控制装置来控制机器、设备或者生产过程等,使其受控物理量自动地按照预定的规律变化,以达到控制目的。
2、开环控制系统定义:被控装置和被控对象之间只有顺向作用,无反向作用特点:系统结构简单、成本低、调整方便;控制精度低;抗干扰能力差。
3、闭环控制系统定义:把输出量直接或者间接的反馈到系统的输入端,形成闭环特点:输出量参与系统的控制;结构复杂、成本高、适应性强;控制精度高;抗干扰能力强。
4、自动控制系统分类恒值系统与随动系统;线性系统与非线性系统;连续系统与离散系统;单输入单输出系统与多输入多输出系统。
5、受控对象:指接收控制量并输出被控制量的装备或设备参考输入量(设定值、给定值):系统的给定输入信号,或称希望值自动控制系统的性能要求:稳定性;准确性,快速性。
6、自动控制理论的发展的三个阶段:经典控制理论;现代控制理论;智能控制理论。
7、列写系统微分方程的一般步骤为:(1)确定系统的输入变量和输出变量(2)从输入端开始,按照信号的传递顺序,依据各变量所遵循的物理、化学等定律,列写各变量之间的动态方程,一般为微分方程组(3)消去中间变量,得到输入变量、输出变量的微分方程(4)标准化拉氏反变换:留数法。
8、传递函数的定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比,称为线性定常系统的传递函数微分方程在时间域,传递函数在复数域传递函数的性质传递函数只适用于线性定常系统;传递函数是在零初始条件下定义的;传递函数可以有量纲;传递函数表示系统的端口关系;传递函数描述了系统的固有特性传递函数的表达式有理分式形式(特征多项式型)零、极点形式(首一型)时间常数形式(尾一型)。
9、动态性能的五个指标延迟时间(稳态值50%);上升时间(稳态值10%-90%,非一阶0-稳态值);峰值时间;调节时间;超调量(或最大超调量)。
10、一阶单位阶跃系统的动态性能指标:调节时间t=3T(5%误差带),t=4T(2%误差带)延迟时间t=0.69T上升时间t=2.20T峰值时间,超调量不存欠阻尼二阶系统的动态性能指标(P72)一对靠的很近或相等的零、极点,彼此将相互抵消,其结果使留数等于零,此类零、极点称为偶极子闭环主导极点,它应满足以下两个条件:(1)在s平面上,距离虚轴比较近,且附近没有其他的零点和极点(2)其实部的绝对值比其他极点实部的绝对值小5倍以上。

[标签:标题]篇一:自动控制原理试题库(有答案的)自动控制理论试卷(A/B卷闭卷)一、填空题(每空1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过值进行的。
2、复合控制有两种基本形式:即按前馈复合控制。
3、两个传递函数分别为G1(s)与G2(s)的环节,以并联方式连接,其等效传递函数为G(s),则G(s)为(用G1(s)与G2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率?n?,阻尼比??,该系统的特征方程为,该系统的单位阶跃响应曲线为。
5、若某系统的单位脉冲响应为g(t)?10e?0.2t?5e?0.5t,则该系统的传递函数G(s)为。
6、根轨迹起始于终止于7、设某最小相位系统的相频特性为?(?)?tg?1(??)?900?tg?1(T?),则该系统的开环传递函数为。
8、PI控制器的输入-输出关系的时域表达式是其相应的传递函数为,由于积分环节的引入,可以改善系统的性能。
二、选择题(每题2 分,共20分)1、采用负反馈形式连接后,则( )A、一定能使闭环系统稳定;B、系统动态性能一定会提高;C、一定能使干扰引起的误差逐渐减小,最后完全消除;D、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果()。
A、增加开环极点;B、在积分环节外加单位负反馈;C、增加开环零点;D、引入串联超前校正装置。
3、系统特征方程为D(s)?s3?2s2?3s?6?0,则系统()A、稳定;B、单位阶跃响应曲线为单调指数上升;C、临界稳定;D、右半平面闭环极点数Z?2。
4、系统在r(t)?t2作用下的稳态误差ess??,说明()A、型别v?2;B、系统不稳定;C、输入幅值过大;D、闭环传递函数中有一个积分环节。
5、对于以下情况应绘制0°根轨迹的是()A、主反馈口符号为“-”;B、除Kr外的其他参数变化时;C、非单位反馈系统;D、根轨迹方程(标准形式)为G(s)H(s)??1。
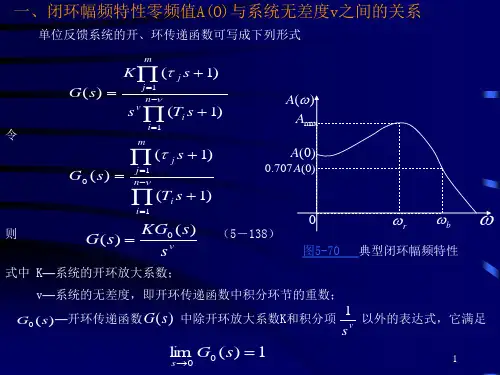
主要内容系统闭环频率特性通过频率特性曲线分析稳态性能指标频域动态性能指标频率域特性指标与时域瞬态指标的关系2)()(1)()()(1s H s G s H s G s H +⋅=4环幅频特性。
闭环幅频特性曲线闭环对数幅频曲线二、由闭环频率特性分析系统的时域响应频率特性分析法比时域性能分析简便,且有成熟的图解法可供使用,但频率特性分析是一种概略性的间接方法,在要求系统性能指标直接而具体时,还需从时域响应面进行讨论。
在已知闭环系统稳定的条件下,可根据系统的闭环幅频特性曲线,对系统的动态过程进行定性分析与定量估算。
51、通常的闭环频域有以下几个指标:V零频幅值:ω=0时闭环幅频特性的数值(反映系统静差(误差))V谐振频率ωr:闭环系统频率特性出现谐振峰值时的频率值V谐振峰值M r:系统闭环频率特性幅值的最大值,反映系统的平稳性,并非所有闭环频率特性的中频段有谐振峰值,若出现了谐振峰值,表明系统的阻尼比较小615M r、σ与ζ的关系曲线当相角裕量γ为30o ~60o 时,对应二阶系统的阻尼比ζ为0.3~0.6在ζ≤0.707时,二阶系统的相角裕量γ与阻尼比ζ之间的关系近似为:ζ=0.01γV谐振频率ωr表征系统瞬态响应的速度。
ωr值越大,响应时间越快。
对于弱阻尼系统(ζ较小),谐振频率ωr与阶跃响应的阻尼振荡频率ωd接近。
V截止频率(带宽频率)ωb当系统闭环幅频特性的幅值M(ω)降到零频率幅值的0.707(或零分贝值以下3dB)时,对应的频率ωb称为截止频率。
0~ωb的频率范围称为带宽它反映系统的快速性和低通滤波特性。
V剪切率ωc幅值=1时的频率ωc,称为剪切率,它既反映系统的相角裕度(相角裕度大,剪切率应较平缓),又表征系统从噪声中辨别信号的能力(剪切率平缓,带宽ωb大,对高频噪声的抑制不利)。
17应注意,剪切频率ωc处斜率平缓(如以-20dB/dec过0dB线)时,系统相角裕量大;而斜率陡峭时,说明具有负相角的环节集图5 剪切率中叠加于此,带来大的负相角,如图5所示,则易造成系统不稳定。
实用文档【机械电子工程根底II 】习题答案一、单项选择题1、开环系统与闭环系统最本质的区别是〔 A 〕A.开环系统的输出对系统无控制作用,闭环系统的输出对系统有控制作用B.开环系统的输入对系统无控制作用,闭环系统的输入对系统有控制作用C.开环系统不一定有反应回路,闭环系统有反应回路D.开环系统不一定有反应回路,闭环系统也不一定有反应回路2、假设f t t t (),,=⎧⎨⎩⎪00515≤<≥,那么L f t [()]=〔 B 〕A.e s s-B.e s s -5C.1sD.15se s 3、f t t ().,=+051其L f t [()]=〔 C 〕 A.s s +052. B.052.s C.1212s s+ D.12s4、以下函数既可用初值定理求其初始值又可用终值定理求其终值的为〔 D 〕A.5252s + B.ss 216+ C.12s -D.12s + 5、假设f t te t ()=-2,那么L f t [()]=〔 B 〕 A.12s + B.122()s + C.12s - D.122()s -6、线性系统与非线性系统的根本区别在于〔 C 〕A.线性系统微分方程的系数为常数,而非线性系统微分方程的系数为时变函数B.线性系统只有一个外加输入,而非线性系统有多个外加输入C.线性系统满足迭加原理,非线性系统不满足迭加原理实用文档D.线性系统在实际系统中普遍存在,而非线性系统在实际中存在较少 7、系统方框图如图示,那么该系统的开环传递函数为〔 B 〕A.1051s + B.2051s s +C.10251s s ()+D.2s8、二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,那么其传递函数为〔 D 〕 A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++D.10054(.)()s s ++9、某系统的传递函数为2s 5)s (G +=,那么该系统的单位脉冲响应函数为〔 A 〕 A.52e t - B.5tC.52e tD.5t10、二阶欠阻尼系统的上升时间t r 定义为〔 C 〕 A.单位阶跃响应到达稳态值所需的时间B.单位阶跃响应从稳态值的10%上升到90%所需的时间C.单位阶跃响应从零第一次上升到稳态值时所需的时间D.单位阶跃响应到达其稳态值的50%所需的时间11、系统类型λ、开环增益K 对系统稳态误差的影响为〔 A 〕 A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小 12、一系统的传递函数为G s KTs ()=+1,那么该系统时间响应的快速性〔 C 〕 A.与K 有关 B.与K 和T 有关 C.与T 有关D.与输入信号大小有关13、一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,那么该系统为〔 C 〕A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为414、瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的〔 B 〕 A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数D.单位斜坡函数15、二阶系统的传递函数为G s Ks s ()=++2212,当K 增大时,其〔 C 〕 A.无阻尼自然频率ωn 增大,阻尼比ξ增大 B.无阻尼自然频率ωn 增大,阻尼比ξ减小 C.无阻尼自然频率ωn 减小,阻尼比ξ减小 D.无阻尼自然频率ωn 减小,阻尼比ξ增大 16、所谓最小相位系统是指〔 B 〕 A.系统传递函数的极点均在S 平面左半平面B.系统开环传递函数的所有零点和极点均在S 平面左半平面C.系统闭环传递函数的所有零点和极点均在S 平面右半平面D.系统开环传递函数的所有零点和极点均在S 平面右半平面 17、一系统的传递函数为G s s ()=+102,那么其截止频率ωb 为〔 A 〕 A. 2rad s / rad s /C.5rad s /D.10rad s /18、一系统的传递函数为G s Ks Ts ()()=+1,那么其相位角ϕω()可表达为〔 B 〕A.--tg T 1ωB.-︒--901tg T ωC.901︒--tg T ωD.tg T -1ω19、一系统的传递函数为G s s ()=+22,当输入r t t ()sin =22时,那么其稳态输出的幅值为〔 A 〕 A.2 B.22/ C.2D.420、延时环节e s ->ττ()0,其相频特性和幅频特性的变化规律是〔 D 〕 A.ϕωω(),()=︒=900L dB B.ϕωωτω(),()=-=L 1 dB C.ϕωωωτ(),()=︒=90L dB D.ϕωωτω(),()=-=L 0 dB21、一单位反应系统的开环传递函数为G s Ks s s ()()()=++12,当K 增大时,对系统性能能的影响是〔 A 〕 A.稳定性降低 B.频宽降低 C.阶跃输入误差增大D.阶跃输入误差减小22、一单位反应系统的开环Bode 图,其幅频特性在低频段是一条斜率为-20dB dec /的渐近直线,且延长线与0dB 线的交点频率为ωc =5,那么当输入为r t t ().=05时,其稳态误差为〔 A 〕C.023、利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N =-中的Z 表示意义为〔 D 〕 A.开环传递函数零点在S 左半平面的个数 B.开环传递函数零点在S 右半平面的个数 C.闭环传递函数零点在S 右半平面的个数 D.闭环特征方程的根在S 右半平面的个数24、关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下表达中正确的选项是〔 B 〕 A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的 B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的 C.乃奎斯特判据是用来判断开环系统稳定性的 D.以上表达均不正确25、以下频域性能指标中根据开环系统来定义的是〔 D 〕 A.截止频率ωb B.谐振频率ωr 与谐振峰值M r C.频带宽度D.相位裕量γ与幅值裕量kg26、一单位反应系统的开环传递函数为G s Ks s K ()()=+,那么该系统稳定的K 值范围为〔 A 〕A.K >0B.K >1C.0<K <10D. K >-127、对于开环频率特性曲线与闭环系统性能之间的关系,以下表达中不正确的有〔 A 〕 A.开环频率特性的低频段表征了闭环系统的稳定性 B.中频段表征了闭环系统的动态特性 C.高频段表征了闭环系统的抗干扰能力D.低频段的增益应充分大,以保证稳态误差的要求28、以下性能指标中不能反映系统响应速度的指标为〔 D 〕 A.上升时间t r B.调整时间t s C.幅值穿越频率ωcD.相位穿越频率ωg29、当系统采用串联校正时,校正环节为G s s s c ()=++121,那么该校正环节对系统性能的影响是〔 D 〕A.增大开环幅值穿越频率ωcB.增大稳态误差C.减小稳态误差D.稳态误差不变,响应速度降低 30、串联校正环节G s As Bs c ()=++11,关于A 与B 之间关系的正确描述为〔 A 〕 A.假设G c (s)为超前校正环节,那么A >B >0 B.假设G c (s)为滞后校正环节,那么A >B >0 C.假设G c (s)为超前—滞后校正环节,那么A≠B D.假设G c (s)为PID 校正环节,那么A=0,B >0 31. 线性系统与非线性系统的根本区别在于〔 C 〕A.线性系统微分方程的系数为常数,而非线性系统微分方程的系数为时变函数B.线性系统只有一个外加输入,而非线性系统有多个外加输入C.线性系统满足迭加原理,非线性系统不满足迭加原理D.线性系统在实际系统中普遍存在,而非线性系统在实际中存在较少实用文档32. 系统方框图如图示,那么该系统的开环传递函数为〔 B 〕A.1051s + B.2051s s +C.10251s s ()+D.2s33. 二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,那么其传递函数为〔 D 〕 A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++D.10054(.)()s s ++34. 某系统的传递函数为2s 5)s (G +=,那么该系统的单位脉冲响应函数为〔 A 〕 A.52e t - B.5tC.52e tD.5t35. 二阶欠阻尼系统的上升时间t r 定义为〔 C 〕 A.单位阶跃响应到达稳态值所需的时间B.单位阶跃响应从稳态值的10%上升到90%所需的时间C.单位阶跃响应从零第一次上升到稳态值时所需的时间D.单位阶跃响应到达其稳态值的50%所需的时间36. 系统类型λ、开环增益K 对系统稳态误差的影响为〔 A 〕 A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小 37. 一系统的传递函数为G s KTs ()=+1,那么该系统时间响应的快速性〔 C 〕 A.与K 有关B.与K 和T 有关C.与T 有关D.与输入信号大小有关38. 一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,那么该系统为〔 C 〕A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为439. 瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的〔 B 〕 A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数D.单位斜坡函数40.二阶系统的传递函数为G s Ks s ()=++2212 ,当K 增大时,其〔 C 〕A.无阻尼自然频率ωn 增大,阻尼比ξ增大B.无阻尼自然频率ωn 增大,阻尼比ξ减小C.无阻尼自然频率ωn 减小,阻尼比ξ减小D.无阻尼自然频率ωn 减小,阻尼比ξ增大 41. 所谓最小相位系统是指〔 B 〕 A.系统传递函数的极点均在S 平面左半平面B.系统开环传递函数的所有零点和极点均在S 平面左半平面C.系统闭环传递函数的所有零点和极点均在S 平面右半平面D.系统开环传递函数的所有零点和极点均在S 平面右半平面 42. 一系统的传递函数为G s s ()=+102,那么其截止频率ωb 为〔 A 〕 A. 2rad s / rad s /C.5rad s /D.10rad s /43. 一系统的传递函数为G s Ks Ts ()()=+1,那么其相位角ϕω()可表达为〔 B 〕A.--tg T 1ωB.-︒--901tg T ωC.901︒--tg T ωD.tg T -1ω44. 一系统的传递函数为G s s ()=+22,当输入r t t ()sin =22时,那么其稳态输出的幅值为〔 A 〕A.2B.22/C.2D.445. 延时环节e s ->ττ()0,其相频特性和幅频特性的变化规律是〔 D 〕 A.ϕωω(),()=︒=900L dB B.ϕωωτω(),()=-=L 1 dB C.ϕωωωτ(),()=︒=90L dB D.ϕωωτω(),()=-=L 0 dB46. 一单位反应系统的开环传递函数为G s Ks s s ()()()=++12,当K 增大时,对系统性能能的影响是〔 A 〕 A.稳定性降低 B.频宽降低 C.阶跃输入误差增大D.阶跃输入误差减小47. 一单位反应系统的开环Bode 图,其幅频特性在低频段是一条斜率为-20dB dec /的渐近直线,且延长线与0dB 线的交点频率为ωc =5,那么当输入为r t t ().=05时,其稳态误差为〔 A 〕C.048. 利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N =-中的Z 表示意义为〔 D 〕 A.开环传递函数零点在S 左半平面的个数 B.开环传递函数零点在S 右半平面的个数 C.闭环传递函数零点在S 右半平面的个数 D.闭环特征方程的根在S 右半平面的个数49. 关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下表达中正确的选项是〔 B 〕A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的C.乃奎斯特判据是用来判断开环系统稳定性的D.以上表达均不正确50.以下频域性能指标中根据开环系统来定义的是〔 D 〕A.截止频率ωbB.谐振频率ωr 与谐振峰值M rC.频带宽度D.相位裕量γ与幅值裕量kg51 一单位反应系统的开环传递函数为G s Ks s K ()()=+,那么该系统稳定的K 值范围为〔 A 〕A.K >0B.K >1C.0<K <10D. K >-152. 对于开环频率特性曲线与闭环系统性能之间的关系,以下表达中不正确的有〔 A 〕 A.开环频率特性的低频段表征了闭环系统的稳定性 B.中频段表征了闭环系统的动态特性 C.高频段表征了闭环系统的抗干扰能力D.低频段的增益应充分大,以保证稳态误差的要求53. 以下性能指标中不能反映系统响应速度的指标为〔 D 〕 A.上升时间t r B.调整时间t s C.幅值穿越频率ωcD.相位穿越频率ωg54. 当系统采用串联校正时,校正环节为G s s s c ()=++121,那么该校正环节对系统性能的影响是〔 D 〕A.增大开环幅值穿越频率ωcB.增大稳态误差C.减小稳态误差D.稳态误差不变,响应速度降低 55. 串联校正环节G s As Bs c ()=++11,关于A 与B 之间关系的正确描述为〔 A 〕 A.假设G c (s)为超前校正环节,那么A >B >0 B.假设G c (s)为滞后校正环节,那么A >B >0 C.假设G c (s)为超前—滞后校正环节,那么A≠B D.假设G c (s)为PID 校正环节,那么A=0,B >0 56. 开环系统与闭环系统最本质的区别是〔 A 〕A.开环系统的输出对系统无控制作用,闭环系统的输出对系统有控制作用B.开环系统的输入对系统无控制作用,闭环系统的输入对系统有控制作用C.开环系统不一定有反应回路,闭环系统有反应回路D.开环系统不一定有反应回路,闭环系统也不一定有反应回路57. 假设f t t t (),,=⎧⎨⎩⎪00515≤<≥,那么L f t [()]=〔 B 〕A.e s s-B.e s s -5C.1sD.15se s 58.f t t ().,=+051其L f t [()]=〔 C 〕 A.s s +052. B.052.s C.1212s s+ D.12s59. 以下函数既可用初值定理求其初始值又可用终值定理求其终值的为〔 D 〕A.5252s + B.ss 216+ C.12s -D.12s + 60. 假设f t te t ()=-2,那么L f t [()]=〔 B 〕 A.12s + B.122()s +C.12s - D.122()s - 61. 系统类型λ、开环增益K 对系统稳态误差的影响为〔 A 〕 A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小 62 一系统的传递函数为G s KTs ()=+1,那么该系统时间响应的快速性〔 C 〕 A.与K 有关 B.与K 和T 有关 C.与T 有关D.与输入信号大小有关63 一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,那么该系统为〔 C 〕A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为464. 瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的〔 B 〕 A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数D.单位斜坡函数65.二阶系统的传递函数为G s Ks s ()=++2212,当K 增大时,其〔 C 〕 A.无阻尼自然频率ωn 增大,阻尼比ξ增大 B.无阻尼自然频率ωn 增大,阻尼比ξ减小 C.无阻尼自然频率ωn 减小,阻尼比ξ减小 D.无阻尼自然频率ωn 减小,阻尼比ξ增大 66. 所谓最小相位系统是指〔 B 〕 A.系统传递函数的极点均在S 平面左半平面B.系统开环传递函数的所有零点和极点均在S 平面左半平面C.系统闭环传递函数的所有零点和极点均在S 平面右半平面D.系统开环传递函数的所有零点和极点均在S 平面右半平面 67. 一系统的传递函数为G s s ()=+102,那么其截止频率ωb 为〔 A 〕 A. 2rad s / rad s /C.5rad s /D.10rad s /68. 一系统的传递函数为G s Ks Ts ()()=+1,那么其相位角ϕω()可表达为〔 B 〕A.--tg T 1ωB.-︒--901tg T ωC.901︒--tg T ωD.tg T -1ω69. 一系统的传递函数为G s s ()=+22,当输入r t t ()sin =22时,那么其稳态输出的幅值为〔 A 〕 A.2 B.22/ C.2D.470. 延时环节e s ->ττ()0,其相频特性和幅频特性的变化规律是〔 D 〕 A.ϕωω(),()=︒=900L dB B.ϕωωτω(),()=-=L 1 dB C.ϕωωωτ(),()=︒=90L dB D.ϕωωτω(),()=-=L 0 dB71. 一单位反应系统的开环传递函数为G s Ks s s ()()()=++12,当K 增大时,对系统性能能的影响是〔 A 〕 A.稳定性降低 B.频宽降低 C.阶跃输入误差增大D.阶跃输入误差减小72. 一单位反应系统的开环Bode 图,其幅频特性在低频段是一条斜率为-20dB dec /的渐近直线,且延长线与0dB 线的交点频率为ωc =5,那么当输入为r t t ().=05时,其稳态误差为〔 A 〕C.073. 利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N =-中的Z 表示意义为〔 D 〕 A.开环传递函数零点在S 左半平面的个数 B.开环传递函数零点在S 右半平面的个数 C.闭环传递函数零点在S 右半平面的个数 D.闭环特征方程的根在S 右半平面的个数74. 关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下表达中正确的选项是〔 B 〕A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的C.乃奎斯特判据是用来判断开环系统稳定性的D.以上表达均不正确75. 以下频域性能指标中根据开环系统来定义的是〔 D 〕 A.截止频率ωbB.谐振频率ωr 与谐振峰值M rC.频带宽度D.相位裕量γ与幅值裕量kg76 一单位反应系统的开环传递函数为G s Ks s K ()()=+,那么该系统稳定的K 值范围为〔 A 〕A.K >0B.K >1C.0<K <10D. K >-177. 对于开环频率特性曲线与闭环系统性能之间的关系,以下表达中不正确的有〔 A 〕 A.开环频率特性的低频段表征了闭环系统的稳定性 B.中频段表征了闭环系统的动态特性 C.高频段表征了闭环系统的抗干扰能力D.低频段的增益应充分大,以保证稳态误差的要求78. 以下性能指标中不能反映系统响应速度的指标为〔 D 〕 A.上升时间t r B.调整时间t s C.幅值穿越频率ωcD.相位穿越频率ωg79. 当系统采用串联校正时,校正环节为G s s s c ()=++121,那么该校正环节对系统性能的影响是〔 D 〕A.增大开环幅值穿越频率ωcB.增大稳态误差C.减小稳态误差D.稳态误差不变,响应速度降低 80. 串联校正环节G s As Bs c ()=++11,关于A 与B 之间关系的正确描述为〔 A 〕 A.假设G c (s)为超前校正环节,那么A >B >0 B.假设G c (s)为滞后校正环节,那么A >B >0 C.假设G c (s)为超前—滞后校正环节,那么A≠B D.假设G c (s)为PID 校正环节,那么A=0,B >0 81. 开环系统与闭环系统最本质的区别是〔 A 〕A.开环系统的输出对系统无控制作用,闭环系统的输出对系统有控制作用B.开环系统的输入对系统无控制作用,闭环系统的输入对系统有控制作用C.开环系统不一定有反应回路,闭环系统有反应回路D.开环系统不一定有反应回路,闭环系统也不一定有反应回路82. 假设f t t t (),,=⎧⎨⎩⎪00515≤<≥,那么L f t [()]=〔 B 〕A.e s s-B.e s s -5C.1sD.15se s 83.f t t ().,=+051其L f t [()]=〔 C 〕 A.s s +052. B.052.s C.1212s s+ D.12s84. 以下函数既可用初值定理求其初始值又可用终值定理求其终值的为〔 D 〕A.5252s + B.ss 216+ C.12s -D.12s + 85. 假设f t te t ()=-2,那么L f t [()]=〔 B 〕 A.12s + B.122()s +C.12s - D.122()s - 86. 线性系统与非线性系统的根本区别在于〔 C 〕A.线性系统微分方程的系数为常数,而非线性系统微分方程的系数为时变函数B.线性系统只有一个外加输入,而非线性系统有多个外加输入C.线性系统满足迭加原理,非线性系统不满足迭加原理D.线性系统在实际系统中普遍存在,而非线性系统在实际中存在较少 87. 系统方框图如图示,那么该系统的开环传递函数为〔 B 〕A.1051s + B.2051s s +C.10251s s ()+D.2s88. 二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,那么其传递函数为〔 D 〕 A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++D.10054(.)()s s ++89. 某系统的传递函数为2s 5)s (G +=,那么该系统的单位脉冲响应函数为〔 A 〕 A.52e t - B.5tC.52e tD.5t90. 二阶欠阻尼系统的上升时间t r 定义为〔 C 〕 A.单位阶跃响应到达稳态值所需的时间B.单位阶跃响应从稳态值的10%上升到90%所需的时间C.单位阶跃响应从零第一次上升到稳态值时所需的时间D.单位阶跃响应到达其稳态值的50%所需的时间91、当系统的输入和输出时,求系统结构与参数的问题,称为( B ) A.最优控制 B.系统辩识 C.系统校正D.自适应控制92、反应控制系统是指系统中有( A ) A.反应回路 B.惯性环节 C.积分环节D.PID 调节器93、( A )=1s a+,(a 为常数)。
机械控制工程基础复习题11、 选择填空(30分,每小题2分)(下列各题均给出数个答案,但只有一个是正确的,请将正确答案的序号写在空白 处)1.1在下列典型环节中,属于振荡环节的是 。
(A) 101.010)(2++=s s s G (B) 101.01)(2++=s s s G (C) 101)(+=s s G 1.2系统的传递函数定义为在零初始条件下输出量的Laplace 变换与输入量的Laplace变换之比,其表达式 。
(A )与输入量和输出量二者有关(B )不仅与输入量和输出量二者有关,还与系统的结构和参数有关 (C )只与系统的结构和参数有关,与输入量和输出量二者无关 1.3系统峰值时间p t 满足 。
(A )0)(=pp o dt t dx (B ))()(∞=o p o x t x (C ))()()(∞⋅∆≤∞-o o p o x x t x其中,)(t x o 为系统的单位阶跃响应。
1.4开环传递函数为G (s )的单位反馈系统的静态速度误差系数的计算式为 。
(A) )(lim 0s G K s v →= (B) )(lim 2s G s K s v →=(C) )(lim 0s sG K s v →=1.5最大百分比超调量(%)p M 的定义式为 。
(A ))()(max (%)∞-=o o p x t x M (B) %100)()()(max (%)∞∞-=o o o p x x t x M(C ))()(max(%)t x t x M i o p = 其中,)(t x i 为系统的输入量,)(t x o 为系统的单位阶跃响应,)(max t x o 为)(t x o 的最大值。
1.6给同一系统分别输入)sin()(11t R t x i ω=和)sin()(2t R t x r i ω=这两种信号(其中,r ω是系统的谐振频率,1ω是系统正常工作频率范围内的任一频率),设它们对应的稳态输出分别为)sin()(1111ϕω+=t C t x o 和)sin()(222ϕω+=t C t x r o ,则 成立。
西北工业大学2020春机考《控制工程基础》作业1单选题1.通常以()评价系统单位阶跃响应的稳态精度。
A.超调量B.调节时间C.稳态误差D.延迟时间答案:C2.系统开环对数幅频特性曲线与()线的交点频率称为系统的截止频率。
A.0oB.数轴C.零分贝D.等分贝答案:C3.稳定环节相角的绝对值()不稳定环节相角的绝对值。
A.大于B.小于C.等于D.无法比较答案:B4.单位脉冲函数的拉氏变换式等于1;单位阶跃函数的拉氏变换式等于()。
A.0B.1C.sD.1/s答案:D5.微分环节的对数幅频与积分环节的()互为镜像。
A.零分贝线B.0o线C.相频曲线D.等分贝线答案:A6.()法主要用于非线性系统的稳定性分析、自激振荡分析及自振荡频率和振幅的计算。
A.实值函数B.矩阵函数C.代数函数D.描述函数答案:D7.微分环节的对数幅频特性曲线为一条在ω()处通过零分贝线的直线,其斜率为20dB/dec。
A.0B.1C.-1D.无穷大答案:B8.乃奎斯特判据是一种应用()曲线来判别闭环系统稳定性的判据。
A.开环频率特性B.闭环频率特性C.幅相频率特性D.数轴答案:A9.一般情况下,超调量愈(),系统的瞬态响应震荡的愈厉害。
A.大B.小C.不变D.不确定答案:A10.系统的稳定性只与闭环()点位置有关。
A.极B.零C.正D.负答案:A11.通常把用二阶微分方程描述的系统称为()系统。
A.一阶B.二阶C.三阶D.四阶答案:B12.若开环系统稳定要使闭环系统稳定的充分必要条件是系统开环幅相频率特性曲线不包围()点。
A.(0,j1)B.(0,j0)C.(1,j0)D.(-1,j0)答案:D13.反馈控制系统的传递函数可以在()下对描述系统的微分方程进行拉氏变换后求得。
A.零初始条件B.无穷大初始条件C.随机条件D.无确定条件答案:A14.典型输入信号中,单位阶跃函数的时域表达式为()。
A.1/sB.1(t)C.1/s2。
自动控制原理试题2. (10分)已知某系统初始条件为零,其单位阶跃响应为)0(8.08.11)(94≥+-=--t e e t h t t ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。
K 表示开环增益。
P 表示开环系统极点在右半平面上的数目。
v 表示系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4.(12分)已知系统结构图如下,试求系统的传递函数)(,)(s E s C1.(10分)已知某单位负反馈系统的开环传递函数为)5(4)(+=S S s G ,求该系统的单位脉冲响应和单位阶跃响应。
3.(10分)系统闭环传递函数为2222)(nn n s s G ωξωω++=,若要使系统在欠阻尼情况下的单位阶跃响应的超调量小于16.3%,调节时间小于6s ,峰值时间小于6.28s ,试在S 平面上绘出满足要求的闭环极点可能位于的区域。
(8分)0,3==p v (a )0,0==p v (b ) 2,0==p v (c ) 题4图 题2图6. (15分)已知最小相位系统的对数幅频特性曲线如下图所示(分段直线近似表示)1、.(10分)已知某单位负反馈系统的开环传递函数为)5(6)(+=s s s G ,试求系统的单位脉冲响应和单位阶跃响应。
3、(10分)已知系统的结构图如下,试求: (1)开环的对数幅频和相频特性曲线;(2)单位阶跃响应的超调量σ%,调节时间ts ; (3)相位裕量γ,幅值裕量h 。
7.(15分)已知系统结构图如下图所示,试求传递函数)()(,)()(s R s E s R s C 。
(1)试写出系统的传递函数G(s);(2)画出对应的对数相频特性的大致形状; (3)在图上标出相位裕量Υ。
3. (10分)已知某系统初始条件为零,其单位阶跃响应为)0(8.08.11)(94≥+-=--t e e t h t t ,试求系统的传递函数及单位脉冲响应。