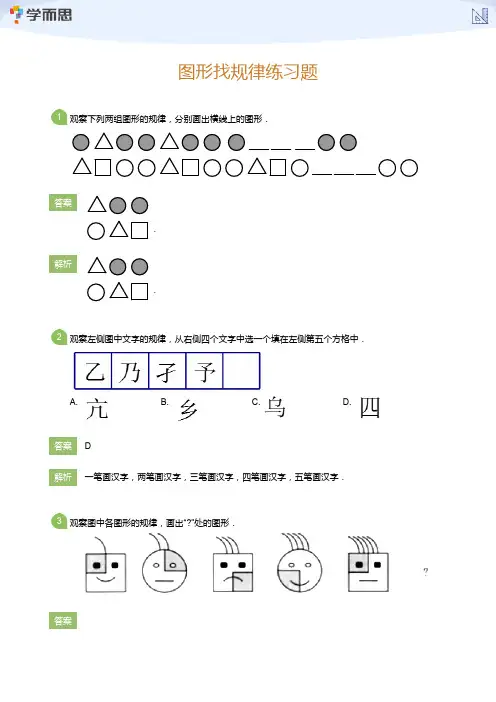
三年级图形找规律

找规律☜知识要点寻找一列数或几幅有联系的图的排列和变化规律，再根据这样的规律，在这列数或图里填上适当的数或图，这样的问题就叫做找规律。

所以，找规律分为数字找规律和图形找规律。

常见的数列规律：1、数列各项只与它的项数有关，或只与它的前一项有关。

如：1,2,4,8,16,32......2、前后几项为一组，以每组的关系找到规律。

如：1,1,2,3,5,8,13......3、数列本身要与其他数列对比才能发现规律。

如：11，12,14,18,26......常见的图形变化规律：1、图形整体变化。

即图形的内部及相对位置没有发生变化，如图形的旋转、翻转。

2、图形的内部及相对位置的变化。

即按某种观察变化使一些图形数量增加或减少。

3、特殊变化。

即某些点、线段、图形的颜色发生变化。

☜精选例题【例1】：找出下面数列的规律，并根据规律在括号里填出适当的数。

（1）4,7,10,13，（）......（2）2,6,18，（）......(3) 1,4,9,16,( ) ......（4）2,6,12,20，（）......☝思路点拨：通过分析数列各项与项数的关系，可以发现：（1）的规律是：前项＋3＝后项，括号里填16。

（2）的规律是：前项×3＝后项，括号里填54。

（3）的规律是：每项依次为：1＝1×1,4＝2×2,9＝3×3,16＝4×4,5×5＝25，所以填25。

（4）的规律是：各项依次为2＝1×2,6＝2×3,12＝3×4,20＝4×5,5×6＝30，所以括号里填30.☝标准答案：（1）4,7,10,13，（16 ）......（2）2,6,18，（54 ）......(3) 1,4,9,16,( 25 ) ......（4）2,6,12,20，（30 ）......✌活学巧用1、找规律填数。

（1）12,16,20,24，（），（）（2）86,84,80，（），72，（）（3）1,4,9,（）,25，36，（）（4）100,81，64，（），36，（），16（5）1,2,4,7,11，（），（）（6）3,8,15,24,35，（），（）【例2】：找出下面数列的规律，并根据规律在括号里填出适当的数。

三年级数学下册第三单元《找规律》教案一、教学目标1. 知识与技能：（1）能够通过观察、实验发现简单图形的排列规律，并应用规律解决实际问题。

（2）培养学生的逻辑思维能力和创新能力。

2. 过程与方法：（1）通过观察、操作、归纳等方法，发现图形的排列规律。

（2）运用数学语言描述规律，提高学生的表达能力和交流能力。

3. 情感态度与价值观：（1）培养学生对数学的兴趣，激发学习积极性。

（2）培养学生合作、探究的精神，培养学生的团队意识。

二、教学内容1. 教学知识点：（1）认识图形排列的规律。

（2）学会用数学语言描述规律。

2. 教学重点：（1）培养学生发现和总结图形排列规律的能力。

（2）培养学生运用规律解决实际问题的能力。

三、教学过程1. 导入新课：（1）利用图片或实物，引导学生观察、发现其中的规律。

（2）激发学生兴趣，引导学生积极参与课堂活动。

2. 自主探究：（1）让学生独立观察、分析图形排列的规律。

（2）学生之间相互交流、讨论，总结规律。

3. 小组合作：（1）分组进行实践活动，让学生应用规律解决实际问题。

（2）培养学生的团队协作能力和创新意识。

4. 课堂讲解：（1）讲解图形排列的规律，引导学生用数学语言描述。

（2）解答学生疑问，巩固所学知识。

5. 练习巩固：（1）设计相关练习题，让学生巩固所学知识。

（2）及时反馈，纠正学生的错误。

四、作业布置1. 观察生活中的图形排列，发现并描述其中的规律。

2. 运用所学知识，解决实际问题。

五、教学反思1. 总结本节课的教学效果，反思教学方法是否适合学生。

2. 关注学生的学习兴趣和积极性，调整教学策略。

3. 针对学生的掌握情况，制定针对性的辅导计划。

六、教学评估1. 课堂表现评估：观察学生在课堂上的参与程度、提问回答情况以及团队合作表现，了解学生的学习状态和兴趣。

2. 练习反馈评估：通过作业和练习题的完成情况，评估学生对知识点的掌握程度和应用能力。

3. 学生互评：鼓励学生之间相互评价，培养学生的批判性思维和自我反思能力。

找规律自主探剪、尝试解答。

1、2、4、6、8、( )、12、( ),16, 18。

2、1,3,6,10,15,( ),( ),36。

3、1,2,4,7,11,16,( ), ( )4、1,4,9,16,( ),( )。

从图中可以看出:搭1个正方形要( )根小木棒,搭2个正方形要( )根小棒,搭3个正方形要( )根小棒,搭4个正方形要( )根小棒,搭9个正方形要( )根小棒。

小军有25根小棒,可以搭出( )个正方形。

练习:1、1,3,5,7,( ),11,( ),15,172、1,1,2,3,5,8,( ), ( ),343、1,3,7,16,31, ( ), ( )4、下面数列的每一项用3个数组成的数表示,依次是:(1,4,7),(2,8,14),(3,12,21)问:第20g个数组内三个数的和是多少?5、有一排加法算:3+2,4+8,5+14,6+2,……按这样的规律排列的第12个加法算式是怎样的?这个算式的结果是多少?6、每两朵红花之间有3多黄花，那么从左往右数第41朵花是（）花，其中红花有（）朵，黄花有（）朵。

7、河堤的一边栽了45棵树。

这些树按1棵柳树、3棵桃树的规律栽种。

河堤的一边共栽了（）棵柳树，（）棵桃树。

8、元旦要到了，教室里要按红、黄、蓝、绿的规律挂彩灯，一共要挂三十四盏灯。

四种颜色的彩灯各需多少盏？9、今天是星期四，妈妈过49天要去喝喜酒，你知道那天是星期几，妈妈周六、周日休息，到那天，她要请假吗？10、上体育课，男生排成一排，按照一至二报数。

这排男生共有25人，第10位同学报（），最后一位同学报（）。

其中共有（）名同学报“一”，共有（）名同学报“二”。

11、王兵在家练习硬笔书法时，写“我们爱科学我们爱科学……”依次写下去，那么第23个字应是（）。

12、有同样大小的红、白、黑珠子共90个。

如果按3个红珠，2个白珠，1个黑珠的顺序进行排列。

黑色的珠子共有几个？第68个珠子是什么颜色?。

宇宙中，好多现象的后边都是规律，科学就是找寻、发现规律。

找规律，需要察看和推理。

填图形，能够培育察看和推理的能力。

填图形，应从图形的个数、形状、性质下手。

【例 1】察看图 1-1 ，并按规律填出空白处的字母。

图 1-1随堂练习 1察看图 1-2 ，并依据图形的变化规律，在（3）中填入适合的图形。

图 1-2【例 2】认真察看图 1-3 ，并依据它的变化规律，在“”处填上适合的图。

随堂练习 2在图 1-5 的空白处填上适合的图形。

【例 3】察看图 1-6 ，并依据变化规律在“”处填上适合的图形。

随堂练习 3察看图 1-8 ，依据变化规律在“”处填上适合的图形图 1-8【例 4】察看图 1-9 ，并依据变化规律在“”处填上适合的图形随堂练习 4龚老师给晶晶带来了三个相同的正方体，每一个正方体的六个面上，都按相同的规律画着“猴”、“猫”、“虎”、“兔”、“狗”、“鸡”六种动物。

龚老师让晶晶收起正方体，而后再一张纸上画了三个正方体的表示图（图 1-11 ）。

请依据这个图说出“猴” 、“狗”对面画的动物。

图 1-11【例 5】依据图 1-12 的摆列规律，第23 个图形是什么小动物随堂练习 5黑棋子和白棋子排成一列，如下图，问：第99 个棋子是什么颜色这99 个棋子中，有多少个白棋子练习题1.察看下列图，在（ 4）中填上适合的图形。

2.察看下边的图形，并在空白处填上适合的图形。

3.在空白处填上适合的图形。

4.一个正方体六个面上分别图上红、黄、绿、蓝、黑五种颜色，此中有两个面涂了相同的颜色。

下列图是这个正方体的三种方法，从图中能够看到三个面所涂的颜色。

问：哪一种颜色涂了两个面5. 依据下列图的摆列规律，第27 个图形是什么动物6.察看下列图，依据（ 1）和（ 2）的变化规律，依据（ 3），在（ 4）中填上适合的图形。

7.察看下列图，在（ 4）中填出适合的图形。

8.察看下列图，在（ 4）中填出适合的图形。

找规律找规律是解决数学问题的一种重要的手段，而规律的寻找既需要有敏锐的观察力，又需要有严密的逻辑推理能力。

为了培养这方面能力，我们将从几何图形的问题入手，逐步分析应从哪些方面来观察思考。

因此，学习本讲的知识有助于养成全面、由浅入深、由简到繁分析问题的良好习惯。

例题讲练例题1想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？解析：图中点的个数从左到右逐次增多，且后面一格比前面一格多两个实心点。

因此第四个格子中应画7个实心点。

练习1想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？例题2观察图形，根据规律，图中“？”处应如何画图？解析：图中阴影三角形在大图形里逆时针旋转。

先在上面，然后在左边，接下来转至下面，按照这个规律，“？”处大图形里的阴影三角形在右边。

练习2按顺序观察下图，并在最后一个图形的空白处填上合适的图形。

例题3找出数的排列规律，在（）里填上适当的数。

（1）3、5、7、9 、（）、（）；（2）25、21、17、13、（）、（）；（3）4、8、16、32、（）、（）；（4）2、4、8、14、22、（）、（）；（5）1、1、2、3、5、（）、（）。

解析：第（1）题：依次用后一个数减去相邻的前一个数，可以发现差都等于2。

第（2）题：依次用前一个数减去相邻的后一个数，可以发现差都等于4。

第（3）题：后一个数是相邻前一个数的2倍。

第（4）题：依次用后一个数减去相邻的前一个数，虽然差在变化，但仔细分析不难发现差是2、4、6、8……，也是有规律的。

第（5）题：依次用前面两个数相加，就等于第三个数。

（1）3、5、7、9、（11）、（13）；（2）25、21、17、13、（9）、（5）；（3）4、8、16、32、（64）、（128）；（4）2、4、8、14、22、（32）、（44）；（5）1、1、2、3、5、（8）、（13）。

练习3找规律在（）里填数。

（1）0、5、10、15、20、（）；（2）27、24、（）、18、15、（）；（3）1、4、5、（）、14、（）；（4）2、20、200、2000、（）、（）；（5）180、177、172、165、（）、145。

数学学科教师辅导教案知识精讲知识点一（【例2】 下面的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形.（1）（2）（3）【例 3】 观察下图的变化规律，画出丙图.【例 4】 有六种不同图案的瓷砖，每种各6块.将它们砌在如下图那样的地面上，使每一横行和每一竖行都没有相同图案的瓷砖.你会怎样设计？？第3组第2组第1组？第3组第2组第1组★★★★★？第3组第2组第1组DC BA丙乙甲DCB A【例 5】 下面各种各样的娃娃头好看吗？认真观察你能找到它们排列的规律吗？根据规律把最后一个画出来.【例 6】 观察图中所给出图形的变化规律，然后在空白处填画上所缺的图形.【例 7】 琪琪特别喜欢蝴蝶，她用直尺和圆规在纸上画了9幅蝴蝶图，并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上，见下图1，她发现这些纸蝴蝶排列挺有规律，突然一阵风来，吹走了3只纸蝴蝶，见下图2.你能找出蝴蝶的排列规律，将图2的3只蝴蝶放入图1的空缺处吗？图1987654321图2B CA【巩固练习】根据前三个方格表中阴影部分的变化规律，填上第（10）个方格表中阴影部分的小正方形内的几个数之和。

【例 11】按照下列图形的变化规律，空白处应是什么样的图形？【巩固练习】按照下列图形的变化规律，空白处应是什么样的图形？【例 12】 请你认真仔细观察，按照下面图形的变化规律，在“?”处画出合适的图形。

【例 13】观察下图的变化规律，在“?”处填入适当的图形.698754321......（10）（3）（2）（1）？？【例 14】下图中的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形.【巩固练习】下面的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形。

【例 15】按照变化规律在“？”处填上合适的图形. （1）（2）【例 16】观察下列各组图的变化规律，并在“？”处画出相关的图形.？？？ihgfedcba（d ）（c ）（b ）（a ）【例 17】仔细观察下列图形的变化，请先回答：（1）在方框（4）中应画出怎样的图形？（2）再按（1）、（2）、（3）……的顺序数下去，第（10）个方框是怎样的图形？【巩固练习】仔细观察下列图形的变化，请先回答：(1)在方框（4）中应画出怎样的图形？(2)再按（1）、（2）、（3）、……的顺序数下去，第（10）个方框是怎样的图形？【例18】顺序观察下面图形，并按其变化规律在“？”处填上合适的图形.（1）（2）（3）（4）11。

图形找规律知识框架找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题：⑴图形数量的变化；⑵图形形状的变化；⑶图形大小的变化；⑷图形颜色的变化；⑸图形位置的变化；⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.例题精讲一、图形规律——数量规律【例 1】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

【考点】图形找规律【难度】3星【题型】填空【解析】（1）数一数，前4个点群包含的点数分别是：1，4，9，16.不难发现，1=1×1,4＝2×2,9＝3×3,16＝4×4,按照这个规律，第5个点群（即方框中的点群）包含的点数是：5×5=25（个）.（2）按发现的规律推出，第十个点群的点数是：10×10=100（个）.（3）前十个点群，所有的点数是：【答案】（1）25，（2）100，（3）385【巩固】观察下面由点组成的图形（点群），请回答：（1）方框内的点群包含个点；（2）第（10）个点群中包含个点；（3）前十个点群中，所有点的总数是。

【考点】图形找规律【难度】3星【题型】填空【解析】（1）数一数可知：前四个点群中包含的点数分别是：1，4，7，10.可以看出，在每相邻的两个数中，后一个数都比前一个数大3.因为方框内应是第（5）个点群，它的点数应该是10+3=13（个）.（2）列表，依次写出各点群的点数，可知第（10）个点群包含有28个点.（3）前十个点群，所有点的总数是：1+4+7+10+13+16+19+22+25+28=145（个）【答案】（1）13，（2）28，（3）145【例 2】下图表示“宝塔”，它们的层数不同，但都是由一样大的小三角形摆成的.仔细观察后，请回答：（1）五层的“宝塔”的最下层包含多少个小三角形？（2）整个五层“宝塔”一共包含多少个小三角形？【考点】图形找规律【难度】3星【题型】解答【解析】（1）数一数“宝塔”每层包含的小三角形数：可见1，3，5，7是个奇数列，所以由这个规律猜出第五层应包含的小三角形是9个.（2）整个五层塔共包含的小三角形个数是：1+3+5+7+9=25（个）.【答案】（1）9，（2）25二、图形规律——旋转、轮换型规律【例 3】琪琪特别喜欢蝴蝶，她用直尺和圆规在纸上画了9幅蝴蝶图，并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上，见下图1，她发现这些纸蝴蝶排列挺有规律，突然一阵风来，吹走了3只纸蝴蝶，见下图2.你能找出蝴蝶的排列规律，将图2的3只蝴蝶放入图1的空缺处吗？【考点】图形找规律 【难度】2星 【题型】填空【解析】 从已摆好的第一行和第一列来看，无论横看或竖看，同一行中3只蝴蝶的翅膀形状各不相同，翅膀上的斑点的形状也各不相同.根据这个规律，剩下的3只蝴蝶图案的排列应该是：6号位置放图案C ；8号位置放图案B ；9号位置放图案A .【答案】A【例 4】 下面的每一个图形都是由△，□，○中的两个构成的。