统计学原理第七章抽样调查

统计学原理抽样调查统计学原理是一门研究数据收集、整理、分析和解释的学科。

在统计学中，抽样调查是一种常用的数据收集方法。

抽样调查通过抽取一部分个体，称为样本，来推断整个总体的特征。

本文将介绍抽样调查的基本原理、常见的抽样方法以及优缺点。

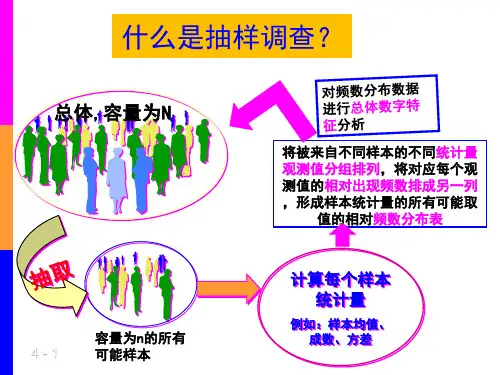
抽样调查的基本原理是从目标总体中抽取一部分个体进行观察，然后将观察结果推广到整个总体。

抽样调查的目的是基于样本的统计数据，得出对总体特征的推断。

在进行抽样调查时，需要考虑以下几个因素：总体的定义、总体的大小、样本的大小、样本的抽取方法以及调查内容。

总体的定义是指研究的对象。

在抽样调查中，总体可以是人群、组织、产品、地域等。

总体的大小是指总体中所包含的个体数量。

样本的大小是指从总体中选取的个体数量。

合理选择样本大小可以在保证统计推断准确性的基础上节约成本和时间。

样本的抽取方法有多种，常见的抽样方法包括随机抽样、分层抽样、系统抽样和整群抽样等。

随机抽样是指以随机的方式从总体中选取个体。

随机抽样可以保证样本的代表性，即样本能够很好地反映总体的特征。

分层抽样是将总体按照一定的特征分成若干层，然后从每一层中选取样本。

通过分层抽样，可以保证各层样本在总体中的比例与总体的比例基本一致。

系统抽样是指从总体中的其中一位置开始，按照一定的间隔选取样本。

整群抽样是将总体分成若干群，然后从每一群中全面抽取样本。

抽样调查的优点在于相对于全面调查，它能够节约时间和成本。

通过从总体中选取一部分个体进行观察，可以得到与全面调查相似的结果。

此外，抽样调查还可以减少调查工作的复杂性和难度。

抽样调查的缺点是存在一定的抽样误差。

抽样误差是指由于样本的随机性导致的样本结果与总体真实结果之间的差异。

为了降低抽样误差，需要采用合理的抽样方法和样本大小，并进行合适的数据分析。

在抽样调查中，可以通过计算抽样误差的置信区间来评估统计结果的可靠性。

置信区间是指对总体特征的一个区间估计，该区间以样本统计量为中心，上下限由样本误差限定。

抽样调查原理及其在应用统计学中的实践经验抽样调查是应用统计学中一项重要的研究方法，它通过从总体中选择一部分样本来推断总体的特征。

本文旨在介绍抽样调查的基本原理，并探讨其在应用统计学中的实践经验。

一、抽样调查原理抽样调查的核心原理是通过选择代表性样本来推断总体的特征。

在进行抽样调查时，需要注意以下几个主要原则：1. 随机性原则：抽样应该具有随机性，即每个个体被选中的概率应该相等且独立于其他个体。

通过随机抽样可以减小选择偏差，使样本更具代表性。

2. 独立性原则：每个个体的选择应该是独立的，即一个个体是否被选中不受其他个体的影响。

独立抽样可以避免个体之间的关联性，确保样本的独立性。

3. 样本容量原则：样本容量应该足够大，以保证对总体特征的准确推断。

样本容量的大小需要根据总体大小、特征分布、研究目的等因素进行合理的估计和确定。

4. 可行性原则：在选择抽样方法时，需要考虑实际操作的可行性。

抽样方法应该简单易行，以便能够快速、准确地获取样本。

二、抽样调查在应用统计学中的实践经验抽样调查在应用统计学中具有广泛的应用，以下是一些实践经验的介绍：1. 问卷调查：问卷调查是一种经常使用的抽样调查方法，通过向样本发放问卷并收集回复来了解人们的意见、态度和行为。

在设计问卷时，需要注意问题的清晰度、选项的全面性以及样本的代表性，以确保获得可靠的结果。

2. 实地观察：实地观察是一种直接观察和记录样本行为或事件的方法。

通过实地观察可以获取真实、客观的数据，对于研究对象的行为和环境有更深入的了解。

在实地观察中，需要选择代表性的样本，科学记录和分析观察结果。

3. 数据挖掘：数据挖掘是从大量数据中发现模式和关联性的过程。

在进行数据挖掘时，需要对数据进行抽样，以提高算法的效率和准确性。

抽样方法的选择要根据研究目的、数据类型和问题特点来确定。

4. 总体推断：通过对样本数据进行统计分析，可以对总体特征进行推断。

总体推断在市场调研、社会调查等领域具有重要的应用，它帮助人们从样本中获取总体特征的信息，支持决策和预测。

抽样调查的一般理论抽样调查是一种统计学上的调查方法，它的基本思想是从总体中抽取一部分样本进行调查，通过对样本数据的分析来推断总体的情况。

抽样调查的一般理论主要包括以下几个方面：1. 抽样的基本概念：抽样是从总体中随机选取一部分单位作为样本进行观察和研究的过程。

总体是指研究对象的全部单位，而样本则是从总体中抽取出来的一部分单位。

抽样调查的目的就是通过样本数据来推断总体的情况。

2. 抽样的原则和方法：抽样的原则主要包括随机性、代表性和广泛性。

随机性是指每个单位被抽取的概率相等，以保证样本的代表性；代表性是指样本能够反映总体的特征和规律，以便通过样本推断总体；广泛性则是指样本应该覆盖总体中的各个部分和层次，以避免出现偏差。

抽样的方法则包括简单随机抽样、分层抽样、整群抽样、系统抽样等。

3. 抽样的误差和样本容量：抽样误差是指由于抽样引起的样本指标与总体指标之间的偏差。

抽样误差是不可避免的，但可以通过增加样本容量和采用更科学的抽样方法来减小误差。

样本容量则是指样本中所包含的单位数，它的大小直接影响到抽样误差的大小和推断的准确性。

4. 抽样推断的原理和方法：抽样推断是通过样本数据来推断总体数据的原理和方法。

其基本原理是概率论中的大数定律和中心极限定理。

抽样推断的方法包括点估计和区间估计。

点估计是通过样本数据直接计算出一个具体的数值作为总体的估计值；区间估计则是通过样本数据计算出一个置信区间，以表示总体参数的可能取值范围。

总之，抽样调查的一般理论是统计学中的重要内容，它为抽样调查提供了科学的依据和指导。

在实际应用中，需要根据具体情况选择合适的抽样方法和样本容量，并对抽样误差进行控制和评估，以保证推断的准确性和可靠性。

第七章抽样本章讨论抽样。

对抽样的统计学原理我们不作详细介绍，重点讨论抽样的过程和具体的操作。

抽样是一项非常重要的技术，在自然科学和社会科学的各个领域广泛运用。

自然科学方面包括化学、天文学、机械工程学和动物学等。

在社会科学研究中，抽样技术可用于实验、调查、内容分析等研究。

7.1 抽样原理7.1.1 为什么要抽样抽样是从一大批研究对象中选出一小群作为研究对象，如从20000人中选出150人。

用抽样方法获得的研究对象称为样本（sample）。

研究中用样本作为具体操作对象比用所有对象要经济得多。

然而研究者感兴趣的不仅仅是样本，他的目的是以小见大，希望把从样本得出的结论推广至全体研究对象。

“管中窥豹，可见一斑”。

数学理论和科学研究的实践业已表明，抽样是非常有效的技术。

如果使用正确，两千多个个体的样本，可有效地代表有两亿个成员的研究对象总体，出错的概率不超过百分之二到四。

这种以小见大，以少胜多并非无稽之谈，而是有缜密的统计学原理为依据，并已一再被经验证据所证实。

并非所有样本都可使结论推而广之，抽取样本必须遵守严密的程序，而且从任何样本得出的结论都必须附带说明，表明其局限性。

7.1.2 总体、个体和抽样框架研究者从一大批研究对象中抽取样本。

这些研究对象是一个个的个体（elements），有时称作个案（cases），可以是个人、群体或组织，也可以是信息、文档，甚至是社会行为（如离婚、吸毒、乱扔垃圾）。

这些都是研究者拟测量或可以测量的事物。

拟定研究对象的全体叫做总体（population）或全域（universe）。

总体是抽样的基础，必须严格界定，没有定义清晰的总体就谈不上抽样。

总体有三个要素：内容、范围和时间。

内容即组成总体的个体单位是什么：人、物还是机构等；范围即总体所处的空间界限，包括地理位置；时间即总体存在的时间界限。

表7.1举例说明了抽样的个体单位（人、企业、医院住院人次、商业广告），地理位置和时间界限。

统计学第七章、第⼋章课后题答案统计学复习笔记第七章参数估计⼀、思考题1．解释估计量和估计值在参数估计中，⽤来估计总体参数的统计量称为估计量。

估计量也是随机变量。

如样本均值，样本⽐例、样本⽅差等。

根据⼀个具体的样本计算出来的估计量的数值称为估计值。

2．简述评价估计量好坏的标准（1）⽆偏性：是指估计量抽样分布的期望值等于被估计的总体参数。

（2）有效性：是指估计量的⽅差尽可能⼩。

对同⼀总体参数的两个⽆偏估计量，有更⼩⽅差的估计量更有效。

（3）⼀致性：是指随着样本量的增⼤，点估计量的值越来越接近被估总体的参数。

3．怎样理解置信区间在区间估计中，由样本统计量所构造的总体参数的估计区间称为置信区间。

置信区间的论述是由区间和置信度两部分组成。

有些新闻媒体报道⼀些调查结果只给出百分⽐和误差（即置信区间），并不说明置信度，也不给出被调查的⼈数，这是不负责的表现。

因为降低置信度可以使置信区间变窄（显得“精确”），有误导读者之嫌。

在公布调查结果时给出被调查⼈数是负责任的表现。

这样则可以由此推算出置信度（由后⾯给出的公式），反之亦然。

4．解释95%的置信区间的含义是什么置信区间95%仅仅描述⽤来构造该区间上下界的统计量(是随机的)覆盖总体参数的概率。

也就是说，⽆穷次重复抽样所得到的所有区间中有95%（的区间）包含参数。

不要认为由某⼀样本数据得到总体参数的某⼀个95%置信区间，就以为该区间以的概率覆盖总体参数。

5．简述样本量与置信⽔平、总体⽅差、估计误差的关系。

1. 估计总体均值时样本量n 为2. 样本量n 与置信⽔平1-α、总体⽅差、估计误差E 之间的关系为与置信⽔平成正⽐，在其他条件不变的情况下，置信⽔平越⼤，所其中： 2222α2222)(E z n σα=n z E σα2=需要的样本量越⼤；与总体⽅差成正⽐，总体的差异越⼤，所要求的样本量也越⼤；与与总体⽅差成正⽐，样本量与估计误差的平⽅成反⽐，即可以接受的估计误差的平⽅越⼤，所需的样本量越⼩。