圆柱体、圆锥体的体积

圆柱体积：V=底面积×高或V=1/2侧面积×高圆锥体积：V=底面积×高÷3圆柱侧面积：S侧=底面周长×高圆柱表面积：S表=侧面积+2个底面积圆柱体积：V=sh圆锥体积：V=sh÷3圆柱侧面积：S=ch/2πrh/πdh圆柱表面积：s=ch+2πr²圆柱体侧面积=底面周长×高圆柱体的表面积=2个底面积+1个侧面积圆柱体的体积=底面积×高（Sh）圆柱体的底面积=圆的面积（πr×r）或（π(d÷2）×(d÷2)）圆锥底面积=圆的面积（πr×r）或（π(d÷2）×(d÷2)（只有一个底面）体积=1/3×与它等底等高的圆柱体积=1/3×底面积×高=1/3sh（圆锥的体积等于与它等底等高的圆柱的体积的1/3）说明：“r”是圆的半径,“d”是圆的直径,在同圆或等圆中,r是d的1/2,d是r的2倍,“S”是面积,“h”是高.一个物体所有面的面积之和叫做它的表面积.一个物体所占空间的大小,叫做这个物体的体积.一个圆锥的体积等于与它等底等高的圆柱的体积的1/3,一个圆柱的体积等于一个与它等底等高的圆锥的体积的3倍. 圆的面积或底面积π×1×1=3.14π×2×2 =12.56π×3×3 =28.26π×4×4 =50.24π×5×5 =78.5π×6×6 =113.04π×7×7 =153.86π×8×8 =200.96π×9×9 =254.34π×10×10 =314。

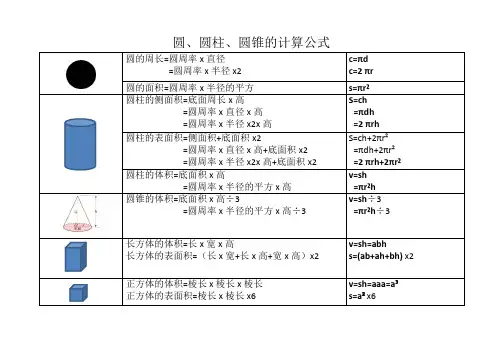
圆、圆柱、圆锥的计算公式
圆的周长=圆周率x直径
=圆周率x半径x2 c=πd c=2 πr
圆的面积=圆周率x半径的平方s=πr²
圆柱的侧面积=底面周长x高
=圆周率x直径x高
=圆周率x半径x2x高S=ch =πdh =2 πrh
圆柱的表面积=侧面积+底面积x2
=圆周率x直径x高+底面积x2
=圆周率x半径x2x高+底面积x2 S=ch+2πr²
=πdh+2πr²=2 πrh+2πr²
圆柱的体积=底面积x高
=圆周率x半径的平方x高v=sh =πr²h
圆锥的体积=底面积x高÷3
=圆周率x半径的平方x高÷3 v=sh÷3 =πr²h÷3
长方体的体积=长x宽x高
长方体的表面积=（长x宽+长x高+宽x高）x2 v=sh=abh
s=(ab+ah+bh) x2
正方体的体积=棱长x棱长x棱长正方体的表面积=棱长x棱长x6 v=sh=aaa=a³s=a²x6。

六年级下册圆柱与圆锥体公式圆柱体公式
圆柱体是一个底部为圆形的立体图形，其公式主要涉及底面积、侧面积和体积的计算。

- 底面积公式：圆柱体的底面积可以通过计算底面的半径r乘
以自身来获得，即：`底面积= π * r * r`，其中π取近似值3.。

- 侧面积公式：圆柱体的侧面积等于侧面高度h乘以底面周长
2πr，即：`侧面积= 2π * r * h`，其中π取近似值3.。

- 体积公式：圆柱体的体积可以通过计算底面积乘以高度h来
获得，即：`体积 = 底面积 * h`。

圆锥体公式
圆锥体是一个底面为圆形且收束于一个顶点的立体图形，其公
式涉及底面积、侧面积和体积的计算。

- 底面积公式：圆锥体的底面积可以通过计算底面的半径r乘以自身来获得，即：`底面积= π * r * r`，其中π取近似值3.。

- 侧面积公式：圆锥体的侧面积等于侧面高度l乘以底面周长2πr除以2，即：`侧面积= π * r * l`，其中π取近似值3.。

- 体积公式：圆锥体的体积可以通过计算底面积乘以高度h再除以3来获得，即：`体积 = (底面积 * h) / 3`。

希望以上公式对你在六年级下册学习圆柱与圆锥体有所帮助！如果有任何问题，请随时向我提问。

圆柱和圆锥是初中数学的重要内容，下面为您详细介绍关于圆柱和圆锥的计算公式。

一、圆柱的计算公式：1.面积公式：圆柱的底面积公式为：S底=π×r²，其中r为底面半径。

圆柱的侧面积公式为：S侧=2π×r×h，其中r为底面半径，h为圆柱的高度。

圆柱的全面积公式为：S全=S底+S侧=π×r²+2π×r×h。

2.体积公式：圆柱的体积公式为：V=S底×h=π×r²×h，其中r为底面半径，h为圆柱的高度。

二、圆锥的计算公式：1.面积公式：圆锥的底面积公式为：S底=π×r²，其中r为底面半径。

圆锥的侧面积公式为：S侧=π×r×l，其中r为底面半径，l为斜高，即从锥顶到底面的距离。

圆锥的全面积公式为：S全=S底+S侧=π×r²+π×r×l。

2.体积公式：圆锥的体积公式为：V=(1/3)×S底×h=(1/3)×π×r²×h，其中r为底面半径，h为圆锥的高度。

三、圆柱和圆锥的应用举例：1. 比如一个圆柱的底面半径为2cm，高度为5cm，求其体积和表面积。

圆柱的底面积为：S底= π×r² = 3.14×2² ≈ 12.56 cm²圆柱的侧面积为：S侧= 2π×r×h = 2×3.14×2×5 ≈ 62.8 cm²圆柱的全面积为：S全 = S底 + S侧= 12.56 + 62.8 ≈ 75.36cm²圆柱的体积为：V = S底×h = 12.56×5 ≈ 62.8 cm³2. 再比如一个圆锥的底面半径为3cm，斜高为4cm，求其体积和表面积。

圆柱体积公式大全表
1. 圆柱体体积公式：
V=πR²H
V为圆柱体的体积，π为圆周率，R为圆柱底面半径，H为圆柱高。

2. 全棱柱体体积公式：
V=a²h
V为全棱柱体的体积，a为底面边长，h为高。

3. 半球体体积公式：
V=2/3πr³
V为半球体的体积，π为圆周率，r为半球体半径。

4. 平行四边形体积公式：
V=1/3a²h
V为平行四边形体积，a为底面边长，h为高。

5. 台阶体积公式：
V=1/3a²h
V为台阶体积，a为底面边长，h为台阶高。

6. 球体体积公式：
V=4/3πr³
V为球体体积，π为圆周率，r为球体半径。

7. 圆台体积公式：
V=πR²H
V为圆台体积，π为圆周率，R为底面半径，H为高。

8. 圆柱台体积公式：
V=(πDiffR² + πR²h)
V为圆柱台体积，π为圆周率，R为底面半径，h为高，DiffR为底部和上部半径的差。

9. 圆筒体积公式：
V=πr²h
V为圆筒体积，π为圆周率，r为圆筒半径，h为高。

10. 椭圆台体积公式：
V=πAh/2
V为椭圆台体积，π为圆周率，A为底部长轴，h为高。

11. 圆锥体积公式：
V=πR²h/3
V为圆锥体积，π为圆周率，R为底面半径，h为高。

12. 球锥体积公式：
V=(3(πR²h - 4/3πr³))/3
V为球锥体积，π为圆周率，R为底面半径，r为顶面半径，h为高。

圆柱体圆锥体面积体积公式圆柱体和圆锥体是几何体中比较常见的形状，它们的面积和体积是计算几何学中的基本知识点。

本文将详细介绍圆柱体和圆锥体的面积和体积公式，并通过数学推导和几何分析，解释这些公式的由来和应用。

首先，我们先来介绍圆柱体的面积和体积公式。

圆柱体是由一个圆面和一个平行于圆面的截面的曲面所围成的立体。

圆柱体的侧面是一个矩形，底面和顶面是两个相等的圆。

圆柱体的表面积由底面、顶面和侧面组成。

底面和顶面都是圆，因此它们的面积公式为：底面积=π*半径^2侧面是一个长方形，它的宽度等于圆的周长（2πr），长度等于圆柱的高（h）。

因此，侧面的面积公式为：侧面积=周长*高=2π*半径*高将底面积和侧面积相加即可得到圆柱体的表面积：圆柱体表面积=底面积+侧面积=π*半径^2+2π*半径*高接下来是圆柱体的体积公式。

圆柱体的体积就是底面积乘以高。

因此，圆柱体的体积公式为：圆柱体体积=底面积*高=π*半径^2*高圆柱体的面积和体积公式是几何学中的基本公式，通过这些公式我们可以方便地计算圆柱体的表面积和体积。

这些公式在实际生活中有着广泛的应用，比如计算柱形容器的容积、圆柱体的表面积等等。

除了圆柱体，我们还可以来看一下圆锥体的面积和体积公式。

圆锥体是由一个圆锥面和一个底面所围成的立体。

圆锥体的底面是一个圆，圆锥体的侧面是一个三角形。

圆锥体的表面积由底面和侧面组成。

底面面积公式同样为：底面积=π*半径^2侧面是一个三角形，它的底边等于圆的周长（2πr），高等于圆锥的斜高（s）。

通过勾股定理可以得到斜高s的值为：s=根号下（高^2+半径^2）因此侧面积=1/2*周长*斜高=1/2*2π*半径*s=π*半径*根号下（高^2+半径^2）将底面积和侧面积相加即可得到圆锥体的表面积：圆锥体表面积=底面积+侧面积=π*半径^2+π*半径*根号下（高^2+半径^2）接下来是圆锥体的体积公式。

圆锥体的体积就是底面积乘以高并除以3、因此，圆锥体的体积公式为：圆锥体体积=1/3*底面积*高=1/3*π*半径^2*高圆锥体的面积和体积公式同样是几何学中的基本公式，通过这些公式我们可以方便地计算圆锥体的表面积和体积。

圆柱和圆锥体积之间的关系
圆柱和圆锥是两种常见的几何体，它们都有一个圆形的底面和一个高，但是圆柱的侧面是一个曲面，而圆锥的侧面是一个锥面。

圆柱和圆锥的体积公式分别是：
圆柱体积：V柱= πr^2h，其中r是底面半径，h是高
圆锥体积：V锥= 1/3πr^2h，其中r是底面半径，h是高
由此可以看出，圆柱和圆锥的体积之间有以下关系：
如果圆柱和圆锥的底面半径和高都相等，那么圆柱的体积是圆锥的体积的3倍，反之，圆锥的体积是圆柱的体积的1/3
如果圆柱和圆锥的高相等，但是体积相等，那么圆锥的底面半径是圆柱的底面半径的根号3倍，反之，圆柱的底面半径是圆锥的底面半径的1/根号3
如果圆柱和圆锥的底面半径相等，但是体积相等，那么圆锥的高是圆柱的高的3倍，反之，圆柱的高是圆锥的高的1/3。

圆柱与圆锥底面积和体积关系
圆柱和圆锥是两种常见的几何体，它们的底面都是圆形。

在比较它们的体积和底面积时，我们可以发现一些有趣的关系。

首先，圆柱和圆锥的底面积很容易计算。

圆柱的底面积为圆的面积，即πr，其中r为圆的半径。

圆锥的底面积也是圆的面积，但是需要乘以一个系数1/3，即底面积为1/3πr。

这是因为圆锥的体积是圆柱体积的1/3。

其次，圆柱和圆锥的体积也可以通过底面积和高来计算。

圆柱的体积为底面积乘以高，即πrh。

圆锥的体积为底面积乘以高再除以3，即1/3πrh。

通过比较圆柱和圆锥的底面积和体积公式，我们可以发现一个有趣的关系：圆锥的体积是圆柱体积的1/3，但是圆锥的底面积却和圆柱一样。

这说明了圆锥的形状是由圆柱截取而来的。

如果我们将圆锥和圆柱的高都设为h，那么它们的比值为1:3。

这个比值可以帮助我们在解决一些几何问题时，快速地计算出圆锥的体积或圆柱的体积，以及它们的比值。

在实际生活中，圆柱和圆锥都有广泛的应用。

圆柱可以用来设计水管、油桶、化学反应釜等容器；圆锥可以用来制作圆锥形桶、圆锥形帐篷、冰淇淋圆锥等。

因此，了解圆柱和圆锥的底面积和体积关系，对于解决实际问题非常有帮助。

- 1 -。

原著的体积计算公式圆柱体的体积公式：体积=底面积×高，如果用h代表圆柱体的高，则圆柱＝s底×h长方体的体积公式：体积=长×宽×高如果用a、b、c分别表示长方体的长、宽、高则长方体体积公式为：v长=abc正方体的体积公式：体积＝棱长×棱长×棱长．如果用a表示正方体的棱长，则正方体的体积公式为v正＝a·a·a＝a³锥体的体积=底面面积×高÷3v圆锥＝s底×h÷3台体体积公式:v=[s上+√(s上s下)+s下]h÷3圆台体积公式:v=(r²+rr+r²)hπ÷3球缺体积公式＝πh²(3r-h)÷3球体积公式：v＝4πr³/3棱柱体积公式：v＝s底面×h＝s直截面×l（l为侧棱长,h为高)棱台体积：v=〔s1＋s2＋开根号（s1*s2）〕／3*h注：v：体积；s1：上表面积；s2：下表面积；h：高。

------几何体的表面积计算公式圆柱体:表面积:2πrr+2πrh体积:πrrh(r为圆柱体上下底圆半径,h为圆柱体高)圆锥体:表面积:πrr+πr[(hh+rr)的平方根]体积:πrrh/3(r为圆锥体低圆半径,h为其高,平面图形名称符号周长c和面积s正方形a—边长c＝4as＝a2长方形a和b－边长c＝2(a+b)s＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半a,b,c－内角其中s＝(a+b+c)/2s＝ah/2＝ab/2·sinc＝[s(s-a)(s-b)(s-c)]1/2＝a2sinbsinc/(2sina)四边形d,d－对角线长α－对角线夹角s＝dd/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角s＝ah＝absinα菱形a－边长α－夹角d－长对角线长d－短对角线长s＝dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长s＝(a+b)h/2＝mh圆r－半径d－直径c＝πd＝2πrs＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数c＝2r＋2πr×(a/360)s＝πr2×(a/360)弓形l－弧长s＝r2/2·(πα/180-sinα)b－弦长＝r2arccos[(r-h)/r]-(r-h)(2rh-h2)1/2h－矢高＝παr2/360-b/2·[r2-(b/2)2]1/2r－半径＝r(l-b)/2+bh/2α－圆心角的度数≈2bh/3圆环r－外圆半径s＝π(r2-r2)r－内圆半径＝π(d2-d2)/4d－外圆直径d－内圆直径椭圆d－长轴s＝πdd/4d－短轴。

圆柱和圆锥的体积之间的关系
圆柱和圆锥是两种不同形状的几何体，它们的体积之间有一定的关系。

首先来看圆柱的体积公式：V = πrh，其中r为圆柱底面半径，h为圆柱高度。

而圆锥的体积公式为：V = 1/3πrh，其中r为圆锥底面半径，h为圆锥高度。

从公式可以看出，圆柱的体积是圆锥的三倍，但这只是当圆柱和圆锥的高度相等时成立。

如果圆柱和圆锥的高度不相等，则它们的体积之间的关系就更加复杂了。

例如，如果圆柱和圆锥的底面半径相等，但圆柱的高度是圆锥高度的两倍，那么圆柱的体积将是圆锥体积的两倍。

但如果圆柱和圆锥的底面半径和高度都不相等，则它们的体积之间的关系将更加复杂，需要通过具体计算来确定。

总之，圆柱和圆锥之间的体积关系是受多个因素影响的，需要根据具体情况进行计算。

- 1 -。

小学数学图形计算公式1、体积公式：1）、圆柱体的体积公式：体积=底面积×高，如果用h代表圆柱体的高，则圆柱=S底×h 。

2）、长方体的体积公式：体积=长×宽×高。

（底面积乘以高 S底·h）如果用a、b、c分别表示长方体的长、宽、高则长方体体积公式为：V长=abc。

3）、正方体的体积公式：体积=棱长×棱长×棱长。

（底面积乘以高 S底·h) 如果用a表示正方体的棱长，则正方体的体积公式为V=a·a·a=a^3。

4）、锥体的体积=底面面积×高÷3 。

圆锥=S底×hx3分之一。

2、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径Ѕ=πr11、长方体的表面积=（长×宽+长×高＋宽×高）×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积小学应用题计算公式1、每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数2、 1倍数×倍数＝几倍数几倍数÷1倍数＝倍数几倍数÷倍数＝1倍数3、速度×时间＝路程路程÷速度＝时间路程÷时间＝速度4、单价×数量＝总价总价÷单价＝数量总价÷数量＝单价5、工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率6、加数＋加数＝和和－一个加数＝另一个加数7、被减数－减数＝差被减数－差＝减数差＋减数＝被减数8、因数×因数＝积积÷一个因数＝另一个因数9、被除数÷除数＝商被除数÷商＝除数商×除数＝被除数10、和差问题的公式：(和＋差)÷2＝大数、(和－差)÷2＝小数11、和倍问题：和÷(倍数－1)＝小数、小数×倍数＝大数、(或者和－小数＝大数)12、差倍问题：差÷(倍数－1)＝小数、小数×倍数＝大数、(或小数＋差＝大数)13、植树问题：1 非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数＝段数＋1＝全长÷株距－1全长＝株距×(株数－1)株距＝全长÷(株数－1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数＝段数－1＝全长÷株距－1全长＝株距×(株数＋1)株距＝全长÷(株数＋1)2 封闭线路上的植树问题的数量关系如下株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数14、盈亏问题：(盈＋亏)÷两次分配量之差＝参加分配的份数(大盈－小盈)÷两次分配量之差＝参加分配的份数(大亏－小亏)÷两次分配量之差＝参加分配的份数15、相遇问题：相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间16、追及问题：追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间17、流水问题：顺流速度＝静水速度＋水流速度逆流速度＝静水速度－水流速度静水速度＝(顺流速度＋逆流速度)÷2水流速度＝(顺流速度－逆流速度)÷218、浓度问题：溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量19、利润与折扣问题：利润＝售出价－成本利润率＝利润÷成本×100%＝(售出价÷成本－1)×100% 涨跌金额＝本金×涨跌百分比折扣＝实际售价÷原售价×100%(折扣＜1)利息＝本金×利率×时间税后利息＝本金×利率×时间×(1－20%)单位换算1、长度：1千米=1000米、1米=10分米、1分米=10厘米、1米=100厘米、1厘米=10毫米2、面积：1平方千米=100公顷、1公顷=10000平方米、1平方米=100平方分米1平方分米=100平方厘米、1平方厘米=100平方毫米、3、体(容)积：1立方米=1000立方分米、1立方分米=1000立方厘米、1立方分米=1升1立方厘米=1毫升、1立方米=1000升、4、重量：1吨=1000 千克、1千克=1000克、1千克=1公斤5、人民币：1元=10角、1角=10分、1元=100分6、时间：1世纪=100年 1年=12月、大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月、平年2月28天, 闰年2月29天、1时=3600秒平年全年365天, 闰年全年366天、1日=24小时 1时=60分、1分=60秒。

圆柱圆锥表面积体积计算题一、圆柱和圆锥的表面积和体积的公式圆柱的表面积公式为：S = 2πr(h + r)，其中 r 是底面半径，h 是高。

圆柱的体积公式为：V = πr^2h。

圆锥的表面积公式为：S = πr^2 + πrl，其中 r 是底面半径，l 是斜边（母线）长度。

圆锥的体积公式为：V = 1/3πr^2h，其中 h 是高。

二、圆柱和圆锥的表面积和体积的题目题型一：已知圆柱的半径或直径和高，求表面积和体积1.已知圆柱的底面半径是2cm，高是5cm，求圆柱的表面积和体积。

2.已知圆柱的底面直径是6cm，高是4cm，求圆柱的表面积和体积。

题型二：已知圆柱的底面周长和高，求表面积和体积3.已知圆柱的底面周长是25.12cm，高是3cm，求圆柱的表面积和体积。

4.已知圆柱的底面周长是15.7cm，高是4cm，求圆柱的表面积和体积。

题型三：已知圆柱的侧面积和高，求表面积和体积5.已知圆柱的侧面积是50.24m²，高是8m，求表面积和体积。

6.已知圆柱的侧面积是219.8m²，高是10m，求表面积和体积。

题型四：已知圆柱的体积和半径或直径，求高和表面积7.已知圆柱的体积是157m³，半径是5m，求高和表面积。

8.已知圆柱的体积是3.14m³，半径是0.1m，求高表面积。

题型四：已知圆锥的半径或直径和高，求体积9.已知圆锥的底面半径是5cm，高是6cm，求圆锥的体积。

10.已知圆锥的底面直径是6cm，高是4cm，求圆锥的体积。

题型五：已知圆锥的底面周长和高，求体积11.已知圆锥的底面周长是18.84cm，高是3cm，求圆锥的体积。

12.已知圆锥的底面周长是9.42cm，高是9cm，求圆锥的体积。

题型六：已知圆锥的体积和半径或直径，求高13.已知圆锥的体积是78.5m³，半径是3m，求高。

14.已知圆锥的体积是1.884m³，直径是4m，求高。

姓名一、知识概述 。

这一讲，我们研究圆柱和圆锥体积的计算问题。

圆柱的体积计算公式是：V ＝Sh 圆锥的体积计算公式是：V ＝ Sh 圆柱的体积等于和它等底等高的圆锥体积的3倍，圆锥的体积等于和它等底等高的圆柱体积的。

通过研究，进一步提高空间想象能力和解决实际问题的能力。

二、精讲精练。

【例1】一个无盖的圆柱形铁皮油桶，高分米，底面直径米。

做这个油桶要铁皮多少平方分米（保留整十数）这个油桶可以装油多少千克（每升油重约千克）练习1：1、一个近似的圆锥形黄沙堆，底面周长米，高6米，每立方米的沙重吨，如果用载重10吨的汽车运，要运多少次2、一个圆柱和一个圆锥等底等高。

（1）如果它们体积的和是48立方厘米，它们的体积各是多少（2）如果它们的体积之差是60立方分米，它们的体积各是多少3、有一种饮料瓶的瓶身呈圆柱形（不包括瓶颈），容积是30立方分米。

现在瓶中装有一些饮料，正放时饮料高度为20厘米，倒放时空余部分的高度为5厘米。

问：瓶内现有饮料多少立方分米3131【例2】一个圆柱形水桶，底面直径4分米，里面装了一些水，把一段直径2分米的圆柱形铁块放入水中，桶里的水上升了分米，这个铁块有多长练习2：1、将一高3分米的圆柱体铁块锻造成一个底面积不变的圆柱体和一个圆锥体，已知锻成的圆柱体高2分米，求锻成的圆锥体的高是多少分米2、一个圆锥体沙堆，底面直径是4米，高为9米。

用这堆沙石在5米宽的公路上铺2厘米厚，能铺多少米长3、在一个底面直径是20厘米的圆柱形容器里，放入一个底面半径3厘米的圆锥形铁块，全部浸没在水中，这时水面上升了厘米。

圆锥形铁块的高是多少厘米【例3】把一个棱长6厘米的正方体木块加工成最大的圆柱，圆柱的体积是多少练习3：1、把一个棱长6分米的正方体加工成一个最大的圆锥体，圆锥的体积是多少2、把一个长、宽、高分别是8厘米、6厘米、4厘米的长方体加工成一个最大的圆锥体，圆锥的体积是多少立方厘米3、如图，把这个扇形做成一个圆锥的的侧面，这个圆锥的高是6厘米，这个圆锥的体积是多少（接头处忽略不计）4厘米【例4】把一个圆柱的高增加8厘米，表面积增加平方厘米，原来圆柱的高是20厘米，求原来圆柱的体积。

圆柱与圆锥体积的关系圆柱和圆锥是我们日常生活中常见的几何体，它们的体积是我们在计算空间容积时经常需要考虑的因素。

那么，圆柱和圆锥的体积之间是否存在某种关系呢？本文将从几何角度出发，探讨圆柱与圆锥体积的关系。

我们来看圆柱的体积公式：V=πr²h，其中r为圆柱的底面半径，h 为圆柱的高度。

这个公式告诉我们，圆柱的体积与其底面半径和高度有关。

如果我们将圆柱的高度h看作是一个变量，那么圆柱的体积就是一个关于h的函数，即V(h)=πr²h。

这个函数是一个一次函数，其图像是一条直线，斜率为πr²，表示当圆柱的高度增加1个单位时，其体积增加πr²个单位。

接下来，我们来看圆锥的体积公式：V=1/3πr²h，其中r为圆锥的底面半径，h为圆锥的高度。

这个公式告诉我们，圆锥的体积与其底面半径和高度有关。

如果我们将圆锥的高度h看作是一个变量，那么圆锥的体积就是一个关于h的函数，即V(h)=1/3πr²h。

这个函数是一个一次函数，其图像也是一条直线，斜率为1/3πr²，表示当圆锥的高度增加1个单位时，其体积增加1/3πr²个单位。

从上面的分析可以看出，圆柱和圆锥的体积都是关于高度的一次函数，其图像都是一条直线。

但是，它们的斜率不同，圆柱的斜率为πr²，圆锥的斜率为1/3πr²。

这意味着，当圆柱和圆锥的高度增加1个单位时，它们的体积增加的速度是不同的。

具体来说，当圆柱和圆锥的高度相等时，圆柱的体积是圆锥的3倍。

圆柱和圆锥的体积之间存在着一定的关系。

虽然它们的体积公式不同，但它们的体积都是关于高度的一次函数，其图像都是一条直线。

通过比较它们的斜率，我们可以发现，当圆柱和圆锥的高度相等时，圆柱的体积是圆锥的3倍。

这个结论在实际生活中也有一定的应用，比如在设计容器时，我们可以根据需要选择圆柱或圆锥形状，以达到最佳的容积效果。

核算体积的公式
1.立方体的体积公式：
立方体是一个具有六个相等的正方形面的立体，它的体积可
以通过边长的立方来计算。

所以立方体的体积公式为：V=边长³。

2.长方体的体积公式：
长方体是一个具有六个矩形面的立体，它的体积可以通过长、宽和高的乘积来计算。

所以长方体的体积公式为：V=长×宽×高。

3.圆柱体的体积公式：
圆柱体是一个具有两个圆面和一个圆柱面的立体，它的体积
可以通过底面积与高的乘积来计算。

所以圆柱体的体积公式为：V=π×半径²×高，其中π取近似值3.14。

4.球体的体积公式：
球体是一个具有无限个等距离于球心的点组成的立体，它的
体积可以通过半径的立方来计算。

所以球体的体积公式为：
V=(4/3)×π×半径³。

5.圆锥体的体积公式：
圆锥体是一个具有一个圆底面和一个顶点的尖锐立体，它的体积可以通过底面积与高的乘积再除以3来计算。

所以圆锥体的体积公式为：V=(1/3)×π×半径²×高。

这些是常见几何体的体积计算公式。

根据不同的几何形状，选择合适的公式进行计算，就可以得到对应几何体的体积。

圆柱的体积怎么算(圆锥的体积怎么算)查看全部您好,今天小篇来为大家解答以上的问题。

圆柱的体积怎么算相信很多小伙伴还不知道,现在让我们一起来看看吧！圆柱的体积怎么算。

圆柱体重量＝圆柱体材料的密度某圆柱体体积＝圆柱体材料的密度某圆柱体底面积某圆柱体高度＝ρ某π某r某r某h。

本文到这结束，希望上面文章对大家有所帮助。

您好,今天小篇来为大家解答以上的问题。

圆柱的体积怎么算相信很多小伙伴还不知道,现在让我们一起来看看吧！1、圆柱体积：V=底面积某高或V=1/2侧面积某高圆锥体积：V=底面积某高÷3圆柱侧面积：S侧=底面周长某高圆柱表面积：S表=侧面积+2个底面积圆柱体重量＝圆柱体材料的密度某圆柱体体积＝圆柱体材料的密度某圆柱体底面积某圆柱体高度＝ρ某π某r某r某h（ρ为圆柱体材料的密度，π为圆周率（取3.14），r为圆柱体底面半径，h为圆柱体高度）。

2、圆柱的两个完全相同的圆面叫做底面（又分上底和下底）；圆柱有一个曲面，叫做侧面；两个底面的对应点之间的距离叫做高（高有无数条）。

3、扩展资料：圆柱性质1、圆柱的两个圆面叫底面，周围的面叫侧面，一个圆柱体是由两个底面和一个侧面组成的。

4、2、圆柱体的两个底面是完全相同的两个圆面。

5、两个底面之间的距离是圆柱体的高。

6、3、圆柱体的侧面是一个曲面，圆柱体的侧面的展开图是一个长方形、正方形或平行四边形（斜着切）。

7、4、圆柱的体积=底面积x高即V=S底面积某h=(π某r某r)h5、等底等高的圆柱的体积是圆锥的3倍6、圆柱体可以用一个平行四边形围成7、圆柱的表面积=侧面积+底面积x28、把圆柱沿底面直径分成两个同样的部分，每一个部分叫半圆柱。

8、这时与原来的圆柱比较，表面积=πr（r+h)+2rh、体积是原来的一半。

9、9、圆柱的轴截面是直径x高的长方形，横截面是与底面相同的圆。