14.4全等三角形的判定(5)

全等三角形的判定方法五种的证明全文共四篇示例，供读者参考第一篇示例：全等三角形（即三角形的所有对应边和角都相等）在几何学中具有重要意义，因为它们有着很多共性特征和性质。

在实际问题中，我们常常需要判定两个三角形是否全等，以便解决一些几何问题。

下面我们将介绍五种判定方法，并给出它们的证明。

一、SSS法则（边边边全等）首先我们来介绍SSS法则，即如果两个三角形的三条边分别相等，则这两个三角形全等。

设有两个三角形ABC和DEF，已知AB=DE，AC=DF，BC=EF。

我们要证明三角形ABC全等于三角形DEF。

【证明过程】由已知条件可知，三角形ABC和三角形DEF的三边分别相等。

所以可以得到以下对应关系：AB=DEAC=DFBC=EF三角形的两边之和大于第三边，所以我们有以下结论：AB+AC>BCDE+DF>EF由于AB=DE，AC=DF，BC=EF，所以根据上述两个不等式可得：AB+AC>BCAB+AC>BC所以三角形ABC与三角形DEF全等。

由于∠C=∠F，所以我们有以下结论：∠A+∠C+∠B=180°∠A+∠F+∠E=180°由于∠C=∠F，所以可以将两个等式相减，得到：∠B-∠E=0∠B=∠E四、HL法则（斜边-直角-斜边全等）由于∠A=∠D，∠B=∠E，所以可以使用AA法则证明三角形ABC 与三角形DEF全等。

我们介绍了五种全等三角形的判定方法以及它们的证明。

这些方法在解决几何问题中起着至关重要的作用，希望大家能够掌握并灵活运用这些方法。

如果遇到类似的题目，可以根据不同情况灵活选择合适的方法来判定三角形的全等关系。

通过不断练习和思考，相信大家能够在几何学习中取得更好的成绩。

【2000字】第二篇示例：全等三角形是指具有完全相同的三边和三角形的一种特殊情况。

在几何学中，全等三角形之间具有一些特殊的性质和关系。

正确判断两个三角形是否全等是解决几何问题的关键。

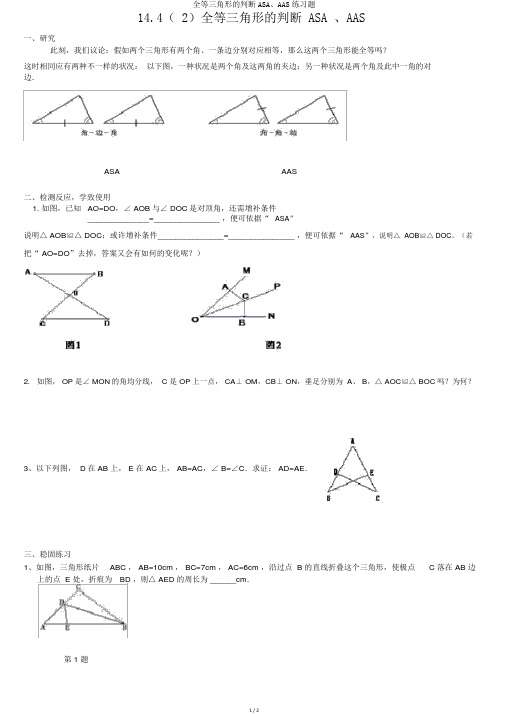
14.4（ 2）全等三角形的判断 ASA 、AAS一、研究此刻，我们议论：假如两个三角形有两个角、一条边分别对应相等，那么这两个三角形能全等吗？这时相同应有两种不一样的状况：以下图，一种状况是两个角及这两角的夹边；另一种状况是两个角及此中一角的对边．ASA AAS二、检测反应，学致使用1. 如图，已知AO=DO，∠ AOB与∠ DOC是对顶角，还需增补条件______________=_______________ ，便可依据“ASA”说明△ AOB≌△ DOC；或许增补条件_______________=_______________ ，便可依据“AAS”，说明△ AOB≌△ DOC。

（若把“ AO=DO”去掉，答案又会有如何的变化呢？）2.如图， OP是∠ MON的角均分线， C 是 OP上一点， CA⊥ OM，CB⊥ ON，垂足分别为 A、 B，△ AOC≌△ BOC吗？为何？3、以下列图， D在 AB 上， E 在 AC上， AB=AC，∠ B=∠C．求证： AD=AE．三、稳固练习1、如图，三角形纸片ABC ， AB=10cm ， BC=7cm ， AC=6cm ，沿过点 B 的直线折叠这个三角形，使极点 C 落在 AB 边上的点 E 处，折痕为BD ，则△ AED 的周长为 ______cm．第 1 题2、已知：如图,∠ 1=∠2 ,∠ 3=∠ 4求证：AC=AB．3．如图， AB⊥ BC，AD⊥ DC，∠ BAC =∠CAD . 试说明： AB=AD .4、已知：如图, FB=CE , AB∥ED , AC∥FD.F、C在直线B E 上．求证： AB=DE , AC=DF．5、如图，在△ ABC中，∠ C=2∠ B,AD 是△ ABC的角均分线，∠ 1=∠B, 试说明： AB=AC+AD6、已知：如图，AB=DC，∠ A=∠ D．试说明：∠ 1=∠2．7.如图， ABC中， D是 AC上一点， BE∥ AC， BE=AD， AE 分别交 BD、 BC于点 F、 G．⑴图中有全等三角形吗？请找出来，并证明你的结论．⑵若连接 DE，则 DE与 AB有什么关系？并说明原因．。

《三角形全等的判定》知识清单一、三角形全等的概念两个三角形能够完全重合，就说这两个三角形全等。

全等三角形的对应边相等，对应角相等。

二、三角形全等的判定方法1、“边边边”（SSS）如果两个三角形的三条边分别对应相等，那么这两个三角形全等。

例如：在三角形 ABC 和三角形 DEF 中，AB ＝ DE，BC ＝ EF，AC ＝ DF，那么三角形 ABC 全等于三角形 DEF。

这个判定方法是三角形全等判定的基础，因为三条边确定了，三角形的形状和大小也就确定了。

2、“边角边”（SAS）如果两个三角形的两条边及其夹角分别对应相等，那么这两个三角形全等。

比如：在三角形 ABC 和三角形 DEF 中，AB ＝ DE，∠A ＝∠D，AC ＝ DF，那么三角形 ABC 全等于三角形 DEF。

需要注意的是，这里的角必须是两条边的夹角。

3、“角边角”（ASA）如果两个三角形的两个角及其夹边分别对应相等，那么这两个三角形全等。

假设在三角形 ABC 和三角形 DEF 中，∠B ＝∠E，BC ＝ EF，∠C ＝∠F，那么三角形 ABC 全等于三角形 DEF。

同样，这里的边必须是两个角的夹边。

4、“角角边”（AAS）如果两个三角形的两个角和其中一个角的对边分别对应相等，那么这两个三角形全等。

例如：在三角形 ABC 和三角形 DEF 中，∠A ＝∠D，∠B ＝∠E，BC ＝ EF，那么三角形 ABC 全等于三角形 DEF。

这一判定方法是由“角边角”推导而来的。

三、直角三角形全等的特殊判定方法1、“斜边、直角边”（HL）对于两个直角三角形，如果斜边和一条直角边分别对应相等，那么这两个直角三角形全等。

比如在直角三角形 ABC 和直角三角形 DEF 中，∠C ＝∠F ＝ 90°，AB ＝ DE，AC ＝ DF，那么直角三角形 ABC 全等于直角三角形 DEF。

四、三角形全等判定的应用1、证明线段相等如果两个三角形全等，那么它们的对应边相等。

全等三角形的判定方法
1.两个三角形的三边分别相等。

2.两个三角形的两个角分别相等，且它们夹的两边也分别相等。

3.两个三角形的一个角相等，且两个角的夹的两边也分别相等。

4.两个三角形的两个角相等，且它们夹的两边分别相等。

5.两个三角形的一个角相等，且两个角的夹的两边分别相等。

6.两个三角形的两个边分别相等，且它们夹的角相等。

7.两个三角形的一边相等，且两个边的夹的角相等。

8.两个三角形的两边分别相等，且它们夹的一个角相等。

9.两个三角形的一边相等，且两个边的夹的一个角相等。

10.两个三角形的一角相等，且两个角的夹的一边也分别相等。

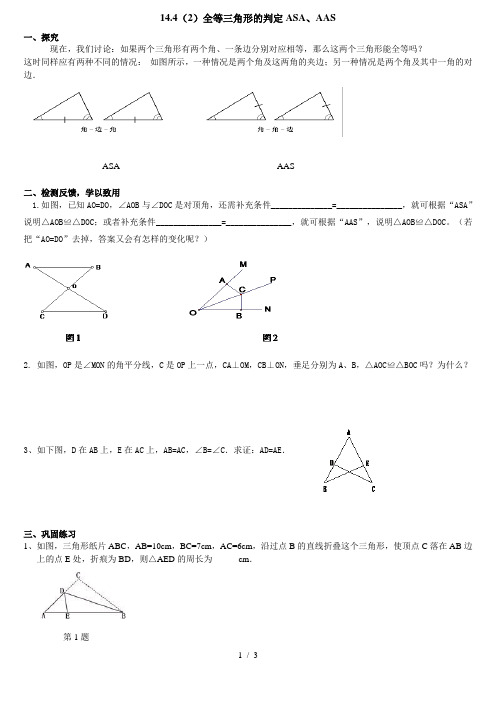
14.4（2）全等三角形的判定ASA、AAS一、探究现在，我们讨论：如果两个三角形有两个角、一条边分别对应相等，那么这两个三角形能全等吗？这时同样应有两种不同的情况：如图所示，一种情况是两个角及这两角的夹边；另一种情况是两个角及其中一角的对边．ASA AAS二、检测反馈，学以致用1.如图，已知AO=DO，∠AOB与∠DOC是对顶角，还需补充条件______________=_______________，就可根据“ASA”说明△AOB≌△DOC；或者补充条件_______________=_______________，就可根据“AAS”，说明△AOB≌△DOC。

（若把“AO=DO”去掉，答案又会有怎样的变化呢？）2. 如图，OP是∠MON的角平分线，C是OP上一点，CA⊥OM，CB⊥ON，垂足分别为A、B，△AOC≌△BOC吗？为什么？3、如下图，D在AB上，E在AC上，AB=AC，∠B=∠C．求证：AD=AE．三、巩固练习1、如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为______cm．第1题2、已知：如图 , ∠1=∠2 , ∠3=∠4求证：AC=AB．3．如图，AB⊥BC，AD⊥DC，∠BAC=∠CAD.试说明：AB=AD .4、已知：如图 , FB=CE , AB∥ED , AC∥FD.F、C在直线 BE上．求证：AB=DE , AC=DF．5、如图，在△ABC中，∠C=2∠B,AD是△ABC的角平分线，∠1=∠B,试说明：AB=AC+AD6、已知：如图，AB=DC，∠A=∠D．试说明：∠1=∠2．7.如图，ΔABC中，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G．⑴图中有全等三角形吗？请找出来，并证明你的结论．⑵若连结DE，则DE与AB有什么关系？并说明理由．。

全等三角形的判定方法五种的证明全等三角形的判定方法有五种，分别是SSS（边边边）、SAS（边角边）、ASA（角边角）、AAS（角角边）和HL（斜边和直角边）。

下面我将从多个角度为你解释这五种判定方法的证明。

首先，我们来看SSS（边边边）判定方法。

假设有两个三角形ABC和DEF，如果它们的对应边长分别相等，即AB=DE，BC=EF，AC=DF，那么根据三角形的性质，这两个三角形是全等的。

这可以通过边长相等所确定的三个顶点的位置关系来证明。

其次，SAS（边角边）判定方法。

假设有两个三角形ABC和DEF，如果它们的一个对应边和夹角分别相等，即AB=DE，∠BAC=∠EDF，BC=EF，那么根据三角形的性质，这两个三角形是全等的。

这可以通过两个边和夹角所确定的三个顶点的位置关系来证明。

第三，ASA（角边角）判定方法。

假设有两个三角形ABC和DEF，如果它们的一个对应角和夹边分别相等，即∠A=∠D，BC=EF，∠B=∠E，那么根据三角形的性质，这两个三角形是全等的。

这可以通过两个角和夹边所确定的三个顶点的位置关系来证明。

其次，AAS（角角边）判定方法。

假设有两个三角形ABC和DEF，如果它们的两对应角和一对应边分别相等，即∠A=∠D，∠B=∠E，AB=DE，那么根据三角形的性质，这两个三角形是全等的。

这可以通过两个角和一对边所确定的三个顶点的位置关系来证明。

最后，HL（斜边和直角边）判定方法。

假设有两个直角三角形ABC和DEF，如果它们的斜边和一个直角边分别相等，即AB=DE，AC=DF，并且它们的一个锐角相等，那么根据三角形的性质，这两个三角形是全等的。

这可以通过斜边和直角边所确定的三个顶点的位置关系来证明。

综上所述，我们可以根据SSS、SAS、ASA、AAS和HL五种全等三角形的判定方法来证明两个三角形是否全等。

这些证明可以从边长、角度和边的组合等多个角度来进行推导和验证。

这些方法在几何推导和证明中起着重要的作用。

第14章全等三角形核心素养整合与提升-2022-2023学年八年级上册初二数学(沪科版)14.1 介绍全等三角形全等三角形是初中数学中的一个重要概念，它是指具有相等对应边和相等对应角的两个三角形。

全等三角形在几何学中有许多重要的性质和应用，掌握全等三角形的相关知识对于初中数学学习非常重要。

14.2 全等三角形的性质全等三角形具有以下性质：1.对应边相等：如果两个三角形是全等的，那么它们的对应边是相等的。

例如，如果三角形ABC与三角形DEF全等，那么AB = DE，AC = DF和BC = EF。

2.对应角相等：如果两个三角形是全等的，那么它们的对应角是相等的。

例如，如果三角形ABC与三角形DEF全等，那么∠A = ∠D，∠B = ∠E和∠C = ∠F。

3.全等三角形的任意两边之比相等：在全等三角形中，任意两边的比值是相等的。

例如，如果三角形ABC与三角形DEF全等，那么AB/DE = AC/DF = BC/EF。

14.3 全等三角形的判定方法判定两个三角形是否全等的方法有多种，其中一些常用的方法有以下几种：1.SSS判定法：如果两个三角形的三条边分别相等，那么这两个三角形是全等的。

2.SAS判定法：如果两个三角形的一边和与之相对的两个角分别相等，那么这两个三角形是全等的。

3.ASA判定法：如果两个三角形的一角和与之相对的两边分别相等，那么这两个三角形是全等的。

4.RHS判定法：如果两个直角三角形的斜边和一个锐角分别相等，那么这两个三角形是全等的。

14.4 全等三角形的应用全等三角形的应用非常广泛，它在几何学和图形的研究中起着重要的作用。

以下是全等三角形在实际问题中的一些应用：1.测量：全等三角形可以用于测量无法直接量度的长度。

通过构造合适的全等三角形，可以利用已知的长度进行计算。

2.角度测量：全等三角形的角度相等性质可以用于测量或计算无法直接量度的角度。

通过构造合适的全等三角形，可以利用已知的角度进行计算。

全等三角形判定条件(六种)
①边角边公理（SAS)有两边和它们的夹角对应相等的两个三角形全等。

②角边角公理（ASA)有两角和它们的夹边对应相等的两个三角形全等。

③推论（AAS)有两角和其中一角的对边对应相等的两个三角形全等。

④边边边公理（SSS)有三边对应相等的两个三角形全等。

⑤斜边、直角边公理（HL)有斜边和一条直角边对应相等的两个直角
三角形全等。

出现两等边三角形、两等腰直角三角形通常用SAS证全等；等腰直角
三角形常见辅助线添法--连结直角顶点和斜边中点；两直角三角形证全等
常用方法：SAS,AAS,HL；出现等腰直角三角形或正方形可能用到K型全等。

核心素养指向的数学学科教学设计改进策略——以“ 14.4（4）全等三角形的判定”为例发布时间：2023-01-09T08:20:15.749Z 来源：《中小学教育》2022年8月16期作者：王素敏[导读] 教育总是随着社会的进步而发展的王素敏上海理工大学附属实验初级中学 200093摘要：教育总是随着社会的进步而发展的，《义务教育课程标准（2022年版）》[1]指出：在课程实施方面需要深化教育改革，主要体现在坚持素养导向、强化学科实践、推进综合学习以及落实因材施教。

初中数学是以课堂教学为主导的学科，课堂教学的质量，决定了整个课程教学的质量。

因此，在新课改之下，初中数学教学需要对课堂教学设计进行合理的优化，行合理的优化，保证课堂教学能够达到最的效果。

《义务教育数学课程标准（2022年版）》[2]指出：有效的教学活动是学生学和教师教的统一、学生是学习的主体，教师是学习的组织者、引导者与合作者。

学生的学习应是一个主动的过程，认真听讲、独立思考、动手实践、自主探究、合作交流等是学习数学的主要方式。

同时标准指出课程目标以学生发展为本。

以核心素养为导向，进一步强调使学生获得数学基础知识、基本技能、基本思想和基本活动经验（简称“四基”）的获得与发展。

因此，加强教学设计研究，注重核心素养的培养是初中数学教师的当务之急，需要教师把学习理论与教学实践联系起来，优化课程教学设计，优化教学过程，切实提高课堂教学效率。

笔者认为可以从以下几个方面入手：关键词：探究教学；数学核心素养；数学思想方法；最近发展区；一、设置情景，融合探究教学探究教学在初中数学课堂教学中的作用毋庸置疑，因此，在优化课堂教学设计的过程中，教师也同样可以在课堂中适当的融合探究教学的理念，通过探究教学来进一步激发学生的探究意识，进一步开拓学生的思维，同时可以提高学生的实践动手能力，因此，笔者在数学中会根据教学的需要，在课堂上引导学生开展探究活动。

以沪教版七年级下册第14章《14.4（4）全等三角形的判定》为例，三角形全等的判定是初中平面几何学习中的基础和核心内容，是今后研究线段相等、角相等的重要方法，是今后研究几何图形不可或缺的工具与方法。