数学人教版八年级上册全等三角形的判定(边边边) (5)

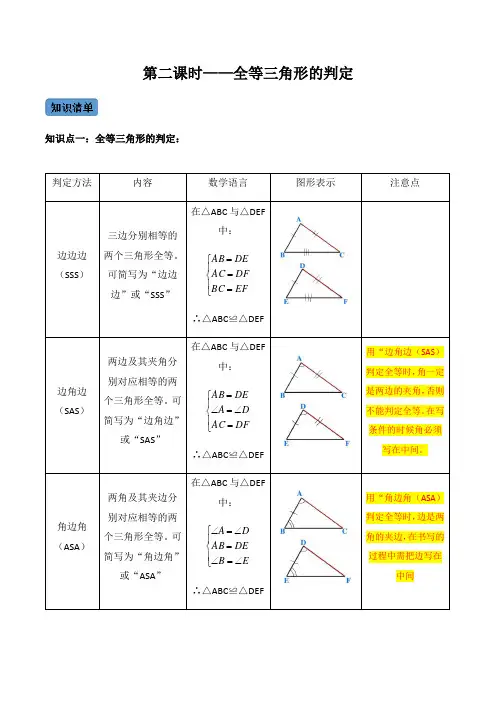
第二课时——全等三角形的判定知识点一：全等三角形的判定：判定方法内容数学语言 图形表示 注意点边边边（SSS ）三边分别相等的两个三角形全等。

可简写为“边边边”或“SSS ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧===EF BC DF AC DE AB ∴△ABC ≌△DEF边角边（SAS ）两边及其夹角分别对应相等的两个三角形全等。

可简写为“边角边”或“SAS ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧=∠=∠=DF AC D A DEAB ∴△ABC ≌△DEF用“边角边（SAS ）判定全等时，角一定是两边的夹角，否则不能判定全等。

在写条件的时候角必须写在中间。

角边角（ASA ）两角及其夹边分别对应相等的两个三角形全等。

可简写为“角边角”或“ASA ”在△ABC 与△DEF中：⎪⎩⎪⎨⎧∠=∠=∠=∠E B DE AB DA ∴△ABC ≌△DEF用“角边角（ASA ）判定全等时，边是两角的夹边，在书写的过程中需把边写在中间特别提示：在写全等三角形的数学语言时，等号左边写“≌”左边三角形的条件，等号右边写“≌”右边三角形的条件。

并且条件的顺序必须和判定条件顺序一致。

方法总结：【类型一：补充证全等条件】1．如图，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC＝DF，只添加一个条件，能判定△ABC≌△DEF的是（）A．BC＝DE B．AE＝DBC．∠A＝∠DEF D．∠ABC＝∠D2．如图，在△ABC和△BAD中，AC＝BD，要使△ABC≌△BAD，则需要添加的条件是（）第2题第3题A．∠BAD＝∠ABC B．∠BAC＝∠ABD C．∠DAC＝∠CBD D．∠C＝∠D3．如图，BC＝BD，添加下列一个条件后，仍无法判定△ABC≌△ABD的是（）A．AC＝AD B．∠ABC＝∠ABD C．∠CAB＝∠DAB D．∠C＝∠D＝90°4．如图，已知点A，D，C，F在同一条直线上，AB＝DE，AD＝CF，要使△ABC≌△DEF，则下列条件可以添加的是（）第4题第5题第7题A．∠B＝∠E B．∠A＝∠EDF C．AC＝DF D．BC∥EF5．如图，已知AB＝AE，∠EAB＝∠DAC，添加一个条件后，仍无法判定△AED≌△ABC的是（）A．AD＝AC B．∠E＝∠B C．ED＝BC D．∠D＝∠C6．下列条件，不能判定两个直角三角形全等的是（）A．两个锐角对应相等B．一个锐角和斜边对应相等C．两条直角边对应相等D．一条直角边和斜边对应相等7．如图，在Rt△ABC与Rt△DCB中，已知∠A＝∠D＝90°，添加一个条件，不能使得Rt△ABC≌Rt△DCB 的是（）A．AB＝DC B．AC＝DB C．∠ABC＝∠DCB D．BC＝BD8．如图，已知AB⊥BD，CD⊥BD，若用“HL”判定Rt△ABD和Rt△CDB全等，则需要添加的条件是（）A．AD＝CB B．∠A＝∠CC．BD＝DB D．AB＝CD【类型二：证明三角形全等】9．请将以下推导过程补充完整．如图，点C在线段AB上，AD∥BE，AC＝BE，AD＝BC，CF平分∠DCE．求证：△DCF ≌△ECF 证明：∵AD ∥BE ∴∠A ＝∠B在△ACD 和△BEC 中()⎪⎩⎪⎨⎧=∠=∠BC AD B A ∴△ACD ≌△BEC （ ）∴CD ＝CE （ ） ∵CF 平分∠DCE ∴ 在△DCF 和△ECF 中()⎪⎩⎪⎨⎧==CE CD CF CF ∴△DCF ≌△ECF （SAS ）10．如图，点C 在BD 上，AB ⊥BD ，ED ⊥BD ，AC ⊥CE ，AB ＝CD ．求证：△ABC ≌△CDE ．11．如图，点A、D、B、E在一条直线上，AD＝BE，AC＝DF，AC∥DF，求证：△ABC≌△DEF．12．如图，点D在线段BC上，AB＝AD，∠1＝∠2，DA平分∠BDE：求证：△ABC≌△ADE．13．天使是美好的象征，她的翅膀就像一对全等三角形．如图AD与BC相交于点O，且AB＝CD，AD＝BC．求证：△ABO≌△CDO．14．如图，在△ABC中，点D在BC的延长线上，DE∥AC，且DE＝BC，AC＝BD．求证：△ABC≌△BED．15．如图，CA＝CD，∠BCE＝∠ACD，BC＝EC．求证：△ABC≌△DEC．16．如图，D、C、F、B四点在一条直线上，AC＝EF，AC⊥BD，EF⊥BD，垂足分别为点C、点F，BF＝CD．试说明：△ABC≌△EDF．17．如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．18．如图，点C、E、B、F在一条直线上，AB⊥CF于B，DE⊥CF于E，AC＝DF，AB＝DE．求证：CE ＝BF．19．如图，AB＝BC，∠BAD＝∠BCD＝90°，点D是EF上一点，AE⊥EF于E，CF⊥EF于F，AE＝CF，求证：Rt△ADE≌Rt△CDF．【类型三：全等三角形的判定与性质】20．如图，在△ABC与△AEF中，点F在BC上，AB＝AE，BC＝EF，∠B＝∠E，AB交EF于点D，∠F AC ＝40°，则∠BFE＝（）第20题第21题A．35°B．40°C．45°D．50°21．如图，在△ABC中，BD平分∠ABC，∠C＝2∠CDB，AB＝12，CD＝3，则△ABC的周长为（）A．21B．24C．27D．3022．如图，AB⊥CD，且AB＝CD，E，F是AD上两点，CE⊥AD，BF⊥AD．若CE＝4，BF＝3，EF＝2，则AD的长为（）第22题第23题A．3B．5C．6D．723．已知：如图，在△ABC，△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD＝CE；②∠ACE+∠DBC＝45°；③BD⊥CE；④∠BAE+∠DAC＝180°．其中结论正确的个数是（）A．1B．2C．3D．424．如图，CB为∠ACE的平分线，F是线段CB上一点，CA＝CF，∠B＝∠E，延长EF与线段AC相交于点D．（1）求证：AB＝FE；（2）若ED⊥AC，AB∥CE，求∠A的度数．25．如图，四边形ABCD中，AD∥BC，E为CD的中点，连结BE并延长交AD的延长线于点F．（1）求证：△BCE≌△FDE；（2）连结AE，当AE⊥BF，BC＝2，AD＝1时，求AB的长．26．如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E．（1）求证：BC＝DC；（2）若∠A＝25°，∠D＝15°，求∠ACB的度数．【类型四：全等三角形的应用】27．如图，要测池塘两端A，B的距离，小明先在地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB，连接DE并测量出它的长度，DE的长度就是A，B间的距离．那么判定△ABC和△DEC全等的依据是（）第27题第28题A．SSS B．SAS C．ASA D．AAS28．打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（）A．带①②去B．带②③去C．带③④去D．带②④去29．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm．第29题第30题30．在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB ＝OC，测得AB＝a，EF＝b，圆形容器的壁厚是（）A ．aB ．bC ．b ﹣aD ．21（b ﹣a ）一、选择题（10题）1．如图为正方形网格，则∠1+∠2+∠3＝（ ）第1题 第2题 第3题A ．105°B ．120°C ．115°D ．135°2．如图，已知∠C ＝∠D ＝90°，添加一个条件，可使用“HL ”判定Rt △ABC 与Rt △ABD 全等．以下给出的条件适合的是（ ）A ．∠ABC ＝∠ABDB ．∠BAC ＝∠BAD C ．AC ＝AD D ．AC ＝BC3．如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．A ．①B ．②C ．③D ．①和②4．根据下列已知条件，能唯一画出△ABC 的是（ ）A．∠C＝90°，AB＝6B．AB＝4，BC＝3，∠A＝30°C．AB＝5，BC＝3D．∠A＝60°，∠B＝45°，BC＝45．如图，测河两岸A，B两点的距离时，先在AB的垂线BF上取C，D两点，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC≌△ABC，从而得到ED＝AB，测得ED的长就是A，B的距离，判定△EDC≌△ABC的依据是（）A．ASA B．SSS C．AAS D．SAS6．如图，已知∠EAC＝∠BAD，AC＝AD，增加下列条件：①AB＝AE；②BC＝ED；③∠C＝∠D；④∠B＝∠D．其中能使△ABC≌△AED的条件有（）A．4个B．3个C．2个D．1个7．如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，则两个木桩离旗杆底部的距离BD与CD的距离间的关系是（）第7题第8题A．BD＞CD B．BD＜CD C．BD＝CD D．不能确定8．如图，AB＝12m，CA⊥AB于点A，DB⊥AB于点B，且AC＝4m，点P从B向A运动，每分钟走1m，点Q从B向D运动，每分钟走2m，P、Q两点同时出发，运动（）分钟后，△CAP与△PQB全等．A．2B．3C．4D．89．把等腰直角三角形ABC，按如图所示立在桌上，顶点A顶着桌面，若另两个顶点距离桌面5cm和3cm，则过另外两个顶点向桌面作垂线，则垂足之间的距离DE的长为（）第9题第10题A．4cm B．6cm C．8cm D．求不出来10．如图，在△AOB和△COD中，OA＝OB，OC＝OD（OA＜OC），∠AOB＝∠COD＝α，直线AC，BD 交于点M，连接OM．下列结论：①AC＝BD，②∠OAM＝∠OBM，③∠AMB＝α，④OM平分∠BOC，其中正确结论的个数是（）A．4B．3C．2D．1二、填空题（6题）11．如图，线段AB，CD相交于点O，AO＝BO，添加一个条件，能使△AOC≌△BOD，所添加的条件的是．12．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．第12题第14题13．在△ABC中，AB＝3cm，AC＝4cm，则BC边上的中线AD的取值范围是．14．在直角三角形中，存在斜边的平方等于两条直角边的平方的和。

全等三角形的证明全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边．(2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角．(3)有公共边的，公共边常是对应边．(4)有公共角的，公共角常是对应角．(5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键．全等三角形的判定方法：(1)边角边定理(SAS)：两边和它们的夹角对应相等的两个三角形全等．(2)角边角定理(ASA)：两角和它们的夹边对应相等的两个三角形全等．(3)边边边定理(SSS)：三边对应相等的两个三角形全等．(4)角角边定理(AAS)：两个角和其中一个角的对边对应相等的两个三角形全等．(5)斜边、直角边定理(HL)：斜边和一条直角边对应相等的两个直角三角形全等．全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．专题1、常见辅助线的做法典型例题找全等三角形的方法：（1）可以从结论出发，寻找要证明的相等的两条线段（或两个角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形全等；（3）可从条件和结论综合考虑，看它们能确定哪两个三角形全等；（4）若上述方法均不可行，可考虑添加辅助线，构造全等三角形。

三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

12．2 三角形全等的判定第1课时 “边边边”学习目标1．三角形全等的“边边边”的条件． 2．了解三角形的稳定性．3．经历探索三角形全等条件的过程，体会利用操作、•归纳获得数学结论的过程． 学习重点三角形全等的条件． 学习难点寻求三角形全等的条件．学习方法：自主学习与小组合作探究 学习过程：一．回顾思考： 1．（1）三角形中已知三个元素，包括哪几种情况？ 三个角、三个边、两边一角、两角一边．（2）到目前为止，可以作为判别两三角形全等的方法有几种？各是什么？三种：①定义__________________________________________________； ②“SAS ”公理__________________________________________________ ③“ASA ”定理__________________________________________________C 'B 'A 'CBA一、情境导入问题提出：一块三角形的玻璃损坏后，只剩下如图①所示的残片，你对图中的残片作哪些测量，就可以割取符合规格的三角形玻璃，与同伴交流．学生活动：观察，思考，回答教师的问题．方法如下：可以将图①的玻璃碎片放在一块纸板上，然后用直尺和铅笔或水笔画出一块完整的三角形．如图②，剪下模板就可去割玻璃了．如果△ABC≌△A′B′C′，那么它们的对应边相等，对应角相等．反之，如果△ABC与△A′B′C′满足三条边对应相等，三个角对应相等，即AB＝A′B′，BC＝B′C′，CA＝C′A′，∠A＝∠A′，∠B＝∠B′，∠C＝∠C′这六个条件，就能保证△ABC≌△A′B′C′.从刚才的实践我们可以发现：只要两个三角形三条对应边相等，就可以保证这两块三角形全等．这种说法对吗？二、合作探究探究点：三角形全等的判定方法——“边边边”【类型一】利用“SSS”判定两个三角形全等如图，AB ＝DE ，AC ＝DF ，点E 、C 在直线BF 上，且BE ＝CF .求证：△ABC ≌△DEF .解析：已知△ABC 与△DEF 有两边对应相等，通过BE ＝CF 可得BC ＝EF ，即可判定△ABC ≌△DEF .证明：∵BE ＝CF ，∴BE ＋EC ＝EC ＋CF ，即BC ＝EF .在△ABC 和△DEF 中，∵⎩⎪⎨⎪⎧BC ＝EF ，AB ＝DE ，AC ＝DF ，∴△ABC ≌△DEF (SSS)．方法总结：判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．【类型二】 “SSS ”与全等三角形的性质结合进行证明或计算如图所示，△ABC 是一个风筝架，AB ＝AC ，AD 是连接点A 与BC 中点D 的支架，求证：AD ⊥BC .解析：要证AD ⊥BC ，根据垂直定义，需证∠1＝∠2，∠1＝∠2可由△ABD ≌△ACD 证得．证明：∵D 是BC 的中点，∴BD ＝CD .在△ABD 和△ACD 中，∵⎩⎪⎨⎪⎧AB ＝AC ，BD ＝CD ，AD ＝AD ，∴△ABD ≌△ACD (SSS)，∴∠1＝∠2(全等三角形的对应角相等)．∵∠1＋∠2＝180°，∴∠1＝∠2＝90°，∴AD ⊥BC (垂直定义)．方法总结：将垂直关系转化为证两角相等，利用全等三角形证明两角相等是全等三角形的间接应用．【类型三】 利用“边边边”进行尺规作图已知：如图，线段a、b、c.求作：△ABC，使得BC＝a，AC＝b，AB＝c.(保留作图痕迹，不写作法)解析：首先画AB＝c，再以B为圆心，a为半径画弧，以A为圆心，b为半径画弧，两弧交于一点C，连接BC，AC，即可得到△ABC.解：如图所示，△ABC就是所求的三角形．方法总结：关键是掌握基本作图的方法，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．【类型四】利用“SSS”解决探究性问题如图，AD＝CB，E、F是AC上两动点，且有DE＝BF.(1)若E、F运动至图①所示的位置，且有AF＝CE，求证：△ADE≌△CBF.(2)若E、F运动至图②所示的位置，仍有AF＝CE，那么△ADE≌△CBF还成立吗？为什么？(3)若E、F不重合，AD和CB平行吗？说明理由．解析：(1)因为AF ＝CE ，可推出AE ＝CF ，所以可利用SSS 来证明三角形全等；(2)同样利用三边来证明三角形全等；(3)因为全等，所以对应角相等，可推出AD ∥CB .解：(1)∵AF ＝CE ，∴AF ＋EF ＝CE ＋EF ，∴AE ＝CF .在△ADE 和△CBF 中，∵⎩⎪⎨⎪⎧AD ＝CB ，DE ＝BF ，AE ＝CF ，∴△ADE ≌△CBF .(2)成立．∵AF ＝CE ，∴AF －EF ＝CE －EF ，∴AE ＝CF .在△ADE 和△CBF 中，∵⎩⎪⎨⎪⎧AD ＝CB ，DE ＝BF ，AE ＝CF ，∴△ADE ≌△CBF .(3)平行．∵△ADE ≌△CBF ，∴∠A ＝∠C ，∴AD ∥BC .方法总结：解决本题要明确无论E 、F 如何运动，总有两个三角形全等，这个在图形中要分清．三、板书设计边边边1．三边分别相等的两个三角形全等．简记为“边边边”或“SSS ”． 2．“边边边”判定方法可用几何语言表示为：在△ABC 和△A 1B 1C 1中，∵⎩⎪⎨⎪⎧AB ＝A 1B 1，BC ＝B 1C 1，AC ＝A 1C 1，∴△ABC ≌△A 1B 1C 1(SSS)．本节课从操作探究活动入手，有效地激发了学生的学习积极性和探究热情，提高了课堂的教学效率，促进了学生对新知识的理解和掌握．从课堂教学的情况来看，学生对“边边边”掌握较好，达到了教学的预期目的．存在的问题是少数学生在辅助线的构造上感到困难，不知道如何添加合理的辅助线，还需要在今后的教学中进一步加强巩固和训练．评价反思 概括总结1. 本节课我们探索得到了三角形全等的条件，又•发现了证明三角形全等的一个规律SSS ．并利用它可以证明简单的三角形全等问题．2.到目前为止，可以作为判别两三角形全等的方法有几种？各是什么？①定义__________________________________________________；②“SAS”公理__________________________________________________③“ASA”定理_________________________________________________④“SSS”定理_________________________________________________12.2 三角形全等的判定第1课时“边边边”AB CD[分析]要证△ABD≌△ACD，可以看这两个三角形的三条边是否对应相等．证明：因为D是BC的中点所以BD=DC在△ABD和△ACD中(AB ACBD CDAD AD=⎧⎪=⎨⎪=⎩公共边)所以△ABD≌△ACD（SSS）．让学生独立思考后口头表达理由，由教师板演推理过程尺规作图：已知：∠BAC．求作：∠B'A'C' ,使∠B'A'C'=∠BAC．让学生初步体验成功的喜悦，同时也明确一下书写过程．巩固练习学练优练习让学生巩固对三角形全等的判定条件的认识，同时也让学生尝试书写推理过程．小结与作业反思小结回顾反思本节课对知识的研究探索过程、小结方法及结论，提炼数学思想，掌握数学规律．再次渗透分类的数学思想，体会分析问题的方法，积累数学活动的经验．布置作业1．必做题：2．选做题：培养学生良好的学习习惯，巩固所学的知识。

第十二章 --全等三角形一、基本概念1.全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；（3）能够完全重合的三角形叫做全等三角形2.全等三角形的表示两个三角形全等用“≌”符号表示；例如：△ABC与△DEF全等，那么我们可以表示为：△ABC≌△DEF。

3.全等三角形的基本性质（1）全等三角形对应边相等；（2）全等三角形对应角相等4.全等三角形的判定方法（1）三边分别相等的两个三角形全等（可以简写成“边边边”或“SSS”）例：在如图所示的三角形中，AB=AC,AD是△ABC的中线，求证△ABD≌△ACD.AB D C（2）两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）例：如图，有一池塘，要测池塘两端A，B的距离，可先在平地上取一点C不经过池塘可以直接到达点A和B。

连接AC并延长到点D，使CD=CA.连接BC并延长到E，使CE=CB.连接DE,那么量出DE的长就是A，B的距离。

为什么？（3）两角和它们的夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）例：如图，点D在AB上，点E在AC上，AB=AC,∠B=∠C。

求证AD=AE.AD EB C（4）两角分别相等且其中一组等角的对边相等的两个三角形全等（可以简写成“角角边”或“AAS”）.例：在△ABC和△DEF中，∠A=∠D,∠B=∠E，BC=EF.求证△ABC≌△DEF（5）斜边和一条直角边分别相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”）例：如图，AC⊥BC，BD⊥AD,垂足分别为C，D，AC=BD.求证BC=AD.5.角平分线的性质及判定性质：角平分线上的点到角两边的距离相等判定：到一个角的两边距离相等的点在这个角的平分线上。

二、灵活运用定理1.判定两个三角形全等的定理中，必须具备三个条件，且至少要有一组边对应相等，因此在寻找全等的条件时，总是先寻找相等的可能性。

（1）已知条件中有两角对应相等，可找：①夹边相等（ASA）②任一组等角的对边相等（AAS）（2）已知条件中有两边对应相等，可找①夹角相等（SAS）②第三组边也相等（SSS）（3）已知条件中有一边一角对应相等，可找①任一组角相等（AAS或ASA）②夹等角的另一组边相等（SAS）三、常见考法（1）利用全等三角形的性质：①证明线段（或角）相等；②证明两条线段的和差等于另一条线段；③证明面积相等（2）利用判定公理来证明两个三角形全等练习题1．（2015•莆田）如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（）A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC2．（2015•茂名）如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（）A．6 B．5 C．4 D．33．（2015•贵阳）如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A=∠C B．∠D=∠B C．AD∥BC D．DF∥BE 4．（2015•青岛）如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE=1，则BC=（）A．B．2 C．3 D．+25．（2015•启东市模拟）如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E．BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中，能使△ABC≌△DEF的条件共有（）A．1组B．2组C．3组D．4组6．（2015•杭州模拟）用直尺和圆规作已知角的平分线的示意图如右，则说明∠CAD=∠DAB 的依据是（）A．SSS B．SAS C．ASA D．AAS 7．（2015•滕州市校级模拟）如图，在下列条件中，不能证明△ABD≌△ACD的是（）A．BD=DC，AB=AC B．∠ADB=∠ADC，BD=DCC．∠B=∠C，∠BAD=∠CAD D．∠B=∠C，BD=DC8．（2015•奉贤区二模）如图，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是（）A．∠B=45°B．∠BAC=90°C．BD=AC D．AB=AC 9．（2015•西安模拟）如图所示，AB∥EF∥CD，∠ABC=90°，AB=DC，那么图中的全等三角形有（）A．4对B．3对C．2对D．1对10．（2015春•泰山区期末）如图，△A BC≌△AEF，AB=AE，∠B=∠E，则对于结论①AC=AF，②∠FAB=∠EAB，③EF=BC，④∠EAB=∠FAC，其中正确结论的个数是（）A．1个B．2个C．3个D．4个二．填空题（共10小题）11．（2015春•沙坪坝区期末）如图，已知△ABC≌△ADE，若AB=7，AC=3，则BE的值为．12．（2015春•张家港市期末）如图，已知Rt△ABC≌Rt△ABCDEC，连结AD，若∠1=20°，则∠B的度数是．13．（2015春•苏州校级期末）如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD=30°，则∠A=°．14．（2015春•万州区期末）如图，已知△ABC≌△ADE，D是∠BAC的平分线上一点，且∠BAC=60°，则∠CAE=．15．（2015•黔东南州）如图，在四边形ABCD中，AB∥CD，连接BD．请添加一个适当的条件，使△ABD≌△CDB．（只需写一个）16．（2014秋•曹县期末）如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是．17．（2015•盐亭县模拟）如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE 的度数是度．18．（2014秋•腾冲县校级期末）如图，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则∠ABC+∠DFE=度．19．（2015•聊城）如图，在△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线．若AB=6，则点D到AB的距离是．20．如图，在△A BC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC=4，DE=2，则△BCD的面积是．三．解答题（共7小题）21．如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB 延长线上一点．（1）求∠EBG的度数．（2）求CE的长．22．已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．（1）求证：△ABD≌△CAE；（2）连接DE，线段DE与AB之间有怎样的位置和数量关系请证明你的结论．23．如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：（1）△AEF≌△CEB；（2）AF=2CD．24．如图：在△ABC中，∠C=90° AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；说明：（1）CF=EB．（2）AB=AF+2EB．25．如图，为了测量一池塘的宽AB，在岸边找到一点C，连接AC，在AC的延长线上找一点D，使得DC=AC，连接BC，在BC的延长线上找一点E，使得EC=BC，测出DE=60m，试问池塘的宽AB为多少请说明理由．练习题参考答案一．选择题（共10小题）1．A 2．A 3．B 4．C 5．C 6．A 7．D 8．D 9．B 10．C 二．填空题（共10小题）11．4 12．70°13．30 14．30°15．AB=CD 16．AC=DE 17．60 18．90 19． 20．4三．解答题（共7小题）21．解：（1）∵△ABE≌△ACD，∴∠EBA=∠C=42°，∴∠EBG=180°﹣42°=138°；（2）∵△ABE≌△ACD，∴AC=AB=9，AE=AD=6，∴CE=AC﹣AE=9﹣6=3．22．证明：（1）∵AB=AC，∴∠B=∠ACD，∵AE∥BC，∴∠EAC=∠ACD，∴∠B=∠EAC，∵AD是BC边上的中线，∴AD⊥BC，∵CE⊥AE，∴∠ADC=∠CEA=90°在△ABD和△CAE中∴△ABD≌△CAE（AAS）；（2）AB=DE，AB∥DE，如右图所示，∵AD⊥BC，AE∥BC，∴AD⊥AE，又∵CE⊥AE，∴四边形ADCE是矩形，∴AC=DE，∵AB=AC，∴AB=DE．∵AB=AC，∴BD=DC，∵四边形ADCE是矩形，∴AE∥CD，AE=DC，∴AE∥BD，AE=BD，∴四边形ABDE是平行四边形，∴AB∥DE且AB=DE．23．证明：（1）∵AD⊥BC，CE⊥AB，∴∠BCE+∠CFD=90°，∠BCE+∠B=90°，∴∠CFD=∠B，∵∠CFD=∠AFE，∴∠AFE=∠B在△AEF与△CEB中，，∴△AEF≌△CEB（AAS）；（2）∵AB=AC，AD⊥BC，∴BC=2CD，∵△AEF≌△CEB，∴AF=BC，∴AF=2CD．24．证明：（1）∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴DE=DC，∵在Rt△DCF和Rt△DEB中，，∴Rt△CDF≌Rt△EBD（HL）．∴CF=EB；（2）∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴CD=CE．在△ADC与△ADE中，∵∴△ADC≌△ADE（HL），∴AC=AE，∴AB=AE+BE=AC+EB=AF+CF+E B=AF+2EB．25．解：AB=60米．理由如下：∵在△ABC和△DEC中，，∴△ABC≌△DEC（SAS），∴AB=DE=60（米），则池塘的宽AB为60米．。

三角形全等的判定“边角边”（7种题型）【知识梳理】全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS ”）.要点诠释：如图，如果AB ＝ ''A B ，∠A ＝∠'A ，AC ＝ ''A C ，则△ABC ≌△'''A B C . 注意：这里的角，指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等，两个三角形不一定全等.如图，△ABC 与△ABD 中，AB ＝AB ，AC ＝AD ，∠B ＝∠B ，但△ABC 与△ABD 不完全重合，故不全等，也就是有两边和其中一边的对角对应相等，两个三角形不一定全等.【考点剖析】题型一：用“边角边”直接证明三角形全等例1．已知：如图，点C 为AB 中点，CD=BE ，CD ∥BE.求证:△ACD ≌△CBE.【解析】证明：∵CD ∥BE ，∴∠ACD=∠B..∵点C 为AB 中点，∴AC=CB.又∵CD=BE ，∴△ACD ≌△CBE （SAS ）【变式1】如图，AC DF =，12∠=∠，如果根据“SAS ”判定ABC DEF △≌△，那么需要补充的条件是（ ）A ．A D ∠=∠B ．AB DE =C ．B E ∠=∠D ．BF CE =【答案】D 【详解】解：需要补充的条件是BF=CE ，∴BF+FC=CE+CF ，即BC=EF ，在△ABC 和△DEF 中，12AC DF BC EF =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△DEF （SAS ）．故选：D ．【变式1】如图，点B ，E ，C ，F 在同一条直线上，AB ＝DE ，BE ＝CF ，∠B ＝∠DEF ．求证：△ABC ≌△DEF ．【解答】证明：∵BE ＝CF ，∴BE+CE ＝CF+EC ．∴BC ＝EF ．在△ABC 和△DEF 中，{AB =DE∠B =∠DEF BC =EF，∴△ABC≌△DEF（SAS）．【变式3】如图，CA＝CD，∠BCE＝∠ACD，BC＝EC．求证：△ABC≌△DEC．【解答】证明：∵∠BCE＝∠ACD，∴∠BCE+∠ACE＝∠ACD+∠ACE，∴∠ACB＝∠DCE，在△ABC和△DEC中，{AC=DC∠ACB=∠DCE BC=EC，∴△ABC≌△DEC（SAS）．【变式4】如图，D、C、F、B四点在一条直线上，AC＝EF，AC⊥BD，EF⊥BD，垂足分别为点C、点F，BF＝CD．试说明：△ABC≌△EDF．【解答】解：∵AC⊥BD，EF⊥BD，∴∠ACB＝∠EFD＝90°，∵BF＝CD，∴BF+CF＝CD+CF，即BC＝DF，在△ABC和△EDF中，{BC=DF∠ACB=∠EFD AC=EF，∴△ABC≌△EDF（SAS）．【变式5】如图，△ABC 中，AB=AC ，点E ，F 在边BC 上，BE=CF ，点D 在AF 的延长线上，AD=AC ，（1）求证：△ABE ≌△ACF ；（2）若∠BAE=30°，则∠ADC= °．【答案】（1）证明见解析；（2）75．【详解】（1）∵AB=AC ，∴∠B=∠ACF ，在△ABE 和△ACF 中，AB AC B ACFBE CF =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACF （SAS ）；（2）∵△ABE ≌△ACF ，∠BAE=30°，∴∠CAF=∠BAE=30°，∵AD=AC ，∴∠ADC=∠ACD ，∴∠ADC=280013︒−︒=75°，故答案为75． 【变式6】（2023春·江苏·七年级统考期末）如图，在ABC 和ADE V 中，AB AC =，AD AE =，90BAC DAE ∠=∠=︒，连接BD CE 、．(1)求证：ABD ACE ≌△△． (2)图中BD 和CE 有怎样的关系？试证明你的结论．【详解】（1）解：90BAC DAE ∠=∠=︒∴BAC CAD DAE CAD ∠+∠=∠+∠∴BAD EAC ∠=∠AB AC =，AD AE =∴ABD ACE ≌△△． （2）解：如图，设BD 和CE 交点为FABD ACE ≌△△∴ACE ABD ∠=∠90BAC ∠=︒∴90ABD DBC ACB ∠+∠+∠=︒∴90ACE DBC ACB ∠+∠+∠=︒即90ECB DBC ∠+∠=︒∴()18090BFC ECB DBC ∠=︒−∠+∠=︒∴BD CE ⊥．题型二：用“边角边”间接证明三角形全等例2、已知：如图，AB ＝AD ，AC ＝AE ，∠1＝∠2．求证：BC ＝DE ．【答案与解析】证明： ∵∠1＝∠2∴∠1＋∠CAD ＝∠2＋∠CAD ，即∠BAC ＝∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE （SAS ）∴BC ＝DE （全等三角形对应边相等）【变式1】如图所示，点O 为AC 的中点，也是BD 的中点，那么AB 与CD 的关系是________．【答案】平行且相等【详解】解：∵点O 为AC 的中点，也是BD 的中点，∴AO=OC ，BO=OD ，又∵∠AOB=∠DOC ，∴△AOB ≌△COD （SAS ）∴AB=CD ，∠A=∠C ，∴AB//CD,即AB 与CD 的关系是平行且相等，故答案为：平行且相等．【变式2】如图，已知AB ∥CD ，AB ＝CD ，∠A ＝∠D ．求证：AF ＝DE ．【详解】证明：∵AB//CD ，∴∠B ＝∠C ，在△ABF 和△DCE 中，A D AB CDB C ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABF ≌△DCE （ASA ），∴AF ＝DE ．【变式3】如图，点E 、F 分别是矩形ABCD 的边 AB 、CD 上的一点，且DF ＝BE .求证：AF=CE .【分析】由SAS 证明△ADF ≌△CBE ，即可得出AF ＝CE ．【详解】证明：∵四边形ABCD 是矩形，∴∠D ＝∠B ＝90°，AD ＝BC ，在△ADF 和△CBE 中，AD BC D B DF BE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADF ≌△CBE （SAS ），∴AF ＝CE ．【变式4】已知ABN 和ACM △位置如图所示，AB AC =，AD AE =，12∠=∠．（1）试说明：BD CE =；（2）试说明：M N ∠=∠．【详解】解：（1）在△ADB 和△AEC 中，12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△AEC （SAS ），∴BD=CE ；（2）∵12∠=∠，∴BAN CAM ∠=∠，∵△ADB ≌△AEC ，∴B C ∠=∠，∴180180B BAN C CAM ︒−∠−∠=︒−∠−∠，即M N ∠=∠．【变式5】如图，将两个一大、一小的等腰直角三角尺拼接 （A 、B 、D 三点共线，AB ＝CB ，EB ＝DB ，∠ABC ＝∠EBD ＝90°），连接AE 、CD ，试确定AE 与CD 的位置与数量关系，并证明你的结论．【答案】AE ＝CD ，并且AE ⊥CD证明：延长AE 交CD 于F ，∵△ABC 和△DBE 是等腰直角三角形∴AB ＝BC ，BD ＝BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD （SAS ）∴AE ＝CD ，∠1＝∠2又∵∠1＋∠3＝90°，∠3＝∠4（对顶角相等）∴∠2＋∠4＝90°，即∠AFC ＝90°∴AE ⊥CD题型三：边角边与倍长中线例3、如图，AD 是△ABC 的中线，求证：AB ＋AC ＞2AD ．【答案与解析】 证明：如图，延长AD 到点E ，使AD ＝DE ，连接CE ．在△ABD 和△ECD 中，∴△ABD ≌△ECD （SAS ）．∴AB ＝CE ．∵AC ＋CE ＞AE ，∴AC ＋AB ＞AE ＝2AD ．即AC ＋AB ＞2AD ．14．如图所示，AD 是△ABC 中BC 边上的中线，若AB =2，AC =6，则AD 的取值范围是__________AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝．【答案】2＜AD ＜4【分析】此题要倍长中线，再连接，构造全等三角形．根据三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边．即可求解．【详解】解：延长AD 到E ，使AD =DE ，连接BE ，∵AD 是△ABC 的中线，∴BD =CD ，在△ADC 与△EDB 中，BD CD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB （SAS ），∴EB =AC ，根据三角形的三边关系定理：6-2＜6+2，∴2＜AD ＜4，故AD 的取值范围为2＜AD ＜4．【点睛】本题主要考查对全等三角形的性质和判定，三角形的三边关系定理等知识点的理解和掌握，能推出6-2＜AE ＜6+2是解此题的关键．题型四：边角边与截长补短例4、已知，如图：在△ABC 中，∠B ＝2∠C ，AD ⊥BC ，求证：AB ＝CD －BD ．【答案与解析】 证明：在DC 上取一点E ，使BD ＝DE∵ AD ⊥BC ，∴∠ADB ＝∠ADE在△ABD 和△AED 中，∴△ABD ≌△AED （SAS ）． ∴AB ＝AE ，∠B＝∠AED ．又∵∠B ＝2∠C ＝∠AED ＝∠C ＋∠EAC ．∴∠C ＝∠EAC ．∴AE ＝EC ．∴AB ＝AE ＝EC ＝CD —DE ＝CD —BD ．【变式】已知，如图，在四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于E ，并且AE ＝（AB ＋AD ）， 求证：∠B ＋∠D ＝180°.【答案】证明：在线段AE 上，截取EF ＝EB ，连接FC ，BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩＝∠∠＝12A EDC B∵CE ⊥AB ，∴∠CEB ＝∠CEF ＝90°在△CBE 和△CFE 中，∴△CBE 和△CFE （SAS ）∴∠B ＝∠CFE∵AE ＝（AB ＋AD ），∴2AE ＝ AB ＋AD∴AD ＝2AE －AB∵AE ＝AF ＋EF ，∴AD ＝2（AF ＋EF ）－AB ＝2AF ＋2EF －AB ＝AF ＋AF ＋EF ＋EB －AB ＝AF ＋AB －AB ，即AD ＝AF在△AFC 和△ADC 中∴△AFC ≌△ADC （SAS ）∴∠AFC ＝∠D∵∠AFC ＋∠CFE ＝180°，∠B ＝∠CFE.∴∠AFC ＋∠B ＝180°，∠B ＋∠D ＝180°.题型五：边边角不能判定两个三角形全等例5．如图，已知AC ＝BD ，添加下列一个条件后，仍无法判定△ABC ≌△BAD 的是（）A ．∠ABC ＝∠BADB ．∠C ＝∠D ＝90° C ．∠CAB ＝∠DBA D ．CB ＝DA【答案】A CEB CEFEC =EC EB EF=⎧⎪∠=∠⎨⎪⎩12(AF ADFAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义）【分析】根据全等三角形的判定方法即可一一判断；【详解】在△ABC 与△BAD 中，AC ＝BD ，AB ＝BA ，A 、SSA 无法判断三角形全等，故本选项符合题意；B 、根据HL 即可判断三角形全等，故本选项不符合题意；C 、根据SAS 即可判断三角形全等，故本选项不符合题意；D 、根据SSS 即可判断三角形全等，故本选项不符合题意；故选：A ． 题型六：尺规作图——利用边角边做三角形例6．（2023春·广东揭阳·七年级统考期末）已知：线段a ，c ，α∠．求作：ABC ．使BC a =，AB c =，ABC α∠=∠．（要求：尺规作图，不写作法，保留作图痕迹）【详解】解：如图所示：【变式1】（2023春·陕西宝鸡·七年级校考阶段练习）尺规作图：已知：线段m ，n ，∠β．求作：ABC ，使AB m =，BC n =，ABC β∠=∠（保留作图痕迹，不写作法）．【详解】解：如图所示：ABC ∴即为所作．题型七：边边边与边角边综合 八年级假期作业）如图，在ABC 中，(1)图中有___________对全等三角形；(2)请选一对加以证明．【详解】（1）图中有3对全等三角形：ABD ACD ≌△△，ABE ACE ≌△△，BDE CDE ≌V V ． 故答案为3；（2）∵D 是BC 的中点，∴BD CD =．在ABD △和ACD 中，AB AC BD CDAD AD =⎧⎪=⎨⎪=⎩， ∴()SSS ABD ACD ≌V V ；∴BAE CAE ∠=∠．在ABE 和ACE △中，AB AC BAE CAEAE AE =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABE ACE △△≌； ∴BE CE =．在BDE △和CDE 中，BE CE BD CDDE DE =⎧⎪=⎨⎪=⎩， ∴()SSS BDE CDE ≌V V ． 【过关检测】一、单选题A ．SSSB ．SASC ．ASAD ．AAS【答案】B 【分析】由题意可知根据“边角边”可证OAB OCD VV ≌即可选择．【详解】解：∵在OAB 和OCD 中，OC OA COD AOB OD OB =⎧⎪∠=∠⎨⎪=⎩， ∴()OAB OCD SAS ≌△△．故判定这两个三角形全等的依据是“SAS ”．故选B ．【点睛】本题考查三角形全等的判定．熟练掌握判定三角形全等的条件是解题关键． 2．（2023春·江西景德镇·七年级统考期末）如图，AB AC =，点D 、E 分别在AC 和AB 边上，且AD AE =，则可得到ABD ACE △△≌，判定依据是（ ）A ．ASAB ．AASC ．SASD ．SSS【答案】C 【分析】根据SAS 证明ABD ACE △△≌，即可求解． 【详解】解：在ABD △与ACE △中，AB AC BAD CAEAD AE =⎧⎪∠=∠⎨⎪=⎩∴ABD ACE △△≌()SAS ，故选：C ． 【点睛】本题考查了全等三角形的判定，熟练掌握全等三角形的判定定理是解题的关键．3．（2023春·四川成都·七年级统考期末）如图，在ABF △和DCE △中，点E 、F 在BC 上，AF DE =，AFB DEC ∠=∠，添加下列一个条件后能用“SAS ”判定ABF DCE ≌△△的是（ ）A ．BE CF =B ．BC ∠=∠ C ．AD ∠=∠ D ．AB DC =【答案】A 【分析】先根据BE CF =得到BF CE =，再根据全等三角形的判定定理进行分析即可．【详解】解：∵BE CF =，∴BE EF CF EF +=+，即BF CE =，A 选项，因为BE CF =，AFB DEC ∠=∠，BF CE =，满足“SAS ”判定ABF DCE ≌△△，符合题意； B 选项，因为B C ∠=∠，AFB DEC ∠=∠，BF CE =，是用“AAS ”判定ABF DCE ≌△△，不符合题意； C 选项，因为A D ∠=∠，AF DE =，AFB DEC ∠=∠，是用“ASA ”判定ABF DCE ≌△△，不符合题意； D 选项，因为AB DC =，AF DE =，AFB DEC ∠=∠，不能判定ABF DCE ≌△△，不符合题意； 故选：A ．【点睛】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键．4．（2023春·四川达州·七年级统考期末）如图，在2×3的正方形方格中，每个正方形方格的边长都为1，则1∠和2∠的关系是（ ）A ．221∠=∠B ．2190∠−∠=︒C ．1290∠+∠=︒D ．12180∠+∠=︒【答案】C 【分析】先证明ABC CDE △△≌，再利用全等三角形的性质和等量代换求解即可． 【详解】解：如图，在ABC 和CDE 中，2901AC CE ACB CED BC DE ==⎧⎪∠=∠=︒⎨⎪==⎩，∴ABC CDE △△≌()SAS ，∴1DCE ∠=∠， ∵290DCE ∠+∠=︒，∴1290∠+∠=︒，故选：C ．【点睛】本题考查了全等三角形的判定与性质，利用网格证明三角形全等是解题的关键．A ．20cmB ．45cmC ．25cmD ．65cm【答案】D 【分析】根据题意可得：OF OG =，OC OD =，利用已知条件判断出OFC OGD ≌，得到CF DG =，即可求出答案．【详解】解：如图：∵O 是FG 和CD 的中点，∴OF OG =，OC OD =，在OFC △和OGD 中，OF OG FOC GODOC OD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS OFC OGD ≌，∴CF DG =，又20cm DG =，∴20cm CF DG ==，∴小明离地面的高度=支点到地面的高度452065cm CF +=+=，故D 正确．故选：D ．【点睛】本题主要考查了三角形全等知识的应用，用数学方法解决生活中有关的实际问题，把实际问题转换成数学问题，用数学方法加以论证，最后进行求解，是一种十分重要的方法． 七年级统考期末）如图，已知在ABC 和BAD 中，直接判定ABC BAD ≌的依据是（ A ．SSSB ．AASC ．ASAD ．SAS【答案】D 【分析】找出两个三角形中已知相等的对应边和对应角，然后根据判定方法即可判断．【详解】解：在ABC 和ABD △中，BC AD ABC BAD AB BA =⎧⎪∠=∠⎨⎪=⎩， ∴()ABC BAD SAS ≌．故选：D ．【点睛】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角． 7．（2023春·上海浦东新·七年级校考阶段练习）如图，AD 平分BAC ∠，AB AC =，连接BD 、CD ，并延长交AC 、AB 于F 、E 点，则图中全等的三角形有( )对．A ．3对B ．4对C ．5对D ．6对【答案】B 【分析】认真观察图形，确定已知条件在图形上的位置，结合全等三角形的判定方法，仔细寻找．【详解】解：AD 平分BAC ∠，BAD CAD ∴∠=∠，在ABD 与ACD 中，AB AC BAD CADAD AD ⎧⎪∠∠⎨⎪⎩＝＝＝，()SAS ABD ACD ∴≌，BD CD ∴=，B C ∠=∠，ADB ADC ∠=∠，又EDB FDC ∠=∠，ADE ADF ∴∠=∠，AED AFD ∴≌，BDE CDF ≌，ABF ACE ≌．AED AFD ∴≌，ABD ACD ≌，BDE CDF ≌，ABF ACE ≌，共4对．故选：B ．【点睛】本题考查三角形全等的判定方法和全等三角形的性质．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．（2023春·河北保定·七年级校考阶段练习）如图，在AOB 和COD △中，OA OB =，OC OD =，AOB COD ∠=∠，AC ，BD 交于点M ，关于结论Ⅰ，Ⅱ，下列判断正确的是（ ）结论Ⅰ：AC BD =；结论Ⅱ：CMD COD ∠>∠A ．Ⅰ对，Ⅱ错B ．Ⅰ错，Ⅱ对C ．Ⅰ，Ⅱ都对D ．Ⅰ，Ⅱ都错【答案】A 【分析】根据已知条件可知三角形的全等，根据全等三角形的性质可知边相等，再根据三角形的内角和即可求出角的大小．【详解】AOB COD ∠=∠，AOB AOD COD AOD ∴∠+∠=∠+∠，AOC BOD ∴∠=∠，∴在AOC 和BOD 中，∴OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩，()AOC BOD SAS ∴≌， AC BD ∴=，故Ⅰ正确；AOC BOD ≌，OCA BDO ∴∠=∠，MDC MDO ODC ∴∠=∠+∠，OCD OCA MCD ∴∠=∠+∠，180()COD OCD ODC ∠=︒−∠+∠，180()CMD MDC MCD ∠=︒−∠+∠，180()CMD MDO ODC MCD ∴∠=︒−∠+∠+∠，180()COD OCA MCD ODC ∠=︒−∠+∠+∠，CMD COD ∴∠=∠，故Ⅱ错误；故选：A ．【点睛】本题考查了全等三角形的性质，熟记对应性质和判定定理是解题的关键． 9．（2023春·江苏·七年级统考期末）如图，在四边形ABCD 中，对角线AC 平分BAD ∠，AD AB >，下列结论正确的是（ ）A ．AD AB CD BC −=−B ．AD AB CD BC −>− C ．AD AB CD BC −<−D ．AD AB −与CD BC −的大小关系无法确定【答案】B 【分析】在AD 上截取AE AB =，BAC EAC ≌，由DE CD CE >−即可求解．【详解】解：如图，在AD 上截取AE AB =，AC 平分BAD ∠，BAC EAC ∴∠=∠，在BAC 和EAC 中AB AE BAC EACAC AC =⎧⎪∠=∠⎨⎪=⎩，∴BAC EAC ≌(SAS )，BC EC ∴=，在CDE 中：DE CD CE >−，AD AB AD AE CD BC −=−>−．故选：B ．【点睛】本题考查了三角形中三边的关系，三角形全等的判定及性质，掌握性质，并根据题意作出辅助线是解题的关键． 10．（2022秋·云南昭通·八年级统考期末）如图，AD 是ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且CE BF ，连接BF CE ，，下列说法： ①DE DF =；②ABD 和ACD 面积相等；③CE BF =；④BDF CDE ≌；⑤CEF F ∠∠=． 其中正确的有（ ）【答案】B 【分析】根据三角形中线的定义可得BD CD =，然后利用“边角边”证明BDF 和CDE 全等，根据全等三角形对应边相等可得CE BF =，全等三角形对应角相等可得F CED ∠∠=，再根据内错角相等，两直线平行可得BF CE ，最后根据等底等高的三角形的面积相等判断出②正确．【详解】解：∵AD 是ABC 的中线，∴BD CD =，在BDF 和CDE 中，BD CD BDF CDEDF DE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BDF CDE ≌，故④正确∴CE BF F CED ∠∠==，，故①正确，∵CEF CED ∠∠=，∴CEF F ∠∠=，故⑤正确，∴BF CE ，故③正确，∵BD CD =，点A 到BD CD 、的距离相等，∴ABD 和ACD 面积相等，故②正确，综上所述，正确的有5个，故选：B ．【点睛】本题考查全等三角形的判定与性质，熟练掌握全等三角形的判定方法并准确识图是解题的关键．二、填空题【答案】120°【分析】先证明,DAG BAC ≌得到GDA CBA ∠=∠，再利用60BAD ∠=︒以及三角形的内角和定理、邻补角的性质可得答案．【详解】解：60,DAE GAC ∠=∠=︒,DAG BAC ∴∠=∠,,AD AB AC AG ==在DAG 与BAC 中，,AD AB DAG BACAG AC =⎧⎪∠=∠⎨⎪=⎩,DAG BAC ∴≌,GDA CBA ∴∠=∠,BEO AED ∠=∠,BOE BAD ∴∠=∠60,BAD ∴∠=︒60,BOE ∴∠=︒120.DOC ∴∠=︒故答案为：120.︒【点睛】本题考查的是三角形全等的判定与性质，等边三角形的判定与性质，邻补角的性质，三角形的内角和定理，掌握以上知识是解题的关键． 七年级统考期末）如图，在锐角ABC 中，24ABC S = 【分析】先根据三角形全等的判定定理与性质可得ME MN =，再根据两点之间线段最短可得BM MN +的最小值为BE ，然后根据垂线段最短可得当BE AC ⊥时，BE 取得最小值，最后利用三角形的面积公式即可得．【详解】如图，在AC 上取一点E ，使AE AN =，连接ME ，AD 是BAC ∠的平分线，EAM NAM ∴∠=∠，在AEM △和ANM 中，AE AN EAM NAMAM AM =⎧⎪∠=∠⎨⎪=⎩，()SAS AEM ANM ∴≌， ME MN ∴=，BM MN BM ME ∴+=+，由两点之间线段最短得：当点,,B M E 共线时，BM ME +取最小值，最小值为BE ，又由垂线段最短得：当BE AC ⊥时，BE 取得最小值，248,ABC S AC ==，1182422AC BE BE ∴⋅=⨯⋅=，解得6BE =，即BM MN +的最小值为6，故答案为：6．【点睛】本题考查了角平分线的定义、三角形全等的判定定理与性质、两点之间线段最短、垂线段最短等知识点，正确找出BM MN +取得最小值时BE 的位置是解题关键． 13．（2023春·广东云浮·八年级校考期中）如图，小明与小红玩跷跷板游戏，已知跷跷板的支点O （即跷跷板的中点）至地面的距离是48cm ，当小红从水平位置CD 下降28cm 时，这时小明离地面的高度是___________cm ．【答案】76【分析】根据题意可得：OF OG =，OC OD =，利用已知条件判断出OFC OGD ≌V V ，得到CF DG =，即可【详解】解：如图：∵O 是FG 和CD 的中点，∴OF OG =，OC OD =，在OFC △和OGD 中，OF OG FOC GODOC OD =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)OFC OGD ≌V V ，∴CF DG =，又28cm DG =，∴28cm CF DG ==，∴小明离地面的高度=支点到地面的高度482876cm CF +=+=，故答案为：76．【点睛】本题主要考查了三角形全等知识的应用，用数学方法解决生活中有关的实际问题，把实际问题转换成数学问题，用数学方法加以论证，最后进行求解，是一种十分重要的方法． 14．（2023春·广东佛山·七年级校考期中）在测量一个小口圆形容器的壁厚(厚度均匀)时，小明用“X 型转动钳”按如图方法进行测量，其中OA OD =，OB OC =，测得3cm AB =，5cm EF =，圆形容器的壁厚是______cm ．【分析】由题证明AOB DOC ≌，由全等三角形的性质可得，AB CD =，即可解决问题．【详解】在AOB 和DOC △中，OA OD AOB DOCBO OC =⎧⎪∠=∠⎨⎪=⎩，(SAS)AOB DOC ∴≌，3cm AB CD ∴==，cm 5EF =Q ，∴圆柱形容器的壁厚是1(53)1(cm)2⨯−=，故答案为：1．【点睛】本题考查了全等三角形的应用，解题的关键是利用全等三角形的性质解决实际问题．【答案】25米/25m【分析】根据SAS 可证明ACB DCE ≌△△，再根据全等三角形的性质可得AB DE =，进而得到答案． 【详解】解：∵点C 是AD 的中点，也是BE 的中点，∴AC DC =，BC EC =，∵在ACB △和DCE △中，AC DC ACB DCEBC EC =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ACB DCE ≌，∵25DE =米，∴25AB =米，故答案为：25米．【点睛】此题考查了全等三角形的应用，关键掌握全等三角形的判定定理和性质定理． 16．（2022秋·陕西宝鸡·八年级统考期末）如图，E 是ABC ∆外一点，D 是AE 上一点，AC BC BE ==，DA DB =，EBD CBD ∠=∠，70C ∠=︒，则BED ∠的度数为___________．【答案】35︒/35度【分析】连接DC ，则DC 垂直平分AB ，可得35ADC DCB ∠=∠=︒，再证明BED BCD ∆≅∆，即可得到35BED DCB ∠=∠=︒．【详解】连接DC ，DA DB =，CA CB =，DC ∴是AB 的垂直平分线，1352DCB ACB ∴∠=∠=︒，在BED 和BCD △中BD BD EBD CBDBE BC =⎧⎪∠=∠⎨⎪=⎩(SAS)BED BCD ∴≌，35BED DCB ∴∠=∠=︒，故答案为：35︒．【点睛】本题主要考查等腰三角形的性质，由条件得到DC 是AB 的垂直平分线再想到证明BED BCD △≌△是解题的关键． 17．（2023·全国·八年级假期作业）如图，AB 与CD 相交于点O ，且O 是AB CD ，的中点，则AOC 与BOD 全等的理由是________．【答案】SAS /边角边【分析】根据全等三角形的判定定理求解即可．【详解】解：∵O 是AB CD ，的中点，∴,,OA OB OC OD ==在AOC 和DOB 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩ ∴()SAS AOC DOB ≌， 故答案为：SAS ．【点睛】此题考查了全等三角形的判定，熟记全等三角形的判定定理是解题的关键．18．（2022秋·山东聊城·八年级统考期末）如图，在ABC ∆中，已知 AB AC =，BD CF = ，BE CD =．若40A ∠=︒，则EDF ∠的度数为__________．【答案】70°【分析】（1）证△BED ≌△CDF ；（2）利用AB=AC 得到∠B 与∠C（3）利用整体法求得∠EDF【详解】∵AB=AC ，∴∠B=∠C∵BD=CF ，BE=CD∴△BED ≌△CDF ，∴∠FDC=∠BED∵∠A=40°∴∠B=∠C=70°∴在△BED 中，∠BED+∠BDE=110°∴∠EDB+∠FDC=110°∴∠EDF=70°【点睛】求角度，常见的方法有：（1）方程思想；（2）整体思想；（3）转化思想本题就是利用全等，结合整体思想求解的角度三、解答题 19．（2023秋·广东广州·八年级统考期末）已知：如图，12BC DC =∠=∠，，求证：ABC ≌ADC △．【答案】见解析【分析】先证明ACB ACD ∠=∠，再结合AC AC =，BC DC =，即可得到结论．【详解】．证明：12∠=∠，ACB ACD ∴∠=∠，AC AC BC DC ==，，ABC ∴≌ADC △．【点睛】本题考查的是全等三角形的判定，掌握“利用SAS 证明两个三角形全等”是解本题的关键． 20．（2021秋·广东广州·八年级广州市第八十九中学校考期中）如图，点E 、F 在BC 上，BF EC =，AB DC =，B C ∠=∠．求证：A D ∠=∠．【答案】证明见解析【分析】证明()SAS ABF DCE ≌△△，然后根据全等三角形的性质即可得出结论．【详解】证明：在ABF △和DCE △中，AB DC B CBF CE =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABF DCE ≌△△， ∵A D ∠=∠．【点睛】本题考查全等三角形的判定和性质．掌握全等三角形的判定是解题的关键．21．（2023春·陕西西安·七年级校考阶段练习）已知：如右图ABCD ，AB CD =．求证：ADC CBA ≌．【答案】见解析【分析】由AB CD ，得ACD CAB ∠=∠，再利用SAS 即可证得结论．【详解】证明：∵ABCD ，∴ACD CAB ∠=∠，在ADC △与CBA △中：AB CD ACD CAB AC CA =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ADC CBA ≌．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ． 22．（2023春·陕西咸阳·七年级统考期末）如图，点D 在线段BE 上，AB CD ，AB DE =，BD CD =．ABD △和EDC △全等吗？为什么？【答案】ADB ECD △≌△，理由见解析【分析】先根据平行线的性质得到ABD EDC =∠∠，再利用SAS 证明ADB ECD △≌△即可得到结论．【详解】解：ADB ECD △≌△，理由如下：∵AB CD ，∴ABD EDC =∠∠，∵AB ED =，BD DC =，∴()SAS ADB ECD △≌△．【点睛】本题主要考查了全等三角形的判定，平行线的性质，熟知边角边证明三角形全等是解题的关键．(1)求证：AEC DFB △△≌； (2)若6AEC S ∆=，求三角形BEC 的面积．【答案】(1)见解析(2)92BEC S =△【分析】（1）根据AE DF ∥得A D ∠=∠，根据AB CD =得AB BC CD BC +=+，即AC DB =，根据ASA 即可证明AEC DFB △△≌； （2）在AEC △中，以AC 为底作EH 为高，则12AEC S EH AC ∆=⋅，12BCE S EH BC ∆=⋅，根据13AB CD BC ==得43AC BC =，6AEC S ∆=，即可得．【详解】（1）证明：∵AE DF ∥，A D ∴∠=∠， ∵AB CD =，AB BC CD BC ∴+=+AC DB ∴=，在AEC △和DFB △中，AE DF A DAC DB =⎧⎪∠=∠⎨⎪=⎩，SAS AEC DFB ∴≌（）△△；（2）解：如图所示，在AEC △中，以AC 为底作EH 为高，12AEC S EH AC ∆∴=⋅，12BCE S EH BC ∆=⋅，∵13AB CD BC ==，43AC BC ∴=，6AEC S ∆=， ΔΔ3 4.54BEC AEC S S ∴==．【点睛】本题考查了三角形的判定与性质，三角形的面积，解题的关键是理解题意，掌握这些知识点． 24．（2023春·福建福州·七年级福州华伦中学校考期末）已知：如图，点,F C 在线段BE 上，AB DE =，B E ∠=∠，BF EC =．求证：A D ∠=∠．【答案】见解析【分析】先根据线段的和差得出BC EF =，进而证明ABC DEF ≌△△，根据全等三角形的性质即可得证． 【详解】证明：∵BF EC =，∴BF FC FC CE +=+，即BC EF =，在,ABC DEF 中，AB DE B EBC EF =⎧⎪∠=∠⎨⎪=⎩，∴ABC DEF ≌△△， ∴A D ∠=∠．【点睛】本题考查了全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．25．（2023·全国·八年级假期作业）如图，在△ABC 中，已知AB AC =，2BAC DAE ∠=∠，且DAE FAE ∆≅∆．求证：ABD ACF ∆≅∆．【答案】见解析【分析】先根据全等三角形的性质以及已知2BAC DAE ∠=∠得出BAD CAF ∠=∠，再利用SAS 即可证出ABD ACF ∆≅∆．【详解】证明：∵DAE FAE ∆≅∆，∴,AD AF DAE FAE =∠=∠．∵2BAC DAE ∠=∠，∴BAD EAC DAE FAE ∠+∠=∠=∠，∵FAC EAC FAE ∠+∠=∠∴BAD CAF ∠=∠．在ABD ∆和ACF ∆中，AB AC BAD CAFAD AF =⎧⎪∠=∠⎨⎪=⎩∴ABD ACF ∆≅∆．【点睛】本题考查了全等三角形的判定和性质，灵活运用这些性质解决问题是本题的关键． 八年级假期作业）如图，在ABC 和V(1)求证：ABD ACE △△≌(2)若35BDA ∠=︒，则【答案】(1)见解析(2)70【分析】（1）根据等式的性质，可得=BAD CAE ∠∠，根据SAS 可得两个三角形全等；（2）根据全等三角形的性质，可得对应角相等，根据等腰三角形的性质，可得ADC AEC ∠∠=，根据等量代换，可得证明结论．【详解】（1）证明：=BAC DAE ∠∠，BAC DAC DAE DAC ∴∠−∠=∠−∠，即=BAD CAE ∠∠．在ABD △和ACE △中，AB AC BAD EACAD AE =⎧⎪∠=∠⎨⎪=⎩，SAS ABD ACE ∴≌（）；（2）证明：ABD ACE ≌△△， ADB AEC ∴∠=∠，AD AE =ADC AEC ∴∠=∠35BDA ADC ∴∠=∠=︒∴223570BDC BDA ∠∠==⨯︒=︒．故答案为：70．【点睛】本题考查了全等三角形的判定与性质，利用SAS 证明三角形全等，利用全等三角形的性质，证明对应角相等，再利用等量代换得出证明结论． 27．（2023春·全国·七年级专题练习）如图，已知点B ，E ，C ，F 在一条直线上，AB DE =，BF CE =，B E ∠=∠．求证：ABC DEF ≌△△【答案】见解析【分析】用边角边定理进行证明即可.【详解】解：∵BF CE =∴BF FC CE FC +=+即：BC EF =在ABC 和DEF 中AB DE B EBC EF =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABC DEF ≌. 【点睛】本题考查边角边定理证明三角形全等，根据题意找到相应的条件是解题关键. 求证：DE BF =．证明：AD BC （已知）∴∠_______=∠_______（两直线平行，内错角相等）AF CE =∴ADE CBF ∴≌（ 【答案】A ；C ；AF EF CE EF −=−；AD BC =；A C ∠=∠；AE CF =；SAS ；全等三角形对应边相等．【分析】根据平行线的性质得到∠A =∠C ，根据等式的性质得到AE CF =，然后证明ADE CBF V V ≌即可得到结论．【详解】证明：AD BC （已知）∴∠A =∠C （两直线平行，内错角相等）AF CE =（已知）∴AF EF CE EF −=−(等式的基本性质)即AE CF =在ADE V 和CBF V 中AD BC A CAE CF =⎧⎪∠=∠⎨⎪=⎩，ADE CBF ∴≌(SAS )DE BF ∴=(全等三角形对应边相等)故答案为：A ；C ；AF EF CE EF −=−；AD BC =；A C ∠=∠；AE CF =；SAS ；全等三角形对应边相等．【点睛】本题考查全等三角形的判定和性质，掌握全等三角形的判定定理是解题的关键．【答案】见解析【分析】根据BE CF =可得BC EF =，根据AC DF ∥可得ACB DFE ∠=∠，即可根据SAS 进行求证．【详解】证明：∵BE CF =，∴BE CE CF CE −=−，即BC EF =，∵AC DF ∥，∴ACB DFE ∠=∠，在ABC 和DEF 中，AC DF ACB DFEBC EF =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABC DEF △△≌． 【点睛】本题主要考查了全等三角形的判定，解题的关键是根据题目所给条件，得出相应的边和角度相等，熟练掌握三角形全等的判定定理． 求证：(1)AE CF =；(2)AE CF ∥；(3)∠=∠AFE CEF ．【答案】(1)见解析(2)见解析(3)见解析【分析】（1）根据“边角边”证明ABE CDF △≌△，即可证得结论；（2）根据全等三角形的性质可得AEB CFD ∠=∠，进而可得结论；（3）由全等三角形的性质可得AE CF =，根据“边角边”证明AEF CFE △≌△，即可证得结论．【详解】（1）证明：在ABE 和CDF 中，∵AB CD =， B D ∠=∠，BE DF =，∴ABE CDF△≌△()SAS ，∴AE CF =； （2）证明：∵ABE CDF △≌△，∴AEB CFD ∠=∠，∴AE CF ∥；（3）证明：∵ABE CDF △≌△，∴AE CF =，又∵AEB CFD ∠=∠，EF FE =，∴AEF CFE △≌△，∴∠=∠AFE CEF ．【点睛】本题考查了全等三角形的判定和性质以及平行线的判定，熟练掌握全等三角形的判定和性质是解题的关键． 求作：ABC ，使 【答案】见解析【分析】先作CAB α∠=∠，再在角的两边上分别截取AC b =，AB c =，从而可得答案．【详解】解：ABC 即为所求．【点睛】本题考查的是作三角形，掌握作一个角等于已知角是解本题的关键． 32．（2023·全国·八年级假期作业）“倍长中线法”是解决几何问题的重要方法．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，具体做法是：如图，AD 是ABC 的中线，延长AD 到E ，使DE AD =，连接BE ，构造出BED 和CAD ．求证：BED CAD △≌△．【答案】见解析【分析】由AD 是ABC 的中线，可得DE AD =，再由EDB ADC ∠=∠，DB DC =，即可证明BED CAD △≌△．【详解】证明：如图所示：，AD 是ABC 的中线，DB DC ∴=，在BED 和CAD 中，ED AD EDB ADCDB DC =⎧⎪∠=∠⎨⎪=⎩，(SAS)BED CAD ∴≌．【点睛】本题主要考查了三角形全等的判定，倍长中线，熟练掌握三角形全等的判定，添加适当的辅助线是解题的关键． 33．（2023春·全国·七年级期末）如图，在ABC 中，D 是BC 延长线上一点，满足CD BA =，过点C 作CE AB ∥，且CE BC =，连接DE 并延长，分别交AC ，AB 于点F ，G ．(1)求证：ABC DCE ≅；(2)若12BD =，2AB CE =，求BC 的长度．【答案】(1)见解析(2)4【分析】（1）根据SAS 证明≌ABC DCE 即可；（2）根据全等三角形的性质解答即可．【详解】（1）∵CE AB ∥，∴B ECD ∠=∠，在ABC 与DCE △中，AB CD B ECDBC CE =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABC DCE ≌；（2）∵≌ABC DCE ，∴,AB CD BC CE ==，∵2AB CE =，∴2CD BC =，∵12BD =，∴312BD CD BC BC =+==∴4BC =．【点睛】此题考查全等三角形的判定和性质，关键是掌握全等三角形的判定和性质．。

12.2全等三角形判定知识要点：三角形全等的判定(1)边边边(SSS)：三边分别相等的两个三角形全等。

(2)边角边(SAS)：两边和它们的夹角分别相等的两个三角形全等。

(3)角边角(ASA)：两角和它们的夹边分别相等的两个三角形全等。

(4)角角边(AAS)：两角和其中一个角的对边分别相等的两个三角形全等。

(5)斜边、直角边(HL)：斜边和一条直角边分别相等的两个直角三角形全等。

一、单选题1．如图，12∠=∠，下列条件中不能使．．．ABD ACD ∆≅∆的是（ ）A ．AB AC = B ．B C ∠=∠ C ．ADB ADC ∠=∠D ．DB DC = 2．如图所示，则下面图形中与图中△ABC 一定全等的三角形是（ ）A ．B ．C ．D ．3．如图，有两个长度相同的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )A．90°B．120°C．135°D．150°4．有一个小口瓶（如图所示），想知道它的内径是多少，但是尺子不能伸到里边直接测，于是拿两根长度相同的细木条，把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（）A．边角边B．角边角C．边边边D．角角边5．如图，用尺规作出∠OBF=∠AOB，作图痕迹MN是A．以点B为圆心，OD为半径的弧B．以点B为圆心，DC为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DC为半径的弧6．如图，已知，，，则图中全等三角形的总对数是A．3 B．4 C．5 D．67．如图，FE=BC，DE=AB，∠B=∠E=40°，∠F=70°，则∠A=( )A．40°B．50°C．60°D．70°8．如图，已知AB∥CF，E为DF的中点，若AB=9cm，CF=5cm，则BD等于（）A．2cm B．3cm C．4cm D．5cm9．如图，已知AC＝DB，AO＝DO，CD＝100 m，则A，B两点间的距离( )A．大于100 m B．等于100 mC．小于100 m D．无法确定10．如图，AB⊥BC且AB=BC，DE⊥CD且DE=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）A．36 B．48 C．72 D．108二、填空题11．如图，若AB＝AD，加上一个条件_____，则有△ABC≌△ADC．12．如图，已知BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=__________．13．如图，已知∠1=∠2=90°，AD=AE，那么图中有____对全等三角形.14．如图，Rt∆ABC 中，∠BAC = 90°，AB =AC ，分别过点B、C 作过点A 的直线的垂线BD、CE ，垂足分别为D、E ，若BD = 4，CE=2，则DE= （_________）15．如图，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，AD ⊥CE ，垂足分别为E ，D ，AD ＝25，DE ＝17，则BE ＝______．三、解答题16．如图，点E ，F 在CD 上，AD CB ，DE CF =，A B ∠=∠，试判断AF 与BE 有怎样的数量和位置关系，并说明理由.17．已知：如图，AB=AC ，PB=PC ，PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ．证明：（1）PD=PE ．（2）AD=AE ．18．已知：如图，AE ∥CF ，AB=CD ，点B 、E 、F 、D 在同一直线上，∠A=∠C ．求证：（1）AB∥CD；（2）BF=DE．19．如图，点M.N在线段AC上，AM=CN，AB∥CD，AB=CD.请说明△ABN≌△CDM的理由；答案1．D 2．B3．A4．A5．D6．D7．D8．C9．B10．C11．BC ＝DC12．150°13．314．615．816．解：AF 与BE 平行且相等，因为AD CB ，所以C D ∠=∠.因为DE CF =，所以CE DF =.又因为A B ∠=∠，所以AFD BEC ∆≅∆.所以AF BE =，AFD BEC ∠=∠.所以AF BE .17．解：证明：（1）连接AP ．在△ABP 和△ACP 中，AB=AC PB=PC AP=AP ⎧⎪⎨⎪⎩，∴△ABP ≌△ACP （SSS ）．∴∠BAP=∠CAP ，又∵PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ，∴PD=PE （角平分线上点到角的两边距离相等）．（2）在△APD 和△APE 中，∵90PAD PAE ADP AEP AP AP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴△APD ≌△APE （AAS ），∴AD=AE ；18．解：（1）∵AB ∥CD ，∴∠B=∠D ．在△ABE 和△CDF 中，A CAB CD B D∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABE ≌△CDF （ASA ），∴∠B=∠D ，∴AB ∥CD ；（2）∵△ABE ≌△CDF ，∴BE=DF ．∴BE+EF=DF+EF ，∴BF=DE ．19．∵AM=CN∴AM+MN=CN+MN即AN=CM∵AB ∥CD∴∠A=∠C在△ABN 和△CDM 中=AN CMA C AB CD=⎧⎪∠∠⎨⎪=⎩∴△ABN ≌△CDM （SAS ）人教版八年级上册12.2全等三角形判定同步练习（包含答案）11 / 11。