离散数学图论习题课共50页文档

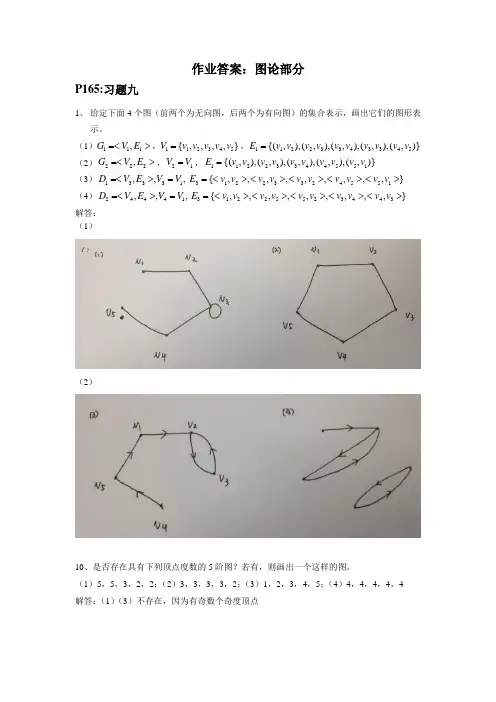
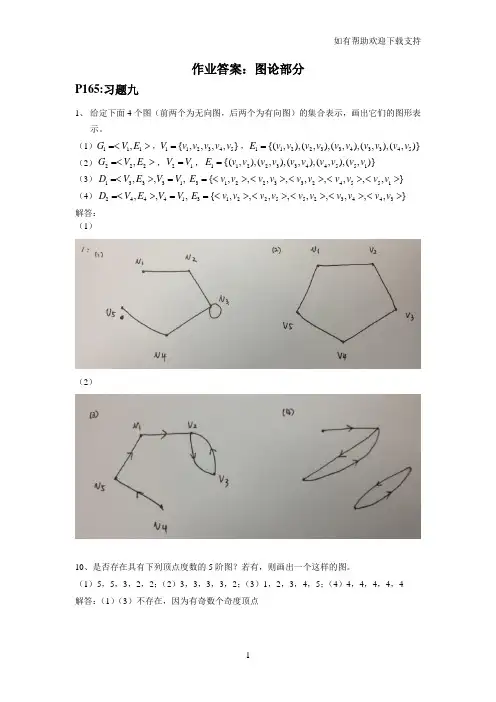
作业答案：图论部分P165:习题九1、 给定下面4个图（前两个为无向图，后两个为有向图）的集合表示，画出它们的图形表示。

（1）111,G V E =<>，112345{,,,,}V v v v v v =，11223343345{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （2）222,G V E =<>，21V V =，11223344551{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （3）13331,,,D V E V V =<>=31223324551{,,,,,,,,,}E v v v v v v v v v v =<><><><><> （4）24441,,,D V E V V =<>=31225523443{,,,,,,,,,}E v v v v v v v v v v =<><><><><> 解答： （1）（2）10、是否存在具有下列顶点度数的5阶图？若有，则画出一个这样的图。

（1）5，5，3，2，2；（2）3，3，3，3，2；（3）1，2，3，4，5；（4）4，4，4，4，4 解答：（1）（3）不存在，因为有奇数个奇度顶点。

14、设G 是(2)n n ≥阶无向简单图，G 是它的补图，已知12(),()G k G k δ∆==，求()G ∆，()G δ。

解答：2()1G n k ∆=--；1()1G n k δ=--。

15、图9.19中各对图是否同构？若同构，则给出它们顶点之间的双射函数。

解答：（c ）不是同构，从点度既可以看出，一个点度序列为4，3，3，3，3而另外一个为4，4，3，3，1（d ）同构，同构函数为12()345x a x bf x x c x d x e=⎧⎪=⎪⎪==⎨⎪=⎪=⎪⎩ 16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。

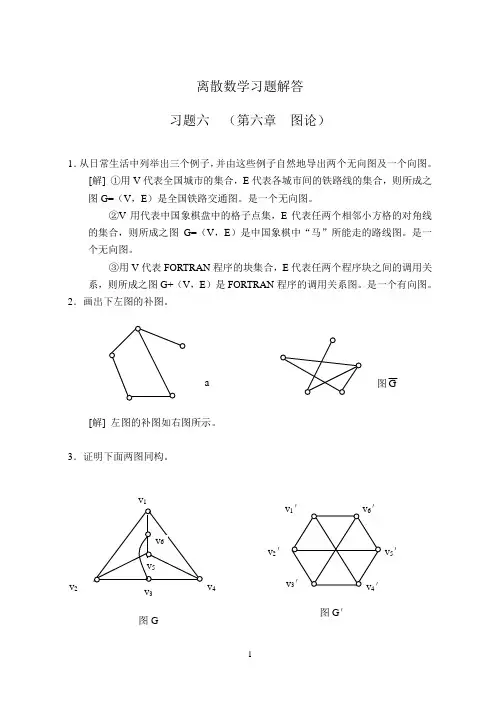
离散数学习题解答 习题六 （第六章 图论）1．从日常生活中列举出三个例子，并由这些例子自然地导出两个无向图及一个向图。

[解] ①用V 代表全国城市的集合，E 代表各城市间的铁路线的集合，则所成之图G=（V ，E ）是全国铁路交通图。

是一个无向图。

②V 用代表中国象棋盘中的格子点集，E 代表任两个相邻小方格的对角线的集合，则所成之图G=（V ，E ）是中国象棋中“马”所能走的路线图。

是一个无向图。

③用V 代表FORTRAN 程序的块集合，E 代表任两个程序块之间的调用关系，则所成之图G+（V ，E ）是FORTRAN 程序的调用关系图。

是一个有向图。

2．画出下左图的补图。

[解] 左图的补图如右图所示。

3．证明下面两图同构。

a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1，v 2)=(v 1′，v 2′) ϕ (v 2)=v 2′ ϕ (v 2，v 3)=(v 2′，v 3′) ϕ (v 3)=v 3′ ϕ (v 3，v 4)=(v 3′，v 4′) ϕ (v 4)=v 4′ ϕ (v 4，v 5)=(v 4′，v 5) ϕ (v 5)=v 5′ ϕ (v 5，v 6)=(v 5′，v 6′) ϕ (v 6)=v 6′ϕ (v 6，v 1)=(v 6′，v 1′) ϕ (v 1，v 4)=(v 1′，v 4′) ϕ (v 2，v 5)=(v 2′，v 5′) ϕ (v 3，v 6)=(v 3′，v 6′)显然使下式成立：ψ (v i ，v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。

4．证明（a ），（b ）中的两个图都是不同构的。

图G 中有一个长度为4的圈v 1v 2v 6v 5v 1，其各顶点的度均为3点，而在图G ′中却没有这样的圈，因为它中的四个度为3的顶点v 1'，v 5'，v 7'，v 3'不成长度的4的圈。

第4章图论综合练习一、单项选择题1．设L是n阶无向图G上的一条通路，则下面命题为假的是( )．(A) L可以不是简单路径，而是基本路径(B) L可以既是简单路径,又是基本路径(C) L可以既不是简单路径，又不是基本路径(D) L可以是简单路径，而不是基本路径答案：A2．下列定义正确的是( )．(A) 含平行边或环的图称为多重图 (B) 不含平行边或环的图称为简单图(C) 含平行边和环的图称为多重图 (D) 不含平行边和环的图称为简单图答案：D3．以下结论正确是 ( )．(A) 仅有一个孤立结点构成的图是零图(B) 无向完全图K n每个结点的度数是n(C) 有n(n>1)个孤立结点构成的图是平凡图(D) 图中的基本回路都是简单回路答案：D4．下列数组中，不能构成无向图的度数列的数组是( )．(A) (1,1,1,2,3) (B) (1,2,3,4,5) (C) (2,2,2,2,2) (D) (1,3,3,3)答案：B5．下列数组能构成简单图的是( )．(A) (0,1,2,3) (B) (2,3,3,3) (C) (3,3,3,3) (D) (4,2,3,3)答案：C6．无向完全图K3的不同构的生成子图的个数为（）．(A) 6 (B) 5 (C) 4 (D) 3答案：C7．n阶无向完全图K n中的边数为（）．(A)2)1(+nn(B)2)1(-nn(C) n (D)n(n+1)答案：B8．以下命题正确的是( )．(A) n (n1)阶完全图K n都是欧拉图(B) n(n 1)阶完全图K n都是哈密顿图(C) 连通且满足m=n－1的图<V,E>(V=n,E=m)是树(D) n(n5)阶完全图K n都是平面图答案：C10．下列结论不正确是( )．(A) 无向连通图G是欧拉图的充分必要条件是G不含奇数度结点(B) 无向连通图G有欧拉路的充分必要条件是G最多有两个奇数度结点(C) 有向连通图D是欧拉图的充分必要条件是D的每个结点的入度等于出度(D) 有向连通图D有有向欧拉路的充分必要条件是除两个结点外，每个结点的入度等于出度 答案：D11．无向完全图K 4是（ ）．（A ）欧拉图 （B ）哈密顿图 （C ）树 答案：B12．有4个结点的非同构的无向树有 ( )个． (A) 2 (B) 3 (C) 4 (D) 5 答案：A13．设G 是有n 个结点，m 条边的连通图，必须删去G 的( )条边，才能确定G 的一棵生成树．(A) 1+-n m (B) m n - (C) 1++n m (D) 1+-m n 答案：A14．设G 是有6个结点的完全图，从G 中删去( )条边，则得到树． (A) 6 (B) 9 (C) 10 (D) 15 答案：C二、 填空题1．数组{1，2，3，4，4}是一个能构成无向简单图的度数序列， 此命题的真值是 . 答案：02．无向完全图K 3的所有非同构生成子图有 个． 答案：43．设图G V ,E ，其中V n ,E m ．则图G 是树当且仅当G 是连通的，且m ． 答案：n －14．连通图G 是欧拉图的充分必要条件是 ． 答案：图G 无奇数度结点5．连通无向图G 有6个顶点9条边，从G 中删去 条边才有可能得到G 的一棵生成树T ． 答案：46．无向图G 为欧拉图，当且仅当G 是连通的，且G 中无 结点． 答案：奇数度7．设图>=<E V G ,是简单图，若图中每对结点的度数之和 ，则G 一定是哈密顿图．答案：V ≥8．如图1所示带权图中最小生成树的权是 ．答案：12三、化简解答题1．设无向图G ＝<V ,E >，V ={v 1，v 2，v 3，v 4，v 5，v 6}， E ={( v 1，v 2), ( v 2，v 2), ( v 4，v 5), ( v 3，v 4), ( v 1，v 3),( v 3，v 1), ( v 2，v 4)}． 1 v 2 v 6 v 53 v 4图2•2 23 • 1 • 7 9 2• 8 • 6 图1(1) 画出图G 的图形；(2) 写出结点v 2, v 4，v 6的度数； (3) 判断图G 是简单图还是多重图． 解：(1) 图G 的图形如图5所示．(2) 0)deg(,3)deg(,4)deg(642===v v v ．(3) 图G 是多重图．作图如图2. 2．设图G ＝<V ，E >，其中V ＝{a ,b ,c ,d ,e }, E ={(a ,b ),(b ,c ),(c ,d ), (a ,e )}试作出图G 的图形，并指出图G 是简单图还是多重图？是连通图吗？说明理由. 解：图G 如图8所示．. 图G 中既无环，也无平行边，是简单图． 图G 是连通图．G 中任意两点都连通.所以，图G 有9个结点．作图如图3．四、计算题1．设简单连通无向图G 有12条边，G 中有2个1度结点，2个2度结点，3个4度结点，其余结点度数为3．求G 中有多少个结点．试作一个满足该条件的简单无向图．解：设图G 有x 个结点，由握手定理21+22+34+3（x 223）＝122 271821243=-+=x x ＝9 故图G 有9个结点．满足该条件的简单无向图如图4所示2．设图G (如图5表示)是6个结点a ,b ,c , d ,e ,f的图，试求，图G 的最小生成树，并计算它的权．解：构造连通无圈的图，即最小生成树，用克鲁斯克尔算法：第一步： 取ab ＝1；第二步： 取af =4 第三步： 取fe ＝3；第四步： 取ad =9 第五步： 取bc =23如图6．权为1+4+3+9+23=403．一棵树T 有两个2度顶点，1个3度顶点；3个4度顶点， 问它有几片树叶？解：设T 有n 顶点，则有n －1条边．T 中有2个 2度顶点，1个3度顶点，3个4度顶点， 其余n －2－1-3个1度顶点．由握手定理： 2·2+1·3+3·4+ (n －2－1-3)=2(n －1) 解得 n =15．于是T 有15-6=9片树叶五、证明题1．若无向图G 中只有两个奇数度结点，则这两个结点一定是连通的．证：用反证法．设G 中的两个奇数度结点分别为u 和v ．假若u 和v 不连通．即它们之间无任何通路，则G 至少有两个连通分支G 1，G 2，且u 和v 分别属于G 1和G 2，于是G 1和G 2各含有一个奇数度结点．这与握手定理的推论矛盾．因而u 和v 一定是连通的．a b ec d 图3图4b • 23 1c • • a 4 • f 9 3d • •e 图6b •23 1 15 c • 25 •a 4 • f 28 9 16 3 d • 15 • e 图5。

离散数学（图论部分）1-4章习题课1. 证明：在10个人中，或有3人互相认识，或有4人互不认识。

证：设x为10人中之任意某人，则在余下9人中：(1) x至少认识其中4人，或(2) x至多认识其中3人（即至少不认识其中6人），两者必居其一。

(1) 若此x认识的4人互不相识，命题得证；否则，互相认识的2人加上x构成互相认识的3人，命题得证。

(2) 若此x不认识的6人中有3人互相认识，命题得证；否则，由Ramsey(3,3)=6知，此6人中至少有3人互不认识，此3人加上x为互不认识的4人，命题得证。

2. 设(a) V={a,b,c,d}，A={<a,b>,<a,c>,<b,c>,<b,d>,<c,d>}(b) V={a,b,c,d,e}，E={(a,b),(a,c),(b,c),(d,e)}画出上述图的图解。

解：略。

3. 试找出K3的全部子图，并指出哪些是生成子图。

解：K3共有17个子图。

其他略。

4. 证明：在至少有2人的团体中，总存在2个人，他们在这个团体中恰有相同数目的朋友。

解：在n个人的团体中，各人可能有的朋友数目为0, 1, 2, 3, …, n-1，共n个数，但其中0和n-1 不能共存，故n个人事实上可能的朋友数目只有n-1个。

由鸽巢原理，命题得证。

5.某次宴会上许多人互相握手。

证明：必有偶数个人握了奇数次手。

证：以人为顶点，握手关系为邻接关系构造一个无向图。

由图的性质，奇数度的顶点必为偶数个，即握了奇数次手的人数必为偶数。

6. 证明：Ramsey(3,4)=9。

（提示：题1的推广）证：在9个人中，不可能每个人都恰好认识其他的3个人（即图的9个顶点不可能每个顶点的度都为3，否则违反图的奇数度的顶点必为偶数个的性质）。

设x不会恰好认识其他的3个人（即deg(x)≠3），则在余下8人中：：(1) x至少认识其中4人，或(2) x至多认识其中2人（即至少不认识其中6人），两者必居其一。

《离散数学》图论部分习题《离散数学》图论部分习题1.已知⽆向图G有12条边，6个3度顶点，其余顶点的度数均⼩于3，问G⾄少有⼏个顶点？并画出满⾜条件的⼀个图形. （24-3*6）/2 +6=92.是否存在7阶⽆向简单图G，其度序列为1、3、3、4、6、6、7.给出相应证明.不存在；7阶⽆向简单图G中最⼤度≤63.设d1、d2、…、d n为n个互不相同的正整数. 证明：不存在以d1、d2、…、d n为度序列的⽆向简单图.Max{d1，d2，…，dn}≥n，n阶⽆向简单图G中最⼤度≤n-14.求下图的补图.5.1)试画⼀个具有5个顶点的⾃补图2)是否存在具有6个顶点的⾃补图，试说明理由。

对于n阶图，原图与其补图同构，边数应相等，均为(n*(n-1)/2)/2，即n*(n-1)/4且为整数，n=4k或n=4k+1，不存在6阶⾃补图。

6.设图G为n(n>2且为奇数)阶⽆向简单图，证明：G与G的补图中奇度顶点个数相等.n(n>2且为奇数)，奇度点成对出现7.⽆向图G中只有2个奇度顶点u和v，u与v是否⼀定连通.给出说明或证明。

只有2个奇度顶点u和v，如果不连通，在u和v在2个连通分⽀上，每个分⽀上仅有⼀个奇度顶点，与握⼿引理相⽭盾。

8.图G如下图所⽰：1)写出上图的⼀个⽣成⼦图.2)δ(G)，κ(G)，λ(G).δ(G)=2，κ(G)=1，λ(G)=2.说明：δ(G)=min{ d(v) | v V } ；κ(G)=min{ |V’| |V’是图G的点割集} ；λ(G)=min{ |E’| |E’是图G的边割集} 9.在什么条件下⽆向完全图K n为欧拉图？n为奇数时10.证明：有桥的图不是欧拉图.假设是欧拉图：桥的端点是u和v，并且图各顶点度均为偶数；桥为割边，删除桥，图不再连通，u和v应该在2各不同的连通分⽀上；且u和v度数变为奇数；由于其他顶点度数均为偶数，则u和v所在的连通分⽀上只有⼀个奇度顶点，与握⼿引理⽭盾。

1兴义民族师范学院数学系10级专科班使用代数结构集合论组合数学离散数学数理逻辑图论初等数论离散数学及其应用兴义民族师范学院2主要内容z 命题、真值、简单命题与复合命题、命题符号化z 联结词¬, ∧, ∨, →, ↔及复合命题符号化z 命题公式及层次z 公式的类型z 真值表及应用基本要求z 深刻理解各联结词的逻辑关系, 熟练地将命题符号化z 会求复合命题的真值z 深刻理解合式公式及重言式、矛盾式、可满足式等概念z 熟练地求公式的真值表，并用它求公式的成真赋值与成假赋值及判断公式类型第一章习题课例2将下列命题符号化.(1)吴颖既用功又聪明.(2)吴颖不仅用功而且聪明.(3)吴颖虽然聪明，但不用功.(4)张辉与王丽都是三好生.(5)张辉与王丽是同学.(1) p∧q解令p:吴颖用功, q:吴颖聪明(2) p∧q(3) ¬p∧q设p:张辉是三好生, q:王丽是三好生(4) p∧q(5) p: 张辉与王丽是同学(1)—(3) 说明描述合取式的灵活性与多样性(4)—(5) 要求分清“与”所联结的成分34例3将下列命题符号化(1) 2 或4 是素数.(2) 2 或3 是素数.(3) 4 或6 是素数.(4) 小元只能拿一个苹果或一个梨.(5) 王小红生于1975 年或1976 年.解：(1) 令p :2是素数, q :4是素数, p ∨q 解：(2) 令p :2是素数, q :3是素数, p ∨q 解：(3) 令p :4是素数, q :6是素数, p ∨q解：(4) 令p :小元拿一个苹果, q:小元拿一个梨(p ∧¬q )∨(¬p ∧q )解：(5) p :王小红生于1975 年, q :王小红生于1976 年,(p ∧¬q )∨(¬p ∧q ) 或p ∨q相容或排斥或5定义1.4设p , q 为两个命题，复合命题“如果p , 则q ”称作p 与q 的蕴涵式，记作p →q ，并称p 是蕴涵式的前件，q 为蕴涵式的后件，→称作蕴涵联结词.规定：p →q 为假当且仅当p 为真q 为假.2. 蕴涵联结词(1)p →q 的逻辑关系：q 为p 的必要条件(2)“如果p , 则q ”有很多不同的表述方法：若p ，就q 只要p ，就q p 仅当q 只有q 才p除非q , 才p 或除非q ，否则非p ，…．(3)当p 为假时，p →q 恒为真，称为空证明(4)常出现的错误：不分充分与必要条件6第一章习题课1.下列句子中，那些是命题？并判断其真假.(1) 古代中国有四大发明. (2) 是无理数. (3)3是素数或4是素数.(4) ,其中是任意实数.(5)你去图书馆吗？(6)2与3都是偶数.(7)刘红与魏新是同学.(8)这朵玫瑰花多美丽呀！(9)吸烟请到吸烟室去！(10)圆的面积等于半径的平方乘以.(11)只有6是偶数，3才能是2的倍数.(12)8是偶数的充分必要条件是8能被3整除.(13)2025年元旦下大雪.5x 235x +<π是命题，真命题是命题，真命题是命题，真命题不是命题，真值不唯一不是命题，疑问句是命题，假命题是命题，真值客观存在，真值视具体情况定不是命题，感叹句不是命题，祈使句是命题，真命题是命题，真命题是命题，假命题是命题，真值客观存在，真值待定78. 将下列命题符号化,并指出各命题的真值.(1)只要，就有.(2) 如果，则.(3) 只有，才有.(4) 除非，才有.(5) 除非，否则.(6) 仅当.32<21<21<21<21<21<21<32≥32<32≥32≥32<解：设p :，q : 21<32<提示：分清必要与充分条件及充分必要条件(1) p →q,真值为：1(2) p →¬q,真值为：1真值为：0(3) ¬q →p,(4) ¬q →p,真值为：0(5) ¬q →p,真值为：0假言易位A →B ⇔¬B →¬A¬q →p ⇔¬p →q(6) p →q,真值为：1补充题3. 用真值表判断下面公式的类型(1)p∧r∧¬(q→p)(2)((p→q) →(¬q→¬p)) ∨r(3)(p→q) ↔(p→r)89(1) p ∧r ∧¬(q →p )矛盾式0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1 p q r 000000001100001001111p ∧r ∧¬(q →p )¬(q →p ) q →p 001(2) ((p→q) →(¬q→¬p)) ∨r永真式111111111111111111110 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1((p→q) →(¬q→¬p)) ∨r ¬q→¬pp→qp q r10练习3解答(3) (p→q) ↔(p→r)非永真式的可满足式1111111111111111110 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1(p→q) ↔(p→r)p→rp→qp q r1112（3）(p ∧q ) →¬p 的真值表1 11 00 10 0(p ∧q ) →¬pp ∧q┐pp q11100111000成真赋值为00，01,1020.列出真值表，求下列公式的成真赋值13（4）¬(p ∨q ) →q 的真值表1 11 00 10 0¬(p ∨q ) →q¬(p ∨q )p ∨qp q111011100001成真赋值为01，10，1120.列出真值表，求下列公式的成真赋值14111100000 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1101010100011000011101111成假赋值为：011¬(¬p ∧q ) ∨¬r¬(¬p ∧q )¬r ¬pp q r¬p ∧q11001111（1）¬(¬p ∧q ) ∨¬r 的真值表21.列出真值表，求下列公式的成假赋值15（2）(¬q ∨r ) ∧(p →q )的真值表0 0 01 1 11 1 01 0 11 0 00 1 10 1 00 0 1(¬q ∨r ) ∧(p →q )p →q ¬q ∨r ¬q p q r 11001111100010110011001110111011成假赋值为：010，100，101，110。