离散数学——图论
- 格式:ppt
- 大小:640.50 KB
- 文档页数:93


离散数学图论矩阵应用实例分析离散数学图论是数学的一个重要分支,它研究的是非连续的结构,其中一个重要的应用领域就是矩阵应用。
本文将对离散数学图论中的矩阵应用进行实例分析,以帮助读者更好地理解和应用相关概念。
一、社交网络中的矩阵应用社交网络是当今社会中非常流行的交流平台,它允许人们在线上建立和维护社交关系。
将社交网络中的用户和关系抽象成图模型,可以用矩阵进行描述和分析。
例如,可以使用邻接矩阵来表示用户之间的关注关系,其中矩阵的行和列代表用户,矩阵的元素代表用户之间的关系强弱。
通过对这个矩阵进行分析,可以了解用户之间的社交网络结构,发现用户群体之间的关联性,进行用户推荐等。
二、交通网络中的矩阵应用交通网络是城市中不可或缺的一部分,它关系到人们的出行和交通组织。
在离散数学图论中,可以使用邻接矩阵来表示交通网络中的道路连接状况。
矩阵的行和列代表交通网络中的节点,通常是城市中的道路,矩阵的元素代表节点之间的连接关系,比如道路的长度或者通行能力。
通过对这个矩阵进行分析,可以计算最短路径、最小生成树等最优化问题,优化交通流动和道路规划。
三、电子电路中的矩阵应用电子电路是离散数学图论中的另一个应用领域,矩阵在描述电路连接和电流传递等方面起到关键作用。
在电路分析中,可以使用节点-支路关系矩阵(Node-Branch Matrix)和支路-节点关系矩阵(Branch-Node Matrix)来描述电路的连接和元件耦合关系。
这两个矩阵的运算可以得到电路的戴维南等效电阻以及电流传递等重要信息,从而分析电路的性能和特性。
四、信息检索中的矩阵应用信息检索是指从大规模的文本数据中提取相关信息的过程。
其中,矩阵常用于描述文本之间的关联和相似性。
例如,可以使用文档-词项矩阵(Document-Term Matrix)来表示文档集合中的词项出现情况。
矩阵的行代表文档,列代表词项,矩阵的元素代表词项在文档中的出现频率。
通过对这个矩阵进行分析,可以进行文本聚类、关键词提取、文档相似度计算等信息检索任务。


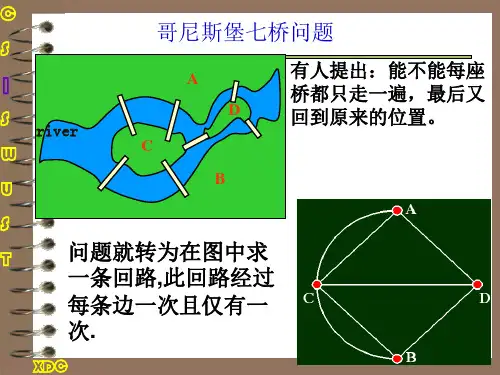


离散数学中常用的图论算法简介图论是高等数学中的一个分支,主要涉及在图中寻找什么样的路径,以及什么样的点之间有什么样的关系。
在计算机科学中,图论的应用越来越广泛。
因为所有的计算机程序都是基于数据结构的,而图是一种最基本的数据结构之一。
离散数学中的图论算法大致可以分为两类:一类是针对稠密图的算法,另一类是针对稀疏图的算法。
稠密图指的是一种图,其中每对顶点都有一条边相连,而稀疏图则是指只有一部分顶点之间相连的图。
以下是一些常见的图论算法的简介。
1. Dijkstra算法Dijkstra算法是一种用于求图中最短路径的算法,也是最常用的图论算法之一。
Dijkstra算法的主要思想是通过贪心策略,从起点出发,逐步扩展最短路径的范围,直到找到终点。
Dijkstra算法可以用来解决单源最短路径问题。
如果图中有n个顶点,算法的时间复杂度为O(n²)。
2. Kruskal算法Kruskal算法是一种用于求最小生成树的算法。
最小生成树指的是,通过连接图中一些顶点形成一棵树,使得这些顶点之间的总权重最小。
Kruskal算法的主要思想是将图中的所有边按照权重进行排序,然后依次加入到生成树中,如果新加入的边会形成环,则不将其加入到生成树中。
如果图中有n个顶点,那么算法的时间复杂度为O(nlogn)。
3. Floyd算法Floyd算法用于求图中任意两个点之间的最短路径。
如果图中所有的权重都是正的,那么Floyd算法的时间复杂度为O(n的三次方),但是如果存在负权重,那么该算法不适用。
关于负权环的处理,可以通过Bellman-Ford算法进行解决。
4. Prim算法Prim算法是一种用于求最小生成树的算法。
与Kruskal算法不同的是,Prim算法是基于顶点集来实现,而不是基于边集。
Prim 算法首先找到一个起点,将其加入到生成树中,然后找到与其相连的边中权重最小的那一条,将其相连的顶点加入到生成树中,重复这一步骤直至所有顶点都被加入到生成树中。



离散数学中的图论应用离散数学是数学中的一个分支,主要研究离散对象和离散结构。
而图论作为离散数学中的一个重要分支,研究的是图这种离散结构的性质和应用。
图论在计算机科学、通信网络、社交网络等领域有着广泛的应用。
本文将从不同的角度介绍离散数学中图论的应用。
一、计算机网络中的图论应用计算机网络是现代信息社会的重要基础设施,而图论在计算机网络中有着广泛的应用。
首先,图论可以用来描述和分析计算机网络的拓扑结构。
计算机网络中的节点和连接可以用图的顶点和边来表示,通过图论的方法可以分析网络的稳定性、可靠性和性能等指标。
其次,图论可以用来解决网络中的路径选择问题。
通过图的最短路径算法,可以找到两个节点之间的最短路径,从而实现数据的快速传输。
另外,图论还可以用来解决网络中的流量控制和路由问题,通过最大流最小割算法可以实现网络资源的合理分配和优化。
二、社交网络中的图论应用随着社交媒体和社交平台的兴起,社交网络成为人们日常生活中重要的一部分。
而图论在社交网络中也有着广泛的应用。
首先,图论可以用来描述和分析社交网络的关系。
社交网络中的用户可以用图的顶点来表示,而用户之间的关系可以用图的边来表示。
通过图的连通性和聚类系数等指标,可以分析社交网络中的社群结构和信息传播等现象。
其次,图论可以用来解决社交网络中的推荐问题。
通过图的相似度算法,可以实现用户之间的兴趣相似度计算和推荐系统的构建。
另外,图论还可以用来解决社交网络中的影响力传播问题,通过图的传播模型可以模拟和预测信息在社交网络中的传播路径和影响力。
三、电路设计中的图论应用电路设计是电子工程中的一个重要领域,而图论在电路设计中有着广泛的应用。
首先,图论可以用来描述和分析电路的拓扑结构。
电路中的器件和连接可以用图的顶点和边来表示,通过图论的方法可以分析电路的稳定性、功耗和延迟等指标。
其次,图论可以用来解决电路中的布线问题。
通过图的最小生成树算法和最短路径算法,可以实现电路的布线优化和信号传输的最优化。