当前位置：文档之家 › 第三章-电路暂态分析1

第三章-电路暂态分析1

  • 格式：docx
  • 大小：1.96 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

电路的暂态分析

电路的暂态分析

对未来研究的建议
1
进一步研究不同电路元件和结构对暂态过程的影 响，探索新的电路元件和结构，以提高电路的性 能和稳定性。
2
结合现代信息技术和人工智能技术，开发更加高 效、智能的电路暂态分析方法和工具，提高分析 的准确性和效率。
3
加强与相关领域的合作与交流，推动电路暂态分 析在其他领域的应用和发展，促进相关领域的科 技进步。
在电子系统中的应用
01
在电子系统中，电路的暂态分析 主要用于信号处理、高速数字电 路等领域。
02
通过暂态分析，可以研究信号的 传输、放大、滤波等过程中的暂 态行为，优化电路的性能，提高 信号的传输质量和稳定性。
在控制工程中的应用
在控制工程中，电路的暂态分析主要用于研究控制系统的 动态特性和稳定性。
电路的暂态分析
目 录
• 引言 • 电路的暂态过程 • 电路的暂态分析方法 • 电路暂态分析的应用 • 电路暂态分析的挑战与展望 • 结论
01 引言
什么是暂态分析
暂态分析是指对电路在某一特定时刻的电流和电压进行计算和分析的过程。在电 路中，由于开关的闭合或断开，或者由于电路中元件的参数变化，可能会引起电 流和电压的瞬态变化。这些瞬态变化通常只在一段时间内存在，因此被称为暂态 。
04 电路暂态分析的应用
在电力系统中的应用
暂态分析在电力系统中主要用于研究 电力系统中的短路故障、雷击、开关 操作等引起的暂态过程，以确保电力 系统的稳定性和可靠性。
通过暂态分析，可以预测和防止电力 系统中的暂态过电压、电流冲击等对 设备造成损坏的情况，同时也可以优 化保护装置的动作时间和性能。
暂态过程的特点
01
02
03
04
非线性

3电路的暂态分析

3电路的暂态分析

0
0
4、R l
s
3
二、电感 L： 单位电流产生的磁链
（单位：H, mH, H）
1、磁通与磁通链（单位：韦伯Wb）
i N Li
u
其中： 为磁通
为磁通链
电感元件
L 为线圈的电感，也称自感
单位：亨H
N 为线圈的匝数
与I的方向符合右手螺旋定则
4
2、自感电动势 当线圈中通过的磁通发生变化时，
18
电容电路
KR
储能元件
uC
+ _U
uC C
E
t
电容为储能元件，它储存的能量为电场能量 ，
其大小为：
WC t uidt 1 cu2
0
2
因为能量的存储和释放需要一个过程，所以有电
容的电路存在过渡过程。
19
电感电路
KR
储能元件
+ t=0
U _
iL
iL
t
电感为储能元件，它储存的能量为磁场能量，
其大小为：
iC
线性微分方程
+
U -
2
R
C uC
RC duC dt
uC
0
iCR + Uc = 0
i C duC dt
设微分方程的通解为：
uC Ae pt
41
求齐次方程的通解：
通解即： RC duC dt
uC
0
的解。
设微分方程的通解为： uC Ae pt
其中:
A为积分常数 P为特征方程式的根
42
求P值:
di 0 dt
u0
所以,在直流电路中电感相当于短路.
7
5、电感是一种储能元件, 储存的磁场能量为：

《电工电子》第3章电路的暂态分析

《电工电子》第3章电路的暂态分析
在直流电路启动过程中，会产生较大的暂态电流和电压，通过暂态分析可以了解启动过程的特性 ，为电路设计和设备选型提供依据。
预测直流电路中的故障
利用暂态分析可以预测直流电路中的短路、断路等故障，从而及时采取维修措施，避免故障扩大 。
优化直流电路的控制策略
通过暂态分析可以了解直流电路在不同控制策略下的响应特性，从而选择最优的控制策略，提高 电路的控制精度和稳定性。
在暂态过程中，电阻的电压和电流会发生变 化，但电阻本身不会储存能量，因此电阻的 暂态响应是被动的，取决于外部电路的变化 。
电阻的阻值决定了电路中电流的大小， 因此在暂态过程中，电阻的阻值会影 响电流的变化速率。
电容的暂态特性
电容的充电和放电过程
当电容两端的电压发生变化时，电容会进行充电或放电， 这个过程需要一定的时间，因此电容的暂态过程相对较长。
稳态过程
电路在稳定状态下的工作过程， 此时电路中各处的电压、电流等 物理量均保持恒定或呈周期性变 化。
暂态分析的重要性
01
02
03
理解电路行为
通过暂态分析，可以深入 了解电路在开关操作、电 源变化等条件下的行为特 性。
优化电路设计
暂态分析有助于优化电路 设计，提高电路的稳定性 和可靠性，减少不必要的 能量损失和电磁干扰。
分析仿真与实验结果之间存在的误差，探 讨误差产生的原因，如元件参数不准确、 测量误差等。
改进建议
总结与反思
根据误差分析结果，提出相应的改进建议 ，如优化仿真模型、提高测量精度等，以 提高暂态分析的准确性。
对整个暂态分析的仿真与实验验证过程进行 总结与反思，总结经验教训，为后续的电路 设计与分析提供参考。
阻尼比与振荡性质
阻尼比是描述振荡衰减快慢的参数。根据阻尼比的大小，二阶电路的振荡可分为过阻尼、 临界阻尼和欠阻尼三种情况。在欠阻尼情况下，电路将呈现持续的振荡现象。

3 电路的暂态分析

3 电路的暂态分析

响应中“三要素”的确定
10 uC ( ) 5 55 5V
6 iL( ) 6 66 3 mA
(2) 初始值f ( 0 ) 的计算 ( 0 ) 、 i ( 0 ) 1) 由t=0- 电路求 u C L 2) 根据换路定则求出
u C (0 ) u C (0 ) iL(0 ) iL(0 )
0
0
( t 0 )
稳态分量
全响应 = 稳态分量 +暂态分量
暂态分量
3.3.1 在在电路的暂态过程中，电路的时间常数τ 愈大，则电流和电压的增长或衰减就（ ） （1）愈快 （2）愈慢 （3）无影响 3.3.2电路的暂态过程从t=0大致经过（ 就可认为到达稳定状态了。 （1） τ （2）（3~5） τ （3）10 τ ）时间，
t RC
s
+ U _
i R
t 0
C
uC (0 -) = 0
+ _ uC
u U Ue U ( 1 e ) C
t RC
d u U C i
iC u C
U R
U
uC
iC
当t=时
u ( ) 63 . 2 % U C

t
3 RC电路的全响应
一阶线性电路暂态分析的三要素法
在直流电源激励的情况下，一阶线性电路微分方 程解的通用表达式： 式中,
f ( t ) f ( ) [ f ( 0 ) f ( )] e
t
f (t ) ：代表一阶电路中任一电压、电流函数
f ( 0 ) -- 初始值 f () -- 稳态值 （三要素） -- 时间常数 利用求三要素的方法求解暂态过程，称为三要素法。 一阶电路都可以应用三要素法求解，在求得 f ( 0 ) 、 f () 和 的基础上,可直接写出电路的响应(电压或电流)。

电工电子学第三章

电工电子学第三章

第三章电路的暂态分析1、研究暂态过程的意义暂态过程是一种自然现象暂态过程是一种自然现象，，对它的研究很重要对它的研究很重要。

暂态过程的存在有利有弊暂态过程的存在有利有弊。

有利的方面有利的方面，，如电子技术中常用它来产生各种波形术中常用它来产生各种波形；；不利的方面不利的方面，，如在暂态过程发生的瞬间态过程发生的瞬间，，可能出现过压或过流可能出现过压或过流，，致使设备损坏备损坏，，必须采取防范措施必须采取防范措施。

设：t =0 时换路---旧稳态的终了瞬间---换路后的初始瞬间0＋0－C(4) 由t=0+时的等效电路求所需的u(0+)、i(0+)。

(0+)、C L Ci L(0+)、i R(0+) 、i S(0+) 。

mA 522210)0(=+×=−L imA155)10(0105)0()0(10)0(=−−−−=−+−+−=+C R S i i i mA10V10S断开=−+U u u C R SR+U 0_CC u i21R u U _++_+_合在1，1合到2，根据换路定则)0()0(U u u C C =−=+SR+U 0_CC u i21Ru +_+_SR+U 0_CC u i21Ru +_+_，和工程上工程上，，t ＝(3~5)τ认为暂态过程结束,电路到达新的稳态新的稳态。

的物理意义: 决定电路暂态过程变化的快慢。

τ的物理意义 决定电路暂态过程变化的快慢。

U0uCτ1 τ 2τ3τ1 < τ 2 < τ3t36.8%U0τ1 τ2 τ321结论： 暂态过程曲线变化越慢， 结论：τ 越大，暂态过程曲线变化越慢，uc 新的稳态所需要的时间越长。

达到 新的稳态所需要的时间越长。

1 SRi+ U0 _2+ uR _uc ( t ) = U 0 eC−t RC+ uC _电路中的电流， 电路中的电流，电阻两 端的电压变化的规律？ 端的电压变化的规律？uR = − uC = −U 0 eU0 uR i= e =− R R−t RCt duC U 0 − RC i=C e =− dt Rt − RC或电路中各量的暂态过程同时发生，也同时结束； 电路中各量的暂态过程同时发生，也同时结束； 并且具有相同的时间常数。

第三章 电路的暂态分析

第三章 电路的暂态分析

注意：这样一个高压将使 电压表损坏，所以直流电 压表不宜固定连接在电感 uV (0 ) RViL (0 ) 2500V 线圈两端。
3.3.2
RL电路接通直流电源
假设在开关合上前，线圈 中未储有能量；在t=0时， 将开关S合上，与直流电 源接通。因为电感中的电 流不能突变 i L (0 ) i L (0 ) 0
3.1电路暂态的基本概念及换路定则
3.1.1电路的稳态与暂态
1、稳态：
（对直流电路）电流和电压是恒定的， （对交流电路）随t按周期性变化的
2、换路：电路状态的变。
如电路接通、断开、改接及元件参数改 变等。
3、暂态：
旧稳态
换路
t(暂态)
新稳态
“稳态”与 “暂态”的概念示例:
S R R
+ _
U
uC
(t 0)
RC放电电路的特点：
uC、uR、i均按指数规律衰减，衰减的速度完
全由电路的参数τ决定
的物理意义: 决定电路过渡过程变化的快慢。
S + _U R C
关于时间常数的讨论
i
uC
uC (t ) U Ue U Ue
t t
RC

RC
uC
t
u C (t ) U Ue
解： ① 开关S在t=0时刻断开，这时电容C原来 所储存的电能通过电阻 R2 放电，因此
uC Ae
t RC
(t 0)
根据换路定则
R2 uC (0 ) uC (0 ) U R1 R2 100 120V=100V 20 100
所以得
A uC (0 ) 100
因电阻与电容串联，所以 t=0时，电阻两端的电压为

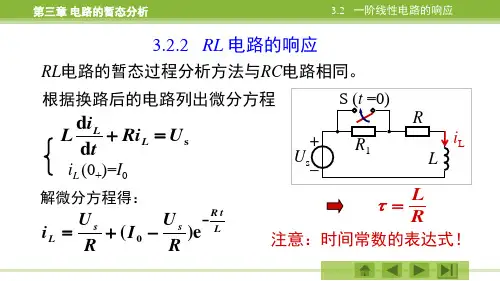
电路的暂态分析_一阶线性电路暂态分析的三要素法

电路的暂态分析_一阶线性电路暂态分析的三要素法
C uC(0+)电压源； L iL(0+)电流源 2.求稳态值f ()
在直流电源作用下， C 开路； L 短路。
第三章 电路的暂态分析
3.3 一阶线性电路暂态分析的三要素法
3.求时间常数
RC电路： ＝RoC
RL电路：
L
Ro
等效电阻Ro的求解方法 ：
换路后将电路除源，从储能元件两端看进去的等效电阻。
t
f () e
三要素法
第三章 电路的暂态分析
3.3 一阶线性电路暂态分析的三要素法
3.3 一阶线性电路暂态分析的三要素法
一阶线性电路指只含有一个储能元件或者可以等效为一
个储能元件的电路。
一阶线性电路在恒定输入激励作用下，全响应的一般
表达式为：
f (t)
f () f (0 )
t
f () e
L uL 1H −
R1
R3
Is R2
iL(0-)
R1
R3
iL(0+)
+
Is
R2
−uL(0+)
第三章 电路的暂态分析
3.3 一阶线性电路暂态分析的三要素法
（2）求uL()
画t =时等效电路 ，uL() =0V
（3）求
3A Is
Ro R1 // R2 R3 2
L 1 0.5 s
Ro 2
Is
（4）求uL(t)
t
uL uL () [uL (0 ) uL ()] e
4e2t V (t 0)
R1 2
R2 2
R3
1 L
1H
+ −uL
R1
R3
+
R2

第3章 电路的暂态分析

第3章 电路的暂态分析

+
S uR uC
duC RC uC U S dt
返回
2 . 解微分方程
RCduC(t)/dt+uC(t) = US ∵ uC(0) = 0 uC(∞) = US
－ t / RC uC(t)=US(1－e )
令τ=RC uC(t)=US(1－e －t/τ) i(t)＝CduC(t)／dt=(US／R) e－t/τ uR(t)＝ i(t) R ＝US e－t/τ
返回
二、求解一阶电路的三要素法 用f (t)表示电路中的某一元件的电压 或电流, f (∞)表示稳态值, f (0+)表示初 始值，τ为时间常数。
返回
例3、换路前电路已处于稳态， t＝0时S断开, 求uC(0+ )、uL(0+)、uR2(0+)、iC(0+ )、iL(0+ )。 S 解： iL ∵ t = 0 ，电路稳态 － R1 iC L uL C 开路，L短路, uC + iL(0－ ) =US/(R1+R2) C R2 US uC(0－ )= iL(0－ ) R2 －
返回
例、已知R1=R2 =10Ω，US=80V，C=10μF, t=0开关S1闭合，0.1ms后，再将S2断开，求 uC的变化规律。(C上初始能量为零) i S1 解： (2) t> (1) 0 < 0.1ms t < 0.1ms uR )=0 uu (t )= uu (C t (0－ )=50.56V R C(0 +)=
习题
通往天堂的班车已到站， 恭喜你!
题解
习题
i1 R1 iC
S
解： ∵t ＝0－，电路稳态。 C 相当于开路， i1(0－ )= i2(0－ )=US/(R1+R2) = 2mA uC(0－ )= i2(0－ ) R2= 6V

第三章电路的暂态分析总结

第三章电路的暂态分析总结

t

时间常数 决定电路暂态过程变化的快慢 令:
RC
时间越长。
越大，曲线变化越慢，u 达到稳态所需要的
C
章目录 上一页 下一页 返回 退出
三、三要素法
在直流电源激励的情况下，一阶线性电路微分方程解的通用表达式：
f ( t ) f ( ) [ f (0 ) f ( )] e
电容电路： uC (0 ) uC (0 ) 注：换路定则仅用于换路瞬间来确定暂态过程中 uC、 iL初始值。
章目录 上一页 下一页 返回
退出
二、初始值的确定
初始值：电路中各 u、i 在 t =0+ 时的数值。
求解要点：
(1) uC( 0+)、iL ( 0+) 的求法。 1) 先由t =0-的电路求出 uC ( 0– ) 、iL ( 0– )； 2) 根据换路定律求出 uC( 0+)、iL ( 0+) 。 (2)其它变量初始值的求法。
3) 由t=0+时的电路，求所需其它各量的 u(0 ) 或 i (0 )
(3) 时间常数 的计算
对于一阶RC电路
R0C
L R0
对于一阶RL电路
1) 对于简单的一阶电路 ，R0=R ; 2) 对于较复杂的一阶电路， R0为换路后的电路除去电源和储能元件后， 在储能元件两端所求得的无源二端网络的等效电阻。 3) 时间常数 决定电路暂态过程变化的快慢
1) 由t =0+等效电路求其它电量的初始值；
2) 在 t =0+的等效电路中电容元件可用一理想电压源替代, 其电压为 uc(0+); 电感元件可用一理想电流源替代，其电流为iL(0+)。

电工学第3章电路的暂态分析1

电工学第3章电路的暂态分析1

一阶电路的三要素分析法
微分与积分电路的构成及波形变换作用 二阶暂态电路简单介绍
第3章：电路的暂态分析
稳态：在一定条件下电路中电压、电流已达到稳定值。 暂态：电路从一种稳态变化到另一种稳态的过渡过程。
K
K R
+ _E
R
+ _E
uC
C
电阻是耗能元件 产生暂态过程的必要条件： ，其上电流 I 随 (1) 电路发生换路 (外因) (2) 电路中含有储能元件 (内因) 电压U成比例变 t 1 t 1 2 2 化，不存在过渡 W C u idt Cu W L ui dt Li 0 0 2 2 过程。 因为能量的存储和释放需要一个过程，所以 有电感或（和）电容的电路存在过渡过程。
a) 电路发生换路； b) 电路中有储能元件C ； c) 电路有储能元件的能量发生变化。 R2 US + R1 C
答案： ( C )
3、下图所示电路在达到稳定状态后减小增加R1， 则该电路（ ）。
a) 因为发生换路，要产生过渡过程 b) 因为C的储能值不变，不产生过渡过程 c) 因为有储能元件且发生换路，要发生过渡过程 R2


(2)若 i L (0 ) I 0 0 , 电感元件用恒流源代替 ， 其值等于I0 ,若i L (0 ) 0 电感元件视为开路。 ,


3.2 一阶电路的暂态响应 用一阶微分方程来描述的电路。电 一阶电路： 路中只含有一个动态元件。 输入为零时，由初始状态产生的 零输入响应： 响应，仅与初始状态有关，而与激励无关。 初始状态为零时，由激励产生的 零状态响应： 响应，仅与激励有关，而与初始状态无关。 由外加输入和储能元件初始储能共同 全响应： 作用在电路中产生的响应。

第3章 电路的暂态分析

第3章 电路的暂态分析

再由t＝ 时刻的电路 的电路： 再由 ＝0＋时刻的电路： 得：
U
i (0+) R1 2 + 6V -
+ R2 4 is(0+) L iL (0+) +
uR2
uR1
-
U 6 i (0 + ) = = =3A R1 2
is（0+）=i（0+）－ L（0+）=3－1=2 A （ ）－i － uR1（0+）=R1i（0+）=2×3=6 A （ × uR2（0+）=R2 iL（0+）=4×1=4 A × 由KVL：uL（0+）= -uR2（0+）= -4 V ：
2 t=0 S 1 + Us i + R uR C + uC
duC 且 i = iC = C dt duC ∴ u R = RC dt duC 故， RC + uC = U s dt
求解一阶线性常微分方程， 求解一阶线性常微分方程， 其解由两部分组成： 其解由两部分组成： 从数学观点解释： 从数学观点解释：
+ U -
i
R1 2 is
R2 4 L iL
6V
S t=0
∵开关闭合前电路已处于稳态，且电路为直流电路 开关闭合前电路已处于稳态， ∴电感相当于短路 则
U 6 iL (0 − ) = i (0 − ) = = =1A R1 + R 2 2 + 4
由换路定则，可得： 由换路定则，可得： iL（0+）=iL（0－）=1 A
）（t≥0） （V）（ ） ）（
三要素法公式
微分方程的通解： 微分方程的通解： 从物理观点解释： 从物理观点解释：

电工技术第三章 电路的暂态分析习题解答

电工技术第三章 电路的暂态分析习题解答

第三章 电路的暂态分析含有电感或电容储能元件的电路，在换路时会出现暂态过程。

本章研究了暂态过程中电压与电流的变化规律。

主要内容：1．暂态过程的基本概念。

2．换路定则：在换路瞬间，电容电流和电感电压为有限值的情况下，电容电压 和电感电流在换路前后的瞬间保持不变。

3．RC 电路的零输入响应、零状态响应和全响应。

4．RL 电路的零输入响应、零状态响应和全响应。

5．一阶线性电路暂态分析的三要素法：一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。

6．暂态过程的应用：对于RC 串联电路，当输入矩形脉冲，若适当的选择参数 和输出，可构成微分电路或积分电路。

[练习与思考]解答3-1-1什么是稳态？什么是暂态？解：当电路的结构、元件参数及激励一定时，电路的工作状态也就一定，且电流和电压为某一稳定的值，此时电路所处的工作状态就称为稳定状态，简称为稳态。

在含有储能元件的电路中，当电路的发生换路时，由于储能元件储的能量的变化，电路将从原来的稳定状态经历一定时间变换到新的稳定状态，这一变换过程称为过渡过程，电路的过渡过程通常是很短的，所以又称暂态过程。

3-1-2什么是暂态过程？产生暂态过程的原因是什么？解：含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程（过渡过程）。

暂态过程产生的内因是电路中含有储能元件，外因是电路发生换路。

3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值？解：初始值是暂态过程的+=0t 时刻的值，稳态值是暂态过程的∞=t 时刻的值。

3-2-2 如何求暂态过程的初始值？解：求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路，求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。

对直流电路，如果换路前电路处于稳态，则电容相当于开路，电感相当于短路。

第三章 -暂态电路

第三章 -暂态电路
第三章 线性电路的暂态分析
概述 3.1 暂态与换路定律 3.2 一阶线性电路的响应 3.3 一阶线性电路暂态分析的三 要素法
3.4 微分电路与积分电路
返回
概述 1、生活中碰到的现象2、暂态现象的危害；3、暂态现象 的利用
3.1 暂态与换路定律
3.1.1 暂态电路的基本概念
1. 激励和响应
电路从电源或者信号源输入的信号称为激励，也称为输入，
电路中的暂态过程虽然十分短暂，但它对电路产生的影响却十 分重要，一方面要充分利用电路的暂态规律来实现震荡信号的产生、 信号波形的改善和变换、电子继电器的延时动作等；另一方面又要 防止电路在暂态过程中产生的过电流或者过电压现象。过电压可能 会击穿电气设备的绝缘，从而影响到设备的安全运行；过电流可能 会产生过大的机械力或引起电气设备和元件的局部过热，从而使其 遭受机械损坏或热损坏，甚至造成人身安全事故。
返回
对于有储能元件(L、C )的电路,当：
1）电路接通电源或从电源断开、短路； 换
2）电路参数或电路结构改变。
路
电路中的 u、i 发生改变，电路从一种稳定 状态变化到另外一种新的稳定状态，这种变 化是不能瞬间完成的，需要经历一个过渡过 程。电路在过渡过程中的工作状态常称为暂 态。
返回
4、电路产生暂态的原因
只要求出“三要素”——f(∞)、f(0+)、，即可直接
写出暂态过程的解。
返回
运用三要素法求解一阶电路暂态过程的步骤:
S iR
t=0
+
+
US –
uC
–
1. 求初始值：
注意：
此时电路尚未
按照换路前的电 换路
路求解: uＣ(0 – )=0 电路处于稳态 ；依换路定律，得： ，

电工学(上)第三章电路的暂态分析讲解

电工学(上)第三章电路的暂态分析讲解
第3章 电路的暂态分析
教学要求： 1. 理解电路的暂态和稳态、零输入响应、零状 态响应、全响应的概念，以及时间常数的物 理意义。 2. 掌握换路定则及初始值的求法。 3. 掌握一阶线性电路分析的三要素法。
稳定状态： 在指定条件下电路中电压、电流已达到稳定值。
暂态过程： 电路从一种稳态变化到另一种稳态的过渡过程。
一阶电路暂态过程的求解方法 一阶电路
仅含一个储能元件或可等效为一个储能元件的线性 电路, 且由一阶微分方程描述，称为一阶线性电路。
求解方法 1. 经典法: 根据激励(电源电压或电流)，通过求解 电路的微分方程得出电路的响应(电压和电流)。
2. 三要素法 求
初始值
稳态值 （三要素） 时间常数
总目录 章目录 返回 上一页 下一页
t =0+时的电流方程中 iL = iL ( 0+)。
总目录 章目录 返回 上一页 下一页
例1．暂态过程初始值的确定
S C R2
已知：换路前电路处稳态，
+ t=0
U
R1
-
L
C、L 均未储能。
试求：电路中各电压和电
流的初始值。
(a)
解：(1)由换路前电路求 uC (0 ), iL(0 )
由已知条件知 uC (0 ) 0, iL(0 ) 0
当电容元件两端加以恒定电压时，其中电 流i为零，故电容元件可视为开路。
总目录 章目录 返回 上一页 下一页
当电容元件两端加以恒定电压时，其中电
流i为零，故电容元件可视为开路。
将式: i dq C du dt dt
两边乘以u，并积分，则得：
t uidt
u Cudu 1 Cu2

电工学-第三章 电路的暂态分析

电工学-第三章 电路的暂态分析

⑵令： 5 = 10(1− e−105 t )
得：
t
=
−
ln 0.5 105
=
6.93×10−6 (S )
3.3.5 在图 3.09 所示电路中，I=10mA，R1=3kΩ，R2=处于稳态。求在 t≥0 时的 uC 和 i1，并作出它们随时间的变化曲线。
+
U1
−
R2
L
U2
−
解： 三要素：
iL (0+ )
= iL (0− )
=
U2 R3
=
20 40
=
0.5( A)
2
iL (∞)
=
U1 R1
+ U2 R3
=
24 60
+
20 40
=
0.4 + 0.5
=
0.9( A)
τ=L=
L
=
4
= 0.2(S)
R R1 // R2 // R3 60 //120 // 40
第三章 电路的暂态分析（B 基本题）
3.3.3 在图 3.07 所示电路中，已知 uC (0-)=0，试求：⑴t≥0 时的 uC 和 i；⑵uC 到达 5V 时 所需时间。
S
10Ω
+
t =0
10V
−
+i u−C 1μF
图3.07 习题3.3.3的图
解：⑴由题意为零状态响应问题。
−t
uC = U (1− e τ )
解： 三要素：
uC (0+ ) = uC (0− ) = 1× 20 −10 = 10(V )
uC (∞)
=
20
10 + 10

电工学第三章习题答案

电工学第三章习题答案

第三章 电路的暂态分析3.2.1 图3.01所示各电路在换路前都处于稳态，试求换路后其中电流i 的初始值(0)i +和稳态值()i ∞。

(b)(a)(c)(d)图3.01解： （a ）A 5.1265.0)0(5.0)0(21)0(=×===−++L L i i i A 326)(==∞i（b ）02662)0(62)0(6)0(=−=−−=−=++c c u u iA 5.1226)(=+=∞i （c ）A 6)0()0(==−+i i A 0)(=∞i（d ）A 75.04364)0(622)0(6)0(=−=−=+−=−++c c u u iA 12226)(=++=∞i3.4.1 在图3.07(a)的电路中，u 为一阶跃电压，如图3.07(b)所示，试求3i 和c u 。

设V 1)0(c =−u 。

(a)图3.07(b)解：s 102)(331312−×=++=C R R R R R τV 22224)(C =+×=∞u V 1)0()0(C C ==−+u u V 2)(500C t e t u −−=mA 75.0)(1)(4)0(31131312322323213=+++++++=+R R R R R R R R R R R R R R R R i mA 144)(3==∞imA 25.01)(5003t e t i −−=3.4.2 电路如图3.08所示，求0t ≥时(1)电容电压C u ，(2)B 点电位B v 和(3)A 点电位A v 的变化规律。

换路前电路处于稳态。

Sk 10图3.08解：(1)求0≥t 时的电容电压C uV 15255)6(0)0()0(C =×+−−==−+C u uV 5.1525510)6(6)(C =×++−−=∞u[]s 1044.010100105//)2510(6123−−×=×××+=τ故V 5.05.1)5.11(5.1)(66103.21044.0C t t e et u ×−×−−=−+=−t =0_时k 10t =0+时+6V Ωk 10（2）求0≥t 时的B 点电位B v注意，+=0t 时，由于电容中存在电流，0CC ≠=dtdu Ci 因此，10K 和5K 电阻中的电流不等。

第三章暂态电路的分析

第三章暂态电路的分析

第三章暂态电路的分析第三章暂态电路的分析⼀. 单项选择题：1. 全响应是指电源激励和储能元件的初始状态均不为零时电路的响应，也就是零输⼊响应和零状态响应的叠加，这是（）在⼀阶线性电路暂态分析中的应⽤： A ．戴维宁定理 B. 诺顿定理 C.叠加定理 D. 结点电压法2. 换路定则适⽤于换路瞬间，下列描述正确的是（）： A. )0()0(+-=L L i i B. )0()0(+-=L L u u C. )0()0(+-=c c i i D. )0()0(+-=R R u u3. RC 电路的初始储能为零，⽽由初始时刻施加于电路的外部激励所引起的响应称为( ) 响应： A.暂态 B. 零输⼊ C. 零状态 D. 全响应 4. RC 电路的响应指数曲线如图1所⽰，该电路的响应形式为（）： A.暂态B. 零输⼊响应C. 零状态响应D. 全响应5. 图2所⽰电路在换路前处于稳态，则换路后电流i 的初始值)0(+i 和稳态值)(∞i 分别为（）： A. 0A ，6A B. 6A ，2A C. 1.5A ，3A D. 6A ，0A6. 电路如图3所⽰，开关断开后，⼀阶电路的时间常数=τ（）： A.C R R R R 2121+ B. C R 2 C. C R R )(21+ D. C R R R R R R 321321)(+++7. 电路如图4所⽰，20=s U V ，Ω==1021R R ，1=L H 。

其零状态响应电流=)(t i （）：A. )1(25t e -- AB. )1(22.0t e -- AC. )1(21.0t e -- AD. )1(10t e -- A8. 图5所⽰电路中，10=I mA ，Ω=k R 31，Ω=k R 32，Ω=k R 33，µ2=C F 。

开关闭合前电路处于稳态。

0≥t 时该电路的响应c u 为（）： A. te10060-V B. te10012-V C. te1060-V D. te2050-V⼆. 填空题：1. 在直流稳态电路中，电感可视作，电容可视作；在⼀阶动态电路的暂态分析中，若换路前储能元件没有初始储能，则在换路后瞬间+=0t 时刻电感可视作，电容可视作。

第三章-电路暂态分析

第三章-电路暂态分析

第二章电路的分析方法the method of analyzing circuit江苏大学电气信息工程学院电工技术（电工学I ）第三章电路的暂态分析the analysis of transient process 江苏大学电气信息工程学院School of electric and information ，UJS内容3.1概述3.2换路定律及初始值的确定3.3RC电路的分析3.4一阶线性电路暂态分析的三要素法3.5RC电路的脉冲响应3.6RL电路的响应暂态分析理解电路的暂态和稳态的概念掌握一阶线性电路分析的三要素法理解零输入响应、零状态响应、全响应的概念掌握换路定律及初始值的求法理解时间常数的物理意义重点3.1 概述一、稳态和暂态的概念：暂态过程：电路从一种稳态变化到另一种稳态的过渡过程。

暂态分析：研究过渡过程中电压或电流随时间的变化规律，即求u （t ）、i （t ）（0≤ t <∞）稳态：电路中的物理量不随时间而变（直流时）或是时间的周期函数（交流时），本章的稳态是指直流电路的稳态暂态：旧稳态新稳态暂态新稳态暂态电路进入新稳态u C =ERE +_Cu tECu o电路原处于旧稳态u C =0CSRE+_Cu （t = 0）一般暂态过程是从稳态开始又结束于另一个稳态稳态是暂态过程的最终状态二、暂态过程的产生原因:电阻电路无过渡过程电阻是耗能元件，其上电流和电压可以突变。

toi ut = 0ER+_iSu电路发生换路是不是所有电路换路时都会产生过渡过程？换路：电路理论中把电路中支路的接通、切断、短路，电源或电路参数的突然改变称为换路。

有电容的电路存在过渡过程。

Cu 不能突变∴212C Cw Cu =不能突变∵电容电路因为电场能量的存储和释放需要一个过程，所以EtCu o有过渡过程u CE KR +_Cu Ci C t=0若c u 发生突变，∞⇒=dtdu i CC 不可能！一般电路则有电感的电路存在过渡过程。

电路的暂态分析_换路定则与电压、电流初始值的确定

电路的暂态分析_换路定则与电压、电流初始值的确定
（3）画t=0+时刻等效电路， 求电路其他部分电压、电流 的初始值。
iC(0 )
uC(0 ) 8 2mA
R2
4
3.1 换路定则与电压电流初始值的确定
S (t=0) R1 iC
+ Us−
R2
C
+ −uC
R1 iC(0+)
+ Us−
R2 C −+uC(0+)
t＝0+时的等效电路
第三章 电路的暂态分析
第三章 电路的暂态分析
1. 稳态与暂态 稳态：电压、电流不随时间变化或周期性重复变化。
过渡过程：电路由一个稳态过渡到另一个稳态需要经历的 中间过程。
暂态：在电路中，过渡过程往往非常短暂，故也称为暂 态过程，简称暂态。
第三章 电路的暂态分析
3.1 换路定则与电压电流初始值的确定
2S R i
uC
Us−+
从t=0－到t=0+的瞬间，电容的电压和电感的电流不会发生
跃变，即：
uC (0 ) uC (0 )
iL (0 ) iL (0 )
第三章 电路的暂态分析
3.1 换路定则与电压电流初始值的确定
注意：
（1）只有uC 、 iL受换路定则的约束，电路中其他电 压、电流都可能发生跃变。
（2）换路定则仅适用于换路瞬间。
3.1 换路定则与电压电流初始值的确定
iC(0 ) 0 ) iC(0 ) ？
+
Us −
iC (0 ) 0 A
R1 R2
iC(0−)
+ uC(0−)
−
第三章 电路的暂态分析
3.1 换路定则与电压电流初始值的确定
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章 电路的暂态分析一、填空题：1. 一阶RC 动态电路的时间常数τ=___RC____,一阶RL 动态电路的时间常数τ=__L/R______。

2. 一阶RL 电路的时间常数越__大/小 _ (选择大或小)，则电路的暂态过程进行的越快 慢/快 （选择快或慢）。

3. 在电路的暂态过程中，电路的时间常数τ愈大，则电压和电流的增长或衰减就 慢 。

4. 根据换路定律，(0)(0)c c u u +-=，()+0L i =()0L i —5. 产生暂态过程的的两个条件为 电路要有储能元件 和 电路要换路 。

6. 换路前若储能元件未储能，则换路瞬间电感元件可看为 开路 ，电容元件可看为 短路 ；若储能元件已储能，则换路瞬间电感元件可用 恒流源 代替，电容元件可用 恒压源 代替。

7. 电容元件的电压与电流在关联参考方向下，其二者的关系式为1u idt C =⎰；电感元件的电压与电流在关联参考方向下，其二者的关系式为di u Ldt =。

8. 微分电路把矩形脉冲变换为 尖脉冲 ，积分电路把矩形脉冲变换为 锯齿波 。

9．下图所示电路中，设电容的初始电压(0)10C u V-=-，试求开关由位置1打到位置2后电容电压上升到90 V 所需要的时间为 4.8*10-3 秒。

Fμ10010. 下图所示电路中，VU u C 40)0(0_==，开关S 闭合后需 0.693**10-3秒时间C u 才能增长到80V ？+U C -11. 下图所示电路在换路前处于稳定状态，在0t =时将开关断开，此时电路的时间常数τ为 （R 1 +R 2 ）C 。

U12. 下图所示电路开关S 闭合前电路已处于稳态，试问闭合开关的瞬间，)0(+L U为 100V 。

1Ai L13. 下图所示电路开关S 闭合已久，t=0时将开关断开，则i L (0-)= 4A ，u C (0+)= 16V ，i C (0+)= 0 。

u c14．下图所示电路，当t=0时将开关闭合，则该电路的时间常数为 0.05S 。

2415. 下图所示电路在换路前都处于稳态，则换路后电流)0(+i 为1.5 A 和)(∞i 3 A 。

+-16. 下图所示电路在换路前都处于稳态，则换路后电流)0(+i 为 0 A 和)(∞i 1.5 A。

+-17. 下图所示电路在换路前都处于稳态，则换路后电流)0(+i 为 6 A 和)(∞i 0 A 。

L 218. 下图所示电路在换路前都处于稳态，则换路后电流)0(+i 为 0.75 A 和)(∞i 1 A 。

+-2Ω19．下图所示电路中，开关Ｓ在闭合前电路处于稳态，电容Ｃ、电感Ｌ无能量储存，在 t = 0时将开关S 闭合，则)0(+i 为 2A 、u C (0+)为 0V 、)(∞i 为 2A 、u ()c ∞为 10V 。

C20. 下图所示电路，已知100E V =，1R M =Ω，50C F μ=，开关在位置1已很久，当0t =时开关由位置1打向位置2，则经过 34.65 秒电流减小到其初始值的一半。

C二、选择题:1. 在直流稳态时，电感元件上（ B ）。

A. 有电流，有电压B. 有电流，无电压C. 无电流，有电压D. 无电流，无电压2. 在直流稳态时，电容元件上（ B ）。

A. 有电压，有电流B. 有电压，无电流C. 无电压，有电流D. 无电压，无电流3. RC电路在零输入条件下，时间常数的意义是（ B ）。

A．电容电压衰减到初始值的0.632倍所需的时间B．电容电压衰减到初始值的0.368倍所需的时间C．过渡过程所需要的时间D．以上说法都不对4. RC电路在零状态下，时间常数的意义是（ A ）。

A．电容电压增加到稳态值的0.632倍所需的时间B．电容电压增加到稳态值的0.368倍所需的时间C．过渡过程所需要的全部时间D．以上说法都不对5. 充电后的电容进行放电的过程属于（ A ）。

A．零输入响应 B．零状态响应 C．全响应D．不能确定6. 电路的暂态过程从t=0大致经过（ B ）时间，工程上就可认为达到稳定状态了。

A.τB.（3～5）τC. 10τD. ∞7. RL 串联电路的时间常数为（ B ）A.RLB. R LC.L RD. 1RL8．在换路瞬间，下列各项中除( D )不能跃变外，其他全可跃变。

A ．电感电压B. 电容电流C.电阻电压 D ．电感中储存的能量9. 下图所示电路开关S 闭合前电路已处于稳态，试问闭合开关瞬间，初始值)0(+L i 和)0(+i 分别为（ B ）。

A. 0A ，1.5AB. 3A, 3A B. 3A, 1.5A D. 1.5A, 3A+-2Ω10. 下图所示电力开关S 闭合前电路已处于稳态，试问闭合开关瞬间，电流初始值)0(+i 为（ C ）。

A. 1AB. 0.8AC. 0AD. 0.4ASi10Ω11. 下图所示电路开关S 闭合前电容元件和电感元件均未能储能，试问开关闭合瞬间发生跃变的是（ B ）。

A.i 和1iB.i 和3iC.2i 和c uD. i 和2i3+U C-12. 下图所示电路开关S 闭合前电路已处于稳态。

当开关闭合后各电流状况为（ B ）。

A. 1i 、2i 、3i 均不变B. 1i 不变、2i 增长为1i 、3i 衰减为零C. 1i 增长、2i 增长、3i 不变D. 1i 、2i、3i 均增长2213．下图所示电路在0t =时刻开关S 闭合，则电容器开始充电，其充电时间常数为（ A ）。

A. 1R C τ= B. 12()R R C τ=+C.123()R R R C τ=++ D. 123(//)R R R C τ=+1U sC14．下图所示电路在换路前处于稳定状态，在t =0瞬间将开关S 闭合，则i C (0+)为( B )。

A ．0.6AB ．0AC ．0.3AD ．－0.6AF15. 下图所示电路在换路前处于稳定状态，在t =0瞬间将开关S 闭合，则iL(0+)为( B )。

A ．1AB ．2AC ．20AD ．10A16. 下图所示电路在换路前处于稳定状态，在0t =时闭合开关，则开关闭合瞬间电容的电压为( B )。

A. 0.2VB. 1VC. 0.8VD. 1.2V17．下图所示电路在换路前处于稳定状态，在0t =时打开开关，电路的时间常数τ为( A )。

A. 0.6mSB. 1.7mSC. 0.66S μD. 0.707S μ40Fμ18. 下图所示电路，在换路前处于稳定状态，在0t =时将开关断开，此时电感电流L i的初始值为（ B ）。

A ．0AB ．0.5AC ．﹣0.5AD ． 1A1019．下图所示电路，在开关打开后电路的时间常数为 ( C ) 。

A ． R 1C B ． R 2C C ． (R 1+R 2)C D ． （R 1//R 2)C20．下图所示电路换路前处于稳定状态，在t=0时开关突然断开则i(0+)为 （ D ）。

A ．1AB ．0AC ．1.5AD ．0.5A9V)t三、计算题：1. 下图所示电路，开关在t=0打开之前已经关闭长时间，求t ≥0时i 1(t)和i 2(t)。

(61012())0.3ti t i t e mA-==（)2. 如图所示电路，开关在未打开前电路处于稳定状态，0t=时，把开关打开，求t>0时电感中的电流i。

(4410() 1.25ti t e mA-⨯=)S (t=0)3. 下图所示电路，开关闭合前已达稳态，在t = 0时开关闭合。

求换路后的电流()Li t。

(12()1tLi t e A-=+)I8V4. 下图所示电路，开关原来长时间地处于断开状态，在t=0时将开关闭合。

用三要素法求iL (t)、i1(t)。

（0t≥）()3210()0.50.5tLi t e A-⨯=+L5. 下图所示电路，开关打开前已达稳定。

在t = 0时开关打开，求换路后电容电压u C (t)的表达式，并画出曲线。

(25u ()126t c t e V-=-)6. 下图所示电路，开关原来长时间地处于断开状态， 在t=0时将开关闭合。

用三要素法求u c (t)、i 1(t)。

（0t ≥）(5u ()48t c t e V -=-)u c7. 下图所示电路，开关原来长时间地处于断开状态，在t=0时将开关S 闭合。

试用三要素法求u C (t)、i C (t)。

（0t ≥）(,)10u ()123t c t e V -=-10()0.0015t C i t e A -=9V8. 下图所示电路在换路前处于稳定。

当将开关从1的位置合到2的位置后，试求()c u t 和()c i t 。

(4610u ()24t c t e V -⨯=-+,4610() 2.4tC i t e A -⨯=-)9. 下图所示电路，开关原来长时间地合在1位置，在t=0时将开关由1位置扳至2位置，用三要素法求i(t)。

（0t ≥）(50()3ti t eA -=-)160mH10. 下图所示电路开关K 原合在“1”的位置，t=0时，开关由“1”合向“2”，换路之前，电路处于稳态，求换路后()c u t 及ci ,并画出它们的变化曲线。

(0.5u ()33t c t e V -=+,0.5()0.75t C i t e A -=-)11. 下图所示电路中，V U 20=，Ω=k R 121，Ω=k R 62，F C μ=101，F C μ=202。

电容元件原先未能储能。

当开关闭合后，试求两串联电容元件两端的电压C u 。

(25u ()20-20tct eV-=)+U -St =0+U C-R 1C 1C 212. 下图所示电路中，mA I 10=，Ω=k R 31，Ω=k R 32，Ω=k R 63，F C μ=2。

在开关S 闭合前电路已处于稳态。

试求0≥t时Cu 和1i ，并作出他们随时间的变化曲线。

(100u ()60t c t e V -=,100()12t C i t e mA-=)Ci +U C-R 1R 3ISt =013. 下图所示电路中，在开关闭合前电路已处于稳态，求开关闭合后的电压C u ，并作出C u 的曲线。

(250u ()1836tc t e V -=+)14. 下图所示电路中，Vu C 10)0(_=，试求0≥t 时的C u 和0u ，并画出它们的变化曲线。

(410u ()5040tc t eV -=-,4100u ()5040tt eV -=+)+O -15. 下图所示电路，开关闭合前电路已稳定，在t=0时将开关闭合，求开关闭合后电路中的()L i t 、()L u t 。

( 3.75()10.25t L i t e A -=+, 3.75u () 1.875t L t e V -=-)+_()t ()L t16. 下图所示电路，开关在位置1已很久，在0t =时开关由1打向2，试求0t ≥时电容上的Cu 和电阻上电流i 。